Photon routing in disordered chiral waveguide QED ladders: Interplay between photonic localization and collective atomic effects

As depicted in Fig. 1, our theoretical model consists of an array of $\mathcal{N}$ number of QEs with a ground state $\ket{g_{j}}$, excited state $\ket{e_{j}}$, transition frequency $\omega_{eg_{j}}$, location $x_{j}$ with respect to the bottom waveguide, $y_{j}$ with respect to the top waveguide, and spontaneous emission rate $\gamma_{j}$, $\forall j=1,2,...,\mathcal{N}$. This emitter chain is simultaneously coupled with two infinitely long one-dimensional waveguides with top and bottom waveguide coupling rates given by $V_{t\alpha_{j}}$ and $V_{b\alpha_{j}}$, respectively, with $\alpha$ representing either left (L) or right (R) direction in the waveguide. For simplicity, we suppose all QEs to be identical, with the ground state energy being set as a reference. Therefore, the free Hamiltonian of the QEs can be expressed as follows

$\displaystyle\hat{\mathcal{H}}_{QE}=\sum^{N}_{j=1}\hbar\widetilde{\omega}_{eg_{j}}\hat{\sigma}^{\dagger}_{j}\hat{\sigma}_{j},$

(1)

where $\widetilde{\omega}_{eg_{j}}:=\omega_{eg_{j}}-i\gamma_{j}$ with $\hat{\sigma}_{j}$ being the $j^{th}$-QE lowering operator following the standard Fermionic anticommutation relation $\{\hat{\sigma}_{i},\hat{\sigma}^{\dagger}_{j}\}=\delta_{ij}$. The spontaneous emission rate $\gamma_{j}$ has been inserted by hand here using the detailed analysis reported in Ref. shen2009theoryI ; shen2009theoryII . The two waveguides in our work are modeled as quantum harmonic oscillators with infinitely many modes, which allows us to write their Hamiltonian in the real-space formalism of quantum optics shen2009theoryI ; shen2009theoryII as

	$\displaystyle\hat{\mathcal{H}}_{W}$	$\displaystyle=-iv_{bg}\hbar\int\left[\hat{c}_{bR}^{{\dagger}}(x)\partial_{x}\hat{c}_{bR}(x)-\hat{c}_{bL}^{{\dagger}}(x)\partial_{x}\hat{c}_{bL}(x)\right]dx$
		$\displaystyle-iv_{tg}\hbar\int\left[\hat{c}_{tR}^{{\dagger}}(y)\partial_{y}\hat{c}_{tR}(y)-\hat{c}_{tL}^{{\dagger}}(y)\partial_{y}\hat{c}_{tL}(y)\right]dy.$		(2)

Here $\hat{c}_{t\alpha}(y)$ and $\hat{c}_{b\alpha}(x)$ represents the photon annihilation operator in the top and bottom waveguide at location $y$ and $x$ in the $\alpha$ direction, respectively. These operators follow the typical Bosonic commutation relations: $[\hat{c}_{t\alpha}(y),\hat{c}_{t\beta}(y^{\prime})]=\delta_{\alpha\beta}\delta(y-y^{\prime})$ and $[\hat{c}_{b\alpha}(x),\hat{c}_{b\beta}(x^{\prime})]=\delta_{\alpha\beta}\delta(x-x^{\prime})$. We have selected two different group velocities $v_{tg}$ and $v_{bg}$ for the top and bottom waveguide, respectively.

Next, two types of interactions are possible in our model. One is the interaction between the QEs and the waveguide fields, while the second is the direct interaction among the QEs due to DDI. The Hamiltonian for the former type $\hat{\mathcal{H}}_{I}$ under the rotating wave approximation can be expressed as

		$\displaystyle\hat{\mathcal{H}}_{I}=\hbar\sum^{N}_{j=1}\sum_{\alpha=L,R}\Bigg{[}\int dx\delta(x-x_{j})\big{(}V_{b\alpha_{j}}\hat{c}^{\dagger}_{b\alpha}(x)\hat{\sigma}_{j}+H.c.\big{)}$
		$\displaystyle+\int dy\delta(y-y_{j})\big{(}V_{t\alpha_{j}}\hat{c}^{\dagger}_{t\alpha}(y)\hat{\sigma}_{j}+H.c.\big{)}\Bigg{]}.$		(3)

Here, the Dirac delta function specifies the location of the $j$th QE in the chain, and the abbreviation $H.c.$ stands for Hermitian conjugate. Finally, by assuming the inter-emitter separation to be smaller than the resonant field wavelength, we introduce an infinitely long-ranged and direct DDI among the emitters agarwal2012quantum . The Hamiltonian for such a DDI is given by

$\displaystyle\hat{\mathcal{H}}_{\rm DDI}=\hbar\sum^{N}_{i=1}\sum\limits_{\begin{subarray}{c}j=1\\ j>i\end{subarray}}^{N}J_{ij}\big{(}\hat{\sigma}^{\dagger}_{i}\hat{\sigma}_{j}+H.c.\big{)}.$

(4)

The DDI parameter (characterizing the strength of the interaction) is known to be sensitively dependent on the inter-emitter separation, as we discuss in the following subsection.

For inter-emitter separation $\mathcal{R}_{ij}$ the DDI parameter $J_{ij}\equiv J\left(\mathcal{R}_{ij}\right)$ is known to obey the following form cheng2017waveguide

	$\displaystyle J_{ij}$	$\displaystyle=\frac{3\Gamma_{0}}{4}\bigg{(}\frac{\cos\mathcal{R}_{ij}}{\mathcal{R}^{3}_{ij}}+\frac{\sin\mathcal{R}_{ij}}{\mathcal{R}^{2}_{ij}}-\frac{\cos\mathcal{R}_{ij}}{\mathcal{R}_{ij}}\bigg{)}$
		$\displaystyle+\cos^{2}\theta\bigg{(}\frac{\cos\mathcal{R}_{ij}}{\mathcal{R}_{ij}}-\frac{3\cos\mathcal{R}_{ij}}{\mathcal{R}^{3}_{ij}}-\frac{3\sin\mathcal{R}_{ij}}{\mathcal{R}^{2}_{ij}}\bigg{)},$		(5)

where the inter-emitter separation is defined as $\mathcal{R}_{ij}=\omega_{eg}|\vec{r}_{i}-\vec{r}_{j}|/c$, with $c$ being the speed of light, $\vec{r}_{i/j}$ identifies the position of $i/j$th emitter. In Eq. (II.2), $\Gamma_{0}$ represents the free space emitter decay rate. $\theta$ is the angle between the dipole moment vector $\vec{p}$ and the emitters relative position vector which is defined as $\cos\theta=\vec{p}\cdot(\vec{r}_{i}-\vec{r}_{j})/\{|\vec{p}||\vec{r}_{i}-\vec{r}_{j}|\}$. Onward, we set $\theta=\pi/2$ for simplicity.

In Fig. 2, we plot the DDI parameter $J$ as a function of inter-emitter separation $L$ between two QEs. As expected from Eq. (II.2), despite being an infinitely long-range interaction, DDI decays quickly as the separation increases. To this end, we observe in periodic and disordered cases that as we approach $L=120nm$, we find $J\rightarrow 0$. Upon comparing the periodic case versus the disordered configuration, we find that for smaller to intermediate inter-emitter separation (i.e., $30nm\lesssim L\lesssim 60nm$), the DDI is slightly higher in the disordered case. For the disorder strength chosen here ($\sigma=0.2\mu$), we found that in the set of iterations in which the separation between the QEs becomes smaller than $\mu$, the DDI enhances considerably (as observed in the form of spikes in $J$ curve for certain separations in Fig. 2). Since the impact of such instances on the overall $J$ value was considerably higher than the iterations in which the random separation was larger than $\mu$, overall DDI remains higher. Note that for larger disorders (i.e., when $\sigma>0.2\mu$), the variation in $J$ fluctuated immensely. Therefore, we identify $\sigma=0.2\mu$ as the border value between the strong disorder case (when $\sigma>0.2\mu$) and the weak disorder case (when $\sigma<0.2\mu)$.

The quantum state of our system restricted to the single-excitation sector of the Hilbert space can be expressed as

	$\displaystyle\ket{\Psi}$	$\displaystyle=\Bigg{[}\sum^{N}_{j=1}\mathcal{A}_{j}\hat{\sigma}_{j}^{\dagger}+\sum\limits_{\alpha=L,R}\Bigg{\{}\int\varphi_{b\alpha}(x)\hat{c}_{b\alpha}^{\dagger}(x)dx$
		$\displaystyle+\int\varphi_{t\alpha}(y)\hat{c}_{t\alpha}^{\dagger}(y)dy\Bigg{\}}\Bigg{]}\ket{\varnothing},$		(6)

where $\ket{\varnothing}=\bigotimes_{j}\ket{g_{j}}\otimes\ket{0_{bR}}\otimes\ket{0_{bL}}\otimes\ket{0_{tR}}\otimes\ket{0_{tL}}$ represents the ground state in which all QEs are unexcited and no photons in the top and bottom waveguide in both left and right direction.

We begin from a rather simple problem, namely, a single-photon routing in a wQED ladder with only two QEs. By setting the origin of coordinates at the location of the first QE, we call inter-emitter separation to be $r_{12}$, the transmission coefficient from Port 2 $\tilde{t}_{b2}$ and from Port 4 i.e. $\tilde{t}_{t2}$ takes the following form:

	$\displaystyle\tilde{t}_{b_{2}}=\frac{4J^{2}+4\Gamma^{2}+\left(\gamma-2i\Delta\right)^{2}+8J\Gamma\sin\left(r_{12}\Delta\right)}{4J^{2}-8ie^{r_{12}\Delta}J\Gamma+\left(\gamma+2\Gamma-2i\Delta\right)^{2}},$		(12a)
	$\displaystyle\tilde{t}_{t_{2}}=\frac{4i\Gamma\left(i\gamma+2\Delta+2J\cos\left(r_{12}\Delta\right)\right)}{4J^{2}-8ie^{r_{12}\Delta}J\Gamma+\left(\gamma+2\Gamma-2i\Delta\right)^{2}},$		(12b)

where we have set $v_{b_{g}}=v_{t_{g}}=1$ such that $r_{12}\Delta$ which in fact is $r_{12}\Delta/v_{g}$ becomes dimensionless. In Fig. 3(a), we present the results for both periodic (translucent curves) and disordered (solid curves) configurations. In the $\gamma\neq 0$ and $J\neq 0$ scenario, the probability of detecting a single photon at Port 4 exhibits two asymmetric resonances around $\Delta=0$ point. As reported in Ref. cheng2017waveguide , such an asymmetry originates from energy decay due to atomic dissipation. From the routing perspective, we observe that in the periodic case, $\sim 74.6\%$ Port 1 to Port 4 routing has been achieved at $\Delta=25.3\Gamma_{0}$. On the other hand, the disorder suppresses the maximum value of Port 4 detection probability to $\sim 65.6\%$ at the same $\Delta$ value.

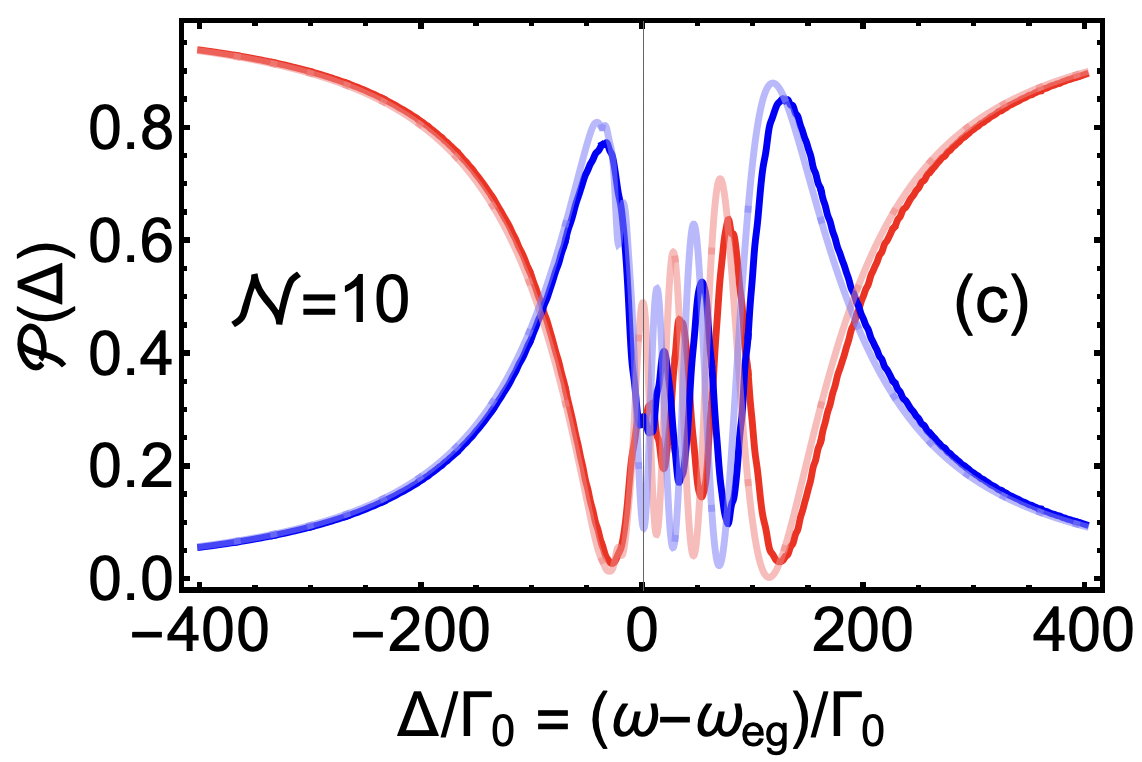
Next, in Fig. 3(b) to Fig. 3(d) we increase the number of QEs from $\mathcal{N}=5$ to $\mathcal{N}=20$ to promote collective emitter interactions. In both periodic and disordered settings, we find that with the increase in the QE number, the number of resonances increases in detection probabilities. As we approach $\mathcal{N}=20$, we notice the emergence of a pattern in detection probabilities where an asymmetric envelope of peaks is formed around $\Delta=0$ along with two major side peaks. These side peaks allow us to achieve a considerably higher degree of routing. For instance, for the periodic case, we find that for $\mathcal{N}=5$, $\mathcal{N}=10$, and $\mathcal{N}=20$ cases, the Port 4 probabilities respectively increase from $\sim 82.8\%$ to $\sim 88.4\%$ to $\sim 93.6\%$. We also note that these values of maximum probabilities exist at larger $\Delta$ values as $\mathcal{N}$ is increased.

This trend of achieving higher Port 4 detection probabilities (improved routing) also extends to the disordered configuration. In the disordered case we observed for $\mathcal{N}=5$, $\mathcal{N}=10$, and $\mathcal{N}=20$ cases the corresponding Port 4 probabilities take the value of $\sim 77.8\%$ at $75.6\Gamma_{0}$, $\sim 85.5\%$ at $\Delta=126.23\Gamma_{0}$, and $\sim 92.9\%$ at $\Delta=202.9\Gamma_{0}$. Additionally, we make two important remarks. First, these higher Port 4 detection probabilities are accompanied by lower Port 2 probabilities, indicating genuine improvement in Port 1 to Port 4 routing as $\mathcal{N}$ increases. Secondly, as the QE number increases, the collective emitter effects shield the routing not only against environmental decoherence (spontaneous emission loss) but also against weak disorder in the emitter locations.

To further highlight the improvement in routing as a function of QE number, in Fig. 4(a), we plot the maximum detection probability at Port 4 (labeled as $\mathcal{P}_{\rm max}$) as a function of $\mathcal{N}$. The blue curve with cyan dots represents the periodic lattice case, while the red curve with orange triangles represents the corresponding disordered lattice. As expected, at $\mathcal{N}=1$, both periodic and disordered cases start from the same value of $\mathcal{P}_{\rm max}\sim 58\%$. However, as we increase the number of emitters, the maximum probability of redirection of single photons to Port 4 increases such that by the time we arrive at $\mathcal{N}>15$, we find that $\mathcal{P}_{\rm max}$ reaches $90\%$. It is essential to notice that the periodic configurations always promote a higher value of $\mathcal{P}_{\rm max}$ as compared to the disordered case, but at $\mathcal{N}=20$, the difference between the periodic and disordered cases minimizes, thus, confirming the dominating nature of collective emitter effects against weak disorder. Next, in Fig. 4(b), we report the detuning values at which $\mathcal{P}_{\rm max}$ has been achieved. We notice that in periodic and disordered cases, the $\Delta_{\rm max}$ follows the (almost) same increasing trend as a function of $\mathcal{N}$.

So far, in the previous results, we have considered a fixed inter-emitter separation of $\lambda_{e}/20$. However, in this work, it is crucial to analyze the impact of inter-emitter separation on the routing protocol. To this end, we introduce routing efficiency $\xi_{\mathcal{N}}$ which for a $\mathcal{N}$-emitter wQED ladder is defined as

$\displaystyle\xi_{\mathcal{N}}=\frac{\left|\tilde{t}_{t\mathcal{N}}\right|^{2}-\left|\tilde{t}_{b\mathcal{N}}\right|^{2}}{\left|\tilde{t}_{t\mathcal{N}}\right|^{2}+\left|\tilde{t}_{b\mathcal{N}}\right|^{2}},$

(13)

where for no-loss problem $-1\leq\xi_{\mathcal{N}}\leq 1$ with $\xi_{\mathcal{N}}=-1$ indicates that the photon appears at Port 2 while $\xi_{\mathcal{N}}=+1$ means photon being routed to Port 4. When spontaneous emission loss is included, the higher positive value of $\xi_{\mathcal{N}}$ would indicate better routing. Explicitly, for $\mathcal{N}=2$ case, the routing efficiency takes the form

$\displaystyle\xi_{2}=-\frac{4J^{2}+\gamma^{2}+4\gamma\Gamma+4\Gamma^{2}-4i\gamma\Delta-8i\Gamma\Delta-4\Delta^{2}-8iJ\Gamma\cos\left(r_{12}\Delta\right)+8J\Gamma\sin\left(r_{12}\Delta\right)}{4J^{2}+\gamma^{2}-4\gamma\Gamma+4\Gamma^{2}-4i\gamma\Delta+8i\Gamma\Delta-4\Delta^{2}+8iJ\Gamma\cos\left(r_{12}\Delta\right)+8J\Gamma\sin\left(r_{12}\Delta\right)},$

(14)

where the last equation holds for both periodic and disordered cases; in the periodic (disordered) case the parameters $r_{12}$ and $J$ are expected to remain fixed (varying).

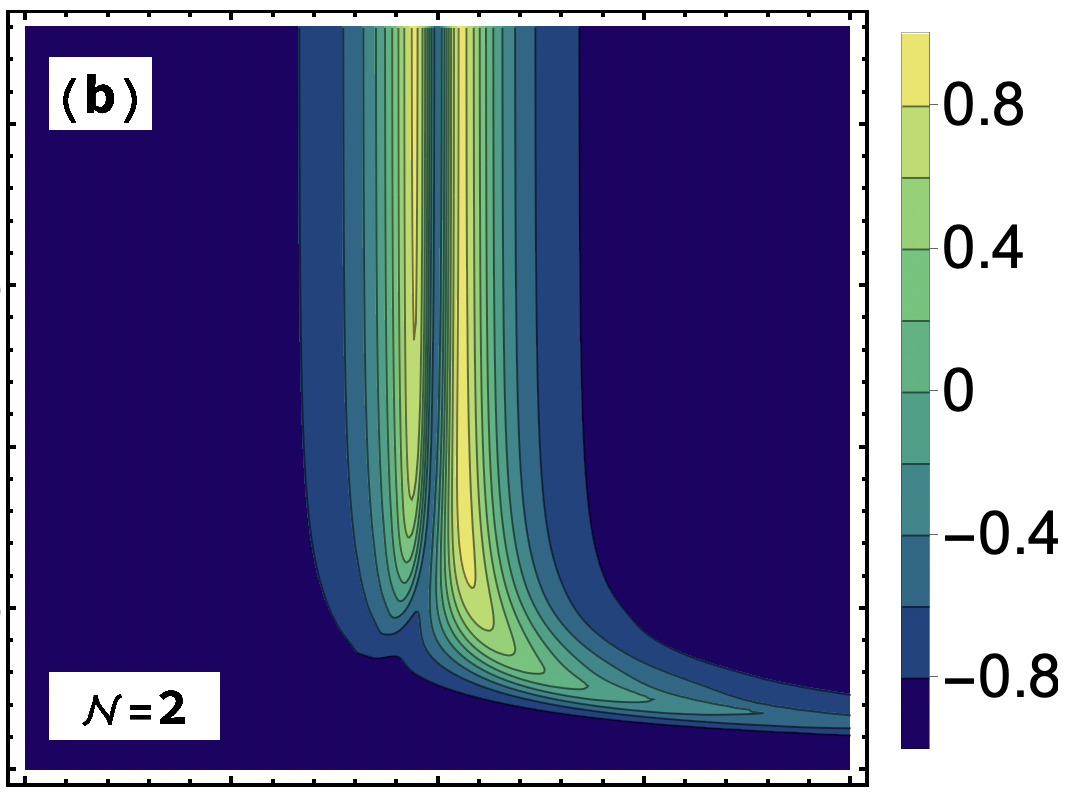
In Fig. 5, we plot routing efficiency for a two- and a five-emitter ladder as a density plot while on the horizontal axis varying the detuning $\Delta$ from $-200\Gamma_{0}$ to $+200\Gamma_{0}$ and on the vertical axis the inter-emitter separation $L$ from $0.01\lambda_{e}$ to $0.23\lambda_{e}$. Both periodic and disordered situations have been presented side-by-side for both cases. We notice that in all four plots, for smaller values of $L$ (say around $L=0.025\lambda_{e}$) $\xi_{\mathcal{N}}$ exhibits branches of positive values of more than $0.8$ value on and on the right side of $\Delta=0$ point. Another similar feature is, as we increase $L$, the right branch of $\xi_{\mathcal{N}}>0$ tends to vanish, and we observe vertical bands of diminishing $\xi_{\mathcal{N}}$ values as we move away from $\Delta=0$. Finally, we find that the difference between periodic and disordered cases is most visible at smaller $L$ values (see, for instance, the behavior of $\xi_{2}$ between $0\leq\Delta\leq 100\Gamma_{0}$ at $L=0.025$). This trend is understandable, as the position disorder for wQED ladders with not a large number of QEs is expected to change the inter-emitter separation or DDI more, which in turn alters the transmission pattern from Port 4 – an argument which is also supported by Fig. 2.

To quantify the degree to which the single photon has been localized in our system due to disorder, we make use of the following definition of localization length $\mathcal{L}$ as reported to be used in one-dimensional electronic systems markos2008wave ; delande2013many

$\displaystyle\mathcal{L}^{-1}=\lim_{\mathcal{N}\rightarrow\infty}\frac{\langle T_{t}\rangle}{\mathcal{N}}.$

(15)

Here, $T_{t}$ represents the transmission probability for Port 4. As evident from Eq. (15), the above definition becomes more and more exact as the number of QEs $\mathcal{N}$ becomes large. However, in the following, we’ll consider the cases with QE numbers up to $\mathcal{N}=20$; therefore, the reported results would represent an approximate behavior of the localization length.

In Fig. 6, we plot the localization length $\mathcal{L}$ as a function of disorder strength (quantified through the standard deviation $\sigma$) for emitter chains with $\mathcal{N}=2,5,10,$ and $20$ QEs. We notice that for relatively weaker disorder (when $\sigma\lesssim 0.075\mu$), the localization length takes a larger value in every case. This indicates that longer emitter chains can localize the photon propagation for the lower disorder. However, as we consider $\sigma>0.1\mu$, irrespective of $\mathcal{N}$, $\mathcal{L}$ decays and reaches considerably lower values (see the behavior of all curves around $\sigma\sim 0.2\mu$), this behavior contrasts with Anderson localization observed in traditional electronic systems with the disorder (for example, semiconductor materials with defects) where strong disorder promotes halting of electron transport wiersma1997localization . Since the DDI has a sensitive dependence on the inter-emitter separation in our case, we argue that with the increasing disorder in our wQED ladder setup, the average inter-emitter separation can be decreased (in some iterations of the averaging process), which will have a drastic effect on DDI. In such cases, we expect the collective emitter effects to be enhanced and lead to improved photon transport (or less photon localization) through the DDI channel, thus producing this non-intuitive trend.