Photon ring polarimetry with next-generation black hole imaging I. M87*
Abstract
The near-horizon region of a black hole impacts linear (LP) and circular polarization (CP) through strong lensing of photons, adding large-scale symmetries and anti-symmetries to the polarized image. To probe the signature of lensing in polarimetry, we utilise a geometric model of concentric, Gaussian rings of equal radius to investigate the transition in the Fourier plane at which the photon ring signal begins to dominate over the direct image. We find analytic, closed-form expressions for the transition radii in total intensity, LP, and CP, wherein the resultant formulae are composed of ratios of tunable image parameters, with the overall “scale” set primarily by the thickness of the direct image. Using these formulae, we compute the transition radii for time-averaged images of M87* simulations at 230 GHz, studying both Magnetically Arrested Disc (MAD) and Standard and Normal Evolution (SANE) configurations for various spin and electron heating models. We compare geometric values to radii obtained directly from the simulations through a coherent averaging scheme. We find that nearly all MAD models have a photon ring-dominated CP signal on long baselines shorter than the Earth diameter at 230 GHz. Across favored models for the M87* accretion flow identified by EHT polarimetric constraints, we quantify the sensitivity and antenna size requirements for the next-generation EHT and the Black Hole Explorer orbiter to detect these features. We find that the stringent requirements for CP favour explorations using long baselines on the ground, while LP remains promising on Earth-space baselines.
1 Introduction
The work by the Event Horizon Telescope (EHT) collaboration in imaging the horizon scale emission of black holes Messier 87* (hereafter M87*) (Event Horizon Telescope Collaboration et al., 2019a, b, 2024a) and Sagittarius A* (hereafter Sgr A*) (Event Horizon Telescope Collaboration et al., 2022a) using very-long-baseline interferometry (VLBI) has opened up a new window in probing the astrophysical features of the strong field gravity regime. The observation of polarised structure in these near-horizon images (Event Horizon Telescope Collaboration et al., 2021a; Roelofs et al., 2023; Event Horizon Telescope Collaboration et al., 2023, 2024b) allows us to study the behaviour of magnetic fields in the vicinity of black holes (Event Horizon Telescope Collaboration et al., 2021b; Tsunetoe et al., 2020; Event Horizon Telescope Collaboration et al., 2024c). Indeed, the Astro2020 Decadal Survey emphasized the role of the EHT in this regime, noting the importance of probing the base of the relativistic jet of M87*, while also recognising the role of such observations to inform our understanding energy extraction from black holes (National Academies of Sciences et al., 2021). More recently, images of the base of the M87* jet at 86 GHz (Lu et al., 2023) have shown a bright ring of light around a flux depression, which taken with EHT results suggest very optically thin emission with rich prospects for accessing gravity signatures near the horizon, in polarization and otherwise.
In the context of future extensions of the EHT, polarimetry has also served as a useful tool for probing the so-called “ photon ring” (Johnson et al., 2020; Gralla et al., 2020a; Wong et al., 2022; Palumbo et al., 2023), a strong lensing feature of photons orbiting the black hole with an appearance that is only weakly dependent on the astrophysical details of the accretion. The “order” indexes the photon ring by the number of half-orbits made by the photon (in the direction of the Boyer-Lindquist co-ordinate system) (Gralla et al., 2020b; Johnson et al., 2020). Here the is the image arising from the “direct” emission and is the secondary image arising from strong lensing. For an equivalent indexing scheme that is covariant but only works when performing “forward” ray tracing from the emitting source to the observer, see Appendix A.3 of Chang et al. (2024). This indexing has been used to probe photon ring signatures in general relativistic magnetohydrodynamic (GRMHD) simulations, (Ricarte et al., 2021; Palumbo & Wong, 2022; Palumbo et al., 2023), EHT observations (Broderick et al., 2022) and for analytic modelling of photon ring structures (Tiede et al., 2022; Cárdenas-Avendaño et al., 2023; Cárdenas-Avendaño & Lupsasca, 2023).
Through both analytic work and GRMHD simulations, there have been several studies of linear (LP) (Himwich et al., 2020; Jiménez-Rosales et al., 2021; Palumbo & Wong, 2022; Palumbo et al., 2023) and circular polarization (CP)(Ricarte et al., 2021; Mościbrodzka et al., 2021) features as proxies for inferring the presence of the photon ring, also leading to a rich interplay with polarimetric features in jets (Mościbrodzka et al., 2017; Davelaar et al., 2019; Kawashima et al., 2021; Tsunetoe et al., 2022; Ogihara et al., 2024).
Now, the EHT observations are performed using only Earth-based stations and therefore the nominal diffraction-limited angular resolution for a given wavelength is limited by the Earth’s diameter . For observations at 230 GHz, this is approximately and the maximum possible baseline length in units of wavelength, is G. In order to improve the limitations on dynamical range and temporal resolution arising due to EHT’s sparse coverage (Event Horizon Telescope Collaboration et al., 2019c), as well to increase the achievable baseline lengths, there are several next-generation black hole imaging missions potentially offering sensitivity to the photon ring signals. The next-generation Event Horizon Telescope (ngEHT) is a ground-based extension to the EHT that aims to install new telescope sites, expand the observing bandwidth to 16 GHz and perform simultaneous multi-frequency observations at 86-230-345 GHz, all of which can lead to high-fidelity, real-time movies of black holes and their associated jets (Doeleman et al., 2023). The Black Hole Explorer (BHEX) mission (Johnson et al., 2024), aims to perform Earth-space VLBI with a single space-based orbiter, providing long baselines enabling photon ring science while also obtaining a dense coverage of the (u,v) plane on short baselines as well, with the aid of simultaneous dual-band observations by leveraging the expansions on the ground.
To study the efficacy of these missions to probe the photon ring, this paper studies its polarimetric features through both, geometric modelling and time-averaged GRMHD simulations. Indeed, while geometric modelling allows to probe lensing structures that are largely agnostic to astrophysical source profiles (Gralla et al., 2020a), simulations help identify features of the accretion flow that are strongly sensitive to the presence of the photon ring (Ricarte et al., 2021; Jiménez-Rosales et al., 2021). The geometric modelling of photon ring signatures of M87* has been studied by several authors in total intensity (Johnson et al., 2020; Gralla et al., 2020a; Lockhart & Gralla, 2022a; Paugnat et al., 2022; Cárdenas-Avendaño & Lupsasca, 2023; Jia et al., 2024), and in LP (Himwich et al., 2020). Gralla (2020) has also studied signatures on long baselines of general narrow features of arbitrary shape and intensity. The polarimetric signature of M87*’s photon ring in GRMHD simulations has also been studied by several authors (Ricarte et al., 2021; Mościbrodzka et al., 2021; Jiménez-Rosales et al., 2021; Palumbo et al., 2023).
The paper is organised as follows. Section 2 introduces the geometric model of the ring. Section 3 explores the photon ring transition signatures of the geometric model in all polarizations. Section 4 analyses transition behavior in a large library of GRMHD simulations in light of the geometric analysis. Section 5 describes detection requirements for ngEHT and BHEX in terms of permissible thermal noise and antenna diameter. Section 6 presents the conclusions and discusses the outlook for future work. Extended derivations of formulae used in the paper, as well as tabulated numerical results from GRMHD, can be found in the appendices.
2 Interferometric Signatures of Analytic Ring Models

Let the image plane be spanned by some two dimensional co-ordinate system and the baseline between the two stations spanned by a dimensionless vector drawn perpendicular to the line of sight. Then, the visibility response of an interferometer formed by this baseline, for an image signature , is given by a two-dimensional Fourier transform:
| (1) |
Here the “tilde” () denotes a quantity in the Fourier/visibility domain. Note that this relation applies for all Stokes parameters where , and represent total intensity, LP and CP respectively.
We consider the visibility domain to be spanned by polar co-ordinates . These co-ordinates are related to the Cartesian co-ordinates via the relation:
| (2) |
2.1 The Model: Concentric, Gaussian Rings
We now specify a geometric model of the image in terms of concentric, Gaussian rings. Such constructions have been used by the EHT to model-fit observations and study the effects on ring parameters of finite imaging resolution (Event Horizon Telescope Collaboration et al., 2019b). The image model is based on the following assumptions:
-
1.
The model for Stokes begins with a pair of symmetric, infinitesimally thin rings, each following Johnson et al. (2020) for a given sub-image :
(3) -
2.
We assume hierarchical total fluxes and thicknesses for the two rings in the model. The thicker ring, corresponding to the signature, has a total flux , radius and a thickness modelled by a Gaussian of thickness (standard deviation) . Similarly, the thinner ring corresponding to the signature has a total flux , radius and Gaussian thickness . Recall that the Gaussian thickness is related to the Full Width at Half Maximum (FWHM) by the relation,
(4) -
3.
The signature for and in Stokes V is proportional to that of Stokes I, with uniform fractional circular polarization and for the and images, respectively. That is, for a given sub-image ,
(5) -
4.
The LP signature is also proprtional to that of Stokes I scaled version of the Stokes I signature in the image domain (Johnson et al., 2020; Palumbo et al., 2020) with scaling described by factors and for the and rings respectively, along with the exponential to produce rotationally symmetric electric vector position angle. That is, for a given sub-image ,
(6)
The total signature in the Fourier domain is a sum of the and visibility responses:
| (7) | ||||
| (8) | ||||
| (9) |
Here is Bessel function of the first kind of order . For the subsequent analysis, we introduce the notation for the image domain ratios flux and polarimetric ratios,
| (10) |
the Fourier domain polarimetric ratios,
| (11) |
and the LP quantity,
| (12) |
Further details of the model can be found in Appendix A. Figure 1 demonstrates how this model approximates the polarized photon ring features of the image domain and the corresponding interferometric transition structures that manifest more subtly in GRMHD simulations.
We further restrict the model by fixing several parameter ranges relative to each other to simplify the model specification and mimic properties of the photon ring often seen in simulations of the M87* and Sgr A* accretion flows:
-
1.
We fix and consider the flux ratio to be a free parameter.
-
2.
Based on insights from Palumbo & Wong (2022), the quantities are assumed to satisfy the complex conjugacy relation
(13) and so and the ratio are free parameters.
-
3.
We assume the fractional circular polarizations and have opposite sign, and take and the ratio to be free parameters.
- 4.
Thus the specifiable parameters of the model (excluding the ring radii which are discussed in the next section) are: and .
3 Polarimetric Photon Ring Signatures: Concentric Gaussian Rings
We now study the transition in at which the signature overtakes the signature in each polarization. Though we consider rings of equal radii for the sake of completeness, an analytic description of such transitions without using this assumption is provided in the Appendix B. The calculation for CP is given below, while for total intensity and LP is given in Appendix B.
For CP, using Equations 7 and 9, we get:
| (14) |
Imposing the condition of equal radii cancels out terms, and taking and common from the numerator and denominator respectively gives:
| (15) |
The condition for to have a negative sign is,
| (16) |
Solving Equation 16 for and using the notation from Equation 10 gives the transition value at which the sign changes as,
| (17) |
A key insight that arises from Equation 16 is that the physical condition of the signal dominating over , is exactly equivalent to the mathematical condition for to change its sign. This further motivates the subsequent analysis of the GRMHD simulations to probe the photon ring signatures in these quantities.
Moreover, noting the fact that in Equation 17 the quantities inside the square root are all ratios and hence dimensionless, it can be inferred that the strongest determinant of is the “resolving out” of the direct image by exceeding . This is evident from rewriting Equation 17 as:
| (18) |
The thickness of the ring is is a crucial factor in comparing simulations with observations (Lockhart & Gralla, 2022b, a) and so Equation 18 and can be a useful tool for geometric modelling of polarimetric signatures of the photon ring. Moreover, the ensuing geometric features can be explored solely by fixing the one parameter of the ring, namely , and then defining the ratios of quantities relating the and ring.
The formulae for total intensity and LP, reproduced from Equations B3 and B8 with the notation of Equation 10, are given by:
| (19) | |||
| (20) |

Using Equations 17, 19 and 20, Figure 2 shows example interferometric quantities as a function of for combinations of model parameters that vary the relative contribution of the photon ring. We investigate the visibility domain signatures in and . We include the ratio to mimic the “universal regime” prediction for isotropic emitters (Johnson et al., 2020) and to make contact with the results of Tiede et al. (2022) for M87*. The Figure demonstrates the advantages of the geometric modelling scheme since after fixing geometric parameters of the rings (i.e and ), the onset of the photon ring transition is primarily governed by the relative polarization ratios (, and ) of the to the image. We find that the the photon ring signal starts to dominate at longer baselines (, tuned by model parameters. Specifically for LP, as the ring becomes more linearly depolarised with respect to the ring (i.e as increases), the transition radius at which the photon ring begins to dominate occurs at longer baselines. For CP, similar trends are observed for the values of the ratio .
4 Comparison with GRMHD Simulations
We now investigate the range of values of for GRMHD simulations of M87*, focusing on LP and CP signatures. We consider a library of time-averaged ray-traced GRMHD and images produced in Palumbo & Wong (2022), which hold fixed the mass at , the distance at Mpc, and the inclination at . The library contains five values of dimensionless spin : -0.94, -0.5, 0, +0.5, and +0.94, where a minus/plus sign indicates retrograde/prograde spin with respect to the large-scale accretion disk. In all cases, the black hole spin is directed away from the observer. The fluid models themselves were produced by iharm3D (Gammie et al., 2003; Prather et al., 2021) and ray-traced using IPOLE (Mościbrodzka & Gammie, 2018) with six values of the electron heating parameter (Mościbrodzka et al., 2016): 1, 10, 20, 40, 80, and 160. This parameter tunes the relative temperatures of ions and electrons as a function of the magnetization of the plasma.
4.1 Methodology: Coherent Annular Averaging

In order to obtain the transition radii directly from the time-averaged images, we utilise a coherent annular averaging (CAA) scheme. Herein, for each image, a polarimetric quantity is studied by making annular averages using a bin width of the order of few G. Throughout this analysis, a bin width of 4G is chosen. Physically, this corresponds to smoothing the small-scale fluctuations in the Fourier domain signal to investigate at which transition radii the photon ring signal first begins to dominate over the direct image. To specify this in the signal, we utilise the change in sign from the to the image-domain polarimetric quantities. For LP and CP, we track the sign change from to and to respectively. In practice, the CAA-based inference scheme is implemented as follows:
-
1.
For a fixed value of the bin width , specify the inner () and outer () radii of the annulus in the Fourier domain:
(21) Then, for each value of in an equally-spaced array from 0 to (say) G, extract the points in the corresponding annuli by performing a boolean & operation as,
(22) -
2.
Mask the interferometric quantity using the values.
-
3.
Take the mean of the resultant masked values and plot them as a function of . These plots are then used to investigate aforementioned transition beyond which the photon ring begins to dominate.
A demonstration of CAA on a time-averaged GRMHD image is given in Figure 4, wherein a MAD model with and is studied. The left panel demonstrates Re() plotted as a function of when no averaging scheme has been applied. The right panel demonstrates the data obtained after implementing CAA. The latter shows a distinct signature in the Fourier plane of a transition point beyond which the character of the signal changes. In subsequent sections, this will be identified as demonstrating the onset of the regime where the photon ring signal begins to dominate over the direct image.
The implementation of CAA is particularly important for due to the phase swings introduced by the null separation (Palumbo et al., 2023), which are smoothed over by this averaging. Similarly for , CAA averages out the spurious phase wraps that arise from the Stokes V and I images not necessarily being exactly proportional to one another.
4.2 Results
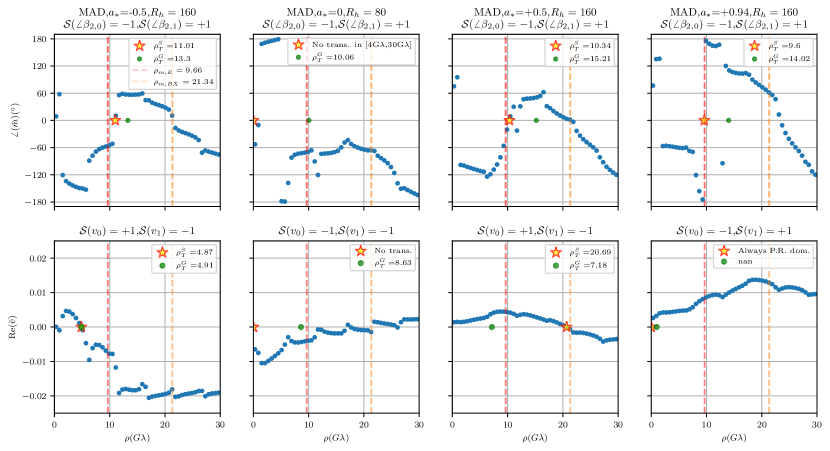
To demonstrate the signal characteristics in LP and CP using CAA, we first consider the four models for M87* at 230 GHz identified by the recent CP results of the EHT (Event Horizon Telescope Collaboration et al., 2023) as having the strongest agreement with EHT polarimetric data constraints; note that these models were not compared to other external criteria, such as jet power. These are MAD models with spin and values of , , and . The transition radii from the CAA scheme as well as from the geometric formulae are given in Figure 3. In the LP plots, the baselines shorter than 4 G are avoided based on insights from Palumbo et al. (2023) to prevent picking up the relative sign difference between the Bessel functions and while the upper limit of 21 G is chosen since this is approximately the maximum baseline of BHEX at 230 GHz. For CP, since there are no such sign complications, the lower and upper bounds are chosen to be 1 G and 21 G respectively. The CP signal for MAD model with and is peculiar since here Stokes V signal has the same sign of and which is inconsistent with our criteria our assigning a change in sign to indicate dominance of the photon ring over the direct image.

Next, we apply the CAA scheme to thehe full suite of GRMHD simulatio. The a graphic summary of the transition radii obtained is provided in Figure 5 and the exact values are tabulated in Table C, which also contains the transition radii for LP and CP for each model obtained from the geometric formulae given in Equations 20 and 17 respectively. To obtain the values from the geometric formulae, the ring widths were obtained using VIDA.jl (Tiede et al., 2020) by fitting a second-order -ring model onto the image.
4.2.1 Inferences and Trends
From the values obtained in Table C, several consistency checks can be performed with previous polarimetric studies of the photon ring. For example, for MAD states with a given spin, as increases, increases, implying a strong depolarization of the photon ring relative to the ring. This is consistent with the findings of (Palumbo & Wong, 2022), which used the same dataset as this paper. Furthermore, Palumbo et al. (2023) studied the MAD model with , and found a clear photon ring transition in LP at around G, which is reasonably close to the values obtained from the LP geometric model ( G) and CAA ( G).
However, trends with respect to are not in general simple. Though increasing tends to produce more jet emission in both MADs and SANEs, the degree to which it also increases the population of cold, depolarizing electrons is generally higher in MADs (Event Horizon Telescope Collaboration et al., 2021b). Abstractly, changing changes the relative balance of different polarizing and depolarizing mechanisms by changing the emission geometry and electron temperature, potentially leaving the simple regime of uniform structures in simply negated in the image. Though other electron thermodynamical post-processing schemes could produce systematically different transition regions this way, the existence of a transition in the Fourier domain can only be undone by a drastic change in optical or Faraday depths, which is difficult to imagine without breaking data consistency with EHT observations.
We now focus on the tabulated values obtained by applying CAA to the GRMHD simulations suite. For the favoured MAD state of M87* (Event Horizon Telescope Collaboration et al., 2021b), the values given in column and allows us to observe several spin-sensitive trends for the LP and CP transition radii respectively. In LP, for retrograde spins, increasing the spin value from to -0.94 while keeping fixed pushes all the photon ring transitions beyond maximum Earth baselines at 230 GHz. The two outliers here are models with spin , with not having a transition and being already beyond the maximal Earth baseline. Next, for , the transition radii values are quite sensitive to whether the spin is prograde/retrograde. All negative spin values are below the maximum Earth baselines (except ) while positive spin values are beyond Earth baselines. Once again and is an outlier. The models with spins do not have this sensitivity to the direction of the spin. However, while all models have transition radii in LP that are beyond the maximal Earth baselines at 230 GHz, the model with and has a transition radius that is just on the edge of this maximal length. We have checked that this result holds even when the bin size is G and so there is some confidence that the transition value is not an artefact of “over-smoothing” of the data.
For the values in CP, most MAD models have transition radii that are accessible from Earth baselines. Furthermore, MAD models with and all produce the majority of their CP flux in the photon ring with a sign flip, causing the photon ring to dominate on all baselines. The mathematical equivalent of this result from the geometric formula is that with the exception of the model with , all MAD models with have and so the logarithm inside the square root in Equation 17 is undefined. Besides this spin, the value in all other cases can be explained by the absence of a sign change thereby implying the non-existence of a transition from the to the regime.
Lastly, we note the particularly interesting case of MADs with . Here, for all values of , there is no transition in the signs of and (i.e both ) and so no transition radii in CP are obtained from the simulations. The absence of such a trend in any other spin values for MAD models indicates the potential utility of CP photon ring signatures to assert a non-zero spin value for M87*. This can complement the recent LP-based analysis by Chael et al. (2023) of M87*’s jet using the Blandford-Znajek mechanism, which crucially requires the black hole to have a non-zero spin.
5 Instrumentation Considerations for Polarimetric Best-Bet Models
In order to address whether ngEHT and BHEX can indeed observe the LP and CP photon ring signatures discussed above, we focus on the four polarimetric best-bet models and consider two main quantities of interest, namely the maximum thermal noise and the antenna size. The thermal noise is a proxy for sensitivity requirements of a baseline while greater antenna diameter implies better performance of the given station.
5.1 Maximum Permissible Thermal Noise
To introduce the notion of maximum permissible thermal noise, we first consider the case for CP. Under the assumption that the thermal noise for and is equal, the thermal noise for their quotient is given by,
| (23) |
Since we require the left hand side to be less than 1, the maximum value would be obtained by equating the right hand side to 1 and solving for . This gives,
| (24) |
For LP, since in Equation 12 is a function of and co-ordinates which can be defined very accurately, the error in it will be only due to the term. Once again, assuming that thermal noise in and is equal, in the high signal-to-noise limit (Chael et al., 2016), the expression for the maximum thermal noise can be obtained analogous to the case for CP, and is given by
| (25) |
An extended derivation of Equations 24 and 25 is given in Appendix LABEL:sec:sensitivity_tn.
For the four best-bet models observed at a fixed inclination of , the maximum thermal noise requirements are plotted in Figure 6. Here we consider baselines between a new antenna and ALMA, since the latter is the most sensitive site in the existing EHT array (Event Horizon Telescope Collaboration et al., 2019c) and has played a crucial role in studying the polarimetric properties of M87* (Goddi et al., 2021). The reference instrumentation specifications for a potential ngEHT site and the BHEX orbiter are tabulated in Table 1.
| Station Type | (K) | (K) | v (GHz) | t (s) | ||||
|---|---|---|---|---|---|---|---|---|
| ngEHT Site | 50 | 270 | 0.25 | 110 | 0.8 | 16 | 600 | 0.88 |
| BHEX Orbiter | 50 | - | - | 50 | 0.8 | 16 | 600 | 0.75 |

From the sensitivity plots, it is noted that for LP, BHEX is sensitive enough to observe the signal with significant improvements in the observation cadence at baselines longer than Earth’s diameter. For the ngEHT, due to limitations of baseline lengths on Earth, LP transitions from the photon ring are likely not detectable despite sufficient sensitivity. For CP, however, the higher sensitivity available on the ground is required. Here, the ngEHT can begin to “sense” the photon ring, albeit requiring maximum thermal noise to be mJy, whereas BHEX will not be sensitive to these signals across any baseline lengths.
5.1.1 Antenna Diameter
For a baseline between a reference station 1 and a new ngEHT/BHEX antenna 2, the antenna diameter for the latter is inversely proportional to the thermal noise on the baseline. The exact expression is derived in the Appendix LABEL:s:antenna_diam. In the context of our analysis, the plots for antenna diameter requirements are given in Figures LABEL:f:diameters_earth and LABEL:f:diameters_space for the ngEHT site-ALMA and BHEX-ALMA baselines respectively. The requirements for the LP and CP signals are different since for them, is and respectively. The detectability inferences from Figures LABEL:f:diameters_earth and LABEL:f:diameters_space are similar to those obtained from studying the thermal noise requirements due to the inverse relationship between the two. However we note that for the ngEHT in probing CP signals, there are clear advantages for choosing a 13 m antenna diameter over 9 m.
6 Conclusions and Outlook
In this paper, we have introduced two approaches to obtain the transition radii in the Fourier domain beyond which the photon ring signal begins to dominate over the direct image. Firstly, by geometrical modelling of the and signals as symmetric, concentric Gaussian rings of equal radii, exact analytical expressions for the transition radii have been found for total intensity, LP and CP. The corresponding formulae are functions solely of tunable model parameters and have a similar mathematical structure. Secondly, a general diagnostic tool, namely CAA, is introduced to systematically obtain the transition radii from the suite of time-averaged GRMHD images. This is applied to the simulation library of M87* at 230 GHz and its polarimetric best-bet models are treated in detail. Lastly, by studying the reference sensitivity and antenna diameter specifications for the ngEHT and BHEX missions, we’ve explored the extent to which these missions can observe the LP and CP photon ring signatures for these best-bet models.
In the context of the M87* model space probed in this paper, we find that Earth-based photon ring detection may have its strongest prospects in sensitivity-limited, astrophysics-forward CP signatures rather than high-resolution imaging. These signatures are relatively insensitive to morphology but may sense the presence of the photon ring in the near future. For BHEX, the prospects for probing the CP signal are sub-optimal, but an overwhelming majority of the signatures in LP are accessible and the nominal sensitivity of BHEX is sufficiently high that Stokes and signatures will likely provide strong morphological sensitivity to the photon ring. However, in the case of morphology that disobeys the trends exploited in this work (for example, if Stokes flips sign across the direct image, as has been seen in some simulations (Tsunetoe et al., 2021)), large discrepancies from rotational symmetry should be apparent even in the Fourier domain. In such cases, there is no substitute for polarimetric imaging.
A natural extension of this work is to performing a similar analysis of M87* at 345 GHz, possibly with the inclusion of more sophisticated geometric models for the image that are currently being used by the EHT (Event Horizon Telescope Collaboration et al., 2019d). It is also timely to perform broad GRMHD library analyses for photon ring detection prospects for Sgr A* as well. Due to its smaller mass, the dynamical timescales of Sgr A* are much shorted than M87* (Event Horizon Telescope Collaboration et al., 2022b) and so it would be instructive to apply the CAA scheme developed in this paper to quantify the range of transition radii as the source evolves. While there has been recent encouraging results in studies of LP detections of the Sgr A* photon ring with the ngEHT (Shavelle & Palumbo, 2024), BHEX may face challenges in detecting Sgr A* due to the diminishment of long-baseline signals caused by diffractive scattering (Johnson & Narayan, 2016). Appropriate orbit selection and observation strategies for the Galactic Center are the object of ongoing work; however, interferometric quotients such as those studied in this paper are innately robust to convolutional corruptions to the image, but will be sensitivity-limited in applications to Sgr A*.
7 Acknowledgements
We thank Paul Tiede for his assistance in the application of VIDA, as well as Michael Johnson and Sheperd Doeleman for many helpful conversations. A.T. gratefully acknowledges the Center for Astrophysics Harvard and Smithsonian, and the Black Hole Initiative for several fruitful discussions and providing a welcoming environment during an extended research visit during May-July 2024. We acknowledge financial support from the National Science Foundation (AST-2307887). This project was funded in part by generous support from Mr. Michael Tuteur and Amy Tuteur, MD. This work was supported by the Black Hole Initiative, which is funded by grants from the John Templeton Foundation (Grant 62286) and the Gordon and Betty Moore Foundation (Grant GBMF-8273) - although the opinions expressed in this work are those of the author(s) and do not necessarily reflect the views of these Foundations.
Appendix A Image and Visibility Domain Formulation of the Model
A.1 The Image Domain
Consider that the sky image of the black hole is constructed as a convolution between an infinitesimally thin ring of diameter convolved with a Gaussian of width . Suppose the image plane is spanned by polar co-ordinates of a thin ring of radius , having peak intensity is given by a delta function (Johnson et al., 2020)
| (A1) |
Here is constructed such that is the total flux density of the image. The Gaussian function having width can be modelled as:
| (A2) |
Several ring modelling papers model the Gaussian in terms of the FWHM (Event Horizon Telescope Collaboration et al., 2019b; Tiede et al., 2022).
Note that due to the absence of any dependence in the equations above, the model is axisymmetric. Now, to construct the geometric model for the image, we require a convolution of the signals given in Equations A1 and A2. The formulation in the image plane is given by (Cárdenas-Avendaño & Lupsasca, 2023):
| (A3) |
Substituting Equation A1 and Equation A2 into Equation A3, we get
| (A4) |
Separating the integral over gives
| (A5) |
Now, the integral can be written in terms of the modified Bessel function of the zeroth order
| (A6) |
with the factor of two 2 arising from the fact that the integrand is even. Thus, the Equation A5 now becomes
| (A7) |
This is the image-domain formulation of a thin ring of radius having a Gaussian width .
A.2 The Visibility Domain
Now for the delta function in Equation A5, it is known that the two-dimensional Fourier transform is given by the Bessel function of the first kind of zeroth order (upto a scale factor ),
| (A8) |
This can be inferred from the fact that for axisymmetric image models, the two dimensional Fourier transform is simply a Hankel transform and the latter for a delta function is simply the Bessel function of zeroth order of the first kind (Thompson et al., 2017).
Furthermore, it is known that the Fourier transform of a Gaussian is also a Gaussian and so for a function of kind in Equation A2, the visibility domain signature is:
| (A9) |
Therefore, since the Fourier transforms of a convolution of two functions is simply the product of the Fourier transform of each of the functions, the signature of our ring model in the visibility domain is:
| (A10) |
This form is common to both and features in our model and by using appropriate scale factors can be mapped to LP and CP models as done in Equations 8 and 9 respectively.
Appendix B Analytic Expressions for Photon Ring Transition Signatures in Polarimetric Quantities
Using the expressions for the Stokes parameters in the Fourier domain for the geometric model given in 7 and 8, we now derive the transition radii in total intensity and LP. The derivation for CP is given in the main text in Section 3.
B.1 Total Intensity (I)
For Stokes in the visibility domain, the dominance of the signature can be intuitively understood with the ratio of the to the term being greater than one. From Equation 7, this implies,
| (B1) |
Physically, this relative dominance is expected to occur at longer baselines (Johnson et al., 2020). Now, assuming equal radii, the terms cancel. Then, making the right equal to 1 to obtain the critical/transition value of , , we get
| (B2) |
Taking the natural logarithm of both sides, after some straightforward algebra, one obtains the expression for the transition radius in total intensity:
| (B3) |
B.2 Linear polarization
For LP, the expression for for our ring model, using Equations 8 and 7, is given by:
| (B4) |
Now, we make two approximations. Firstly, we assume equal radii of the and rings, i.e . Secondly, we assume,
| (B5) |
which is valid in the range of Earth-space baselines of interest to future observations (Palumbo et al., 2023). Now, as a consequence of this, the Bessel function terms cancel out of the numerator and the denominator, and after cancelling out we are left with,
| (B6) |
Now, asserting the requirement of criticality as in total intensity, the mathematical condition to be solved for the transition radii is,
| (B7) |
Here since only and are complex quantities, using the magnitude corresponded to using their absolute values. Taking to the right side, performing a natural logarithm on both sides, and solving for , gives:
| (B8) |
Appendix C Transition Radii for M87* at 230 GHz
The Table lists the transition radii in LP and CP obtained using the Equations 20 and 17 as well as from time-averaged GRMHD simulations of M87* at 230 GHz. The rows in bold are the best-bet models for M87* hedged by the recent polarimetric results of the EHT for M87* (Event Horizon Telescope Collaboration et al., 2023).
| Flux | ||||||||||||||||||||||||||||||
| MAD | -0.94 | 1 | 7.17 | 0.67 | 5.6 | -1.0 | 1.0 | 1.0 | -1.0 | 1.03 | 1.55 | 8.61 | 12.44 | 9.56 | 1.06 | |||||||||||||||
| MAD | -0.94 | 10 | 6.92 | 0.66 | 5.15 | -1.0 | 1.0 | 1.0 | -1.0 | 1.23 | 0.62 | 9.17 | 13.18 | 7.29 | 1.16 | |||||||||||||||
| MAD | -0.94 | 20 | 6.91 | 0.66 | 4.96 | -1.0 | 1.0 | 1.0 | -1.0 | 1.37 | 0.49 | 9.35 | 13.69 | 6.33 | 1.04 | |||||||||||||||
| MAD | -0.94 | 40 | 6.75 | 0.66 | 4.75 | -1.0 | 1.0 | 1.0 | -1.0 | 1.8 | 0.45 | 10.12 | 13.83 | 6.07 | 1.22 | |||||||||||||||
| MAD | -0.94 | 80 | 6.39 | 0.64 | 4.52 | -1.0 | 1.0 | 1.0 | -1.0 | 2.58 | 0.52 | 11.44 | 13.37 | 6.71 | 4.89 | |||||||||||||||
| MAD | -0.94 | 160 | 5.9 | 0.61 | 4.25 | -1.0 | 1.0 | 1.0 | -1.0 | 4.05 | 0.68 | 13.35 | 13.06 | 8.13 | 5.94 | |||||||||||||||
| MAD | -0.5 | 1 | 6.44 | 0.46 | 5.58 | -1.0 | -1.0 | 1.0 | 1.0 | 0.81 | 2.88 | 8.88 | 0.0 | 12.05 | 0.0 | |||||||||||||||
| MAD | -0.5 | 10 | 6.76 | 0.47 | 4.88 | -1.0 | 1.0 | 1.0 | -1.0 | 0.99 | 2.14 | 8.63 | 5.81 | 10.53 | 6.04 | |||||||||||||||
| MAD | -0.5 | 20 | 6.98 | 0.48 | 4.65 | -1.0 | 1.0 | 1.0 | -1.0 | 1.12 | 0.84 | 8.55 | 5.38 | 7.76 | 5.77 | |||||||||||||||
| MAD | -0.5 | 40 | 6.97 | 0.48 | 4.4 | -1.0 | 1.0 | 1.0 | -1.0 | 1.57 | 0.5 | 9.29 | 5.41 | 5.95 | 5.08 | |||||||||||||||
| MAD | -0.5 | 80 | 6.69 | 0.47 | 4.13 | -1.0 | 1.0 | 1.0 | -1.0 | 2.65 | 0.41 | 10.76 | 5.95 | 5.05 | 4.79 | |||||||||||||||
| MAD | -0.5 | 160 | 6.26 | 0.46 | 3.86 | -1.0 | 1.0. | 1.0 | -1.0 | 6.36 | 0.4 | 13.3 | 11.01 | 4.91 | 4.87 | |||||||||||||||
| MAD | 0 | 1 | 5.73 | 0.47 | 5.8 | -1.0 | 1.0 | -1.0 | -1.0 | 0.98 | 1.37 | 10.72 | 15.02 | 11.71 | 0.0 | |||||||||||||||
| MAD | 0 | 10 | 5.83 | 0.45 | 4.98 | -1.0 | 1.0 | -1.0 | -1.0 | 1.0 | 0.74 | 10.12 | 14.41 | 9.11 | 0.0 | |||||||||||||||
| MAD | 0 | 20 | 6.22 | 0.46 | 4.82 | -1.0 | 1.0 | -1.0 | -1.0 | 1.0 | 0.73 | 9.38 | 15.72 | 8.37 | 0.0 | |||||||||||||||
| MAD | 0 | 40 | 6.63 | 0.46 | 4.68 | -1.0 | 1.0 | -1.0 | -1.0 | 1.19 | 0.8 | 9.21 | 0.0 | 8.06 | 0.0 | |||||||||||||||
| MAD | 0 | 80 | 7.0 | 0.46 | 4.52 | -1.0 | 1.0 | -1.0 | -1.0 | 2.18 | 1.19 | 10.06 | 0.0 | 8.63 | 0.0 | |||||||||||||||
| MAD | 0 | 160 | 7.29 | 0.46 | 4.34 | -1.0 | 1.0 | -1.0 | -1.0 | 4.06 | 1.49 | 10.81 | 0.0 | 8.72 | 0.0 | |||||||||||||||
| MAD | +0.5 | 1 | 5.17 | 0.48 | 5.6 | -1.0 | 1.0 | -1.0 | 1.0 | 0.99 | 0.34 | 11.81 | 15.98 | 7.19 | 5.22 | |||||||||||||||
| MAD | +0.5 | 10 | 4.96 | 0.47 | 4.85 | -1.0 | 1.0 | -1.0 | 1.0 | 1.02 | 0.35 | 11.91 | 13.71 | 6.8 | 5.63 | |||||||||||||||
| MAD | +0.5 | 20 | 5.12 | 0.47 | 4.77 | -1.0 | 1.0 | -1.0 | 1.0 | 1.08 | 0.41 | 11.65 | 13.43 | 7.51 | 6.83 | |||||||||||||||
| MAD | +0.5 | 40 | 5.24 | 0.48 | 4.73 | -1.0 | 1.0 | -1.0 | 1.0 | 1.47 | 0.62 | 12.38 | 12.73 | 9.25 | 7.45 | |||||||||||||||
| MAD | +0.5 | 80 | 5.32 | 0.48 | 4.7 | -1.0 | 1.0 | -1.0 | 1.0 | 2.74 | 6.51 | 14.02 | 12.75 | 16.22 | 4.92 | |||||||||||||||
| MAD | +0.5 | 160 | 5.38 | 0.48 | 4.66 | -1.0 | 1.0 | 1.0 | -1.0 | 4.67 | 0.43 | 15.21 | 10.34 | 7.18 | 20.69 | |||||||||||||||
| MAD | +0.94 | 1 | 5.73 | 0.7 | 5.54 | -1.0 | 1.0 | -1.0 | 1.0 | 1.01 | 0.28 | 10.71 | 15.02 | 5.38 | 0.0 | |||||||||||||||
| MAD | +0.94 | 10 | 5.35 | 0.67 | 5.01 | -1.0 | 1.0 | -1.0 | 1.0 | 1.02 | 0.12 | 11.18 | 14.43 | nan | 0.0 | |||||||||||||||
| MAD | +0.94 | 20 | 5.42 | 0.68 | 4.99 | -1.0 | 1.0 | -1.0 | 1.0 | 1.04 | 0.1 | 11.09 | 14.45 | nan | 0.0 | |||||||||||||||
| MAD | +0.94 | 40 | 5.52 | 0.68 | 5.04 | -1.0 | 1.0 | -1.0 | 1.0 | 1.19 | 0.09 | 11.36 | 13.17 | nan | 0.0 | |||||||||||||||
| MAD | +0.94 | 80 | 5.57 | 0.67 | 5.12 | -1.0 | 1.0 | -1.0 | 1.0 | 1.72 | 0.07 | 12.39 | 9.6 | nan | 0.0 | |||||||||||||||
| MAD | +0.94 | 160 | 5.58 | 0.66 | 5.21 | -1.0 | 1.0 | -1.0 | 1.0 | 3.17 | 0.02 | 14.02 | 9.6 | nan | 0.0 | |||||||||||||||
| SANE | -0.94 | 1 | 11.52 | 0.94 | 13.96 | -1.0 | 1.0 | 1.0 | 1.0 | 5.46 | 0.72 | 8.42 | 16.03 | 6.14 | 0.0 | |||||||||||||||
| SANE | -0.94 | 10 | 6.95 | 0.61 | 5.86 | -1.0 | 1.0 | 1.0 | -1.0 | 32.14 | 1.33 | 15.36 | 6.03 | 9.62 | 11.03 | |||||||||||||||
| SANE | -0.94 | 20 | 6.57 | 0.58 | 5.67 | -1.0 | 1.0 | 1.0 | -1.0 | 38.0 | 0.71 | 16.45 | 6.17 | 8.37 | 6.0 | |||||||||||||||
| SANE | -0.94 | 40 | 6.28 | 0.56 | 5.47 | -1.0 | 1.0 | 1.0 | -1.0 | 36.26 | 0.56 | 17.08 | 6.8 | 7.87 | 6.07 | |||||||||||||||
| SANE | -0.94 | 80 | 6.03 | 0.54 | 5.28 | -1.0 | 1.0 | 1.0 | -1.0 | 32.35 | 0.52 | 17.52 | 12.41 | 7.73 | 6.67 | |||||||||||||||
| SANE | -0.94 | 160 | 5.85 | 0.53 | 5.11 | -1.0 | 1.0 | 1.0 | -1.0 | 29.82 | 0.54 | 17.87 | 12.65 | 8.05 | 11.12 | |||||||||||||||
| SANE | -0.5 | 1 | 10.29 | 0.58 | 17.88 | -1.0 | 1.0 | 1.0 | 1.0 | 0.93 | 0.7 | 7.57 | 4.31 | 7.19 | 0.0 | |||||||||||||||
| SANE | -0.5 | 10 | 7.11 | 0.58 | 5.3 | -1.0 | 1.0 | 1.0 | 1.0 | 9.25 | 1.26 | 12.92 | 8.39 | 9.03 | 0.0 | |||||||||||||||
| SANE | -0.5 | 20 | 6.91 | 0.42 | 5.05 | -1.0 | 1.0 | 1.0 | 1.0 | 9.67 | 3.43 | 13.28 | 9.6 | 11.37 | 0.0 | |||||||||||||||
| SANE | -0.5 | 40 | 6.69 | 0.4 | 4.84 | -1.0 | 1.0 | 1.0 | -1.0 | 9.16 | 9.22 | 13.53 | 9.3 | 13.54 | 10.55 | |||||||||||||||
| SANE | -0.5 | 80 | 6.45 | 0.39 | 4.56 | -1.0 | 1.0 | 1.0 | -1.0 | 9.51 | 2.26 | 13.99 | 6.4 | 11.01 | 10.53 | |||||||||||||||
| SANE | -0.5 | 160 | 6.25 | 0.37 | 4.24 | -1.0 | 1.0 | 1.0 | -1.0 | 8.22 | 1.25 | 14.03 | 5.93 | 9.61 | 10.55 | |||||||||||||||
| SANE | 0 | 1 | 8.24 | 0.49 | 18.48 | 1.0 | -1.0 | -1.0 | -1.0 | 0.56 | 1.1 | 8.62 | 6.59 | 9.8 | 0.0 | |||||||||||||||
| SANE | 0 | 10 | 9.38 | 0.68 | 10.09 | -1.0 | -1.0 | -1.0 | -1.0 | 2.02 | 1.25 | 8.62 | 0.0 | 7.9 | 0.0 | |||||||||||||||
| Flux | ||||||||||||||||||||||||||||||
| SANE | 0 | 20 | 6.87 | 0.37 | 5.26 | -1.0 | 1.0 | -1.0 | -1.0 | 10.76 | 1.8 | 13.6 | 5.98 | 10.15 | 0.0 | |||||||||||||||
| SANE | 0 | 40 | 6.55 | 0.32 | 4.49 | -1.0 | 1.0 | -1.0 | -1.0 | 11.68 | 2.22 | 14.11 | 5.99 | 10.76 | 0.0 | |||||||||||||||
| SANE | 0 | 80 | 6.38 | 0.3 | 4.31 | -1.0 | 1.0 | -1.0 | -1.0 | 8.42 | 2.83 | 13.8 | 5.98 | 11.52 | 0.0 | |||||||||||||||
| SANE | 0 | 160 | 6.2 | 0.29 | 4.18 | -1.0 | 1.0 | -1.0 | -1.0 | 7.49 | 2.89 | 13.91 | 6.03 | 11.83 | 0.0 | |||||||||||||||
| SANE | +0.5 | 1 | 7.39 | 0.65 | 10.21 | -1.0 | 1.0 | -1.0 | 1.0 | 0.92 | 0.23 | 9.45 | 5.78 | 5.81 | 4.65 | |||||||||||||||
| SANE | +0.5 | 10 | 6.56 | 0.66 | 7.53 | 1.0 | -1.0 | -1.0 | -1.0 | 0.7 | 1.48 | 9.18 | 20.95 | 11.04 | 0.0 | |||||||||||||||
| SANE | +0.5 | 20 | 5.86 | 0.67 | 6.74 | -1.0 | -1.0 | -1.0 | -1.0 | 0.41 | 1.7 | 8.07 | 0.0 | 12.46 | 0.0 | |||||||||||||||
| SANE | +0.5 | 40 | 5.71 | 0.71 | 5.56 | -1.0 | -1.0 | -1.0 | -1.0 | 1.35 | 1.91 | 11.64 | 0.0 | 12.6 | 0.0 | |||||||||||||||
| SANE | +0.5 | 80 | 5.82 | 0.87 | 4.42 | -1.0 | -1.0 | -1.0 | -1.0 | 3.56 | 0.68 | 13.4 | 0.0 | 8.47 | 0.0 | |||||||||||||||
| SANE | +0.5 | 160 | 5.6 | 1.23 | 3.82 | -1.0 | 1.0 | -1.0 | -1.0 | 5.47 | 0.41 | 14.83 | 4.81 | 5.63 | 0.0 | |||||||||||||||
| SANE | +0.94 | 1 | 6.12 | 0.77 | 6.91 | -1.0 | 1.0 | 1.0 | 1.0 | 1.06 | 0.01 | 10.79 | 13.8 | nan | 0.0 | |||||||||||||||
| SANE | +0.94 | 10 | 4.89 | 0.71 | 5.85 | -1.0 | 1.0 | -1.0 | 1.0 | 2.4 | 0.55 | 15.6 | 8.58 | 10.37 | 10.23 | |||||||||||||||
| SANE | +0.94 | 20 | 5.04 | 0.74 | 5.56 | -1.0 | 1.0 | -1.0 | 1.0 | 5.69 | 1.95 | 17.29 | 9.35 | 14.37 | 11.6 | |||||||||||||||
| SANE | +0.94 | 40 | 12.06 | 0.79 | 4.51 | -1.0 | 1.0 | -1.0 | 1.0 | 15.37 | 0.73 | 7.94 | 10.15 | 4.2 | 4.07 | |||||||||||||||
| SANE | +0.94 | 80 | 6.56 | 0.84 | 3.84 | -1.0 | 1.0 | -1.0 | 1.0 | 14.93 | 0.03 | 14.36 | 9.7 | nan | 2.57 | |||||||||||||||
| SANE | +0.94 | 160 | 7.08 | 0.95 | 3.54 | -1.0 | 1.0 | 1.0 | 1.0 | 17.11 | 0.27 | 13.4 | 9.13 | nan | 0.0 | |||||||||||||||
Appendix D Sensitivity and Antenna Diameter Considerations
D.1 Maximum Permissible Thermal Noise
Here we derive the expression for the maximum thermal noise in the CP () and LP () signal respectively.
Starting with CP, since , the error is given by,
| (D1) |
Assuming , and taking the square root of both sides, we get,
| (D2) |
Since the left-hand-side is required to be less than 1, to find its maximum value, the right hand-hand-side has to be equated to 1, such that the maximum thermal noise, , in is:
| (D3) |
For LP, note that can be written in terms of Stokes and as
| (D4) |
and so assuming , we get:
| (D5) |
Now, for , in the high signal-to-noise limit, the error can be approximated in a manner similar to Equation LABEL:eq:cp_error (Chael et al., 2016), giving:
| (D6) |
Assuming , taking the square root of both sides, using Equation LABEL:eq:lp_error_cond and once again imposing the condition of the right-hand-side to be equal to 1, we get the expression for the maximum thermal noise in as:
| (D7) |
The Equations LABEL:eq:cp_err_eqn and LABEL:eq:lp_err_eqn are used to generate the plots in Figure 6 in the main text.
D.2 Quantifying Antenna Diameter Requirements
Consider the baseline formed by two stations 1 and 2 with the baseline thermal noise given by . This can be written in terms of the station parameters, namely the System Equivalent Flux Densities (SEFD1 and SEFD2) measured in Jansky (Jy), bandwidth measured in Hertz (Hz) and coherence time measured in seconds (s),
| (D8) |
For any given station, hereafter Station 2, the SEFD is given in terms of the effective system temperature , antenna area and aperture efficiency , by the formula,
| (D9) |
where J/K is the Boltzmann constant. Now, since Jansky is not a standard (SI) unit while all other quantities are specified in terms of their SI units, it is important to note the following unit conversion:
| (D10) |
Keeping this conversion in mind, and approximating for station 2 the area of the single-dish antenna with diameter by , substituting Equation LABEL:eq:sefd_def into Equation LABEL:eq:tnoise_def, making the unit conversion from Equation LABEL:eq:jansky_SI and solving for diameter , we get:
| (D11) |
This formula is used to compute the plots given in Figure LABEL:f:diameters_earth.
For the ground-based ngEHT site, a reasonable value of , can be obtained from standard values of the receiver temperature at 230 GHz, forward efficiency of the antenna , atmospheric temperature and opacity as (Doeleman et al., 2023),
| (D12) |
For BHEX, the diameter plot is given in Figure LABEL:f:diameters_space. A summary of the parameters used to make the plots is given in Table 1.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/903b223b-f04a-4b38-976f-70ab28e86faa/x7.png)
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/903b223b-f04a-4b38-976f-70ab28e86faa/x8.png)
References
- Broderick et al. (2022) Broderick, A. E., Pesce, D. W., Gold, R., et al. 2022, ApJ, 935, 61, doi: 10.3847/1538-4357/ac7c1d
- Cárdenas-Avendaño & Lupsasca (2023) Cárdenas-Avendaño, A., & Lupsasca, A. 2023, Phys. Rev. D, 108, 064043, doi: 10.1103/PhysRevD.108.064043
- Cárdenas-Avendaño et al. (2023) Cárdenas-Avendaño, A., Lupsasca, A., & Zhu, H. 2023, Phys. Rev. D, 107, 043030, doi: 10.1103/PhysRevD.107.043030
- Chael et al. (2023) Chael, A., Lupsasca, A., Wong, G. N., & Quataert, E. 2023, ApJ, 958, 65, doi: 10.3847/1538-4357/acf92d
- Chael et al. (2016) Chael, A. A., Johnson, M. D., Narayan, R., et al. 2016, ApJ, 829, 11, doi: 10.3847/0004-637X/829/1/11
- Chang et al. (2024) Chang, D. O., Johnson, M. D., Tiede, P., & Palumbo, D. C. M. 2024, arXiv e-prints, arXiv:2405.04749, doi: 10.48550/arXiv.2405.04749
- Davelaar et al. (2019) Davelaar, J., Olivares, H., Porth, O., et al. 2019, A&A, 632, A2, doi: 10.1051/0004-6361/201936150
- Doeleman et al. (2023) Doeleman, S. S., Barrett, J., Blackburn, L., et al. 2023, Galaxies, 11, 107, doi: 10.3390/galaxies11050107
- Event Horizon Telescope Collaboration et al. (2019a) Event Horizon Telescope Collaboration, Akiyama, K., Alberdi, A., et al. 2019a, ApJ, 875, L1, doi: 10.3847/2041-8213/ab0ec7
- Event Horizon Telescope Collaboration et al. (2019b) —. 2019b, ApJ, 875, L4, doi: 10.3847/2041-8213/ab0e85
- Event Horizon Telescope Collaboration et al. (2019c) —. 2019c, ApJ, 875, L2, doi: 10.3847/2041-8213/ab0c96
- Event Horizon Telescope Collaboration et al. (2019d) —. 2019d, ApJ, 875, L6, doi: 10.3847/2041-8213/ab1141
- Event Horizon Telescope Collaboration et al. (2021a) Event Horizon Telescope Collaboration, Akiyama, K., Algaba, J. C., et al. 2021a, ApJ, 910, L12, doi: 10.3847/2041-8213/abe71d
- Event Horizon Telescope Collaboration et al. (2021b) —. 2021b, ApJ, 910, L13, doi: 10.3847/2041-8213/abe4de
- Event Horizon Telescope Collaboration et al. (2022a) Event Horizon Telescope Collaboration, Akiyama, K., Alberdi, A., et al. 2022a, ApJ, 930, L12, doi: 10.3847/2041-8213/ac6674
- Event Horizon Telescope Collaboration et al. (2022b) —. 2022b, ApJ, 930, L15, doi: 10.3847/2041-8213/ac6736
- Event Horizon Telescope Collaboration et al. (2023) —. 2023, ApJ, 957, L20, doi: 10.3847/2041-8213/acff70
- Event Horizon Telescope Collaboration et al. (2024a) —. 2024a, A&A, 681, A79, doi: 10.1051/0004-6361/202347932
- Event Horizon Telescope Collaboration et al. (2024b) —. 2024b, ApJ, 964, L25, doi: 10.3847/2041-8213/ad2df0
- Event Horizon Telescope Collaboration et al. (2024c) —. 2024c, ApJ, 964, L26, doi: 10.3847/2041-8213/ad2df1
- Gammie et al. (2003) Gammie, C. F., McKinney, J. C., & Tóth, G. 2003, ApJ, 589, 444, doi: 10.1086/374594
- Goddi et al. (2021) Goddi, C., Martí-Vidal, I., Messias, H., et al. 2021, ApJ, 910, L14, doi: 10.3847/2041-8213/abee6a
- Gralla (2020) Gralla, S. E. 2020, Phys. Rev. D, 102, 044017, doi: 10.1103/PhysRevD.102.044017
- Gralla et al. (2020a) Gralla, S. E., Lupsasca, A., & Marrone, D. P. 2020a, Phys. Rev. D, 102, 124004, doi: 10.1103/PhysRevD.102.124004
- Gralla et al. (2020b) —. 2020b, Phys. Rev. D, 102, 124004, doi: 10.1103/PhysRevD.102.124004
- Himwich et al. (2020) Himwich, E., Johnson, M. D., Lupsasca, A., & Strominger, A. 2020, Phys. Rev. D, 101, 084020, doi: 10.1103/PhysRevD.101.084020
- Jia et al. (2024) Jia, H., Quataert, E., Lupsasca, A., & Wong, G. N. 2024, arXiv e-prints, arXiv:2405.08804, doi: 10.48550/arXiv.2405.08804
- Jiménez-Rosales et al. (2021) Jiménez-Rosales, A., Dexter, J., Ressler, S. M., et al. 2021, MNRAS, 503, 4563, doi: 10.1093/mnras/stab784
- Johnson & Narayan (2016) Johnson, M. D., & Narayan, R. 2016, ApJ, 826, 170, doi: 10.3847/0004-637X/826/2/170
- Johnson et al. (2020) Johnson, M. D., Lupsasca, A., Strominger, A., et al. 2020, Science Advances, 6, eaaz1310, doi: 10.1126/sciadv.aaz1310
- Johnson et al. (2024) Johnson, M. D., Akiyama, K., Baturin, R., et al. 2024, arXiv e-prints, arXiv:2406.12917, doi: 10.48550/arXiv.2406.12917
- Kawashima et al. (2021) Kawashima, T., Toma, K., Kino, M., et al. 2021, ApJ, 909, 168, doi: 10.3847/1538-4357/abd5bb
- Lockhart & Gralla (2022a) Lockhart, W., & Gralla, S. E. 2022a, MNRAS, 517, 2462, doi: 10.1093/mnras/stac2743
- Lockhart & Gralla (2022b) —. 2022b, MNRAS, 509, 3643, doi: 10.1093/mnras/stab3204
- Lu et al. (2023) Lu, R.-S., Asada, K., Krichbaum, T. P., et al. 2023, Nature, 616, 686, doi: 10.1038/s41586-023-05843-w
- Mościbrodzka et al. (2017) Mościbrodzka, M., Dexter, J., Davelaar, J., & Falcke, H. 2017, MNRAS, 468, 2214, doi: 10.1093/mnras/stx587
- Mościbrodzka et al. (2016) Mościbrodzka, M., Falcke, H., & Shiokawa, H. 2016, A&A, 586, A38, doi: 10.1051/0004-6361/201526630
- Mościbrodzka & Gammie (2018) Mościbrodzka, M., & Gammie, C. F. 2018, MNRAS, 475, 43, doi: 10.1093/mnras/stx3162
- Mościbrodzka et al. (2021) Mościbrodzka, M., Janiuk, A., & De Laurentis, M. 2021, MNRAS, 508, 4282, doi: 10.1093/mnras/stab2790
- National Academies of Sciences et al. (2021) National Academies of Sciences, Engineering, & Medicine. 2021, Pathways to Discovery in Astronomy and Astrophysics for the 2020s (The National Academies Press), doi: 10.17226/26141
- Ogihara et al. (2024) Ogihara, T., Kawashima, T., & Ohsuga, K. 2024, ApJ, 969, 22, doi: 10.3847/1538-4357/ad429a
- Özel et al. (2022) Özel, F., Psaltis, D., & Younsi, Z. 2022, ApJ, 941, 88, doi: 10.3847/1538-4357/ac9fcb
- Palumbo & Wong (2022) Palumbo, D. C. M., & Wong, G. N. 2022, ApJ, 929, 49, doi: 10.3847/1538-4357/ac59b4
- Palumbo et al. (2023) Palumbo, D. C. M., Wong, G. N., Chael, A., & Johnson, M. D. 2023, ApJ, 952, L31, doi: 10.3847/2041-8213/ace630
- Palumbo et al. (2020) Palumbo, D. C. M., Wong, G. N., & Prather, B. S. 2020, ApJ, 894, 156, doi: 10.3847/1538-4357/ab86ac
- Paugnat et al. (2022) Paugnat, H., Lupsasca, A., Vincent, F. H., & Wielgus, M. 2022, A&A, 668, A11, doi: 10.1051/0004-6361/202244216
- Prather et al. (2021) Prather, B., Wong, G., Dhruv, V., et al. 2021, The Journal of Open Source Software, 6, 3336, doi: 10.21105/joss.03336
- Ricarte et al. (2021) Ricarte, A., Qiu, R., & Narayan, R. 2021, MNRAS, 505, 523, doi: 10.1093/mnras/stab1289
- Roelofs et al. (2023) Roelofs, F., Johnson, M. D., Chael, A., et al. 2023, ApJ, 957, L21, doi: 10.3847/2041-8213/acff6f
- Shavelle & Palumbo (2024) Shavelle, K. M., & Palumbo, D. C. M. 2024, arXiv e-prints, arXiv:2407.09750, doi: 10.48550/arXiv.2407.09750
- Thompson et al. (2017) Thompson, A. R., Moran, J. M., & Swenson Jr, G. W. 2017, Interferometry and Synthesis in Radio Astronomy, 3rd edn. (Springer Open)
- Tiede et al. (2020) Tiede, P., Broderick, A. E., & Palumbo, D. C. M. 2020, arXiv e-prints, arXiv:2012.07889, doi: 10.48550/arXiv.2012.07889
- Tiede et al. (2022) Tiede, P., Johnson, M. D., Pesce, D. W., et al. 2022, Galaxies, 10, 111, doi: 10.3390/galaxies10060111
- Tsunetoe et al. (2022) Tsunetoe, Y., Mineshige, S., Kawashima, T., et al. 2022, ApJ, 931, 25, doi: 10.3847/1538-4357/ac66dd
- Tsunetoe et al. (2020) Tsunetoe, Y., Mineshige, S., Ohsuga, K., Kawashima, T., & Akiyama, K. 2020, PASJ, 72, 32, doi: 10.1093/pasj/psaa008
- Tsunetoe et al. (2021) —. 2021, PASJ, 73, 912, doi: 10.1093/pasj/psab054
- Wong et al. (2022) Wong, G. N., Prather, B. S., Dhruv, V., et al. 2022, ApJS, 259, 64, doi: 10.3847/1538-4365/ac582e