Photon recoil and laser focusing limits to Rydberg gate fidelity

This section discusses how momentum kicks to atoms during gate pulses affect the fidelity of the gate. The most basic example of this situation is a 3-state atom in a one dimensional harmonic trap with the absorbed and emitted photons parallel to the allowed motion. In a typical implementation a laser may cause a transition from the qubit state $|1\rangle$ but leave state $|0\rangle$ untouched. We will limit the treatment to the case where the atom is excited from state $|1\rangle$ to Rydberg state $|R\rangle$ and then de-excited as part of the gate. For simplicity, the discussion below is in the wave function picture but all of the results in Sec. V are obtained using density matrices.

A reduction in gate fidelity occurs because the laser pulses create entanglement between the internal states of the atom and its center of mass degrees of freedom, which has been pointed out in several previous worksJaksch et al. (2000); Saffman and Walker (2005); Li et al. (2013); Keating et al. (2015). Consider the case where the atom starts in a separable wave function of the form of Eq. (1). A short laser pulse of duration $\delta t$ excites state $|1\rangle$ to state $|R\rangle$ and in the process gives the atom a momentum kick $\hbar K$. After a delay $\tau$ much shorter than the vibrational period of the atom trap, a second laser pulse in the same direction de-excites state $|R\rangle$ to state $|1\rangle$ giving the atom a momentum kick $-\hbar K$ from the stimulated emission. Although the second momentum kick undoes the change in momentum from the first, the spatial wave function for state $|1\rangle$ will not be the same as that for the state $|0\rangle$ because there will be a change in position, $\delta x=\hbar K\tau/M$, and an extra phase accumulation due to the change in kinetic energy during $\tau$. The final wave function can be written as

where the $c_{j}$ are as before, the $\psi_{\rm f,0}$ is normalized to one, and the integral of the sum $|\psi_{\rm f,1}|^{2}+|\psi_{\rm f,R}|^{2}$ is normalized to one. Typically, the norm in state $|1\rangle$ is much larger than that in state $|R\rangle$.

The entanglement between the spatial and internal degrees of freedom results in decoherence in the internal states. A measure of the decoherence is

where

which has a magnitude $0\leq|\chi|\leq 1$. When $|\chi|=1$, no entanglement occurred between the spatial and internal states and there is only an overall phase difference between $\psi_{\rm f,0}(x)$ and $\psi_{\rm f,1}(x)$. This is the desired outcome of the gate pulses. There is decoherence for the case $|\chi|<1$ which can occur even when the norm of $\psi_{\rm f,1}$ is unity because the laser kicks can cause this part of the wave function to evolve into a different region of Hilbert space. From the process described in the previous paragraph, there will be both a magnitude less than one and a complex phase for $\chi$. See the appendices, Sec. A for a derivation of $\chi$ for four different excitation styles. We give both the magnitude and phase for $\chi$, but the projection having a norm less than one is more problematic because the change in phase can be compensated for.

Although not due to photon kicks from absorption or emission, there is a source of decoherence due to transient population with double Rydberg characterKeating et al. (2015). This entanglement between the internal states of the atom and the atom motion arises because the Rydberg-Rydberg interaction depends on the separation of the atoms leading to an impulse along the line connecting the atoms, but only when the atoms start in the $|11\rangle$ state. We will only consider the case where the duration of the gate pulses is much smaller than the trap period. In this limit, the Rydberg-Rydberg interaction leads to an impulse due to the force between the atoms when they are both excited. This term only enters the $\psi_{\rm f,11}$ part of the wave function and consists of a phase accumulation $\phi=-V_{RR}\tau_{RR}/\hbar$ where

is effectively the time spent in the double Rydberg state and $P_{RR}$ is the probability both atoms are in the Rydberg state when starting in the $|11\rangle$ state.

Defining the $y$-direction as pointing from atom 1 to 2, the spatial dependence of the extra phase accumulation can be approximated as $\phi=6{\sf B}(y_{2}-y_{1})\tau_{RR}/r_{12}$ where the $y_{j}$ are displacements from the respective trap centers, with $r_{12}$ the distance between the center of the traps, and $\hbar{\sf B}=V_{RR}(r_{12})$; this assumes a $1/r_{12}^{6}$ dependence on the Rydberg-Rydberg interaction and the displacements are small compared to the trap separation. Outside of an overall, irrelevant phase factor, the projection of the $|00\rangle$, $|01\rangle$, or $|10\rangle$ components on that of $|11\rangle$ are the same and is

where $\psi_{\rm f,ii^{\prime}}$ are the spatial components of the wave function Eq. (21), $\omega_{\perp}$ is the trap frequency in the $y$-direction, and $T_{\rm eff}$ is defined in Eq. (62). We used the identity $\langle M\omega_{\perp}^{2}y^{2}\rangle=k_{B}T_{\rm eff}$ to generalize Eq. (7) to a thermal distribution.

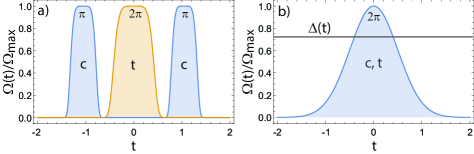
The atomic level structure is shown in Fig. 1. Atoms, each with stable ground states $\ket{0},\ket{1}$, are individually trapped in harmonic potentials. State $\ket{1}$ is optically coupled to Rydberg state $\ket{R}$ while off-resonant excitation of $\ket{0}$ is assumed negligible. The small contribution to gate infidelity from this off-resonant coupling has been considered in Zhang et al. (2012); Theis et al. (2016). Rydberg excitation is typically implemented as a one- or two-photon process. In the latter case the photons can be sufficiently detuned from an intermediate level that the additional photon scattering is negligible. The two-photon excitation has the advantage that using a counterpropagating geometry the momentum transfer is substantially smaller than for a one-photon implementation.

The two protocols we analyze in detail are shown in Fig. 2. The first is the $\pi-2\pi-\pi$ protocol, the fidelity of which using constant amplitude pulses has been analyzed in detail in Zhang et al. (2012). Neglecting the motional effects considered here, the gate fidelity is limited by atomic structure parameters to less than ${\mathcal{F}}\sim 0.998$. Higher fidelity reaching ${\mathcal{F}}>0.9999$ can be achieved using shaped pulsesTheis et al. (2016). The gap between the control atom $\pi$ pulses plays a dominant role in the sensitivity of this protocol to motional decoherenceWilk et al. (2010).

The second protocol we consider consists of a single adiabatic pulse applied simultaneously to both atoms with a Gaussian amplitude profile and constant detuning as shown in Fig. 2b. This gate is similar in concept to the Rydberg dressing gateKeating et al. (2015), and other adiabatic gate protocolsMitra et al. (2020); Saffman et al. (2020), but has a simplified implementation requiring only a single pulse with a constant laser detuning.

The entanglement mechanism of a single adiabatic pulse can be understood from analysis of the coherent part of the atomic dynamics depicted in Fig. 1. Consider first the simplified one-atom problem described by

in the basis $(\ket{1},\ket{R})$. Here we have ignored the far detuned coupling of $\ket{0}$ to the Rydberg state. $\hat{H}_{1}$ has eigenvalues $\hbar\lambda_{1,2}=\hbar(-\Delta\pm\sqrt{\Delta^{2}+|\Omega|^{2}})/2$ and eigenvectors ${\bf u}_{1,2}$. At the beginning of the Gaussian pulse $\Omega(0)=0$ and the state is $\ket{\psi}=\ket{1}=\begin{pmatrix}1\\ 0\end{pmatrix}={\bf u}_{1}.$ As long as the evolution is adiabatic $\ket{\psi(t)}={\bf u}_{1}$ at all times so the atom returns to the ground state independent of the length of the pulse. This imparts robustness with respect to the amplitude of $\Omega(t)$.

The adiabatic condition is $|\frac{d\theta}{dt}|\ll|\lambda_{2}-\lambda_{1}|=\sqrt{\Delta^{2}+|\Omega|^{2}}$ with $\theta$ the mixing angle. The dynamical phase acquired by the state during an adiabatic pulse of duration $T$ is $\phi_{01}=\phi_{10}=\int_{0}^{T}dt\,\lambda_{1}(t)=\int_{0}^{T}dt\,(\Delta(t)+\sqrt{\Delta^{2}(t)+|\Omega(t)|^{2}})/2$. Setting $\Delta$ constant and $\Omega(t)=\Omega_{\rm max}\left(e^{-(t-T/2)^{2}/\sigma^{2}}-e^{-T^{2}/4\sigma^{2}}\right)/\left(1-e^{-T^{2}/4\sigma^{2}}\right)$ the phase can be found numerically as a function of $\Delta,\Omega_{\rm max}$, and $\sigma.$

When the qubits are symmetrically excited the Hamiltonian in the two-atom symmetric basis $(\ket{11},\frac{\ket{1R}+\ket{R1}}{\sqrt{2}},\ket{RR})$ is

Here $\Omega$ is the one atom Rabi frequency coupling states $\ket{1}$ and $\ket{R}$. Diagonalizing $\hat{H}_{2}$ we obtain eigenvalues $\hbar\lambda_{1,2,3}$ and eigenvectors ${\bf u}_{1,2,3}.$ Explicit expressions for the eigenvalues are given in Saffman (2016). As for the case of a single Rydberg coupled atom the dynamical phase $\phi_{11}$ is found from integrating the relevant eigenvalue over the duration of the pulse. The result depends on $\Delta,\Omega_{\rm max},\sigma$, and $\sf B$. For any value of $\sf B$, which is fixed by the choice of Rydberg states and the interatomic spacing ${\bf r}_{12}$, we have two free parameters $\Delta/\Omega_{\rm max}$ and $\sigma$ which can be chosen to satisfy the condition on the phases for an entangling $C_{Z}$ gate.

Examples of valid gate parameters for different interaction strengths are given in Sec. V.2. As we will show the adiabatic gate can achieve high fidelity for a wide range of interaction strengths including the limit of strong blockade when $|{\sf B}|\gg\Omega_{\rm max}$ as well as the opposite limit of $|{\sf B}|\ll\Omega_{\rm max}$. In the latter case the doubly excited state $\ket{RR}$ is populated which leads to additional motional errors from Rydberg - Rydberg forces.

We will quantify the fidelity of the $C_{Z}$ gate by calculating the fidelity of the Bell state $|B\rangle=(|00\rangle+|11\rangle)/\sqrt{2}$ which can be prepared by a perfect gate operation. The sequence starts with the separable state $\ket{11}$. Applying the Hadamard gate to both qubits gives

Applying the Rydberg $C_{Z}$ gate (defined to be ${\rm diag}(C_{Z})=[1,-1,-1,-1]$) followed by a Hadamard gate on qubit 2 gives the Bell state, $|B\rangle$ under perfect operation. In what follows, we will evaluate the implementation of the $C_{Z}$ gate by starting in a separable density matrix

where the $\rho_{s}$ contains the spatial information about the two atom system and could be an eigenstate or a thermal state of the two atoms. We will then solve the density matrix equation for the $C_{Z}$ gate

where $\hat{H}(t)$ is the time-dependent Hamiltonian which will include the kick from photon absorption or emission. In the calculations, we will simulate the case where the qubit $|1\rangle$ can be excited to a Rydberg state $|R\rangle$. For the two-atom Hamiltonian we use $\hat{H}={\hat{H}}_{1}\otimes{\hat{I}}+{\hat{I}}\otimes{\hat{H}}_{1}+{\hat{H}}_{2}$ where ${\hat{H}}_{1}$ is a one-atom operator and ${\hat{H}}_{2}$ describes the Rydberg interaction.

As a basic example, plane wave light propagating in the $x$-direction will give a one atom Hamiltonian

where $H_{C}$ represents the kinetic energy and confining potential for each atom, $\Delta$ is the detuning of the laser connecting states $|1\rangle$ and $|R\rangle$, $K$ is the photon wave number, and $\Omega$ is the Rabi frequency. In addition to the one atom Hamiltonian, there is a Rydberg-Rydberg interaction

where $\hbar{\sf B}$ is the energy shift of the pair Rydberg state. The Rydberg state can decay by spontaneous photon emission or by absorption or emission of black-body photons. If the Rydberg state decays, the time to return to the ground state manifold can be large compared to the gate duration and there are many more hyperfine ground states than the qubit pair. Thus, we will use the pessimistic approximation that all of the radiative loss goes to states outside of the qubit pair or the Rydberg state. This population can be assigned to the single dark state $|d\rangle$ giving

where $j$ labels the two atoms.

Various gate protocols have different time dependence in the coupling $\Omega(t)$, and the detuning $\Delta(t)$. In some cases, the confining potential $H_{C,j}$ can depend on time and on the internal state of the atom.

In practice, we solve the density matrix equations using a basis set of harmonic oscillator states at angular frequency $\omega$ for the center of mass motion; in cases where more than 1D motion is important, we will distinguish between angular frequencies of the center of mass motion parallel, $\omega_{\parallel}$, or perpendicular, $\omega_{\perp}$, to the beam propagation direction. This gives

where $|i\rangle$ are the internal states $|0\rangle$, $|1\rangle$, $|R\rangle$, or $|d\rangle$ and the $v$ indicate the vibrational quantum numbers where each $v_{j}$ could be 1, 2, or 3 indices depending on the spatial dimension of the simulation. The number of vibrational states needed for convergence depends on the temperature in the simulation (more states are needed as $k_{B}T/(\hbar\omega)$ increases) and the photon momentum (more states are needed as $K$ increases).

The reduced density matrix is defined as

where we will not use a special symbol for the reduced density matrix since it has 4 indices instead of the 8 for the full density matrix. The reduced density matrix is used in the calculation of the gate fidelity.

After solving the time dependent density matrix equation, Eq. (13), for the $C_{Z}$ gate, we add a phase to state $|1\rangle$ and then apply a Hadamard gate to qubit 2. The phase is chosen to maximize the Bell state fidelity. We assume the phase on state $|1\rangle$ and the Hadamard gate can be perfectly implemented irrespective of the vibrational state. The Bell state fidelity is defined as Sackett et al. (2000)

The $C_{Z}$ gate protocol is designed to make $\cal F$ as large as possible. The requirement for scalable quantum computation depends on the error correction schemeTerhal (2015), but ${\cal F}>0.99$ is generally considered a minimum fidelity below which very large numbers of qubits are required.

To simplify many of the derivations, we will use a wave function picture to track the effects from a gate although all of the results are ultimately derived from the density matrix in Eq. (19). The initial state can be written as

where $|{\rm in}\rangle$ is defined in Eq. (12). A gate will cause a manipulation of the spatial part of the wave function depending on the internal state. Ignoring the part of the wave function left in the states outside of the qubit pair, the wave function after the gate has the form

where the $\psi_{f,ii^{\prime}}$ have the effects of different interactions between the atoms and have norm $\sim 1$.

Applying the Hadamard gate to qubit 2 gives the final state

From this, taking $|\Psi\rangle\langle\Psi|$ and integrating over the spatial coordinates gives the components of the reduced density matrix

To see how entanglement between the internal qubit state and the atomic center of mass motion affects the Bell fidelity, the $\pi-2\pi-\pi$ Rydberg blockade gate is instructive. In this case, a first pulse excites qubit 1 to the Rydberg state if it is in state $|1\rangle$, a second pulse excites qubit 2 from state $|1\rangle$ to the Rydberg state and back to state $|1\rangle$ if qubit 1 is not in the Rydberg state, and a last pulse de-excites qubit 1 from the Rydberg state back to $|1\rangle$. We will consider three contributions to infidelity: axial momentum kicks, laser focusing, and radiative losses.

The finite spatial extent of an atom’s position combined with spatial variation of the laser intensity due to focusing leads to infidelity in the gate. In this section, we will only treat this effect. There are several trends to consider. As the laser waist decreases, the spatial variation of the intensity increases across the spatial extent of the atom position leading to decreased fidelity. The fidelity decreases with increasing temperature due to the increasing spatial extent. The fidelity increases as the trap frequency increases due to the decreasing spatial extent.

To obtain the infidelity due to laser focusing, the projection derived in Sec. F will be used. The decreased norm in each term can be found by noting that in $\psi_{f,00}$ neither atom is excited, $\psi_{f,10}$ atom 1 is excited, $\psi_{f,01}$ atom 2 is excited, and $\psi_{f,11}$ has no effect since the $2\pi$ pulse changes the sign of the $\psi_{11}$ term not excited to $\psi_{R1}$ in the first $\pi$ pulse. Unlike the previous section, the main effect is the change in the norm of the state associated with the transition to the Rydberg state and back. In this case, the different wave functions can be written as

Substituting the projections into Eq. (IV.1.1), gives

where $\varepsilon^{(G)}$ is defined in Eq. (91). Dropping all terms involving $\varepsilon^{2}$ the Bell state fidelity, Eq. (19), gives

If the excitation is due to two photon absorption, the $1/w_{0}^{2}$ is the sum of the squares of the inverse waists and the $1/x_{R}^{2}$ is the sum of the squares of the inverse Rayleigh ranges.

The contribution to the infidelity due to radiative losses can be computed from the form of Eq. (III.2) by considering the decrease in magnitude in each part of the wave function. We will take the most pessimistic interpretation that radiative losses due to spontaneous emission or blackbody radiation lead to transitions outside of the qubit states on the time scale relevant to the gate. Assuming the Rydberg lifetime is much shorter than the gate duration, the change in norm leads to

Using Eqs. (III.2) and (19) and dropping terms quadratic in $\tau$ leads to the infidelity

where $\Gamma$ is the inverse of the Rydberg lifetime due to radiative losses, $\tau_{1}$ is the time between the two $\pi$ pulses, and $\tau_{2}=\delta t/2$ with $\delta t$ the duration of the $2\pi$ pulse.

Another possible gate protocol involves exciting both qubits simultaneously with the same laser pulse. We will let $\Omega(t)$ have a Gaussian envelope with fixed detuning $\Delta$. This will give a $C_{Z}$ if the detuning, duration, and Rydberg-Rydberg interaction, $\hbar{\sf B}$, are chosen appropriately. The one atom Hamiltonian is Eq. (14) with

the only time dependent part.

As in the previous section, the final wave function has the form of Eq. (21) where the $\psi_{f,ii^{\prime}}$ have the effects of different kicks. The $\psi_{f,00}$ has no kick from the photon momentum, the $\psi_{f,10}$ has a kick on qubit 1 and no kick on qubit 2, the $\psi_{f,01}$ has the same kick on qubit 2 and no kick on qubit 1, and the $\psi_{f,11}$ has a kick on both qubits. There are small kicks from far detuned transitions which will be ignored. The results from Sec. D.3 can be used to compute the effect on $\psi_{f,10}$ and $\psi_{f,01}$. The effect on $\psi_{f,11}$ is more difficult to obtain because it involves both qubits.

Because there are 4 electronic states involved and two different atomic momenta, we were not able to derive an expression for the projections involving $\psi_{f,11}$. However, we have found a formula using qualitative arguments that gives good agreement with all of the calculations we have performed with the full density matrix. The idea is to treat the adiabatic pulse on the $\psi_{f,11}$ state as giving the same kick to each atom. In analogy to Eq. (78), we define the duration of the kick on an individual atom as half of the Rydberg population integrated over the pulse:

where $P_{R1}(t)$ is the probability for atom 1 to be in the Rydberg state and atom 2 is in state $|1\rangle$, $P_{1R}(t)$ is the reverse identification, and $P_{RR}(t)$ is the probability that both atoms are in the Rydberg state. For the symmetric excitation of this gate, $P_{R1}(t)=P_{1R}(t)$. This calculation requires hardly any computer time compared to solving the full density matrix equations including the vibrational states. This leads to the identification

with the projections from Eq. (79)

where $\tau_{a}$ is from Eq. (78) and $\tau_{R}$ is from Eq. (34).

Ignoring all terms quadratic in the $\varepsilon$, the projections in Eq. (III.2) give:

where $\tau_{a}$ is from Eq. (78) and $\tau_{R}$ is from Eq. (34). Both of these times are computed using only the internal states of the atoms. Combining these factors, the the Bell state infidelity due to the photon momentum kicks is

which can be compared to the same expression for the $\pi-2\pi-\pi$ gate of the previous section, Eq. (27). Although the details are different, the gates have the same scaling with photon kick $\hbar K$, atom mass $M$, and effective temperature $T_{\rm eff}$. An advantage of the adiabatic gate is that the time spent in the Rydberg state, as measured by $\tau_{a}$ and $\tau_{R}$, can be substantially shorter than the spacing of the $\pi$-pulses $\tau_{1}$ in the $\pi-2\pi-\pi$ gate for the same excitation Rabi frequency. This gate also has the advantage that it can reach high fidelity for both large and small $\sf B$, the latter case being useful for gates acting on qubits with large spatial separations.

In addition to the axial momentum kick, the Rydberg lifetime and the laser focus will contribute to infidelity. It is not obvious how to analytically account for these effects for this adiabatic gate. However, they can be accounted for by solving the small set of density matrix equations that do not include the effect from axial recoil.

The first tests will involve parameters for the $\pi-2\pi-\pi$ gate of Ref. Graham et al. (2019). To model the pulses, we use

where the $\Omega_{j,\rm max}$ give the appropriate $\pi$ pulses for atom 1 and $2\pi$ pulse for atom 2, $\tau_{1}=1.0044$ $\mu$s is the time between pulses for atom 1, $\delta t_{1}=0.14$ $\mu$s is the duration of each of the atom 1 pulses, and $\delta t_{2}=0.22$ $\mu$s is the duration of the atom 2 pulse. Because of the order of magnitude difference between $\tau_{1}$ and $\tau_{2}=\delta t_{2}/2$, the Bell state infidelity is $1-{\cal F}\simeq\varepsilon^{(1)}/2$.

Figure 3 shows the infidelity, $1-{\cal F}$ in Eq. (27), for these parameters as a function of the trapping frequency when the atoms start in the motional ground state. For this case, we assume a scenario where the trapping potential is magic so that the potential is the same for all states. The finite lifetime of the Rydberg state is not included in this calculation, but the horizontal lines show the contribution to the infidelity due to the Rydberg finite lifetime for 66S (solid) and 106S (dotted) states. The solid red line is from numerically solving the density matrix calculation; the approximation, Eq. (85), that includes the trapping potential is the green dotted line that overlays the exact result. This shows that the small width of the individual $\pi$-pulses has a negligible contribution to $\varepsilon^{(1)}$. The blue dashed line is the exact result when the trapping potential is turned off during the calculation, Eq. (67). Because this calculation has $\sim 1$ $\mu$s between $\pi$-pulses, it is not surprising that Eq. (67) becomes noticeably different from calculations with the trap on when $f\sim 100$ kHz. For these calculations, convergence to better than 0.01% was achieved using a maximum vibrational quantum number of 10.

It is, perhaps, a surprise that there is more, not less, decoherence as the trapping frequency increases. Intuition suggests that higher frequencies lead to less effects from atom recoil due to the larger energy spacing. However, because the durations are short, the size of the energy spacings are not relevant. The main effect is from the spatial size of the initial state and how far the atom moves during the sequence of laser pulses. The spatially smaller states at higher frequency have less overlap with the unkicked states. At the higher frequencies, the infidelity due to the axial photon kick can be larger than that from radiative losses even when the atom is in the motional ground state.

For the laser parameters of the previous paragraph, we now compare the approximation, Eq. (73), to the full calculation with the trapping potential for a thermal distribution. Results from calculations with three different trap frequencies are shown in Fig. 4. These calculations include the trapping potential during the laser manipulations. The results from the approximation, Eq. (73), are indistinguishable from the full solution on the scale shown. As in Fig. 3, the horizontal lines are the infidelity due to finite Rydberg lifetime of the 66S (solid) and 106S (dotted) states. The fidelity is ${\cal F}>0.995$ for the temperatures plotted. The best value for the 50 kHz trapping potential is ${\cal F}\simeq 0.999$. The maximum number of vibrational states was used for the 20 kHz calculation at 5 $\mu$K because the 10 kHz calculation was only performed to 1.5 $\mu$K; the maximum number of vibrational states for this case was $\sim 100$.

Figure 4 shows that the decoherence increases linearly with the temperature once $k_{B}T$ is larger than $\sim\hbar\omega_{\parallel}$. Also, the decoherence is nearly independent of the frequency of the trapping potential when this condition is satisfied because the smallest relevant length scale is the thermal de Broglie wavelength. Since the approximation, Eq. (73), is accurate, we can use it to derive an expression for the decoherence when $\varepsilon^{(1)}$ is small:

where ${\rm coth}(x)=(e^{x}+e^{-x})/(e^{x}-e^{-x})$. The limits are

which shows the linear dependence on the temperature when the atoms are hot compared to the quantum energies. It also shows that the decoherence does not depend on the trap frequency at high temperatures. Another point of comparison is to remember that the average number of vibrational quanta is $\langle n\rangle=1/\{\exp[\hbar\omega_{\parallel}/(k_{B}T)]-1\}$. When $k_{B}T=\hbar\omega_{\parallel}$, the average vibrational quanta is $\langle n\rangle\simeq 0.58$ and the fractional error in the high temperature form of the decoherence is 8%. When $k_{B}T=2\hbar\omega_{\parallel}$ then $\langle n\rangle\simeq 1.54$ and the fractional error is 2%. This illustrates how quickly the trap frequency becomes irrelevant to the decoherence.

As a physical example, we consider the case from Ref. Madjarov et al. (2020) where Sr is excited from the ³P₀ metastable state to ³S₁ Rydberg states using a single 317 nm photon. The time scale for a $2\pi$ pulse was of order 100 ns. Using their estimated temperature of $2.5/\sqrt{10}$ $\mu$K$=0.8$ $\mu$K gives $\varepsilon^{(1)}\simeq 1.5\times 10^{-4}$. However, if the gate is composed of more than one pulse, the duration can be longer. The decoherence increases to $\varepsilon^{(1)}\simeq 1.3\times 10^{-3}$ if $\tau_{1}=300$ ns.

The scale of the projection error can be compared to the decoherence from decay of the Rydberg state. Figure 5 shows the $\varepsilon^{(1)}$ for calculations in a 10 kHz trap for three different temperatures (2, 5, and 10 $\mu$K) as a function of the time, $\tau_{1}$, between the $\pi$-pulses. This emphasizes that the infidelity from Rydberg state decay scales linearly with $\tau_{1}$ while that from recoil is proportional to the square of the time. For short times between pulses, the main error will be due to the decay of the Rydberg state. For pulses with $\tau_{1}\sim 1$ $\mu$s, the atoms need to be cold for the projection error to be smaller than the decay probability.

The infidelity due to laser focusing, Eq. (30), does not depend on the duration of the gate as long as the duration is much less than the trap period. This infidelity has the strongest dependence on the effective temperature of the mechanisms examined in this paper. Figure 6 shows the infidelity, Eq. (30), for 3 different transverse trap frequencies: 10 kHz (solid red), 20 kHz (blue dashed), and 50 kHz (green dotted). For this calculation and that of Fig. 7, we assumed the terms with $x_{R}$ are less than 10% of the transverse decoherence and have been dropped. The effective waist is $\sqrt{2}$ $\mu$m and there is assumed misalignment of $y_{0}=100$ nm. This figure illustrates how sensitive the infidelity is to the transverse trap frequency: at high temperature, the infidelity is proportional to $1/f_{\perp}^{4}$. This figure also shows how high temperature exacts a high penalty because the infidelity scales like $T^{2}$ in this limit.

Figure 7 shows how the axial displacement, $y_{0}$, can quickly degrade the fidelity of the $\pi-2\pi-\pi$ gate. This graph uses the same parameters as Fig. 6 except the temperatures and frequencies are fixed: the curves use 10, 20, or 50 kHz and 1 or 5 $\mu$K. As with Fig. 6, it is clear that larger temperatures dramatically degrade the fidelity as do lower trap frequencies. Figure 7 demonstrates the importance of alignment for the gate fidelity since the infidelity, Eq. (30), has a quartic dependence on $y_{0}$. It is interesting that the infidelity from displacement of the focused beam is greater than that due to finite Rydberg lifetime for displacements larger than $\sim 200$ nm even for the $66S$ state; this value is $\sim 1/10$ the waist of the individual beams.

Because the infidelity is proportional to the atom temperature for $k_{B}T>\hbar\omega$, the change in vibrational character due to gate pulses should be examined. This effect can be estimated using the heating of the atom’s center of mass motion due to the time delay between the pulses. The kick shifts the position which leads to heating. For reasonable gate parameters, this effect will be negligible except for high frequency traps at the lowest temperatures. The center of mass energy will change by the amount

which is the recoil energy times $(\omega\tau_{1})^{2}$. Since $\omega\tau_{1}$ will be much less than one, this shows the energy will increase by a small fraction of the recoil energy per gate. To give an idea of the size of the two effects, for $\tau_{1}=1.00$ $\mu$s and $\lambda_{\rm eff}=822.9\leavevmode\nobreak\ \rm nm$, the change in energy from Eq. (44) is 0.42 nK per kick for a 10 kHz trap, 1.7 nK per kick for 20 kHz, and 11 nK per kick for 50 kHz.

As a comparison, the change in energy that occurs when the trap is turned off for a time $\tau\simeq\tau_{1}+4\delta t_{1}\simeq 1.56$ $\mu$s and then turned back on is $\Delta E=(k_{B}T_{\rm eff}/2)(\omega\tau)^{2}$. For this effect, the size of the energy change increases with each time the trap is turned off and back on. Taking $<E>=k_{B}T_{\rm eff}$, The temperature after $N$ gates is $T_{N}=T_{\rm eff}\exp[N(\omega\tau_{1})^{2}/2]$. For 100 gates, $T=T_{\rm eff}e^{0.48}=1.62T_{\rm eff}$ for a 10 kHz trap, $e^{1.92}T_{\rm eff}=6.83T_{\rm eff}$ for a 20 kHz trap, and $e^{12}T_{\rm eff}=1.6\times 10^{5}T_{\rm eff}$ for a 50 kHz trap. Clearly, several approximations break down for the 50 kHz trap before this limit is reached. Nevertheless this result indicates that turning on and off a 50 kHz trap is not a good idea. Fortunately it is possible to design traps that present the same trapping potential for ground and Rydberg atoms so it is feasible to leave the trap potential on continuouslyZhang et al. (2011).