Phase-Dependent Damping Rate of Josephson Plasmons in the Nonequilibrium Steady State
Abstract
We calculate the damping rate of Josephson plasmons due to thermally excited quasiparticles in a nonequilibrium steady state. It is known that the experimentally observed dependence of the damping rate on the phase difference behaves in the opposite way to that of the theory. It is shown that this problem can be solved by calculating the damping rate by incorporating changes in the electronic state at the resonant frequency. When the phase difference is large, the broadening of the one-particle state is large due to the presence of a dc current and brings about the effective thermalization, so that the nonequilibrium correction becomes small. Conversely, when the phase difference is small, the nonequilibrium correction becomes large and causes a smaller damping rate due to a reduction in the effective temperature. This dependence of the nonequilibrium correction on the phase difference results in a damping rate that is consistent with experimental results.
1 Introduction
The Josephson current, which depends on the phase difference between two superconductors in the tunnel junction, has a non-dissipative current and a dissipative current, [1, 2] and there is a so-called cosine term problem in the latter. The problem is that there is an inconsistency between theory and experiment about the sign of the phase-dependent term of the dissipative current proportional to the cosine of the phase difference. [4, 3] Theory shows that the sign of this term is positive, [5, 6] but experiments on the damping rate of the Josephson plasmon show that the sign of this term is negative. [7, 8, 9]
In recent years, this term has been studied in relation to the energy relaxation in superconducting qubits. [10, 11] The experiment carried out at very low temperatures showed that in the limit of small excitation frequencies, the sign of the cosine term is positive, [12] as in theory. As in this study experiments on superconducting qubits are mainly aimed at extremely low temperatures where thermally excited quasiparticles can be neglected.
On the other hand, in previous experiments in which the negative sign of the cosine term was observed, thermally excited quasiparticles are thought to be responsible for the damping rate of Josephson plasmons. This is because these experiments were conducted at relatively high temperatures ( with and being the temperature and the transition temperature, respectively), and the theoretical calculations were also performed for the case where the thermal excitation gives a finite value of the damping rate. For this reason, the previous cosine term problem at relatively high temperatures, rather than at low temperatures where superconducting qubits work, is considered to be unsolved.
Up until now, theoretical calculations for the cosine term problem have focused only on the sign of the cosine term. [13, 14, 15, 16] Experiments have shown that as the phase difference becomes smaller, the damping rate of Josephson plasmons decreases. Therefore, rather than extracting only the cosine term and examining its sign, it is necessary to examine the dependence of the entire term in the dissipative current on the phase difference.
In this study, we consider that at the resonance frequency of Josephson plasmons, the one-particle state of electrons is in a nonequilibrium steady state due to the external field at this frequency. We calculate the damping rate based on this electronic state. A finite phase difference occurs under the dc current which changes the resonance frequency. The presence of this phase difference causes a broadening of the peak around the gap edge in the density of state. Therefore the nonequilibrium correction differs depending on the magnitude of the phase difference, and the resulting variation of the effective temperature (this is known as the Éliashberg effect [17]) leads to the phase-dependent damping rate due to quasiparticle excitations.
The structure of this paper is as follows. In Sect. 2, we give a formulation based on the quasiclassical approximation in the nonequilibrium steady state, and derive the expression of the damping rate from the current. Section 3 gives the results of the numerical calculations based on this formulation. First, we show the calculated results of the damping rate without correction terms, and show that it gives the same behavior as in the previous studies. Next, we give the results of the damping rate in a nonequilibrium steady state, and show that the nonequilibrium correction plays a major role in the dependence of the damping rate on the phase difference. Section 4 provides a discussion of these results.
2 Formulation
2.1 The expression of the current
We give the expression of the current from which the damping rate is derived. This quantity is experimentally obtained from the impedance measurements, [7] and the expression of the impedance is given as follows. (We set with the velocity of light.) By introducing the capacitance ( and are the thickness and the area of the junction, respectively), we obtain from the Maxwell equation, [18] in which and are the induced and external currents, respectively [19] ( is the vector potential with its frequency ). With use of , which is obtained below (Sect. 2.3), the impedance () is written as . Here, with and being the plasma frequency [20] and the critical current [21] in the Josephson junction, respectively. and are the superconducting order parameters of two superconductors consisting the Josephson junction (the magnitude of the gap is assumed to be equal for two superconductors), and is the tunnel resistance in the normal state. is the damping rate and its expression is given in Sect. 2.3.
The expression of the current is obtained by using the quasiclassical Green functions. The following relation holds from the kinetic equations for quasiclassical Green functions: [22]
| (1) |
and are the retarded (advanced) and Keldysh quasiclassical Green functions, respectively, and and are the self-energies. The superscripts and are indices representing two superconductors consisting the Josephson junction. , means a matrix in the Nambu space, and indicates taking the trace. This leads to the following relation between the current () and the temporal variation of the charge ():
| (2) |
( is the density of states which is assumed to be equal for two superconductors, and the volumes of superconductors are set to be 1 and not written explicitly below.)
We take account of the tunneling effect as the self-energy correction [23] as follows.
| (3) |
Here,
| (4) |
(. The case of zero voltage is studied in this paper.) is replaced by in . With use of the perturbative expansion by
| (5) |
We use the monochromatic field such as
| (6) |
and the oscillating terms ( with ) will be neglected below:
| (7) |
This approximation holds in the case that the strength of the external field is much smaller than : [24] . From Eqs. (2) and (5) up to the linear response the current is written as follows.
| (8) |
with . The first line of Eq. (8) reduces to the supercurrent .
2.2 The nonequilibrium steady state
In this subsection we derive the one-particle Green functions which are used to calculate the current [Eq. (8)]. These functions are modified by the tunneling effect and the external field. The latter effect makes the system in the nonequilibrium state, and the kinetic equations for quasiclassical Green’s functions are written as follows. [25]
| (9) |
and
| (10) |
with , , and
| (11) |
[The superscript (a) in means the anomalous term in Keldysh Green function.] By omitting the oscillating part as noted above in Eq. (7) and using the perturbative expansion Eq. (5) and
| (12) |
Eqs. (9) and (10) are rewritten as follows.
| (13) |
with
| (14) |
and
| (15) |
with
| (16) |
and
| (17) |
Here, and in the above equations represent the inelastic scattering effect which is needed to dissipate absorbed energies and maintain the nonequilibrium steady state under the external fields, and the expression of this effect will be specified below. There also exist the equations with and interchanged in the above equations.
We introduce the following phase transformation to describe the current-carrying state due to the finite phase difference ();
| (18) |
and multiply the right (left) of Eq. (13) by (its complex conjugate ). This equation is rewritten as
| (19) |
Here, we put
| (20) |
| (21) |
| (22) |
| (23) |
with , , , , and
| (24) |
Then the solutions to Eq. (19) are written as
| (25) |
with . From and , only the sign of component is reversed, and other than that, the same results as the above equations are obtained.
Similarly Eq. (15) is rewritten as
| (26) |
Here, ,
| (27) |
| (28) |
and
| (29) |
[, , and are the components of as in Eq. (24). The -component is omitted because it is confirmed to be small by numerical calculations and its contribution to the damping rate is negligible.] By introducing the quantity
| (30) |
in which the equality of these three quantities follows from the normalization conditions for the quasiclassical Green functions, Eq. (26) is reduced to
| (31) |
here,
| (32) |
and has a meaning of the nonequilibrium correction to the distribution function. is obtained by solving Eq. (31).
2.3 Derivation of the damping rate from the current
From Eq. (8), the rf current term is written as
| (33) |
Using the quasiclassical Green functions in the previous subsection, this current is rewritten as with and being given as follows.
| (34) |
and
| (35) |
We introduce the dimensionless damping rate such as
| (36) |
with
| (37) |
and
| (38) |
We call and the quasiparticle term and the interference term, [3] respectively. The finite values of these two terms are brought about by the thermal excitation of quasiparticles.
3 Results of the Numerical Calculations
3.1 The damping rate in the absence of correction terms
In this subsection we show results of the damping rate in which the corrections by the tunneling effect and the nonequilibrium distribution are not included. In this case quasiclassical Green functions, Eq. (25), are approximated as follows.
| (39) |
here . When these quantities and are used, Eq. (35) results in
| (40) |
with
| (41) |
and
| (42) |
here, means a step function. This result is similar to that obtained previously in Refs. 5 and 26.
We calculate numerically. The superconducting gap at absolute zero is set to be the unit of energy .
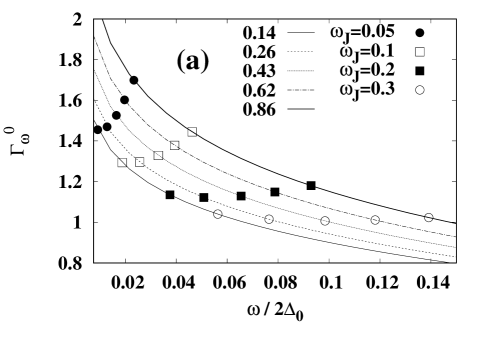

Figure 1 shows the dependence of the damping rate on and . The lines show the dependence of the damping rate on and each curve takes a different value of . The points show the damping rate corresponding to each value of . Since the possible range of values of differs depending on the value of , the dependence of the damping rate on also differs. As the value of becomes smaller, the tendency for the damping rate to increase becomes stronger as a function of because increases with decreasing . This causes the damping rate to have a positive slope as a function of . When the value of is large, takes a wide range of values, so the dependence of the damping rate on becomes small. There is no significant difference between and , but the positive slope as a function of is greater at higher temperatures.
The above dependence of the damping rate on mainly comes from the interference term as shown in Fig. 2.


Figure 2 shows the decomposition of the damping rate into the quasiparticle term () and the interference term (). As is clear from Eq. (41), the quasiparticle term has no explicit dependence on in the absence of correction terms. Then takes values on the same curve for all values of and , and the dependence of the quasiparticle term on simply follows its dependence on . The damping rate due to the quasiparticle term becomes smaller as the value of increases. On the other hand, since the interference term is itself proportional to [Eq. (42)], the dependence of on is determined mainly by the interference term rather than the quasiparticle term. Then the damping rate increases with increasing the value of . At higher temperatures, there are more thermally excited quasiparticles, and the dependence of the damping rate on becomes weaker. The factor of becomes more effective in the damping rate at high , and this leads to the difference between and in Fig. 1.
3.2 The damping rate in the nonequilibrium steady state
In this subsection, we consider the damping rate when a nonequilibrium distribution function is introduced as in Eq. (32) and the one-particle state is modified by a phase-dependent current as in Eq. (25). Since the thermalization is brought about by low-energy excitations, we take account of the interaction between electrons and acoustic phonons as the self-energy due to inelastic scattering introduced in Eqs. (14) and (17). The concrete expressions of and are similar to those of Eqs. (59) and (60) in Ref. 27 except that has -components in this calculation as in Eq. (20).
Numerical calculations below are performed in the same way as in Ref. 27, but there is a difference because of the existence of the phase-dependent term. Using Eq. (34) with , the numerically calculated value of the resonance frequency at shows the same dependence on and as though its absolute value is slightly shifted to the high-frequency side under the influence of the external field as in Ref. 28. The smallness of this shift is related to that in the superconducting gap due to the nonequilibrium correction, which is small as compared to the change in the absorption spectrum at frequencies below the gap edge as shown in Fig. 4 of Ref. 27. We neglect this small shift, and use as the resonance frequency in the calculation of the damping rate below.


Figure 3 shows the damping rate of Josephson plasmons at several values of the resonance frequency in the nonequilibrium steady state. [ is the coupling constant between electrons and acoustic phonons introduced in Eqs. (59) and (60) in Ref. 27. The value of ( is the velocity of sound) in these two equations is set to be in the numerical calculations as in Ref. 27, and this value will not be written explicitly hereafter.] Unlike the case without these corrections in Fig. 1, the dependence of the damping rate on differs depending on the value of because the nonequilibrium correction varies depending on the resonance frequency. The graphs of in the case of are shown in Fig. 3, but unlike Fig. 1, the dependence on differs depending on the values of due to the nonequilibrium correction. (To avoid complexity, only the case of is shown.) It can be seen that the damping rate becomes smaller with increasing , and the sign of the slope of is negative as a function of in contrast to the case of in Fig. 1. This is because, as shown below, for the larger values of the nonequilibrium correction becomes larger, which results in a decrease in the damping rate. This result of the dependence on is different from previous theories [5, 6] on the damping rate, and agrees with experimental results. [7, 8, 9] The results for and are similar except for the magnitude of the values, but there are differences in the damping rate as a function of , especially for small values of . At the dependence of on is smaller than that of . This is related to the result that the sign of the slope of as a function of changes from negative to positive as the temperature rises, which will be shown later. This also agrees with the experimental results that the sign of the slope changes near .
The effect of the nonequilibrium distribution on the damping rate can be seen by considering the following quantities:
| (43) |
The factor in Eq. (35) is equal to with .


Figure 4(a) shows the effect of the nonequilibrium correction on the thermal distribution . For both and , the effect of becomes larger with increasing . Furthermore, the sign of changes near the energy gap and becomes negative around energies at which the density of states is large. Therefore, has the effect of lowering the effective temperature. Since the reduction in the effective temperature is greater at the resonance frequencies with smaller phase differences, the sign of the slope of the damping rate is negative as a function of as shown in Fig. 3. This dependence of the nonequilibrium correction on is due to the broadening of the density of states in the current-carrying state.
Figure 4(b) shows the effect of the phase-dependent current on the density of states. For both and , the peak of the density of states becomes broad with decreasing , which is similar to the results in Ref. 29. This is because, as in the superconductors including paramagnetic impurities, [30, 31] the effect of time-reversal symmetry breaking due to the phase-dependent current on the density of states becomes more pronounced for the smaller values of . However, as shown below, this variation of the density of states itself does not make a qualitative difference in the dependence of the damping rate on as compared to the case without corrections.


Figure 5 shows the damping rate at several values of the resonance frequency in the absence of the nonequilibrium correction: . Here, and are those of Eqs. (37) and (38) in which is set to be 0. Unlike the results in Fig. 3, the dependence of on is hardly affected by the value of and shows almost the same curve when the value of is the same (the case of is shown for comparison). This is almost the same as in the calculation with the bare Green functions in Fig. 1. This shows that the negative slope of the damping rate as a function of in Fig. 3 is caused not by the current-induced change in the density of states in Fig. 4(b), but by the change in the nonequilibrium distribution in Fig. 4(a). By comparing the results between and , it can be seen that there is a difference in the slope of the damping rate which is similar to that in the case of Fig. 1. The dependence of the damping rate on arises from the interference term. This can be seen by decomposing into the quasiparticle term and the interference term.


Figure 6 shows the decomposition of the damping rate into the quasiparticle term () and the interference term () in the case of . The results are almost the same as those in Fig. 2, and the quasiparticle term takes values on almost the same curve regardless of the values of and . (The reduction of the quasiparticle term at small resonance frequencies is due to the broadening of the density of states.) The interference terms take values on different curves depending on the values of , but its dependence on hardly changes depending on the values of . This shows that, as mentioned above, the dependence of the damping rate on does not qualitatively change in the presence of the phase-dependent current without the nonequilibrium corrections. There are studies in which the sign of the interference term becomes negative when a phenomenological parameter that smooths out the Riedel peak is introduced, [14, 32] but this calculation showed that the sign of the interference term remains positive in the current-carrying state.
When the nonequilibrium correction is taken into account, the above behaviors of the quasiparticle and the interference terms change qualitatively.


Figure 7 shows the decomposition of the damping rate in Fig. 3 into the quasiparticle term and the interference term [Eqs. (37) and (38), respectively]. Compared to the results in Figs. 2 and 6, the quasiparticle term has a greater dependence on , and the damping rate is suppressed with increasing due to the effective temperature lowering by the nonequilibrium correction. In the same way this correction suppresses also the interference term as a function of as compared to the results in Figs. 2 and 6. These behaviors bring about a negative slope in the damping rate as a function of as shown in Fig. 3.
In Fig. 3, as a function of , the negative slope at is less steep than that at . This is attributed to the large inelastic scattering effect at high temperatures, which results in relatively small nonequilibrium correction at high due to the strong thermalization as shown in Fig. 4(a). In Fig. 8, this effect of the inelastic scattering is shown in a different way by changing the values of the coupling constant () between electrons and acoustic phonons.

Figure 8 shows the dependence of the damping rate on for different values of and . The sign of the slope of the damping rate as a function of changes from negative to positive as temperature increases for a fixed . This change in sign occurs similarly when increasing at a fixed temperature. This shows that the inelastic scattering induces a change in the sign of the slope at high temperatures.
4 Summary and Discussion
In this paper, we calculated the dependence of the damping rate on the phase difference at the resonance frequency. We considered that the electronic state is in a nonequilibrium steady state due to an external field with this resonance frequency. In this state, the nonequilibrium distribution function is dependent on the phase difference, and then the damping rate changes depending on this difference. When the phase difference is large, the time-reversal symmetry breaking causes a broadening of the one-particle density of states as in the presence of paramagnetic impurities. As compared to the case where the phase difference is small and the density of states has a sharp peak, this broadening has effects of strengthening the thermalization and reducing the nonequilibrium correction. Therefore, when the phase difference is small, the reduction of the effective temperature is larger than that in the case of a large phase difference. This difference in the effective temperature depending on the phase difference causes the dependence of the damping rate due to thermally excited quasiparticles on the phase difference.
As a result, the damping rate becomes smaller with decreasing phase difference (increasing ). On the other hand, the interference term has originally an explicit dependence on the phase difference, which causes an increase in the damping rate as the phase difference becomes smaller. Therefore, the actual dependence of the damping rate on the phase difference is determined by the competition between the nonequilibrium correction and the phase difference term in the interference term. The calculations in this paper showed that the former can be predominant over the latter and the damping rate becomes smaller with decreasing the phase difference. This is consistent with experimental results showing that the damping rate has a negative slope as a function of . As the temperature rises, the effect of the inelastic scattering by acoustic phonons increases, and the nonequilibrium correction becomes smaller due to the strong thermalization. Therefore, at high temperatures, the interference term becomes predominant in the damping rate, and it is possible that the damping rate increases with decreasing phase difference. This means that the sign of the slope of the damping rate as a function of can change at high temperatures. This behavior qualitatively agrees with the experimental results.
Other previous studies have assumed that the dependence of the damping rate on the phase difference arises only from the interference term, and have discussed the sign of this term. [14, 15] Since these studies considered the zero frequency limit, the dependence of the quasiparticle term on the frequency was not taken into account. In experiments, the frequency is finite, and is about . [7] In our study, it was shown that even at a value of , the dependence of the damping rate on the frequency exists due to the nonequilibrium correction in the quasiparticle term.
Considering the comparison with the experiment, in our calculation and at and , respectively, by using an experimental value . [7] This is almost consistent with the experimental value at . Though it is difficult to control the effect of inelastic scattering experimentally, the magnitude of electron–phonon scattering varies depending on materials. [33] Therefore, it is possible to verify this theory by examining the temperatures at which the dependence of the damping rate on the phase difference changes for various materials.
Acknowledgment
The numerical computation in this work was carried out at the Yukawa Institute Computer Facility.
References
- [1] B. D. Josephson, Phys. Lett. 1, 251 (1962).
- [2] B. D. Josephson, Adv. Phys. 14, 419 (1965).
- [3] D. N. Langenberg, Rev. Phys. Appl. 9, 35 (1974).
- [4] A. Barone and G. Paternò, Physics and Applications of the Josephson Effect (Wiley, New York, 1982). Chap. 2, Sect. 6.
- [5] R. E. Harris, Phys. Rev. B 10, 84 (1974).
- [6] U. K. Poulsen, Rev. Phys. Appl. 9, 41 (1974).
- [7] N. F. Pedersen, T. F. Finnegan, and D. N. Langenberg, Phys. Rev. B 6, 4151 (1972).
- [8] O. H. Soerensen, J. Mygind, and N. F. Pedersen, Phys. Rev. Lett. 39, 1018 (1977).
- [9] S. Rudner and T. Claeson, J. Appl. Phys. 50, 7070 (1979).
- [10] G. Catelani, J. Koch, L. Frunzio, R. J. Schoelkopf, M. H. Devoret, and L. I. Glazman Phys. Rev. Lett. 106, 077002 (2011).
- [11] J. Leppäkangas, M. Marthaler, and G. Schön, Phys. Rev. B 84, 060505(R) (2011).
- [12] I. M. Pop, K. Geerlings, G. Catelani, R. J. Schoelkopf, L. I. Glazman, and M. H. Devoret, Nature 508, 369 (2014).
- [13] K. Hida and Y. Ono, J. Low Temp. Phys. 29, 355 (1977).
- [14] A. B. Zorin, I. O. Kulik, K. K. Likharev, and J. R. Schrieffer, Sov. J. Low Temp. Phys. 5, 537 (1979).
- [15] A. M. Gulyan and G. F. Zharkov, Sov. Phys. JETP, 62, 89 (1985).
- [16] A. Levy Yeyati, A. Martín-Rodero, and J. C. Cuevas, J. Phys. Condens. Matter 8, 449 (1996).
- [17] G. M. Éliashberg, JETP Lett. 11, 114 (1970).
- [18] A. J. Dahm, A. Denenstein, T. F. Finnegan, D. N. Langenberg, and D. J. Scalapino, Phys. Rev. Lett. 20, 859 (1968).
- [19] D. Pines and P. Nozières, The Theory of Quantum Liquids (W.A. Benjamin, New York, 1966). Chap. 4, Sect. 7.
- [20] P. W. Anderson, in Lectures on the Many-Body Problem, ed. by E. R. Caianiello (Academic Press, New York, 1964), Vol. 2.
- [21] V. Ambegaokar and A. Baratoff, Phys. Rev. Lett. 10, 486 (1963).
- [22] J. Voutilainen, T. T. Heikkilä, and N. B. Kopnin, Phys. Rev. B 72, 054505 (2005).
- [23] A. F. Volkov, Sov. Phys. JETP, 41, 376 (1974)
- [24] A. V. Semenov, I. A. Devyatov, P. J. de Visser, and T. M. Klapwijk, Phys. Rev. Lett. 117, 047002 (2016).
- [25] G. M. Éliashberg, Sov. Phys. JETP 34, 668 (1972).
- [26] A. I. Larkin and Yu. N. Ovchinnikov, Sov. Phys. JETP 24, 1035 (1967).
- [27] T. Jujo, J. Phys. Soc. Jpn. 92, 074706 (2023).
- [28] P. J. de Visser, D. J. Goldie, P. Diener, S. Withington, J. J. A. Baselmans, and T. M. Klapwijk, Phys. Rev. Lett. 112, 047004 (2014).
- [29] E. V. Bezuglyi, A. S. Vasenko, V. S. Shumeiko, and G. Wendin, Phys. Rev. B 72, 014501 (2005).
- [30] A. A. Abrikosov and L. P. Gor’kov, Sov. Phys. JETP 12, 1243 (1961).
- [31] S. Skalski, O. Betbeder-Matibet, and P. R. Weiss, Phys. Rev. 136, A1500 (1964).
- [32] F. Sheldon, S. Peotta, and M. Di Ventra, Eur. Phys. J. Appl. Phys. 81, 10601 (2018).
- [33] S. B. Kaplan, C. C. Chi, D. N. Langenberg, J. J. Chang, S. Jafarey, and D. J. Scalapino, Phys. Rev. B 14, 4854 (1976).