Phase control of magnons in the van der Waals antiferromagnet NiPS3
Abstract
We demonstrate phase control of magnons in the van der Waals antiferromagnet NiPS3 using optical excitation by polarized light. The sign of the coherent precession of spin amplitude changes upon (1) reversing the helicity of a circularly polarized pump beam, or (2) rotating the polarization of a linearly polarized pump by . Because these two excitation pathways have comparable generation efficiency, the phase of spin precession can be continuously tuned from 0 to by controlling the polarization state of the pump pulse. The ability to excite magnons with a desired phase has potential applications in the design of a spin-wave phased array and ultrafast spin information processing.
Coherent optical excitation of low energy collective modes is an important tool for both fundamental research and integration of materials into information technologies. One of the most prominent examples are magnons, the collective excitations of magnetic order [1, 2]. Magnons in insulators can propagate over macroscopic distances without Joule heating, making them promising for energy-efficient computing [3]. While recent years have seen rapid advances in all-electrical control of incoherent magnons [3, 4, 5, 6], these methods forego the potential of coherence. The phase information carried by coherent magnons provides an opportunity to design wave-based logic circuits that allow for non-Boolean computing, with the potential to operate faster and more efficiently than traditional Boolean logic circuits [7, 8, 9, 10]. In another application, tuning the relative phase of an array of spin wave emitters allows control over the direction of wavefront propagation. This enables the creation of a ”spin-wave phased-array antenna” which is desirable for spin based information processing [11, 12].
While phase control of microwave-excited spin waves has been achieved through varying applied magnetic field [7] or microwave amplitude [13], such techniques are limited to ferromagnetic resonances within the gigahertz frequency range. Aiming at higher operation speeds, the focus of magnonics research is shifting from ferromagnetic materials towards antiferromagnets, which have the potential for terahertz bandwidth applications [14, 15, 16]. Two-dimensional (2D) van der Waals (vdW) antiferromagnets have attracted attention as they may serve as atomically-thin magnonic devices [17, 18, 19, 20, 21, 22, 23]. Among them, the transition metal thiophosphates PS3 (: Mn, Fe, Ni) are of particular interest because of their ultrafast spin dynamics [24, 25, 26]. While FePS3 and MnPS3 show easy-axis type antiferromagnetism [27, 28, 29, 30], NiPS3 is a -type easy-plane antiferromagnet [31, 32, 33], offering promise as a platform to explore 2D magnetic phenomena such as the Berezinski-Kosterlitz-Thouless transition and long-distance spin transport via spin superfluidity [34, 35].
Optical pump-probe methods are powerful tools to excite and detect picosecond time-scale spin dynamics, and a number of antiferromagnetic resonances have been detected using these techniques [36, 37, 38, 39, 40, 41, 25, 24, 42]. Despite this intense study, reports of phase control of optically-excited spin waves are limited to ferromagnets, and in these reports only partial shifts in phase have been achieved [11, 43]. Realizing full phase control from to of light-induced antiferromagnetic magnons has remained a challenge.
In this Letter, we demonstrate full phase control of coherent magnon excitations in the vdW antiferromagnet NiPS3, achieved by varying the helicity of the pump photons. The unique feature of NiPS3 that enables optical control of spin wave phase is the coexistence of two excitation mechanisms with comparable efficiency: one arising from linearly polarized (LP) light and the other from circular polarized (CP) light. In both cases the generation mechanism is fully coherent; the sign of the spin wave amplitude flips upon reversing circular polarization from left to right and rotating the linear polarization by . This indicates that the excitation of magnons takes place through a non-thermal process, with the potential to control of spin-wave phase via the light-matter interaction.
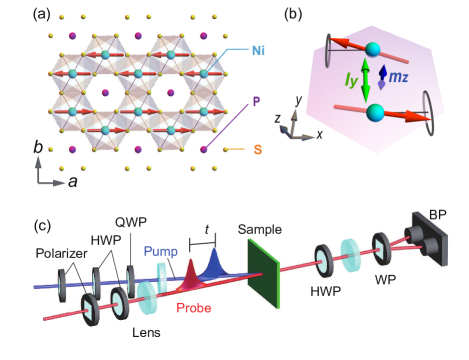
NiPS3 crystallizes in a monoclinic structure with the space group . The local magnetic moments are carried by the Ni2+ ions with [44, 45, 46]. Trigonally distorted NiS6 octahedra form an edge-sharing layered honeycomb lattice in the plane, see Fig. 1(a). The trigonal axis is perpendicular to the plane [47]. Below the Néel temperature = 155 K, Ni2+ coplanar spins form ferromagnetic zig-zag chains along the axis that are antiferromagnetically coupled along the axis (Fig. 1(a)). The easy plane is slightly tilted from basal plane [32, 31, 32, 33]. In the following, we use Cartesian coordinates , , and , where L denotes a Néel vector.
The spin wave dynamics of such a biaxial antiferromagnet, in which spins are strongly confined to a plane and weakly oriented within that plane, is characterized by two magnon modes [48]. In the lower frequency mode the Néel vector traces an ellipse with major axis in the magnetic easy plane (Fig. 1(b)) while the higher frequency mode the major axis is perpendicular to the easy plane. A previous pump-probe study of NiPS3 showed that the lower frequency in-plane mode can be excited by a linearly polarized pump with a wavelength tuned to be resonant with a - transition of Ni2+ [24].
We studied the dynamics of the in-plane mode of NiPS3 as function of photon polarization using the setup shown schematically in Fig. 1(c). The tunable light source is an optical parametric amplifier (OPA) pumped by a regeneratively amplified laser, producing 100 fs pulses at 5 kHz repetition rate. The OPA output, which was used as the pump, was tuned to 1240 nm to coincide with the transition from the ground state to the excited state of Ni2+ ions. The probe wavelength was 800 nm. The polarization rotation of the transmitted probe light was detected using a Wollaston prism and balanced photodetector.
Single crystals of NiPS3 were grown by a chemical vapor transport method [49]. Stoichiometric amounts of Ni, P, and S were mixed and the resulting powder mixture was loaded in a quartz tube. The ampoule was heated at 800∘ (heating zone) and 700∘ (growth zone) for a week. The obtained crystals were characterized by powder x-ray diffraction and Superconducting Quantum Interference Device (SQUID) magnetometry, and then mechanically exfoliated on a copper substrate with a hole of diameter 500 m. The thickness of the sample was 10 m. The sample was mounted in a He closed-cycled refrigerator.
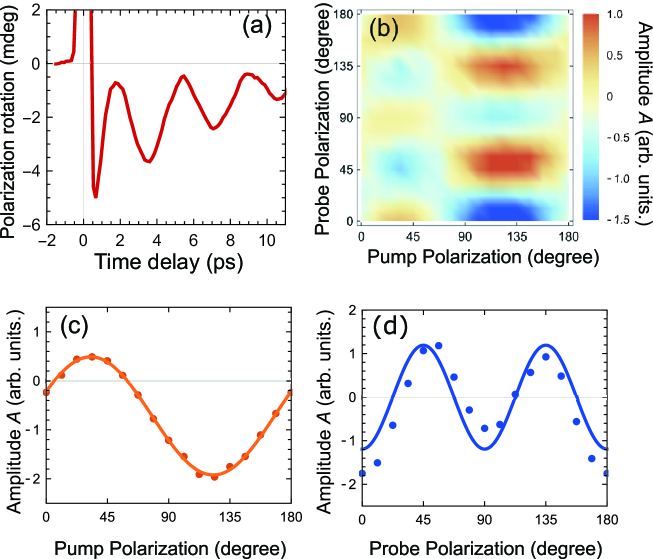
We first measured the properties of magnon generation and detection with linearly polarized light. Fig. 2(a) shows an example of photogenerated spin precession in NiPS3 which can be fit to,
| (1) |
where , , and are an amplitude, frequency, decay time, and initial phase of the oscillations, respectively. is a second-order polynomial that describes the smooth background on which the oscillations are superposed. An overview the dependence of the spin precession amplitude on pump and probe polarization is shown as a color map a function of polarization of the pump and probe beams is shown as a color map in Fig. 2(b). First, we note that the dependence on polarization demonstrates that the both the excitation and detection mechanisms is coherent, that is, magnons are generated and detected via a non-thermal light-matter interaction. Vertical and horizontal cuts through this plane clarify the dependence of on polarization direction. The horizontal cut plotted in Fig. 2(c) shows that at fixed probe angle, in this case . Finally, the vertical cut at fixed pump polarization shows that in this case . [50, 24]. Below we discuss how the dependence on the polarization of the pump and probe arise in an antiferromagnet with the symmetry of NiPS3.
In the phenomenological model of the light-matter interaction the energy of the magneto-optical interaction is given by, [50, 51, 41, 52],
| (2) |
where is the amplitude of the electric field of light. For light propagating in the direction we consider the and components, which have the form and , respectively. Here is the azimuthal angle of rotation about the axis and is the relative phase of the and components of the electric field. LP corresponds to , while CP corresponds to , . The time-dependent function takes different forms depending on the type of excitation. For the displacive-type excitation [53, 54], it is proportional to the Heaviside step function, while for the impulsive magnon excitation [50, 41], it is proportional to Dirac delta function. The susceptibility tensor is given by [50], where the lowercase and are the light-induced changes in the Nel vector and magnetization, respectively and the denote the components of the equilibrium Néel vector. When absorption is negligible, the Onsager reciprocity relation gives . Here we assume that this relation holds, because the pump and probe photon energies are below the parity-allowed charge transfer transition, leaving only the parity-forbidden weak transition. Consequently, the third rank axial tensor and fourth rank polar tensor are purely real and satisfy and . The tensor components that are relevant to the in-plane mode are and , as the other components are either associated with the out-of-plane mode or vanish in the 2/m point group (see the Supplementary Information). The magneto-optical interaction energy of the lower frequency magnon mode can therefore be written as
| (3) |
where is proportional to the intensity of the pump light ( and are sketched in Fig. 1(b). Eq. (3) shows that the dependence on pump polarization shown in Fig. 2 follows directly from the symmetry of NiPS3. Note that in addition to coupling via linearly polarized light () to fluctuations in , coupling via circularly polarized light () to is allowed.
The detection of spin precession by the probe occurs via the inverse of the couplings described above and can arise from oscillations of and/or . Fluctuations in give rise to magnetic linear birefringence, which has been shown [50] to manifest as the dependence on probe polarization that we observe (see Fig. 2(d)). Fluctuations in give rise to Faraday rotation which is independent of . Hence, the detection of the in-plane magnon at the probe wavelength used in our measurements occurs via the magnetic linear birefringence associated with rather than the Faraday rotation mediated by .
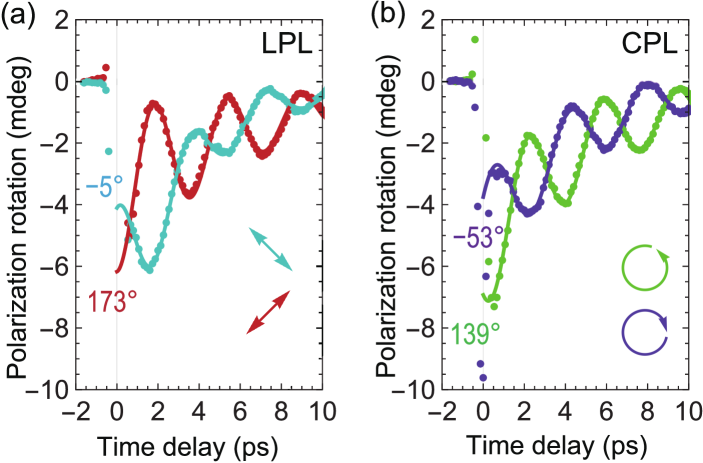
Although the probe couples only , the pump pulse can generate oscillations of both and , via coupling to linearly and circularly polarization, respectively. The key to phase control of spin precession in NiPS3 is that both the LP and CP modes of magnon generation are not only nonzero, but comparable in magnitude. This is illustrated in Figs. 3(a) and 3(b), which show time-resolved probe polarization rotation for LP, and CP pump pulses, respectively, plotted on the same time and amplitude scales. The comparable magnitude of precession generated by LP and CP pump photons is notable, as in other systems the relative efficiency of magnon excitation varies by orders of magnitude [41, 51]. The spin precession frequency is THz for LP and THz for CP, showing that the same spin wave mode is excited in both cases. Moreover, this frequency is consistent with the low-energy in-plane magnon mode found in the previous optical pump-probe [24] and electron spin resonance studies [55]. As illustrated in the Fig. 3(a) inset, the two responses to LP excitation shown are obtained by rotating the pump polarization by ; the resulting change in phase arises from the term in the light-matter interaction . Fig. 3(b) shows that the phase of the spin precession also changes by for CP pumping upon reversing the helicity, arising in this case from the factor in .
In addition to the sign reversal on changing polarization, Fig. 3 also displays the initial phase, for each of the curves. As we discuss below, the initial phase reflects the nature of the magnon generation mechanism [52, 41, 51]). The free energy of the easy-plane type antiferromagnet can be written as [24]
| (4) |
where and are the effective exchange field and anisotropy field, respectively. Dynamics described by Landau-Lifshitz equations,
| (5) |
| (6) |
where and . Linearizing the equations leads to the following differential equations for the in-plane magnon mode,
| (7) |
| (8) |
where and . Eqs. (7) and (8) describe spin oscillation at frequency with normal coordinate . The phase of the oscillation after the pulsed excitation is determined by the torque functions, . To illustrate the dynamics after pulsed excitation at , we consider the case of LP pump, where . For the impulsive generation mechanism with being the laser pulse duration, integrating the equations of motion gives, , whereas the displacive mechanism yields . Hence, LP pump induces () time dependence of for the impulsive (displacive) mechanism. In the case of excitation with CP light (), Eqs. (7) and (8) predict and for impulsive and displacive excitation, respectively.
Our experimental results show cosine-like time dependence for the LP pump (Fig. 3(a)) while the CP pump induces a superposition of sine and cosine dependence (Fig. 3(b)) of . This indicates that the displacive-type excitation plays a dominant role for the LP pump, while both impulsive- and displacive-type excitation processes contribute to the generation of the in-plane magnon mode for CP pumping. Coexistence of impulsive and displacive excitation mechanisms have been observed previously in both coherent phonon excitation [56] and coherent magnon excitation [11].
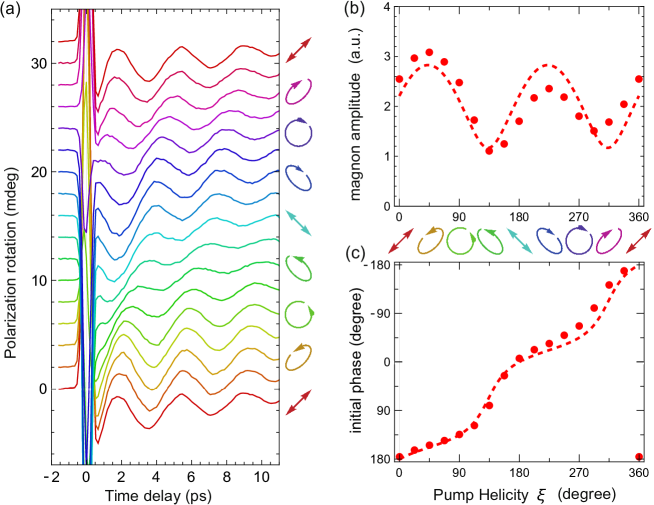
With this understanding of the magnon generation and detection mechanisms, we turn to the demonstration of phase control shown in Fig. 4. The polarization of the pump beam is tuned continuously between LP and CP by transmission through a half-wave plate (HWP) and quarter-wave plate (QWP), as shown in Fig. 1(c). Varying the angle of the HWP, with the QWP fixed, continuously tunes the helicity without changing the azimuthal angle . Figure 4(a) shows time traces of the spin precession, for several at . As the pump helicity is tuned, the phase of the oscillation shifts monotonically. Figures 4(b) and (c) display the phase and amplitude of the spin wave oscillation, obtained by fitting the traces to Eq.(1), as function of pump helicity. Fig. 4(b) demonstrates continuous tuning of the phase of the coherent magnon excitation from 0 to 2.
The dashed lines through the data points are obtained by summing the contributions from the CP and LP components of the elliptical pump pulses. The probe polarization rotation can be described by
| (9) |
where () and () denote the amplitude and initial phase for the case of the LP (CP) pump, respectively. The parameters and are obtained from measurements with pure LP and CP pump. Eq. 9 yields a resultant helicity dependent magnon oscillation, where,
| (10) |
and
| (11) |
In principle, all magnetic systems in which magnons can be generated by both CP and LP light can manifest the phase control phenomenon described above. Indeed, both CP and LP excitation has been reported in other easy-plane type antiferromagnets, such as in FeBO3 [41] and NiO [51]. However, magnon phase control was not demonstrated, likely due to the fact that the magnon excitation by LP light is approximately two orders of magnitude more efficient than excitation by CP light [41, 51].
To conclude, we performed time-resolved pump-probe measurements of the in-plane magnon mode in the antiferromagnet NiPS3. The amplitude of spin precession was comparable for LP and CP pump processes, yet their initial phase is different. By tuning the pump helicity, the phase of the spin oscillation shifts from 0 to 2 with little change in amplitude, thus establishing a reliable scheme for magnon phase control in the ultrafast regime. This technique paves the way for the construction of magnon-based devices such as spin-wave logic circuits [7, 8] and phased array [11, 12]. Moreover, excitation of antiferromagnetic magnons can generate terahertz electromagnetic radiation [25], and thus control the magnon phase may be useful for example as terahertz phased array antennas.
We acknowledge support from the Quantum Materials program under the Director, Office of Science, Office of Basic Energy Sciences, Materials Sciences and Engineering Division, of the U.S. Department of Energy, Contract No. DE-AC02-05CH11231. J.O received support from the Gordon and Betty Moore Foundation’s EPiQS Initiative through Grant GBMF4537 at UC Berkeley. S.T. is supported by JSPS Overseas Research Fellowships.
References
- Kruglyak et al. [2010] V. Kruglyak, S. Demokritov, and D. Grundler, Journal of Physics D: Applied Physics 43, 264001 (2010).
- Barman et al. [2021] A. Barman, G. Gubbiotti, S. Ladak, A. O. Adeyeye, M. Krawczyk, J. Gräfe, C. Adelmann, S. Cotofana, A. Naeemi, V. I. Vasyuchka, et al., Journal of Physics: Condensed Matter 33, 413001 (2021).
- Kajiwara et al. [2010] Y. Kajiwara, K. Harii, S. Takahashi, J.-i. Ohe, K. Uchida, M. Mizuguchi, H. Umezawa, H. Kawai, K. Ando, K. Takanashi, et al., Nature 464, 262 (2010).
- Cornelissen et al. [2015] L. J. Cornelissen, J. Liu, R. A. Duine, J. B. Youssef, and B. J. van Wees, Nature Physics 11, 1022 (2015).
- Lebrun et al. [2018] R. Lebrun, A. Ross, S. A. Bender, A. Qaiumzadeh, L. Baldrati, J. Cramer, A. Brataas, R. A. Duine, and M. Kläui, Nature 561, 222 (2018).
- Lebrun et al. [2020] R. Lebrun, A. Ross, O. Gomonay, V. Baltz, U. Ebels, A. L. Barra, A. Qaiumzadeh, A. Brataas, J. Sinova, and M. Kläui, Nature Communications 11, 6332 (2020).
- Schneider et al. [2008] T. Schneider, A. A. Serga, B. Leven, B. Hillebrands, R. L. Stamps, and M. P. Kostylev, Applied Physics Letters 92, 022505 (2008).
- Kostylev et al. [2005] M. Kostylev, A. Serga, T. Schneider, B. Leven, and B. Hillebrands, Applied Physics Letters 87, 153501 (2005).
- Chumak et al. [2015] A. V. Chumak, V. I. Vasyuchka, A. A. Serga, and B. Hillebrands, Nature physics 11, 453 (2015).
- Csaba et al. [2014] G. Csaba, A. Papp, and W. Porod, Journal of Applied Physics 115, 17C741 (2014).
- Yoshimine et al. [2014] I. Yoshimine, T. Satoh, R. Iida, A. Stupakiewicz, A. Maziewski, and T. Shimura, Journal of applied physics 116, 043907 (2014).
- Song et al. [2019] M. Song, K.-W. Moon, C. Hwang, and K.-J. Kim, Physical Review Applied 11, 024027 (2019).
- Ustinov et al. [2013] A. B. Ustinov, B. A. Kalinikos, and E. Lähderanta, Journal of Applied Physics 113, 113904 (2013).
- Jungwirth et al. [2016] T. Jungwirth, X. Marti, P. Wadley, and J. Wunderlich, Nature nanotechnology 11, 231 (2016).
- Baltz et al. [2018] V. Baltz, A. Manchon, M. Tsoi, T. Moriyama, T. Ono, and Y. Tserkovnyak, Reviews of Modern Physics 90, 015005 (2018).
- Němec et al. [2018] P. Němec, M. Fiebig, T. Kampfrath, and A. V. Kimel, Nature Physics 14, 229 (2018).
- Huang et al. [2017] B. Huang, G. Clark, E. Navarro-Moratalla, D. R. Klein, R. Cheng, K. L. Seyler, D. Zhong, E. Schmidgall, M. A. McGuire, D. H. Cobden, et al., Nature 546, 270 (2017).
- Gong et al. [2017] C. Gong, L. Li, Z. Li, H. Ji, A. Stern, Y. Xia, T. Cao, W. Bao, C. Wang, Y. Wang, et al., Nature 546, 265 (2017).
- Fei et al. [2018] Z. Fei, B. Huang, P. Malinowski, W. Wang, T. Song, J. Sanchez, W. Yao, D. Xiao, X. Zhu, A. F. May, et al., Nature materials 17, 778 (2018).
- Cai et al. [2019] X. Cai, T. Song, N. P. Wilson, G. Clark, M. He, X. Zhang, T. Taniguchi, K. Watanabe, W. Yao, D. Xiao, et al., Nano letters 19, 3993 (2019).
- Long et al. [2020] G. Long, H. Henck, M. Gibertini, D. Dumcenco, Z. Wang, T. Taniguchi, K. Watanabe, E. Giannini, and A. F. Morpurgo, Nano letters 20, 2452 (2020).
- Khan et al. [2020] Y. Khan, S. M. Obaidulla, M. R. Habib, A. Gayen, T. Liang, X. Wang, and M. Xu, Nano Today 34, 100902 (2020).
- Wang et al. [2020] M.-C. Wang, C.-C. Huang, C.-H. Cheung, C.-Y. Chen, S. G. Tan, T.-W. Huang, Y. Zhao, Y. Zhao, G. Wu, Y.-P. Feng, et al., Annalen der Physik 532, 1900452 (2020).
- Afanasiev et al. [2021] D. Afanasiev, J. R. Hortensius, M. Matthiesen, S. Mañas-Valero, M. Šiškins, M. Lee, E. Lesne, H. S. van Der Zant, P. G. Steeneken, B. A. Ivanov, et al., Science advances 7, eabf3096 (2021).
- Belvin et al. [2021] C. A. Belvin, E. Baldini, I. O. Ozel, D. Mao, H. C. Po, C. J. Allington, S. Son, B. H. Kim, J. Kim, I. Hwang, et al., Nature communications 12, 4837 (2021).
- Mertens et al. [2022] F. Mertens, D. Mönkebüscher, U. Parlak, C. Boix-Constant, S. Mañas-Valero, M. Matzer, R. Adhikari, A. Bonanni, E. Coronado, A. M. Kalashnikova, et al., Advanced Materials , 2208355 (2022).
- Lançon et al. [2016] D. Lançon, H. Walker, E. Ressouche, B. Ouladdiaf, K. Rule, G. McIntyre, T. Hicks, H. M. Rønnow, and A. Wildes, Physical Review B 94, 214407 (2016).
- Chandrasekharan and Vasudevan [1994] N. Chandrasekharan and S. Vasudevan, Pramana 43, 21 (1994).
- Kurosawa et al. [1983] K. Kurosawa, S. Saito, and Y. Yamaguchi, Journal of the Physical Society of Japan 52, 3919 (1983).
- Ressouche et al. [2010] E. Ressouche, M. Loire, V. Simonet, R. Ballou, A. Stunault, and A. Wildes, Physical Review B 82, 100408 (2010).
- Joy and Vasudevan [1992] P. Joy and S. Vasudevan, Physical Review B 46, 5425 (1992).
- Wildes et al. [2015] A. R. Wildes, V. Simonet, E. Ressouche, G. J. Mcintyre, M. Avdeev, E. Suard, S. A. Kimber, D. Lançon, G. Pepe, B. Moubaraki, et al., Physical Review B 92, 224408 (2015).
- Kim et al. [2019] K. Kim, S. Y. Lim, J.-U. Lee, S. Lee, T. Y. Kim, K. Park, G. S. Jeon, C.-H. Park, J.-G. Park, and H. Cheong, Nature Communications 10, 1 (2019).
- Seifert et al. [2022] U. F. Seifert, M. Ye, and L. Balents, Physical Review B 105, 155138 (2022).
- Takei et al. [2014] S. Takei, B. I. Halperin, A. Yacoby, and Y. Tserkovnyak, Physical Review B 90, 094408 (2014).
- Satoh et al. [2010] T. Satoh, S.-J. Cho, R. Iida, T. Shimura, K. Kuroda, H. Ueda, Y. Ueda, B. Ivanov, F. Nori, and M. Fiebig, Physical review letters 105, 077402 (2010).
- Bossini et al. [2016] D. Bossini, S. Dal Conte, Y. Hashimoto, A. Secchi, R. V. Pisarev, T. Rasing, G. Cerullo, and A. V. Kimel, Nature communications 7, 1 (2016).
- Satoh et al. [2015] T. Satoh, R. Iida, T. Higuchi, M. Fiebig, and T. Shimura, Nature Photonics 9, 25 (2015).
- Baierl et al. [2016] S. Baierl, M. Hohenleutner, T. Kampfrath, A. Zvezdin, A. V. Kimel, R. Huber, and R. Mikhaylovskiy, Nature Photonics 10, 715 (2016).
- Kalashnikova et al. [2007] A. Kalashnikova, A. Kimel, R. Pisarev, V. Gridnev, A. Kirilyuk, and T. Rasing, Physical review letters 99, 167205 (2007).
- Kalashnikova et al. [2008] A. Kalashnikova, A. Kimel, R. Pisarev, V. Gridnev, P. Usachev, A. Kirilyuk, and T. Rasing, Physical Review B 78, 104301 (2008).
- Zhang et al. [2020] X.-X. Zhang, L. Li, D. Weber, J. Goldberger, K. F. Mak, and J. Shan, Nature Materials 19, 838 (2020).
- Chernov et al. [2018] A. I. Chernov, M. A. Kozhaev, A. Khramova, A. N. Shaposhnikov, A. R. Prokopov, V. N. Berzhansky, A. K. Zvezdin, and V. I. Belotelov, Photonics Research 6, 1079 (2018).
- Bernasconi et al. [1988] M. Bernasconi, G. Marra, G. Benedek, L. Miglio, M. Jouanne, C. Julien, M. Scagliotti, and M. Balkanski, Physical Review B 38, 12089 (1988).
- Brec [1986] R. Brec, in Intercalation in Layered Materials (Springer, 1986) pp. 93–124.
- Ouvrard et al. [1985] G. Ouvrard, R. Brec, and J. Rouxel, Materials research bulletin 20, 1181 (1985).
- Wildes et al. [2022] A. Wildes, J. Stewart, M. Le, R. Ewings, K. Rule, G. Deng, and K. Anand, Physical Review B 106, 174422 (2022).
- Rezende et al. [2019] S. M. Rezende, A. Azevedo, and R. L. Rodríguez-Suárez, Journal of Applied Physics, Journal of Applied Physics 126, 151101 (2019).
- Ho et al. [2021] C.-H. Ho, T.-Y. Hsu, and L. C. Muhimmah, npj 2D Materials and Applications 5, 8 (2021).
- Satoh et al. [2017] T. Satoh, R. Iida, T. Higuchi, Y. Fujii, A. Koreeda, H. Ueda, T. Shimura, K. Kuroda, V. Butrim, and B. Ivanov, Nature communications 8, 638 (2017).
- Tzschaschel et al. [2017] C. Tzschaschel, K. Otani, R. Iida, T. Shimura, H. Ueda, S. Günther, M. Fiebig, and T. Satoh, Physical Review B 95, 174407 (2017).
- Gridnev [2008] V. Gridnev, Physical Review B 77, 094426 (2008).
- Hansteen et al. [2006] F. Hansteen, A. Kimel, A. Kirilyuk, and T. Rasing, Physical Review B 73, 014421 (2006).
- Atoneche et al. [2010] F. Atoneche, A. Kalashnikova, A. Kimel, A. Stupakiewicz, A. Maziewski, A. Kirilyuk, and T. Rasing, Physical Review B 81, 214440 (2010).
- Mehlawat et al. [2022] K. Mehlawat, A. Alfonsov, S. Selter, Y. Shemerliuk, S. Aswartham, B. Büchner, and V. Kataev, Physical Review B 105, 214427 (2022).
- Garrett et al. [1996] G. A. Garrett, T. Albrecht, J. Whitaker, and R. Merlin, Physical Review Letters 77, 3661 (1996).