Perturbation-Restrained Sequential Model Editing

Jun-Yu Ma^1,2, Hong Wang², Hao-Xiang Xu^1,2, Zhen-Hua Ling^1,2, Jia-Chen Gu³
¹National Engineering Research Center of Speech and Language Information Processing
²University of Science and Technology of China ³University of California, Los Angeles
{mjy1999,wanghong1700,nh2001620}@mail.ustc.edu.cn,
[email protected], [email protected]
Corresponding author.

Abstract

Model editing is an emerging field that focuses on updating the knowledge embedded within large language models (LLMs) without extensive retraining. However, current model editing methods significantly compromise the general abilities of LLMs as the number of edits increases, and this trade-off poses a substantial challenge to the continual learning of LLMs. In this paper, we first theoretically analyze that the factor affecting the general abilities in sequential model editing lies in the condition number of the edited matrix. The condition number of a matrix represents its numerical sensitivity, and therefore can be used to indicate the extent to which the original knowledge associations stored in LLMs are perturbed after editing. Subsequently, statistical findings demonstrate that the value of this factor becomes larger as the number of edits increases, thereby exacerbating the deterioration of general abilities. To this end, a framework termed Perturbation Restraint on Upper bouNd for Editing (PRUNE) is proposed, which applies the condition number restraints in sequential editing. These restraints can lower the upper bound on perturbation to edited models, thus preserving the general abilities. Systematically, we conduct experiments employing three popular editing methods on three LLMs across four representative downstream tasks. Evaluation results show that PRUNE can preserve considerable general abilities while maintaining the editing performance effectively in sequential model editing. The code and data are available at https://github.com/mjy1111/PRUNE.

1 Introduction

Despite the remarkable capabilities of large language models (LLMs), they encounter challenges such as false or outdated knowledge, and the risk of producing toxic content [65, 46, 29, 28]. Given the prohibitively high cost of retraining LLMs to address these issues, there has been a surge in focus on model editing [12, 41, 43, 44, 42, 39, 64, 27, 40], which aims at updating the knowledge of LLMs cost-effectively. Existing model editing methods can be roughly classified into either parameter-modifying methods [43, 41, 42] that directly modify a small subset of model parameters, or parameter-preserving methods [44, 63] that integrate additional modules without altering the model parameters. In this paper, we study the parameter-modifying editing methods.

Sequential model editing involves making successive edits to the same model over time to continuously update knowledge, as illustrated in Figure 1(a). Recent studies [21, 22, 37] indicate that parameter-modifying editing methods significantly compromise the general abilities of LLMs as the number of edits increases, such as summarization, question answering, and natural language inference. However, these studies neither provide a theoretical analysis of the bottleneck of the general abilities of the edited models, nor propose a solution to preserve these abilities in sequential editing. These affect the scalability of model editing and pose a substantial challenge to the continual learning of LLMs.

Refer to caption — Figure 1: (a) Illustration of sequential model editing. (b) The condition number of edited matrix rapidly increases as the number of edits increases. (c) Comparison of general downstream task performance before editing, after regular editing, and after restrained editing by PRUNE. (d) Comparison of editing performance after regular editing and after restrained editing by PRUNE. $f_{W}$ , $f_{W_{n}}$ and $f_{\overline{W}_{n}}$ denote the models that are unedited, regularly edited $n$ times, and restrainedly edited by PRUNE respectively. $W$ is denoted as a matrix to be edited.

In light of the above issues, we first theoretically analyze through matrix perturbation theory [38, 54, 60] to elucidate a crucial factor affecting the general abilities during sequential editing: the condition number [50, 13, 52] of the edited matrix. The condition number of a matrix represents its numerical sensitivity and therefore can be used to indicate the extent to which the original knowledge associations stored in LLMs are perturbed after editing. As shown in Figure 1(b), our statistical findings demonstrate that the condition number of the edited matrix substantially increases as the number of edits increases, thereby exacerbating the perturbation of original knowledge and the deterioration of general abilities. Therefore, we assume that the bottleneck of the general abilities during sequential editing lies in the escalating value of the condition number.

Towards continual and scalable model editing, we propose Perturbation Restraint on Upper bouNd for Editing (PRUNE) based on the above analysis, which applies the condition number restraints in sequential editing to preserve general abilities and maintain new editing knowledge simultaneously. Specifically, the condition number of the edited matrix is restrained by reducing the large singular values [1, 57] of the edit update matrix. Consequently, the upper bound on perturbation to the edited matrix is lowered, thus reducing the perturbation to the original knowledge associations and preserving the general abilities of the edited model, as shown in Figure 1(c). Additionally, we observe that these larger singular values often encapsulate redundant editing overfitting information, so regularizing them will not affect the newly editing knowledge, as shown in Figure 1(d). In this way, the new editing knowledge is embedded into LLMs without affecting their original general abilities. Overall, the proposed editing framework requires only minimal computing resources, and is adaptable to be coupled with multiple existing editing methods.

To validate the effectiveness of the proposed PRUNE, our study comprehensively evaluates the edited LLMs for both general abilities and editing performance in sequential editing scenarios. Extensive empirical research involves three popular editing methods, including MEND [43], ROME [41], and MEMIT [42], which are analyzed based on three representative LLMs including GPT-2 XL (1.5B) [48], LLaMA-2 (7B) [53], and LLaMA-3 (8B). Four representative downstream tasks including reasoning [8], summarization [19], open-domain QA [31], and natural language inference [11] are employed to extensively demonstrate the impact of model editing on the general abilities of LLMs. Experimental results demonstrate that the proposed PRUNE can preserve considerable general abilities and maintain almost all editing performance in sequential editing.

In essence, our research offers three significant contributions: (1) This study theoretically analyzes that the escalating value of the condition number of the edited matrix is the bottleneck of sequential model editing. (2) The PRUNE framework based on the analysis is proposed to preserve the general abilities of the edited model while retaining the editing knowledge. (3) Experimental results including both editing performance and four downstream task performance across three editing methods on three LLMs demonstrate the effectiveness of the proposed method.

2 Related Work

Model Editing Methods

From the perspective of whether the model parameters are modified, existing editing methods can be divided into parameter-modifying [43, 41, 42, 12] and parameter-preserving methods [44, 25, 63]. This paper focuses on the former. Previous works have investigated the role of MLP layers in Transformer, showing that MLP layers store knowledge, which can be located in specific neurons and edited [16, 10, 17]. KE [3] and MEND [43] train a hypernetwork to get gradient changes to update model parameters [43]. Besides, Meng et al. [41] and Meng et al. [42] used Locate-Then-Edit strategy, which first located multi-layer perceptron (MLP) storing factual knowledge, and then edited such knowledge by injecting new key-value pair in the MLP module. Parameter-preserving methods do not modify model weights but store the editing facts with an external memory. For example, Mitchell et al. [44] stored edits in a base model and learned to reason over them to adjust its predictions as needed.

Model Editing Evaluation

Some works investigate the paradigm for model editing evaluation [67, 9, 39, 35, 26, 61, 15, 40]. Cohen et al. [9] introduced the ripple effects of model editing, suggesting that editing a particular fact implies that many other facts need to be updated. Ma et al. [39] constructed a new benchmark to assess the edited model bidirectionally. Besides, Li et al. [35] explored two significant areas of concern: Knowledge Conflict and Knowledge Distortion. These early studies mainly evaluate edited models per edit rather than sequentially, and they focus narrowly on basic factual triples. Recently, some works assess the impact of editing methods on the general abilities of LLMs in sequential editing scenarios. These studies [21, 22, 37] have conducted comprehensive experiments, showing the parameter-modifying methods significantly degrade the model performance on general downstream tasks.

Matrix Perturbation Theory

It plays a crucial role in the field of artificial intelligence (AI) by providing a systematic framework to understand the impact of small changes or perturbations in various AI algorithms and models. Some studies [24, 47, 49] delve into the interpretability of LLMs, revealing how minor alterations in input features or model parameters influence the model’s predictions. This understanding helps uncover significant feature connections within the model architecture. Moreover, it has been instrumental in assessing and enhancing the robustness of models [5, 20, 6]. Furthermore, Bird et al. [2] and Dettmers et al. [14] have employed it for sensitivity analysis to identify critical factors affecting algorithm performance. It also contributes to the development of efficient optimization techniques [34, 7, 30], improving convergence rates and stability of optimization algorithms.

Compared with previous works [41, 42, 62, 21, 22, 37] that are the most relevant, a main difference should be highlighted. They neither theoretically investigate the reasons for general ability degradation, nor propose methods to maintain these abilities during sequential editing. In contrast, our study makes the first attempt to theoretically explore the bottleneck of general abilities in sequential editing and proposes the PRUNE framework to preserve these abilities for continual model editing.

3 Analysis on Bottleneck of Sequential Model Editing

3.1 Preliminary

Model Editing

This task involves modifying the memorized knowledge contained in LMs. Various kinds of complex learned beliefs such as logical, spatial, or numerical knowledge are expected to be edited. In this paper, following previous work [41, 67, 42, 64], we study editing factual knowledge in the form of (subject s, relation r, object o), e.g., (s = United States, r = President of, o = Donald Trump). An LM is expected to recall a memory representing $o$ given a natural language prompt $p(s,r)$ such as “The President of the United States is”. Editing a fact is to incorporate a new knowledge triple $(s,r,o^{*})$ in place of the current one $(s,r,o)$ . An edit is represented as $e=(s,r,o,o^{*})$ for brevity. Given a set of editing facts $\mathcal{E}=\left\{e_{1},e_{2},\ldots\right\}$ and an original model $f_{\theta_{0}}$ , sequential model editing operationalizes each edit after the last edit¹¹1This paper studies editing a single fact at a time and leaves the exploration of batch editing as future work., i.e., $K(f_{\theta_{n-1}},e_{n})=f_{\theta_{n}}$ , where $f_{\theta_{n}}$ denotes the model after $n$ edits.

Singular Value Decomposition

SVD [1] is a fundamental and effective matrix factorization technique for analyzing matrix structures. Formally, an SVD of a matrix $W\in\mathbb{R}^{p\times q}$ is given by $W=U\Sigma V^{\mathrm{T}}$ , where $U=[u_{1},u_{2},...,u_{p}]\in\mathbb{R}^{p\times p}$ , $V=[v_{1},v_{2},...,v_{q}]\in\mathbb{R}^{q\times q}$ , and $\Sigma\in\mathbb{R}^{p\times q}$ . $u_{i}$ and $v_{i}$ are the column vectors of $U$ and $V$ , and constitute an orthonormal basis of $\mathbb{R}^{p}$ and $\mathbb{R}^{q}$ respectively. $\Sigma$ is a diagonal matrix whose diagonal entries are given by the singular values of $W$ in descending order. Additionally, the SVD of $W$ could also be formulated as: $W=\sum_{i=1}^{\min\{p,q\}}\sigma_{i}u_{i}v_{i}^{\mathrm{T}}$ , where $\sigma_{i}$ is singular value, and $\sigma_{1}\geq\sigma_{2}\geq...\geq\sigma_{\min\{p,q\}}\geq 0$ . In the scenario of this paper, $W$ is a full-rank matrix, so $\sigma_{\min\{p,q\}}>0$ .

3.2 Matrix Perturbation Theory Analysis

Previous works [16, 41, 23, 59] have analyzed and located that the MLP modules in Transformer [55] store various kinds of knowledge [45, 56]. The MLP module of the $l$ -th Transformer layer consists of two projection layers, where the first and second layers are denoted as $W_{fc}^{l}$ and $W_{proj}^{l}$ respectively. $W_{proj}^{l}$ is considered as a linear associative memory which stores knowledge in the form of key-value pairs $(k_{i},v_{i})$ , and is usually regarded as the editing area [41, 42]. In this paper, $W_{proj}^{l}$ is denoted as $W$ for brevity. $W$ is assumed to store many key-value pairs $P=\{(k_{i},v_{i})\mid i=1,2,...\}$ which satisfies $Wk_{i}=v_{i}$ , where $k_{i}\in\mathbb{R}^{q}$ and $v_{i}\in\mathbb{R}^{p}$ . Assuming $\mid\mathcal{E}\mid=N$ in sequential model editing, an edit update matrix $\Delta W_{j}$ is calculated for the edit $e_{j}$ and added to $W$ , which can be formulated as: $W_{N}=W+\sum_{j=1}^{N}\Delta W_{j}$ with $\Delta W_{j}$ calculated from $f_{\theta_{j-1}}$ .

Problem Modeling

To explore the reasons for the general ability degradation of edited models, we begin by noting that most of the key-value pairs of $P$ correspond to facts unrelated to editing. For the sake of analysis, only the matrix $W$ of a single layer is assumed to be modified. We intuitively hypothesize that for the facts that are irrelevant to the editing fact, the cumulative modifications applied during sequential model editing may lead to significant mismatches in the associations between the original key-value pairs $P$ . Specifically, consider a key-value pair $(k_{i},v_{i})\in P$ . After applying an edit $e_{j}$ that generates $\Delta W_{j}$ and adding it to $W$ , if the extracted value $v_{i}$ remains unchanged, the corresponding key $k_{i}$ needs to be adjusted with an adjustment denoted as $\Delta k^{j}_{i}$ . Mathematically, this can be represented as²²2As $W_{j}\in\mathbb{R}^{p\times q}$ , and we observed $p<q$ in LLMs, so there will be $\Delta k^{j}_{i}$ that satisfies this formula. $W_{N}(k_{i}+\sum_{j=1}^{N}\Delta k^{j}_{i})=v_{i}$ after $N$ edits. However, during the editing process, it’s challenging to guarantee such adjustments completely, leading to inaccuracies in the knowledge extracted from the edited model. To delve deeper, let’s analyze how the key $k_{i}$ changes (i.e., $\sum_{j=1}^{N}\Delta k^{j}_{i}$ ) when its corresponding value $v_{i}$ remains unchanged after $N$ edits.

Perturbation Analysis of Single Edit

According to matrix perturbation theory [38, 54, 60], the edit update matrix $\Delta W$ from an edit can be regarded as a perturbation³³3We obtained some $\Delta W_{j}$ and found $\|\Delta W_{j}\|\ll\|W\|$ , which satisfies the definition of perturbation. for $W$ , so we first analyze the situation where $W\in\mathbb{R}^{p\times q}$ is appended with a perturbation $\Delta W$ . Define $W^{\dagger}$ is the generalized inverse [51] of $W$ , $\|\ast\|$ represents 2-norm, and $\tilde{W}=W+\Delta W$ .

Theorem 3.1 Consider $Wk=v$ , there exists $\Delta k$ such that $\tilde{k}=k+\Delta k$ satisfies $\tilde{W}\tilde{k}=v$ . Let $k=W^{\dagger}v$ and $\tilde{k}=\tilde{W}^{\dagger}v$ , and $\Delta W$ is an acute perturbation of $W$ . Then:

\frac{\|\Delta k\|}{\|k\|}=\frac{\|k-\tilde{k}\|}{\|k\|}\leq\hat{\kappa}\frac{\|\Delta E_{11}\|}{\|W\|}+\Psi_{2}\left(\frac{\hat{\kappa}\Delta E_{12}}{\|W\|}\right)+\hat{\kappa}^{2}\frac{\|\Delta E_{12}\|}{\|W\|}\left(\eta^{-1}g(v)+\frac{\|\Delta E_{21}\|}{\|W\|}\right),

(1)

where $\Delta E_{11}$ , $\Delta E_{12}$ , and $\Delta E_{21}$ are directly related to $\Delta W$ . $\Psi_{2}(F)$ is a monotonically increasing function of $\|F\|$ and $g(v)$ is a function about $v$ . $\hat{\kappa}=\|W\|\|\tilde{W}_{11}^{-1}\|$ , where $\tilde{W}_{11}$ is square and related to the reduced form of $W$ . Each term on the right-hand side involves $\hat{\kappa}$ , which means that the upper bound on the perturbation of the vector $k$ is constrained by $\hat{\kappa}$ . Readers can refer to Appendix A.3 for the details and proof of this theorem. However, calculating $\|\tilde{W}_{11}^{-1}\|$ involves the reduced form of $W$ , which incurs unnecessary additional overhead. Therefore, we consider the following theorem and give an alternative estimation.

Theorem 3.2 Let $\kappa=\|W\|\|{W}^{\dagger}\|$ , and suppose that $\gamma\equiv 1-\frac{\kappa\|\Delta E_{11}\|}{\|W\|}>0$ . Then:

\|\tilde{W}^{\dagger}\|\leq\frac{\|W^{\dagger}\|}{\gamma}.

(2)

According to Theorem 3.2, $\|\tilde{W}^{-1}_{11}\|\leq\frac{\|W_{11}^{-1}\|}{\gamma}=\frac{\|W^{\dagger}\|}{\gamma},$ so $\hat{\kappa}\leq\frac{\kappa}{\gamma}$ . Here $\kappa=\|W\|\|{W}^{\dagger}\|=\frac{\sigma_{max}}{\sigma_{min}}$ is the condition number of $W$ , where $\sigma_{\text{max}}$ and $\sigma_{\text{min}}$ are the maximum and minimum singular values of $W$ , respectively. Combining Theorem 3.1, we know that the larger $\kappa$ is, the greater the upper bound on the perturbation of the vector $k$ . Readers can refer to Appendix A for the full theoretical analysis.

3.3 Change Trend of Condition Number

As mentioned above, we have analyzed that the condition number of the edited matrix can be used to indicate the upper bound on the perturbation of the key-value pair associations by a single edit. In order to explore the impact of sequential model editing on these associations, the change trend of the condition number of the edited matrix during sequential editing is illustrated in Figure 2.

Surprisingly, we observed that regardless of the editing methods employed, the condition number of the edited matrix exhibited a rapid increase as the number of edits increased, especially after a large number of edits. According to Theorem 3.1, the adjustment norm $\|\Delta k^{n}_{i}\|_{2}$ corresponding to the $n$ -th edit tends to increase as the number of edits $n$ increases. It underscores that when the number of edits is relatively large, the upper bound on the perturbation caused by subsequent edits to the key-value pair associations becomes very large, further disrupting the stored original knowledge and exacerbating the deterioration of general abilities.

4 PRUNE: Perturbation Restraint on Upper bouNd for Editing

According to the analysis in Section 3, the bottleneck of the general abilities during sequential editing lies in the escalating value of the condition number. In this section, a framework termed Perturbation Restraint on Upper bouNd for Editing (PRUNE) is proposed, which applies the condition number restraints to preserve general abilities and maintain new editing knowledge simultaneously.

Table 1: The maximum singular values of

\sum_{j=1}^{N}\Delta W_{j}

with three edting methods. Other settings are the same as those illustrated in Figure 2.

Edits ( $N$ )	ROME	MEMIT	MEND
10	7.25	7.46	14.08
50	11.38	15.63	75.53
100	15.62	23.39	127.89
200	57.61	935	191.04

Principle

Given an edited matrix with $N$ edits, $W_{N}=W+\sum_{j=1}^{N}\Delta W_{j}$ , as shown in Figure 2, its maximum singular value is constantly increasing, while the minimum singular value is basically unchanged as the number of edits $N$ increases. This directly leads to the increasing condition number of the edited matrix. Therefore, our motivation is to restrain the maximum singular value of the edited matrix to lower the upper bound on the perturbation. If we directly perform SVD operation on $W_{N}$ and reduce its singular values, the original $W$ will be inevitably destroyed. Consequently, an analysis of the singular values of $\sum_{j=1}^{N}\Delta W_{j}$ is conducted, and the results in Table 1 present that its maximum singular value becomes very large when $N$ is large. We assume that this is the main reason why the maximum singular value of $W_{N}$ is large, our method therefore aims to restrain the large singular values of $\sum_{j=1}^{N}\Delta W_{j}$ .

Design

Firstly, SVD is operated on the original $W$ and $\sum_{j=1}^{N}\Delta W_{j}$ respectively as:

W=\sum_{i=1}^{\min\{p,q\}}\sigma_{i}u_{i}v_{i}^{\mathrm{T}},\quad\quad\sum_{j=1}^{N}\Delta W_{j}=\sum_{i=1}^{\min\{p,q\}}\hat{\sigma}_{i}\hat{u}_{i}\hat{v}_{i}^{\mathrm{T}}.

(3)

This paper considers $W$ to be the main part, and any singular value in $\sum_{j=1}^{N}\Delta W_{j}$ should be ensured not to obviously exceed the maximum singular value of $W$ . Subsequently, if any singular value $\hat{\sigma}_{i}$ of $\sum_{j=1}^{N}\Delta W_{j}$ is greater than the maximum singular value of $W$ , it will be restrained with a function $F$ , otherwise it remains unchanged, which could be formulated as:

\overline{\sigma}_{i}=\left\{\begin{array}[]{ll}F(\hat{\sigma}_{i}),&\text{ if }\hat{\sigma}_{i}>max\{\sigma_{i}\},\\ \hat{\sigma}_{i},&\text{ if }\hat{\sigma}_{i}\leq max\{\sigma_{i}\}.\end{array}\right.

(4)

F(\hat{\sigma}_{i})=\operatorname{log}_{\alpha}(\hat{\sigma}_{i})-\operatorname{log}_{\alpha}(max\{\sigma_{i}\})+max\{\sigma_{i}\}.

(5)

In the main paper, we use the $\operatorname{log}$ function in $F$ to restrain $\hat{\sigma}_{i}$ . Here ${\alpha}$ is a hyperparameter to control the degree of restraints, readers can refer to Appendix B.3 for its details for experiments. Besides, we also provide the definition and results of $\operatorname{linear}$ function in Appendix C.3. Finally, we obtain the restrained edited matrix $\overline{W}_{N}$ to replace ${W}_{N}$ :

\overline{W}_{N}=W+\sum_{i=1}^{\min\{p,q\}}\overline{\sigma}_{i}\hat{u}_{i}\hat{v}_{i}^{\mathrm{T}}.

(6)

In this way, the condition number of the edited matrix is reduced (see Appendix C.4) and the upper bound on perturbation is significantly restrained.

5 Experiments

In this section, both the downstream task performance and editing performance of three editing methods on three LLMs were evaluated in sequential model editing. The proposed PRUNE was plug-and-play which can be coupled with these editing methods.

5.1 Base LLMs and Editing Methods

Experiments were conducted on three LLMs including GPT-2 XL (1.5B) [48], LLaMA-2 (7B) [53] and LLaMA-3 (8B)⁴⁴4https://llama.meta.com/llama3/. Three popular editing methods were selected as the baselines including MEND [43], ROME [41], and MEMIT [42]. Readers can refer to Appendix B.1 for the details of these editing methods.

5.2 Editing Datasets and Evaluation Metrics

Two popular model editing datasets Zero-Shot Relation Extraction (ZsRE) [33] and CounterFact [41] were adopted in our experiments. ZsRE is a QA dataset using question rephrasings generated by back-translation as the equivalence neighborhood. A key distinction between CounterFact and ZsRE datasets is that ZsRE contains true facts, while CounterFact contains counterfactual examples where the new target has a lower probability when compared to the original answer [22]. Readers can refer to Appendix B.2 for examples of each dataset.

To assess the editing performance of editing methods, following previous works, three fundamental metrics were employed: efficacy, generalization and locality [3, 43, 41, 42]. Given an original model $f_{\theta_{0}}$ , an edited model $f_{\theta_{n}}$ with $n$ times sequential editing. Each edit $e_{i}=(s_{i},r_{i},o_{i},o_{i}^{*})$ has an editing prompt $p_{i}$ , paraphrase prompts $\mathcal{P}^{G}_{i}$ , and locality prompts $\mathcal{P}^{L}_{i}$ .

Efficacy validates whether the edited models could recall the editing fact under editing prompt $p_{i}$ . The assessment is based on Efficacy Score (ES) representing as: $\mathbb{E}_{i}[\mathbbm{1}[\,P_{f_{\theta_{n}}}(o^{*}_{i}\,|\,p_{i})>P_{f_{\theta_{n}}}(o_{i}\,|\,p_{i})]\,]$ , where $\mathbbm{1}$ is the indicator function.

Generalization verifies whether the edited models could recall the editing fact under the paraphrase prompts $\mathcal{P}^{G}_{i}$ via Generalization Score (GS): $\mathbb{E}_{i}\,[\,\mathbb{E}_{p\in\mathcal{P}^{G}_{i}}[\mathbbm{1}[\,P_{f_{\theta_{n}}}(o^{*}_{i}\,|\,p)>P_{f_{\theta_{n}}}(o_{i}\,|\,p)]\,]$ .

Locality verifies whether the output of the edited models for inputs out of editing scope remains unchanged under the locality prompts $\mathcal{P}^{L}_{i}$ via Locality Score (LS): $\mathbb{E}_{i}\,[\,\mathbb{E}_{p_{l}\in\mathcal{P}^{L}_{i}}[\mathbbm{1}[\,P_{f_{\theta_{n}}}(o_{l}\,|\,p_{l})>P_{f_{\theta_{n}}}(o^{*}_{i}\,|\,p_{l})]\,]\,]$ , where $o_{l}$ was the original answer of $p_{l}$ .

Different from previous studies that assess the edited models after each individual edit [22, 62], this paper evaluated whether the final edited models after completing all edits can still recall all preceding edits, which is more challenging and common in real-world.

5.3 Downstream Tasks, Datasets and Metrics

To explore the side effects of sequential model editing on the general abilities of LLMs, four representative tasks with corresponding datasets were adopted for assessment, including:

Reasoning on the GSM8K [8], and the results were measured by solve rate.

Summarization on the SAMSum [19], and the results were measured by the average of ROUGE-1, ROUGE-2 and ROUGE-L following Lin [36].

Open-domain QA on the Natural Question [31], and the results were measured by exact match (EM) with the reference answer after minor normalization as in Chen et al. [4] and Lee et al. [32].

Natural language inference (NLI) on the RTE [11], and the results were measured by accuracy of two-way classification.

For each dataset, some examples were randomly sampled for evaluation. Details of prompts for each tasks were shown in Appendix B.4.

5.4 Results of General Abilities

Figure 3 illustrates the downstream task performance of edited models with LLaMA-2 (7B) on the CounterFact dataset. Due to page limitation, results of other LLMs and datasets were put in Appendix C.1. These results were analyzed from the following perspectives.

Current editing methods significantly compromised general abilities. As depicted by the dashed lines of Figure 3, both the ROME and MEMIT methods initially maintained relatively stable performance in downstream tasks when the number of edits was small ( $\leq$ 100). However, as the number of edits surpassed 200, a noticeable decline in performance was observed across all tasks for both methods. Additionally, the MEND method exhibited significant performance degradation after just 20 sequential edits, indicating its inadequacy as a sequential model editing method. Furthermore, when comparing LLMs of different sizes, a general trend emerged: larger models suffered more pronounced compromises in their general abilities when subjected to the same number of edits. For instance, with 300 edits, MEMIT’s performance on GPT2-XL remained largely unchanged, whereas it dwindled to nearly 0 on LLaMA-2 and LLaMA-3.

The performance decline was gradual initially but accelerated with increasing edit count. This trend aligned with the fluctuation observed in the size of the condition number, as depicted in Figure 2. When the number of edits was small, the condition number was small, and each new edit introduced relatively minor perturbations to the model. However, as the number of edits increased, the condition number underwent a substantial increase. Consequently, each subsequent edit exerted a significant perturbation on the model, leading to a pronounced impairment of its general abilities. These results substantiated the analysis presented in Section 3.3.

The proposed PRUNE can preserve considerable general abilities. As shown by the solid lines of Figure 3, when MEMIT was coupled with PRUNE and subjected to 200 edits, its downstream tasks performance remained close to that of the unedited model. However, for the unrestrained MEMIT, downstream task performance had plummeted to nearly 0 by this point. This consistent trend was also observed with ROME and MEND. Nevertheless, for models edited using the unrestrained MEND method, performance degradation was stark after just 20 edits. Even with the addition of PRUNE, preservation could only be extended up to 40 edits. This suggests that while PRUNE effectively preserves general abilities, it does have an upper limit determined by the unrestrained editing method.

5.5 Results of Editing Performance

Figure 4 shows different metrics used for measuring the editing performance of edited models with LLaMA-2 (7B) on the CounterFact dataset. Other results across models and datasets were put in Appendix C.2. Three conclusions can be drawn here.

Previous editing facts were forgotten as the number of edits increased. As shown by the dashed lines of Figure 4, the decline in efficacy and generalization suggests that in sequential editing scenarios, post-edited models gradually forget knowledge acquired from previous edits after a few iterations. Comparing these editing methods, we also observed a notable drop in efficacy and generalization after hundreds of edits with ROME and MEMIT, whereas these values decreased significantly after only 30 edits with MEND. This indicates that in sequential editing scenarios, the MEND method struggled to successfully integrate new knowledge into LLMs after several edits.

Unrelated facts were perturbed as the number of edits increased. The locality metric served as an indicator of perturbation for unrelated facts. It became evident that for each editing method, the locality decreased significantly. Additionally, an observation emerged: when the locality of the edited model was low, the performance of downstream tasks was also low. This observation underscores that perturbations of irrelevant knowledge compromise the general abilities of the edited model.

PRUNE can effectively maintain the editing performance. This is shown by the solid lines of Figure 4 and could be analyzed from two aspects. On the one hand, when the number of edits was small, the editing performance of each editing method coupled with PRUNE was about the same as the unrestrained method. On the other hand, it significantly mitigated the forgetting of editing facts and the perturbation of irrelevant facts when the number of edits was large during the sequential editing. Specifically, when the number of edits reached 150, the editing performance of MEMIT was very low. But when coupled with PRUNE, its performance remained relatively stable.

5.6 Editing Facts Forgetting Analysis

In section 3, the analysis was conducted to elucidate the reasons behind the degradation in general abilities with an increasing number of edits. Subsequent experiments quantitatively demonstrated the effectiveness of the proposed PRUNE. Here, we delve into qualitative analysis to explain why editing facts are forgotten and how PRUNE can mitigate this forgetting.

Initially, a set of editing facts $\mathcal{E}=\left\{e_{1},e_{2},\ldots\right\}$ was collected, where $\mid\mathcal{E}\mid=200$ . ROME was employed for analysis, and the original matrix was defined as $W$ . During sequential editing, ROME computed key-value pairs $(k^{e}_{j},v^{e}_{j})$ of the last subject token to generate $\Delta W_{j}$ for each edit $e_{j}$ to incorporate new facts, satisfying the equation: $W_{j}\cdot k^{e}_{j}=v^{e}_{j}$ . However, when evaluating editing performance, the edited model obtained from the last edit was utilized, thus computing values⁵⁵5Since ROME only modifies one matrix, the $k^{e}_{j}$ remains the same across these edited models.: $W_{200}\cdot k^{e}_{j}=\hat{v}^{e}_{j}$ . After adopting PRUNE to ROME, this equation became $\overline{W}_{200}\cdot k^{e}_{j}=\overline{v}^{e}_{j}$ . We hypothesized that if $\hat{v}^{e}_{j}$ was similar to $v^{e}_{j}$ , the editing fact $e_{j}$ could be maintained.

Denote $V_{Current}=\{v^{e}_{j}\}$ , $V_{Editing}=\{\hat{v}^{e}_{j}\}$ , and $V_{Prune}=\{\overline{v}^{e}_{j}\}$ . Specifically, these corresponding values of the first 100 edits were used, as they are more prone to be forgotten than the last 100. Principal Component Analysis (PCA) [18] was employed to visualize these values. The first two principal components of each value were calculated and illustrated, as they can represent most of its features [66]. As shown in Figure 5, on the one hand, the discrepancy between the principal components of $V_{Current}$ and $V_{Editing}$ was markedly large. This indicates that after 200 edits to the model, the values corresponding to the first 100 facts stored in the edited matrix are severely corrupted, leading to significant forgetfulness. On the other hand, after adopting PRUNE, the discrepancy between the principal components of $V_{Current}$ and $V_{Prune}$ was small. This demonstrates that PRUNE effectively maintains the values and mitigates the forgetting of editing facts.

6 Conclusion

In this paper, a theoretical analysis is firstly conducted to elucidate that the bottleneck of the general abilities during sequential editing lies in the escalating value of the condition number. Subsequently, a plug-and-play framework called PRUNE is proposed to apply restraints to preserve general abilities and maintain new editing knowledge simultaneously. Comprehensive experiments on various editing methods and LLMs demonstrate the effectiveness of this method. We aspire that our analysis and method will catalyze future research on continual model editing.

Limitations & Future Work

The limitations of our work are discussed as follows. Firstly, while this paper focuses on editing a single fact at a time in sequential model editing, some studies have explored updating hundreds or thousands of facts simultaneously in batch editing. Therefore, investigating batch-sequential editing could enhance the scalability of model editing and remains further research. Secondly, for the experimental settings, it is necessary to explore the performance of larger-size models and more editing methods on more downstream tasks. Thirdly, the current focus of editing knowledge primarily revolves around factual knowledge. However, it is also important to investigate whether editing other types of knowledge will affect general abilities and whether PRUNE is effective in this situation. Additionally, the proposed PRUNE is only applied once after the completion of the last edit. But it could also be utilized multiple times during the sequential editing process, and we intuitively believe that this approach would be more conducive to preserving the general abilities of the model. These aspects are yet to be fully understood and warrant a more comprehensive study.

References

Albano et al. [1988] Alfonso M Albano, J Muench, C Schwartz, AI Mees, and PE Rapp. Singular-value decomposition and the grassberger-procaccia algorithm. Physical review A, 38(6):3017, 1988.
Bird et al. [2020] Sarah Bird, Miro Dudík, Richard Edgar, Brandon Horn, Roman Lutz, Vanessa Milan, Mehrnoosh Sameki, Hanna Wallach, and Kathleen Walker. Fairlearn: A toolkit for assessing and improving fairness in ai. Microsoft, Tech. Rep. MSR-TR-2020-32, 2020.
Cao et al. [2021] Nicola De Cao, Wilker Aziz, and Ivan Titov. Editing factual knowledge in language models. In Marie-Francine Moens, Xuanjing Huang, Lucia Specia, and Scott Wen-tau Yih, editors, Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing, EMNLP 2021, Virtual Event / Punta Cana, Dominican Republic, 7-11 November, 2021, pages 6491–6506. Association for Computational Linguistics, 2021. doi: 10.18653/v1/2021.emnlp-main.522. URL https://doi.org/10.18653/v1/2021.emnlp-main.522.
Chen et al. [2017] Danqi Chen, Adam Fisch, Jason Weston, and Antoine Bordes. Reading wikipedia to answer open-domain questions. In Regina Barzilay and Min-Yen Kan, editors, Proceedings of the 55th Annual Meeting of the Association for Computational Linguistics, ACL 2017, Vancouver, Canada, July 30 - August 4, Volume 1: Long Papers, pages 1870–1879. Association for Computational Linguistics, 2017. doi: 10.18653/V1/P17-1171. URL https://doi.org/10.18653/v1/P17-1171.
Chen et al. [2023] Shuo Chen, Jindong Gu, Zhen Han, Yunpu Ma, Philip H. S. Torr, and Volker Tresp. Benchmarking robustness of adaptation methods on pre-trained vision-language models. In Alice Oh, Tristan Naumann, Amir Globerson, Kate Saenko, Moritz Hardt, and Sergey Levine, editors, Advances in Neural Information Processing Systems 36: Annual Conference on Neural Information Processing Systems 2023, NeurIPS 2023, New Orleans, LA, USA, December 10 - 16, 2023, 2023. URL http://papers.nips.cc/paper_files/paper/2023/hash/a2a544e43acb8b954dc5846ff0d77ad5-Abstract-Datasets_and_Benchmarks.html.
Chen et al. [2024] Zhuotong Chen, Zihu Wang, Yifan Yang, Qianxiao Li, and Zheng Zhang. PID control-based self-healing to improve the robustness of large language models. CoRR, abs/2404.00828, 2024. doi: 10.48550/ARXIV.2404.00828. URL https://doi.org/10.48550/arXiv.2404.00828.
Cheng et al. [2023] Wenhua Cheng, Weiwei Zhang, Haihao Shen, Yiyang Cai, Xin He, and Kaokao Lv. Optimize weight rounding via signed gradient descent for the quantization of llms. CoRR, abs/2309.05516, 2023. doi: 10.48550/ARXIV.2309.05516. URL https://doi.org/10.48550/arXiv.2309.05516.
Cobbe et al. [2021] Karl Cobbe, Vineet Kosaraju, Mohammad Bavarian, Mark Chen, Heewoo Jun, Lukasz Kaiser, Matthias Plappert, Jerry Tworek, Jacob Hilton, Reiichiro Nakano, Christopher Hesse, and John Schulman. Training verifiers to solve math word problems. CoRR, abs/2110.14168, 2021. URL https://arxiv.org/abs/2110.14168.
Cohen et al. [2023] Roi Cohen, Eden Biran, Ori Yoran, Amir Globerson, and Mor Geva. Evaluating the ripple effects of knowledge editing in language models. CoRR, abs/2307.12976, 2023. doi: 10.48550/ARXIV.2307.12976. URL https://doi.org/10.48550/arXiv.2307.12976.
Da et al. [2021] Jeff Da, Ronan Le Bras, Ximing Lu, Yejin Choi, and Antoine Bosselut. Analyzing commonsense emergence in few-shot knowledge models. In Danqi Chen, Jonathan Berant, Andrew McCallum, and Sameer Singh, editors, 3rd Conference on Automated Knowledge Base Construction, AKBC 2021, Virtual, October 4-8, 2021, 2021. doi: 10.24432/C5NK5J. URL https://doi.org/10.24432/C5NK5J.
Dagan et al. [2005] Ido Dagan, Oren Glickman, and Bernardo Magnini. The PASCAL recognising textual entailment challenge. In Joaquin Quiñonero Candela, Ido Dagan, Bernardo Magnini, and Florence d’Alché-Buc, editors, Machine Learning Challenges, Evaluating Predictive Uncertainty, Visual Object Classification and Recognizing Textual Entailment, First PASCAL Machine Learning Challenges Workshop, MLCW 2005, Southampton, UK, April 11-13, 2005, Revised Selected Papers, volume 3944 of Lecture Notes in Computer Science, pages 177–190. Springer, 2005. doi: 10.1007/11736790\_9. URL https://doi.org/10.1007/11736790_9.
Dai et al. [2022] Damai Dai, Li Dong, Yaru Hao, Zhifang Sui, Baobao Chang, and Furu Wei. Knowledge neurons in pretrained transformers. In Smaranda Muresan, Preslav Nakov, and Aline Villavicencio, editors, Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics (Volume 1: Long Papers), ACL 2022, Dublin, Ireland, May 22-27, 2022, pages 8493–8502. Association for Computational Linguistics, 2022. doi: 10.18653/v1/2022.acl-long.581. URL https://doi.org/10.18653/v1/2022.acl-long.581.
Dedieu [1997] Jean-Pierre Dedieu. Condition operators, condition numbers, and condition number theorem for the generalized eigenvalue problem. Linear algebra and its applications, 263:1–24, 1997.
Dettmers et al. [2023] Tim Dettmers, Ruslan Svirschevski, Vage Egiazarian, Denis Kuznedelev, Elias Frantar, Saleh Ashkboos, Alexander Borzunov, Torsten Hoefler, and Dan Alistarh. Spqr: A sparse-quantized representation for near-lossless LLM weight compression. CoRR, abs/2306.03078, 2023. doi: 10.48550/ARXIV.2306.03078. URL https://doi.org/10.48550/arXiv.2306.03078.
Gandikota et al. [2023] Rohit Gandikota, Joanna Materzynska, Jaden Fiotto-Kaufman, and David Bau. Erasing concepts from diffusion models. CoRR, abs/2303.07345, 2023. doi: 10.48550/ARXIV.2303.07345. URL https://doi.org/10.48550/arXiv.2303.07345.
Geva et al. [2021] Mor Geva, Roei Schuster, Jonathan Berant, and Omer Levy. Transformer feed-forward layers are key-value memories. In Marie-Francine Moens, Xuanjing Huang, Lucia Specia, and Scott Wen-tau Yih, editors, Proceedings of the 2021 Conference on Empirical Methods in Natural Language Processing, EMNLP 2021, Virtual Event / Punta Cana, Dominican Republic, 7-11 November, 2021, pages 5484–5495. Association for Computational Linguistics, 2021. doi: 10.18653/v1/2021.emnlp-main.446. URL https://doi.org/10.18653/v1/2021.emnlp-main.446.
Geva et al. [2022] Mor Geva, Avi Caciularu, Kevin Ro Wang, and Yoav Goldberg. Transformer feed-forward layers build predictions by promoting concepts in the vocabulary space. In Yoav Goldberg, Zornitsa Kozareva, and Yue Zhang, editors, Proceedings of the 2022 Conference on Empirical Methods in Natural Language Processing, EMNLP 2022, Abu Dhabi, United Arab Emirates, December 7-11, 2022, pages 30–45. Association for Computational Linguistics, 2022. doi: 10.18653/v1/2022.emnlp-main.3. URL https://doi.org/10.18653/v1/2022.emnlp-main.3.
Gewers et al. [2022] Felipe L. Gewers, Gustavo R. Ferreira, Henrique Ferraz de Arruda, Filipi Nascimento Silva, Cesar H. Comin, Diego R. Amancio, and Luciano da Fontoura Costa. Principal component analysis: A natural approach to data exploration. ACM Comput. Surv., 54(4):70:1–70:34, 2022. doi: 10.1145/3447755. URL https://doi.org/10.1145/3447755.
Gliwa et al. [2019] Bogdan Gliwa, Iwona Mochol, Maciej Biesek, and Aleksander Wawer. SAMSum corpus: A human-annotated dialogue dataset for abstractive summarization. In Lu Wang, Jackie Chi Kit Cheung, Giuseppe Carenini, and Fei Liu, editors, Proceedings of the 2nd Workshop on New Frontiers in Summarization, pages 70–79, Hong Kong, China, November 2019. Association for Computational Linguistics. doi: 10.18653/v1/D19-5409. URL https://aclanthology.org/D19-5409.
Gong et al. [2024] Zhuocheng Gong, Jiahao Liu, Jingang Wang, Xunliang Cai, Dongyan Zhao, and Rui Yan. What makes quantization for large language model hard? an empirical study from the lens of perturbation. In Michael J. Wooldridge, Jennifer G. Dy, and Sriraam Natarajan, editors, Thirty-Eighth AAAI Conference on Artificial Intelligence, AAAI 2024, Thirty-Sixth Conference on Innovative Applications of Artificial Intelligence, IAAI 2024, Fourteenth Symposium on Educational Advances in Artificial Intelligence, EAAI 2014, February 20-27, 2024, Vancouver, Canada, pages 18082–18089. AAAI Press, 2024. doi: 10.1609/AAAI.V38I16.29765. URL https://doi.org/10.1609/aaai.v38i16.29765.
Gu et al. [2024] Jia-Chen Gu, Hao-Xiang Xu, Jun-Yu Ma, Pan Lu, Zhen-Hua Ling, Kai-Wei Chang, and Nanyun Peng. Model editing can hurt general abilities of large language models. CoRR, abs/2401.04700, 2024. doi: 10.48550/ARXIV.2401.04700. URL https://doi.org/10.48550/arXiv.2401.04700.
Gupta et al. [2024] Akshat Gupta, Anurag Rao, and Gopala Anumanchipalli. Model editing at scale leads to gradual and catastrophic forgetting. CoRR, abs/2401.07453, 2024. doi: 10.48550/ARXIV.2401.07453. URL https://doi.org/10.48550/arXiv.2401.07453.
Gupta et al. [2023] Anshita Gupta, Debanjan Mondal, Akshay Krishna Sheshadri, Wenlong Zhao, Xiang Lorraine Li, Sarah Wiegreffe, and Niket Tandon. Editing commonsense knowledge in GPT. CoRR, abs/2305.14956, 2023. doi: 10.48550/ARXIV.2305.14956. URL https://doi.org/10.48550/arXiv.2305.14956.
Harder et al. [2020] Frederik Harder, Matthias Bauer, and Mijung Park. Interpretable and differentially private predictions. In The Thirty-Fourth AAAI Conference on Artificial Intelligence, AAAI 2020, The Thirty-Second Innovative Applications of Artificial Intelligence Conference, IAAI 2020, The Tenth AAAI Symposium on Educational Advances in Artificial Intelligence, EAAI 2020, New York, NY, USA, February 7-12, 2020, pages 4083–4090. AAAI Press, 2020. doi: 10.1609/AAAI.V34I04.5827. URL https://doi.org/10.1609/aaai.v34i04.5827.
Hartvigsen et al. [2023] Tom Hartvigsen, Swami Sankaranarayanan, Hamid Palangi, Yoon Kim, and Marzyeh Ghassemi. Aging with GRACE: lifelong model editing with discrete key-value adaptors. In Alice Oh, Tristan Naumann, Amir Globerson, Kate Saenko, Moritz Hardt, and Sergey Levine, editors, Advances in Neural Information Processing Systems 36: Annual Conference on Neural Information Processing Systems 2023, NeurIPS 2023, New Orleans, LA, USA, December 10 - 16, 2023, 2023. URL http://papers.nips.cc/paper_files/paper/2023/hash/95b6e2ff961580e03c0a662a63a71812-Abstract-Conference.html.
Hase et al. [2023] Peter Hase, Mohit Bansal, Been Kim, and Asma Ghandeharioun. Does localization inform editing? surprising differences in causality-based localization vs. knowledge editing in language models. CoRR, abs/2301.04213, 2023. doi: 10.48550/ARXIV.2301.04213. URL https://doi.org/10.48550/arXiv.2301.04213.
Hu et al. [2024] Chenhui Hu, Pengfei Cao, Yubo Chen, Kang Liu, and Jun Zhao. Wilke: Wise-layer knowledge editor for lifelong knowledge editing. CoRR, abs/2402.10987, 2024. doi: 10.48550/ARXIV.2402.10987. URL https://doi.org/10.48550/arXiv.2402.10987.
Huang et al. [2023] Lei Huang, Weijiang Yu, Weitao Ma, Weihong Zhong, Zhangyin Feng, Haotian Wang, Qianglong Chen, Weihua Peng, Xiaocheng Feng, Bing Qin, and Ting Liu. A survey on hallucination in large language models: Principles, taxonomy, challenges, and open questions. CoRR, abs/2311.05232, 2023. doi: 10.48550/ARXIV.2311.05232. URL https://doi.org/10.48550/arXiv.2311.05232.
Ji et al. [2023] Ziwei Ji, Nayeon Lee, Rita Frieske, Tiezheng Yu, Dan Su, Yan Xu, Etsuko Ishii, Yejin Bang, Andrea Madotto, and Pascale Fung. Survey of hallucination in natural language generation. ACM Comput. Surv., 55(12):248:1–248:38, 2023. doi: 10.1145/3571730. URL https://doi.org/10.1145/3571730.
Jiang et al. [2024] Shuoran Jiang, Qingcai Chen, Youcheng Pan, Yang Xiang, Yukang Lin, Xiangping Wu, Chuanyi Liu, and Xiaobao Song. Zo-adamu optimizer: Adapting perturbation by the momentum and uncertainty in zeroth-order optimization. In Michael J. Wooldridge, Jennifer G. Dy, and Sriraam Natarajan, editors, Thirty-Eighth AAAI Conference on Artificial Intelligence, AAAI 2024, Thirty-Sixth Conference on Innovative Applications of Artificial Intelligence, IAAI 2024, Fourteenth Symposium on Educational Advances in Artificial Intelligence, EAAI 2014, February 20-27, 2024, Vancouver, Canada, pages 18363–18371. AAAI Press, 2024. doi: 10.1609/AAAI.V38I16.29796. URL https://doi.org/10.1609/aaai.v38i16.29796.
Kwiatkowski et al. [2019] Tom Kwiatkowski, Jennimaria Palomaki, Olivia Redfield, Michael Collins, Ankur P. Parikh, Chris Alberti, Danielle Epstein, Illia Polosukhin, Jacob Devlin, Kenton Lee, Kristina Toutanova, Llion Jones, Matthew Kelcey, Ming-Wei Chang, Andrew M. Dai, Jakob Uszkoreit, Quoc Le, and Slav Petrov. Natural questions: a benchmark for question answering research. Trans. Assoc. Comput. Linguistics, 7:452–466, 2019. doi: 10.1162/TACL\_A\_00276. URL https://doi.org/10.1162/tacl_a_00276.
Lee et al. [2019] Kenton Lee, Ming-Wei Chang, and Kristina Toutanova. Latent retrieval for weakly supervised open domain question answering. In Anna Korhonen, David R. Traum, and Lluís Màrquez, editors, Proceedings of the 57th Conference of the Association for Computational Linguistics, ACL 2019, Florence, Italy, July 28- August 2, 2019, Volume 1: Long Papers, pages 6086–6096. Association for Computational Linguistics, 2019. doi: 10.18653/V1/P19-1612. URL https://doi.org/10.18653/v1/p19-1612.
Levy et al. [2017] Omer Levy, Minjoon Seo, Eunsol Choi, and Luke Zettlemoyer. Zero-shot relation extraction via reading comprehension. In Roger Levy and Lucia Specia, editors, Proceedings of the 21st Conference on Computational Natural Language Learning (CoNLL 2017), Vancouver, Canada, August 3-4, 2017, pages 333–342. Association for Computational Linguistics, 2017. doi: 10.18653/v1/K17-1034. URL https://doi.org/10.18653/v1/K17-1034.
Li et al. [2020] Hui-Jia Li, Lin Wang, Yan Zhang, and Matjaž Perc. Optimization of identifiability for efficient community detection. New Journal of Physics, 22(6):063035, 2020.
Li et al. [2023] Zhoubo Li, Ningyu Zhang, Yunzhi Yao, Mengru Wang, Xi Chen, and Huajun Chen. Unveiling the pitfalls of knowledge editing for large language models. CoRR, abs/2310.02129, 2023. doi: 10.48550/ARXIV.2310.02129. URL https://doi.org/10.48550/arXiv.2310.02129.
Lin [2004] Chin-Yew Lin. ROUGE: A package for automatic evaluation of summaries. In Text Summarization Branches Out, pages 74–81, Barcelona, Spain, July 2004. Association for Computational Linguistics. URL https://aclanthology.org/W04-1013.
Lin et al. [2024] Zihao Lin, Mohammad Beigi, Hongxuan Li, Yufan Zhou, Yuxiang Zhang, Qifan Wang, Wenpeng Yin, and Lifu Huang. Navigating the dual facets: A comprehensive evaluation of sequential memory editing in large language models. CoRR, abs/2402.11122, 2024. doi: 10.48550/ARXIV.2402.11122. URL https://doi.org/10.48550/arXiv.2402.11122.
Luo and Tseng [1994] Zhi-Quan Luo and Paul Tseng. Perturbation analysis of a condition number for linear systems. SIAM Journal on Matrix Analysis and Applications, 15(2):636–660, 1994.
Ma et al. [2023] Jun-Yu Ma, Jia-Chen Gu, Zhen-Hua Ling, Quan Liu, and Cong Liu. Untying the reversal curse via bidirectional language model editing. CoRR, abs/2310.10322, 2023. doi: 10.48550/ARXIV.2310.10322. URL https://doi.org/10.48550/arXiv.2310.10322.
Ma et al. [2024] Jun-Yu Ma, Jia-Chen Gu, Ningyu Zhang, and Zhen-Hua Ling. Neighboring perturbations of knowledge editing on large language models. CoRR, abs/2401.17623, 2024. doi: 10.48550/ARXIV.2401.17623. URL https://doi.org/10.48550/arXiv.2401.17623.
Meng et al. [2022] Kevin Meng, David Bau, Alex Andonian, and Yonatan Belinkov. Locating and editing factual associations in GPT. In NeurIPS, 2022. URL https://arxiv.org/abs/2202.05262.
Meng et al. [2023] Kevin Meng, Arnab Sen Sharma, Alex J. Andonian, Yonatan Belinkov, and David Bau. Mass-editing memory in a transformer. In The Eleventh International Conference on Learning Representations, ICLR 2023, Kigali, Rwanda, May 1-5, 2023. OpenReview.net, 2023. URL https://openreview.net/pdf?id=MkbcAHIYgyS.
Mitchell et al. [2022a] Eric Mitchell, Charles Lin, Antoine Bosselut, Chelsea Finn, and Christopher D. Manning. Fast model editing at scale. In The Tenth International Conference on Learning Representations, ICLR 2022, Virtual Event, April 25-29, 2022. OpenReview.net, 2022a. URL https://openreview.net/forum?id=0DcZxeWfOPt.
Mitchell et al. [2022b] Eric Mitchell, Charles Lin, Antoine Bosselut, Christopher D. Manning, and Chelsea Finn. Memory-based model editing at scale. In Kamalika Chaudhuri, Stefanie Jegelka, Le Song, Csaba Szepesvári, Gang Niu, and Sivan Sabato, editors, International Conference on Machine Learning, ICML 2022, 17-23 July 2022, Baltimore, Maryland, USA, volume 162 of Proceedings of Machine Learning Research, pages 15817–15831. PMLR, 2022b. URL https://proceedings.mlr.press/v162/mitchell22a.html.
Pearl [2001] Judea Pearl. Direct and indirect effects. In Jack S. Breese and Daphne Koller, editors, UAI ’01: Proceedings of the 17th Conference in Uncertainty in Artificial Intelligence, University of Washington, Seattle, Washington, USA, August 2-5, 2001, pages 411–420. Morgan Kaufmann, 2001. URL https://dslpitt.org/uai/displayArticleDetails.jsp?mmnu=1&smnu=2&article_id=126&proceeding_id=17.
Peng et al. [2023] Baolin Peng, Michel Galley, Pengcheng He, Hao Cheng, Yujia Xie, Yu Hu, Qiuyuan Huang, Lars Liden, Zhou Yu, Weizhu Chen, and Jianfeng Gao. Check your facts and try again: Improving large language models with external knowledge and automated feedback. CoRR, abs/2302.12813, 2023. doi: 10.48550/arXiv.2302.12813. URL https://doi.org/10.48550/arXiv.2302.12813.
Qin et al. [2022] Bin Qin, Fu-Lai Chung, and Shitong Wang. KAT: A knowledge adversarial training method for zero-order takagi-sugeno-kang fuzzy classifiers. IEEE Trans. Cybern., 52(7):6857–6871, 2022. doi: 10.1109/TCYB.2020.3034792. URL https://doi.org/10.1109/TCYB.2020.3034792.
Radford et al. [2019] Alec Radford, Jeffrey Wu, Rewon Child, David Luan, Dario Amodei, Ilya Sutskever, et al. Language models are unsupervised multitask learners. OpenAI blog, 1(8):9, 2019.
Singh et al. [2024] Chandan Singh, Jeevana Priya Inala, Michel Galley, Rich Caruana, and Jianfeng Gao. Rethinking interpretability in the era of large language models. CoRR, abs/2402.01761, 2024. doi: 10.48550/ARXIV.2402.01761. URL https://doi.org/10.48550/arXiv.2402.01761.
Smith [1967] Russell A Smith. The condition numbers of the matrix eigenvalue problem. Numerische Mathematik, 10:232–240, 1967.
Stewart and Sun [1990] Gilbert W Stewart and Ji-guang Sun. Matrix perturbation theory. (No Title), 1990.
Sun [2000] Ji-guang Sun. Condition number and backward error for the generalized singular value decomposition. SIAM Journal on Matrix Analysis and Applications, 22(2):323–341, 2000.
Touvron et al. [2023] Hugo Touvron, Louis Martin, Kevin Stone, Peter Albert, Amjad Almahairi, Yasmine Babaei, Nikolay Bashlykov, Soumya Batra, Prajjwal Bhargava, Shruti Bhosale, Dan Bikel, Lukas Blecher, Cristian Canton-Ferrer, Moya Chen, Guillem Cucurull, David Esiobu, Jude Fernandes, Jeremy Fu, Wenyin Fu, Brian Fuller, Cynthia Gao, Vedanuj Goswami, Naman Goyal, Anthony Hartshorn, Saghar Hosseini, Rui Hou, Hakan Inan, Marcin Kardas, Viktor Kerkez, Madian Khabsa, Isabel Kloumann, Artem Korenev, Punit Singh Koura, Marie-Anne Lachaux, Thibaut Lavril, Jenya Lee, Diana Liskovich, Yinghai Lu, et al. Llama 2: Open foundation and fine-tuned chat models. CoRR, abs/2307.09288, 2023. doi: 10.48550/arXiv.2307.09288. URL https://doi.org/10.48550/arXiv.2307.09288.
Vaccaro [1994] Richard J Vaccaro. A second-order perturbation expansion for the svd. SIAM Journal on Matrix Analysis and Applications, 15(2):661–671, 1994.
Vaswani et al. [2017] Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N. Gomez, Lukasz Kaiser, and Illia Polosukhin. Attention is all you need. In Isabelle Guyon, Ulrike von Luxburg, Samy Bengio, Hanna M. Wallach, Rob Fergus, S. V. N. Vishwanathan, and Roman Garnett, editors, Advances in Neural Information Processing Systems 30: Annual Conference on Neural Information Processing Systems 2017, December 4-9, 2017, Long Beach, CA, USA, pages 5998–6008, 2017. URL https://proceedings.neurips.cc/paper/2017/hash/3f5ee243547dee91fbd053c1c4a845aa-Abstract.html.
Vig et al. [2020] Jesse Vig, Sebastian Gehrmann, Yonatan Belinkov, Sharon Qian, Daniel Nevo, Yaron Singer, and Stuart M. Shieber. Investigating gender bias in language models using causal mediation analysis. In Hugo Larochelle, Marc’Aurelio Ranzato, Raia Hadsell, Maria-Florina Balcan, and Hsuan-Tien Lin, editors, Advances in Neural Information Processing Systems 33: Annual Conference on Neural Information Processing Systems 2020, NeurIPS 2020, December 6-12, 2020, virtual, 2020.
Wall et al. [2003] Michael E Wall, Andreas Rechtsteiner, and Luis M Rocha. Singular value decomposition and principal component analysis. In A practical approach to microarray data analysis, pages 91–109. Springer, 2003.
Wang et al. [2023] Peng Wang, Ningyu Zhang, Xin Xie, Yunzhi Yao, Bozhong Tian, Mengru Wang, Zekun Xi, Siyuan Cheng, Kangwei Liu, Guozhou Zheng, and Huajun Chen. Easyedit: An easy-to-use knowledge editing framework for large language models. CoRR, abs/2308.07269, 2023. doi: 10.48550/arXiv.2308.07269. URL https://doi.org/10.48550/arXiv.2308.07269.
Wang et al. [2024] Xiaohan Wang, Shengyu Mao, Ningyu Zhang, Shumin Deng, Yunzhi Yao, Yue Shen, Lei Liang, Jinjie Gu, and Huajun Chen. Editing conceptual knowledge for large language models. CoRR, abs/2403.06259, 2024. doi: 10.48550/ARXIV.2403.06259. URL https://doi.org/10.48550/arXiv.2403.06259.
Wedin [1972] Per-Åke Wedin. Perturbation bounds in connection with singular value decomposition. BIT Numerical Mathematics, 12:99–111, 1972.
Wu et al. [2023] Suhang Wu, Minlong Peng, Yue Chen, Jinsong Su, and Mingming Sun. Eva-kellm: A new benchmark for evaluating knowledge editing of llms. CoRR, abs/2308.09954, 2023. doi: 10.48550/ARXIV.2308.09954. URL https://doi.org/10.48550/arXiv.2308.09954.
Yao et al. [2023] Yunzhi Yao, Peng Wang, Bozhong Tian, Siyuan Cheng, Zhoubo Li, Shumin Deng, Huajun Chen, and Ningyu Zhang. Editing large language models: Problems, methods, and opportunities. In Houda Bouamor, Juan Pino, and Kalika Bali, editors, Proceedings of the 2023 Conference on Empirical Methods in Natural Language Processing, EMNLP 2023, Singapore, December 6-10, 2023, pages 10222–10240. Association for Computational Linguistics, 2023. URL https://aclanthology.org/2023.emnlp-main.632.
Yu et al. [2024] Lang Yu, Qin Chen, Jie Zhou, and Liang He. MELO: enhancing model editing with neuron-indexed dynamic lora. In Michael J. Wooldridge, Jennifer G. Dy, and Sriraam Natarajan, editors, Thirty-Eighth AAAI Conference on Artificial Intelligence, AAAI 2024, Thirty-Sixth Conference on Innovative Applications of Artificial Intelligence, IAAI 2024, Fourteenth Symposium on Educational Advances in Artificial Intelligence, EAAI 2014, February 20-27, 2024, Vancouver, Canada, pages 19449–19457. AAAI Press, 2024. doi: 10.1609/AAAI.V38I17.29916. URL https://doi.org/10.1609/aaai.v38i17.29916.
Zhang et al. [2024] Ningyu Zhang, Yunzhi Yao, Bozhong Tian, Peng Wang, Shumin Deng, Mengru Wang, Zekun Xi, Shengyu Mao, Jintian Zhang, Yuansheng Ni, Siyuan Cheng, Ziwen Xu, Xin Xu, Jia-Chen Gu, Yong Jiang, Pengjun Xie, Fei Huang, Lei Liang, Zhiqiang Zhang, Xiaowei Zhu, Jun Zhou, and Huajun Chen. A comprehensive study of knowledge editing for large language models. CoRR, abs/2401.01286, 2024. doi: 10.48550/ARXIV.2401.01286. URL https://doi.org/10.48550/arXiv.2401.01286.
Zhang et al. [2023] Yue Zhang, Yafu Li, Leyang Cui, Deng Cai, Lemao Liu, Tingchen Fu, Xinting Huang, Enbo Zhao, Yu Zhang, Yulong Chen, Longyue Wang, Anh Tuan Luu, Wei Bi, Freda Shi, and Shuming Shi. Siren’s song in the AI ocean: A survey on hallucination in large language models. CoRR, abs/2309.01219, 2023. doi: 10.48550/arXiv.2309.01219. URL https://doi.org/10.48550/arXiv.2309.01219.
[66] Chujie Zheng, Fan Yin, Hao Zhou, Fandong Meng, Jie Zhou, Kai-Wei Chang, Minlie Huang, and Nanyun Peng. On prompt-driven safeguarding for large language models. In ICLR 2024 Workshop on Secure and Trustworthy Large Language Models.
Zhong et al. [2023] Zexuan Zhong, Zhengxuan Wu, Christopher D. Manning, Christopher Potts, and Danqi Chen. Mquake: Assessing knowledge editing in language models via multi-hop questions. In Houda Bouamor, Juan Pino, and Kalika Bali, editors, Proceedings of the 2023 Conference on Empirical Methods in Natural Language Processing, EMNLP 2023, Singapore, December 6-10, 2023, pages 15686–15702. Association for Computational Linguistics, 2023. URL https://aclanthology.org/2023.emnlp-main.971.

Appendix A Theoretical Analysis Based on Perturbation Theory

Here, we provide a detailed analysis and proof of Section 3.2. We begin by introducing some definitions and then present several preliminary lemmas and theorems. These lemmas and theorems are finally used to prove Theorem 3, which is most relevant to our problem discussed in Section 3.2.

A.1 Definition

We discuss the problem $Ax=b$ , where $\tilde{A}$ is a perturbation of $A$ given by $\tilde{A}=A+E$ . We assume $b$ remains unchanged and $\tilde{x}$ represents the corresponding change, satisfying $\tilde{A}\tilde{x}=b$ . Here $A\in\mathbb{C}^{m\times n}$ , $b\in\mathbb{C}^{m}$ .

It is noteworthy that in the following derivation, $A^{H}$ denotes the conjugate transpose of $A$ , $A^{\dagger}$ represents the generalized inverse of $A$ , and $\|\ast\|$ represents 2-norm [51].

To simplify the problem, we apply a rotation. Specifically, let $V=(V_{1}\ V_{2})$ be a unitary matrix with $R(V_{1})=R(A^{H})$ , and let $U=(U_{1}\ U_{2})$ be a unitary matrix with $R(U_{1})=R(A)$ , where $R$ refers to the rank. Then

U^{H}AV=\begin{pmatrix}U_{1}^{H}AV_{1}&U_{1}^{H}AV_{2}\\ U_{2}^{H}AV_{1}&U_{2}^{H}AV_{2}\end{pmatrix}=\begin{pmatrix}A_{11}&0\\ 0&0\end{pmatrix},

(7)

where $A_{11}$ is square and nonsingular. If we set

U^{H}EV=\begin{pmatrix}U_{1}^{H}EV_{1}&U_{1}^{H}EV_{2}\\ U_{2}^{H}EV_{1}&U_{2}^{H}EV_{2}\end{pmatrix}=\begin{pmatrix}E_{11}&E_{12}\\ E_{21}&E_{22}\end{pmatrix},

(8)

then

U^{H}\tilde{A}V=\begin{pmatrix}A_{11}+E_{11}&E_{12}\\ E_{21}&E_{22}\end{pmatrix}=\begin{pmatrix}\tilde{A}_{11}&E_{12}\\ E_{21}&E_{22}\end{pmatrix}.

(9)

We will call these transformed, partitioned matrices the reduced form of the problem. Many statements about the original problem have revealing analogues in the reduced form.

In this form, $x$ is replaced by $V^{H}x$ and $b$ is replaced by $U^{H}b$ . If $x$ and $b$ are partitioned in the forms

x=\begin{pmatrix}x_{1}\\ x_{2}\end{pmatrix},\quad b=\begin{pmatrix}b_{1}\\ b_{2}\end{pmatrix},

(10)

where $x_{1},b_{1}\in\mathbb{C}^{r}$ , then

x_{1}=A_{11}^{-1}b_{1}

(11)

and

x_{2}=0.

(12)

Moreover, the norm of the residual vector

r=b-Ax

(13)

is given by

\|r\|=\|b_{2}\|.

(14)

Here, we define the symbol $\eta$ :

\eta=\frac{\|A\|\|x\|}{\|b\|},

(15)

and for any $F\in\mathbb{C}^{k\times r}$ ( $k\geq r$ ) the symbol $\Psi(F)$ , for the spectral norm:

\Psi_{2}(F)=\frac{\|F\|}{(1+\|F\|^{2})^{1/2}}.

(16)

A.2 Preliminary Lemmas & Theorems

After introducing some definitions, we give some preliminary lemmas and theorems, which are used to prove Theorem 3.

Lemma 1 Let

\kappa(A)=\|A\|\|A^{-1}\|

be the condition number of $A$ . If $\tilde{A}$ is nonsingular, then

\frac{\|\tilde{A}^{-1}-A^{-1}\|}{\|\tilde{A}^{-1}\|}\leq\kappa(A)\frac{\|E\|}{\|A\|}.

(17)

If in addition

\frac{\|E\|}{\|A\|}\kappa(A)<1,

then $\tilde{A}$ is perforce nonsingular and

\|\tilde{A}^{-1}\|\leq\frac{\|A^{-1}\|}{1-\kappa(A)\frac{\|E\|}{\|A\|}}.

(18)

Moreover

\frac{\|\tilde{A}^{-1}-A^{-1}\|}{\|A^{-1}\|}\leq\frac{\kappa(A)\frac{\|E\|}{\|A\|}}{1-\kappa(A)\frac{\|E\|}{\|A\|}}.

(19)

Lemma 2 In the reduced form the matrices $A$ and $\tilde{A}$ are acute if and only if $A_{11}$ is nonsingular and

E_{22}=E_{21}\tilde{A}_{11}^{-1}E_{12}.

(20)

In this case, if we set

F_{21}=E_{21}\tilde{A}_{11}^{-1}\quad\text{and}\quad F_{12}=\tilde{A}_{11}^{-1}E_{12},

then

\tilde{A}=\begin{pmatrix}I\\ F_{21}\end{pmatrix}\tilde{A}_{11}\begin{pmatrix}I&F_{12}\end{pmatrix}

and

\tilde{A}^{\dagger}=\begin{pmatrix}I&F_{12}\end{pmatrix}^{\dagger}\tilde{A}_{11}^{-1}\begin{pmatrix}I\\ F_{21}\end{pmatrix}^{\dagger}.

(21)

Lemma 3 The matrix

\begin{pmatrix}I\\ F\end{pmatrix}

satisfies

\left\|\begin{pmatrix}I\\ F\end{pmatrix}^{\dagger}\right\|\leq 1

(22)

and

\left\|\begin{pmatrix}I\\ F\end{pmatrix}^{\dagger}-\begin{pmatrix}I&0\end{pmatrix}\right\|=\Psi_{2}(F).

(23)

Theorem 1 Let $\tilde{A}$ be an acute perturbation of $A$ , and let

\hat{\kappa}=\|A\|\|\tilde{A}_{11}^{-1}\|.

(24)

Then

\frac{\|\tilde{A}^{\dagger}-A^{\dagger}\|}{\|A^{\dagger}\|}\leq\hat{\kappa}\frac{\|E_{11}\|}{\|A\|}+\Psi_{2}\left(\frac{\hat{\kappa}E_{12}}{\|A\|}\right)+\Psi_{2}\left(\frac{\hat{\kappa}E_{21}}{\|A\|}\right).

(25)

Proof.

Let

I_{21}=\begin{pmatrix}I\\ 0\end{pmatrix},\quad I_{12}=\begin{pmatrix}I&0\end{pmatrix},

(26)

J_{21}=\begin{pmatrix}I\\ F_{21}\end{pmatrix},\quad J_{12}=\begin{pmatrix}I&F_{12}\end{pmatrix}.

(27)

$\tilde{A}^{\dagger}=J_{12}^{\dagger}A_{11}^{-1}I_{21}^{\dagger}$ , hence

\tilde{A}^{\dagger}-A^{\dagger}=(J_{12}^{\dagger}-I_{12}^{\dagger})A_{11}^{-1}I_{21}^{\dagger}+J_{12}^{\dagger}A_{11}^{-1}(J_{21}^{\dagger}-I_{21}^{\dagger})+J_{12}^{\dagger}(\tilde{A}_{11}^{-1}-A_{11}^{-1})J_{21}^{\dagger}.

(28)

From Lemma 1 we have the following bound:

\|J_{12}^{\dagger}(\tilde{A}^{-1}_{11}-A_{11}^{-1})J_{21}^{\dagger}\|\leq\|A_{11}^{-1}\|\hat{\kappa}\frac{\|E_{11}\|}{\|A_{11}\|}.

(29)

By Lemma 3

\|(J_{12}^{\dagger}-I_{12}^{\dagger})A_{11}^{-1}I^{\dagger}_{21}\|\leq\|A_{11}^{-1}\|\|J^{\dagger}_{12}-I^{\dagger}_{12}\|=\|A_{11}^{-1}\|\Psi_{2}(F_{12})

(30)

=\|A_{11}^{-1}\|\Psi_{2}(\tilde{A}_{11}^{-1}E_{12})

(31)

\leq\|A_{11}^{-1}\|\Psi_{2}\left(\frac{\hat{\kappa}E_{12}}{\|A\|}\right),

(32)

and likewise

\|J_{12}^{\dagger}A_{11}^{-1}(J_{21}^{\dagger}-I_{21}^{\dagger})\|\leq\|A_{11}^{-1}\|\Psi_{2}\left(\frac{\hat{\kappa}E_{21}}{\|A\|}\right)\leq\|A^{\dagger}\|\Psi_{2}\left(\frac{\hat{\kappa}E_{21}}{\|A\|}\right).

(33)

∎

Theorem 2 In Theorem 1, let

\kappa=\|A\|\|{A}^{\dagger}\|,

(34)

and suppose that

\|A^{\dagger}\|\|E_{11}\|<1,

(35)

so that

\gamma\equiv 1-\frac{\kappa\|E_{11}\|}{\|A\|}>0.

(36)

Then

\|\tilde{A}^{\dagger}\|\leq\frac{\|A^{\dagger}\|}{\gamma},

(37)

and

\frac{\|\tilde{A}^{\dagger}-A^{\dagger}\|}{\|A^{\dagger}\|}\leq\frac{\kappa\|E_{11}\|}{\gamma\|A\|}+\Psi_{2}\left(\frac{\kappa E_{21}}{\gamma\|A\|}\right)+\Psi_{2}\left(\frac{\kappa E_{12}}{\gamma\|A\|}\right).

(38)

Proof.

From the equation $\tilde{A}^{\dagger}=J_{12}^{\dagger}\tilde{A}_{11}^{-1}J_{21}^{\dagger}$ , we have

\|\tilde{A}^{\dagger}\|\leq\|J_{12}^{\dagger}\|\|\tilde{A}_{11}^{-1}\|\|J_{21}^{\dagger}\|\leq\|\tilde{A}_{11}^{-1}\|.

(39)

By Lemma 1,

\|\tilde{A}^{-1}_{11}\|\leq\frac{\|A_{11}^{-1}\|}{\gamma}=\frac{\|A^{\dagger}\|}{\gamma},

(40)

which establishes (37). Also $\hat{\kappa}\leq\frac{\kappa}{\gamma}$ , and the inequality (38) follows from (25).

∎

A.3 Core Theorem

Finally, we give the core theorem used in main paper. Some symbols and definitions have been claimed in Appendix A.1 and A.2.

Theorem 3 Let ${x}=A^{\dagger}{b}$ and $\tilde{{x}}=\tilde{A}^{\dagger}{b}$ , where $\tilde{A}=A+E$ , and $E$ is an acute perturbation of $A$ . Then

\frac{\|{x}-\tilde{{x}}\|}{\|{x}\|}\leq\hat{\kappa}\frac{\|E_{11}\|}{\|A\|}+\Psi_{2}\left(\frac{\hat{\kappa}E_{12}}{\|A\|}\right)+\hat{\kappa}^{2}\frac{\left\|E_{12}\right\|}{\|A\|}\left(\eta^{-1}\frac{\|{b}_{2}\|}{\|{b}_{1}\|}+\frac{\|E_{21}\|}{\|A\|}\right).

(41)

Proof.

By Lemma 2, write

\tilde{x}-x=J_{12}^{\dagger}(\tilde{A}_{11}^{-1}-A_{11}^{-1})b_{1}+(J_{12}^{\dagger}-I_{12}^{\dagger})A_{11}^{-1}b_{1}+J_{12}^{\dagger}\tilde{A}_{11}^{-1}(J_{21}^{\dagger}-I_{21}^{\dagger})b.

(42)

Then

\|J_{12}^{\dagger}(\tilde{A}_{11}^{-1}-A_{11}^{-1})b_{1}\|\leq\hat{\kappa}\frac{\|E_{11}\|}{\|A\|}\|x\|,

(43)

and

\|(J^{\dagger}_{12}-I^{\dagger}_{12})A_{11}^{-1}b_{1}\|\leq\Psi_{2}\left(\frac{\hat{\kappa}E_{12}}{\|A\|}\right)\|x\|.

(44)

Now

\displaystyle J^{\dagger}_{12}\tilde{A}_{11}^{-1}(J^{\dagger}_{21}-I^{\dagger}_{21})b

\displaystyle=J^{\dagger}_{12}\tilde{A}_{11}^{-1}((I+F^{H}_{21}F_{21})^{-1}-I)b_{1}+J^{\dagger}_{12}\tilde{A}_{11}^{-1}(I+F^{H}_{21}F_{21})^{-1}F^{H}_{21}b_{2}.

(45)

To bound the first term in (45), note that

(I+F^{H}_{21}F_{21})^{-1}-I=-(I+F^{H}_{21}F_{21})^{-1}F^{H}_{21}F_{21}.

Hence

$\displaystyle\\|J_{12}\tilde{A}_{11}^{-1}((I+F^{H}_{21}F_{21})-I)b_{1}\\|$	$\displaystyle\leq\\|\tilde{A}_{11}^{-1}\\|\\|(I+F^{H}_{21}F_{21})^{-1}\\|\\|F^{H}_{21}\\|\\|F_{21}b_{1}\\|$
	$\displaystyle\leq\\|\tilde{A}_{11}^{-1}\\|\\|E_{21}\tilde{A}_{11}^{-1}b_{1}\\|$
	$\displaystyle\leq\\|\tilde{A}_{11}^{-1}\\|\\|E_{21}\\|^{2}\\|{x}\\|$
	$\displaystyle=\left(\frac{\hat{\kappa}\\|E_{21}\\|_{2}}{\\|A\\|}\right)^{2}\\|{x}\\|.$	(46)

For the second term in (45) we have

$\displaystyle\\|J_{21}^{\dagger}\tilde{A}_{11}^{-1}(I+F^{H}_{21}F_{21})^{-1}F_{21}b_{2}\\|$	$\displaystyle\leq\\|\tilde{A}_{11}^{-1}\\|^{2}\\|E_{21}\\|\\|b_{2}\\|$
	$\displaystyle=\\|\tilde{A}_{11}^{-1}\\|^{2}\\|E_{21}\\|\frac{\\|b_{2}\\|}{\\|b_{1}\\|}\eta^{-1}\\|x\\|\\|A\\|$
	$\displaystyle\leq\eta^{-1}\hat{\kappa}^{2}\frac{\\|E_{21}\\|\\|b_{2}\\|}{\\|A\\|\\|b_{1}\\|}\\|x\\|.$	(47)

The bound (41) follows on combining (42)–(47).

∎

Readers can refer to this work [51] for more details of perturbation analysis.

Returning to our problem, consider $Wk=v$ , where $(k,v)\in P$ . Let $\tilde{W}=W+\Delta W$ , where $\Delta W$ is the corresponding perturbation matrix. Assuming $v$ remains constant, there exists $\Delta k$ such that $\tilde{k}=k+\Delta k$ satisfies $\tilde{W}\tilde{k}=v$ . And we have $k=W^{\dagger}v$ and $\tilde{k}=\tilde{W}^{\dagger}v$ . Applying Theorem 3, we obtain

\frac{\|\Delta k\|}{\|k\|}=\frac{\|k-\tilde{k}\|}{\|k\|}\leq\hat{\kappa}\frac{\|\Delta E_{11}\|}{\|W\|}+\Psi_{2}\left(\frac{\hat{\kappa}\Delta E_{12}}{\|W\|}\right)+\hat{\kappa}^{2}\frac{\|\Delta E_{12}\|}{\|W\|}\left(\eta^{-1}\frac{\|v_{2}\|}{\|v_{1}\|}+\frac{\|\Delta E_{21}\|}{\|W\|}\right),

(48)

where $\Delta E_{11}$ , $\Delta E_{12}$ , $\Delta E_{21}$ , and $\Delta W$ are directly related, and each term on the right-hand side involves $\hat{\kappa}$ . This means that the relative perturbation of the vector $k$ is constrained by $\hat{\kappa}$ . According to Theorem 2, $\hat{\kappa}\leq\frac{\kappa}{\gamma}$ , where $\kappa=\|W\|\|{W}^{\dagger}\|$ is the condition number of $W$ . This indicates that $\kappa$ is a robust indicator of the impact of $\Delta W$ on the vector $k$ .

Appendix B Experimental Setup

B.1 Baseline Editing Methods

Three popular model editing methods were selected as baselines including:

$\bullet$

MEND [43]⁶⁶6https://github.com/eric-mitchell/mend: it learned a hypernetwork to produce weight updates by decomposing the fine-tuning gradients into rank-1 form.
$\bullet$

ROME [41]⁷⁷7https://github.com/kmeng01/rome: it first localized the factual knowledge at a specific layer in the transformer MLP modules, and then updated the knowledge by directly writing new key-value pairs in the MLP module.
$\bullet$

MEMIT [42]⁸⁸8https://github.com/kmeng01/memit: it extended ROME to edit a large set of facts and updated a set of MLP layers to update knowledge.

The ability of these methods was assessed based on EasyEdit⁹⁹9https://github.com/zjunlp/EasyEdit [58], an easy-to-use knowledge editing framework which integrates the released codes and hyperparameters from previous methods.

B.2 Editing Datasets and Evaluation Metrics

Table 2 shows the examples of two datasets.

Table 2: The editing datasets of both CounterFact and ZsRE.

Datasets	Editing prompt
CounterFact	In America, the official language is
ZsRE	Which was the record label for New Faces, New Sounds?

Besides, following previous works [41, 43, 42], the editing performance metrics for the CounterFact dataset and ZsRE dataset are efficacy, generalization and locality, but there are some computational differences. In the main paper, the metrics of editing performance are calculated for the CounterFact dataset. For the ZsRE dataset, here are the details:

Efficacy validates whether the edited models could recall the editing fact under editing prompt $p_{i}$ . The assessment is based on Efficacy Score (ES) representing as: $\mathbb{E}_{i}[\mathbbm{1}[\,\operatorname{argmax}_{o}P_{f_{\theta_{n}}}(o\,|\,p_{i})=o^{*}_{i}]\,]$ .

Generalization verifies whether the edited models could recall the editing fact under the paraphrase prompts $\mathcal{P}^{G}_{i}$ via Generalization Score (GS): $\mathbb{E}_{i}\,[\mathbb{E}_{p\in\mathcal{P}^{G}_{i}}[\mathbbm{1}[\,\operatorname{argmax}_{o}P_{f_{\theta_{n}}}(o\,|\,p)=o^{*}_{i}]\,]$ .

Locality verifies whether the output of the edited models for inputs out of editing scope remains unchanged under the locality prompts $\mathcal{P}^{L}_{i}$ via Locality Score (LS): $\mathbb{E}_{i}\,[\mathbb{E}_{p_{l}\in\mathcal{P}^{L}_{i}}[\mathbbm{1}[\,\operatorname{argmax}_{o}P_{f_{\theta_{n}}}(o\,|\,p_{l})=o_{l}]\,]\,]$ , where $o_{l}$ was the original answer of $p_{l}$ .

B.3 Hyperparameters of PRUNE

When conducting experiments, for different editing methods, LLMs and editing datasets, the hyperparameter $\alpha$ in function $F$ of PRUNE is different. Table 3 shows the details of this hyperparameter. $e$ is the base of the natural logarithm.

Table 3: The hyperparameters

\alpha

for PRUNE.

Datasets	Models	ROME	MEMIT	MEND
CounterFact	GPT-2 XL	1.2	1.2	1.2
	LLaMA-2	1.2	$e$	1.2
	LLaMA-3	1.5	$e$	-
ZsRE	LLaMA-2	1.2	$e$	$e$

B.4 Task Prompts

The prompts for each downstream task were illustrated in Table 4.

Table 4: The prompts to LLMs for evaluating their zero-shot performance on these general tasks.

Reasoning:

Q: {QUESTION} A: Let’s think step by step. {HINT} Therefore, the answer (arabic numerals) is:

NLI:

{SENTENCE1} entails the {SENTENCE2}. True or False? answer:

Open-domain QA:

Refer to the passage below and answer the following question. Passage: {DOCUMENT} Question: {QUESTION}

Summarization:

{DIALOGUE} TL;DR:

B.5 Experiments Compute Resources

We used NVIDIA A800 80GB GPU for experiments. For LLaMA-2 (7B) and LLaMA-3 (8B), it occupies about 40+GB memory and costs about 3 hours for each editing method to run 200 edits and then to test downstream tasks . For GPT-2 XL (1.5B), it needs 10+GB and costs about 1.5 hours for each editing method to run 200 edits and then to test downstream tasks.

Appendix C Experimental Results

C.1 Results of General Abilities

Figure 6 and 7 show the downstream task performance of edited models with GPT-2 XL and LLaMA-3 (8B) on CounterFact dataset. Figure 8 shows the downstream task performance of edited models with LLaMA-2 (7B) on ZsRE dataset. Due to limitations of computing resources, experiments were conducted using only LLaMA-2 (7B) on the ZsRE dataset. We will supplement experiments with other LLMs in the future.

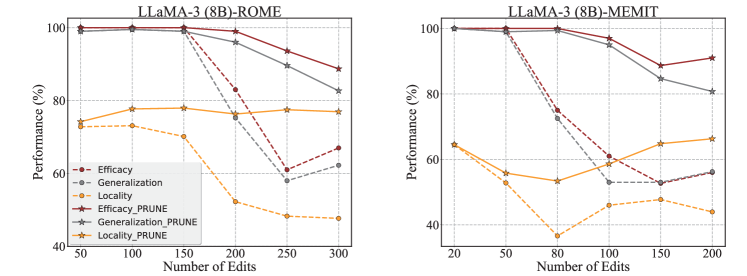
C.2 Results of Editing Performance

Figure 9 and 10 shows the editing performance of edited models with GPT-2 XL and LLaMA-3 (8B) on CounterFact dataset. Figure 11 shows the editing performance of edited models with LLaMA-2 (7B) on ZsRE dataset.

C.3 Results of another function for PRUNE

In the main paper, $\operatorname{log}$ function is used in $F$ in PRUNE to restrain $\hat{\sigma}_{i}$ . Here we use the $\operatorname{linear}$ function, which could be represented as: $F(\hat{\sigma}_{i})=\frac{1}{\beta}*\hat{\sigma}_{i}+\frac{\beta-1}{\beta}*max\{\sigma_{i}\}$ . Here $\beta>1$ was a hyperparameter and was set as 2 in this section. Figure 12 and 13 respectively show some downstream task performance and editing performance with $\operatorname{linear}$ function on CounterFact dataset.

Compared with Figure 6 and 9, we observed that although the $\operatorname{linear}$ function in PRUNE played a role in preserving general abilities and maintaining editing performance, its effectiveness was noticeably inferior to that of the $\operatorname{log}$ function when the number of edits was large.

C.4 Condition number with PRUNE

Figure 14 shows after coupling with PRUNE, the condition number of MEMIT is significantly restrained.

Appendix D Broader Impacts

This work offers significant advancements in the field of model editing for LLMs. By addressing the challenge of preserving general abilities while performing sequential edits, PRUNE facilitates continual learning and adaptability in LLMs. This can lead to several positive impacts, such as:

Enhanced Adaptability. It enables LLMs to update their knowledge base quickly and accurately without extensive retraining. This adaptability is crucial in dynamic environments where up-to-date information is vital, such as real-time translation services, personalized learning systems, and interactive virtual assistants.

Resource Efficiency. By mitigating the need for full retraining, PRUNE significantly reduces computational resources and energy consumption. This aligns with sustainable AI and makes it more feasible to deploy LLMs in resource-constrained settings.

Improved Performance in Specialized Tasks. PRUNE’s ability to perform targeted edits without compromising overall model performance can enhance LLMs’ effectiveness in specialized domains, such as medical diagnostics, legal analysis, and technical support, where precise and updated knowledge is essential.

While this work offers many benefits, there are potential negative societal impacts that must be considered:

Misuse for Malicious Purposes. The capability to edit LLMs efficiently could be exploited to inject harmful or biased information into models, thereby spreading disinformation or propaganda. This risk is particularly concerning in applications involving social media and news dissemination where LLMs might generate or amplify misleading content.

Fairness. Unintended biases could be introduced during the editing process, potentially exacerbating existing biases in LLMs. This could lead to unfair treatment or misrepresentation of specific groups, especially if the editing is not conducted with proper oversight and consideration of ethical implications.

Privacy Concerns. The ability to update models quickly might also pose privacy risks, as models could be edited to include sensitive or personal information. Ensuring that editing processes do not compromise individual privacy is critical, particularly in applications involving personal data.

To mitigate these potential negative impacts, several strategies could be implemented:

Gated Release and Monitoring. Limiting access to the framework through gated releases and monitoring its usage can help prevent misuse.

Bias and Fairness Audits. Conducting regular audits to assess and address biases in the model editing process can help ensure that edits do not unfairly impact any specific group. Developing guidelines for ethical editing practices is also essential.

Privacy Protection Measures. Establishing clear protocols for handling sensitive data during the editing process can help protect privacy. Anonymization and encryption techniques should be employed to safeguard personal information.

By considering both the positive and negative impacts and implementing appropriate mitigation strategies, this work can contribute to the responsible and ethical advancement of model editing technologies.

$\displaystyle\\|J_{12}\tilde{A}_{11}^{-1}((I+F^{H}_{21}F_{21})-I)b_{1}\\|$	$\displaystyle\leq\\|\tilde{A}_{11}^{-1}\\|\\|(I+F^{H}_{21}F_{21})^{-1}\\|\\|F^{H}_{21}\\|\\|F_{21}b_{1}\\|$
	$\displaystyle\leq\\|\tilde{A}_{11}^{-1}\\|\\|E_{21}\tilde{A}_{11}^{-1}b_{1}\\|$
	$\displaystyle\leq\\|\tilde{A}_{11}^{-1}\\|\\|E_{21}\\|^{2}\\|{x}\\|$
	$\displaystyle=\left(\frac{\hat{\kappa}\\|E_{21}\\|_{2}}{\\|A\\|}\right)^{2}\\|{x}\\|.$	(46)

$\displaystyle\\|J_{21}^{\dagger}\tilde{A}_{11}^{-1}(I+F^{H}_{21}F_{21})^{-1}F_{21}b_{2}\\|$	$\displaystyle\leq\\|\tilde{A}_{11}^{-1}\\|^{2}\\|E_{21}\\|\\|b_{2}\\|$
	$\displaystyle=\\|\tilde{A}_{11}^{-1}\\|^{2}\\|E_{21}\\|\frac{\\|b_{2}\\|}{\\|b_{1}\\|}\eta^{-1}\\|x\\|\\|A\\|$
	$\displaystyle\leq\eta^{-1}\hat{\kappa}^{2}\frac{\\|E_{21}\\|\\|b_{2}\\|}{\\|A\\|\\|b_{1}\\|}\\|x\\|.$	(47)