Personalized Federated Learning with Attention-based Client Selection
Abstract
Personalized Federated Learning (PFL) relies on collective data knowledge to build customized models. However, non-IID data between clients poses significant challenges, as collaborating with clients who have diverse data distributions can harm local model performance, especially with limited training data. To address this issue, we propose FedACS, a new PFL algorithm with an Attention-based Client Selection mechanism. FedACS integrates an attention mechanism to enhance collaboration among clients with similar data distributions and mitigate the data scarcity issue. It prioritizes and allocates resources based on data similarity. We further establish the theoretical convergence behavior of FedACS. Experiments on CIFAR10 and FMNIST validate FedACS’s superiority, showcasing its potential to advance personalized federated learning. By tackling non-IID data challenges and data scarcity, FedACS offers promising advances in the field of personalized federated learning.
1 Introduction
Federated learning is a collaborative learning paradigm that allows multiple clients to work together while ensuring the preservation of their privacy Yang et al. (2019a). By leveraging the collective knowledge and data from all participating clients, federated learning aims to achieve better learning performance compared with individual client efforts McMahan et al. (2017). This collaborative nature has made federated learning increasingly popular, finding numerous practical applications where data decentralization and privacy are paramount. The privacy-preserving solutions offered by federated learning have found extensive applications in domains such as healthcare, smart cities, and finance Zheng et al. (2022); Yang et al. (2019b); Xu et al. (2021).
However, the effectiveness of the collaborative approach in federated learning is highly dependent on the distribution of data among the clients. While federated learning performs exceptionally well when data distribution among clients is independent and identically distributed (IID), this is not the case in many real-world scenarios Kairouz et al. (2021). When the global model, which is collectively trained across decentralized clients, encounters diverse datasets with varying statistical characteristics, it may face challenges in effectively generalizing to the unique local data of each client Zhao et al. (2018); Jiang et al. (2019). The performance of the global model may be suboptimal on certain clients’ data due to differences in data distributions and patterns. This limitation becomes more pronounced as the diversity among local data from different clients continues to increase Deng et al. (2020).
To address this issue, personalized federated learning (PFL) techniques have been proposed, which aim to overcome the limitations of traditional federated learning by incorporating personalized adaptation in local clients. Instead of relying solely on a single global model, PFL allows each client to tailor the model to her specific data distribution, preferences, and local context Kulkarni et al. (2020). Most existing PFL methods focus on taking the global model as an initial model for local training or incorporating the global model into the loss function Deng et al. (2020); Li et al. (2021); T Dinh et al. (2020); Fallah et al. (2020). However, recent work by Huang et al. Huang et al. (2021) challenges the assumption that a single global model can adequately fit all clients in personalized cross-silo federated learning with non-IID data. In particular, they argue that the misassumption of a universally applicable global model remains a fundamental bottleneck Huang et al. (2021). However, their claims lack substantial theoretical foundations or sufficient empirical evidence. To shed light on this issue, Mansour et al. Mansour et al. (2020) provide theoretical insights into the generalization of the uniform global model and demonstrate that the discrepancy between local and global distributions influences the disparity between local and global models. In this study, we present an empirical example to further validate the idea that a single global model cannot adequately fit all clients. Table 1 presents the learning performance of local training models and two PFL methods Fallah et al. (2020); Li et al. (2021). For each dataset, we utilize a Dirichlet distribution with the parameter of 0.5 to partition it, and subsequently, we sample 50 data points from the training dataset for the training process. Specifically, Ditto-P and PerAvg-P represent the results of personalized models, while Ditto-G and PerAvg-G reflect the performance of global models generated by the respective algorithms. It is evident from the table that the global models produced by the PFL methods struggle to achieve satisfactory generalization across clients and, in some cases, even perform worse than the locally trained models. This empirical example highlights the need for novel approaches that go beyond the simple fine-tuning of global models and account for the inherent heterogeneity in data distributions among clients.
| Dataset | CIFAR10 dir = 0.5 | FMNIST dir = 0.5 |
|---|---|---|
| Local | 77.29 | 75.98 |
| Ditto-P | 77.33 | 78.79 |
| Ditto-G | 39.47 | 76.34 |
| PerAvg-P | 73.07 | 74.07 |
| PerAvg-G | 28.90 | 69.14 |
Motivated by the insights gained from Huang et al. (2021) and recognizing the challenges posed by the scarcity of data in specific areas such as medical care, in this paper, we propose a PFL algorithm with an Attention-based Client Selection mechanism (FedACS) that aims to overcome the dependency on a single global model and leverage the model information from other clients to develop a personalized model for each client. By employing an attention mechanism, FedACS allows clients to receive and process personalized messages tailored to their specific model parameters, enhancing the effectiveness of collaboration. Additionally, we provide the convergence of our proposed FedACS method in general scenarios, ensuring the reliability and stability of the algorithm. This demonstrates that the proposed method can effectively converge to optimal solutions for personalized models in general settings. To evaluate the effectiveness of the proposed methods, we conduct extensive experiments on various datasets and settings, allowing for a comprehensive performance evaluation. The results of the experiments demonstrate the superior performance of the proposed methods compared to those of existing approaches.
2 Personalized Federated Learning
2.1 Formulation
Standard federated learning (FL) aims to train a global model by aggregating local models contributed by multiple clients without the need for their raw data to be centralized. In FL, there are clients communicating with a server to solve the problem: to find a global model . The function denotes the expected loss over the data distribution of the client . One of the first FL algorithms is FedAvg McMahan et al. (2017), which uses local stochastic gradient descent (SGD) updates and builds a global model from a subset of clients.
However, the performance of the global model tends to degrade when faced with clients whose data distributions differ significantly from the global training data distribution. On the other hand, local models trained on the respective data distributions match the distributions at inference time, but their generalization capabilities are limited due to the data scarcity issue Mansour et al. (2020). Personalized federated learning (PFL) can be viewed as a middle ground between pure local models and global models, as it combines the generalization properties of the global model with the distribution matching characteristic of the local model Li et al. (2021); Fallah et al. (2020); T Dinh et al. (2020); Deng et al. (2020).
In PFL, the goal is to train personalized models for individual clients while respecting data privacy and accommodating user-specific requirements. The problem can be framed as:
Instead of solving the traditional PFL problem, Huang et al. Huang et al. (2021) argued that the fundamental bottleneck in personalized cross-silo federated learning with non-IID data is that the misassumption of one global model can fit all clients. Therefore, they proposed a different approach by adding a regularized term with -norm of model weights distances among clients and formulate the PFL problem as:
| (1) |
in which is a matrix that contains clients’ local models as its columns and is a regularization parameter. is known as “client-side personalization" in the context of PFL. is a regularization term designed to help clients with similar data distributions collaboratively train their own models.
2.2 Our proposed method: FedACS
We propose a novel federated attention-based client selection algorithm (FedACS) (as illustrated in Algorithm1) to solve the optimization problem (1). In this paper, we mainly consider:
| (2) |
where is the normalized score to measure data distribution similarity. It is worth mentioning that the formation of is easy to generate into other functions, like Huang et al. (2021). The above formulation implies that locally optimizing the objective function requires each client to collect the other clients’ model parameters for computation. However, researchers find that adversaries can infer data information in the training set based on the model parameters, and directly gathering model parameters will violate the principles of federated learning to protect data privacy Fredrikson et al. (2015); Shokri et al. (2017); Hitaj et al. (2017). To address this dilemma, we leverage the idea of incremental optimization Bertsekas et al. (2011). Specifically, we iteratively optimize by alternatively optimizing and until convergence. Note that FedACS handles the refinement of on the server side. We introduce an intermediate model for each client, and these intermediate models form the model matrix in the same way as . In the -th iteration, we first apply a gradient descent step to update :
| (3) |
where is the collection of local models from the last round and is the learning rate. Under the definition (2), the gradient of ’s -th column is . In this paper, we use the cosine similarity of the model parameters instead of the data similarity to avoid the accessibility of the server to local data, i.e. .
As mentioned above, the performance of a local model could be adversely affected if each client averages information from those with different data distributions. Thus, in practice, we also introduce to control the degree of collaboration. We adopt a dynamic strategy to define for each round. After gathering the parameters from clients at the -th round, the server first computes the similarity of the model to generate the similarity matrix , then is calculated by the -quantile of all elements in . We can adjust the ratio to alter the degree of collaboration. Modifying can effectively mitigate the aggregation effect that arises from initial training rounds, where the model parameters fail to accurately represent the underlying data distribution accurately. After having , we only consider the model similarity greater than and calculate as follows:
| (4) |
Since the similarity of the client model to itself is always 1 and greater than . Like the attention mechanism in deep learning, clients with highly similar data distributions receive higher similarity scores, enabling the server to assign greater weights to their models during the combination Vaswani et al. (2017). By differentiating between models based on their relevance and informativeness, the server can selectively assign the most pertinent models to each client rather than treating all models equally. Furthermore, the server can collect weights from clients and utilize the attention mechanism to optimize effectively while still ensuring the preservation of data privacy for all the involved clients.
After optimizing on the server, FedACS then optimizes on clients’ devices by taking as initialization of and computes locally by:
| (5) |
The update of draws inspiration from local fine-tuning in FL that takes the global model as initialization and updates the local models with several gradient steps to fit local data distribution. Considering the scarcity of data, it is more efficient to use as an initial value instead of incorporating it into the objective function. . This research is driven by prior studies that have shown difficulties in achieving high training accuracy when the data is either limited or unevenly spread out, thus highlighting the significance of a carefully selected starting pointLi et al. (2019).
By iteratively optimizing through alternating between and optimization, FedACS continues this process until a predefined maximum number of iterations, , is reached.
2.3 Relation to FedAMP
We note that the usage of the regularization term in FedACS bears resemblance to FedAMPHuang et al. (2021), a method that also applies attentive message passing to facilitate similar clients to collaborate more. However, FedACS differs from FedAMP in the update steps. First, when computing the intermediate model matrix , FedAMP combines all client models for each client, while FedACS only uses information from clients who share similar data distribution to further reduce the influence from unrelated clients. Meanwhile, if we set the threshold then the calculation of is the same as that in FedAMP. Second, for each round, FedAMP updates by , which means the needs to reach the local optimal. However, it is not easy to be satisfied when data is insufficient on local devices, and when the learning rate is small enough, the update function in FedAMP will be simplified to without using local data information. Additionally, the Euclidean distance version of FedAMP incorporates an -term regularization, which adds the Euclidean distance of the models to the objective function without using weighted scores. However, this approach provides limited assistance to the server in effectively assigning similar clients’ models to each client, thereby underutilizing the potential of the attention mechanism. As discussed above, the limitation of data may adversely influence the performance of FedAMP, while our proposed FedACS will not suffer from this issue. The experiment results also demonstrate our conjectures.
2.4 Convergence analysis of FedACS
In this subsection, we provide the convergence analysis of FedACS under suitable conditions without the special requirement of the convexity of the objective function. We start with the definition of -approximate first-order stationary point.
Definition 1. A point is considered an -approximate First-Order Stationary Point (FOSP) for the problem (1) if it satisfies
Consistent with the analysis performed in various incremental and stochastic optimization algorithms Bertsekas et al. (2011); Nemirovski et al. (2009); Huang et al. (2021), we introduce the following assumption and present the main result of the paper.
Assumption 1. There exists a constant such that and hold for every , where is the subdifferential of and is the Frobenius norm.
Theorem 2.1.
Assuming the validity of Assumption 1 and considering the continuous differentiability of functions and , with gradients that exhibit Lipschitz continuity with a modulus , if and , then the model matrix sequence generated by Algorithm 1 satisfies the following.
| (6) |
where . Additionally, if and satisfies and , then
| (7) |
Remark. Theorem 1 implies that for any , FedACS needs at most iterations to find an -approximate stationary point of problem (1) such that . It also establishes the global convergence of FedACS to a stationary point of problem (1) when is smooth and non-convex. We are unable to provide proof due to page limitations.
3 Experiments
3.1 Experimental settings
We evaluate the performance of FedACS and compare it with the state-of-the-art PFL algorithms, including Ditto Li et al. (2021), PerAvg Fallah et al. (2020), pFedMe T Dinh et al. (2020), APFL Deng et al. (2020), and FedAMP Huang et al. (2021). The first three methods are local fine-tuning methods, using the global model to help fine-tune local models. FedAMP is a method that focuses on adaptively facilitating pairwise collaborations among clients. To ensure the completeness of our experiments, we have also included the results obtained using the standard FL method FedAvg McMahan et al. (2017). The performance of all methods is evaluated by the mean test accuracy across all clients. We perform five experiments for each dataset and partition configuration, wherein we record both the mean and variance of the test accuracy. All methods are implemented in PyTorch 1.8 running on NVIDIA 3090.
We use two public benchmark data sets, FMNIST (FashionMNIST) Xiao et al. (2017) and CIFAR10 Krizhevsky et al. (2009). First, we simulate the non-IID and data-sufficient settings by employing two classical data split methods to distribute the data among 100 clients. These methods include: 1) a pathological non-IID data setting, where the dataset is partitioned in a non-IID manner, assigning two classes of samples to each client; and 2) a practical non-IID data setting, where the dataset is partitioned in a non-IID manner following a Dirichlet 0.5 distribution McMahan et al. (2017). To simulate scenarios where data insufficiency is encountered during training for each dataset, we adopt two distinct data settings: 1) a pathological non-IID data setting that distributes data into 100 clients following Dirichlet 0.5 distribution, and each user only keeps 50 pieces of data samples for training to simulate the scenario where clients lack sufficient training data: 2) a practical non-IID data setting that distributes data into 500 clients following Dirichlet 0.5 distribution to simulate the scenario of a large number of clients and only some clients participate in each round.

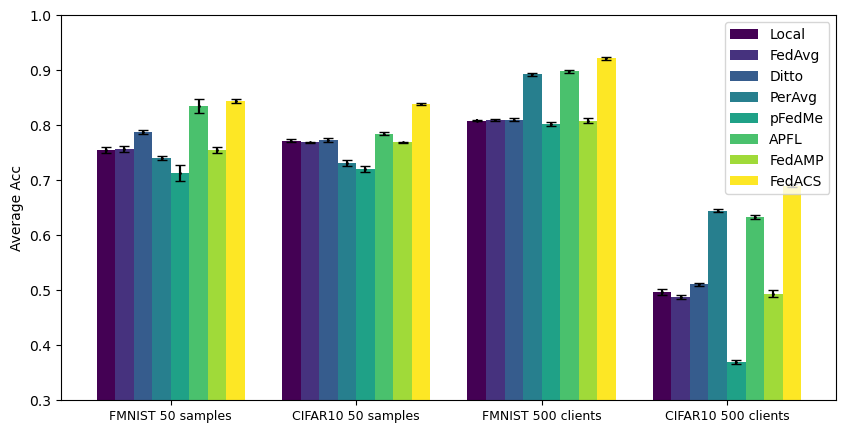
3.2 Results on the sufficient non-IID data setting
Figure 1(a) presents the mean accuracy and standard deviation per method and sufficient data setting. The two histograms on the left display the performance of PFL methods under pathological settings, while the right-side histograms illustrate the results when the data is partitioned according to the Dirichlet 0.5 distribution. It can be observed that FedACS performs comparably to most PFL methods, but with lower standard deviations. This similarity in performance may be attributed to the availability of sufficient data, allowing the global model to possess adequate generalization ability, while its local fine-tuning enables better adaptation to local data distributions. The abundance of training data simplifies the classification task for each client, as evidenced by the strong performance of models trained solely on local datasets. However, non-IID data settings pose challenges for global federated learning methods Huang et al. (2021). FedAvg’s performance on Cifar10 declines noticeably because it introduces instability in the gradient-based optimization process. This instability arises from aggregating personalized models trained on non-IID data from different clients Zhang et al. (2021). APFL achieves the best performance in the pathological setting by adaptively learning the model and leveraging the relationship between local and global models, thus increasing the diversity of local models as learning progresses Deng et al. (2020). On the other hand, we can observe that pFedMe struggles to achieve good performance, as it focuses on solving the bilevel problem by using the aggregation of data from multiple clients to improve the global model rather than optimize local performance.
3.3 Results on the insufficient non-IID data setting
Figure 1(b) presents the mean accuracy and standard deviation per method and insufficient data setting. The two histograms on the left depict the mean accuracy with only 50 data samples per client, whereas those on the right showcase the results when the data is divided among 500 clients. It is evident that FedACS outperforms all other methods with smaller standard deviations in both the FMNIST and CIFAR10 datasets. The three local fine-tuning PFL methods face challenges across different datasets and settings, highlighting the fundamental bottleneck in PFL with non-IID data. By relying solely on a misleading global model, the significance of local data distribution in PFL is underestimated, and a single global model fails to capture the intricate pairwise collaboration relationships between clients. It is evident that PerAvg outperforms pFedMe in all settings. Both methods incorporate a “meta-model" during training, but PerAvg utilizes it as an initialization to optimize a one-step gradient update for its personalized model. On the other hand, pFedMe simultaneously pursues both personalized and global models. As discussed in Section 2.3, leveraging the meta-model for a single local update step may yield better results when local devices have limited data. The reason behind PerAvg’s suboptimal performance in scenarios where each client possesses only 50 data samples can be attributed to its requirement of three data batches for a single update step. Consequently, the training process becomes insufficient due to the limited amount of data available. As discussed in Section 2.3, FedAMP fails to leverage the potential of the attention mechanism, resulting in underutilization. Additionally, it requires a large amount of local data to achieve local optima in each round, which is often unrealistic in many federated learning scenarios.
3.4 Ablation study of data distribution
To analyze the performance of FedACS with varying Dirichlet distribution parameter , we conducted experiments under conditions of limited data on two datasets, with each client retaining only 50 data samples for training. The results, encompassing both mean and variance of test accuracy, are presented in the table. As increases, the non-IIDness in the data decreases, leading to a more uniform data distribution. This results in improved generalization capabilities for the global model. While the model performance exhibits enhancement, it is recommended to encourage users to involve a larger pool of participants in FedACS to further elevate the overall model performance.
| Dataset | |||||
|---|---|---|---|---|---|
| CIFAR10 | 81.720.45 | 83.840.19 | 84.970.36 | 85.760.14 | 85.420.42 |
| FMNIST | 84.260.38 | 84.330.35 | 85.570.24 | 86.130.34 | 88.420.22 |
4 Conclusion
In this paper, we proposed FedACS to address the challenge of data heterogeneity and improve overall FL performance. Our approach leveraged the attention aggregation mechanism, allowing clients to identify and collaborate with those who can provide valuable information. This allowed FedACS to avoid being constrained by a single global model and instead optimize personalized models based on each client’s local data distribution. We also analyzed the complexity of FedACS in achieving first-order optimality. Furthermore, we conducted a series of numerical experiments to demonstrate the superiority of FedACS in various non-IID settings. The results highlighted its effectiveness in handling data scarcity compared to other methods.
References
- Bertsekas et al. (2011) Dimitri P Bertsekas et al. Incremental gradient, subgradient, and proximal methods for convex optimization: A survey. Optimization for Machine Learning, 2010(1-38):3, 2011.
- Deng et al. (2020) Yuyang Deng, Mohammad Mahdi Kamani, and Mehrdad Mahdavi. Adaptive personalized federated learning. arXiv preprint arXiv:2003.13461, 2020.
- Fallah et al. (2020) Alireza Fallah, Aryan Mokhtari, and Asuman Ozdaglar. Personalized federated learning with theoretical guarantees: A model-agnostic meta-learning approach. Advances in Neural Information Processing Systems, 33:3557–3568, 2020.
- Fredrikson et al. (2015) Matt Fredrikson, Somesh Jha, and Thomas Ristenpart. Model inversion attacks that exploit confidence information and basic countermeasures. In Proceedings of the 22nd ACM SIGSAC conference on computer and communications security, pages 1322–1333, 2015.
- Hitaj et al. (2017) Briland Hitaj, Giuseppe Ateniese, and Fernando Perez-Cruz. Deep models under the gan: information leakage from collaborative deep learning. In Proceedings of the 2017 ACM SIGSAC conference on computer and communications security, pages 603–618, 2017.
- Huang et al. (2021) Yutao Huang, Lingyang Chu, Zirui Zhou, Lanjun Wang, Jiangchuan Liu, Jian Pei, and Yong Zhang. Personalized cross-silo federated learning on non-iid data. In Proceedings of the AAAI Conference on Artificial Intelligence, volume 35, pages 7865–7873, 2021.
- Jiang et al. (2019) Yihan Jiang, Jakub Konečnỳ, Keith Rush, and Sreeram Kannan. Improving federated learning personalization via model agnostic meta learning. arXiv preprint arXiv:1909.12488, 2019.
- Kairouz et al. (2021) Peter Kairouz, H Brendan McMahan, Brendan Avent, Aurélien Bellet, Mehdi Bennis, Arjun Nitin Bhagoji, Kallista Bonawitz, Zachary Charles, Graham Cormode, Rachel Cummings, et al. Advances and open problems in federated learning. Foundations and Trends® in Machine Learning, 14(1–2):1–210, 2021.
- Krizhevsky et al. (2009) Alex Krizhevsky, Geoffrey Hinton, et al. Learning multiple layers of features from tiny images. 2009.
- Kulkarni et al. (2020) Viraj Kulkarni, Milind Kulkarni, and Aniruddha Pant. Survey of personalization techniques for federated learning. In 2020 Fourth World Conference on Smart Trends in Systems, Security and Sustainability (WorldS4), pages 794–797. IEEE, 2020.
- Li et al. (2021) Tian Li, Shengyuan Hu, Ahmad Beirami, and Virginia Smith. Ditto: Fair and robust federated learning through personalization. In International Conference on Machine Learning, pages 6357–6368. PMLR, 2021.
- Li et al. (2019) Xiang Li, Kaixuan Huang, Wenhao Yang, Shusen Wang, and Zhihua Zhang. On the convergence of fedavg on non-iid data. arXiv preprint arXiv:1907.02189, 2019.
- Mansour et al. (2020) Yishay Mansour, Mehryar Mohri, Jae Ro, and Ananda Theertha Suresh. Three approaches for personalization with applications to federated learning. arXiv preprint arXiv:2002.10619, 2020.
- McMahan et al. (2017) Brendan McMahan, Eider Moore, Daniel Ramage, Seth Hampson, and Blaise Aguera y Arcas. Communication-efficient learning of deep networks from decentralized data. In Artificial intelligence and statistics, pages 1273–1282. PMLR, 2017.
- Nemirovski et al. (2009) Arkadi Nemirovski, Anatoli Juditsky, Guanghui Lan, and Alexander Shapiro. Robust stochastic approximation approach to stochastic programming. SIAM Journal on optimization, 19(4):1574–1609, 2009.
- Shokri et al. (2017) Reza Shokri, Marco Stronati, Congzheng Song, and Vitaly Shmatikov. Membership inference attacks against machine learning models. In 2017 IEEE symposium on security and privacy (SP), pages 3–18. IEEE, 2017.
- T Dinh et al. (2020) Canh T Dinh, Nguyen Tran, and Josh Nguyen. Personalized federated learning with moreau envelopes. Advances in Neural Information Processing Systems, 33:21394–21405, 2020.
- Vaswani et al. (2017) Ashish Vaswani, Noam Shazeer, Niki Parmar, Jakob Uszkoreit, Llion Jones, Aidan N Gomez, Lukasz Kaiser, and Illia Polosukhin. Attention is all you need. Advances in neural information processing systems, 30, 2017.
- Xiao et al. (2017) Han Xiao, Kashif Rasul, and Roland Vollgraf. Fashion-mnist: a novel image dataset for benchmarking machine learning algorithms. arXiv preprint arXiv:1708.07747, 2017.
- Xu et al. (2021) Jie Xu, Benjamin S Glicksberg, Chang Su, Peter Walker, Jiang Bian, and Fei Wang. Federated learning for healthcare informatics. Journal of Healthcare Informatics Research, 5:1–19, 2021.
- Yang et al. (2019a) Qiang Yang, Yang Liu, Tianjian Chen, and Yongxin Tong. Federated machine learning: Concept and applications. ACM Transactions on Intelligent Systems and Technology (TIST), 10(2):1–19, 2019a.
- Yang et al. (2019b) Wensi Yang, Yuhang Zhang, Kejiang Ye, Li Li, and Cheng-Zhong Xu. Ffd: A federated learning based method for credit card fraud detection. In Big Data–BigData 2019: 8th International Congress, Held as Part of the Services Conference Federation, SCF 2019, San Diego, CA, USA, June 25–30, 2019, Proceedings 8, pages 18–32. Springer, 2019b.
- Zhang et al. (2021) Xinwei Zhang, Mingyi Hong, Sairaj Dhople, Wotao Yin, and Yang Liu. Fedpd: A federated learning framework with adaptivity to non-iid data. IEEE Transactions on Signal Processing, 69:6055–6070, 2021.
- Zhao et al. (2018) Yue Zhao, Meng Li, Liangzhen Lai, Naveen Suda, Damon Civin, and Vikas Chandra. Federated learning with non-iid data. arXiv preprint arXiv:1806.00582, 2018.
- Zheng et al. (2022) Zhaohua Zheng, Yize Zhou, Yilong Sun, Zhang Wang, Boyi Liu, and Keqiu Li. Applications of federated learning in smart cities: recent advances, taxonomy, and open challenges. Connection Science, 34(1):1–28, 2022.
Appendix
Appendix A Missing Proofs
A.1 Proof of Theorem 2.1
See 2.1
Proof.
The proof of the theorem is motivated by the analysis from Huang et al..Huang et al. (2021) Define the function as
where is the Lipschitz constant of . Also, here we denote to be the optimal solution of the minimization problem: In chapter 3.1, we defined the update of , . Then follow the updates:
Following Assumption 1, we have . Besides, from the Lipschitz continuous property of , it holds that
Thus, we have
| (8) |
Moreover, the update of : together with the definition of , yields
Following Assumption 1, we have . Besides, from the Lipschitz continuous property of , it holds that
Thus, we have
| (9) |
Since is the optimal solution of , we have
which implies
| (10) |
From Huang et al.,Huang et al. (2021) we claim that
Upon adding (12) with (9) and combining , we get
| (13) |
The second inequality is from the definition of that .
We now consider the case where for all By summing up (LABEL:GWW) from to , we obtain
| (14) |
From the definition of , we can verify that , and where is the optimal value of . Also, using the definition of and taking the fact that is Lipschitz continuous with the constant 2, we can obtain that
Combining this, (14), and , we have
| (15) |
besides, we can bound as
When , combining the above equations with (9) gives us
| (16) |