Periodic Activities of Repeating Fast Radio Bursts from Be/X-ray Binary Systems

First, we make a discussion about starquakes of the NS induced by the spin evolution. When the spin period of the NS changes, the oblateness ($\varepsilon$) and the moment of inertia ($I$) will change to readjust the stellar shape. The oblateness of the NS is defined as $\varepsilon\equiv|I-I_{0}|/I$, where the non-rotating moment of inertia of the NS is taken as $I_{0}=10^{45}\,\mathrm{g\,cm^{2}}$. The rigidity of the NS resists this change and this corresponding energy is defined as the strain energy $E_{\text{strain}}=\mathcal{B}\left(\varepsilon-\varepsilon_{0}\right)^{2}$, where $\mathcal{B}$ is the coefficient and $\varepsilon_{0}$ is a reference oblateness without strain energy. The mean stress is

where $V$ is the volume of the NS, and $\mu=2\mathcal{B}/V$ is the mean shear modulus ¹¹1The shear modulus of the crust of the NS can be represented by (e.g., Thompson & Duncan, 1995; Douchin & Haensel, 2001; Piro, 2005) $\mu\simeq 6.0\times 10^{30}\,\mathrm{erg\,cm^{-3}}\rho_{\text{n}}^{4/3}(Z/50)^{2}(615/A)^{4/3}[(1-X_{\text{n}})/0.4]^{4/3}$, where $\rho_{\text{n}}=2.8\times 10^{14}~{}{\rm g~{}cm^{-3}}$ is the nuclear density, $Z$ is the number of protons per ion, $A$ is the number of nucleons in a nucleus and $X_{\text{n}}$ denotes the fraction of neutrons outside nuclei. Because the shear modulus of the NS crust during the accretion process is a little bit softer (e.g., Haensel & Zdunik, 2008; Zdunik et al., 2008), here we adopt $\mu\sim 10^{31}\,\mathrm{erg\,cm^{-3}}$ in this process. of the NS. There is a critical stress value $\sigma_{\text{c}}$, above which, i.e., $\sigma>\sigma_{\text{c}}$, a starquake can take place.

The total energy of the NS can be estimated by (Baym & Pines, 1971; Shapiro & Teukolsky, 1983)

where $E_{\text{grav}}=E_{0}+\mathcal{A}\varepsilon^{2}$ is the gravitational energy of the rotating NS, with the energy of the nonrotating star $E_{0}=-3M_{\text{NS}}^{2}G/(5R_{\text{NS}})$ and the coefficient $\mathcal{A}=-1/5E_{0}$ for a self-gravitating incompressible sphere, $E_{\text{rot}}=\mathcal{L}^{2}/(2I)$ is the rotation energy, with the stellar angular momentum $\mathcal{L}=I\Omega$ and the angular velocity of the NS $\Omega=2\pi/P_{\text{NS}}$. By minimizing the total energy $E$, $\varepsilon$ satisfies

where $\partial I(\varepsilon)/\partial\varepsilon=I_{0}$. By setting $\mathcal{B}=0$, the reference oblateness is $\varepsilon_{0}=I_{0}\Omega_{0}^{2}/(4\mathcal{A})$, where $\Omega_{0}$ is the angular velocity of the NS with completely unstressed crust.

When the stress $\sigma$ in Eq.(1) reaches the critical stress $\sigma_{\text{c}}$, a starquake is produced. The reference oblateness as a reference point shifts $\Delta\varepsilon_{0}$, and thus the actual oblateness of the NS shifts

According to the conservation of the angular momentum, $\Delta\varepsilon=|\Delta\Omega/\Omega|$, where $\Delta\Omega$ is the difference between the angular velocity after and before the starquake. Based on the observation of pulsar glitches, $\Delta\varepsilon$ can span several orders of magnitude from $\Delta\varepsilon\approx 10^{-12}$ to $\Delta\varepsilon\approx 10^{-5}$ (Espinoza et al., 2011). Lai et al. (2018) gives an estimation of $\Delta\varepsilon\sim 10^{-10}$ for the Crab pulsar and $\Delta\varepsilon\sim 10^{-11}$ for the Vela pulsar from the observations (Espinoza et al., 2011). Then the stress relieved during a starquake can be represented by

According to Eq.(1) and Eq.(3), the stress in the crust will start to build up again after starquakes at a rate

where $\dot{\Omega}$ is the change rate of angular velocity of the NS. The next starquake occurs after a time (Haskell & Melatos, 2015)

i.e., the waiting time of the NS starquakes, where $\dot{\Omega}$ can be derived by the torque $N$ on the NS, i.e., $N=I_{0}\dot{\Omega}$. In the following part, we will derive $N$ on the NS in/out of the Be star disk.

Because the accretion process of the NS in a BeXRB system is still unclear, both disk accretion (e.g., Okazaki & Negueruela, 2001; Xu & Li, 2019) and wind accretion (e.g., Ikhsanov, 2007; Shakura et al., 2012) are possible scenarios. During the NS is in the disk of the Be star, if the interaction radius between the accreted material and the NS magnetosphere $R_{\mathrm{in}}$ and the radius of the light cylinder $R_{\text{lc}}$ satisfies $R_{\mathrm{in}}<R_{\text{lc}}=c/\Omega\simeq 4.8\times 10^{7}(P_{\text{NS}}/0.01\,\mathrm{s})\,\mathrm{cm}$, there will exist the interaction between the accreted material and the magnetosphere of the NS. In this situation, an accretion torque $N_{\rm acc}$ would change the NS spin evolution, leading to spin up or spin down ²²2We define the corotation radius as $R_{\rm co}$ where the local Keplerian angular velocity of the accreted material equals the angular velocity of the NS. If $R_{\rm in}<R_{\rm co}$, i.e., accretor state, the material in the inner boundary would be faster than the rotation velocity of the NS, and flows along the magnetic field lines onto the NS (Frank et al., 2002), which casues that accretion occurs and accelerates the rotation of the NS by the angular momentum transfer. If $R_{\rm co}<R_{\rm in}<R_{\rm lc}$, i.e., propeller state, accretion is forbidden, because the velocity of the accretion disk is less than the rotation velocity of the NS. The material of the accretion disk is thrown out by centrifugal force, which takes away angular momentum and decelerates the NS.. $N_{\rm acc}$ can be represented by (e.g., Ghosh & Lamb, 1979b; Lü et al., 2012)

where $\dot{M}$ is the accretion rate of the NS, “$+$” corresponds to the spin-up case, and “$-$” corresponds to the spin-down case. The total torque can be represented by $N_{\text{tot}}=N_{\rm acc}+N_{\mathrm{rad}}$, with the radiation torque of the NS to be $N_{\mathrm{rad}}$. Because $|N_{\text{tot}}|\gg|N_{\mathrm{rad}}|$, the starquakes in both the accretor and propeller states would have the same waiting time ³³3Here we only consider the direction of the accretion disk of the NS is the same as that of the NS spin..

The interaction radius between the accreted material and the NS magnetosphere $R_{\text{in}}$ can be evaluated by $R_{\text{in}}=\xi R_{\text{A}}$. $\xi\sim 0.01-1$ is taken for the disk accretion (e.g., Ghosh & Lamb, 1979a; Filippova et al., 2017) and $\xi\sim 1$ is taken for the wind accretion (e.g., Lü et al., 2012), respectively. The Alfvén radius $R_{\text{A}}=[\mu_{\text{NS}}^{4}/(2GM_{\text{NS}}\dot{M}^{2})]^{1/7}$ is where the magnetic pressure of an NS is equal to the shock pressure of accreted material, with the accretion rate $\dot{M}$. $\mu_{\text{NS}}=B_{\text{NS}}R^{3}_{\text{NS}}/2$ is the magnetic moment of the NS, with the surface magnetic field of the NS to be $B_{\text{NS}}$. Thus, $R_{\text{in}}$ is represented by

The Eddington luminosity is defined as $L_{\text{Edd}}\equiv 4\pi GM_{\text{NS}}m_{\text{p}}c/\sigma_{\text{T}}$, where $m_{\text{p}}$ is the mass of proton and $\sigma_{\text{T}}$ is the Thompson cross section. The rate of Eddington accretion is $\dot{M}_{\text{Edd}}\simeq 10^{18}\left(R_{\text{NS}}/10^{6}\,\mathrm{cm}\right)\,\mathrm{g\,s^{-1}}$. For BeXRB system, the X-ray luminosity of the type Type I outbursts is about $10^{36}-10^{37}\,\mathrm{erg\,s^{-1}}$. If we assume that all the kinetic energy of the accretion matter is converted to the luminosity of type Type I outbursts, i.e., $L=1/2\dot{M}v_{\mathrm{ff}}^{2}=GM_{\text{NS}}\dot{M}/R_{\text{NS}}$, with the free-fall velocity $v_{\text{ff}}=\sqrt{2GM_{\text{NS}}/R_{\text{NS}}}$, we can derive that the accretion rate of the NS is about $0.1\dot{M}_{\text{Edd}}$.

According to Eq.(7), the waiting time of two starquakes induced by accretion of the NS in the Be star disk can be represented by

with $\mu=10^{31}\,\mathrm{erg\,cm^{-3}}$ (e.g., Thompson & Duncan, 1995; Douchin & Haensel, 2001; Piro, 2005), $M_{\text{NS}}=1.4M_{\odot}$, $R_{\text{NS}}=1.2\times 10^{6}\,\mathrm{cm}$, and $|N_{\text{acc}}|\gg|N_{\mathrm{dip}}|$. Here, we take $P_{\text{NS}}=0.01\,\mathrm{s}$ as a reference value, which is consistent with the observation of SAX J0635+0533 with a spin period $0.0338\,\mathrm{s}$ (Kaaret et al., 1999; Cusumano et al., 2000). If $P_{\text{NS}}=0.02\,\mathrm{s}$, $\Delta\varepsilon=10^{-13}$, $\xi=0.1$, $B_{\text{NS}}=10^{13}\,\mathrm{G}$, $M_{\text{NS}}=1.4M_{\odot}$, $R_{\text{NS}}=1.2\times 10^{6}\,\mathrm{cm}$ and $\dot{M}=\dot{M}_{\text{Edd}}$, we obtain $R_{\mathrm{in}}\simeq 5.3\times 10^{7}\,\mathrm{cm}<R_{\mathrm{lc}}\simeq 9.5\times 10^{7}\,\mathrm{cm}$ and $t_{\text{s}}\simeq 4.9\,\mathrm{day}$. Thus, in an active window of FRB 180916B, there would be several starquakes, leading to several FRBs occurring in the active window. If $\xi=0.5$, $P_{\text{NS}}=0.01\,\mathrm{s}$, $B_{\text{NS}}=10^{13}\,\mathrm{G}$, $M_{\text{NS}}=1.4M_{\odot}$, $R_{\text{NS}}=1.2\times 10^{6}\,\mathrm{cm}$ and $\dot{M}=\dot{M}_{\text{Edd}}$, $R_{\mathrm{in}}\simeq 2.6\times 10^{8}\,\mathrm{cm}>R_{\mathrm{lc}}\simeq 4.8\times 10^{7}\,\mathrm{cm}$, without interaction between the accreted material and the magnetosphere of the NS, the NS will spin down through radiation which will be discussed later.

When the crust of the NS cracks, the magnetic field near the surface would be disturbed, and further propagates as Alfvén waves into the magnetosphere (e.g., Thompson & Duncan, 1995; Kumar & Bošnjak, 2020; Lu et al., 2020; Yang & Zhang, 2021). The released energy can be evaluated by

where $\Delta R$ is the thickness of the crust and $\zeta$ is the magnetic energy conversion factor. Therefore, the energy released by the magnetic energy in the NS crust is enough to produce FRBs.

When the NS is outside the disk of the Be star or $R_{\rm in}>R_{\rm lc}$, the accretion will be very weak. Taking $|\dot{\Omega}|=2\pi P_{\text{NS}}^{-2}\dot{P}_{\text{NS}}$ into Eq.(7), the interval between two starquakes due to the radiation of the NS can be estimated by

where $\dot{P}_{\text{NS}}$ is the period derivative of the NS, with typical value in range $10^{-20}\,\mathrm{s\,s^{-1}}$ to $10^{-10}\,\mathrm{s\,s^{-1}}$ (Taylor et al., 1993), The other parameters are taken as $\mu=10^{31}\,\mathrm{erg\,cm^{-3}}$, $M_{\text{NS}}=1.4M_{\odot}$, and $R_{\text{NS}}=1.2\times 10^{6}\,\mathrm{cm}$. This interval is much longer than the orbit period of the BeXRB system, thus it is unlikely to produce radio bursts when the NS moves outside the disk of the Be star.

In Figure 2, we plot the parameter space of period and magnetic field of the NS. The area enclosed by the red dashed line, purple dash-dotted line and blue dotted line satisfies $t_{\text{s}}<6.1\,\mathrm{day}$, $t_{\text{s}}^{\prime}>16.29\,\mathrm{day}$ and $R_{\mathrm{in}}<R_{\mathrm{lc}}$, which is suitable to explain FRB 180916B period activity. In this area, different colors denote different $t_{\text{s}}$. The parameters are taken as $\mu=10^{31}\,\mathrm{erg\,cm^{-3}}$, $\xi=0.1$, $\Delta\varepsilon=10^{-13}$, $\dot{M}=\dot{M}_{\text{Edd}}$, $\dot{P}_{\text{NS}}=10^{-18}\,\mathrm{s\,s^{-1}}$, $M_{\text{NS}}=1.4M_{\odot}$, and $R_{\text{NS}}=1.2\times 10^{6}\,\mathrm{cm}$.

When the crust fractures, Alfvén waves would be generated at the surface of the NS by the starquake and propagate into the magnetosphere, further produce FRBs at a large radius (Kumar & Bošnjak, 2020; Lu et al., 2020; Yang & Zhang, 2021). About tens of NS radius, the plasma density in the magnetosphere is not enough to screen the parallel electric field associated with the Alfvén wave, leading to a charge starved region. In this scenario, FRBs could be emitted by bunching coherent curvature radiation due to two-stream instability (Kumar & Bošnjak, 2020; Lu et al., 2020; Yang et al., 2020) or coherent plasma radiation (Yang & Zhang, 2021).

We assume that the disk of the Be star is coplanar with the orbit of the NS for simplify, and FRBs are produced when the NS passes through the disk of the Be star. In Figure 1, the Be star is at the left focus of the orbit. The NS moves counterclockwise. The point $N$ is where the NS starts to move into the disk of the Be star, and the point $N^{\prime}$ is where the NS is beginning to move outside of the disk of the Be star. We define

where $\theta$ is the azimuth angle of the NS relative to the Be star, $a$ is the length of semi-major axis of the orbit, and $e$ is the orbital eccentricity. The area swept out by a line joining the Be star and the NS from the point $N$ to the point $N^{\prime}$ can be calculated by $\Delta S_{\text{NS}}(\theta_{0},2\pi-\theta_{0})$, where $\theta_{0}$ is the initial azimuth angle at the point $N$. Setting the phase of the orbit periastron as 0.5, the phase at any azimuth angle, $\theta_{x}$, of the orbit can be represented by $\phi(\theta_{x})=\Delta S_{\text{NS}}(\theta_{0},\theta_{x})/S_{\text{NS}}-\Delta S_{\text{NS}}(\theta_{0},\pi)/S_{\text{NS}}+0.5$.

According to the Kepler’s third law, the length of semi-major axis of the orbit should meet $a=\left[G(M_{\star}+M_{\text{NS}})P_{\text{orb}}^{2}/4\pi^{2}\right]^{1/3}\simeq 4.8\times 10^{12}\,\mathrm{cm}$, where the orbit period is $P_{\text{orb}}=16.29\,\mathrm{day}$, the mass of the Be star is taken as $M_{\star}=15M_{\odot}$ and the mass of the NS is $M_{\text{NS}}=1.4M_{\odot}$. The total area of the orbit is $S_{\text{NS}}=\pi\left(1-e^{2}\right)^{1/2}a^{2}$. We define the active fraction of the period as the duty cycle. According to Kepler’s second law, the duty cycle can be represented by

with the active window of FRB 180916B to be $\Delta P_{\text{orb}}$.

The abscissa of the point $N$ satisfies $x_{\text{K}}=(-a^{2}+aR_{\text{disk}})/c_{\text{e}}$ and $x_{\text{K}}=R_{\text{disk}}\cos(\theta_{0})-c_{\text{e}}$, with $c_{\text{e}}$ the focal length of the orbit and $R_{\text{disk}}$ the radius of the disk. For a given orbit period and active window, $R_{\text{disk}}$ and $\theta_{0}$ are functions $e$, respectively, as shown in Figure 3. The larger the eccentricity $e$, the larger the disk radius $R_{\text{disk}}$ and the smaller the initial azimuth angle $\theta_{0}$ are required.

Next, we establish a three-dimensional model to describe the density distribution of the Be star disk. The disk of the Be star is usually a Keplerian disk (e.g., Lee et al., 1991; Okazaki, 1991; Quirrenbach et al., 1997; Rivinius et al., 2013). The velocity at the horizontal distance $r$ to the central star is $v=\sqrt{GM_{\star}/r}$, where $G$ is Newton’s gravitational constant. In the $z$ direction vertical to the disk, the gas pressure is balanced with the gravitational force, i.e.,

where $\rho$ and $P$ are the density and pressure of the matter, respectively. The height $H(r)$ at radius $r$ is estimated by

with the isothermal sound speed $c_{s}=(kT/\mu_{\text{m}}m_{\mathrm{H}})^{1/2}$, where $\mu_{\text{m}}=0.61$ is the mean molecular weight for a solar composition, $T$ is the isothermal electron temperature and $m_{\mathrm{H}}$ is the mass of hydrogen. The temperature of the disk is roughly constant, $T\sim 2\times 10^{4}\,\mathrm{K}$, within $100R_{\star}$ in the radial direction (e.g., Millar & Marlborough, 1998, 1999). The density structure of the Be star disk can be represented radially as a power law and vertically with an exponential decay, (e.g., McGill et al., 2013), i.e.,

where the base density $\rho_{0}$ for most of Be stars ranges from $10^{-13}\,\mathrm{g\,cm^{-3}}$ to $10^{-10}\,\mathrm{g\,cm^{-3}}$ (e.g., Carciofi et al., 2007; Jones et al., 2008; Tycner et al., 2008) and the index $\eta$ ranges from $2$ to $5$ (e.g., Waters et al., 1987; Dougherty et al., 1994)

In order to calculate the optical depth of a burst along a certain propagation direction, we first define the direction vector of the line of sight. In the reference frame centered on the Be star, the direction vector of the line of sight can be expressed as $(\cos(\beta_{0})\cos(\alpha_{0}),\cos(\beta_{0})\sin(\alpha_{0}),\sin(\beta_{0}))$, with direction angle $\alpha_{0}$ and vertical angle $\beta_{0}$. When the NS moves in the disk of Be star, the optical depth of free-free absorption along the line of sight is calculated by

with the attenuation coefficient (e.g., Draine, 2011)

where $T=T_{4}10^{4}\,\mathrm{K}$ is the temperature, $\nu=\nu_{9}10^{9}\,\mathrm{Hz}$ is the frequency, $Z_{i}\sim 1$ is the charge of ions, $g_{\text{ff}}(\nu,T)$ is the Gaunt factor for the free-free emission, and $n_{i}\approx n_{e}$ is assumed with the ion density $n_{i}$ and electron density $n_{e}=\rho/\mu_{\rm e}m_{\rm H}$, with the mean molecular weight per electron $\mu_{\rm e}=1.2$ for a solar composition. If $\tau_{\nu}>1$, the observed flux of an FRB would be significantly reduced by free-free absorption. According to Eq.(18), in the following part, we will calculate the burst rate at different frequencies from a certain propagation path after the free-free absorption.

When the NS is in the Be star disk, it will accrete the material and trigger FRBs by starquakes as discussed above in Section 2.1. We assume that the burst rate during the active window satisfying a Gaussian distribution as a function of phase (also see the observation result of Figure 4 in Pastor-Marazuela et al. (2020)). The burst rate reaches the maximum near the periastron, and decreases when the NS is away from the periastron, because the accretion rate depends on the density of the Be star disk. Such a Gaussian burst rate is also consistent with pulse shapes of Type I outbursts of BeXRBs (e.g., Wilson et al., 2002; Baykal et al., 2008; Wilson et al., 2008). The burst rate at $1\,\mathrm{GHz}$ as a function of phase can be represented by

where $\mathcal{R}_{0}$ is the normalized constant, $\sigma_{\phi}$ is the standard deviation, and $\phi_{0}=0.5$. According to Extended Figure 1 of Pastor-Marazuela et al. (2020), for bursts of the same fluence, FRB 180916B is around over an order of magnitude more active at $150\,\mathrm{MHz}$ than at $1.4\,\mathrm{GHz}$. Thus, the ratio of burst rates in $1.4\,\mathrm{GHz}$ and $150\,\mathrm{MHz}$ is $\mathcal{R}_{1.4\,\mathrm{GHz}}/\mathcal{R}_{150\,\mathrm{MHz}}=(1.4\,\mathrm{GHz}/150\,\mathrm{MHz})^{-1}$. Furthermore, we assume that the burst rate at different frequencies can be represented by

with $\alpha\approx-1$ as a typical value.

We further generate a sample of FRBs with different frequencies at different phases. The fluences of FRBs, $f_{\nu}(\phi)$, at a phase $\phi$ are assumed to satisfy a normal distribution of $N(\mu_{f_{\nu}},\sigma_{f_{\nu}}^{2})$, where $\mu_{f_{\nu}}$ is the average fluence and $\sigma_{f_{\nu}}$ is the standard deviation. According to Extended Figure 1 of Pastor-Marazuela et al. (2020), the fluence of the low-frequency bursts is higher than that of high-frequency bursts. The average fluence at $1.4\,\mathrm{GHz}$ of FRB 180916B is a few Jy ms, however at $150\,\mathrm{MHz}$ is a few hundred Jy ms. We assume the average fluence at different frequencies $\nu$ as a power law, i.e.,

where $\mu_{f_{1\,\mathrm{GHz}}}$ is the average fluence at $1\,\mathrm{GHz}$, and $\gamma$ is the power law index with $\gamma\approx-2$ as a typical value.

Involving the absorption of the disk of the Be star, the observed fluence of each burst at phase $\phi$ can be estimated by

The observed burst rate $\mathcal{R}_{\nu,\text{obs}}$ is determined by the fluence threshold of a specific telescope. When $f_{\text{$\nu$,obs}}(\phi)$ of a burst is greater than the threshold, it is regarded as observable. The thresholds of Apertif, CHIME and LOFAR are about $1\,\mathrm{Jy\,ms}$ (Pastor-Marazuela et al., 2020), $5.3\,\mathrm{Jy\,ms}$ (CHIME/FRB Collaboration et al., 2020a), $50\,\mathrm{Jy\,ms}$ (Pastor-Marazuela et al., 2020), respectively. Next, in order to explain the activity window of FRB 180916B, we will simulate the observable active window of FRBs affected by the free-free absorption of the disk of the Be star.

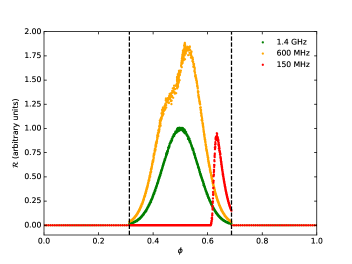
In general, the radius of Be stars, $R_{\star}$, ranges from $\sim 3R_{\odot}$ to $\sim 13R_{\odot}$ and the radius of the Be star disk, $R_{\text{disk}}$, ranges from about $1.5R_{\star}$ to $17R_{\star}$ (Rivinius et al., 2013). The mass of the Be star is $>8M_{\odot}$ (Reig, 2011). The eccentricity of binary orbits can be 0.1 to 0.9 (Ziolkowski, 2002). If the central star is a B0 main-sequence star, the typical parameters are $R_{\star}=7.41R_{\odot}$, $M_{\star}=17.8M_{\odot}$ (Allen, 1973). In order to explain the observation properties of the frequency-dependent active window of FRB 180916B, we find that the following parameters are appropriate: the radius of Be star is $R_{\star}=5R_{\odot}$, the mass of the Be star is $M_{\star}=15M_{\odot}$, the temperature of the disk is $T=2\times 10^{4}\,\mathrm{K}$, the index of the density structure of the disk is $\eta=4.5$, the base density of the density structure is $\rho_{0}=1.6\times 10^{-13}\,\mathrm{g\,cm^{-3}}$, the orbital eccentricity is $e=0.35$, the standard deviation of the burst rate is $\sigma_{\phi}=0.065$, the reference burst rate is $\mathcal{R}_{0}=100\,\mathrm{h^{-1}}$, the index of the burst rate with frequency is $\alpha=-1.0$, the average fluence of bursts at $1\,\mathrm{GHz}$ is $\mu_{f_{1\,\mathrm{GHz}}}=5\,\mathrm{Jy\,ms}$, the standard deviation of fluence of bursts is $\sigma_{f_{\nu}}=0.3\mu_{f_{\nu}}$, the power law index of the average fluence with frequency is $\gamma=-2.0$, and the direction of the burst is $\alpha_{0}=-0.7\pi$ and $\beta_{0}=-0.05\pi$. Then the disk of the Be star is about $67.4R_{\odot}$. The frequency-dependent burst rate with phase is shown in Figure 4. We can see that the peaks of active windows of high-frequency and low-frequency bursts appear at different phases. Low-frequency bursts are observed later than the high-frequency in an orbital cycle. Bursts with frequency of $600\,\mathrm{MHz}$ have wider periodic activity window. The dotted red line denotes the burst rate at $150\,\mathrm{MHz}$. Because of the absorption, it has the greatest influence on the $150\,\mathrm{MHz}$ bursts and the burst rate at $600\,\mathrm{MHz}$ does not follow the shape of Gaussian model. The above results are consistent with the observation properties of FRB 180916B.

When the NS is in the Be star disk, the observed DM will also change with orbit phase. In general, the total observed DM can be divided into (Deng & Zhang, 2014; Zhang, 2018) ${\rm DM_{tot}}={\rm DM_{MW}}+{\rm DM_{IGM}}+({\rm DM_{host}}+{\rm DM_{src}})/(1+z)$, where $\rm{DM_{MW}}$ and $\rm{DM_{IGM}}$ are the contributions from the Milky Way and the intergalactic medium, respectively, $\rm{DM_{host}}$ and $\rm{DM_{src}}$ are the contributions from the host galaxy and source local environment in the rest frame of the FRB, respectively, and $z$ is the redshift of the FRB. Yang & Zhang (2017) investigated the various possibilities that may cause DM variations of an FRB and finds that only the near-source plasma can cause observable DM variations. In a BeXRB system, we mainly consider the DM variations contributed from $\rm{DM_{src}}$, i.e., $\rm{DM_{disk}}$, the dispersion measure contribution from the Be star disk.

Different from an observable increasing DM of FRB 121102 (e.g., Oostrum et al., 2020; Zhao et al., 2021), there is no obvious DM variation with phase for FRB 180916B, and the largest DM variation is about $4\,\mathrm{pc\,cm^{-3}}$ (see top panel of Extended Figure 7 in Pastor-Marazuela et al., 2020). Based on the density profile of the Be star disk, Eq.(17), we obtain $\rm{DM_{disk}}$ at different phases, as is shown in Figure 5. The parameters are taken the same with Figure 4. The red part corresponds to the DM in active window, and the blue part corresponds to the DM in the non-active window. In non-active window, since the NS moves out of the Be star disk, the burst rate is much lower according to Eq.(12.), although it also appears DM variation at some certain line-of-sight directions. For the given parameters satisfying the properties of the observed frequency-dependent active window of FRB 180916B, we find that the dispersion measure contribution from the Be star disk is $<1\,\mathrm{pc\,cm^{-3}}$.