Performance Evaluation and Modeling of Cryptographic Libraries for MPI Communications
Abstract
In order for High Performance Computing (HPC) applications with data security requirements to execute in the public cloud, the cloud infrastructure must ensure privacy and integrity of data. To meet this goal, we consider incorporating encryption in the Message Passing Interface (MPI) library. We empirically evaluate four contemporary cryptographic libraries, OpenSSL, BoringSSL, Libsodium, and CryptoPP using micro-benchmarks and NAS parallel benchmarks on two different networking technologies, 10Gbps Ethernet and 40Gbps InfiniBand. We also develop accurate models that allow us to reason about the performance of encrypted MPI communication in different situations, and give guidance on how to improve encrypted MPI performance.
Index Terms:
MPI, encrypted communication, performance modeling, benchmark.1 Introduction
There is a current trend that more and more High Performance Computing (HPC) applications are moved to execute in the public cloud. Some of these applications process sensitive data, such as medical, financial, and engineering documents. In order for such HPC applications to run on the cloud, the cloud infrastructure for HPC must provide privacy and integrity. A very large number of HPC applications are developed based on the Message Passing Interface (MPI) library, the de facto communication library for message passing applications. Incorporating privacy and integrity mechanisms in the MPI library will allow MPI applications to run in the public cloud with strong security guarantees.
The existing efforts to secure MPI libraries with encryption contain severe security flaws. For example, ES-MPICH2 [1], the first such MPI library, uses the weak ECB (Electronic Codebook) mode of operation that has known vulnerabilities [2, page 89]. In addition, no existing encrypted MPI libraries provide meaningful data integrity, meaning that data could potentially be modified without being detected. Hence, it is urgent to apply modern cryptographic theory and practice to properly secure MPI communications.
In recent years, significant efforts have been put in the hardware and software to improve the performance of security operations. Recent processors from all major CPU vendors have introduced hardware support for cryptographic operations (e.g., Intel AES-NI instructions to accelerate the AES algorithm, or the x86 CLMUL instruction set to improve the speed of finite-field multiplications). Modern cryptographic libraries, including OpenSSL [3], BoringSSL [4], Libsodium [5] and CryptoPP [6], all support hardware-accelerated cryptographic operations. All of these libraries received intensive security review; and some (OpenSSL and CryptoPP) even passed the Federal Information Processing Standards (FIPS) 140-2 validation. These libraries have different usability, functionality, and performance. Moreover, recent technology advances have shifted the communication bottleneck from the network links to the network end-points. As a result, the computationally intensive encryption operations may introduce significant overheads to MPI communications when security mechanisms are incorporated in the MPI library. It is thus critical find out which library is the best option for MPI communications, and to understand the overheads introduced due to the cryptographic operations.
In this work, we develop encrypted MPI libraries that are built on top of four cryptographic libraries OpenSSL, BoringSSL, Libsodium, and CryptoPP. Using these libraries, we empirically evaluate the performance of encrypted MPI communications with micro benchmarks and NAS parallel benchmarks [7] on two networking technologies, 10Gbps Ethernet and 40Gbps InfiniBand QDR. The main conclusions include the following:
-
•
Different cryptographic libraries result in very different overheads. Specifically, OpenSSL and BoringSSL are on par with each other; and their performance is much higher than that of Libsodium and CryptoPP, on both Ethernet and InfiniBand.
-
•
For individual communication, encrypted MPI introduces relative small overhead for small messages and large overhead for large messages. For example, on the 10Gbps Ethernet, even for BoringSSL, encrypted MPI under the AES-GCM encryption scheme [8] introduces 5.9% overhead for 256-byte messages and 78.3% for 2MB messages in the ping-pong test. On the 40Gbps InfiniBand, BoringSSL introduces 80.9% overhead for 256-byte messages and 215.2% overhead for 2MB messages in the ping-pong test. This calls for developing new techniques to optimize the combination of encryption and MPI communications.
-
•
For more practical scenarios, the cryptographic overhead is not as significant. On average, BoringSSL only introduces 12.75% overhead on Ethernet and 17.93% overhead on InfiniBand for NAS parallel benchmarks (class C running on 64 processes and 8 nodes).
To gain a theoretical understanding of the performance of encrypted MPI point-to-point communication, we investigate the modeling of encrypted MPI point-to-point communication in two settings: a single point-to-point communication like the Ping-Pong test and multiple concurrent point-to-point communications like the OSU Multiple-Pair benchmark [9]. We show that the performance of encrypted MPI point-to-point communication can be accurately modeled using the Hockney model [10] that has been used to model MPI communication [11, 12, 13, 14, 15, 16], and the max-rate model of Gropp et al. [17] that was proposed to model concurrent communications. Moreover, the parameters of our models can be derived from independent benchmarking of conventional MPI and encryption libraries. The simplicity of our models offers a simple and intuitive explanation for the performance of encrypted MPI point-to-point communication across different cryptographic libraries and networks, and allows for accurate prediction of encrypted MPI point-to-point communication performance as technology advances. Using these models, we reason about the performance of encrypted MPI point-to-point communication in different situations and discuss the potential benefits of some optimization techniques to improve the performance of encrypted MPI communication.
2 Related work
Prior systems of encrypted MPI. There have been a few proposed systems for adding encryption to MPI libraries, and some have even been implemented [1, 18, 19, 20, 21]. Existing systems, however, suffer from notable security vulnerabilities, as we will elaborate below.
First, privacy—the main goal of those systems—is seriously flawed because of the insecure crypto algorithms or the misuse of crypto algorithms. For example, ES-MPICH2 [1] is the first MPI library that integrates encryption to MPI communication, but its implementation is based on a weak encryption scheme, the Electronic Codebook (ECB) mode of operation. While ECB is still included in several standards, such as NIST SP 800-38A, ANSI X3.106, and ISO 8732, it has been known to be insecure [2, page 89]. For another example of an insecure choice of encryption, consider the system VAN-MPICH2 [20] that relies on one-time pads for encryption. It however implements one-time pads as substrings of a big key . Thus when encrypting many large messages, it is likely that there are two messages and whose one-time pads and are overlapping substrings of , say the last 8 KB of is also the first 8 KB of . In that case, one can obtain the xor of and , where is the last 8 KB of and is the first 8 KB of . If and are English texts there are known methods to recover them from their xor value [22].
Next, no existing system provides meaningful data integrity. Some do suggest that integrity may be added via digital signatures [1, 20], but this is impractical because all existing digital signature schemes are expensive. Some consider encrypting each message together with a checksum (obtained via a cryptographic hash function such as SHA-2) [19], but this approach does not provide integrity if one uses classical encryption schemes such as the Cipher Block Chaining (CBC) mode of encryption [23]. Others believe that encrypting data via the ECB mode also provides integrity [1, 18], but it is well-known that classical encryption schemes such as ECB or CBC provide no integrity at all [2, page 109].
We note that the insecurity of the systems above has never been realized in the literature. MPI communication therefore is in dire need of strong encryption that provides both privacy and integrity. In addition, in recent years, hardware support for efficient cryptographic operations, such as Intel’s AES-NI instructions, has become ubiquitous. These advances are fully exploited by modern cryptographic libraries to improve encryption speed. Yet there is currently a lack of understanding of how these libraries perform in the MPI environment. Our paper fills this gap, giving (i) the first implementation that properly encrypts MPI communication to provide genuine privacy and integrity, and (ii) a systematic benchmarking to investigate the overheads of modern cryptographic libraries for MPI communication on contemporary clusters. Unlike prior work with insecure, ad hoc encryption schemes, our implementation is based on the Galois-Counter Mode (GCM) that provably delivers both privacy and integrity [24].
Performance modeling. Modeling the performance of communication systems has a long history; and many models have been developed. Most notable performance models include the Hockney model [10], the LogP model [25], the LogGP model [26], and the PLogP model [27]. A good summary of these performance models is given in [28]. The Hockney model is widely used and has been used to analyze MPI communication algorithms [11, 12, 13, 14, 15, 16]. In this work, we show that the Hockney model can be used for the encrypted Ping Pong setting, and the recent max-rate model [17] for concurrent one-to-one flows can be used for multi-threading encryption. In hindsight, encrypted communication can be viewed as ordinary MPI communication over a private, authenticated channel, and thus it is understandable why conventional models for MPI communication continue to work well for encrypted settings.
3 Background
3.1 Encryption Schemes
A bird’s-eye view of encryption. A (symmetric) encryption scheme is a triple of algorithms . Initially, the sender and receiver somehow manage to share a secret key that is randomly generated by Gen. Each time the sender wants to send a message to the receiver, she would encrypt , and then send the ciphertext in the clear. The receiver, upon receiving , will decrypt . An encryption scheme is commonly built on top of a blockcipher (such as AES and 3DES).
Standard documents, such as NIST SP 800-38A [8] and 800-38D [29], specify several modes of encryption. Many of them, such as Electronic Codebook (ECB), Cipher Block Chaining (CBC), Counter (CTR), Galois/Counter Mode (GCM), and Counter with CBC-MAC (CCM), are well-known and widely used. However, these schemes are not equal in security and ease of correct use. The ECB mode, for example, is insecure [2]. CBC and CTR modes provide only privacy, meaning that the adversary cannot even distinguish ciphertexts of its chosen messages with those of uniformly random messages of the same length. They however do not provide data integrity in the sense that the adversary cannot modify ciphertexts without detection.111 Actually, the adversary can still replace a ciphertext with a prior one; this is known as replay attack. Here we do not consider such attacks. Among the standardized encryption schemes, only GCM and CCM satisfy both privacy and integrity, but GCM is the faster one [30]. Therefore, in this paper, we will focus on GCM; one does not need to know technical details of GCM to understand our paper.
GCM Overview. According to NIST SP 800-38D, the blockcipher for GCM must be AES, and correspondingly, the key length is either or bits. The longer key length means better security against brute-force attacks, but also slower speed. In this paper, we consider both 128-bit key (the most efficient version) and 256-bit key (the most secure one). AES-GCM is a highly efficient scheme [30], provably meeting both privacy and integrity [24]. Due to its strength, AES-GCM appears in several network protocols, such as SSH, IPSec, and TLS.
Syntactically, AES-GCM is a nonce-based encryption scheme, meaning that to encrypt plaintext , one needs to additionally provide a nonce , i.e., a public value that must appear at most once per key. The same nonce is required for decryption, and thus the sender needs to send both the nonce and the ciphertext to the receiver. See Fig. 1 for an illustration of the encrypted communication via GCM. In AES-GCM, nonces are 12-byte long, and one often implements them via a counter, or pick them uniformly at random. In addition, each ciphertext is -byte longer than the corresponding plaintext, as it includes a -byte tag to determine whether the ciphertext is valid.

3.2 Cryptographic Libraries
In our implementation, we consider the following cryptographic libraries: OpenSSL [3], BoringSSL [4], Libsodium [5], and CryptoPP [6]. They are all in the public domain, are widely used, and have received substantial scrutiny from the security community.
OpenSSL is one of the most popular cryptographic libraries, providing a widely used implementation of the Transport Layer Security (TLS) and Secure Sockets Layer (SSL) protocols. Due to its importance, there has been a long line of work in checking the security of OpenSSL, resulting in the discovery of several important vulnerabilities, such as the notorious Heartbleed bug [31]. As a popular commercial-grade toolkit, OpenSSL is used by many systems. BoringSSL is Google’s fork of OpenSSL, providing the SSL library in Chrome/Chromium and Android OS.
Libsodium is a well-known cryptographic library that aims for security and ease of correct use. It provides several benefits such as portability, cross-compilability, and API-compatibility, and supports bindings for all common programming languages. As a result, Libsodium has been used in a number of applications, such as the cryptocurrency Zcash and Facebook’s OpenR (a distributed platform for building autonomic network functions). It however only supports AES-GCM with 256-bit keys.
CryptoPP is another popular open-source cryptographic library for C++. It is widely adopted in both academic and commercial usage, including WinSSHD (an SSH server for Windows), Steam (a digital distribution platform purchasing and playing video games), and Microsoft SharePoint Workspace (a document collaboration software).
4 MPI with encrypted communication
We developed two MPI libraries whose communication is encrypted via AES-GCM (for both -bit and -bit keys); one library is based on MPICH-3.2.1 for Ethernet and the other on MVAPICH2-2.3 for InfiniBand. Specifically, encryption is added to the following MPI routines:
-
•
Point-to-point: MPI_Send, MPI_Recv, MPI_ISend, MPI_IRecv, MPI_Wait, and MPI_Waitall.
-
•
Collective: MPI_Allgather, MPI_Alltoall, MPI_Alltoallv, and MPI_Bcast.
The underlying cryptographic library is user-selectable among OpenSSL, BoringSSL, Libsodium, and CryptoPP. With encryption incorporated at the MPI layer, our prototypes can run on top of any underlying network. As our main focus of this work is to benchmark the performance of encrypted MPI libraries, we did not implement a key distribution mechanism; this is left as a future work. In our experiments, the encryption key was hardcoded in the source code.
To illustrate the high-level ideas of our implementation, consider the pseudocode of our Encrypted_Alltoall routine in Algorithm 1. Within this code, we use to denote the sampling of a uniformly random -byte string, and for the concatenation of two strings and . The encryption and decryption routines of AES-GCM are Enc and Dec, respectively. Intuitively, the ordinary MPI_Alltoall is used to send/receive just ciphertexts and their corresponding nonces. That is, one would need to encrypt the sending messages before calling MPI_Alltoall—each message with a fresh random nonce, and then decrypt the receiving ciphertexts. If a sending message is -byte long then the corresponding data that MPI_Alltoall sends is -byte long, since it consists of (i) a -byte nonce, and (ii) a ciphertext that is -byte longer than its plaintext.
We note that although the pseudocode above seems straightforward, in an actual implementation, there are some low-level subtleties when one has to deal with non-blocking communication. For example, for Encrypted_IRecv, our implementation performs decryption inside MPI_Wait to ensure the non-blocking property.
5 Experiments
We empirically evaluated the performance of our encrypted MPI libraries to (i) understand the encryption overheads in MPI settings, and (ii) determine the best cryptographic library to use with MPI. Below, we will first describe the system of our experiments, the benchmarks, and our methodology. Later, in Section 5.1 and Section 5.2, we will report the experiment results on Ethernet and Infiniband respectively.
System setup. The experiments were performed on a cluster with the following configuration. The processors are Intel Xeon E5-2620 v4 with the base frequency of 2.10 GHz. Each node has 8 cores and 64GB DDR4 RAM and runs CentOS 7.6. Each node is equipped with two types of network interface cards: a 10 Gigabit Ethernet card (Intel 82599ES SFI/SFP+) and a 40 Gigabit InfiniBand QDR one (Mellanox MT25408A0-FCC-QI ConnectX). Allocated nodes were chosen manually. For each experiment, the same node allocation was repeated for all measurements. All ping-pong results use two processes on different nodes.
We implemented our prototypes on top of MPICH-3.2.1 (for Ethernet) and MVAPICH2-2.3 (for Infiniband). The baseline and our encrypted MPI libraries were compiled with the standard set of MPICH and MVAPICH compilation flags and optimization level O2. In addition, we compiled all the cryptographic libraries (OpenSSL 1.1.1, BoringSSL, CryptoPP 7.0, and Libsodium 1.0.16) separately using their default settings and linked them with MPI libraries during the linking phase of MPICH and MVAPICH.
Benchmarks. We consider the following suites of benchmarks:
-
•
Encryption-decryption: The encryption-decryption benchmark measures the encryption and decryption performance. For each data size, it measures the time for performing 500,000 times the simple encryption and then decryption of the data using a single thread.
-
•
Ping-pong: This benchmark measures the uni-directional throughput when two processes communicate back and forth repeatedly using blocking send and receive. We ran several experiments, each corresponding to a particular message size within the range from 1B to 2MB. In each experiment measurement, the two processes send messages of the designated size back and forth 10,000 times if the message size is less than 1MB, and 1,000 times otherwise. For encrypted communication, each message results in an additional 28-byte overhead, as we need to send a 12-byte nonce and a 16-byte tag per ciphertext. Those bytes are excluded in the throughput calculation.
-
•
OSU micro-benchmark 5.4.4 [9]: We used the Multiple Pair Bandwidth Test benchmark in OSU suite to measure aggregate uni-directional throughput when multiple senders in one node communicate with their corresponding receivers in another node, via non-blocking send and receive. In each experiment measurement, the sender iterates 100 times; in each iteration, it sends 64 messages of the designated size to the receiver and wait for the replies before moving to the next iteration. Again, we excluded the 28-byte overhead per message in calculating the throughput.
We also used OSU suite to measure performance of collective communication routines. Each experiment measurement consists of 100 iterations.
-
•
NAS parallel benchmarks [7]: To measure performance of (encrypted) MPI in applications, we used the BT, CG, FT, IS, LU, MG, and SP in the NAS parallel benchmarks; all experiments used Class C size.
Benchmark methodology. For ping-pong, OSU benchmarks, and NAS benchmarks, we first ran each experiment at least 20 times, up to 100 times, until the standard deviation was within 5% of the arithmetic mean. If after 100 measurements, the standard deviation was still too big then we would keep running the experiment until the 99% confidence interval was within 5% of the mean. The variability for encryption and decryption is much smaller. Hence, each result for the encryption-decryption benchmark is obtained by running the benchmark at least 5 times until the standard deviation was within 5% of the arithmetic mean.
To evaluate the scalability of our implementation, we used four different settings (e.g. 4 rank/4 node, 16 rank/4 node, 16 rank/8 node and 64 rank/8 node) for OSU and NAS benchmarks.
What we report. In our experiments, BoringSSL and OpenSSL delivered very similar performance. This is not surprising, since BoringSSL is a fork of OpenSSL. In addition, the benchmarks yielded the same trends for both 128-bit and 256-bit keys. We therefore only report the results of BoringSSL (256-bit key), Libsodium, and CryptoPP (256-bit key).
5.1 Ethernet Results
Encryption-decryption. Before we get into the details of the communication benchmark results, it is instructive to understand the performance of AES-GCM, since it helps us to have a better understanding of the performance of the encrypted MPI libraries. The average throughputs of AES-GCM-256 with different data sizes are shown in Fig. 2. It is clear that different encryption libraries have very different encryption and decryption performance. There are two ways to interpret the results here. First, one can view this as the convergence of the ping-pong performance when the network speed becomes much faster than encryption and descryption. Also, since for AES-GCM, the encryption and decryption speed is roughly the same, the reported performance here is a half of the encryption throughput (that is also decryption throughput). Thus we can predict that for most experiments, among the three encrypted MPI libraries, BoringSSL is the best, and then Libsodium, and finally CryptoPP.

Ping-pong. The ping-pong performance of the baseline and the encrypted MPI libraries is shown in Table I for small messages, and in Fig. 3 for medium and large messages. For 1KB data, BoringSSL appears to slightly outperform the baseline, but recall that we are reporting the mean values with 5% deviation, so this only means that BoringSSL has close performance to the baseline.
| 1B | 16B | 256B | 1KB | |
|---|---|---|---|---|
| Unencrypted | 0.050 | 0.83 | 7.01 | 17.03 |
| BoringSSL | 0.045 | 0.78 | 6.62 | 17.05 |
| Libsodium | 0.046 | 0.79 | 6.62 | 17.02 |
| CryptoPP | 0.029 | 0.48 | 6.85 | 17.02 |

For large messages, say 2MB ones, encrypted MPI libraries have poor performance compared to the baseline: even the fastest BoringSSL yields 78.3% overhead, and CryptoPP’s overhead is much worse, nearly 400%. These performance results can be explained as follows.
-
•
The running time of an encrypted MPI library consists of (i) the encryption-decryption cost, and (ii) the underlying MPI communications, which roughly corresponds to the baseline performance.
-
•
For BoringSSL, on 2MB messages, the encryption-decryption throughput of AES-GCM-256 (1381 MB/s) is about 1.32 times that of the ping-pong throughput of the baseline (1038 MB/s). Estimatedly, BoringSSL’s ping-pong time would be roughly times slower than that of the baseline. This is consistent with the reported 78.3% overhead above.
-
•
For CryptoPP, on 2MB messages, the encryption-decryption throughput of AES-GCM-256 (273 MB/s) much worse, just around 26% of the ping-pong performance of the baseline (1038 MB/s). One thus can estimate that CryptoPP’s ping-pong time would be about times slower than that of the baseline. This is again consistent with the reported 400% overhead above.
For small messages, encrypted MPI libraries often perform reasonably well, since the encryption-decryption throughput of AES-GCM-256 is quite higher than the ping-pong throughput of the baseline. For example, for 256-byte messages, the encryption-decryption throughput of Libsodium is 409.67 MB/s, much higher than the 7.01 MB/s baseline ping-pong throughput. Consequently, Libsodium has just 5.89% overhead for 256-byte messages.
OSU Multiple-Pair Bandwidth. The Multiple-Pair performance of the baseline and the encrypted MPI libraries, for 1B, 16KB, and 2MB messages, is shown in Figure 4.



For medium and large messages, as the number of pairs increases, the relative performance of the encrypted MPI libraries becomes much better, because (i) the network bandwidth remains the same, yet the computational power doubles, and (ii) encryption/decryption can overlap with MPI communications. When there is just a single pair, even BoringSSL cannot encrypt fast enough to keep up with the network speed. However, when there are 8 pairs, even CryptoPP can reach the baseline performance, for 16KB messages. These results suggest that (1) the overhead for a single communication flow may be significant, but (2) in modern multi-core machines, when multiple flows happen concurrently, the performance of encrypted MPI libraries may be on par with the baseline.
For small messages, the situation is different, because the network bandwidth is not fully used. As shown in Fig. 4, for 1B-data, the baseline throughput keeps increasing as the number of pairs increases. In contrast, for medium and large messages, the baseline throughput is saturated when there are just two pairs of senders and receivers. Consequently, even when there are 8 pairs, BoringSSL still incurs 61.67% overhead, and CryptoPP is far worse, resulting in 506.25% overhead.
Collective communication. The average running time of Encrypted_Bcast and Encrypted_Alltoall, for the 64-rank and 8-node setting, is shown in Tables II and III, respectively.
| 1B | 16KB | 4MB | |
|---|---|---|---|
| Unencrypted | 31.15 | 231.75 | 9,594.75 |
| BoringSSL | 37.15 | 246.17 | 13,892.74 |
| Libsodium | 35.54 | 264.37 | 18,322.19 |
| CryptoPP | 54.97 | 278.65 | 29,301.96 |
| 1B | 16KB | 4MB | |
|---|---|---|---|
| Unencrypted | 159.13 | 6,562.82 | 1,966,299.47 |
| BoringSSL | 329.60 | 7,691.08 | 2,210,546.32 |
| Libsodium | 452.76 | 8,937.74 | 2,535,104.93 |
| CryptoPP | 1,221.98 | 9,462.90 | 3,297,402.93 |
To understand the performance of Encrypted_Bcast, recall that each encrypted broadcast consists of an ordinary MPI_Bcast and an encryption and a decryption per node. Hence the encryption overhead of the three encrypted MPI libraries, illustrated in Fig. 5, loosely mirrors their encryption-decryption throughput of Fig. 2.
-
•
For example, for large messages (say 2MB), the encryption-decryption throughput of BoringSSL (1381 MB/s) is around 2.37 times that of Libsodium (583 MB/s). On the other hand, the encryption overhead in Encrypted_Bcast of BoringSSL (44.8%) is 2.03 times smaller than that of Libsodium (90.96%), approximating the ratio 2.37 above.
-
•
As another example, for BoringSSL, the encryption-decryption throughput for 2MB messages is about the same as that for 16KB messages. Thus one would expect the encryption cost for 4MB messages in Encrypted_Bcast would be about times that for 16KB messages. Indeed, for 4MB messages, BoringSSL spends about 4,298 s on encryption/decryption, which is about 298 times its encryption/decryption time for 16KB messages (14.42 s).


The trend of Encrypted_Alltoall, illustrated in Fig. 5, is similar.
-
•
For example, for 16KB messages, the encryption-decryption throughput of BoringSSL (1332 MB/s) is about times that of CryptoPP (568 MB/s). The encryption overhead of BoringSSL in Encrypted_Alltoall (17.19%) is 2.57 times smaller than that of CryptoPP (44.19%).
-
•
As another example, for CryptoPP, the encryption-decryption throughput for 2MB messages (273 MB/s) is about a half of that for 16 KB messages (568 MB/s). Thus one would expect the encryption cost for 4MB messages in Encrypted_Alltoall would be about times that for 16KB messages. Indeed, for 4MB messages, CryptoPP spends about 1,331,103 s on encryption/decryption, which is about 459 times its encryption/decryption time for 16KB messages (2900 s).
and 8-node, on Ethernet.
| CG | FT | MG | LU | BT | SP | IS | |
|---|---|---|---|---|---|---|---|
| Unencrypted | 7.01 | 12.04 | 2.55 | 18.04 | 22.83 | 21.99 | 4.06 |
| BoringSSL | 8.55 | 12.81 | 3.01 | 19.05 | 27.40 | 24.46 | 4.52 |
| Libsodium | 9.62 | 13.67 | 3.09 | 19.48 | 28.70 | 26.30 | 4.71 |
| CryptoPP | 11.67 | 15.53 | 3.33 | 23.13 | 29.52 | 27.37 | 4.83 |
NAS benchmarks. To understand encryption overheads in a more realistic setting, we evaluated the encrypted MPI libraries under NAS parallel benchmarks. The results are shown in Table IV. Overall, BoringSSL’s total running time is 99.81 seconds, whereas the baseline’s running time is 88.52 seconds, and thus BoringSSL’s overhead is 12.75%.222 Conventionally, one would compute BoringSSL’s overhead of each benchmark (BT, CG, FT, etc) and then report the average of them as BoringSSL’s average overhead. However, as pointed out by several papers [32, 33], averaging over ratios is meaningless. Following the recommendation of those papers, here we instead derived BoringSSL’s overhead from its total timing of all NAS benchmarks and that of the baseline. Likewise, Libsodium’s and CryptoPP’s overhead are 19.25% and 30.33% respectively. These results again support our thesis that encryption overheads may not be prohibitive for realistic scenarios where there are multiple concurrence communication flows.
5.2 Infiniband Results
Encryption-decryption. It turns out that the MVAPICH2-2.3 compiler, even with the same O2 flag, results in higher encryption-decryption performance than the gcc 4.8.5 compiler for some libraries. Fig. 6 shows the average encryption-decryption throughput of AES-GCM-256 code compiled by the MVAPICH compiler. In particular, the performance of CryptoPP for message size greater than 64KB is dramatically improved. It seems natural to predict that while CryptoPP is still the last among the three encrypted MPI libraries, for large messages, its performance will be close to that of Libsodium.

Ping-pong. The ping-pong performance of the baseline and the encrypted MPI libraries is shown in Table V for small messages, and illustrated in Fig. 7 for medium and large messages.

Again, for large messages, the performance of the encrypted MPI libraries is much lower than that of the baseline, but the situation is much worse than the Ethernet setting. For example, for 2MB messages, even BoringSSL results in a 215.2% overhead. With InfiniBand, the baseline ping-pong throughput is significantly higher than that with Ethernet while the encryption-decryption throughput remains the same: the encryption-decryption throughput of AES-GCM-256 is much lower than the ping-pong throughput of the baseline. For example, for 2MB messages, the encryption-decryption throughput of AES-GCM-256 in BoringSSL (1384 MB/s) is just around 46% of the baseline ping-pong throughput (3023 MB/s), and thus estimatedly, BoringSSL’s ping-pong time would be about times slower than that of the baseline. This is consistent with the reported 215.2% overhead above.
256-bit Encryption Key on Infiniband.
| 1B | 16B | 256B | 1KB | |
|---|---|---|---|---|
| Unencrypted | 0.57 | 9.61 | 82.34 | 272.84 |
| BoringSSL | 0.22 | 4.02 | 45.51 | 142.23 |
| Libsodium | 0.27 | 4.86 | 50.66 | 133.06 |
| CryptoPP | 0.05 | 0.98 | 17.27 | 61.08 |
For small messages, the situation is somewhat better, but even BoringSSL would yield poor performance. For example, for 256-byte messages, BoringSSL has a 80.93% overhead.
OSU Multiple-Pair Bandwidth. The Multiple-Pair performance of the baseline and the encrypted MPI libraries, for 1B, 16KB, and 2MB messages, is shown in Figure 8.



Like the Ethernet setting, for medium and large messages, although the encryption overhead is substantial when there is only one pair of communication, when the number of pairs increases, the throughput of encrypted MPI libraries is much closer to the baseline throughput. However, for medium message size (say 16KB), even when there are eight communication flows, BoringSSL only achieves 2561 MB/s, which is just 81.8% of the baseline throughput of 3128 MB/s. This gap is due to the speed difference between Ethernet and Infiniband.
For small messages, the trend is at first similar to that of the Ethernet setting, but when the number of pairs increases from 4 pairs to 8 pairs, the baseline throughput is throttled, probably due to network contention. This decrease also happens for medium and large messages, but not as conspicuously as the case of small messages. Due to the plummeting of the baseline throughput, for 8 pairs and one-byte messages, BoringSSL’s overhead is just 29.91%, whereas for 4 pairs, its overhead is 308.33%.
Collective Communication. The average running time of Encrypted_Bcast and Encrypted_Alltoall for the 64-rank and 8-node setting, is shown in Tables VI and VII respectively. The trend, as illustrated in Fig. 9, is similar to that of the Ethernet setting, but the overhead is much worse, because Infiniband latency is lower.
| 1B | 16KB | 4MB | |
|---|---|---|---|
| Unencrypted | 4.14 | 28.58 | 3,780.27 |
| BoringSSL | 7.64 | 52.08 | 8,204.73 |
| Libsodium | 6.68 | 75.81 | 13,294.35 |
| CryptoPP | 25.25 | 85.43 | 23,344.63 |
| 1B | 16KB | 4MB | |
|---|---|---|---|
| Unencrypted | 21.48 | 5,352.84 | 657,145.51 |
| BoringSSL | 435.70 | 6,789.17 | 1,013,896.50 |
| Libsodium | 736.29 | 7,977.41 | 1,305,389.60 |
| CryptoPP | 1,187.75 | 8,744.08 | 2,049,864.38 |


NAS benchmarks. The results of NAS benchmarks for Infiniband are shown in Table VIII. Here the overheads of BoringSSL, Libsodium, and CryptoPP are 17.93%, 24.27% and 29.41% respectively. CryptoPP’s overhead in Infiniband is slightly less than that in Ethernet, because the compiler in the former setting uses more aggressive optimizations than its Ethernet counterpart, which drastically improves the performance of CryptoPP, as shown in Figures 2 and 6. These results again reiterate our thesis that even in very fast networks, encryption overheads may not be prohibitive for practical scenarios.
and 8-node, on Infiniband.
| CG | FT | MG | LU | BT | SP | IS | |
|---|---|---|---|---|---|---|---|
| Unencrypted | 6.55 | 10.00 | 3.59 | 18.36 | 24.56 | 24.20 | 3.04 |
| BoringSSL | 8.36 | 10.77 | 4.20 | 19.73 | 33.35 | 26.87 | 3.20 |
| Libsodium | 9.87 | 11.52 | 4.28 | 20.04 | 34.62 | 28.55 | 3.33 |
| CryptoPP | 10.47 | 11.89 | 4.41 | 22.82 | 34.96 | 28.97 | 3.35 |
6 Modeling Encrypted MPI Point-to-Point Communication
To further understand the performance of encrypted MPI communications, we develop performance models that can predict the performance of encrypted MPI point-to-point communication in two settings: single-pair point-to-point communication like the Ping-Pong test and (concurrent) multiple-pair point-to-point communication like the OSU Multiple-Pair benchmark [9]. Our models extend the Hockney model [10] and the max-rate model [17], and are able to predict the performance of encrypted MPI point-to-point communication in the two settings accurately. We will describe the models and validate them with measured data in Section 5, on both Ethernet and Infiniband. We show that the parameters for our models can be obtained by independent benchmarking of the MPI and cryptographic libraries. Using the models, we reason about the performance of encrypted MPI point-to-point communication in different system settings and suggest potential optimization techniques to improve the performance of encrypted MPI communication.
6.1 Modeling Single-pair Encrypted MPI Point-to-point Communication
Modeling communication. If encryption and decryption are extremely fast then the performance of encrypted communication will converge to that of the conventional MPI communication. Therefore, let’s begin by recalling how to model unencrypted point-to-point communication. There are several models in the literature, such as LoP [25] or LoGP [26]. Among them, a popular one is the Hockney model [10], where the time to send or receive a message of bytes is modeled as
Here, is the network latency, and is the inverse of the asymptotic bandwidth. We will use different values of the parameters for the eager phase (i.e., message size is smaller than KB on Ethernet) and the rendezvous phase (i.e., message size is bigger than KB on Ethernet), since MPI implementations will use different protocols for these phases.
To obtain the parameters of the Hockney model, we use linear least squares on latency measurements from the Ping-Pong benchmarks in Section 5 to find the best fitting .333 If the linear regression results in a meaningless negative then we will instead let be the average latency of Ping-Pong benchmarks for one-byte data, and then find the best fitting via linear least squares. The values of those parameters are given in Table IX.
| (s) | (s/B) | ||
|---|---|---|---|
| Ethernet | Eager | 32.74 | |
| Rendezvous | 117.30 | ||
| Infiniband | Eager | 3.40 | |
| Rendezvous | 7.17 |
Modeling encryption-decryption. It is also instructive to study encryption-decryption alone, as this is a special case of encrypted communication on a very fast network. We model the time of encrypting and then decrypting a message of bytes as
where is the initial overhead, and is the encryption-decryption rate. To obtain the parameters and , we again use linear least squares on the latency measurements of the encryption-decryption benchmarks in Section 5. The values of those parameters are given in Table X.
| (s) | (s/B) | |
|---|---|---|
| BoringSSL | 0.53 | |
| Libsodium | 0.48 | |
| CryptoPP (MPICH) | 5.51 | |
| CryptoPP (MVAPICH) | 5.16 |
Modeling encrypted communication. An encrypted single-flow point-to-point communication consists of the following sequential operations: (i) encrypting the message at the sender, (ii) transmitting the encrypted message from the sender to the receiver, and (iii) decrypting the ciphertext at the receiver. If we ignore the 28-byte expansion in encryption then the time in completing the encrypted communication of an -byte message can be modeled as
If we let and then we obtain
| (1) |
Intuitively, encrypted communication can be viewed as conventional MPI communication over a private and authenticated channel, thus Eq. (1) is the Hockney model for communication over this network. Since this Hockney model takes both communication and encryption into account, we will call it the enhanced Hockney model.
An advantage of the enhanced Hockney model above is that the parameters and can be obtained without implementing encrypted MPI. In fact, one can use available benchmarks of conventional MPI implementations and cryptographic libraries to obtain , and compute and . In other words, the independent benchmarking results summarized in Table IX (for MPI libraries) and Table X (for cryptographic libraries), can directly derive the model parameters for the enhanced Hockney model. Consider, for example, small messages (Eager protocol) with BoringSSL on InfiniBand. From Table IX, we have and ; from Table X, we have and . Hence, for the encrypted single-flow MPI point-to-point communication, the enhanced Hockney model has the parameters and for small messages. The model parameters for other combinations of libraries and systems can be derived similarly.
Using parameters derived from independent benchmarking of MPI and encryption libraries, we validate the enhanced Hockney models for single-pair encrypted MPI communications by comparing the model’s predicted performance to the measured performance of our encrypted MPI libraries with the Ping-Pong benchmark on different systems. Three encryption libraries, BoringSSL, Libsodium, and CryptoPP, and two networks, InfiniBand and Ethernet are studied. Results for OpenSSL are similar to those for BoringSSL and are not reported. As shown in Fig. 10, for all configurations, our enhanced Hockney models capture the trend of encrypted communication with reasonable accuracy.






6.2 Modeling Multiple-pair Encrypted MPI Point-to-point Communication
We consider the performance of multiple concurrent pairs of encrypted MPI point-to-point communications like the OSU multiple-pair benchmark.
Modeling communication. Again, we begin by recalling how to model the performance of concurrent unencrypted, point-to-point communications. Under the Hockney model [10], the time of senders from one node to transmit -byte messages to corresponding receivers in another node is
where is the network latency, and is the inverse of the network bandwidth. We use different values of the parameters for the eager phase (meaning message size is smaller than 128KB on Ethernet) and the rendezvous phase (meaning message size is bigger than 128KB on Ethernet).
We use linear least-squares on latency measurements from the (unencrypted) Multiple-Pair benchmarks in Section 5 to obtain the best fitting . The values of those parameters are given in Table XI. 444Since OSU Multiple-Pair benchmark uses non-blocking sends and Ping Pong uses blocking sends, the parameter of the former is smaller than that of the latter. Moreover, as OSU Multiple-Pairs benchmark sends 64 messages back-to-back, its latency is an order of magnitude smaller than that of the Ping Pong benchmark.
| (s) | (s/B) | ||
|---|---|---|---|
| Ethernet | Eager | 3.84 | |
| Rendezvous | 16.35 | ||
| Infiniband | Eager | 1.02 | |
| Rendezvous | 2.38 |
Modeling encryption-decryption. To understand how encryption performance scales with multiple threads, we consider the setting in which there are threads, each encrypting and then decrypting an -byte message. We follow the max-rate model of Gropp et al. [17] for concurrent point-to-point communications by viewing multi-threading encryption-decryption as unencrypted Multiple-Pair communication over a very fast network, and encryption as injecting a message to a network card. Specifically, the latency is modeled as
where is the initial cost, and models the encryption rate of threads, capturing the fact that adding more threads will slow down the per-thread performance.
To obtain the training data for deriving the parameters, we run the encryption-decryption benchmark in Section 5 for BoringSSL for threads. To account for the pipelining effect of AES-NI and whether a message fits the L1 cache (32 KB), we divide the message size into three corresponding levels—small (up to 256B), moderate (larger than 256B but smaller than 32KB), and large (32KB or more)—and use different parameters for each level. To obtain the parameters , we use Matlab’s non-linear least square on the latency measurements from the experiment above to find the best fitting choice.555Specifically, we use Matlab’s command lsqnonlin. The values of are given in Table XII.
| Phase | (s) | (B/s) | (B/s) |
|---|---|---|---|
| Small | 1.8 | ||
| Moderate | 2.66 | ||
| Large | 3.44 |
Modeling encrypted communication. Multiple-pair MPI communication is more complicated than single-pair ping-pong communication in that there are different ways that the multiple-pair communication can be performed. Hence the models for multiple-pair communication will depend on the ways that the multiple-pair communication is performed. We will use the model for the OSU multiple-pair benchmark to illustrate how multiple-pair encrypted MPI point-to-point communication can be obtained from independent benchmarking results for MPI and encryption libraries, that is, from and .
In the OSU multiple-pair benchmark, the performance is measured for iterations of 64-round loops. For each iteration, each sender encrypts a message of bytes and then sends the ciphertext to its receiver via a non-blocking send; with our encrypted library implementation, each receiver waits for all 64 ciphertexts to arrive and decrypt them. In modeling this multiple-pair communication, we make the following assumptions:
-
•
The encryption time and decryption time for a message are the same.666In modern machines that support AES-NI and CLMUL instruction set, AES-GCM encryption is often slightly faster than decryption, but the speed difference is small.
-
•
The transmission of the -th message (via non-blocking send) and the encryption of the -th message can happen concurrently. Likewise, the receiver can simultaneously decrypt a ciphertext of the -th message while receiving the ciphertext of the -th message.
In this communication, each sender will first encrypt the bytes data, which takes time (half of the encryption and description time), after that, there are 63 overlapped encryptions and communications, which takes time, and one last communication, that takes time. Hence, the encryption and sending time can be modeled as
Since the receiver waits for all 64 ciphertexts to arrive and decrypt them, the total time for a 64-round loop in the encrypted Multiple-Pair experiment can be modeled as
and thus the average time for a single round is
Notice that the model for multiple-pair encrypted MPI point-to-point communication, is derived from and . Hence the model parameters for multiple-pair communication can also be derived from independent benchmarking results for the MPI library and encryption libraries.





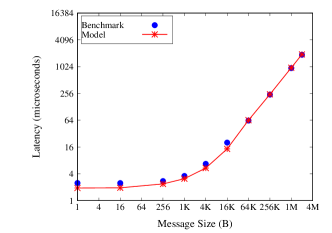


We validate the model by comparing the predicted performance from the model to the measured performance using the OSU Multiple-Pair benchmark [9] with the three encryption libraries and two networks (Ethernet and InfiniBand). Fig. 11 shows the results for Ethernet and Fig. 12 shows the results for InfiniBand.
6.3 Discussion
An advantage of our models for both single-pair and multiple-pair communications is that the parameters can be obtained from the available benchmarks of conventional MPI and encryption, meaning that using these models, one does not need to implement encrypted MPI in order to understand encrypted MPI communication performance. As shown earlier, these models capture the performance trend and predict the performance with reasonable accuracy for different libraries and networks. Hence, the models allow us to reason about the performance of encrypted MPI communications.
We will use examples to show that the models give simple and intuitive explanation of the performance results across different cryptographic libraries and different networks in Section 5. Consider for example the single-pair communication. For large messages, and are dominated by and respectively, and thus the encryption overhead (for throughput) is
For example, the overhead of BoringSSL for large messages is predicted to be
for Ethernet, which is consistent with the Ping-pong benchmark results in Figure 3 in Section 5—the measured results have an overhead of 78.3% for 2MB messages. For InfiniBand, the overhead of BoringSSL for large messages is predicted to be
where as the measured results of the Ping-pong benchmark in Figure 7 in Section 5 have an overhead of 215% for 2MB messages.
Consider now the multiple-pair communication:
There are two situations depending on the relative speed of communication and encryption. For a slow network such that , we have , and the encryption overhead (for throughput) is
meaning that the overhead is inversely proportional to : the larger the value of (pairs of communications), the smaller the overhead. Both 10Gbps Ethernet and 40Gbps InfiniBand has when . This overhead trend is observed in Figure 4 and Figure 8. Plugging in the values of and from Table XII and from Table XI will give a reasonable estimation of the overheads for OSU multiple pair benchmarking results.
For a faster network such that , , meaning that the communication cost can be completely hidden. However, the performance will be bounded by the encryption speed, which can be much slower than the network speed.
Clearly, there is a gap between what single-core encryption can provide and what a high-speed network can consume. The gap is likely to increase since (1) we reach the limit of Moore’s law and single-core computing performance will not drastically improve, and (2) communication technology is still improving as the network bandwidth continues to increase. As such, efficient encrypted MPI communication will be even more challenging in the future.
The models can give guidance on the techniques to achieve higher encrypted MPI communication performance as well as the potential benefits of such techniques. Consider for example to improve the single-pair encrypted performance. One potential technique is to overlap encryption with communication. For large messages, this can be achieved by chopping the message into small segments, then encrypting (and decrypting) each segment, and using non-blocking communication to overlap communication with encryption and decryption as in streaming encryption [34]. Using this technique, . For systems with a slow network such as an 10Gbps Ethernet where , we have : the encryption overhead can virtually be completely removed. However, for a faster network such as 40Gbps InfiniBand where , . Consider for example, encrypted communication for large message with BoringSSL on InfiniBand, we have (Table IX) and (Table X), hence . Thus, even with the encryption and communication overlapping technique, the encryption overhead will roughly be . This overhead is further be improved by using multiple threads to perform concurrent encryption and decryption. This technique with multiple threads will be more attractive for future systems since they will likely to have more (idle) cores in each node.
7 Conclusion
We considered adding encryption to MPI communications for providing privacy and integrity. Four widely used cryptographic libraries, OpenSSL, BoringSSL, CryptoPP, and Libsodium, were studied in this paper. We found that the encryption overhead differs drastically across libraries, and that BoringSSL (and OpenSSL) achieves the best performance in most settings. Moreover, when individual communication is considered, encryption overhead can be quite large. However, in practical scenarios when multiple communication flows are carried out concurrently, the overhead is not significant. In particular, our evaluation with the NAS parallel benchmarks shows that using the best cryptographic library BoringSSL, our implementation on average only introduces 12.75% overhead on Ethernet and 17.93% overhead on Infiniband.
We then show that the Hockney model accurately model encrypted Ping Pong performance. Moreover, the model parameters can be obtained from benchmark results of a conventional MPI library and a cryptographic library, meaning that one does not even need to implement encrypted MPI. In addition, we show how to decompose the performance of encrypted Multiple-Pair benchmark into the unencrypted Multiple-Pair cost and the multi-threading encryption cost, and model these components via the Hockney model and the max-rate model. These models allow us to reason about the performance of encrypted MPI communication across different cryptographic libraries and platforms, and estimate the potential performance gain for different optimization techniques.
Acknowledgments
We thank Sriram Keelveedhi for helpful discussions and Prof. Weikuan Yu at Florida State University for providing the computing infrastructure for software development and performance measurement. This material is based upon work supported by the National Science Foundation under Grants CICI-1738912, CRI-1822737, CNS-1453020, and CRII-1755539. Any opinions, findings, and conclusions or recommendations expressed in this material are those of the author(s) and do not necessarily reflect the views of the National Science Foundation. This work used the Extreme Science and Engineering Discovery Environment (XSEDE), which is supported by National Science Foundation grant number ACI-1548562. This work used the XSEDE Bridges resource at the Pittsburgh Supercomputing Center (PSC) through allocation TG-ECS190004.
References
- [1] X. Ruan, Q. Yang, M. I. Alghamdi, S. Yin, and X. Qin, “ES-MPICH2: A Message Passing Interface with enhanced security,” IEEE Trans. Dependable Secur. Comput., vol. 9, no. 3, pp. 361–374, May 2012. [Online]. Available: http://dx.doi.org/10.1109/TDSC.2012.9
- [2] J. Katz and Y. Lindell, Introduction to modern cryptography. CRC press, 2014.
- [3] “OpenSSL: The open source toolkit for SSL/TLS,” http://www.openssl.org, 2018.
- [4] “BoringSSL,” https://boringssl.googlesource.com/boringssl, 2018.
- [5] “The Sodium cryptography library (Libsodium),” https://libsodium.gitbook.io/doc, 2018.
- [6] W. Dai, “CryptoPP,” https://www.cryptopp.com, 2018.
- [7] D. Bailey, E. Barszcz, J. Barton, D. Browning, R. Carter, L. Dagum, R. Fatoohi, P. Frederickson, T. Lasinski, R. Schreiber, H. Simon, V. Venkatakrishnan, and S. Weeratunga, “The NAS Parallel Benchmarks,” Int. J. High Perform. Comput. Appl., vol. 5, no. 3, pp. 63–73, Sep. 1991. [Online]. Available: http://dx.doi.org/10.1177/109434209100500306
- [8] M. J. Dworkin, “NIST SP 800-38A. Recommendation for block cipher modes of operation: Methods and techniques,” 2001.
- [9] “OSU Benchmarks,” http://mvapich.cse.ohio-state.edu/benchmarks/.
- [10] R. W. Hockney, “The communication challenge for mpp: Intel paragon and meiko cs-2,” Parallel Comput., vol. 20, no. 3, pp. 389–398, Mar. 1994. [Online]. Available: http://dx.doi.org/10.1016/S0167-8191(06)80021-9
- [11] R. Thakur, R. Rabenseifner, and W. Gropp, “Optimization of collective communication operations in mpich.” International Journal of High Performance Computing Applications, vol. 19, pp. 49–66, 01 2005.
- [12] A. Faraj and X. Yuan, “Automatic generation and tuning of mpi collective communication routines,” in ACM International Conference on Supercomputing (ICS), 06 2005, pp. 393–402.
- [13] R. Rabenseifner and J. L. Träff, “More efficient reduction algorithms for non-power-of-two number of processors in message-passing parallel systems,” in Recent Advances in Parallel Virtual Machine and Message Passing Interface, D. Kranzlmüller, P. Kacsuk, and J. Dongarra, Eds. Berlin, Heidelberg: Springer Berlin Heidelberg, 2004, pp. 36–46.
- [14] A. Faraj, P. Patarasuk, and X. Yuan, “Bandwidth efficient all-to-all broadcast on switched clusters,” International Journal of Parallel Programming, vol. 36, no. 4, pp. 426–453, Aug 2008. [Online]. Available: https://doi.org/10.1007/s10766-007-0047-0
- [15] P. Patarasuk, X. Yuan, and A. Faraj, “Techniques for pipelined broadcast on ethernet switched clusters,” Journal of Parallel and Distributed Computing, vol. 68, no. 6, pp. 809 – 824, 2008. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0743731508000154
- [16] P. Patarasuk and X. Yuan, “Bandwidth optimal all-reduce algorithms for clusters of workstations,” J. Parallel Distrib. Comput., vol. 69, no. 2, pp. 117–124, Feb. 2009. [Online]. Available: http://dx.doi.org/10.1016/j.jpdc.2008.09.002
- [17] W. Gropp, L. N. Olson, and P. Samfass, “Modeling mpi communication performance on smp nodes: Is it time to retire the ping pong test,” in Proceedings of the 23rd European MPI Users’ Group Meeting. ACM, 2016, pp. 41–50.
- [18] B. Balamurugan, P. V. Krishna, G. V. Rajya Lakshmi, and N. S. Kumar, “Cloud cluster communication for critical applications accessing C-MPICH,” in 2014 International Conference on Embedded Systems (ICES 2014), July 2014, pp. 145–150.
- [19] M. A. Maffina and R. S. RamPriya, “An improved and efficient message passing interface for secure communication on distributed clusters,” in 2013 International Conference on Recent Trends in Information Technology (ICRTIT 2013), July 2013, pp. 329–334.
- [20] V. Rekhate, A. Tale, N. Sambhus, and A. Joshi, “Secure and efficient message passing in distributed systems using one-time pad,” in 2016 International Conference on Computing, Analytics and Security Trends (CAST 2016), Dec 2016, pp. 393–397.
- [21] S. Shivaramakrishnan and S. D. Babar, “Rolling curve ECC for centralized key management system used in ECC-MPICH2,” in 2014 IEEE Global Conference on Wireless Computing Networking (GCWCN 2014), Dec 2014, pp. 169–173.
- [22] J. Mason, K. Watkins, J. Eisner, and A. Stubblefield, “A natural language approach to automated cryptanalysis of two-time pads,” in Proceedings of the 13th ACM conference on Computer and communications security (CCS 2006). ACM, 2006, pp. 235–244.
- [23] J. H. An and M. Bellare, “Does encryption with redundancy provide authenticity?” in International Conference on the Theory and Applications of Cryptographic Techniques (EUROCRYPT 2001). Springer, 2001, pp. 512–528.
- [24] D. A. McGrew and J. Viega, “The security and performance of the Galois/Counter Mode (GCM) of operation,” in International Conference on Cryptology in India (INDOCRYPT 2004). Springer, 2004, pp. 343–355.
- [25] D. Culler, R. Karp, D. Patterson, A. Sahay, K. E. Schauser, E. Santos, R. Subramonian, and T. von Eicken, “Logp: Towards a realistic model of parallel computation,” in Proceedings of the Fourth ACM SIGPLAN Symposium on Principles and Practice of Parallel Programming, ser. PPOPP ’93. New York, NY, USA: ACM, 1993, pp. 1–12. [Online]. Available: http://doi.acm.org/10.1145/155332.155333
- [26] A. Alexandrov, M. F. Ionescu, K. E. Schauser, and C. Scheiman, “Loggp: Incorporating long messages into the logp model for parallel computation,” Journal of Parallel and Distributed Computing, vol. 44, no. 1, pp. 71 – 79, 1997. [Online]. Available: http://www.sciencedirect.com/science/article/pii/S0743731597913460
- [27] T. Kielmann, H. E. Bal, and K. Verstoep, “Fast measurement of logp parameters for message passing platforms,” in Parallel and Distributed Processing, J. Rolim, Ed. Berlin, Heidelberg: Springer Berlin Heidelberg, 2000, pp. 1176–1183.
- [28] J. Pjesivac-Grbovic, T. Angskun, G. Bosilca, G. E. Fagg, E. Gabriel, and J. J. Dongarra, “Performance analysis of mpi collective operations,” in 19th IEEE International Parallel and Distributed Processing Symposium, April 2005, pp. 8 pp.–.
- [29] M. J. Dworkin, “NIST SP 800-38D. Recommendation for block cipher modes of operation: Galois/Counter Mode (GCM) and GMAC,” 2007.
- [30] T. Krovetz and P. Rogaway, “The software performance of authenticated-encryption modes,” in International Workshop on Fast Software Encryption (FSE 2011). Springer, 2011, pp. 306–327.
- [31] “The Heartbleed Bug,” http://heartbleed.com/.
- [32] P. J. Fleming and J. J. Wallace, “How not to lie with statistics: the correct way to summarize benchmark results,” Communications of the ACM, vol. 29, no. 3, pp. 218–221, 1986.
- [33] T. Hoefler and R. Belli, “Scientific benchmarking of parallel computing systems: twelve ways to tell the masses when reporting performance results,” in Proceedings of the international conference for high performance computing, networking, storage and analysis (SC 2015). ACM, 2015, p. 73.
- [34] V. Tung Hoang, R. Reyhanitabar, P. Rogaway, and D. Vizar, “Online authenticated-encryption and its nonce-reuse misuse-resistance,” in Annual Cryptology Conference (CRYPTO 2015), vol. 9215, 08 2015.