Performance Analysis and Optimization for RIS-Assisted Multi-User Massive MIMO Systems with Imperfect Hardware
Abstract
The paper studies a reconfigurable intelligent surface (RIS)-assisted multi-user uplink massive multiple-input multiple-output (MIMO) system with imperfect hardware. At the RIS, the paper considers phase noise, while at the base station, the paper takes into consideration the radio frequency impairments and low-resolution analog-to-digital converters. The paper derives approximate expressions for the ergodic achievable rate in closed forms under Rician fading channels. For the cases of infinite numbers of antennas and infinite numbers of reflecting elements, asymptotic data rates are derived to provide new design insights. The derived power scaling laws indicate that while guaranteeing a required system performance, the transmit power of the users can be scaled down at most by the factor when goes infinite, or by the factor when and go infinite, where is the number of antennas and is the number of the reflecting units. Furthermore, an optimization algorithm is proposed based on the genetic algorithm to solve the phase shift optimization problem with the aim of maximizing the sum rate of the system. Additionally, the optimization problem with discrete phase shifts is considered. Finally, numerical results are provided to validate the correctness of the analytical results.
Index Terms:
Reconfigurable Intelligent Surface (RIS), massive MIMO, phase noise, radio frequency impairments, analog-to-digital converter, achievable rateI Introduction
As fifth generation (5G) commercial networks began to be deployed in 2020, there is an increasing demand for the future communication systems to support the ever-increasing number of devices while guaranteeing the high quality of the communication service [1]. Massive multiple-input multiple-output (MIMO) has been widely used to enhance the system performance, since it can efficiently reduce multi-user interference and scale down the transmit power of users [2, 3, 4]. Recently, reconfigurable intelligent surface (RIS), also known as intelligent reflecting surface (IRS) or large intelligent surface (LIS), has been proposed as a promising technique to extend the coverage and improve the spectrum efficiency (SE) and energy efficiency (EE) of communication networks [5, 6, 7, 8, 9, 10]. RIS is mainly composed of numerous reflecting elements, each of which imposes an independent phase shift on the incident signals. In particular, by carefully tuning the phase shifts, RIS can shape the wireless radio propagation environment to be customized to meet specific targets. Different from the relay, the reflecting elements at RIS require no active hardware components such as radio frequency (RF) chains and amplifiers, which significantly reduce the power consumption and hardware cost. Furthermore, RIS can work in the full-dulplex mode without the self-loop interference [11].
Due to its appealing advantages, RIS has attracted extensive research attention from both academia and industry. For instance, the authors in [12] studied an RIS-assisted single-user downlink system, derived the upper bound expression of the SE, and optimized the phase shifts at the RIS. In the case where the working base station (BS) was interfered by another BS, the authors in [13] obtained tractable expressions for the data rates under both instantaneous and statistical channel state information (CSI). In [14], the authors applied RIS to Internet of Things, analyzed the system performance and proposed a time-length allocation scheme for minimizing the energy consumption. The authors in [15] investigated a multi-RIS downlink system with imperfect location information of the users, and analyzed the impacts of the system parameters with derived approximate expressions for the ergodic AR. In [16], the authors studied a multi-pair system assisted by RIS, and utilized the genetic algorithm (GA) to solve the phase shift optimization problem for maximizing the sum ergodic achievable rate (AR). In [17], the authors in took into account the interplay of the responses between the phase shift and the amplitude in an RIS-assisted single-user system. The authors in [18] investigated a downlink RIS-assisted massive MIMO system with statistical CSI at the BS, and optimized the beamformings at the RIS and the BS. The authors in [19] derived closed-form sum rates for RIS-assisted uplink systems under spatially correlated Rician Fading, and jointly optimized the phase-shifting matrix and the transmit covariance matrix. In [20], the authors focused on an RIS-assisted multi-user uplink massive MIMO system, and proposed a GA-based algorithm for maximizing the sum ergodic AR according to the derived closed-form expressions.
It should be noted that the assumption of perfect hardware was considered in the aforementioned works. However, in practice, communication systems suffer from imperfect hardware, which leads to hardware impairments (HIs), such as oscillator phase noise, in-phase/quadrature-phase (I/Q) imbalance, non-linearities and quantization errors [21, 22]. Although compensation algorithms can alleviate the effects of HIs [23, 24, 25], the residual HIs still degrade and limit the system performance. Therefore, it is necessary to take HIs into consideration when analyzing practical systems. The authors in [26] considered HIs at the transmitters in an RIS-assisted single-user downlink system. They first obtained closed-form solutions for the optimal beamforming at the multi-antenna source, and then optimized the phase shifts at the RIS for maximizing the signal-to-noise ratio (SNR). In [27], the secrecy rate was studied in RIS-assisted systems with HIs at the transmitters of the BS. The authors proposed an iterative method to optimize the beamforming vectors at both the BS and the RIS. For a multi-RIS-assisted full-duplex system, the authors in [28] investigated the impacts of HIs at the transceivers of the BS and users, and jointly optimized the beamformings at the BS and the RISs and the transmit power of the users for maximizing the sum AR.
Moreover, in massive MIMO systems, the BS is equipped with a large number of antennas, which requires a large number of analog-to-digital converters/digital-to-analog converters (ADCs/DACs), leading to a high power consumption and hardware cost. To address this, researchers use low-resolution ADCs/DACs to reduce the power consumption and hardware cost while sacrificing a certain system performance [29, 30, 31]. The authors in [32] investigated an RIS-assisted single-user uplink system with low-resolution ADCs at the BS, and derived the AR expressions and analyzed the system performance. In [33], an RIS-assisted multi-user downlink system with low-resolution DACs was studied. The authors derived the approximate expressions for AR and optimized the phase shifts at the RIS.
On the other hand, the phase noise has recently gain much attention in RIS-assisted systems, which is generated from the non-ideal reconfiguration of the phase shifts at the RIS in practical systems [34]. Considering phase noise at the RIS, the authors in [35] studied an RIS-assisted system with two legitimate nodes and one eavesdropper, and analyzed the system performance based on the secrecy rate. The authors in [36] considered RIS-assisted single-user systems with phase noise and transceiver HIs, and analyzed the EE under Rayleigh fading channels. The authors in [37] extended the work to imperfect CSI cases, and studied the power scaling laws. In [38], the authors investigated the SE and EE of an RIS-assisted downlink system with phase noise and RF impairments, assuming determined line-of-sight (LoS) channels. The authors in [39] derived the closed-form expressions for the AR of an RIS-assisted downlink system with phase noise and transceiver HIs, and optimized the phase shifts for maximizing the SNR. The authors in [40] optimized the transmit power, the beamformings at the BS and the RIS of an RIS-assisted multi-user system with phase noise and transceiver HIs under correlated Rayleigh fading channels and instantaneous CSI. In [41], assuming correlated Rayleigh fading channels and statistical CSI, the authors studied the channel estimation, and optimized the phase shifts of RIS-assisted multi-user systems with phase noise and transceiver HIs.
In this paper, we focus on an RIS-assisted multi-user uplink massive MIMO system under Rician fading channels and with imperfect hardware. We jointly consider the phase noise at the RIS, and the RF impairments and low-resolution ADCs at the BS. Based on that, we derive the closed-form expressions for the ergodic AR, analyze the system performance and optimize the phase shifts. The main contributions of this paper are summarized as follows:
-
•
We investigate an RIS-assisted multi-user uplink massive MIMO system under Rician fading channels and with imperfect hardware. The channels between the users and the RIS and that between the RIS and the BS are modelled as Rician fading. Furthermore, we jointly consider the phase noise at the RIS, and the RF impairments and low-resolution ADCs at the BS, due to the imperfect hardware.
-
•
We derive approximate expressions for the ergodic AR in closed forms. Based on that, asymptotic data rates are obtained with infinite number of antennas and of reflecting elements , when the RIS is aligned to a specific user and when the RIS is aligned to none of the users. Besides, we study the power scaling laws of the users. We find that while guaranteeing a required system performance, the transmit power of the users can be scaled down at most by the factor when goes infinite, or by the factor when and go infinite.
-
•
We propose an optimization algorithm based on GA, which can be applied to solving the continuous and the discrete phase shift optimization problems for maximizing the sum rates of the system. Moreover, we verify in simulations that the proposed optimization algorithm can largely improve the sum rates of the considered system.
The remainder of this paper is organized as follows: Section II models the RIS-assisted multi-user uplink massive MIMO system under Rician fading channels and with imperfect hardware. Section III derives the approximate expressions for ergodic AR, and analyzes the system performance. Section IV proposes an algorithm based on GA to solve the continuous and discrete phase shift optimization problems for maximizing the sum rates of the system. Section V provides the simulation results. Section VI gives a brief conclusion.
Notations: In this paper, we use lower case letters, bold lower case letters and bold upper case letters to denote scalars, vectors and matrices, respectively. The matrix inverse, conjugate-transpose, transpose and conjugate operations are respectively denoted by the superscripts , , and . We use , and to denote trace, Euclidean 2-norm and the expectation operations, respectively. And denotes the th element of matrix . The matrix denotes an identity matrix. In addition, we denote a circularly symmetric complex Gaussian vector with zero mean and covariance by .
II System Model
We investigate a multi-user uplink communication system with imperfect hardware, where single-antenna users transmit signals to a BS equipped with large-scale arrays of antennas. As shown in Fig. 1, the direct links between the users and the BS are blocked by obstacles such as buildings and trees. Therefore, we employ an RIS with elements to assist the communications between the users and the BS.
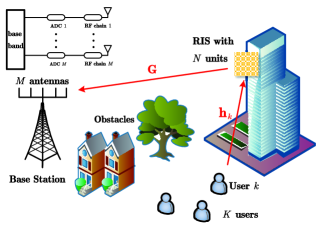
II-A Channel Model
The channels from the users to the RIS and from the RIS to the BS follow the Rician fading distribution, which can be expressed respectively as
| (1) |
| (2) |
where scalars and are respectively the large-scale fading coefficients between user and the RIS, and between the RIS and the BS. Scalars and stand for the Rician factors of the channels between user and the RIS, and between the RIS and the BS, respectively. Vector and matrix are the non-line-of-sight (nLoS) parts of the channels with independently and identically distributed (i.i.d) elements following the distribution of . Vector and matrix are the LoS parts of the channels, which are expressed respectively as
| (3) |
| (4) |
where and represent the azimuth angles of arrival (AoA) and elevation AoA at the RIS from user , respectively. and are the azimuth angles of departure (AoD) and elevation AoD from the RIS to the BS, respectively. and stand for the azimuth AoA and elevation AoA at the BS from the RIS, respectively. Furthermore, it is assumed that uniform square planar arrays are equipped at both the RIS and the BS with size of and , respectively. Thus, the ith element of vector is expressed as [20], [38]
| (5) |
where is the antenna/unit spacing, and is the carrier wavelength.
| (14) |
| (18) |
| (19) |
II-B Data Transmission with Imperfect Hardware
Since the RIS is employed to assist the communications between the users and the BS, the signals are first transmitted to the RIS, then reflected to the BS. Therefore, when the RIS and the BS have ideal configurations, the received signal at the BS can be expressed as
| (6) |
where with representing the signal transmitted from user and subject to . , and is the transmit power of user . stands for the phase shift matrix, and is the phase shift at the unit of the RIS. is the additive white Gaussian noise (AWGN) at the BS, whose elements follow i.i.d .
However, in real scenarios, the imperfect hardware at the RIS and the BS should be taken into consideration , which would limit the system performance. To address this, we consider the phase noise at the RIS, the RF impairments and low-resolution ADCs at the BS.
The phase noise is induced by the imperfection of the reflecting elements, or by the imperfect channel estimation [34]. In this paper, it is modelled as
| (7) |
where follows a zero-mean Von Mises distribution with the probability density function (PDF) of [41]
| (8) |
with being the concentration parameter.
Then, we adopt the extended error vector magnitude (EEVM) model to depict the impacts of the RF impairments, such as I/Q imbalance and carrier frequency offset [42, 31, 38]. Thus, the received signal at the RF chains is re-expressed as
| (9) |
where with representing the amplitude attenuation and phase shift for the th RF chain. The scalar satisfies , while follows a uniform distribution of with . Additionally, vector stands for the additive distortion noise at the RF chains, where has the distribution of . In the following analysis, we assume , and for for simplicity, which means all the RF chains have the same level of imperfections.
Moreover, the BS uses low-resolution ADCs to reduce the hardware cost and power consumption, the impacts of which can be modelled by the additive quantization noise model (AQNM) [29, 31]. Therefore, the quantized signals can be obtained as
| (10) |
where , and is the inverse of the signal-to-quantization-noise ratio. For the quantization bits , the values of are listed in Table I, while for , we have . Vector represents the additive Gaussian quantization noise, which is uncorrelated with . The matrix satisfies , which yields
| (11) |
where is the vector whose mth element is 1, while the rest elements are zero.
| 1 | 2 | 3 | 4 | 5 | |
|---|---|---|---|---|---|
| 0.3634 | 0.1175 | 0.03454 | 0.009497 | 0.002499 |
After the quantization, the BS adopts the maximal-ratio-combining (MRC) processing. Then, the processed signal is obtained as
| (12) |
where the beamforming matrix is given by . Herein, we focus on the signal transmitted from user , which is obtained as
| (13) |
Note that at the right hand side of (13), the first term is the desired signal from user ; the second term is the multi-user interference from the other users; the third and the fourth terms are generated from the distortion noise and the AWGN at RF chains, respectively; the last term is from the quantization noise.
III Achievable Rate Analysis
In this section, we investigate the uplink ergodic AR of this multi-user massive MIMO system and the impacts of the system settings, such as the number of the reflecting elements at the RIS and the number of the antennas at the BS.
According to (13), the uplink ergodic AR for user is expressed as (14) at the bottom of this page, where the power of the distortion noise, the AWGN, and the quantization noise are respectively expressed as
| (15) |
| (16) |
| (17) |
Based on (14), we present the following theorem.
Theorem 1
Proof:
See Appendix A. ∎
It can be readily observed from Theorem 1 that the uplink ergodic AR of user depends on , , the AoA at the BS, the AoA and AoD at the RIS, the power of users, the large-scale fading coefficients, the Rician factors, the phase shifts and noise at the RIS, the RF impairments, and the quantization bit and accuracy.
In particular, when the Rician factors satisfy , and , the Rician fading channels expressed in (1) and (2) degenerate to Rayleigh fading channels, where only the nLoS parts of the channels remain. The following remark discusses the uplink ergodic AR with Rayleigh fading channels under the considered system.
Remark 1
III-A Asymptotic Analysis
According to (54) in Appendix A, it is noted that and the equality holds when the RIS is aligned to user . Specifically, the phase shifts aligned to user at the RIS should satisfy
| (20) |
In this case, we assume that is bounded when . Therefore, when the RIS is aligned to user , the numerator in (18) is on the order of .
To obtain the order of the denominator in (18), we need to focus on the term in (79) and (82) first, which can be further expressed as
| (21) |
Step is because . On the other hand, for fixed , we have
| (22) |
which yields
| (23) |
According to (21), it is noted that is below the order of , which means is not the term which dominates the order of the denominator. Since the quantization noise is proportional to the power of the received signals, the denominator is on the order of . Thus, the fraction in (18) is on the order of . Then, we have the following corollary:
Corollary 1
It can be seen from Corollary 1 that the converged uplink ergodic AR for user is determined by , the quantization parameter , and the scalar which is related to the RF impairments.
Furthermore, we can find that the impact of the phase noise at the RIS vanishes in the converged AR for user . This is because when the RIS is aligned to user , the signal transmitted from user is on the order of , while the interference from the other users is on the order of . Then as goes to infinity, the signal transmitted from user becomes dominant. On the other hand, the phase noise at the RIS is multiplicative to the transmitted signal, and the quantization noise at the ADCs is proportional to the signal power. Therefore, the impact of phase noise at the RIS vanishes as the equal parts of coefficients in the numerator and denominator are eliminated.
When none of the users is aligned to the RIS, we assume that is bounded for . In this case, both of the numerator and the denominator in the fraction of (18) are on the order of . Then, we have the following conclusion.
Corollary 2
In Corollary 2, the converged uplink ergodic AR for user is determined by the power of the users, the large-scale fading coefficients, the Rician factors, and the level of phase noise.
| (30) |
| (31) |
III-B Power Scaling Laws
An important feature of massive MIMO is that it reduces the transmit power of the users proportionally to the number of antennas while maintaining the required system performance. As such, to gather valuable insights on energy savings, we investigate the power scaling laws of the users..
We scale down the power as , , with fixed , where is the power scaling factor deciding the power scaling level. Then, from (18) in Theorem 1, as the number of antennas , we have
| (26) |
where and are respectively defined as (27) and (28)
| (27) |
| (28) |
and , , and are respectively given by (39), (57), and (86) in Appendix A.
It is noted that the converged AR is determined by the power scaling factor . When , the converged AR goes to zero as . This is because the transmit power is aggressively scaled down with a large , which certainly degrades the system performance. When , the converged AR is a non-zero value as . It means the system performance can be maintained when the transmit power is scaled down. Furthermore, when , the transmit power can be scaled down by the factor at most while guaranteeing the required system performance. Therefore, we obtain the following corollary.
Corollary 3
Corollary 3 illustrates the power scaling law related to . Theoretically, the transmit power of the users can be further cut down according to the number of reflecting elements at the RIS in the considered RIS-assisted system. The following corollary shows the power scaling law related to and , when none of the users is aligned to the RIS.
Corollary 4
When none of the users is aligned to the RIS, as the number of antennas and reflecting elements , the transmit power of the users can be scaled down at most to , , with fixed , then the uplink ergodic AR for user in the RIS-assisted multi-user uplink massive MIMO system converges to (30) at the bottom of this page.
Corollary 4 investigates the power scaling law in the case where none of the users is aligned to the RIS. Moreover, the following Corollary 5 investigates the power scaling law in the case where the RIS is aligned to user .
Corollary 5
When the RIS is aligned to user , as the number of antennas and reflecting elements , the transmit power of user can be scaled down at most to , while the transmit power of other users is scaled down to , , with fixed , then the uplink ergodic AR for user in the RIS-assisted multi-user uplink massive MIMO system converges to (31) at the bottom of this page.
IV Phase Shift Optimization
Theorem 1 shows that the uplink ergodic AR depends on the phase shift of the RIS. Thus, to enhance the system performance, we can optimize the phase shifts at the RIS for maximizing the sum uplink ergodic AR.
From (18), the sum uplink ergodic AR of the RIS-assisted multi-user uplink massive MIMO system can be expressed as
| (32) |
Since the phase shift at each unit of the RIS lies in the range of , the phase shift optimization problem can be expressed as
| (33) |
where is the sum uplink ergodic AR defined in (32), is the phase shift matrix, and is the phase shift at unit of the RIS. According to (18) and (32), the expression for the objective function of Problem (IV) is complicated, which makes the problem challenging to be solved. Herein, we apply GA to solve our phase shift optimization problem.
Simulating the evolution of nature population, GA mainly includes five parts: population initialization, fitness evaluation & sort, selection, crossover and mutation. By tailoring it to our phase shift optimization problem, we further discuss the five parts of GA.
1) Population initialization: In the beginning, individuals are generated in the initial population. For the phase shifts at the reflecting elements of the RIS, each individual has one chromosome containing genes. Furthermore, the value of each gene is initially generated in .
2) Fitness evaluation & sort: The fitness value of the individual is evaluated by the fitness function, which is given by
| (34) |
where is the sum uplink ergodic AR corresponding to individual . Since we use the objective function in Problem (IV) as the fitness function, the individual corresponding to a higher sum uplink ergodic AR has a higher fitness value. Then, individuals are sorted by the fitness values given in (34) as LIST 1.
3) Selection: The selection operation is to choose individuals from the current population as parents. Before the selection operation, we choose the top individuals in LIST 1 as elite individuals, which are directly copied to the next generation. The operation for the elite individuals is to make sure that the optimal individuals in the current population are passed to the next. Then, we scale the fitness values of the individuals in LIST 1 as follows:
| (35) |
where is the fitness value of the th individual in LIST 1. Based on (35), the selection algorithm is given in Algorithm 1, which is used to select one parent once at a time.
4) Crossover: The crossover operation needs two parents. Simply, we execute the selection operation two times to generate two parents for one crossover operation. The crossover algorithm is given in Algorithm 2, where stands for the crossover probability, and and are generated from the selection operation.
5) Mutation: The mutation operation is after the crossover operation. Each gene of the child generated from the crossover operation can mutate under the mutation probability . The mutation operation is shown in Algorithm 3. Finally, the child after the mutation operation is added to the next generation.
Based on Algorithms 1-3, we propose a GA for the phase shift optimization problem (IV) to obtain the optimal phase shifts along with the maximum sum rate . The GA is given in Algorithm 4. Additionally, the complexity of the proposed GA-based algorithm is , where is the population size, and is the number of generations evaluated which is determined by the convergence behavior of the GA [43].
It is noted that the phase shifts vary in a continuous range of in Problem (IV). However, in practical scenarios, the phase shifts are usually discrete values in the range of . In that case, the phase shift optimization problem can be formulated as
| (36) |
where the range of the phase shifts is divided into bits. It is readily to be seen that with a larger , the phase shifts can be adjusted more accurately. When the values of the genes are generated from the discrete range, Algorithm 4 can be applied to solve Problem (IV) with discrete phase shifts as to solve Problem (IV).
V Numerical Results
In this section, numerical results are provided. Similar to the settings in [44] and [20], we consider a scenario placed in an XYZ Cartesian coordinate system, where the BS is at coordinate , and the RIS is at . Users are assumed to be randomly distributed within the circle in Plane with the center at . The values for the AoA and AoD of the BS and the RIS are generated from a uniform distribution in . Furthermore, we set the spacing distance at the BS and the RIS as , the number of users as , the Rician factors as and , , the transmit power of users as dBm, , the parameter of the phase noise as , the amplitude and phase parameters of RF impairments as and , the noise power as dBm, and the ADC quantization bits as . The large-scale fading coefficient is modeled as
| (37) |
where is the distance between the source and the destination. is the path-loss exponent, which is assumed to be in this section. Additionally, the simulation results in this section are obtained by averaging over 2000 Monte Carlo realizations.
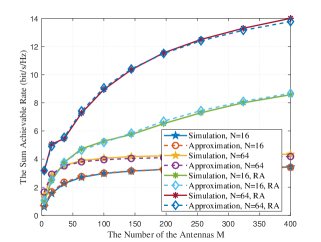
In Fig. 2, we study how the sum rates vary with the number of the antennas at the BS, setting the number of the reflecting elements at the RIS as and . The curves marked with “Simulation” are obtained based on (14), while the curves marked with “Approximation” are obtained according to (18) in Theorem 1. Two cases are considered: 1) Case 1: the phase shifts at the RIS are fixed, each of which is randomly generated from a uniform distribution in ; 2) Case 2: the phase shifts at the RIS are obtained by applying the GA in Algorithm 4 to Problem (IV). The parameters of the GA are set as: the population is , the number of elites is , the crossover probability is , the mutation probability is , and the number of the termination iteration times is . It can be seen that the approximation curves match well with the simulation curves, which supports the results in Theorem 1. Moreover, it is noted that the sum rates with the optimized phase shifts obtained by Algorithm 4 are better than that with the fixed phase shifts. Furthermore, the sum rates increase with in Case 2 with the optimized phase shifts, while for Case 1 with the fixed phase shifts, the sum rates first increase and then tend to be saturated with . Additionally, the sum rates with are higher than that with in both Case 1 and 2. Therefore, we can improve the performance of the RIS-assisted multi-user massive MIMO system by increasing and , while using the optimized phase shifts obtained by the proposed GA in Algorithm 4.
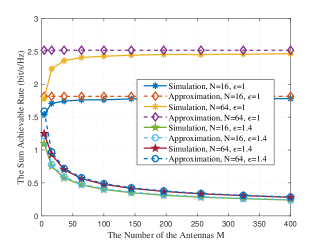
In Fig. 3, we investigate the power scaling laws of the users. Two groups of the fixed phase shifts are considered, which are obtained by using the GA in Algorithm 4 with and respectively, when . We set the power as , , with fixed dB. The curves marked with “Approximation” in Fig. 3 are obtained according to (26). It can be seen that when the power scaling factor , as , the sum rates converge to zero in both cases with and . This is because the transmit power is scaled down too fast with . Furthermore, when , as , the sum rates converge to non-zero limits in both cases with and . It means the system maintains a required performance when the transmit power is scaled down by the factor , which validates our analysis in Section III.
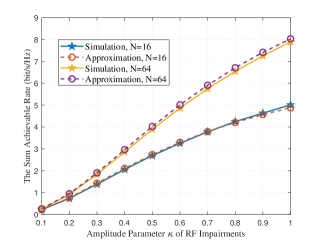
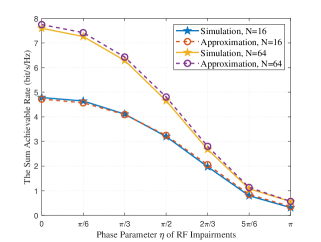
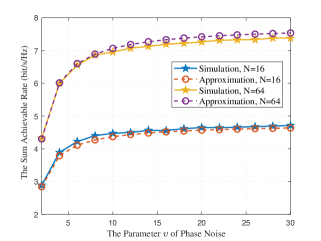
Fig. 4 shows the impacts of the phase noise at the RIS on the sum rates. It can be seen that the sum rates increase as the concentration parameter increases. For both and cases, the increase of the sum rates is rapid when is small, and then slows down when is large. Since the phase noise at the unit of the RIS follows a Von Mises distribution, a higher concentration parameter means the fluctuation for lies in a smaller range. Specifically, when , we have , which means there is no phase noise at the RIS. Therefore, the sum rates converge to the case without phase noise as the concentration parameter grows to infinity, which is consistent with the results in Fig. 4, where the sum rates first increase and then become saturated as increases.
Fig. 5 and 6 focus on the impacts of RF impairments on the sum rates while setting . In Fig. 5, we can find that the sun rates increase with the amplitude parameter in both and cases. It should be mentioned that means RF impairments have no impacts on the amplitude of the receiving signals. Thus, a smaller stands for severer RF impairments, causing larger reduction of the system performance, as is shown in Fig. 5. In Fig. 6, it is observed that the sun rates decrease with the phase parameter in both and cases. This is because when is large, the phase shifts brought by RF impairments would lie in a large range, which leads to poor system performance.
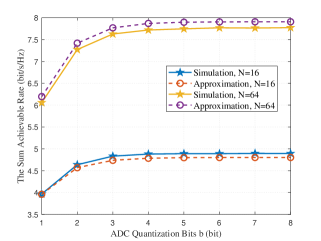
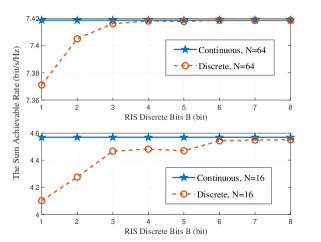
Fig. 7 depicts how the sum rates vary with the ADC quantization bits . It is readily seen that in both and cases, the sum rates first increase fast with , and then become saturated. It is well known that the power consumption and hardware cost of wireless systems increase rapidly as ADC quantization bits increases.. Thus, Fig. 7 indicates that we can choose for the considered system to obtain a balance between system performance, power consumption and hardware cost.
Finally, we make a comparison between the cases with continuous phase shifts and with discrete phase shifts in Fig. 8. The phase shifts for the curves marked with ”Discrete” is obtained by applying Algorithm 4 to Problem (IV) with discrete phase shifts. The RIS discrete bits is defined in (IV). In practical scenarios, discrete phase shifts are used, while the continuous phase shifts are considered for ideal scenarios. Therefore, it is essential to study the system performance with discrete phase shifts. From Fig. 8, the sum rates with the optimized discrete phase shifts increase as increases, and converge to that with the optimized continuous phase shifts. It is noted that and are reasonable choices for the discrete case with and , respectively, since they achieve the performance for the corresponding continuous cases, while a higher leads to more cost.
VI Conclusion
The paper studied an RIS-assisted multi-user uplink massive MIMO system under Rician fading channels and with imperfect hardware at both the RIS and BS. At the RIS, the paper used Von Mises distribution to model the phase noise, while at the BS, the paper adopted EEVM model for RF impairments and AQNM for low-resolution ADCs. Based on that, asymptotic data rates were obtained with infinite and , when the RIS was aligned to a specific user and when the RIS was aligned to none of the users. Besides, the paper investigated the power scaling laws of the users, and showed that while guaranteeing a required system performance, the transmit power of the users can be scaled down at most by the factor when goes infinite, or by the factor when and go infinite. Furthermore, an optimization algorithm was proposed based on GA, which can be applied to solve the continuous and discrete phase shift optimization problems for maximizing the sum rates of the system. Numerical results were provided to support the main results. The numerical results revealed that the sum rate of the considered system can be improved by increasing and . Moreover, the impacts of the parameters of the imperfect hardware on the system performance were revealed. The numerical results also revealed that when , and are reasonable choices for the discrete cases with and , respectively.
| (45) |
| (46) |
| (51) |
| (52) |
| (53) |
It should be aware that the considered system model can be further extended to investigate a more practical scenario. For example, this work considered perfect CSI, while perfect CSI is usually hard to obtain in practical. Furthermore, due to the large number of antennas at BS and reflecting units at RIS, channels are usually correlated with each other in a practical RIS-assisted massive MIMO system. Therefore, the future work would take channel estimation and channel correlation into consideration to provide more insights for RIS-assisted massive MIMO systems.
Appendix A Proof of Theorem 1
First, we review some key preliminary results given in the following lemmas.
Lemma 1: [45, Lemma 1] If and are both sums of nonnegative random variables and , then we get the following approximation
| (38) |
Note that it is not necessary for the random variables and to be independent. In addition, the approximation becomes more accurate as and increase.
Lemma 2: If is a random variable following zero-mean Von Mises distribution with a concentration parameter , the characteristic function of , , equals to when . In other words, we have
| (39) |
where represents the modified Bessel function of the first kind and order .
Proof:
The Bessel Function of the first kind and order is given by
| (40) |
and the corresponding Modified Bessel Function is given by
| (41) |
When , we can obtain
| (42) |
On the other hand, the PDF of is given by
| (43) |
Then the characteristic function with can be calculated as
| (44) |
∎
From (14), by using Lemma 1, we can obtain (45) at the top of this page. Then, we start to derive the expectations in (45) one by one.
Based on (1) and (2), the term can be written as (VI) at the top of this page, where the matrix is defined as
| (47) |
Therefore, can be expressed as
| (48) |
where step is obtained by removing the zero-expectation terms. Then, we focus on deriving the expectation . Note that
| (49) |
where the term in (A) is expressed as
| (50) |
and , and in (A) are respectively expressed as (51)-(53) at the bottom of the page, where the terms and are defined as
| (54) |
| (62) |
| (63) |
| (64) |
| (65) |
| (66) |
Thus, the expectation can be calculated as
| (55) |
Step is obtained by removing zero-valued terms. The expectation in (55) is further calculated as
| (56) |
where scalar is defined as
| (57) |
The is given by (39) in Lemma 2. Additionally, it is well known that , since is real. The other expectations in (55) can be obtained in a similar way, which are respectively expressed as follows:
| (58) |
| (59) |
| (60) |
| (61) |
Then, we arrived at (62) at the bottom of this page. Similar to the calculation for , the rest expectations in (48) can be obtained as (63)-(66) at the bottom of this page. Substituting (62)-(66) into (48), we can obtain
| (67) |
where the coefficients , , and are respectively given by
| (68) |
| (69) |
| (70) |
| (71) |
| (74) |
| (75) |
| (76) |
| (77) |
Similar to (VI), we expand as
| (72) |
Thus, the expectation can be expressed as
| (73) |
Step in (73) is obtained by removing the zero terms. Again, similar to the calculation for , the expectations in (73) are obtained as (74)-(77) at the bottom of this page. Therefore, the expectation can be obtained as
| (78) |
where the coefficients - are respectively given by
| (79) |
| (80) |
| (81) |
| (82) |
| (91) |
| (94) |
Then, we focus on the expectations , and . According to (15)-(17), they can be expanded respectively as
| (83) |
| (84) |
| (85) |
To obtain the expectations in (83) and (84), we calculate the value of , which is shown as follows:
| (86) |
where steps and are obtained by substituting (2) and (1) into the derivation respectively and then removing the zero terms. Step is based on the calculation
| (87) |
Thus, we have
| (88) |
| (89) |
Furthermore, to obtain the expectation in (85), we need additionally derive the expectation in in (11), which can be further expressed as
| (90) |
where is the vector whose mth element is 1, while the rest elements are zero. The last expectation in (90) can be calculated as (A) at the top of this page, where step is based on the following calculations:
| (92) |
| (93) |
By using (90) and (A), we arrive at (94) at the top of this page. Therefore, from (11), (86) and (94), we can obtain
| (95) |
References
- [1] Y. Zhou, L. Tian, L. Liu, and Y. Qi, “Fog computing enabled future mobile communication networks: A convergence of communication and computing,” IEEE Commun. Mag., vol. 57, no. 5, pp. 20–27, May 2019.
- [2] H. Q. Ngo, H. A. Suraweera, M. Matthaiou, and E. G. Larsson, “Multipair full-duplex relaying with massive arrays and linear processing,” IEEE J. Sel. Areas Commun., vol. 32, no. 9, pp. 1721–1737, Sep. 2014.
- [3] B. Sun, Y. Zhou, J. Yuan, and J. Shi, “Interference cancellation based channel estimation for massive MIMO systems with time shifted pilots,” IEEE Trans. Wireless Commun., vol. 19, no. 10, pp. 6826–6843, Oct. 2020.
- [4] Z. Peng, X. Chen, W. Xu, C. Pan, L.-C. Wang, and L. Hanzo, “Analysis and optimization of massive access to the IoT relying on multi-pair two-way massive MIMO relay systems,” IEEE Trans. Commun., vol. 69, no. 7, pp. 4585–4598, Jul. 2021.
- [5] S. Hu, F. Rusek, and O. Edfors, “Beyond massive MIMO: The potential of data transmission with large intelligent surfaces,” IEEE Trans. Signal Process., vol. 66, no. 10, pp. 2746–2758, May 2018.
- [6] M. Di Renzo, A. Zappone, M. Debbah, M.-S. Alouini, C. Yuen, J. de Rosny, and S. Tretyakov, “Smart radio environments empowered by reconfigurable intelligent surfaces: How it works, state of research, and the road ahead,” IEEE J. Sel. Areas Commun., vol. 38, no. 11, pp. 2450–2525, Nov. 2020.
- [7] z. Özdogan, E. Björnson, and E. G. Larsson, “Intelligent reflecting surfaces: Physics, propagation, and pathloss modeling,” IEEE Wireless Commun. Lett., vol. 9, no. 5, pp. 581–585, May 2020.
- [8] W. Yan, X. Yuan, and X. Kuai, “Passive beamforming and information transfer via large intelligent surface,” IEEE Wireless Commun. Lett., vol. 9, no. 4, pp. 533–537, Apr. 2020.
- [9] C. Pan, H. Ren, K. Wang, J. F. Kolb, M. Elkashlan, M. Chen, M. Di Renzo, Y. Hao, J. Wang, A. L. Swindlehurst, X. You, and L. Hanzo, “Reconfigurable intelligent surfaces for 6G systems: Principles, applications, and research directions,” IEEE Commun. Mag., vol. 59, no. 6, pp. 14–20, Jun. 2021.
- [10] X. Wei, D. Shen, and L. Dai, “Channel estimation for RIS assisted wireless communications—part i: Fundamentals, solutions, and future opportunities,” IEEE Commun. Lett., vol. 25, no. 5, pp. 1398–1402, May 2021.
- [11] Z. Peng, Z. Zhang, C. Pan, L. Li, and A. L. Swindlehurst, “Multiuser full-duplex two-way communications via intelligent reflecting surface,” IEEE Trans. Signal Process., vol. 69, pp. 837–851, Feb. 2021.
- [12] Y. Han, W. Tang, S. Jin, C.-K. Wen, and X. Ma, “Large intelligent surface-assisted wireless communication exploiting statistical CSI,” IEEE Trans. Veh. Technol., vol. 68, no. 8, pp. 8238–8242, Aug. 2019.
- [13] Y. Jia, C. Ye, and Y. Cui, “Analysis and optimization of an intelligent reflecting surface-assisted system with interference,” IEEE Trans. Wireless Commun., vol. 19, no. 12, pp. 8068–8082, Dec. 2020.
- [14] G. Yu, X. Chen, C. Zhong, D. W. Kwan Ng, and Z. Zhang, “Design, analysis, and optimization of a large intelligent reflecting surface-aided b5g cellular internet of things,” IEEE Internet Things J., vol. 7, no. 9, pp. 8902–8916, Sep. 2020.
- [15] X. Hu, C. Zhong, Y. Zhang, X. Chen, and Z. Zhang, “Location information aided multiple intelligent reflecting surface systems,” IEEE Trans. Commun., vol. 68, no. 12, pp. 7948–7962, Dec. 2020.
- [16] Z. Peng, T. Li, C. Pan, H. Ren, W. Xu, and M. D. Renzo, “Analysis and optimization for RIS-aided multi-pair communications relying on statistical CSI,” IEEE Trans. Veh. Technol., vol. 70, no. 4, pp. 3897–3901, Apr. 2021.
- [17] Y. Zhang, J. Zhang, M. D. Renzo, H. Xiao, and B. Ai, “Performance analysis of RIS-aided systems with practical phase shift and amplitude response,” IEEE Trans. Veh. Technol., vol. 70, no. 5, pp. 4501–4511, May 2021.
- [18] J. Zhang, J. Liu, S. Ma, C.-K. Wen, and S. Jin, “Large system achievable rate analysis of ris-assisted MIMO wireless communication with statistical CSIT,” IEEE Trans. Wireless Commun., vol. 20, no. 9, pp. 5572–5585, Sep. 2021.
- [19] K. Xu, J. Zhang, X. Yang, S. Ma, and G. Yang, “On the sum-rate of RIS-assisted MIMO multiple-access channels over spatially correlated rician fading,” IEEE Trans. Commun., vol. 69, no. 12, pp. 8228–8241, Dec. 2021.
- [20] K. Zhi, C. Pan, H. Ren, and K. Wang, “Power scaling law analysis and phase shift optimization of RIS-aided massive MIMO systems with statistical CSI,” IEEE Trans. Commun., vol. 70, no. 5, pp. 3558–3574, May 2022.
- [21] X. Zhang, M. Matthaiou, M. Coldrey, and E. Björnson, “Impact of residual transmit RF impairments on training-based MIMO systems,” IEEE Trans. Commun., vol. 63, no. 8, pp. 2899–2911, Aug. 2015.
- [22] X. Xia, D. Zhang, K. Xu, W. Ma, and Y. Xu, “Hardware impairments aware transceiver for full-duplex massive MIMO relaying,” IEEE Trans. Signal Process., vol. 63, no. 24, pp. 6565–6580, Dec. 2015.
- [23] T. Schenk, RF imperfections in high-rate wireless systems : impact and digital compensation. Germany: Springer, 2008.
- [24] C. Studer, M. Wenk, and A. Burg, “MIMO transmission with residual transmit-RF impairments,” in Proc. Int. ITG Workshop Smart Antennas, Feb. 2010, pp. 189–196.
- [25] E. Björnson, M. Matthaiou, and M. Debbah, “Massive MIMO with non-ideal arbitrary arrays: Hardware scaling laws and circuit-aware design,” IEEE Trans. Wireless Commun., vol. 14, no. 8, pp. 4353–4368, Aug. 2015.
- [26] H. Shen, W. Xu, S. Gong, C. Zhao, and D. W. K. Ng, “Beamforming optimization for IRS-aided communications with transceiver hardware impairments,” IEEE Trans. Commun., vol. 69, no. 2, pp. 1214–1227, Feb. 2021.
- [27] G. Zhou, C. Pan, H. Ren, K. Wang, and Z. Peng, “Secure wireless communication in RIS-aided MISO system with hardware impairments,” IEEE Wireless Commun. Lett., vol. 10, no. 6, pp. 1309–1313, Jun. 2021.
- [28] M. A. Saeidi, M. J. Emadi, H. Masoumi, M. R. Mili, D. W. K. Ng, and I. Krikidis, “Weighted sum-rate maximization for multi-IRS-assisted full-duplex systems with hardware impairments,” IEEE Trans. Cogn. Commun. Netw., vol. 7, no. 2, pp. 466–481, Jun. 2021.
- [29] P. Dong, H. Zhang, W. Xu, and X. You, “Efficient low-resolution ADC relaying for multiuser massive MIMO system,” IEEE Trans. Veh. Technol., vol. 66, no. 12, pp. 11 039–11 056, Dec. 2017.
- [30] P. Dong, H. Zhang, Q. Wu, and G. Y. Li, “Spatially correlated massive MIMO relay systems with low-resolution ADCs,” IEEE Trans. Veh. Technol., vol. 69, no. 6, pp. 6541–6553, Jun. 2020.
- [31] L. Xu, X. Lu, S. Jin, F. Gao, and Y. Zhu, “On the uplink achievable rate of massive MIMO system with low-resolution ADC and RF impairments,” IEEE Commun. Lett., vol. 23, no. 3, pp. 502–505, Mar. 2019.
- [32] K. Zhi, C. Pan, H. Ren, and K. Wang, “Uplink achievable rate of intelligent reflecting surface-aided millimeter-wave communications with low-resolution ADC and phase noise,” IEEE Wireless Commun. Lett., vol. 10, no. 3, pp. 654–658, Mar. 2021.
- [33] J. Dai, Y. Wang, C. Pan, K. Zhi, H. Ren, and K. Wang, “Reconfigurable intelligent surface aided massive MIMO systems with low-resolution DACs,” IEEE Commun. Lett., vol. 25, no. 9, pp. 3124–3128, Sep. 2021.
- [34] M.-A. Badiu and J. P. Coon, “Communication through a large reflecting surface with phase errors,” IEEE Wireless Commun. Lett., vol. 9, no. 2, pp. 184–188, Feb. 2020.
- [35] J. D. Vega Sánchez, P. Ramírez-Espinosa, and F. J. López-Martínez, “Physical layer security of large reflecting surface aided communications with phase errors,” IEEE Wireless Commun. Lett., vol. 10, no. 2, pp. 325–329, Feb. 2021.
- [36] Y. Liu, E. Liu, and R. Wang, “Energy efficiency analysis of intelligent reflecting surface system with hardware impairments,” in Proc. IEEE GLOBECOM, Dec. 2020, pp. 1–6.
- [37] Y. Liu, E. Liu, R. Wang, and Y. Geng, “Channel estimation and power scaling of reconfigurable intelligent surface with non-ideal hardware,” in Proc. IEEE WCNC, Mar. 2021, pp. 1–6.
- [38] S. Zhou, W. Xu, K. Wang, M. Di Renzo, and M.-S. Alouini, “Spectral and energy efficiency of IRS-assisted MISO communication with hardware impairments,” IEEE Wireless Commun. Lett., vol. 9, no. 9, pp. 1366–1369, Sep. 2020.
- [39] Z. Xing, R. Wang, J. Wu, and E. Liu, “Achievable rate analysis and phase shift optimization on intelligent reflecting surface with hardware impairments,” IEEE Trans. Wireless Commun., vol. 20, no. 9, pp. 5514–5530, Sep. 2021.
- [40] A. Papazafeiropoulos, C. Pan, A. Elbir, V. Nguyen, P. Kourtessis, and S. Chatzinotas, “Asymptotic analysis of max-min weighted SINR for IRS-assisted MISO systems with hardware impairments,” IEEE Wireless Commun. Lett., 2021, to be published, doi: 10.1109/LWC.2021.3095678.
- [41] A. Papazafeiropoulos, C. Pan, P. Kourtessis, S. Chatzinotas, and J. M. Senior, “Intelligent reflecting surface-assisted MU-MISO systems with imperfect hardware: Channel estimation and beamforming design,” IEEE Trans. Wireless Commun., vol. 21, no. 3, pp. 2077–2092, Mar. 2022.
- [42] T. C. W. Schenk and E. R. Fledderus, “RF impairments in high-rate wireless systems - understanding the impact of TX/RX-asymmetry,” in Proc. 3rd Int. Symp. ISCCSP, Mar. 2008, pp. 117–122.
- [43] Z. Ye, C. Pan, H. Zhu, and J. Wang, “Tradeoff caching strategy of the outage probability and fronthaul usage in a cloud-RAN,” IEEE Trans. Veh. Technol., vol. 67, no. 7, pp. 6383–6397, Jul. 2018.
- [44] C. Pan, H. Ren, K. Wang, W. Xu, M. Elkashlan, A. Nallanathan, and L. Hanzo, “Multicell MIMO communications relying on intelligent reflecting surfaces,” IEEE Trans. Wireless Commun., vol. 19, no. 8, pp. 5218–5233, May 2020.
- [45] Q. Zhang, S. Jin, K. Wong, H. Zhu, and M. Matthaiou, “Power scaling of uplink massive MIMO systems with arbitrary-rank channel means,” IEEE J. Sel. Top. Sign. Proces., vol. 8, no. 5, pp. 966–981, Oct. 2014.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/a00a316e-578c-4ce5-9208-f85812db0b09/x9.png) |
Zhangjie Peng received the B.S. degree from Southwest Jiaotong University, Chengdu, China, in 2004, and the M.S. and Ph.D. degrees from Southeast University, Southeast University, Nanjing, China, in 2007, and 2016, respectively, all in Communication and Information Engineering. He is currently an Associate Professor at the College of Information, Mechanical and Electrical Engineering, Shanghai Normal University, Shanghai 200234, China. His research interests include reconfigurable intelligent surface (RIS), cooperative communications, information theory, physical layer security, and machine learning for wireless communications. |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/a00a316e-578c-4ce5-9208-f85812db0b09/x10.png) |
Xianzhe Chen received the B.E. degree in information engineering from Zhejiang University, Zhejiang, China, in 2019, and the M.E. degree in information and communication engineering from Shanghai Normal University, Shanghai, China, in 2022. He is currently pursuing the Ph.D. degree with the Department of Electrical and Computer Engineering, The University of British Columbia, Vancouver, Canada. His major research interests include reconfigurable intelligent surfaces, massive multiple-input multiple-output systems and relaying communications. |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/a00a316e-578c-4ce5-9208-f85812db0b09/x11.png) |
Cunhua Pan received the B.S. and Ph.D. degrees from the School of Information Science and Engineering, Southeast University, Nanjing, China, in 2010 and 2015, respectively. From 2015 to 2016, he was a Research Associate at the University of Kent, U.K. He held a post-doctoral position at Queen Mary University of London, U.K., from 2016 and 2019.From 2019 to 2021, he was a Lecturer in the same university. From 2021, he is a full professor in Southeast University. His research interests mainly include reconfigurable intelligent surfaces (RIS), intelligent reflection surface (IRS), ultra-reliable low latency communication (URLLC) , machine learning, UAV, Internet of Things, and mobile edge computing. He has published over 120 IEEE journal papers. He is currently an Editor of IEEE Wireless Communication Letters, IEEE Communications Letters and IEEE ACCESS. He serves as the guest editor for IEEE Journal on Selected Areas in Communications on the special issue on xURLLC in 6G: Next Generation Ultra-Reliable and Low-Latency Communications. He also serves as a leading guest editor of IEEE Journal of Selected Topics in Signal Processing (JSTSP) Special Issue on Advanced Signal Processing for Reconfigurable Intelligent Surface-aided 6G Networks, leading guest editor of IEEE Vehicular Technology Magazine on the special issue on Backscatter and Reconfigurable Intelligent Surface Empowered Wireless Communications in 6G, leading guest editor of IEEE Open Journal of Vehicular Technology on the special issue of Reconfigurable Intelligent Surface Empowered Wireless Communications in 6G and Beyond, and leading guest editor of IEEE ACCESS Special Issue on Reconfigurable Intelligent Surface Aided Communications for 6G and Beyond. He is Workshop organizer in IEEE ICCC 2021 on the topic of Reconfigurable Intelligent Surfaces for Next Generation Wireless Communications (RIS for 6G Networks), and workshop organizer in IEEE Globecom 2021 on the topic of Reconfigurable Intelligent Surfaces for future wireless communications. He is currently the Workshops and Symposia officer for Reconfigurable Intelligent Surfaces Emerging Technology Initiative. He is workshop chair for IEEE WCNC 2024, and TPC co-chair for IEEE ICCT 2022. He serves as a TPC member for numerous conferences, such as ICC and GLOBECOM, and the Student Travel Grant Chair for ICC 2019. He received the IEEE ComSoc Leonard G. Abraham Prize in 2022. |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/a00a316e-578c-4ce5-9208-f85812db0b09/x12.png) |
Maged Elkashlan received the PhD degree in Electrical Engineering from the University of British Columbia in 2006. From 2007 to 2011, he was with the Commonwealth Scientific and Industrial Research Organization (CSIRO) Australia. During this time, he held visiting faculty appointments at University of New South Wales, University of Sydney, and University of Technology Sydney. In 2011, he joined the School of Electronic Engineering and Computer Science at Queen Mary University of London. He also holds a visiting faculty appointment at Beijing University of Posts and Telecommunications. His research interests fall into the broad areas of communication theory and signal processing. Dr. Elkashlan is an Editor of the IEEE TRANSACTIONS ON VEHICULAR TECHNOLOGY and the IEEE TRANSACTIONS ON MOLECULAR, BIOLOGICAL AND MULTI-SCALE COMMUNICATIONS. He was an Editor of the IEEE TRANSACTIONS ON WIRELESS COMMUNICATIONS from 2013 to 2018 and the IEEE COMMUNICATIONS LETTERS from 2012 to 2016. He received numerous awards, including the 2022 IEEE Communications Society Leonard G. Abraham Prize, and best paper awards at the 2014 and 2016 IEEE ICC, 2014 CHINACOM, and 2013 IEEE VTC-Spring. |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/a00a316e-578c-4ce5-9208-f85812db0b09/x13.png) |
Jiangzhou Wang (Fellow, IEEE) is a Professor at the University of Kent, U.K. His research interest is in mobile communications. He has published over 400 papers and 4 books. He was a recipient of the 2022 IEEE Communications Society Leonard G. Abraham Prize and the 2012 IEEE Globecom Best Paper Award. Professor Wang is a Fellow of the Royal Academy of Engineering, U.K., Fellow of the IEEE, and Fellow of the IET. He was the Technical Program Chair of the 2019 IEEE International Conference on Communications (ICC2019), Shanghai, the Executive Chair of the IEEE ICC2015, London, and the Technical Program Chair of the IEEE WCNC2013. He was an IEEE Distinguished Lecturer from 2013 to 2014. He has served as an Editor for a number of international journals, including IEEE Transactions on Communications from 1998 to 2013. |