Pauli nonlocality and the nucleon effective mass
Abstract
A study of the nucleon mean-field potential in nuclear matter (NM) is done within an extended Hartree-Fock (HF) formalism, using the CDM3Y6 density dependent version of the M3Y interaction which is associated with the nuclear incompressibility MeV. The momentum dependence of nucleon optical potential (OP) in NM at the saturation density is shown to be due mainly to its exchange term up to fm-1, so that the Pauli nonlocality is expected to be the main origin of the nucleon effective mass at low momenta. Because nucleons in neutron-rich NM at are either weakly bound or unbound by the in-medium nucleon-nucleon interaction, the determination of the effective mass of nucleon scattered on targets with neutron excess at low energies should be of interest for the mean-field studies of neutron star matter. For this purpose, the folding model is used to calculate the nonlocal nucleon OP for the optical model analysis of elastic nucleon scattering on 40,48Ca, 90Zr, and 208Pb targets at energies MeV, to probe the model reliability and validate the WKB local approximation to obtain the local folded nucleon OP. The nucleon effective mass is then carefully deduced from the momentum dependence of the local folded nucleon OP which is resulted from the Pauli nonlocality of the exchange term. The obtained values agree well with the nucleon effective mass given by the extended HF calculation of the single-particle potential in asymmetric NM. The neutron-proton effective mass splitting determined at from the central strength of the real folded nucleon OP for 48Ca, 90Zr, and 208Pb targets has been found to depend linearly on the neutron-proton asymmetry parameter as , in a good agreement with the recent empirical constraints.
I Introduction
Over a wide range of the single-particle energies, the nucleon motion in medium is overwhelmingly governed by the nuclear mean field, known as the shell-model potential for bound states and optical potential (OP) for scattering states. The single-particle potential is also a key quantity in the mean-field studies of the equation of state (EOS) of nuclear matter (NM) as well as the structure of finite nuclei [1, 2]. The nucleon OP was widely studied in the Brueckner-Hartree-Fock (BHF) calculations of NM using free nucleon-nucleon (NN) interaction [2, 3, 4, 5], and in the mean-field calculations of NM on the Hartree-Fock (HF) level using different choices of the effective NN interaction [6, 7, 8, 9, 10, 11]. The mean-field description of nucleon OP in the NM limit provide an important physics input for the microscopic models of nucleon OP of finite nuclei, in particular, different versions of the folding model [11, 12, 13, 14, 15].
The microscopic studies of NM have repeatedly shown the impact by the Pauli blocking and increasing strength of higher-order NN correlations at high densities [2]. These in-medium effects are considered as the physics origin of the density dependence introduced into various effective NN interactions used in the nuclear structure and reaction studies. In the present work, we employ the CDM3Y6 density dependent version [16] of the M3Y interaction [20] which was used successfully in the HF studies of NM [6, 7, 21, 22, 23], and in the folding model calculation of the nucleon and nucleus-nucleus OP at low and medium energies [16, 13, 14, 24, 25, 26, 11, 17]. The CDM3Yn density dependence (n=1-6) of the original M3Y interaction [20] was first parametrized in Ref. [16] to reproduce the saturation of symmetric NM on the HF level. The CDM3Y3 and CDM3Y6 versions were later modified to take into account the rearrangement term (RT) of the single-particle potential in NM into the folding calculation of the nucleon-nucleus and nucleus-nucleus OP [11, 17], based on the Hugenholtz and van Hove (HvH) theorem [27, 28] which is exact for all interacting Fermi systems independently of the interaction between fermions.
When the antisymmetrization of the nucleon-nucleus system is taken explicitly into account, the exchange term of the folded nucleon-nucleus potential becomes nonlocal in coordinate space [12, 15], and a nonlocal folding model of nucleon OP using the CDM3Yn interaction was suggested in Ref. [29], with the RT properly taken into account. The calculable -matrix method [30, 31] is used to solve the OM equation with the nonlocal kernel of the folded nucleon OP. This method was well tested in the OM analysis of elastic nucleon scattering at energies up to 40 MeV [32], using the phenomenological nonlocal nucleon OP [33, 34, 35, 36].
The momentum dependence of nucleon OP at the NM saturation density is due mainly to the exchange term up to fm-1, and the antisymmetrization of the nucleon-nucleus system is, therefore, the main origin of the momentum dependence of nucleon OP at low momenta. As a result, it becomes possible to determine the nucleon effective mass from the momentum dependence of the folded nucleon OP of finite nuclei, based on the WKB local approximation, in the OM analysis of low-energy elastic nucleon scattering on target nuclei with neutron excess. The present work is our first attempt to determine the radial- and isospin dependence of the nucleon effective mass near the saturation density () from the radial strengths of the real folded nucleon OP. The obtained results for allowed us to determine the neutron-proton effective mass splitting at for 48Ca, 90Zr, and 208Pb targets, which is complementary to the values obtained in different mean-field calculations of asymmetric NM.
The knowledge about the nucleon effective mass is of wide importance for different nuclear physics and nuclear astrophysics studies [37, 38, 39, 40, 41]. In particular, the direct link of the nucleon effective mass to the density dependence of nuclear symmetry energy [5, 42, 43], the liquid-gas phase transition in the neutron-rich NM, and the temperature profile of hot protoneutron stars [44] and neutrino emission therefrom [45].
II Single-particle potential in nuclear matter
An effective density-dependent NN interaction is the essential input for the mean-field calculation of NM, and we recall briefly the CDM3Yn density dependent versions of the M3Y interaction used in our model. Originally, parameters of the CDM3Yn density dependence were parametrized [16] to reproduce the NM saturation properties on the HF level. These parameter sets were extended later to include a realistic isovector part [23, 11, 14] as well as the rearrangement term of the single-particle potential [11]. The HF results for the energy per nucleon of NM obtained with the CDM3Yn interaction are compared in Fig. 1 with results of the ab initio variational calculation using the Argonne V18 interaction [46]. One can see a nice agreement of the HF results with those of the ab initio calculation over a wide range of densities.

We note that the functional CDM3Yn density dependence of the original M3Y interaction [20] was parametrized [16] to reproduce on the HF level the saturation of symmetric NM at , as well as to give a realistic (real) nucleus-nucleus OP within the double-folding model that properly describes the nuclear rainbow pattern observed in elastic -nucleus and light heavy-ion refractive scattering. The rainbow scattering data were proven to be sensitive to the real OP at small distances where the dinuclear overlap density is reaching up to twice the saturation density [24], so that the use of the CDM3Yn interaction is well validated for the low-energy domain of nuclear EOS (see Fig. 1).
According to Landau theory for an infinite system of interacting fermions [47], the single-particle energy is determined [11] as derivative of the energy per nucleon of NM with respect to the nucleon momentum distribution
| (1) |
is, thus, the change of the NM energy at density caused by the removal or addition of a nucleon with the momentum . The single-particle potential consists of both the HF and rearrangement terms
| (2) |
with the explicit expressions of given in Ref. [11]. At the Fermi momentum determined from Eqs. (1)-(2) is exactly the Fermi energy given by the Hugenholtz-van Hove (HvH) theorem [27], which is satisfied on the HF level only when the effective NN interaction is density independent, with the RT equal zero [11, 48]. In the mean-field calculation (1)-(2), the RT originates naturally from the density dependence of the in-medium NN interaction that implicitly accounts for the higher-order NN correlations as well as three-body force [1, 4, 5].
For the spin-saturated NM, the (spin-independent) direct (D) and exchange (EX) parts of the CDM3Yn interaction [16, 14] are used in the HF calculation of NM
| (3) |
The radial dependence of the isoscalar (IS) and isovector (IV) terms is kept unchanged as that used for the original M3Y interaction [20]. The IS density dependence was determined [16] to reproduce the saturation of NM on the HF level. The IV density dependence was determined [11] based on the isospin dependence of nucleon OP given by the BHF calculation of NM by Jeukenne, Lejeune and Mahaux (JLM) [49], and and fine tuned by the folding model description of the charge exchange reaction to the isobar analog states in medium-mass nuclei [26].
Using the exact expression of the RT given by the HvH theorem, a compact method was suggested [11] to account for the RT on the HF level by adding a correction term to the CDM3Yn density dependence, , used in the HF-type calculation of the single-particle potential
| (4) |
where are the ordinary plane waves. Treating explicitly the isospin dependence, the single-particle potential (4) is expressed [11] in terms of the IS and IV parts as
| (5) | |||||
where (-) sign pertains to proton and (+) sign to neutron. and are, respectively, the IS and IV parts of the single-particle potential given by the density independent M3Y interaction
| (6) |
| (7) |
Because the original M3Y interaction is momentum independent, the momentum dependence of the single-particle potential (5) is due to the exchange term of , with the nucleon momentum determined self-consistently as
| (8) |

The extended HF approach (4)-(8) provides a consistent description of both the single-particle potential for bound nucleons, with , and nucleon optical potential, with . Such an approach is the well-known continuous approximation for the single-particle potential [1, 50], where nucleon OP in NM is determined as the mean-field potential felt by nucleon being scattered on NM at energy . The momentum of scattered nucleon is determined by the same relation (8) but with replaced by the nucleon incident energy . In this way, the energy- and momentum dependence of nucleon OP are treated on the same footing as illustrated in Fig. 2. Therefore, an important constraint for the present approach is that at the energy dependence of the potential (5) should agree reasonably with the observed energy dependence of nucleon OP. The single-particle potential (5) evaluated for symmetric NM at the saturation density using the CDM3Y6 interaction is compared with the empirical data [51, 52, 53] for nucleon OP at in Fig. 2. One can see that the inclusion of the RT significantly improves the agreement with the empirical data at energies MeV. Moreover, the momentum dependence of nucleon OP in this low-energy region is found nearly linear and due mainly to the Pauli exchange term in Eq. (4).
It should be noted here that the Pauli exchange term in Eq. (4) gives a good agreement of the energy (or momentum) dependence of nucleon OP with the empirical data at low energies only. At higher energies ( MeV or fm-1) the agreement becomes worse, and nucleon OP (5) is more attractive compared to the empirical data (see, e.g., Fig. 3 in Ref. [17]). Such a behavior of nucleon OP given by the HF calculation is well expected in light of the effective G-matrix interaction derived from the solution of Brueckner–Bethe–Goldstone equation [12], where both the direct and exchange parts of the G matrix interaction are energy dependent. This is also the reason why a slight linear energy dependence was added to the CDM3Y6 interaction, in terms of factor [16], for the double-folding calculation of nucleus-nucleus OP at medium energies. Consequently, the nucleon effective mass at high momenta originates not only from the Pauli nonlocality, but also from the higher-order NN correlations in nuclear medium. The present work is focused, however, on the determination of at low energies ( MeV) and corresponding momenta fm-1 from the momentum dependence of nucleon OP, which is due entirely to the Pauli nonlocality as shown above.
III Folding model of nucleon optical potential
III.1 Nonlocal folded nucleon OP
The folding model of nucleon OP [12, 13, 15] is known to generate the first-order term of the microscopic nucleon OP defined in Feshbach’s formalism of nuclear reactions [54]. The success of the folding approach in the OM description of elastic nucleon-nucleus scattering at low and medium energies confirms that the folded nucleon OP is the dominant part of the microscopic nucleon OP. In a consistent mean-field consideration, the central OP for elastic nucleon scattering on a target nucleus is evaluated using the same Eq. (4), but with plane waves replaced by the single-particle wave functions of target nucleons
| (9) |
The antisymmetrization of the nucleon-nucleus system is done in the HF manner, taking into account explicitly the nucleon knock-on exchange. As a result, the exchange term of the folded nucleon OP (9) becomes nonlocal in coordinate space [12], and the OM equation for elastic nucleon scattering at energy becomes an integro-differential equation
| (10) |
where is the spin-orbit potential and is the Coulomb potential used for elastic proton scattering only. The scattering wave function is obtained from the solution of the OM equation (10) at each nucleon-nucleus distance . Based on the CDM3Yn interaction (3) with the RT included, the mean-field part of nucleon OP consists of the local direct potential and the exchange integral involving a nonlocal density-dependent kernel . Making explicit the isospin degrees of freedom, the mean-field part of nucleon OP can be expressed (in the Lane manner) in terms of the IS and IV components as
| (11) |
where (-) sign pertains to proton OP and (+) sign to neutron OP. The IS and IV parts of the direct folded potential and nonlocal exchange kernel (11) are given through the IS and IV nucleon density matrices, respectively, as
| (12) |
where . The nucleon density matrix is determined from the single-particle wave functions of target nucleons as
| (13) |
The direct potential is readily obtained by folding the nucleon densities with the direct part of the density dependent CDM3Yn interaction (3), including the contribution of the RT, as
| (14) |
where the signs are used in the same way as in Eqs. (5) and (11), and the contribution of the RT to the IV part of the direct potential via is the same for both the proton and neutron OP. The exact treatment of the nonlocal exchange term is cumbersome and involves the explicit angular-momentum dependence of the exchange kernel. Using the multipole decomposition of the radial Yukawa function of the exchange part of the CDM3Yn interaction (3)
| (15) |
we obtain, after integrating out the angular dependence, the radial equation for each partial wave
| (16) |
where is the radial part of nucleon scattering wave function , is the s.o. coupling coefficient determined as if , and if . The nonlocal density-dependent exchange kernel is then obtained at each partial wave as
| (17) | |||||
| (24) | |||||
| (31) | |||||
Here is the radial part of the single-particle wave function of target nucleon. The (-) sign is used with proton OP and (+) sign with neutron OP, and the contribution of the RT to the IV part of the exchange kernel is also the same for both proton and neutron OP as found for the IV part of the direct potential (14). The explicit representation of nucleon OP in terms of the IS and IV parts should be helpful in revealing the contribution of valence neutrons to the total OP. Furthermore, the charge exchange form factor (FF) of the reaction to the isobar analog state (IAS) is determined, in the Lane isospin coupling scheme, entirely by the IV part of nucleon OP [26, 55]. Therefore, the present nonlocal folding model can also be used to calculate the nonlocal charge exchange FF of the Fermi transition to IAS in the folding model study of IAS reaction.
III.2 Local approximation for the folded nucleon OP
Although the nucleon OP is well established to be nonlocal in the coordinate space due to the Pauli blocking (as discussed above) and nonelastic channel coupling, the nucleon OP of some local form is widely used in numerous OM analyses of elastic nucleon-nucleus scattering. The obtained elastic scattering wave function (dubbed as the distorted wave) is then used as a key input in different DWBA or coupled-channel calculations of direct nuclear reactions. We briefly discuss here the validity of the local folding model [13, 14] of nucleon OP, which has been successfully used to study elastic nucleon scattering.
Applying a local WKB approximation [18, 19] for the change in the scattering wave function in the OM equation (10) induced by the exchange of spatial coordinates of scattered nucleon and target nucleon, we obtain
| (32) |
where the local momentum of scattered nucleon is energy- and radial dependent. Inserting Eq. (32) into Eq. (10), the nonlocal exchange integral becomes localized and energy (momentum) dependent. The local exchange term of the folded nucleon OP can then be evaluated separately using the nonlocal nucleon density matrix
| (33) | |||||
where the signs are used in the same way as in Eq. (11). The local momentum of scattered nucleon is determined self-consistently from the real folded nucleon OP as
| (34) |
Thus, the momentum- and energy dependences of the local folded nucleon OP of finite nuclei are directly interrelated and also determined on the same footing as in the NM limit (see Fig. 2). The method to evaluate the direct (14) and exchange (33) folded potentials is given in more details in, e.g., Ref. [13]. Using a realistic local approximation for the nonlocal density matrix in Eq. (33), the nuclear density obtained in any structure model or directly deduced from electron scattering data can be used in the folding model calculation of the local nucleon OP.
III.3 Elastic nucleon scattering on 40,48Ca, 90Zr, and 208Pb targets
To validate the use of the local folded nucleon OP to deduce the nucleon effective mass, we show here results of the folding model analysis of low-energy elastic nucleon scattering using both the nonlocal and local folded nucleon OP. Namely, the nonlocal and local folding models of nucleon OP discussed above are used to calculate nucleon OP for the OM study of elastic neutron and proton scattering on 40,48Ca, 90Zr, and 208Pb targets. Because the nonlocal folding calculation (12)-(13) requires the explicit single-particle wave functions of target nucleons, we have used the single-particle wave functions given by the HF calculation of finite nuclei based upon a complete basis of spherical Bessel functions [56] and finite-range D1S Gogny interaction [57].

To obtain a complex folded nucleon OP, it is necessary to have a realistic complex parametrization of the density dependent CDM3Yn interaction. For this purpose, the imaginary density dependence of the CDM3Y6 interaction was determined using the same density dependent functional as that used for the real interaction (3), with the parameters adjusted to reproduce, at each energy, the imaginary nucleon OP in NM given by the JLM parametrization of the BHF results [49] on the HF level [14]. The complex nonlocal and local folded OP’s were then used as input for the OM calculation of elastic nucleon scattering using the calculable -matrix method [30, 31]. In the present OM calculation, both the nonlocal and local folded OP’s are supplemented by the local Coulomb and spin-orbit potentials taken from the global systematics CH89 of nucleon OP [52].


The reliability of the folded OP is best to be probed in the OM analysis of elastic neutron scattering from a heavy target at low energies, where the Coulomb interaction is absent and the mean-field dynamics is well established. For this purpose, elastic Pb scattering data measured accurately at energies of 26, 30.4, and 40 MeV [58, 59, 60] turned out to be a very good test ground. Given parameters of the real CDM3Yn interaction fine-tuned by the HF description of NM shown in Fig. 1, no renormalization of the real part of both the nonlocal and local folded OP was allowed in the present OM study to test its proximity to the real nucleon OP. The imaginary folded OP based on the JLM parametrization delivers a good OM description of elastic proton scattering, but it gives a stronger absorption of neutron OP, and an overall renormalization of the imaginary part of both nonlocal and local folded neutron OP by a factor was found necessary for a good OM description of the considered neutron scattering data. From the OM results obtained for elastic Pb scattering shown in Fig. 3 one can see that both the nonlocal and local folded OP deliver the same good OM description of data over the whole angular range, which validates the local approximation (33)-(34) for the exchange term of the folded neutron OP. We note that, in the absence of the Coulomb interaction, the (diffractive) oscillation of elastic neutron scattering cross section at small angles can be properly reproduced only with the inclusion of the RT into the folding calculation [29]. A good accuracy of the local approximation for the folded OP can also be seen in the OM results obtained for elastic neutron scattering on the medium-mass 40,48Ca and 90Zr targets shown in Fig. 4.

The elastic Pb scattering data measured at 30.4, 35, and 45 MeV [64, 65] are compared in Fig. 5 with the OM results given by the folded proton OP. Both the nonlocal and local folded OP were found to give the same good OM description of elastic Pb data at the forward and medium angles, while the data points at backward angles are better reproduced by the nonlocal folded OP, especially, at 45 MeV. We note that the OM results shown in Figs. 5 and 6 were obtained without renormalizing the (complex) strength of the folded proton OP. Like the OM result obtained for elastic Pb scattering at MeV, one can also see a more pronounced difference given by the nonlocal folded proton OP at medium and large scattering angles from the results obtained for elastic Ca scattering at energies MeV shown in Fig. 6, which indicates the need of taking into account exactly the Pauli nonlocality of the folded proton OP at these medium energies.
IV Nucleon effective mass
As discussed in Sec. II, the momentum dependence of the single-particle potential in NM at low momenta is determined mainly by the exchange term which results on a nonlocal single-nucleon potential in the coordinate space. At positive energy () the single-nucleon potential (4)-(5) can be treated as nucleon OP in NM, with the associated nucleon effective mass determined [1, 37] as
| (35) |
where is the free nucleon mass. In general, the nucleon effective mass arises from both the momentum- and energy dependence of the single-particle potential [1], known as the - and -effective masses, which characterize the spacetime nonlocality. Within the time independent HF formalism [11], the total nucleon effective mass is determined by the same relation (35), and it is associated with the spatial nonlocality of the nucleon mean-field potential. At the Fermi momentum () , the nucleon effective mass (35) is obtained naturally from the Fermi energy (1) by the Hugenholtz-van Hove theorem [27]. The knowledge about at the saturation density and different neutron-proton asymmetries is essential for the determination of the nuclear symmetry energy and its slope parameter , the two key ingredients of the EOS of neutron rich NM [41, 42].

The neutron and proton effective masses (35) obtained from the single-particle potential (4)-(5) in asymmetric NM at the saturation density with are shown in Fig. 7 as dashed and dotted lines, respectively. Although the values are still poorly known at high NM densities and/or large values, the empirical nucleon effective mass in symmetric NM () at the saturation density is well established to be around [37]. Our extended HF calculation of NM using the CDM3Yn interaction gives at and (see Fig. 9), in a good agreement with the empirical data. The isospin dependence of the nucleon effective mass is governed by the neutron-proton effective mass splitting
| (36) |
which is associated directly with the nuclear symmetry energy and its slope parameter. The knowledge of is also of importance for the determination of the neutron/proton ratio during stellar evolution or cooling of protoneutron star [38, 40, 41]. Depending on the isospin dependence of the in-medium NN interaction, one obtains very different results for the neutron-proton effective mass splitting. A survey of different mean-field studies in Ref. [41] shows that values depend linearly on the neutron-proton asymmetry parameter , and are ranging widely from negative- to positive values, up to . An analysis of the empirical constraints for the density dependence of nuclear symmetry energy [38] from both the nuclear physics experiments and astrophysical observations has led to the empirical constraint . Our extended HF calculation of asymmetric NM using the CDM3Y6 interaction gives at the Fermi momentum, which is well inside the empirical boundary.
For many years, the nucleon effective mass in finite nuclei has been a focus of different nonrelativistic and relativistic nuclear structure studies (see, e.g., Refs. [68, 69, 70]) which provided accurate estimates of the values for the single-particle states of bound nucleons (with ). Although the neutron- and proton effective masses, and the corresponding single-particle energies and spectroscopic factors are well described by the structure studies, it remains difficult to deduce therefrom an explicit isospin dependence of or the neutron-proton effective mass splitting (36). The method often used so far for this purpose is to deduce the isospin dependence of the nucleon effective mass from the isospin dependence of the phenomenological nucleon OP given by the best OM fit to elastic nucleon scattering data at different energies [39]. In the present work, we aim to determine the nucleon effective mass from the semi-microscopic nucleon OP predicted by the local folding model presented in Sec. III.2. Given a good OM description of elastic nucleon scattering at low energies by the local folded nucleon OP shown Sec. III.3, it is reasonable to determine the effective mass of nucleon scattered by the mean field of target from the momentum dependence of the real folded OP as
| (37) | |||||
| (38) |
Here are the direct and exchange parts of the local neutron (or proton) folded OP determined from Eqs. (14) and (33), respectively. The energy or momentum dependence of the folded nucleon OP (38) is embedded in the exchange term only, which was shown in Sec. III.2 to be resulted from the Pauli nonlocality of the folded nucleon OP. The in-medium momentum of scattered nucleon is determined self-consistently from the real folded nucleon OP by Eq. (34).
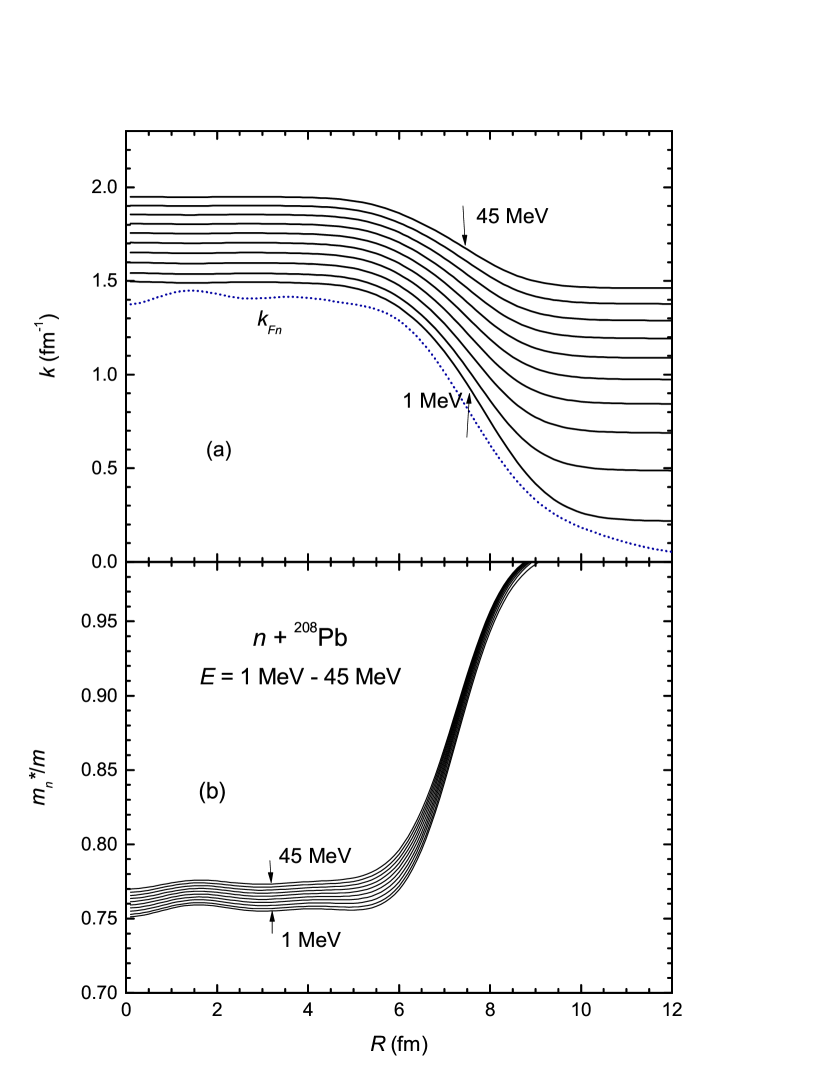
It is obvious from Eq. (34) that the momentum of scattered nucleon depends explicitly on the nucleon-nucleus distance , and the nucleon effective mass (38) is, therefore, also radial dependent. The in-medium momentum of scattered neutron determined from the real folded Pb OP at energies of MeV is shown in panel (a) of Fig. 8, and one can see that at each energy the neutron momentum changes gradually from its maximum of about fm-1 in the center to fm-1 at the surface, lying above the corresponding Fermi momentum. Over the same radial range, the neutron effective mass is changing from about to unity at the surface. Such a radial dependence of is similar to that found in the nuclear structure studies [68, 69, 70]. However, the latter is usually enhanced to above unity at the surface for the bound single-particle states lying close to the Fermi level.

From the radial dependence of the neutron effective mass and the neutron- and total ground-state densities of 208Pb shown in panel (a) of Fig. 9, it is straightforward to infer the density dependence of the effective mass of neutron scattered off 208Pb target at different energies, over the density range . One can see in panel (a) of Fig. 9 that the average total density in the center of 208Pb target is , and the neutron- and proton effective masses determined at distances fm (shown in panels (b) of Figs. 9 and 10) can represent, therefore, the corresponding values in asymmetric NM at , and neutron-proton asymmetry . Because of the target valence neutrons, the deduced value in the target center is smaller than the total difference in neutron- and proton numbers . Since our local folding model (14) and (33) predicts the real nucleon OP at or , approaching the Fermi momentum from above, we have computed the real folded nucleon OP for 48Ca, 90Zr, and 208Pb targets at MeV (i.e., 50 keV above the Fermi level), and deduced the neutron- and proton effective masses using Eq. (38). The obtained results are presented in Table 1 and shown in Figs. 7 as rhombuses and circles. One can see that the values obtained at and for these targets follow approximately the trend given by the extended HF calculation of the single-particle potential in NM.

| Nucleus | 48Ca | 90Zr | 208Pb |
|---|---|---|---|
It is interesting that the neutron-proton effective mass splitting (36) obtained from the values given in Table 1 also depends linearly on the asymmetry parameter, , which is within the empirical boundary of deduced from the terrestrial nuclear physics experiments and astrophysical observations [38]. In neutron-rich NM, nucleons at are not bound by the in-medium NN interaction (see, e.g., Fig 1 in Ref. [11]), and the results obtained above for at should be appropriate for nucleons in the outer core of neutron star which are bound by gravitation only. We note further that the value estimated from the folded nucleon OP of finite nuclei is slightly lower than that given by nucleon OP in NM using the same interaction, , and the value estimated from the phenomenological nucleon OP [40], based on the extensive OM analysis of elastic nucleon scattering.
We note finally that the nucleon effective mass is given entirely by the momentum dependence of the exchange term of the folded nucleon OP, so that the nucleon effective masses presented in Table 1 and shown in Fig. 7 originated solely from the spacial Pauli nonlocality of nucleon OP at low energies. We have considered the energy region MeV, and found that the nucleon effective mass (38) depends weakly on the energy. For example, and for 208Pb target, and this result agrees fairly with the empirical energy dependence of about established for the isoscalar effective mass of nucleons lying above the Fermi level [37].
V Summary
The generalized folding model of the nonlocal nucleon OP, with the exchange potential calculated exactly in the HF manner and rearrangement term properly included, has been used for the OM analysis of elastic neutron and proton scattering on 40,48Ca, 90Zr, and 208Pb targets at different energies, where the WKB local approximation for the exchange term of the nonlocal folded nucleon OP is validated by a consistently good OM description of the considered elastic data.
Given the accurate local approximation for the nonlocal folded nucleon OP, a compact method is proposed to determine the nucleon effective mass at low momenta from the in-medium momentum dependence of the local folded nucleon OP, which originates mainly from the Pauli nonlocality. The results obtained for the effective mass of nucleon being scattered by the target mean-field potential at MeV and fm-1 seem to follow closely the isospin dependence of predicted by the extended HF calculation of single-particle potential in asymmetric NM, using the same density dependent CDM3Y6 interaction.
The neutron-proton effective mass splitting (36) given by the values obtained from the real folded nucleon OP of finite nuclei at low energies was found to depend also linearly on the asymmetry parameter . At positive energies lying slightly above the Fermi level, the value determined at the center of finite nuclei (with the average density ) is slightly smaller than that obtained from the extended HF calculation of the single-particle potential of nucleons in asymmetric NM at , where the Pauli exchange has been shown as the main origin of nucleon effective mass.
Because nucleons at density in the outer core of neutron star are mainly bound by gravitation, not by the (in-medium) density dependent NN interaction, the values obtained in this work from the folded nucleon OP of finite nuclei with neutron excess could be of complementary interest for the mean-field studies of the EOS of neutron star matter.
Acknowledgments
The authors are indebted to Pierre Descouvemont for his helpful discussions and comments on the calculable -matrix method [30, 31]. We also thank Bao-An Li for his communication and suggestion on the nucleon effective mass. The present research has been supported, in part, by the National Foundation for Scientific and Technological Development of Vietnam (NAFOSTED Project No. 103.04-2021.74).
References
- [1] C. Mahaux, P.F. Bortignon, R.A. Broglia, and C.H. Dasso, Phys. Rep. 120, 1 (1985).
- [2] M. Baldo and C. Maieron, J. Phys. G 34, R243 (2007).
- [3] I. Bombaci and U. Lombardo, Phys. Rev. C 44, 1892 (1991).
- [4] W. Zuo, I. Bombaci, and U. Lombardo, Phys. Rev. C 60, 024605 (1999).
- [5] W. Zuo, I. Bombaci, and U. Lombardo, Eur. Phys. J. A 50, 12 (2014).
- [6] D.T. Khoa and W. von Oertzen, Phys. Lett. B304, 8 (1993).
- [7] D.T. Khoa and W. von Oertzen, Phys. Lett. B342, 6 (1995).
- [8] C. Xu, B.A. Li, and L.W. Chen, Phys. Rev. C 82, 054607 (2010).
- [9] R. Chen, B.J. Cai, L.W. Chen, B.A. Li, X.H. Li, and C. Xu, Phys. Rev. C 85, 024305 (2012).
- [10] C. Xu, B.A. Li, and L.W. Chen, Eur. Phys. J. A 50, 21 (2014).
- [11] D.T. Loan, B.M. Loc, and D.T. Khoa, Phys. Rev. C 92, 034304 (2015).
- [12] K. Amos, P. J. Dortmans, S. Karataglidis, H. V. von Geramb, and J. Raynal, Adv. Nucl. Phys. 25, 275, (2001).
- [13] D.T. Khoa, E. Khan, G. Colò, and N.V. Giai, Nucl. Phys. A 706, 61 (2002).
- [14] D.T. Khoa, H.S. Than, and D.C. Cuong, Phys. Rev. C 76, 014603 (2007).
- [15] K. Minomo, K. Ogata, M. Kohno, Y. R. Shimizu, and M. Yahiro, J. Phys. G 37, 085011 (2010).
- [16] D.T. Khoa, G.R. Satchler, and W. von Oertzen, Phys. Rev. C 56 (1997) 954.
- [17] D.T. Khoa, N.H. Phuc, D.T. Loan, and B.M. Loc, Phys. Rev. C 94, 034612 (2016).
- [18] B. Sinha, Phys. Rep. 20, 1 (1975).
- [19] F.A. Brieva and J.R. Rook, Nucl. Phys. A 291, 317 (1977).
- [20] N. Anantaraman, H. Toki, and G.F. Bertsch, Nucl. Phys. A 398, 269 (1983).
- [21] D.T. Khoa, W. von Oertzen, and A.A. Ogloblin, Nucl. Phys. A 602, 98 (1996).
- [22] H.S. Than, D.T. Khoa, and N.V. Giai, Phys. Rev. C 80, 064312 (2009).
- [23] D.T. Loan, N.H. Tan, D.T. Khoa, and J. Margueron, Phys. Rev. C 83, 065809 (2011).
- [24] D.T. Khoa, W. von Oertzen, H.G. Bohlen, and S. Ohkubo, J. Phys. G34, R111 (2007).
- [25] N.D. Chien and D.T. Khoa, Phys. Rev. C 79, 034314 (2009).
- [26] D.T. Khoa, B.M. Loc, and D.N. Thang, Eur. Phys. J. A 50, 34 (2014).
- [27] N.M. Hugenholtz and L. Van Hove, Physica 24, 363 (1958).
- [28] L. Satpathy, V.S. Uma Maheswari, and R.C. Nayak, Phys. Rep. 319, 85 (1999).
- [29] D.T. Loan, D.T. Khoa, and N.H. Phuc, J. Phys. G 47, 035106 (2020).
- [30] P. Descouvemont and D. Baye, Rep. Prog. Phys. 73, 36301 (2010).
- [31] P. Descouvemont, Comp. Phys. Comm. 200, 199 (2016).
- [32] D.T. Loan, N.H. Phuc, and D.T. Khoa, Communications in Physics 28, 323 (2018).
- [33] F. Perey and B. Buck, Nucl. Phys. 32, 353 (1962).
- [34] Y. Tian, D.Y. Pang, and Z.Y. Ma, Int. J. Mod. Phys. E 24 1550006 (2015).
- [35] A.E. Lovell, P.L. Bacq, P. Capel, F.M. Nunes, and L.J. Titus, Phys. Rev. C 96, 051601(R) (2017).
- [36] M.I. Jaghoub, A.E. Lovell, and F.M. Nunes, Phys. Rev. C 98, 024609 (2018).
- [37] P.E. Hodgson, Contemp. Phys. 24, 491 (1983).
- [38] B.A. Li and X. Han, Phys. Lett. B 727, 276 (2013).
- [39] X.H. Li, W.J. Guo, B.A. Li, L.W. Chen, F.J. Fattoyev, and W.G. Newton, Phys. Lett. B 743, 408 (2015).
- [40] B.A. Li and L.W. Chen, Modern Physics Letters A 30, 1530010 (2015).
- [41] B.A. Li, B.J. Cai, L.W. Chen, and J. Xu, Prog. Part. Nucl. Phys. 99, 29 (2018).
- [42] C.J. Horowitz, E.F. Brown, Y. Kim, W.G. Lynch, R. Michaels, A. Ono, J. Piekarewicz, M.B. Tsang, and H.H. Wolter, J. Phys. G 41, 093001 (2014).
- [43] B.A. Li, L.W. Chen, and C.M. Ko, Phys. Rep. 464, 113 (2008).
- [44] N.H. Tan, D.T. Loan, D.T. Khoa, and J. Margueron, Phys. Rev. C 93, 035806 (2016).
- [45] M. Baldo, G.F. Burgio, H.J. Schulze, and G. Taranto, Phys. Rev. C 89, 048801 (2014).
- [46] A. Akmal, V.R. Pandharipande, and D.G. Ravenhall, Phys. Rev. C 58, 1804 (1998).
- [47] A. B. Migdal, Theory of Finite Fermi Systems and Applications to Atomic Nuclei (Interscience, New York, 1967).
- [48] P. Czerski, A. De Pace, and A. Molinari, Phys. Rev. C 65, 044317 (2002).
- [49] J.P. Jeukenne, A. Lejeune, and C. Mahaux, Phys. Rev. C 16, 80 (1977).
- [50] C. Mahaux and R. Sartor, Adv. Nucl. Phys. 20, 1 (1991).
- [51] A. Bohr and B.R. Mottelson, Nuclear Structure, vol.I, p.237 (W.A. Benjamin, Inc., New York, 1969).
- [52] R.L. Varner, W.J. Thompson, T.L. McAbee, E.J. Ludwig, and T.B. Clegg, Phys. Rep. 201, 57 (1991).
- [53] S. Hama, B.C. Clark, E.D. Cooper, H.S. Sherif, and R.L. Mercer, Phys. Rev. C 41, 2737 (1990).
- [54] H. Feshbach, Theoretical Nuclear Physics, Vol. II (Wiley, New York, 1992).
- [55] B.M. Loc, D.T. Khoa, and R.G.T. Zegers, Phys. Rev. C 89, 024317 (2014).
- [56] H.S. Than, E. Khan, and N.V. Giai, J. Phys. G 38, 025201 (2011).
- [57] J.F. Berger, M. Girod, and D. Gogny, Comp. Phys. Comm. 63, 365 (1991).
- [58] R.W. Finlay, J.R.M. Annand, T.S. Cheema, J. Rapaport, and F.S. Dietrich, Phys. Rev. C 30, 796 (1984).
- [59] J. Rapaport, T.S. Cheema, D.E. Bainum, R.W. Finlay, and J.D. Carlson, Nucl. Phys. A 313, 1 (1979).
- [60] R.P. DeVito, D.T. Khoa, S.M. Austin, U.E.P. Berg, and B.M. Loc, Phys. Rev. C 85, 024619 (2012).
- [61] G.M. Honoré, W. Tornow, C.R. Howell, R.S. Pedroni, R.C. Byrd, R.L. Walter, and J.P. Delaroche, Phys. Rev. C 33, 1129 (1986).
- [62] J.M. Mueller, R.J. Charity, R. Shane, L.G. Sobotka, S.J. Waldecker, W.H. Dickhoff, A.S. Crowell, J.H. Esterline, B. Fallin, C.R. Howell, et al., Phys. Rev. C 83, 064605 (2011).
- [63] Y. Wang and J. Rapaport, Nucl. Phys. A 517, 301 (1990).
- [64] W.T.H. van Oers, Huang Haw, N.E. Davison, A. Ingemarsson, B. Fagerström, and G. Tibell, Phys. Rev. C 10, 307 (1974).
- [65] L.N. Blumberg, E.E. Gross, A. van der Woude, A. Zucker, and R. H. Bassel, Phys. Rev. 147, 812 (1966).
- [66] R.H. McCamis, T.N. Nasr, J. Birchall, N.E. Davison, W.T.H. van Oers, P.J.T. Verheijen, R.F. Carlson, A.J. Cox, B.C. Clark, E.D. Cooper, S. Hama, and R.L. Mercer, Phys. Rev. C 33, 1624 (1986).
- [67] A. Koning and J. Delaroche, Nucl. Phys. A 713, 231 (2003).
- [68] N.V. Giai and P.V. Thieu, Phys. Lett. 126B, 421 (1983).
- [69] E. Litvinova and P. Ring, Phys. Rev. C 73, 044328 (2006).
- [70] M. Zalewski, P. Olbratowski, and W. Satula, Phys. Rev. C 81, 044314 (2010).