PatchComplete: Learning Multi-Resolution Patch Priors for 3D Shape Completion on Unseen Categories

Understanding how to reconstruct 3D shapes is an essential task for 3D machine perception. In particular, the task of shape completion to predict a complete shape from partial input observations has been studied by various works toward understanding 3D shape structures. Recently, many works have leveraged deep learning techniques to learn strong data-driven priors for shape completion, focusing on various different representations, e.g. volumetric grids [45, 14], continuous implicit functions [31, 22, 30, 7, 40, 36, 37], point clouds [32], and meshes [12, 20, 34, 35]. These works tend to focus on strong synthetic supervision on a small set of train categories, achieving impressive performance on unseen shapes from train categories, but often struggling to generalize to unseen classes. We focus on learning more generalizable, local shape priors in order to effectively reconstruct complete shapes on unseen class categories.

Several works have been developed to tackle the challenging task of few-shot or zero-shot shape reconstruction, as observations in-the-wild often contain a wide diversity of objects. In the few-shot scenario where several examples of novel categories are available, Wallace and Hariharan [42] learn to refine a given category prior. Michalkiewicz et al. [23] further propose to learn compositional shape priors for single-view reconstruction.

In the zero-shot scenario without any examples seen for novel categories, Naeem et al. [25] learn priors from seen categories to generate segmentation masks for unseen categories. Zhang et al. [48] additionally proposed to use spherical map representations to learn priors for the reconstruction of novel categories. Thai et al. [39] recently developed an approach to transfer knowledge from an RGB image for shape reconstruction. We also tackle a zero-shot shape reconstruction task, by learning a multi-resolution set of strong local shape priors to compose a reconstructed shape.

Several recent works have explored learning shape priors by leveraging a VQ-VAE backbone with autoregressive prediction to perform shape reconstruction [24, 46]. In contrast, we propose to learn multi-resolution shape priors without requiring any sequence interpretation, which enables direct applicability to real-world scan data that often contains noise and clutter. Additionally, hierarchical reconstruction has shown promising results for shape reconstruction [2, 6]. Our approach also takes a multi-resolution perspective, but learns explicit shape and local patch priors and their correlation to input partial observations for robust shape completion.

Our method aims to learn effective 3D shape priors that enable general shape completion from partial input scan data, on novel class categories not seen during training. Key to our approach is the observation that 3D shapes often share repeated local patterns – for instance, chairs, tables, and nightstands all share a support surface, and chair or table legs can share a similar structure with lamp rods. Inspired by this, we regard a complete object as a set of substructures, where each substructure represents a local geometric region. We thus propose PatchComplete to learn such local priors and assemble them into a complete shape from a partial scan. An overview of our approach is shown in Figure 2.

We first learn local shape priors from ground-truth train objects. We represent both the input partial scan $\mathcal{S}$ and the ground-truth shape $\mathcal{G}$ as 3D truncated signed distance field grids of size $D^{3}$. Figure 3 illustrates the process of learning local shape priors. We learn to build mappings from local regions in incomplete input observations to local priors based on complete shapes, in order to robustly reconstruct the complete shape output.

We first aim to learn patch-based priors, which we extract from learnable global shape priors $\{\mathcal{T}^{c}\}$. We denote $\mathcal{G}^{c}$ as the set of ground-truth train objects in the $c$-th category. These $\{\mathcal{T}^{c}\}$ priors are initialized per train category $c$ based on mean-shift clustering within shapes in $\mathcal{G}^{c}$. Thus $\mathcal{T}^{c}$ is a set of representative samples in each category, which are encoded parallel to the input scan $\mathcal{S}$.

Both encoders are analogously structured as 3D convolutional encoders which spatially downsample by a factor of $R$, resulting in a 3D encoding of size $N^{3}$; $N=D/R$. The input encoding (from $\mathcal{S}$) are uniformly chunked into patches $\{\mathcal{Q}_{i}\}$, $i$=1,…,$N^{3}$; similarly, the encoded priors (from $\{\mathcal{T}^{c}\}$) are chunked into patches $\{\mathcal{K}^{c}_{i}\}$.

We then use each local part $\mathcal{Q}_{i}$ to query for the most informative encodings of complete local regions $\{\mathcal{K}^{c}_{i}\}$, building this mapping based on cross-attention [41]. Then for each input patch, we calculate its similarity with all local patches in representative shapes on training categories:

$$\mathrm{Attention}(\mathcal{Q}_{i},\mathcal{K})=\mathrm{softmax}(\frac{\mathcal{Q}_{i}\cdot{\mathcal{K}}^{T}}{d/2}),\\ \mathcal{K}=\{\mathcal{K}^{c}_{i}|i=1,...,N^{3},c=1,...,C\},$$

(1)

where $d$ is the dimension of the encoded vectors of $\mathcal{Q}_{i},\mathcal{K}^{c}_{i}$; $C$ is the category number. We then reconstruct complete shape patches $\{\mathcal{P}_{i}\}$ by:

$$\mathcal{P}_{i}=\mathrm{Attention}(\mathcal{Q}_{i},\mathcal{K})\cdot\mathcal{V}$$

(2)

where $\mathcal{V}=\{\mathcal{V}^{c}_{i}\}$ is the set of $N^{3}$ chunks (of resolution $R$) from shapes in all categories $\{\mathcal{T}^{c}\}$, where each $\mathcal{V}^{c}_{i}$ is paired with $\mathcal{K}^{c}_{i}\in\mathcal{K}$. We can then recompose $\{\mathcal{P}_{i}\}$ to the predicted full shape $P$.

In Section 3, we learn to complete shapes in a single patch resolution $R$. Since local substructures may exist at various scales, we learn patch priors under varying resolutions, which we then use to decode a complete shape. We use three patch resolutions ($R$=4, 8, 32), for which we learn patch priors. This results in three pairs of trained {input encoder, prior encoder} (see Figure 3). Given a partial input scan $\mathcal{S}$, each pair outputs a set of 1) input patch features $\{\mathcal{Q}^{R}_{i}\}$, and 2) prior patch features $\mathcal{K}^{R}$, under the resolution of $R$=4, 8, 32. In this section, we decode a complete shape from these multi-resolution patch priors.

Since $\mathcal{K}^{R}$ stores the patch priors, we use it as the (key, value) term into an attention module, where each input patch feature $\mathcal{Q}^{R}_{i}$ is used to query for the most informative prior features in $\mathcal{K}^{R}$ under different resolutions, from which we complete partial patches in feature spaces with a multi-scale fashion. We formulate this process by

$$\mathcal{O}^{R}_{i}=\mathrm{Concat}\left[\mathcal{Q}^{R}_{i},\mathrm{Attention}(\mathcal{Q}^{R}_{i},\mathcal{K}^{R})\cdot\mathcal{K}^{R}\right],R=4,8,32,$$

(3)

where we concatenate input patch feature with the attention result to compensate information loss on observable regions. This outputs $\{\mathcal{O}^{R}_{i}\}$ as the intermediate feature of the $i$-th patch; $i=1,...,N_{R}^{3}$. $N_{R}$ denotes the number of patches under the resolution $R$; $N_{R}=D/R$. We recompose all generated patch features into a volume $\mathcal{O}^{R}=\{\mathcal{O}^{R}_{i}|i=1,...,N_{R}^{3}\}$. Note that the dimension of each grid feature in $\{\mathcal{Q}^{R}_{i}\}$ and $\mathcal{K}^{R}$ equals to $d$ (see Eq. 1). Then $\mathcal{O}^{R}$ is with the dimension of $N_{R}^{3}\times 2d$.

We then sequentially use 3D convolution decoders to upsample and concatenate $\mathcal{O}^{R}$ from low to high resolution to fuse all the shape features as in

$$\begin{split}\mathcal{O}^{R_{r+1}}&=\mathrm{Concat}\left[\mathrm{Upsample}(\mathcal{O}^{R_{r}}),\mathcal{O}^{R_{r+1}}\right],R_{r}|_{r=1,2,3}=32,8,4,\\ \mathcal{O}_{pred}&=\mathrm{Conv}(\mathrm{Upsample}(\mathcal{O}^{R_{3}})).\end{split}$$

(4)

In Eq. 4, $\mathcal{O}^{R_{r}}$ has a lower resolution than $\mathcal{O}^{R_{r+1}}$. We then use deconvolution layers to upsample $\mathcal{O}^{R_{r}}$ to match the resolution of $\mathcal{O}^{R_{r+1}}$, and then concatenate them together. We recursively fuse $\mathcal{O}^{R_{r}}$ into $\mathcal{O}^{R_{r+1}}$, which produces $\mathcal{O}^{R_{3}}$ as the final fusion result with the resolution of $(D/4)^{3}$. An extra upsampling followed by a convolution layer is adopted to upsample $\mathcal{O}^{R_{3}}$ into our shape prediction $\mathcal{O}_{pred}$ with the dimension of $D^{3}$.

In training the feature fusion, we fix all parameters from the {input encoder, prior encoder} under the three resolutions, since they are pre-trained on Section 3 and provide better-learned priors and attention maps under these strong constraints. The whole pipeline for this section can be found in Figure 4.

We use an $\ell_{1}$ loss to supervise the TSDF value regression. We weight the $\ell_{1}$ loss to penalize false predictions based on the predicted signs as Eq. 5 shows, which represents whether this voxel grid is occupied or not. It is also used in the loss function in Section 3.

$$\mathcal{L}=w_{occ}\ell_{1}(\mathcal{O}^{occ}_{pred},\mathcal{O}_{gt})+w_{empty}\ell_{1}(\mathcal{O}^{empty}_{pred},\mathcal{O}_{gt})+\ell_{1}(\mathcal{O}^{correct}_{pred},\mathcal{O}_{gt}).$$

(5)

In Eq. 5, $\mathcal{O}^{empty}_{pred}$ represents the false positive TSDF values, where the ground truth has negative signs and the prediction has positive signs, which in general indicates the missing predictions. $\mathcal{O}^{occ}_{pred}$ represents false negative TSDF values, where the ground truth has positive signs and the prediction has negative signs, which indicates extra predictions. $\mathcal{O}^{correct}_{pred}$ means those predicted TSDF values with the same signs as the ground-truth. During training, we choose the weight for false positive ($w_{empty}$) as 5, and the weight for false negative ($w_{occ}$) as 3.

We train our approach on a single NVIDIA A6000 GPU, using an Adam optimizer with batch size 32 for a synthetic dataset and batch size 16 for a real-world dataset, and an initial learning rate of 0.001. We train for 80 epochs until convergence, and then decrease the learning rate by half after epoch 50. We use the same settings for learning priors and the multi-resolution decoding, which train for 4 and 15.5 hours respectively. For additional network architecture details, we refer to the supplemental material.

Note that for training for real scan data, we first pre-train on synthetic data and then fine-tune only the input encoder. We use 112 shape priors in our method, which are clustered from 3202 train shapes, and represented as TSDFs with truncation of 2.5 voxels.

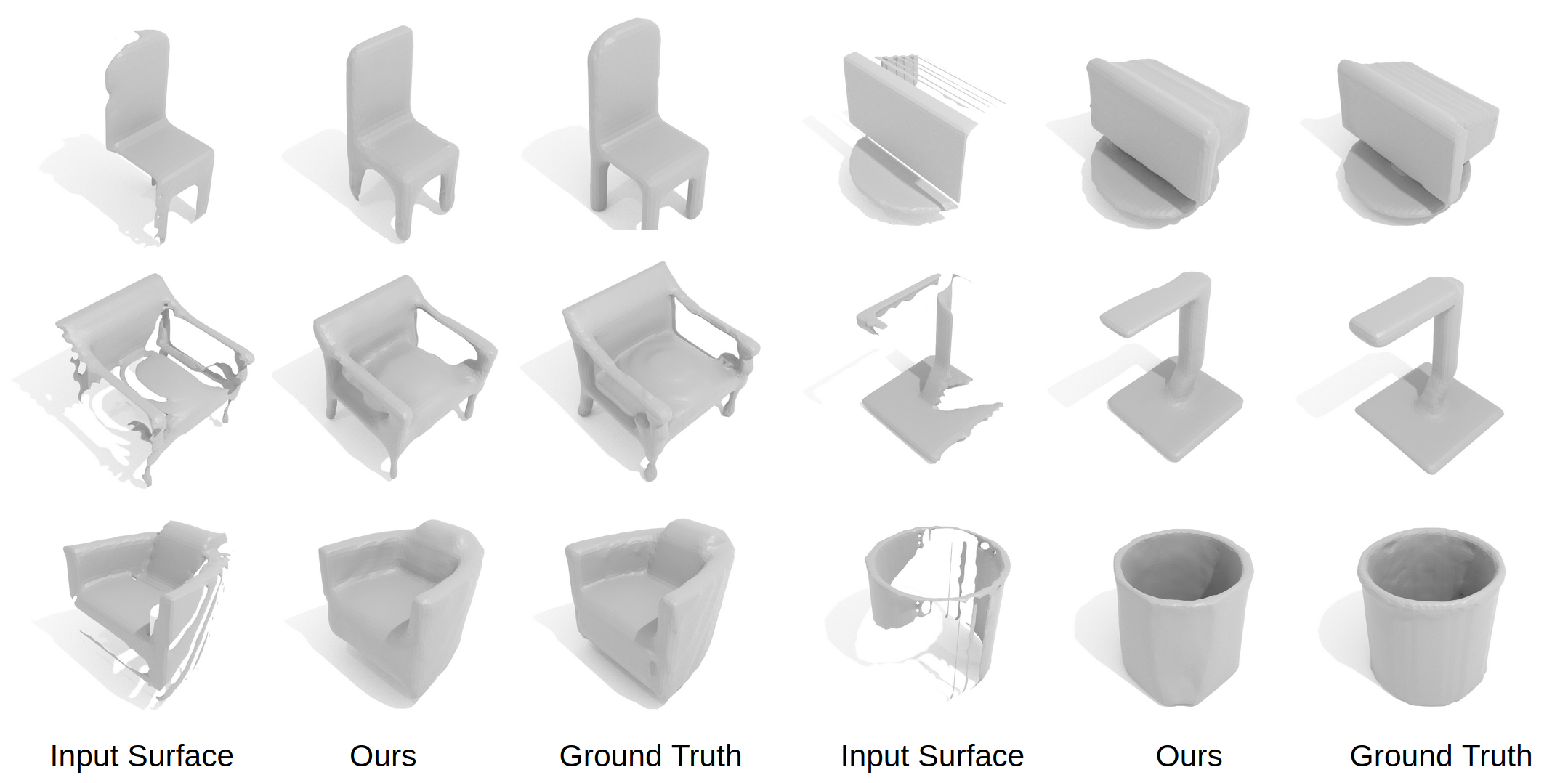
In Table 1, we evaluate our approach in comparison with prior arts on unseen class categories of synthetic ShapeNet [5] data. Our approach on learning attention-based correlation to learned local shape priors results in notably improved reconstruction performance, with coherent global and local structures, as shown in Figure 5. In Table 1, our work outperforms other baselines both instance-wise and category-wise. One of the key factors is that our method learns multi-scale patch information from seen categories to complete unseen categories with enough flexibility, while most of the other baselines are designed for 3D shape completion on known categories, which hardly leverage shape priors across categories.

Table 2 evaluates our approach in comparison with prior arts on real scanned objects from unseen categories in ScanNet [11]. Here, input scans are not only partial but often contain noise and clutter; our multi-resolution learned priors enable more robust shape completion in this challenging scenario. Results in Figure 6 further demonstrate that our approach presents more coherent shape completion than prior methods by using cross-attention with learnable priors, which better preserves the global structures in coarse and cluttered environments.

While PatchComplete has presented a promising step towards learning more generalizable shape priors, various limitations remain. For instance, output shape completion is limited by the dense voxel grid resolution in representing fine-scale geometric details. Additionally, detected object bounding boxes are required for real scan data as input to independent shape completion predictions, while formulation considering other objects in the scene or an end-to-end framework could learn more effectively from global scene contextual information.