Parton Distribution Functions for discovery physics at the LHC††thanks: Presented at XXIX Cracow Epiphany Conference on Physics at the Electron-Ion Collider and Future Facilities
Abstract
At the LHC we are colliding protons, but it is not the protons that are doing the interacting. It is their constituents the quarks, antiquarks and gluons-collectively known as partons. We need to know how what fractional momentum of the proton each of these partons takes at the energy scale of LHC collisions, in order to understand LHC physics. Such parton momentum distributions are known as PDFs (Parton Distribution Functions) and are a field of study in their own right. However, it is now the case that the uncertainties on PDFs are a major contributor to the background to the discovery of physics Beyond the Standard Model (BSM). Firstly in searches at the highest energy scales of a few TeV and secondly in precision measurements of Standard Model (SM) parameters such as the mass of the W-boson, , or the weak mixing angle, , which can provide indirect evidence for BSM physics in their deviations from SM values.
1 Introduction to the determination of PDFs
PDFs were traditionally determined from meausurements of the differential cross sections of Deep Inelastic Scattering. In such processes a lepton is scattered from the proton at high enough energy that it sees the parton constituents of the proton. The process is seen as proceeding by the emission of a virtual boson from the incoming lepton and this boson striking a quark, or antiquark, within the proton. The 4-momentum transfer squared, , between the lepton and the proton is always negative and the scale of the process is given by . To calculate the cross sections for these scattering processes we require that is large enough that we may apply perturbative quantum chromodynamics, QCD. This requires GeV2.
The formalism is presented here briefly, for a full explanation and references see [1]. The form for the differential cross-section for charged lepton-nucleon scattering via neutral current (NC, ie neutral mediating virtual bosons, ) is given by
| (1) |
where and , , are measureable kinematic variables given in terms of the scattered lepton energy and scattering angle and the incoming beam momenta of lepton and proton. The three structure functions, , depend on the nucleon structure as follows, to leading order (LO) in perturbative QCD. (Here by leading order we mean to zeroth order in )
| (2) |
where, for unpolarised lepton scattering,
| (3) |
| (4) |
and
| (5) |
where,
| (6) |
The term in arises from interference and the term in arises purely from exchange, where accounts for the effect of the propagator relative to that of the virtual photon, and is given by
| (7) |
The other factors in the expressions for and are the quark charge, , NC electroweak vector, , and axial-vector,, couplings of quark and the corresponding NC electroweak couplings of the electron, . At low only the term is sizeable and it depends only on the quark-charge-squared, see Eq 2. In the simple Quark Parton Model the structure functions depend ONLY on the kinematic variable , so the structure functions scale, and can be identified as the fraction of the proton’s momentum taken by the struck quark or antiquark. QCD improves on this prediction by taking into account the interactions of the partons, such that a quark can radiate a gluon before, or after, being struck and indeed a gluon may split into a quark-antiquark pair and one of these is the struck parton. This modification leads to the dependence of the structure functions on the scale of the probe, , as well as on . However, this dependence, or scaling deviation, is slow, it is logarithmic and is calculated through the DGLAP evolution equations. We can already see from the equations that measuring the structure functions will give us information on quarks and antiquarks, but measuring their scaling violations will also give us information on the gluon distribution and furthermore, if we calculate beyond leading order we will also see that the longitudinal structure function depends on the gluon distribution. If we also consider charged current (CC) lepton scattering via the and bosons we find that we tell apart u- and d-type flavoured quarks and antiquarks. Scattering with neutrinos rather than charge lepton probes give similar information.
The current state of the art is calculations to NNLO in QCD. At this order the relation of the structure functions to the parton distributions becomes a lot more complicated. However it is completely caluclable so that, given the parton distributions at some low scale , we can evolve them to any higher scale using the NNLO DGLAP equations and then calculate the measurable structure functions using the NNLO relationships between the structure functions and the parton distributions. This allows us to confront these predictions with the measurements. But how do we know the parton distribution functions at . We don’t! We have to parametrise them. The parameters are then fitted in a fit of the predictions to the data. Given that there are typically data points and parameters, the success of such fits is what has given us confidence that QCD IS the theory of the strong interaction.
2 Uncertainties on PDFs and consequences for the LHC
Several groups worldwide perform these sort of fits to determine PDFs. In doing so they make different choices about paramterisations, about model inputs to the calculation and about methodology. PDFs are typically parametrised at the starting scale by
| (8) |
where is a polynomial in or , which could be an ordinary polynomial, a Chebyshev or Bernstein polynomial, or indeed could actually be given by a neural net. Some parameters are fixed by the number and momentum sum-rules, but for others chosing to fix or free them constitute model choices. For example; the heavier quarks are often chosen to be generated by gluon splitting, but they could be parametrised; the strange and antistrange quarks can be set equal, or parametrised separately. Other choices are the value of the starting scale ; the choice of data accepted for the fit and the kinematic cuts applied to them; the choice of heavy quark scheme and the choice of heavy quark masses input. Although the HERA collider DIS data [2] form the backbone of all modern PDF fits, earlier DIS fixed-target data has also been used as well as Drell-Yan data from fixed target scattering and in particlar, and production data from the Tevatron and indeed from the LHC. High jet data from both Tevatron and LHC have also been used and more recently LHC production data, spectra, or + jet data and + heavy flavour data have all been used.
Given that groups make different choices, how are we doing? Fig 1 (top left) show comparisons of the latest NNLO gluon PDFs from the three global PDF fitting groups, NNPDF3.1, CT18A, MSHT20 [3] at a typical low scale 111Other notable PDF analyses are HERAPDF2.0 [2], ABMP16 [4], and ATLASpdf21 [5] but none of these include such a wide range of data. Looking at this plot we have the impression that the level of agreement between the three groups is not bad. However, if we look at the ratio of the gluon pdfs to that of NNPDF3.1 in Fig 1 (top right), we see that the situation is only good (within ) at middling . Disagreement at low and high is quite signficant. Although this is illustrated only for the gluon, the situation is similar for all PDFs.




To see how this affects physics at the LHC we must first consider how these cross sections are calculated in order that we can make sense of a definition of parton-parton luminosities.
where is the parton-parton cross-section at a hard scale and is the parton momentum density of parton in hadron at a factorisation scale (and similarly for ). The initial parton momenta are . The hard scale could be provided by jet or Drell-Yan lepton-pair mass, for example. Strictly the scale involved in the definition of in the cross-section (the renormalisation scale) could be different from the factorisation scale for the partons, but it is usual to set the two to be equal and indeed the choice is often made. We have assumed the factorisation theorem. A parton-parton luminosity is the normalised convolution of just the parton distribution part of the above equation for LHC cross-sections [6]. The gluon-gluon luminosities for NNPDF3.1, MSHT20 and CT18 is shown in the bottom left part of Fig 1 in ratio to NNPDF3.1. The -axis is the c.of.m energy of the system which is produced in the gluon-gluon collision, . We can see that the luminosities are in good agreement at the the Higgs mass, but less so at smaller and larger scales.
We may ask the question has the LHC data decreased the uncertainty on the PDFs. In Fig. 2 (left) we compare the NNPDF31 gluon distribution with and without the LHC data in ratio. We can see that the LHC data has decreased the uncertainty and changed the shape. But we cannot draw a conclusion on the basis of one PDF alone. The NNPDF3.1 analysis makes specific choices of which jet production data to use, which distributions to use etc., and specific choices of how to treat the correlated systematic uncertainties for these data. Other PDF fitting groups make different choices. We need to look at the progress made by all three groups. Fig. 1 (bottom right) shows a comparison of the gluon-gluon luminosity for all three groups for the previous generation of PDFs, NNPDF3.0, MMHT14, CT14 [7], for which very little LHC data were used. If we compare this with the recent gluon-gluon luminosity plot in Fig. 1 (bottom left) we see that, whereas each group has reduced its uncertainties, their central values were in better agreement at the Higgs mass for the previous versions! Thus analysis of new data can introduce discrepancies.
An effort to combine the three PDFs, called PDF4LHC15, was performed for the previous versions, and a new combination, called PDF4LHC21 [9], as been performed for the most recent versions. The combination procedure uses MC replicas from all three PDFs and then compresses them with minimal loss of information. Altough the overall uncertainties of PDF4LHC21 are smaller than those of PDF4LHC15. The improvement is not as dramatic as one might have hoped, precisely because of deviation in central values. Since PDF4LHC21 the NNPDF group have updated to NNPDF4.0 [8], which has considerably reduced uncertainties compared to NNPDF3.1. However, this is mostly due to a new methodology rather than due to new data. Unfortunately this puts the NNPDF4.0 central values further from those of CT and MSHT in some regions, such that there is no big improvement in the combination of all three.
To illustrate the impact for direct searches for BSM physics from PDF uncertainties Fig. 2 (right) illustrates two types of searches done in dilepton production using 13 TeV ATLAS data, one for a 3 TeV and one for contact interactions at 20 TeV. The panel below the main plot shows the ratio of data to SM background and the grey uncertainty and on this shows the projected systematic uncertainty band of the measurement. A major contributor to this uncertainty is the PDF uncertainty of the background calculation. Whereas a resonant at higher scale could likely be distinguished from the background this is far less clear for the gradual change in shape induced by the contact interaction. Indeed this could potentially be accommodated in small changes to the input PDF parameters such that it would remain hidden.


Given that no searches for BSM physics at high scale have given a significant signal, the effects of BSM are also investigated indirectly by making precision measurements of SM parameters such as the mass of the W-boson, , or the weak mixing angle, , which can provide indirect evidence for BSM physics in their deviations from SM values. For example, is predicted in terms of other SM parameters but there is a contribution from higher order loop diagrams which would include any BSM effects. This would raise the value of noticeably if the scale of the BSM effects is not very far above presently excluded limits. The recent meausurement from CDF [11] is GeV, well above the SM prediction of GeV. However, many other measurements are not discrepant and the next most accurate is the ATLAS 7 TeV measurement GeV. Obviously, one would like to improve the accuracy on this LHC measurement, but a major part of the 19 MeV uncertainty is MeV coming from PDF uncertainty. The LHC PDF uncertainty is larger than that of CDF because the LHC 7 TeV collisions are mostly sea quark-antiquark collisions at , whereas the CDF collisions are mostly valence-valence collisions at . To substantially reduce the LHC PDF uncertainty one requires PDF uncertainties of in the relevant range.
The vital question for both direct and indirect searches is whether the PDF uncertainty can be reduced in future. A study of potential improvements from the High-Luminosity Phase of the LHC was made [12] asssuming a luminosity of of data. The processes considered were those which have not yet reached the limit in which the data uncertainties are systematic dominated e.g. higher mass Drell-Yan, , direct photon, at very high , higher scale jet production and higher scale production. Two different sets of assumptions were made about the systematic uncertainties, pessimistic and optimistic. For the pessimistic case there is no improvement in systematic uncertainties, for the optimistic case one assumes that a better knowledge of the data gained from higher statistics could result in a reduction of the size of systematic uncertainties by a factor of 0.4, and in the role of correlations between systematics uncerrainties by a factor of 0.25. Improvements of in the PDF uncertainties of about a factor of two are predicted for gluon, and quarks and antiquarks. Whereas this looks very promising -reducing the PDF4LHC PDF uncertainty from to over the relevant range for measurement, with little difference in pessimistic and optimistic assumptions- we should remember that a) we aim for accuracy on PDFs, and b) such a pseudo-data analysis is necessarily over-optimistic in that it assumes that the future data are fully consistent with each other and that systematic uncertainties have well-behaved Gaussian behaviour. In reality this is never the case - this is why tolerance, , values in the CT and MSHT analyses are set at .
A further issue highlighted by a recent ATLAS PDF analysis [5] is that there can be correlations of systematic uncertainties between data sets as well as within them. The ATLAS analysis used many different types of ATLAS data. Amongst these were inclusive jets, and boson + jets, in lepton + jet mode. The systematic uncertainties on the jet measurements are correlated between these data sets and an egregious example of this is the relatively large uncertainties on the jet energy scale. The ATLAS analysis showed that the difference in the resulting PDFs between accounting for these correlations and not accounting for them can exceed at the relevant energy scale and region for production, see Fig 3 (top part).
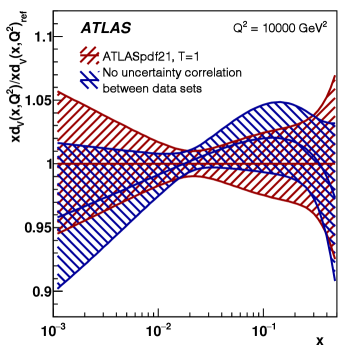



Thus PDFs cannot become accurate without accounting for such correlations. The information needed to do this was not avalable to the global PDF fitting groups prior to this ATLAS analysis, and it needs to become available for many more data sets included in their fits.
This ATLAS analysis also made a study in which data at very high scale GeV ( GeV2) are cut. Most of the data cut are the high- jet production data. If new physics at high scale makes a subtle change to the shape of jet high- spectra, it will also make a change to the PDF parameters when fitted. Thus there may be a difference in PDFs fitting or not fitting high scale data. Fig 3 (bottom part) shows such a comparison for the gluon and PDFs, which are most affected by this cut. There is no significant difference even at very high-.
A further limitation on PDF accuracy is scale uncertainty. The ATLASPDF21 analysis included scale uncertainties on the NNLO predictions for inclusive production, which is the only process included for which these uncertainties are comparable to the experimental unceratinties, for the other processes scale uncertainties are significantly smaller. Comparing the PDFs with and without accounting for these scale uncertainties showed that discrepancies in central PDF values can also come from this source. But the situation may be worse than this. MSHT have recently performed an approximate N3LO analysis [13]. The MSHT20 N3LO and NNLO gluon differences are very strong at low- and low scale and this difference persists to LHC scales such that there is still a discrepancy at GeV2 and . This translates into a difference in gluon-gluon luminosity at the Higgs mass! This difference is a consequence of the much stronger differences at low- and low and such differences will matter more as we go to higher energies and/or to more forward physics at the LHC. However, we will also need an improved theoretical understanding of low- physics, such as resummation and non-linear effects due to parton recombination, to fully exploit this region, see for example [14] and references therein.
So how could we improve the PDFs in future? A dedicated lepton-hadron collider would provide the most accurate PDFs. The reason that a lepton-hadron collider can improve PDF uncertainty more than a hadron-hadron machine is that the inclusive DIS process, from which most of the information comes, can be analysed by a single team, with a consistent treatment of systematic uncertainties across the whole kinematic plane. This situation does not appertain at the LHC where different teams analyse the many different processes which are input to the PDF fits. Whereas there are common conventions for measurement, complete consistency is rarely obtained, particularly since the optimal treatment of data evolves with time and analyses proceed at different paces.
Proposals for an LHeC or even an FCC-eh machine at CERN have been made and these would improve the PDFs very substantially across a kinematic region ranging down to and up to for the LHeC (FCCeh) respectively [15]. Such a collider will also be able to shed light on low-£x£ physics. The EIC collider at Brookhaven is an approved project which will extend the kinematic region of accurate measurement to higher at low scales [16] and this would benefit studies at the LHC scales, firstly because DGLAP evolution percolates from high to low as the scale increases and secondly because the momentum sum-rule ties all regions together.
3 Summary
The precision of present PDFs needs improvement in order to aid discovery physics, both at high scale and in the precision measurement of SM parameters. Substantial improvement should come from the HL-LHC run, but the desired accuracy of can only be achieved at a future lepton-hadron collider. The EIC with improve accuracy at high , but for low- physics an LHeC or FCC-eh is necessary.
References
- [1] R C E Devenish and A M Cooper-Sarkar, ’Deep Inelastic Scattering’, Oxford University Press 2004
- [2] H.Abramowicz et al. [ZEUS and H1 Collaboration], Eur Phys J C75(2015)580, arXiv:1506.06042
- [3] NNPDF arXiv:1706.00428; MSHT arXiv:2012.04684; CTEQ arXiv:1912.10053
- [4] ABMP arXiv:1609.03327
- [5] ATLAS Collaboration, Eur Phys J C82(2022)438, arXiv:2112.11266
- [6] https://web.pa.msu.edu ¿ les houchesluminosity
- [7] NNPDF arXiv:1410.8849; MMHT arXiV:1412.3989; CTEQ arXiv:1506.07443
- [8] NNPDF arXiV: 2109.02653
- [9] PDF4LHC group, arXiv:2203.05506; arXiv:1510.03856
- [10] ATLAS Collaboration, Phys Lett B 761(2016)372, arXiV:1607.03669
- [11] CDF Collaboration, Science 376(2022)6589
- [12] R A Khalek et al, arXiv:1810.03639
- [13] MSHT arXiV:2207.04739
- [14] xFitter developers, H Abdolmaleki et al, Eur.Phys.C78(2018),621, arXIV:1804.00064; M Bonvini, arXiV:1812.01958; N Armesto et al, Phys Rev D105(2022)11
- [15] Max Klein, https://indico.cern.ch ¿ caseLHeCmaxklein
- [16] T J Hobbs, PDFs at the Electron Ion Collder, Snowmass-CPM Oct20 HOBBS