Parton collisional effect on the conversion of geometry eccentricities into momentum anisotropies in relativistic heavy-ion collisions

We trace the collisional history of the initially produced partons during the source evolution in Pb+Pb collisions. The total number of parton-parton scatterings suffered by each parton before its freezing out is difined as $N_{coll}$.

Fig. 1 shows the $N_{coll}$ distributions of the freezeout partons for different centrality classes. As expected, partons in central Pb+Pb collisions on average suffer more partonic collisions than non-central collisions before freezing out as the energy density is higher in more central collisions. The probability distribution shows a non-monotonic $N_{coll}$ dependence in central collisions which is different from that of the peripheral collisions. A peak around $N_{coll}$ $\sim$ 6 is observed for the 0-10$\%$ most central collisions. The average number of $N_{coll}$ in 0-10$\%$ centrality is found to be roughly three times as large as that in 40-60$\%$ centrality. It indicates that the fraction of partons which never collided with other partons decreases from peripheral to central collision class.

We study in particular the spatial evolution of the initial partons in ultra-relativistic heavy-ion collisions. Figs. 2 and  3 present the two-dimensional distributions of the initial partons [plots (a)-(c)] and freezeout partons [plots (d)-(f)] in central and peripheral Pb+Pb collisions, where the initial parton distributions in the collision zone are compared with the final parton distributions for different $N_{coll}$ intervals. We find that partons suffering small $N_{coll}$ tend to distribute in the outer region close to the source surface whereas partons with large $N_{coll}$ are seen concentrating more in the central area. This is consistent with the expectation that due to the energy density distribution of the bulk matter, outgoing partons from the inner source suffers more collisions when passing through the bulk matter than partons close to the source surface.

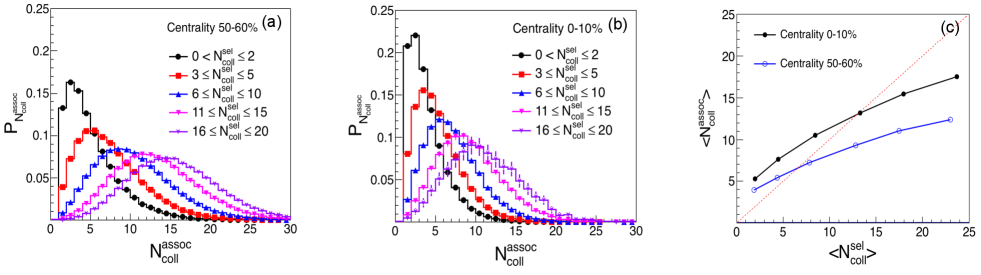
We further investigate the partonic collision history of some selected partons before their freezing out. For a selected parton, we define those partons which collided with the selected parton during its evolution as “associated partons” of the selected parton. The numbers of parton collisions for the selected parton and associated parton are defined as $N^{sel}_{coll}$ and $N^{assoc}_{coll}$, respectively. Fig. 4 (a) and (b) show the $N^{assoc}_{coll}$ probability distributions for five $N^{sel}_{coll}$ intervals of the selected partons for peripheral and central Pb+Pb collisions, respectively. One can find that for a selected freezeout parton which suffered $N^{sel}_{coll}$ collisions, the number of collisions that its associated partons suffer ($N^{assoc}_{coll}$) can be distributed over a wide range. For example, for a selected parton with a small $N^{sel}_{coll}$, a long-tailed $N^{assoc}_{coll}$ distribution can be observed suggesting that many large-$N^{assoc}_{coll}$ partons play an important role in the collisional history of small-$N^{sel}_{coll}$ parton. We quantitatively extract the mean value of $N^{assoc}_{coll}$ for each $N^{sel}_{coll}$ intervals and plot the relations as shown in Fig. 4(c). One can find that $\langle N^{assoc}_{coll}\rangle$ is larger than $\langle N^{sel}_{coll}\rangle$ at small $\langle N^{sel}_{coll}\rangle$, which indicates the partons which suffer a small number of collisions prefer to collide with the partons which suffer a larger number of collisions. But with the increasing of $\langle N^{sel}_{coll}\rangle$, $\langle N^{assoc}_{coll}\rangle$ tends to be close to and then less than $\langle N^{sel}_{coll}\rangle$. It indicates that the partons which suffer a large number of collisions prefer to collide with the partons which suffer a small number of collisions. In this sense, all partons are complemented with each other during the whole evolution of the partonic phase in Pb+Pb collisions.

Azimuthal anisotropy coefficients $v_{n}$ (n = 2,3..) are typically used to characterize the different orders of harmonic flow of the collision system. In simulation studies, one can calculate $v_{n}$ with respect to the participant plane of the collision event Voloshin et al. (2008b). The $n$th-order participant plane angle $\psi_{n}$ for a single event is in the form:

where $r$ and $\varphi_{PP}$ are the position and azimuthal angle of each parton in the transverse plane in the initial stage of AMPT and the bracket $\langle...\rangle$ denotes per-event average. Then $v_{n}$ with respect to the participant plane $\psi_{n}\left\{PP\right\}$ is defined as

where $\phi$ in this study is the azimuthal angle of parton in the momentum space, and the average $\langle\cdots\rangle$ denotes event average. The above method for $v_{n}$ calculation is referred to as participant plane method. Participant plane method takes into account initial geometric fluctuation effect, and has been widely used in many studies Derradi de Souza et al. (2012).

Besides the participant plane method, the multi-particle cumulant method was also proposed for studying flow via particle correlations. It has been successfully used in both model and experimental studies to quantified the harmonic flow Bilandzic et al. (2011); Zhou et al. (2016); Abelev et al. (2014). Usually, the two- and four-particle cumulants can be written as

The integral flow can be derived directly from two- and four-particle cumulants through the following equations

and estimation of differential flow is according to

where the $d_{n}\left\{2\right\}$ and $d_{n}\left\{4\right\}$ are the two- and four-particle differential cumulants as defined in Ref. Bilandzic et al. (2011).

By extracting the parton information in AMPT simulation, we study the collisional effects on the development of partonic flow and eccentricity in the early stage of the heavy-ion collisions.

Fig. 5 shows the simulation results of the anisotropic flow of freezeout partons as a function of $N_{coll}$ in Pb+Pb collisions at $\sqrt{s_{NN}}$ = 5.02 TeV. The second and third order flow harmonics of the freezeout partons are defined as $v^{f}_{2}$ and $v^{f}_{3}$ respectively. Similar to the probablity distribution of $N_{coll}$, $v^{f}_{2}$ shows non-monotonic $N_{coll}$ dependence for central collisions. A maximum value of $v^{f}_{2}$ around $N_{coll}$ $\sim$ 5 is observed for 0-10$\%$ centrality. For the periphral collisions, $v^{f}_{2}$ shows a similar decreasing trend and is comparably much larger in magnitude than that of the central collisions in magnitude. It generally shows that partons with larger $N_{coll}$ tends to have smaller $v^{f}_{2}$ indicating that with increasing $N_{coll}$ the momentum azimuthal distribution of freezeout partons tend to be isotropic. This could be because large $N_{coll}$ partons come mostly from the center where the effective gradients are small. In other words, large $N_{coll}$ partons are less sensitive to the geometry than small $N_{coll}$ partons which are closer to the surface. The same conclusion also holds for $v^{f}_{3}$ but which originates basically from the initial-state fluctuations.

Besides the participant plane method, we further studied $v^{f}_{n}$ based on multi-particle cumulant methods. Fig. 6 shows the two-particle ($v_{2}\left\{2\right\}$) and four-particle ($v_{2}\left\{4\right\}$) cumulant flow results. Comparisons are made with the results from the participant plane method. It is generally found that $v^{f}_{2}$ from cumulant methods are similar in trend with the $v^{f}_{2}$ results from participant plane method. An ordering of $v_{2}\left\{2\right\}>v_{2}\left\{part\right\}>v_{2}\left\{4\right\}$ is observed, because $v_{2}\left\{2\right\}$ involves flow fluctuations but $v_{2}\left\{4\right\}$ suppresses non-flow contributions.

Towards a more quantitative study, we compare the flow anisotropies of the initial partons ($v^{i}_{n}$) and final freezeout partons ($v^{f}_{n}$) for n = 2,3. Note that the averaged $v_{n}$ for all the initial partons is zero due to the isotropy of initial azimuthal distribution in the AMPT model. As can be seen in Fig. 7, showing the change of $v_{n}$ from the initial to the final stage of the partonic evolution, the parton-parton collisions generally make $v_{2}$ and $v_{3}$ increase for different $N_{coll}$ regions. For the partons with a larger number of $N_{coll}$, the change of $v_{2}$ and $v_{3}$ is smaller, since they are more probably located at the center of the source where more collisions may randomize their motion.

In order to quantitatively study the collisional effect on the flow harmonics, we examine the change of parton $v_{n}$ after $N_{coll}$ collisions, i.e. $\Delta$$v_{n}$ = $v^{f}_{n}$ - $v^{i}_{n}$. Fig. 8 shows the $\Delta$$v_{n}$ (n = 2,3) in Pb+Pb collisions as a function of $N_{coll}$. Results are compared for different flow methods. Significant centrality dependence can be seen for $\Delta$$v_{n}$. It is interesting to see that in central collisions $\Delta$$v_{2}$ shows non-monotonic $N_{coll}$ dependence whereas $\Delta$$v_{3}$ presents monotonic $N_{coll}$ dependence. As shown in Fig. 7, the initial intrinsic parton $v_{n}$ is quite tiny, the gain in $v_{n}$ is primarily due to the partonic scatterings throughout the source evolution. In general, $\Delta$$v_{n}$ decreases with increasing of $N_{coll}$ indicating that small $N_{coll}$ partons contribute to most of the flow anisotropies.

Initial geometry anisotropy of the QGP matter is a main source responsible for generating the final flow anisotropy in relativistic heavy-ion collisions. Thus, it is important to study the partonic effect on the initial spatial anisotropy. In nuclear-nuclear collisions, the spatial anisotropy of the collision zone in the transverse plane (perpendicular to the beam direction) can be characterized by the eccentricity $\varepsilon_{n}$. It has been argued that the magnitude and trend of the eccentricity imply testable predictions for final-state hadronic flow Miller and Snellings (2003); Lacey et al. (2011); Drescher and Nara (2007); Broniowski et al. (2007).

The definition of the $n$th-order harmonic eccentricity in the coordinate space of the participant nucleons or partons for single collision event is in the form:

where $r$ and $\varphi$ are position and azimuthal angle of each nucleon or parton in the transverse plane. $\varepsilon_{n}\left\{part\right\}$ characterizes the eccentricity through the distribution of participant nucleons or partons which naturally contains event-by-event fluctuation. $\varepsilon_{n}\left\{part\right\}$ defined in this way is usually named as “participant eccentricity”.

We study the parton collisional effects on the partonic eccentricity in Pb+Pb collisions. Fig. 9 shows the AMPT results of the second and third order eccentricities calculated with Eq. (7). Eccentricities of the initial and final freezeout partons are denoted as $\varepsilon^{i}_{n}\left\{part\right\}$ and $\varepsilon^{f}_{n}\left\{part\right\}$ respectively. Similarly to the flow harmonics, partonic scattering is found to play an important role in the evolution of eccentricities. $\varepsilon_{n}$ of the freezeout partons is larger at larger $N_{coll}$. One can see in the figures that parton collisions generally reduce $\varepsilon_{n}$ which is consistent with our expectation - during the expansion of the QGP source, the transition of the initial pressure gradient from coordinate space to the momentum space will significantly diminish the spatial anisotropy.

In addition, we studied $\Delta$$\varepsilon_{n}$=$\varepsilon^{f}_{n}\left\{part\right\}$ - $\varepsilon^{i}_{n}\left\{part\right\}$ as a function of the number of parton collisions for different centrality classes. The results for second and third order harmonics are shown in Fig. 10 (a) and (b), respectively. We find that $\Delta$$\varepsilon_{2}$ and $\Delta$$\varepsilon_{3}$ exhibit clear decreasing $N_{coll}$ dependences. Quantitative difference are seen between the results for $\Delta$$\varepsilon_{2}$ and $\Delta$$\varepsilon_{3}$ , because $\varepsilon_{3}$ is purely driven by initial fluctuations but $\varepsilon_{2}$ is driven by initial geometry.

Impressive progress has been made in studying the final-state flow response to the initial eccentricity in relativistic heavy-ion collisions Petersen et al. (2012); Niemi et al. (2013). The success of hydrodynamical models tells us that elliptic flow $v_{2}$ and triangular flow $v_{3}$ are mainly driven by the linear response to the initial ellipticity and triangularity of the source geometry. As space-momentum correlation is also expected to be built during the partonic evolution stage, quantitative study of the partonic flow response in a event-by-event transport model is also important for understanding the development of final flow .

Based on the AMPT model simulations, we studied $N_{coll}$ effects on the flow response by looking into the ratio $\Delta$$v_{n}$/$\Delta$$\varepsilon_{n}$. Since $\Delta$$\varepsilon_{n}$ (n = 2,3) are negative and $\Delta$$v_{n}$ (n = 2,3) are positive over all the $N_{coll}$ classes, one could take the absolute value of $\Delta$$v_{n}$/$\Delta$$\varepsilon_{n}$ as an estimation of the flow conversion efficiency. Fig. 11 and  12 show the results for the flow conversion efficiency with respect to $\Delta$$\varepsilon_{n}$ and $\varepsilon^{i}_{n}$ as a function of $N_{coll}$. Considering absolute value, results in both figures show similar trend. The ratio of $\Delta$$v_{n}$/$\Delta$$\varepsilon_{n}$ presents obvious $N_{coll}$ dependences for different centrality classes. We observe that for both elliptic and triangular flow the conversion efficiency is strongest in the collision class of 0-10%. It indicates that more collisions in more central collisions help transfer $\varepsilon_{n}$ into $v_{n}$, which is a normal concept about the flow conversion efficiency which is an integral effect of all $N_{coll}$ partons. For the differential $N_{coll}$ dependence, $\Delta$$v_{n}$/$\Delta$$\varepsilon_{n}$ (n = 2,3) presents a smooth increasing trend from small to large $N_{coll}$, which indicates that the larger $N_{coll}$ is, the lower the flow conversion efficiency is. The feature seems against common sense, but it can be understood through the above results that parton collisional contribution to flow change $\Delta$$v_{n}$ is more significant at smaller $N_{coll}$ whereas that to eccentricity change $\Delta$$\varepsilon_{n}$ is more significant at larger $N_{coll}$, i.e. changes of $\Delta$$v_{n}$ and $\Delta$$\varepsilon_{n}$ are not in sync with respect to $N_{coll}$. But since small-$N_{coll}$ and large-$N_{coll}$ partons are complemented with each other during the evolution, it is actually hard to fairly say which should be given the first credit to the generation of the final flow. In the limit of long evolution time, final eccentricity $\varepsilon^{f}_{n}$ is supposed to approach zero, and we observe the similar results for $\Delta$$v_{n}$/$\varepsilon^{i}_{n}$ except with the opposite sign, as shown in Fig.  12.