Particle-in-cell simulations of the tearing instability for relativistic pair plasmas

Here we present results from simulations aimed at measuring the tearing growth rate and verifying equation (11). We note that, unlike classical references Laval et al. (1966) and Coppi et al. (1966), we are considering the case of a pair plasma composed of positrons and electrons with equal mass. We expect pair plasmas with non-relativistic temperatures to occur as a result of radiative cooling. Furthermore, our general conclusions should be relevant for electron-proton plasmas as well, as the predictions of the growth rate from Zelenyi & Krasnosel’skikh (1979) with electron-proton mass ratios only differ by a factor of order unity (as long as the temperature ratio also remains of order unity). We will examine two regimes holding $a/\rho_{L,C}=2.5$ and $a/\rho_{L,C}=5$ constant, and varying the temperature, in the regime where $T/m_{e}c^{2}\ll 1$. This means that we are also varying $u_{d}/c$, in contrast with the next section where we will hold $a/\rho_{L,R}=1/(u_{d}/c)$ constant. Please note the different usage of classical and relativistic Larmor radii, $\rho_{L,C}$ and $\rho_{L,R}$ in the paragraph above.

For the cases with $a/\rho_{L,C}=2.5$, we use 1024 particles-per-cell, $L_{y}/a=20.5$ and $L_{x}=L_{y}/2$ with a resolution of 18.6 grid cells per $a$. We take a time step of $dt=0.035a/c<dx/c/\sqrt{2}=0.0376a/c$ to satisfy the Courant condition. For the case with $a/\rho_{L,C}=5$, to avoid issues with numerical heating, we use 4096 particles-per-cell. We use the same system size, the same resolution of grid cells per $a$, and the same time step as for $a/\rho_{L,C}=2.5$. The parameters of each of these runs can be found in Table 1.

We track the evolution of the perpendicular magnetic field energy $B_{y}^{2}/4\pi$ as a function of time, along with the kinetic energy of the particles in the Harris sheet, the total magnetic field energy, and the total electric field energy. In Figure 1, we present an example case where $T/m_{e}c^{2}=0.00125$ and $a/\rho_{L,C}=2.5$. The magnetic energy $B_{y}^{2}/4\pi$ is dominated by noise up until $t\gamma_{th}\sim 2.5$ ($tc/a\approx 900$), where we have normalized to the theoretical linear growth rate $\gamma_{th}$ given by equation (11). This time, therefore, corresponds to a couple of e-folding times. We then measure a best fit of the growth rate between $t\gamma_{th}=3.08-4.4$, obtaining a growth rate $\gamma_{m}a/c=0.00277$, which matches very well with equation (11) ($\gamma_{th}a/c=0.00275$). In the time interval between $t\gamma_{th}=7.7-7.8$, the signal begins to grow faster ($\gamma a/c=0.0081$), as measured in Figure 1 (d). This faster growth rate is close to the linear prediction for $a/\rho_{L,C}=1$ ($\gamma a/c=0.011$). While the growth rate fits an exponential, it corresponds to multiple interacting modes, and we call this period the fast-growing nonlinear stage. Soon after the signal saturates, and a significant portion of the free energy of the magnetic field $B_{x}^{2}/4\pi$ is transferred to both the $B_{y}^{2}/4\pi$ signal and kinetic energy of the plasma, as seen in Figure 1 (a,c), which shows the transfer of magnetic energy in purple to kinetic energy in red, and in Figure 1 (b,d) which shows that $B_{y}$ in green constitutes a significant portion of the total magnetic energy in purple. The noise in the kinetic energy is larger than that of the $B_{y}^{2}/4\pi$ signal, so it is not useful for calculating a reliable slope. However, in Figure 1 (b) at late times $t\gamma_{th}\sim 6.6$, the slope of the kinetic energy becomes comparable to that of $B_{y}^{2}/4\pi$. The electric field energy $E_{z}^{2}/4\pi$ does not increase appreciably until the fully nonlinear stage.

We will now provide a potential explanation for the faster nonlinear growth stage that works in both relativistic and nonrelativistic regimes. In the nonlinear stage of the instability, the local $B_{x}$ decreases around the x-line effectively increasing $\rho_{L}$. This increase coincides with an increased ratio $\rho_{L}/a$ as long as $a$ does not grow too much, and simulations show that $a$, on the contrary, shrinks during this nonlinear stage. We thus expect an increase in the instability growth rate from equation (11) or in relativistic cases equation (10), until $\rho_{L}/a\sim 1$, where the assumptions behind the derivation of equations (9–11) break down. For increasingly wide $\rho_{L}/a$ the growth rate will stop increasing with $\rho_{L}/a$ and begin to decrease; thus its maximal value should be at $\rho_{L}/a\sim 1$. We test this prediction in the classical and relativistic temperature regimes. We will show in the relativistic part of Section 4 that when varying $T/m_{e}c^{2}$ (classical temperatures), keeping $\rho_{L,R}/a=u_{d}/c$ constant, the peak growth rate indeed occurs when $\rho_{L,C}/a\sim 1$. We also provide evidence of a maximum when varying $u_{d}/c$ and keeping $T/m_{e}c^{2}$ constant. While in the classical regime, a wider $\rho_{L,C}/a$ can occur if either $T/m_{e}c^{2}$ or $u_{d}/c$ change, in the relativistic regime, a wider $\rho_{L,R}/a$ implies a faster $u_{d}/c$. In particular, we expect the maximal value for relativistic cases where $\rho_{L,R}/a=u_{d}/c\sim 1$, because this is the maximal growth rate according to the predictions of Hoshino (2020). One should note that this is in a highly nonlinear stage, and thus linear growth rates can only be used as a rough estimate of the dynamics. On the other hand, we will show that this estimation gives a rather accurate prediction of the peak nonlinear growth rate. As we showed in Section 2, force balance implies that $\rho_{L}\approx d_{e}\sim 1/\sqrt{n}$ (in both classical and relativistic regimes). In the regions where $B_{x}$ decreases, the density $n$ also decreases, and this force balance appears to hold. Following this logic, if there were a background population, the growth of $d_{e}$ would be limited to the background value $d_{e}(n_{b})$, and the fastest nonlinear growth might also be limited to the prediction for $\rho_{L}/a=d_{e}(n_{b})/a$ instead of $\rho_{L}/a=1$. We check this prediction at the end of this section.

In Figure 2 we show a map of the $B_{y}$ component of the magnetic field from the same example case from Figure 1, for two representative times. The first time at $t\gamma_{th}=3.363$ corresponds to the linear stage, where the signal has just grown beyond the noise. It is clear in the upper current sheet that the dominant mode is at $ka=2\pi ma/(2L_{x})\approx 0.6$ ($m=2$). This matches very well with the predicted value from Zelenyi’s model $ka=1/\sqrt{3}\approx 0.58$. The later time $t\omega_{pe}=7.205$ corresponds to a late stage of the linear growth rate, where the dominant mode shifts to a lower $k$ ($m=1$). Soon after, the growth moves into the fast-growing nonlinear stage. The start of the nonlinear stage matches with the prediction from Hoshino (2021) based on the theory from Galeev et al. (1978), that once $B_{y}/B_{0}>k\rho_{L}$ an explosive nonlinear stage occurs. In our case, assuming $ka=1/\sqrt{3}$, $k\rho_{L,C}\equiv 0.23$, which is on the same order as the $B_{y}/B_{0}$ seen in 1(b).

To better understand how to characterize tearing instability (before it reaches a strongly nonlinear stage), we present in Figure 3 a spatial map of several quantities that characterize the tearing mode, with selected contours of magnetic flux overlaid to highlight the magnetic islands. We have chosen $B_{y}$ to measure the growth rates because the signal is visible at times as early as $t\gamma_{th}=3$, however, after around $t\gamma_{th}=5$, one can see in Figure 1 (b) that a majority of the energy is being transferred to the kinetic energy in the Harris sheet. This energy goes to both heating and bulk flows. We show a map of $B_{y}$ in Figure 3 (a) similar to what we saw in Figure 2, but at $t\gamma_{th}=5.284$ and zoomed in on the current sheet. The energy is mainly converted into thermal energy. The temperature is shown in Figure 3 (b), where there is an overall heating with cooling at the x-points (eg. at $x/a\approx-5,y/a\approx 5$). The energy going into the bulk flows includes a flow in the $x$ direction away from the x-points and toward the o-points (eg. at $x/a\approx-10,y/a\approx 0$), which can be seen in Figure 3 (c). As the plasma moves with this flow, the density decreases at the x-points, and increases at the o-points as seen in Figure 3 (d). This flow also drags the out-of-plane current with it as seen in Figure 3 (e). The total kinetic energy in the current therefore also increases.

Although we do not plot this here, the energy associated with the quantities in Figure 3 (when applicable) all grow at the same growth rate during the linear stage, taking energy from the $B_{x}$ component of the magnetic field outside of the current sheets. We now report how much energy was transferred to each quantity by $t\gamma_{th}=5.284$, the time associated with Figure 3. The source of free energy is in the $B_{x}$ component; the total energy in $B_{x}$ drops by a factor of $3.3\times 10^{-4}$ its value at $t\gamma_{th}=0.48$. The energy predominantly goes to the thermal energy i.e. about $90\%$ plus an additional increase of $16\%$ due to numerical heating, while $13\%$ of the energy goes into $B_{y}$. The energy going into the bulk flows is about an order of magnitude less, about equally distributed between $1.3\%$ in the out-of-plane direction associated with the current, and $1.2\%$ in the in-plane directions associated with reconnection outflows along the $x$ direction. The energy going into $E_{z}$ is even less and the signal is not visible. This energy distribution between the different quantities is consistent with Figure 1 which shows that the loss of energy in the total magnetic field in purple (predominantly associated with $B_{x}$) matches the gain in kinetic energy (predominantly thermal energy) (Zenitani, 2017; Pucci et al., 2018a). The energy in $B_{y}$ is about an order of magnitude less at $t\gamma_{th}=5.284$. At later times, all of these quantities convert the linear wave number mode to lower wave number modes and eventually evolve into a fast-growing nonlinear state of multiple interacting modes.

Unlike the $a/\rho_{L,C}=2.5$ case, when $a/\rho_{L,C}=5$ the instability saturates before significant energy is released, i.e., before the fast-growing nonlinear stage of the instability is reached. For example, we show in Figure 4 (a-b) the energy evolution for the case with $T/m_{e}c^{2}=0.005$. We can measure a growth rate $\gamma_{m}a/c=0.00150$ which matches theory $\gamma_{th}a/c=0.00194$, in the linear stage (between $t\gamma_{th}=1.55-3.88$). However, after $t\gamma_{th}\sim 4.23$ the growth saturates. The evolution continues without significant growth up to $t\gamma_{th}\sim 6.87$. We would like to point out that this saturation effect is dependent on the noise. We performed a similar set of simulations, not presented here, with much fewer particles-per-cell that were noisier and less accurate but obtained the same growth rates. In this noisier case, the signal was able to grow to the fast-growing nonlinear stage without saturating.

We found however that by increasing the length of the box to $L_{x}=L_{y}$ (twice as long), we get a similar linear growth rate $\gamma_{m}a/c=0.00194$ (matching theory almost perfectly). The wave number also remains consistent with theory with $ka=2\pi ma/(2L_{x})\approx 0.6$ (now with a higher $m=4$). However, in this case, the instability does reach a fast-growing nonlinear stage. As we saw previously, the growth rate increases until it reaches $\gamma a/c=0.0296$ close to the prediction corresponding to $a/\rho_{L,C}=1$, $\gamma a/c=0.0217$. In Figure 4, we highlight the difference between the case with the smaller box ($L_{x}=L_{y}/2$) in Figure 4(a-b) and an identical case except ($L_{x}=L_{y}$) in Figure 4(c-d). In the case with the larger box, significant energy is released as shown in Figure 4(c), and the nonlinear growth rate is measurable in Figure 4(d).

We illustrate in Figure 5 the time right before the nonlinear phase (at $t\gamma_{th}=5.241$), where either the growth of $B_{y}$ saturates (when $L_{x}=L_{y}/2$) (a) or it blows up (when $L_{x}=L_{y}$) (b). In both cases, the tearing has moved from the linear $ka\approx 1/\sqrt{3}$ to the lowest $k$ that fits in the box (only 1 magnetic island). Furthermore, we note that at this stage, the current sheets begin to interact. Once again we see that the nonlinear stage matches the prediction from Hoshino (2021). Assuming $ka=1/\sqrt{3}$, we calculate the normalized wavelength $k\rho_{L,C}\equiv 0.12$. While the $B_{y}/B_{0}$ in Figure 5(a) never exceeds this value and thus no explosive reconnection phase is observed, it exceeds this value in Figure 5(b) and we do see an explosive phase.

From the start of the simulation, the tension from the bent magnetic field lines pulls the plasma toward the center of the magnetic islands, driving the instability. Meanwhile, the upstream magnetic field is also bent providing a stabilizing force on the inflow. During the linear phase of the tearing instability, the driving force is stronger than the stabilizing force. However, in the nonlinear regime, the stabilizing force can dominate. In the simulation with the large box, the aspect ratio of the island which is proportional to $L_{x}/a$ is also larger, and thus the driving force which is proportional to $1/a$ remains large compared to the stabilizing force which is proportional to $1/L_{x}$. This argument for saturation may also explain the transfer we see from the Zelenyi prediction $ka=1/\sqrt{3}$ to the smallest mode that fits in the box $ka=2\pi a/L_{x}$.

We find similar results for all of our simulations. For all temperatures with $a/\rho_{L,C}=2.5$, we measure the growth rates in the range $t\omega_{pe}=3.30-4.39\omega_{pe}/\gamma_{th}$. We find that the measured growth rate $\gamma_{m}$ matches the theory $\gamma_{th}$ shown in Table 1. We also measure the growth rates for the non-linear stage $\gamma_{m,nl}$, in the ranges $t_{st,nl}-t_{fi,nl}$ also found in Table 1. We find that the nonlinear growth rate matches the linear prediction for $a/\rho_{L,C}=1$. For the cases with $a/\rho_{L,C}=5$ we measure the growth rate that is consistent with the theory (both in Table 1) in the range $t\omega_{pe}=1.55-3.88\omega_{pe}/\gamma_{th}$, which is earlier than the interval used in the set of simulations with $a/\rho_{L,C}=2.55$ because we have less noise due to the increased particles-per-cell. The peak growth rate for the nonlinear stage is again measured for the simulations with $L_{x}=L_{y}$ and is reported along with the time range of the measurement in Table 1. The growth rates in the linear stage of these simulations also match the theory well and are listed in Table 1.

These results are summarized in Figure 6. We indicate the growth rates for the linear stage with solid circles $a/\rho_{L,C}=2.5$ (red) and $a/\rho_{L,C}=5$ (blue), and the corresponding theory equation (11) is plotted as a line with the same color. These measurements match remarkably well with the theory. We indicate the growth rates for the nonlinear stage with x’s for $a/\rho_{L,C}=2.5$ and $a/\rho_{L,C}=5$ (Measured from simulation with $L_{x}=L_{y}$), with the same color scheme. The nonlinear growth rate can be well estimated by the black line which corresponds to equation (11) with $a/\rho_{L,C}=1$.

The fast-growing nonlinear growth rate when $a/\rho_{L,C}=5$ is a factor close to $5^{3/2}\approx 11$ faster than the linear growth rate. However, earlier in this section, we hypothesized that although a background plasma would not affect the linear growth rate, the fast-growing nonlinear growth rate can be limited by the background. The linear growth rate is a function of $\rho_{L,C}/a\approx d_{e,C}/a$ [equation (11)]. While the fast-growing nonlinear growth rate can be estimated by the linear prediction assuming $\rho_{L,C}/a=1$, with a background, we predict it is given by the linear prediction replacing $\rho_{L,C}/a$ with the background inertial length $d_{e,C}(n_{b})/a=\rho_{L,C}/a\sqrt{n_{0}/n_{b}}$, rather than $1$. To test this hypothesis, we performed a simulation identical to the case with $a/\rho_{L,C}=5$, $T/m_{e}c^{2}=0.005$, and $L_{x}=L_{y}$, but with a background density of $n_{b}/n_{0}=0.1$. The simulation showed both a similar linear growth rate and a slower nonlinear growth rate, that match this prediction. Using a low pass filter described in the next section to mitigate noise from the background population, we measure a linear growth rate of $\gamma_{m}a/c=0.00197$, which is consistent with the theoretical value of $\gamma_{th}a/c=0.00194$. The fast-growing nonlinear growth rate was measured as $\gamma_{m,nl}a/c=0.0297$ for the case with no background, close to the linear prediction for $a/\rho_{L}=1$, namely $\gamma a/c=0.0217$. With the background density $n_{b}/n_{0}=0.1$, the ratio $a/d_{e,C}(n_{b})=5\sqrt{0.1}$, suggesting a nonlinear growth rate $\gamma_{nl}a/c=0.0109$, about half the growth rate for the case with no background. The measured nonlinear growth rate was $\gamma_{m,nl}a/c=0.0095$, matching our predictions.

In this section, we examine a wider range of temperatures while keeping $u_{d}/c$ constant (instead of $\rho_{L,C}$ like the previous section); from $T/m_{e}c^{2}=2.74\times 10^{-5}\ll 1$ to $T/m_{e}c^{2}=7.2\gg 1$, separated by factors of 4, thus exploring a range of both classical and relativistic temperatures. We examine three cases with $u_{d}/c=0.8,0.2,$ and $0.05$, which respectively correspond to $a/\rho_{L,R}=c/u_{d}=1.25,5$ and $20$ for relativistic temperatures (see Table 2 for a list of all the simulations.). Here we explore regimes beyond the scope of the Zelenyi model, i.e. equations (7–8). When we keep $\rho_{L,R}/a$ constant while varying $T/m_{e}c^{2}$, as a consequence we are also varying $\rho_{L,C}/a$, and for increasingly small temperatures, $a/\rho_{L,C}$ decreases. Therefore, for many of our simulations $a/\rho_{L,C}$ is smaller than $1$, and since the temperature is classical, the assumption that $\rho_{L}/a\ll 1$ breaks down.

Note that it is, in fact, possible to have a current sheet where $a<\rho_{L,C}$. When there are strong gradients in the magnetic field and few particles to sustain a current, the particles can be accelerated beyond the thermal velocity. The current is thus composed of beams of particles trapped in a magnetic potential without the possibility of making Larmor orbits.

For the $u_{d}/c=0.8$ case, $a/\rho_{L,R}=1.25$, so even for large temperatures the assumption $\rho_{L}/a\ll 1$ breaks down. However, this region is in the scope of the predictions from Hoshino (2020) included in equation (8). This model predicts that $\rho_{L,R}/a=u_{d}/c\approx 0.8$ is the optimal value for the maximum growth rate (higher $u_{d}/c$ leads to a suppression of the instability.).

For each simulation, we use 1024 particles-per-cell, $L_{y}/a=21.4$, and $L_{x}/a=10.7$ with a resolution of 18 grid cells per $a$. We always choose a time step to satisfy the Courant condition. Let us first consider the classical regime where $T/m_{e}c^{2}\ll 1$. Just as in the previous section, we calculate growth rates, both in the linear stage and in the nonlinear stage where the growth rate rapidly increases, by calculating a line of best fit of the $B_{y}$ component of the energy. Note that no faster nonlinear stage is found for cases where $\rho_{L,C}/a>1$ and the assumption that $\rho_{L}/a\ll 1$ breaks down. This is expected because in these cases, the growth rate is already at its maximum with respect to $\rho_{L,C}/a$. For some cases, we also perform identical simulations with increased length in the $x$ direction $L_{x}=L_{y}$ and $2L_{y}$, which will be identified in the text when they are used.

Before discussing the measurement of the growth rate in the relativistic regime, let us briefly discuss the expected particle noise that seeds the instability. In a classical Maxwellian distribution, there are fewer particles with high $v/c$ leading to predominantly low $k$ noise in the magnetic field. This is due to the large inter-spacial distance between these energetic particles. In contrast, for ultra-relativistic temperatures, there is only weak $k$ dependence as nearly all particles have the same value of $v/c\approx 1$. Therefore, in the relativistic regime, the particle noise with high $ka$ contributes significantly to the magnetic energy in $B_{y}^{2}/4\pi$, making it difficult to measure the growth rate of the signal simply from the evolution of the energy in $B_{y}^{2}/4\pi$. While one might expect a similar effect when $u_{d}/c$, rather than $T/m_{e}c^{2}$, becomes relativistic, the faster growth rates associated with faster $u_{d}/c$ can more easily overcome the noise. Furthermore, the in-plane thermal noise is reduced by $1/\Gamma_{d}$ after being boosted into the moving frame. An increasing temperature, on the other hand, keeping $u_{d}/c$ constant, can only slow the growth rate.

An example of the evolution of the energy of the particles, electromagnetic fields, and the energy in the $B_{y}$ component of the magnetic field is shown in Figure 7 for the case where $T/m_{e}c^{2}=2$ and $u_{d}/c=0.2$. Note that in this case, we have doubled the length to $L_{x}=L_{y}$, which gives similar results to the standard case where $L_{x}=L_{y}/2$, but will help us to measure the growth rate. Like in the previous section, we normalize the time to the theoretical growth rate $\gamma_{th}=0.0295$. However, here we have calculated the theoretical growth rate using the relativistic model, equation (10). As expected the noise of the magnetic field dominates throughout the linear stage, and a measurement cannot be taken. Furthermore, the scale separation between the noise in the different energy channels is no longer significant. The energy in the $B_{y}$ component of the magnetic field is a factor of $v_{T}/c$ less than the electric field energy, which itself is a factor of $v_{T}/c$ less than total magnetic field and kinetic energy, as seen in Figure 1 in the nonrelativistic case when $v_{T}\ll c$. With relativistic temperatures ($v_{T}\sim c$), this separation is no longer present, making a measurement more difficult. However, around $t\gamma_{th}\sim 8$ the system reaches the nonlinear stage, and like in the classical case the growth rate increases rapidly and overcomes the noise. We can thus measure a nonlinear growth rate between $t\gamma_{th}\sim 8.3-8.9$ of $\gamma a/c=0.0848$. Again, like in the classical case, Figure 7 (a) shows in the nonlinear regime significant energy originally from the $B_{x}$ component of the electromagnetic field is converted to kinetic energy.

To measure the linear growth rate, we put the magnetic field grid through a low pass filter, keeping only $ka\lesssim 1$ ($m\equiv k_{x}L_{x}/\pi$ and $k_{y}L_{y}/\pi\leqq 6$) which are the modes that we expect to grow and constitute our signal. To have a better resolution in $k$-space, we use simulations with $L_{x}=L_{y}$, i.e. double the length of our fiducial runs. In Figure 8, we show the evolution of this filtered magnetic energy evolution compared to the curve of the unfiltered magnetic field shown in dashed lines, and we can measure a growth rate between $t\gamma_{th}\sim 3.1-6.2$ of $\gamma_{m}a/c=0.0206$, which is comparable to the theoretical value $\gamma_{th}a/c=0.0295$.

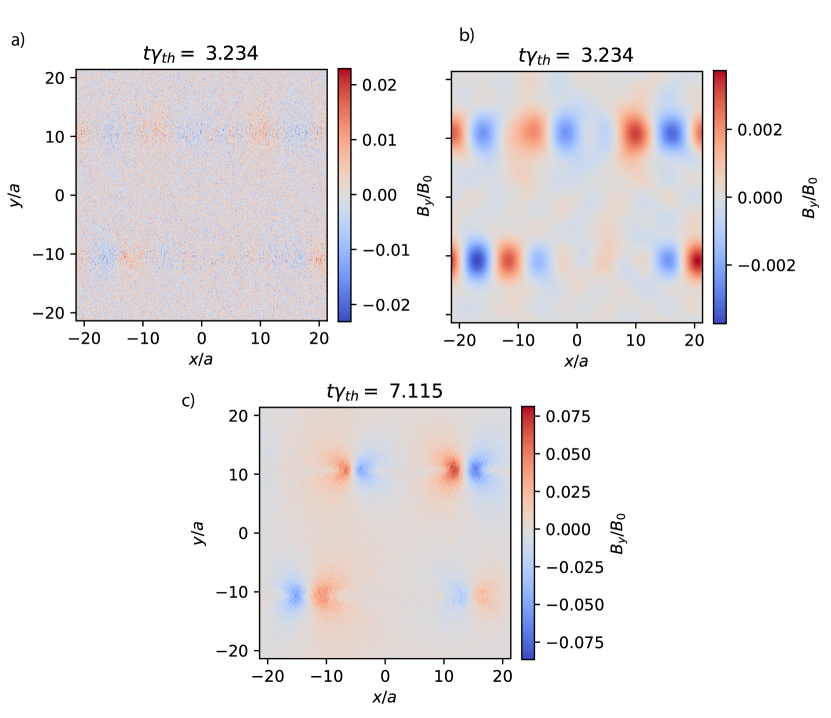
Figure 9 (a) illustrates the significant noise in the linear growth stage in a map of the magnetic field, while a low $k$ signal is visible. Figure 9 (b) shows that the low pass filter removes this noise while retaining the low $k$ signal. Finally, Figure 9 (c) shows the signal once it has grown beyond the noise. At this point, it has already reached a nonlinear stage, where the smallest $ka$ dominates and the growth rate begins to blow up.

In Figure 10 we summarize the temperature dependence on the growth rate for the various values of $u_{d}/c$ from all our simulations, which can also be found in Table 2. The standard measurements of the linear phase are marked by circles, while the simulations measured in larger boxes ($L_{x}=L_{y}$) using a low pass filter are marked by stars. The nonlinear growth rate was also measured for the $u_{d}/c=0.2$ and $u_{d}=0.05$ cases, and the results are indicated by x’s for the standard simulation with $L_{x}=L_{y}/2$, +’s for the simulations with $L_{x}=L_{y}$, and stars for $L_{x}=2L_{y}$. This is an equivalent plot to Figure 6 from the classical part of Section 4, which is also the growth rate as a function of temperature. Figure 6 would fit in the low temperature and $u_{d}/c$ regime (lower left corner of Figure 10), remembering that while here $a/\rho_{L,R}=u_{d}/c$ is held constant, in Figure 6, $a/\rho_{L,C}$ is held constant.

Let us first examine the familiar classical regime of the $u_{d}/c=0.05$ simulations for temperatures above $T/m_{e}c^{2}\approx 2\times 10^{-3}$ ($a/\rho_{L,C}=1.26$), where the simulated growth rates follow the prediction for the classical regime, equation (9) (left blue line). For lower temperatures, the current thickness $a/\rho_{L,C}<1$, and the growth rates fit the predictions for $\rho_{L,C}/a=1$ (indicated by the black line). A better approximation, at least for electron-ion plasmas, is given by Pritchett et al. (1991), who looks in the small $a/\rho_{L,C}\sim 1$ regime, finding a similar limit for $a/\rho_{L,C}\ll 1$. Also Brittnacher et al. (1995) finds an analytic expression that works well for both regimes of $a/\rho_{L,C}$. Finally, for temperatures larger than $T/m_{e}c^{2}\approx 0.45$, the growth rates follow equation (10) (horizontal blue line). Similarly, the $u_{d}/c=0.2$ simulations follow equation (9) between $T/m_{e}c^{2}\approx 3\times 10^{-2}$ ($a/\rho_{L,C}=1.22$) and $T/m_{e}c^{2}\approx 0.45$ (left green line). Note that the range of validity for equation (9) is shorter than in the $u_{d}/c=0.05$ case. For lower temperatures, the growth rates follow predictions for $\rho_{L,C}/a=1$, and for relativistic temperatures beyond $T/m_{e}c^{2}\approx 0.45$, they follow equation (10) (horizontal green line). The growth rate does not match equation (10) precisely but is smaller by a factor of $1.5$, a factor similar to the $\sim 1.7-2$ found in Hoshino (2020) and Zenitani & Hoshino (2007), who only considered values of $u_{d}/c\geq 0.3$. We can see in these curves that, as claimed in the previous section, for constant $u_{d}/c$, the growth rate reaches a peak near $a/\rho_{L,C}=1$.

For $u_{d}/c=0.8$ (points marked in red), at no point does the growth rate match equation (9) (indicated by the red line on the left), as it is always true that $\rho_{L,C}/a>1$, breaking the assumptions of the model. In the classical temperature regime, the growth rate matches the predicted value from equation (11) for $\rho_{L,C}/a=1$ (black line), until $T/m_{e}c^{2}\approx 0.1$ when the growth rate becomes independent of the temperature as predicted by equation (10) (indicated by the horizontal red line) for relativistic plasmas. Like in the $u_{d}/c=0.2$ case, the prediction overestimates the growth rate by a factor of $\sim 1.5$. We also expect, as claimed in the previous section, that for constant $T/m_{e}c^{2}$, a peak growth rate occurs near $a/\rho_{L,C}=1$. In Hoshino’s model for the relativistic temperature regime i.e. equation (10), the growth rate for small $u_{d}/c$ is proportional to $(u_{d}/c)^{3/2}$, and for large $u_{d}/c$ (implying $a/\rho_{L,R}<1$) it is proportional to $(u_{d}/c)^{-1}\sim 1/\Gamma_{d}$, leading to a peak in between at moderate $u_{d}/c\sim 1$. For the coldest temperatures simulated, when $a/\rho_{L,C}<1$ the growth rate also decreases with $1/u_{d}$, and thus a peak growth rate also exists when $a/\rho_{L,C}\sim 1$.

Although not shown in the figure, we performed one simulation identical to our previous simulations with $T/m_{e}c^{2}=2$ and $L_{x}=L_{y}$, but this time with $u_{d}/c=10$ to confirm Hoshino’s model for large drift velocities. We were able to measure a growth rate between $t\gamma_{th}=2.8-8.4$ of $\gamma_{m}a/c=0.027$ using both the growth with and without the low pass filter (The thermal noise is greatly reduced in the boosted frame.). This value is consistent with the theoretical value $\gamma_{m}a/c=0.034$ from equation (10), with only a factor of 1.3 overestimation. The wave number at the start of the measurement was $ka=0.47$, which is consistent with the wave numbers $ka=0.3-0.5$ reported in Hoshino (2020).

We measure the nonlinear growth rate in simulations where $a/\rho_{L,C}>1$, for all cases where $u_{d}/c=0.2$ and several cases where $u_{d}/c=0.05$. In the cases when $u_{d}/c=0.05$ and $T/m_{e}c^{2}>0.028$ ($a/\rho_{L,C}>4.7$), the growth rate saturates early and therefore there is no measurement presented. Like in the previous section, we double the length, increasing to $L_{x}=L_{y}$, which allows a wave number as low as $ka=0.16$ at the $m=1$ mode, and find that the growth reaches the fast-growing nonlinear stage where significant energy is released before saturation occurs. Once again when $u_{d}/c=0.05$ and $T/m_{e}c^{2}>0.5$ ($a/\rho_{L,C}>20$), the growth rate saturates early for the $L_{x}=L_{y}$ case, and likewise we double the length again ($L_{x}=2L_{y}$), which allows a wave number as low as $ka=0.08$ at the $m=1$ mode and reach the fast-growing nonlinear stage. (The growth rate does eventually reach the fast-growing nonlinear stage without doubling $L_{x}$ due to a slow growth after saturation.) Beyond this temperature is considered the relativistic regime, and $a/\rho_{L,R}=20$. Unsurprisingly, we do not see any more early saturation as we increase the temperature. We expect the fast-growing nonlinear stage can always be reached, for a sufficiently long system. An important question remains; how does this critical length scale with the $\rho_{L}/a$?