Partially Ordered Sets Corresponding to the Partition Problem

Susumu Kubo

Abstract

The partition problem is a well-known basic NP-complete problem. We mainly consider the optimization version of it in this paper. The problem has been investigated from various perspectives for a long time and can be solved efficiently in practice. Hence, we might say that the only remaining task is to decide whether the problem can be solved in polynomial time in the number $n$ of given integers.

We propose two partially ordered sets (posets) and present a novel methodology for solving the partition problem. The first poset is order-isomorphic to a well-known poset whose structures are related to the solutions of the subset sum problem, while the second is a subposet of the first and plays a crucial role in this paper. We first show several properties of the two posets, such as size, height and width (the largest size of a subset consisting of incomparable elements). Both widths are the same and $O(2^{n}/n^{3/2})$ for $n$ congruent to $0$ or $3$ (mod $4$ ). This fact indicates the hardness of the partition problem. We then prove that in general all the candidate solutions correspond to the elements of the second poset, whose size is $2^{n}-2\binom{n}{\lfloor n/2\rfloor}$ . Since a partition corresponds to two elements of the poset, the number of the candidate partitions is half of it, that is, $2^{n-1}-\binom{n}{\lfloor n/2\rfloor}$ . We finally prove that the candidate solutions can be reduced based on the partial order. In particular, we give several polynomially solvable cases by considering the minimal elements of the second poset.

Our approach offers a valuable tool for structural analysis of the partition problem and provides a new perspective on the P versus NP problem.

1 Introduction

The partition problem is formulated as follows: given positive integers $c_{1},\ldots,c_{n}$ , the objective is to decide whether there exists a subset $S$ of $\{1,\ldots,n\}=:[n]$ such that $\Delta(S)=0$ , where

\Delta(S):=\sum_{i\in S}c_{i}-\sum_{i\in[n]\setminus S}c_{i}.

(1)

In this paper, we mainly consider the optimization version of it: to find a subset $S$ of $[n]$ that minimizes the absolute value $|\Delta(S)|$ . Without loss of generality, we can assume that the integers are indexed in non-increasing order, that is,

c_{1}\geq c_{2}\geq\cdots\geq c_{n},

and that $c_{n}\geq 0$ for the simplicity of proof though originally $c_{n}>0$ .

The partition problem is one of Karp’s 21 NP-complete problems [11] and is also one of Garey and Johnson’s six basic NP-complete problems [5]. Therefore, the optimization version is known to be NP-hard. It has important applications such as task scheduling [3, 21], and is equivalent to the two-identical-parallel-machine scheduling problem to minimize the makespan.

The problem has been investigated from various perspectives. Several optimal algorithms give exact solutions in exponential time in $n$ [5, 8, 12, 17]. Moreover, a variety of heuristic and metaheuristic algorithms have been developed [1, 4, 9, 10, 16]. Thus, we can solve the problem efficiently in practice. An “easy-hard” phase transition was observed and the solution structure has been studied based on the notion and tools from statistical mechanics [2, 6, 7, 15]. An algebraic expression was presented based on the max-plus algebra [13]. We might say that the only remaining task is to decide whether the problem can be solved in polynomial time in $n$ .

Furthermore, the number of solutions to the subset sum problem, a special case of which is the partition problem, has been studied. The subset sum problem with positive inputs is to decide whether there exists a subset $S$ of $[n]$ such that

\sum_{i\in S}c_{i}=t,

where $t$ is a given constant, a target. Let $N(\{c_{1},...,c_{n}\},t)$ denote the number of the solutions. It is known that

N\left(\{c_{1},...,c_{n}\},t\right)\leq N\left([n],\left\lfloor\frac{n(n+1)}{4}\right\rfloor\right)

[14, 19]. The number $N\left([n],\lfloor n(n+1)/4\rfloor\right)$ is Sequence A025591 in the On-Line Encyclopedia of Integer Sequences [22] and is known to be $O(2^{n}/n^{3/2})$ for $n$ congruent to $0$ or $3$ (mod $4$ )[20]. The inequality is established using the properties of a partially ordered set (poset).

The poset is a well-known poset, denoted by $M(n)$ in Stanley’s paper [19, Subsection 4.1.2]. The elements of $M(n)$ are all the subsets of $[n]$ . Let $A$ and $B$ be two subsets of $[n]$ with elements $a_{1},a_{2},\ldots,a_{j}$ and $b_{1},b_{2},\ldots,b_{k}$ , respectively, and assume that the elements of $A$ and $B$ are indexed in decreasing order. The partial order is defined as follows: $A\leqslant B$ if and only if $j\leq k$ and $a_{i}\leq b_{i}$ for $i\in[j]$ .

To the best of our knowledge, there is no work applying the poset to the partition problem in terms of optimization.

Main results

To define two posets that correspond to the partition problem, we first consider the set $\mathbb{R}^{n}$ of $n$ -dimensional vectors of real numbers. Let $\mathbf{x}=(x_{1},\ldots,x_{n})\in\mathbb{R}^{n}$ and $\mathbf{y}=(y_{1},\ldots y_{n})\in\mathbb{R}^{n}$ , and define a partial order on the set: $\mathbf{x}\preceq\mathbf{y}$ if and only if

	$\displaystyle x_{1}$	$\displaystyle\leq y_{1},$
	$\displaystyle x_{1}+x_{2}$	$\displaystyle\leq y_{1}+y_{2},$
		$\displaystyle\;\;\vdots$
	$\displaystyle x_{1}+x_{2}+\cdots+x_{n}$	$\displaystyle\leq y_{1}+y_{2}+\cdots+y_{n}.$

In other words, $\mathbf{x}\preceq\mathbf{y}$ means that any entry of the cumulative sum of $\mathbf{x}$ is less than or equal to the corresponding one of $\mathbf{y}$ .

Let us define a poset $P(n)$ that corresponds to the partition problem. Let $P(n)$ be the set of all $n$ -dimensional vectors with entries in $\{1,-1\}$ . The size of $P(n)$ is of course $2^{n}$ . The partial order is defined to be the restriction of $\preceq$ on $P(n)$ , denoted by $\preceq_{P}$ . The poset is order-isomorphic to $M(n)$ under the mapping $f$ from $P(n)$ to $M(n)$ defined by the following rule: Given $\mathbf{v}=(v_{1},\dots,v_{n})\in P(n)$ , we have that $i\in f(\mathbf{v})$ if and only if $v_{n+1-i}=1$ .

Example.

The Hasse diagrams of $M(5)$ and $P(5)$ are shown in Figures 1 and 2 respectively. We can see that the two posets are order-isomorphic under $f$ . For example, $f((1,-1,1,-1,-1))=\{5,3\}$ . Note that a partial order is shown horizontally due to space limitation, though it is usually shown vertically. The horizontal position indicates rank.

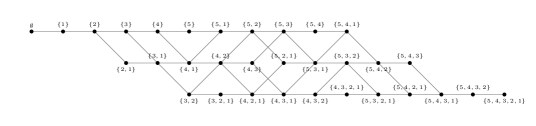
Refer to caption — Figure 1: The Hasse diagram of $M(5)$ .

Let us define another poset $Q(n)$ to be the subset of $P(n)$ obtained by deleting from $P(n)$ the elements that are less than or greater than $\mathbf{0}$ , that is, $Q(n)=P(n)\setminus\{{\mathbf{v}\in P(n)}\colon{\mathbf{v}\preceq\mathbf{0}}\allowbreak\text{or }{\mathbf{0}\preceq\mathbf{v}}\},$ where $\mathbf{0}=(0,\dots,0)$ . The partial order is defined to be the restriction of $\preceq_{P}$ on $Q(n)$ , denoted by $\preceq_{Q}$ . The poset $Q(n)$ can be constructed by truncating the upper part and lower part of $P(n)$ . The size of $Q(n)$ is proved to be $2^{n}-2\binom{n}{\lfloor n/2\rfloor}$ .

Example.

Let us consider $Q(n)$ for $n\leq 6$ . We can easily see that $Q(1)=Q(2)=\emptyset$ and $Q(3)=\{(1,-1,-1),(-1,1,1)\}$ , the elements of which are incomparable. The Hasse diagrams of $Q(4),Q(5)$ and $Q(6)$ are shown in Figure 3.

To investigate the relationship between the partition problem and the posets $P(n)$ and $Q(n)$ , we rewrite the difference (1) of the partition problem. There is a one-to-one correspondence between $P(n)$ and the set of all subsets of $[n]$ . We introduce a mapping $\mathbf{p}$ from $2^{[n]}$ to $P(n)$ . To each subset $S$ of $[n]$ , we assign $\mathbf{p}(S)=(p_{1},\dots,p_{n})$ defined by

p_{i}=\begin{cases}\phantom{-}1&\text{ if }i\in S\\ -1&\text{ if }i\notin S.\end{cases}

Let $\mathbf{c}=(c_{1},c_{2},\ldots,c_{n})$ . Then

\Delta(S)=\mathbf{p}(S)\cdot\mathbf{c},

where the dot indicates the usual inner product. Note that $\mathbf{p}([n]\setminus S)=-\mathbf{p}(S)$ and hence $\Delta([n]\setminus S)=-\mathbf{p}(S)\cdot\mathbf{c}$ , the absolute value of which is equal to $\lvert\Delta(S)\rvert$ . A pair of two elements $\mathbf{p}(S)$ and $-\mathbf{p}(S)$ corresponds to the partition $\{S,\;[n]\setminus S\}$ . We can show that we have only to consider $Q(n)$ for solving the partition problem.

Theorem 1.

The candidate solutions to the partition problem are the subsets that correspond to the elements of $Q(n)$ .

The number of the candidate partitions is half of the size of $Q(n)$ , i.e., $2^{n-1}-\binom{n}{\lfloor n/2\rfloor}$ , since a partition comprises a subset and its complement. Furthermore, the candidate solutions can be reduced based on the partial order of $Q(n)$ .

Theorem 2.

Given an instance $\mathbf{c}$ of the partition problem, the following holds:

(1)

If $\mathbf{p}(S)\cdot\mathbf{c}\geq 0$ for some subset $S$ of $[n]$ satisfying $\mathbf{p}(S)\in Q(n)$ , then $\lvert\mathbf{p}(S)\cdot\mathbf{c}\rvert\leq\lvert\mathbf{p}(S^{\prime})\cdot\mathbf{c}\rvert$ for any $S^{\prime}$ that satisfies $\mathbf{p}(S^{\prime})\preceq_{Q}-\mathbf{p}(S)$ or $\mathbf{p}(S)\preceq_{Q}\mathbf{p}(S^{\prime})$ .
(2)

If $\mathbf{p}(S)\cdot\mathbf{c}\leq 0$ for some subset $S$ of $[n]$ satisfying $\mathbf{p}(S)\in Q(n)$ , then $\lvert\mathbf{p}(S)\cdot\mathbf{c}\rvert\leq\lvert\mathbf{p}(S^{\prime})\cdot\mathbf{c}\rvert$ for any $S^{\prime}$ that satisfies $\mathbf{p}(S^{\prime})\preceq_{Q}\mathbf{p}(S)$ or $-\mathbf{p}(S)\preceq_{Q}\mathbf{p}(S^{\prime})$ .

Using this result, we provide several polynomially solvable cases by considering the minimal elements of $Q(n)$ .

Theorem 3.

Let $\mathbf{v}$ be a minimal element of $Q(n)$ . If $\mathbf{v}\cdot\mathbf{c}\geq 0$ , then the subset $S$ such that $\mathbf{p}(S)=\mathbf{v}$ is a solution and the optimal value is $\mathbf{v}\cdot\mathbf{c}$ .

All the minimal elements are explicitly obtained, as shown in Proposition 15. This is a generalization of the obvious fact that the subset $\{1\}$ is a solution and the optimal value is $c_{1}-(c_{2}+\cdots+c_{n})$ if $c_{1}-(c_{2}+\cdots+c_{n})\geq 0$ , which is the case where the minimal element is $(1,-1,\dots,-1)$ .

Our results are very simple once we realize them. However, the realization was the hard part. The key points are to use $\{1,-1\}$ instead of $\{1,0\}$ when defining the posets and not to limit the candidate solutions to half by assuming, for instance, that a subset of $[n]$ always contains $1$ . We believe that our approach offers a valuable tool for structural analysis of the partition problem and provides a new perspective on the P versus NP problem.

The organization in the paper

The paper is organized as follows. In Section 2 we provide some fundamental concepts relevant to posets and the properties of $P(n)$ and $Q(n)$ . In Section 3 we explore the relationship between the partition problem and the posets and prove our main results.

2 Two posets corresponding to the partition problem

2.1 Preliminaries

In this subsection, we review some standard facts on posets and give some properties of the poset $M(n)$ .

Let $(P,\preceq)$ be a finite poset. We simply denote the poset by $P$ and define the relation $\prec$ by $x\prec y$ if and only if $x\preceq y$ and $x\neq y$ . A subset of $P$ is a chain if it is totally ordered, and a subset of $P$ is an antichain if no pair of elements in it is comparable. A chain is a maximal chain if no other element can be added to it without losing the property of being totally ordered. The height (width) of $P$ is the largest size of a chain (antichain, resp.) in $P$ . An element of $P$ is a maximal (minimal) element if it is not less (greater, resp.) than any other element. An element of $P$ is the greatest (least) element if it is greater (less, resp.) than any other element.

A poset $P$ is graded¹¹1There are several competing definitions for graded posets. if it is equipped with a rank function $\rho$ from $P$ to $\mathbb{Z}$ that satisfies:

(i)

if $x\prec y$ , then $\rho(x)<\rho(y)$ ;
(ii)

if $y$ covers $x$ , i.e., $x\prec y$ and there is no $z\in P$ such that $x\prec z\prec y$ , then $\rho(y)=\rho(x)+1$ .

An element $x\in P$ has rank $i$ if $\rho(x)=i$ . By setting the minimum value of the rank function to zero, any graded poset $P$ can be partitioned into $P=\bigcup_{i=0}^{r}P_{i}$ , where $P_{i}=\{x\in P\colon\rho(x)=i\}$ . We denote the size of $P_{i}$ by $s_{i}$ . The poset $P$ is rank-symmetric if $s_{i}=s_{r-i}$ for each $i$ . The poset $P$ is rank-unimodal if $s_{0}\leq s_{1}\leq\cdots\leq s_{i}\geq s_{i+1}\geq\cdots\geq s_{r}$ for some $i$ , and $P$ is Sperner if the width of $P$ is equal to $\max_{i}\{s_{i}\}$ . The width is lower bounded by $\max_{i}\{s_{i}\}$ since every $P_{i}$ is an antichain. In a Sperner poset, the largest one among $P_{0},P_{1},\ldots,P_{r}$ provides an antichain of maximum size.

A poset $P$ is a lattice if any two elements $x,y\in P$ have a least upper bound and a greatest lower bound, denoted by $x\vee y$ and $x\wedge y$ respectively. A lattice $L$ is distributive if $x\vee(y\wedge z)=(x\vee y)\wedge(x\vee z)$ for each $x,y,z\in L$ .

The poset $M(n)$ has the following properties [18]:

•

The rank function with minimum rank 0 is the sum of elements of a subset. The maximum rank is $n(n+1)/2$ .
•

The poset $M(n)$ is rank-symmetric, rank-unimodal and Sperner. Therefore, its width is equal to the size of the middle rank, which is $N\left([n],\left\lfloor n(n+1)/4\right\rfloor\right)$ .
•

Its height is $n(n+1)/2+1$ .
•

The poset $M(n)$ is a distributive lattice with the greatest element $[n]$ and the least element $\emptyset$ .

2.2 Properties of the two posets

We will provide the properties of $P(n)$ and $Q(n)$ . We need first to become familiar with some elementary properties of the partial order $\preceq$ .

Proposition 4.

For $\mathbf{x},\mathbf{y},\mathbf{z}\in\mathbb{R}^{n}$ , the following holds:

(1)

$\mathbf{x}\preceq\mathbf{y}\Longleftrightarrow\mathbf{x}+\mathbf{z}\preceq\mathbf{y}+\mathbf{z}$ .
(2)

$\mathbf{x}\preceq\mathbf{y}$ and $\,k\geq 0\Longrightarrow k\mathbf{x}\preceq k\mathbf{y}$ .
(3)

$\mathbf{x}\preceq\mathbf{y}$ and $\,k\leq 0\Longrightarrow k\mathbf{y}\preceq k\mathbf{x}$ .

Proof.

Straightforward. ∎

In particular, $\mathbf{x}\preceq\mathbf{y}$ is equivalent to $\mathbf{0}\preceq\mathbf{y}-\mathbf{x}$ . In order to examine the poset $P(n)$ , we define two operators. Let us denote the $i$ th entry of a vector $\mathbf{v}$ by $v_{i}$ hereafter.

Definition 5 (Addition operator).

For $k\in[n]$ , the addition operator $\mathcal{A}^{(k)}$ takes the input $\mathbf{v}\in P(n)$ with $v_{k}=-1$ and sets the $k$ th entry to $1$ , that is,

\left(\mathcal{A}^{(k)}\mathbf{v}\right)_{i}=\begin{cases}1&\text{ if }\;i=k\\ v_{i}&\text{ if }\;i\neq k.\end{cases}

For other elements $\mathbf{v}$ , the operation $\mathcal{A}^{(k)}\mathbf{v}$ is not defined.

Definition 6 (Swap operator).

For $j$ , $k\in[n]$ with $j<k$ , the swap operator $\mathcal{S}^{(j,k)}$ takes the input $\mathbf{v}\in P(n)$ with $v_{j}=-1$ and $v_{k}=1$ , and swaps $v_{j}$ and $v_{k}$ , that is,

\left(\mathcal{S}^{(j,k)}\mathbf{v}\right)_{i}=\begin{cases}\phantom{-}1&\text{ if }\;i=j\\ -1&\text{ if }\;i=k\\ \phantom{-}v_{i}&\text{ if }\;i\notin\{j,k\}.\end{cases}

For other elements $\mathbf{v}$ , the operation $\mathcal{S}^{(j,k)}\mathbf{v}$ is not defined.

We prove some relationships between the operators and the partial order $\preceq_{P}$ .

Proposition 7.

In the poset $P(n)$ , $\mathbf{v}\prec_{P}\mathbf{w}$ if and only if $\mathbf{w}$ is obtained from $\mathbf{v}$ by applying addition and/or swap operators.

Proof.

Assume that $\mathbf{w}$ is obtained from $\mathbf{v}$ by applying addition and/or swap operators. For each $\mathbf{u}\in P(n)$ and any possible integers $j$ and $k$ , we have $\mathbf{u}\prec_{P}\mathcal{A}^{(k)}\mathbf{u}$ and $\mathbf{u}\prec_{P}\mathcal{S}^{(j,k)}\mathbf{u}$ . Therefore, $\mathbf{v}\prec_{P}\mathbf{w}$ .

Conversely, assume that $\mathbf{v}\prec_{P}\mathbf{w}$ . Let $\mathbf{x}=\mathbf{w}-\mathbf{v}$ . Then $x_{i}$ is $\pm 2$ or $0$ for $i\in[n]$ . Denote the indices of $x_{i}$ ’s equal to $-2$ by $k_{1},\ldots,k_{l}$ in increasing order. Since any entry of the cumulative sum of $\mathbf{x}$ is nonnegative, we can pair each entry equal to $-2$ with an entry equal to 2 on the left, that is, we can choose distinct indices $j_{1},\ldots,j_{l}$ of $x_{i}$ ’s equal to $2$ such that $j_{1}<k_{1},\cdots,j_{l}<k_{l}$ . Hence, $\mathbf{x}$ is decomposed as follows:

	$\displaystyle\mathbf{x}$	$\displaystyle=(\underbrace{0,\ldots,0}_{j_{1}-1},2,\underbrace{0,\ldots,0}_{k_{1}-j_{1}-1},-2,0,\ldots,0)+\dots+(\underbrace{0,\ldots,0}_{j_{l}-1},2,\underbrace{0,\ldots,0}_{k_{l}-j_{l}-1},-2,0,\ldots,0)$
		$\displaystyle\quad+(\underbrace{0,\ldots,0}_{i_{1}-1},2,0,\ldots,0)+\dots+(\underbrace{0,\ldots,0}_{i_{m}-1},2,0,\ldots,0),$

where $i_{1},\dots,i_{m}$ are the indices of the remaining $2$ ’s. Since the indices are all distinct, we have $\mathbf{w}=\mathcal{A}^{(i_{m})}\cdots\mathcal{A}^{(i_{1})}\mathcal{S}^{(j_{l},k_{l})}\cdots\mathcal{S}^{(j_{1},k_{1})}\mathbf{v}.$ This means that $\mathbf{w}$ is obtained from $\mathbf{v}$ by applying addition and/or swap operators. ∎

Proposition 8.

In the poset $P(n)$ , $\mathbf{w}$ covers $\mathbf{v}$ if and only if $\mathbf{w}$ is obtained from $\mathbf{v}$ by applying a single operator of the addition operator $\mathcal{A}^{(n)}$ and the swap operators $\mathcal{S}^{(1,2)},\ldots,\mathcal{S}^{(n-1,n)}$ .

Proof.

Assume that $\mathbf{w}$ covers $\mathbf{v}$ , that is, $\mathbf{v}\prec_{P}\mathbf{w}$ and there is no $\mathbf{u}\in P(n)$ such that $\mathbf{v}\prec_{P}\mathbf{u}\prec_{P}\mathbf{w}$ . Suppose, contrary to our claim, that $\mathbf{w}$ is not obtained from $\mathbf{v}$ by one of the operators. We have the following three cases:

Case 1: $\mathbf{w}$ is obtained from $\mathbf{v}$ by two or more addition and/or swap operators. Then there exists $\mathbf{u}\in P$ such that $\mathbf{v}\prec_{P}\mathbf{u}\prec_{P}\mathbf{w}$ since one of the operators always makes the input larger. This is a contradiction.

Case 2: $\mathbf{w}=\mathcal{A}^{(i)}\mathbf{v}$ for some $i\in[n-1]$ . Then $v_{i}=-1$ . If $v_{i+1}=1$ then $\mathbf{w}=\mathcal{A}^{(i+1)}\mathcal{S}^{(i,i+1)}\mathbf{v}$ . If $v_{i+1}=-1$ then $\mathbf{w}=\mathcal{S}^{(i,i+1)}\mathcal{A}^{(i+1)}\mathbf{v}$ . Both lead to Case 1, a contradiction.

Case 3: $\mathbf{w}=\mathcal{S}^{(j,k)}\mathbf{v}$ for some $j$ and $k$ with $k-j\geq 2$ . Then $v_{j}=-1$ and $v_{k}=1$ . If $v_{j+1}=1$ then $\mathbf{w}=\mathcal{S}^{(j+1,k)}\mathcal{S}^{(j,j+1)}\mathbf{v}$ . If $v_{j+1}=-1$ then $\mathbf{w}=\mathcal{S}^{(j,j+1)}\mathcal{S}^{(j+1,k)}\mathbf{v}$ . Both lead to Case 1, a contradiction.

Conversely, assume that $\mathbf{w}$ is obtained from $\mathbf{v}$ by applying one of the operators. It is clear that $\mathbf{v}\prec_{P}\mathbf{w}$ . Suppose, contrary to our claim, that there exists $\mathbf{u}\in P(n)$ such that $\mathbf{v}\prec_{P}\mathbf{u}\prec_{P}\mathbf{w}$ . If $\mathbf{w}=\mathcal{A}^{(n)}\mathbf{v}$ , then $v_{i}=w_{i}$ for $i\in[n-1]$ , $v_{n}=-1$ and $w_{n}=1$ . Thus, $u_{i}=v_{i}=w_{i}$ for $i\in[n-1]$ and $u_{n}$ must be equal to $\pm 1$ , which is a contradiction. If $\mathbf{w}=\mathcal{S}^{(k,k+1)}\mathbf{v}$ for some $k\in[n-1]$ , then $v_{i}=w_{i}$ for $i\notin\{k,k+1\}$ , $v_{k}=-1$ , $v_{k+1}=1$ , $w_{k}=1$ and $w_{k+1}=-1$ . Thus, $u_{i}=v_{i}=w_{i}$ for $i\in[k-1]$ , $u_{k}+u_{k+1}=0$ , and $u_{i}=v_{i}=w_{i}$ for $i\in[n]\setminus[k+1]$ , which is also a contradiction. ∎

Proposition 9.

The poset $P(n)$ is order-isomorphic to $M(n)$ .

Proof.

We need to show that $\mathbf{v}\preceq_{P}\mathbf{w}$ if and only if $f(\mathbf{v})\leqslant f(\mathbf{w})$ for each $\mathbf{v}$ and $\mathbf{w}$ in $P(n)$ .

Assume that $\mathbf{v}\preceq_{P}\mathbf{w}$ . From Proposition 7 it follows that $\mathbf{w}$ is obtained from $\mathbf{v}$ by applying addition and/or swap operators. An addition operator increases 1’s of the input by one and a swap operator shifts one of 1’s of the input to the left. Now let $\mathbf{v}$ have $m$ 1’s. Then $\mathbf{w}$ has at least $m$ 1’s, which implies that $f(\mathbf{w})$ has at least as many elements as $f(\mathbf{v})$ . The $m$ left-most 1’s of $\mathbf{w}$ do not lie more to the right than the 1’s of $\mathbf{v}$ , which implies that in decreasing order the $i$ th element of $f(\mathbf{w})$ is not less than that of $f(\mathbf{v})$ for $i\in[m]$ . Hence, $f(\mathbf{v})\leqslant f(\mathbf{w})$ .

Conversely, assume that $f(\mathbf{v})\leqslant f(\mathbf{w})$ . Let $f(\mathbf{v})=\{a_{1},\ldots,a_{j}\}$ and $f(\mathbf{w})=\{b_{1},\ldots,b_{k}\}$ in decreasing order. Then $j\leq k$ , which means that $\mathbf{w}$ has at least as many 1’s as $\mathbf{v}$ , and $a_{i}\leq b_{i}$ for $i\in[j]$ , which means that the $j$ left-most 1’s of $\mathbf{w}$ do not lie more to the right than the 1’s of $\mathbf{v}$ . By the properties of addition and swap operators, $\mathbf{w}$ is obtained from $\mathbf{v}$ by applying addition and/or swap operators, that is, $\mathbf{v}\preceq_{P}\mathbf{w}$ . ∎

The poset $P(n)$ has the following symmetry.

Proposition 10.

In the poset $P(n)$ , $\mathbf{v}\prec_{P}\mathbf{w}$ if and only if $-\mathbf{w}\prec_{P}-\mathbf{v}$ .

Proof.

For each $\mathbf{v}\in P(n)$ , it holds that $-\mathbf{v}\in P(n)$ . The statement follows immediately from Proposition 4 (3). ∎

It follows from Proposition 9 and its proof and Proposition 10 that the poset $P(n)$ has the following properties:

•

The rank function with minimum rank 0 is

$\frac{1}{2}\left(\mathbf{v}\cdot\mathbf{c}_{0}+\frac{1}{2}n(n+1)\right)$ (2)

for $\mathbf{v}\in P(n)$ , where $\mathbf{c}_{0}=(n,n-1,\ldots,2,1)$ .
•

The poset $P(n)$ is rank-symmetric, rank-unimodal and Sperner.
•

Its width is $N\left([n],\left\lfloor n(n+1)/4\right\rfloor\right)$ .
•

Its height is $n(n+1)/2+1$ .
•

The poset $P(n)$ has a certain symmetry: $\mathbf{v}\prec_{P}\mathbf{w}\Longleftrightarrow-\mathbf{w}\prec_{P}-\mathbf{v}$ .
•

The poset $P(n)$ is a distributive lattice. The greatest element and the least one are respectively $(1,\ldots,1)$ and $(-1,\ldots,-1)$ .

Remark.

An element of $P(n)$ can be also regarded as a path of the random walk on the integer number line which starts at 0 and at each step moves $+1$ or $-1$ . The relation $\mathbf{v}\preceq_{P}\mathbf{w}$ means that the path corresponding to $\mathbf{v}$ does not “exceed” the one corresponding to $\mathbf{w}$ . Figure 4 shows an example.

We investigate the other poset $Q(n)$ . Hereafter, let $n\geq 3$ . We will show some properties of $Q(n)$ .

Let $R_{+}(n)=\{\mathbf{v}\in P(n)\colon\mathbf{0}\prec\mathbf{v}\}$ and $R_{-}(n)=\{\mathbf{v}\in P(n)\colon\mathbf{v}\prec\mathbf{0}\}$ . We can see that the subposets $R_{+}(n)$ and $R_{-}(n)$ of $P(n)$ are sublattices of $P(n)$ . The least element of $R^{+}(n)$ is $(1,-1,1,-1,...)$ , the rank of which in $P(n)$ is $n/4+n(n+1)/4$ if $n$ is even and $(n+1)/4+n(n+1)/4$ if $n$ is odd. The elements of $R_{+}(n)$ are not in the middle rank of $P(n)$ . This is true for $R_{-}(n)$ by the symmetry of $P(n)$ . Therefore, we obtain the next proposition.

Proposition 11.

The width of $Q(n)$ is the same as that of $P(n)$ .

For the size of $Q(n)$ , the next proposition holds.

Proposition 12.

The size of $Q(n)$ is $2^{n}-2\binom{n}{\lfloor n/2\rfloor}$ .

Proof.

By definition, $\#Q(n)=\#P(n)-\#R_{+}(n)-\#R_{-}(n)$ , where $\#$ indicates the size of a set. Since $\#P(n)=2^{n}$ and $\#R_{+}(n)=\#R_{-}(n)$ , it is sufficient to show that $\#R_{+}(n)=\binom{n}{\lfloor n/2\rfloor}$ . Let us regard the elements of $R_{+}(n)$ as the paths of the random walk. The size is the number of $n$ -step paths from 0 never going below 0 (for example, see $\mathbf{w}$ in Figure 4). Denote the number by $X_{n}$ and define $X_{0}=1$ . Then we have

X_{n}=\begin{cases}2X_{n-1}-C_{(n-1)/2}&\text{ if $n$ is odd}\\ 2X_{n-1}&\text{ if $n$ is even},\end{cases}

where $C_{m}$ is the number of $2m$ -step paths from 0 to 0 never going below 0, known as the Catalan number. The sequence $X_{n}$ is known to be $\binom{n}{\lfloor n/2\rfloor}$ . ∎

The poset $Q(n)$ also has the symmetry.

Proposition 13.

In the poset $Q(n)$ , $\mathbf{v}\prec_{Q}\mathbf{w}$ if and only if $-\mathbf{w}\prec_{Q}-\mathbf{v}$ .

Proof.

For each $\mathbf{v}\in Q(n)$ , we show that $-\mathbf{v}\in Q(n)$ . Suppose, contrary to our claim, that $-\mathbf{v}\notin Q(n)$ . Then $-\mathbf{v}\prec\mathbf{0}$ or $\mathbf{0}\prec-\mathbf{v}$ , which contradicts $\mathbf{v}\in Q(n)$ . The statement follows immediately from Proposition 4 (3). ∎

Proposition 14.

The poset $Q(n)$ is graded and one of the rank functions is the same as the rank function (2) of $P(n)$ .

Proof.

Denote the rank function of $P(n)$ by $\rho$ . We show that a rank function of $Q(n)$ is $\rho$ . Since $Q(n)$ is a subposet of $P(n)$ , if $\mathbf{v}\prec_{Q}\mathbf{w}$ then $\rho(\mathbf{v})<\rho(\mathbf{w})$ . When $\mathbf{w}$ covers $\mathbf{v}$ in $Q(n)$ , suppose, contrary to our claim, that $\rho(\mathbf{w})\geq\rho(\mathbf{v})+2$ . Then there exists some $\mathbf{u}\in P(n)\setminus Q(n)$ such that $\mathbf{v}\prec_{P}\mathbf{u}\prec_{P}\mathbf{w}$ and $\rho(\mathbf{u})=\rho(\mathbf{v})+1$ . Since $\mathbf{u}$ is not in $Q(n)$ , $\mathbf{u}\prec\mathbf{0}$ or $\mathbf{0}\prec\mathbf{u}$ . If $\mathbf{u}\prec\mathbf{0}$ then $\mathbf{v}\prec\mathbf{0}$ . If $\mathbf{0}\prec\mathbf{u}$ then $\mathbf{0}\prec\mathbf{w}$ . Either case is a contradiction. ∎

Let $\ell=\lfloor(n-1)/2\rfloor$ . For $k\in\{0,1,\dots\ell\}$ we denote by $\mathbf{m}_{k}$ the element of $Q(n)$

(\underbrace{1,\ldots,1}_{k},\underbrace{-1,\ldots,-1}_{k+1},1,\ldots,1).

Thus, $-\mathbf{m}_{k}$ stands for the element of $Q(n)$

(\underbrace{-1,\ldots,-1}_{k},\underbrace{1,\ldots,1}_{k+1},-1,\ldots,-1).

Proposition 15.

The maximal (minimal) elements of $Q(n)$ are $\mathbf{m}_{0}$ , $\mathbf{m}_{1}$ , $\ldots,\mathbf{m}_{\ell}\>(-\mathbf{m}_{0}$ , $-\mathbf{m}_{1}$ , $\ldots,-\mathbf{m}_{\ell}$ , resp.).

Proof.

We first prove that $\mathbf{m}_{k}$ for $k\in\{0,1,\dots\ell\}$ is maximal. It is sufficient to show that the elements covering $\mathbf{m}_{k}$ on $P(n)$ are not in $Q(n)$ . If $n$ is even, then the last entry of $\mathbf{m}_{k}$ is always $1$ for each $k$ . From this fact and Proposition 8 it follows that the unique element covering $\mathbf{m}_{k}$ is $\mathcal{S}^{(2k+1,2k+2)}\mathbf{m}_{k}$ , that is,

(\underbrace{1,\ldots,1}_{k},\underbrace{-1,\ldots,-1}_{k},1,-1,1,\ldots,1),

which is greater than $\mathbf{0}$ . If $n$ is odd, then the last entry of $\mathbf{m}_{k}$ might be $-1$ . The unique element covering $\mathbf{m}_{k}$ is $\mathcal{S}^{(2k+1,2k+2)}\mathbf{m}_{k}$ if $k<\ell$ , and $\mathcal{A}^{(n)}\mathbf{m}_{k}$ , that is,

(\underbrace{1,\ldots,1}_{k},\underbrace{-1,\ldots,-1}_{k},1)

if $k=\ell$ . Both are greater than $\mathbf{0}$ .

We next prove that no other elements are maximal. Consider a maximal element $\mathbf{v}\in Q(n)$ . Now we distinguish two cases.

Case 1: $\mathbf{v}$ contains no $(-1,1)$ sequence. Then $\mathbf{v}$ is a vector with $1$ ’s up to some position (possibly none) and then $-1$ ’s for the rest of the entries, that is, $(1,\ldots,1)$ , $(-1,\ldots,-1)$ or $(1,\ldots,1,-1,\ldots,-1)$ . The first two are not obviously in $Q(n)$ . Since $\mathbf{v}\in Q(n)$ and $\mathcal{A}^{(n)}\mathbf{v}\in R_{+}(n)$ , the sum $v_{1}+\cdots+v_{n}$ must be equal to $-1$ . Therefore, $\mathbf{v}$ is

(\underbrace{1,\ldots,1}_{(n-1)/2},\underbrace{-1,\ldots,-1}_{(n-1)/2},-1),

where $n$ is odd. This is exactly $\mathbf{m}_{\ell}$ .

Case 2: $\mathbf{v}$ contains $(-1,1)$ sequences. We assume that the left-most sequence lies at the $j$ th and $(j+1)$ th positions. Then $\mathcal{S}^{(j,j+1)}\mathbf{v}\in R_{+}(n)$ . Hence, $v_{1}+\cdots+v_{j}$ must be equal to $-1$ . If $\mathbf{v}$ contains another $(-1,1)$ sequence at the $j^{\prime}$ th and $(j^{\prime}+1)$ th positions, then $\mathcal{S}^{(j^{\prime},j^{\prime}+1)}\mathbf{v}\in Q(n)$ , which contradicts the maximality. Therefore, the subsequences $(v_{1},\ldots,v_{j-1})$ and $(v_{j+2},\ldots,v_{n})$ contain no $(-1,1)$ sequence. By a similar argument to Case 1, they are $(1,\ldots,1)$ , $(-1,\ldots,-1)$ , $(1,\ldots,1,-1,\ldots,-1)$ or empty. Since $v_{1}+\cdots+v_{j-1}=0$ , we get

(v_{1},\ldots,v_{j-1})=(\underbrace{1,\ldots,1}_{(j-1)/2},\underbrace{-1,\ldots,-1}_{(j-1)/2}),

where $j$ is odd (if $j=1$ then the subsequence is empty). On the other hand, if $v_{n}=-1$ then $\mathcal{A}^{(n)}\mathbf{v}\in Q(n)$ , which contradicts the maximality. Hence, $(v_{j+2},\ldots,v_{n})$ is $(1,\dots,1)$ or empty. Consequently, $\mathbf{v}$ is

(\underbrace{1,\ldots,1}_{(j-1)/2},\underbrace{-1,\ldots,-1}_{(j-1)/2},-1,1,\underbrace{1,\ldots,1}_{n-(j+1)}),

which is exactly $\mathbf{m}_{k}$ , where $k=(j-1)/2$ and $j\leq n-1$ . Note that $k\in\{0,1,\dots,\ell\}$ if $n$ is even and $k\in\{0,\dots,\ell-1\}$ if $n$ is odd.

By symmetry, if $\mathbf{v}$ is a maximal element, then $-\mathbf{v}$ is a minimal element.

∎

Lemma 16.

In the poset $Q(n)$ with $n\geq 4$ , a minimal element $-\mathbf{m}_{k}$ is less than a maximal element $\mathbf{m}_{k^{\prime}}$ with $k^{\prime}\neq k$ , that is, $-\mathbf{m}_{k}\prec_{Q}\mathbf{m}_{k^{\prime}}$ .

Proof.

Let $k_{0}=\min\{k,k^{\prime}\}$ and $k_{1}=\max\{k,k^{\prime}\}$ . If $k_{0}<k_{1}\leq 2k_{0}+1$ , then

\mathbf{m}_{k^{\prime}}-(-\mathbf{m}_{k})=(\underbrace{2,\ldots,2}_{k_{0}},\underbrace{0,\ldots,0}_{k_{1}-k_{0}},\underbrace{-2,\ldots,-2}_{2k_{0}+1-k_{1}},\underbrace{0,\ldots,0}_{2(k_{1}-k_{0})},2,\ldots,2),

which is greater than $\mathbf{0}$ since $k_{0}\geq 2k_{0}+1-k_{1}$ . If $2k_{0}+1<k_{1}$ , then

\mathbf{m}_{k^{\prime}}-(-\mathbf{m}_{k})=(\underbrace{2,\ldots,2}_{k_{0}},\underbrace{0,\ldots,0}_{k_{0}+1},\underbrace{2,\ldots,2}_{k_{1}-(2k_{0}+1)},\underbrace{0,\ldots,0}_{k_{1}+1},2,\ldots,2),

which is evidently greater than $\mathbf{0}$ . ∎

Note that in the case where $n=3$ , the maximal elements $\mathbf{m}_{0}=(-1,1,1)$ and $\mathbf{m}_{1}=(1,-1,-1)$ are also minimal elements.

Proposition 17.

The height of $Q(n)$ is

	$\displaystyle\frac{1}{2}n(n-1)-\left(n-\frac{3}{2}\ell\right)(\ell+1)+1$	$\displaystyle\text{ for }\>n\leq 7,\text{ and}$
	$\displaystyle\frac{1}{2}(n-2)(n-3)+1$	$\displaystyle\text{ for }\>n\geq 8.$

Proof.

We first consider the case where $n\geq 4$ . From Lemma 16 it follows that two elements $-\mathbf{m}_{k}$ and $\mathbf{m}_{k^{\prime}}$ with $k^{\prime}\neq k$ are comparable. Let us take a maximal chain containing the two elements. Since $Q(n)$ is graded, the size of the maximal chain is $\rho(\mathbf{m}_{k^{\prime}})-\rho(-\mathbf{m}_{k})+1$ , where $\rho$ denotes the rank function (2) of $P(n)$ and $Q(n)$ . Therefore, the height is

\max_{k\neq k^{\prime}}\left\{\rho(\mathbf{m}_{k^{\prime}})-\rho(-\mathbf{m}_{k})+1\right\}.

(3)

Since $\rho(\mathbf{v})=\left(\mathbf{v}\cdot\mathbf{c}_{0}+n(n+1)/2\right)/2$ for $\mathbf{v}\in Q(n)$ , we have

	$\displaystyle\rho(\mathbf{m}_{k^{\prime}})$	$\displaystyle=\frac{1}{2}n(n+1)-n(k^{\prime}+1)+\frac{3}{2}k^{\prime}(k^{\prime}+1),$
	$\displaystyle\rho(-\mathbf{m}_{k})$	$\displaystyle=n(k+1)-\frac{3}{2}k(k+1).$

Substituting these expressions into (3), we obtain

\max_{k\neq k^{\prime}}\left\{\frac{3}{2}\left(k-\frac{2n-3}{6}\right)^{2}+\frac{3}{2}\left(k^{\prime}-\frac{2n-3}{6}\right)^{2}-3\left(\frac{2n-3}{6}\right)^{2}+\frac{1}{2}n(n-3)+1\right\}.

The objective function is symmetric in $k$ and $k^{\prime}$ , and we can assume that $k>k^{\prime}$ . In the $k$ - $k^{\prime}$ plane the farthest point from the center point $\left((2n-3)/6,(2n-3)/6\right)$ provides the maximum value. Therefore, the candidate points are $(1,0)$ and $(\ell,0)$ . Determining the position of the center point relative to the line $k=(1+\ell)/2$ , equidistant from the two points, we conclude that the optimal point is $(\ell,0)$ for $n\leq 7$ and $(1,0)$ for $n\geq 8$ . Hence, the height is $n(n-1)/2-(n-3\ell/2)(\ell+1)+1$ for $n\leq 7$ and $(n-2)(n-3)/2+1$ for $n\geq 8$ .

In the case where $n=3$ , the height is $1$ , which is obtained by the expression above for $n\leq 7$ . ∎

Summarizing, we have the following properties of $Q(n)$ :

•

The rank function with minimum rank 0 is

$\frac{1}{2}\left(\mathbf{v}\cdot\mathbf{c}_{0}+\frac{1}{2}n(n+1)\right)-n$

for $\mathbf{v}\in Q(n)$ .
•

Its size is $2^{n}-2\binom{n}{\lfloor n/2\rfloor}$ .
•

The poset $Q(n)$ is rank-symmetric and Sperner.
•

Its width is the same as that of $P(n)$ , i.e., $N\left([n],\left\lfloor n(n+1)/4\right\rfloor\right)$ .
•

Its height is $n(n-1)/2-\left(n-3\ell/2\right)(\ell+1)+1$ for $n\leq 7$ and $(n-2)(n-3)/2+1$ for $n\geq 8$ .
•

The poset $Q(n)$ also has the same symmetry as $P(n)$ : $\mathbf{v}\prec_{Q}\mathbf{w}\Longleftrightarrow-\mathbf{w}\prec_{Q}-\mathbf{v}$ .
•

The minimal elements and the maximal ones are respectively $-\mathbf{m}_{0},-\mathbf{m}_{1},\ldots,-\mathbf{m}_{\ell}$ and $\mathbf{m}_{0},\mathbf{m}_{1},\ldots,\mathbf{m}_{\ell}$ .

It does not seem easy to determine whether $Q(n)$ is rank-unimodal or not. As a side note, we observed that $Q(n)$ is rank-unimodal for $n\leq 21$ .

3 Relationship between the partition problem and the posets

We will discuss the relationship between the partition problem and the posets $P(n)$ and $Q(n)$ . We first show the relationship between the difference of the partition problem and the partial order $\preceq_{P}$ or $\preceq_{Q}$ . To this end, we introduce another expression of the difference $\mathbf{p}(S)\cdot\mathbf{c}$ . Let $\mathbf{d}=(d_{1},\dots,d_{n})$ defined by $d_{i}=c_{i}-c_{i+1}$ for $i\in[n]$ , where $c_{n+1}=0$ . Note that $\mathbf{d}\geq\mathbf{0}$ , which is a componentwise inequality. Denote the cumulative sum of $\mathbf{p}(S)$ by $\mathbf{r}(S)$ , that is, $\mathbf{r}(S)=(p_{1},p_{1}+p_{2},\dots,p_{1}+\dots+p_{n})$ when $\mathbf{p}(S)=(p_{1},p_{2},\dots,p_{n})$ . Then $\mathbf{p}(S)\cdot\mathbf{c}=\mathbf{r}(S)\cdot\mathbf{d}$ . In addition, the relation $\mathbf{p}(S)\preceq_{P}\mathbf{p}(S^{\prime})$ can be succinctly written as the componentwise inequality $\mathbf{r}(S)\leq\mathbf{r}(S^{\prime})$ .

Proposition 18.

Given two subsets $S$ and $S^{\prime}$ of $[n]$ , the inequality $\mathbf{p}(S)\cdot\mathbf{c}\leq\mathbf{p}(S^{\prime})\cdot\mathbf{c}$ holds for any $\mathbf{c}$ if and only if $\mathbf{p}(S)\preceq_{P}\mathbf{p}(S^{\prime})$ .

Proof.

We denote $\mathbf{p}(S)$ and $\mathbf{p}(S^{\prime})$ by $(p_{1},\ldots,p_{n})$ and $(p^{\prime}_{1},\ldots,p^{\prime}_{n})$ , respectively.

We first assume that $\mathbf{p}(S)\cdot\mathbf{c}\leq\mathbf{p}(S^{\prime})\cdot\mathbf{c}$ for any $\mathbf{c}$ . Suppose, contrary to our claim, that $p_{1}+\cdots+p_{k}>p^{\prime}_{1}+\cdots+p^{\prime}_{k}$ for some $k\in[n]$ . Take

\mathbf{c}^{\prime}=(\underbrace{1,\ldots,1}_{k},0,\ldots,0).

Then $\mathbf{p}(S)\cdot\mathbf{c}^{\prime}>\mathbf{p}(S^{\prime})\cdot\mathbf{c}^{\prime}$ , which is a contradiction.

We next prove the converse. We assume that $\mathbf{p}(S)\preceq_{P}\mathbf{p}(S^{\prime})$ , that is, $\mathbf{r}(S)\leq\mathbf{r}(S^{\prime})$ . Suppose, contrary to our claim, that $\mathbf{p}(S)\cdot\mathbf{c}>\mathbf{p}(S^{\prime})\cdot\mathbf{c}$ for some $\mathbf{c}$ . Then we have $(\mathbf{r}(S)-\mathbf{r}(S^{\prime}))\cdot\mathbf{d}>0$ . Since $\mathbf{r}(S)-\mathbf{r}(S^{\prime})$ is nonpositive and $\mathbf{d}$ is nonnegative, the left-hand side is nonpositive, a contradiction. ∎

A similar statement holds for the poset $Q(n)$ .

Corollary 19.

Given two subsets $S$ and $S^{\prime}$ of $[n]$ satisfying $\mathbf{p}(S)$ , $\mathbf{p}(S^{\prime})\in Q(n)$ , the inequality $\mathbf{p}(S)\cdot\mathbf{c}\leq\mathbf{p}(S^{\prime})\cdot\mathbf{c}$ holds for any $\mathbf{c}$ if and only if $\mathbf{p}(S)\preceq_{Q}\mathbf{p}(S^{\prime})$ .

We next provide subsets unnecessary to be considered in the partition problem.

Lemma 20.

If a subset $S$ of $[n]$ satisfies $\mathbf{p}(S)\prec\mathbf{0}$ or $\mathbf{0}\prec\mathbf{p}(S)$ , then there exists some subset $S^{\prime}$ of $[n]$ , not equal to $S$ or $[n]\setminus S$ , such that $\lvert\mathbf{p}(S^{\prime})\cdot\mathbf{c}\rvert\leq\lvert\mathbf{p}(S)\cdot\mathbf{c}\rvert$ for any $\mathbf{c}$ .

Proof.

We denote $\mathbf{p}(S)$ by $(p_{1},\ldots,p_{n})$ . For the complement of $S$ , we have $\mathbf{p}([n]\setminus S)=-\mathbf{p}(S)$ and $\lvert\mathbf{p}([n]\setminus S)\cdot\mathbf{c}\rvert=\lvert\mathbf{p}(S)\cdot\mathbf{c}\rvert$ . Without loss of generality, we can thus assume that $\mathbf{p}(S)\prec\mathbf{0}$ . We need to consider two cases:

Case 1: $\mathbf{p}(S)$ contains no $(-1,1)$ sequence. Since $\mathbf{p}(S)\prec\mathbf{0}$ , it holds that $S=\emptyset$ . Take $\{n\}$ as $S^{\prime}$ . Then $\mathbf{p}(S)\prec_{P}\mathbf{p}(S^{\prime})$ and $\mathbf{p}(S^{\prime})\prec\mathbf{0}$ . It follows from the former relation and Proposition 18 that $\mathbf{p}(S)\cdot\mathbf{c}\leq\mathbf{p}(S^{\prime})\cdot\mathbf{c}$ holds for any $\mathbf{c}$ . The latter relation is equivalent to $\mathbf{r}(S^{\prime})\leq\mathbf{0}$ . The inner product of $\mathbf{r}(S^{\prime})$ with the nonnegative vector $\mathbf{d}$ is nonpositive. Thus, $\mathbf{r}(S^{\prime})\cdot\mathbf{d}=\mathbf{p}(S^{\prime})\cdot\mathbf{c}\leq 0$ for any $\mathbf{c}$ . Therefore, $\mathbf{p}(S)\cdot\mathbf{c}\leq\mathbf{p}(S^{\prime})\cdot\mathbf{c}\leq 0$ for any $\mathbf{c}$ .

Case 2: $\mathbf{p}(S)$ contains $(-1,1)$ sequences. We assume that the left-most sequence lies at the $j$ th and $(j+1)$ th positions. Take $S^{\prime}$ such that $\mathbf{p}(S^{\prime})=\mathcal{S}^{(j,j+1)}\mathbf{p}(S)$ . Then $\mathbf{p}(S)\prec_{P}\mathbf{p}(S^{\prime})$ by Proposition 7. On the other hand, subtracting $-\mathbf{p}(S)$ from $\mathbf{p}(S^{\prime})$ , we have

\mathbf{p}(S^{\prime})-(-\mathbf{p}(S))=(2p_{1},\ldots,2p_{j-1},0,0,2p_{j+2},\ldots,2p_{n}).

This gives $\mathbf{p}(S^{\prime})\prec_{P}-\mathbf{p}(S)$ , since $\mathbf{p}(S)\prec\mathbf{0}$ . Consequently, it follows from Proposition 18 that $\mathbf{p}(S)\cdot\mathbf{c}\leq\mathbf{p}(S^{\prime})\cdot\mathbf{c}\leq-\mathbf{p}(S)\cdot\mathbf{c}$ for any $\mathbf{c}$ . ∎

By this lemma, it turns out that it is unnecessary to consider the elements of $P(n)\setminus Q(n)$ . We then show that in general we must consider all the elements of $Q(n)$ .

Lemma 21.

Let a subset $S$ of $[n]$ satisfy $\mathbf{p}(S)\in Q(n)$ . Then there exists some $\mathbf{c}$ such that $\lvert\mathbf{p}(S)\cdot\mathbf{c}\rvert<\lvert\mathbf{p}(S^{\prime})\cdot\mathbf{c}\rvert$ for any $S^{\prime}$ that satisfies $\mathbf{p}(S^{\prime})\in Q(n)$ and is not equal to $S$ or $[n]\setminus S$ .

Proof.

We will prove this by contradiction. Suppose that for any $\mathbf{c}$ there exists some $S^{\prime}$ such that $\lvert\mathbf{p}(S^{\prime})\cdot\mathbf{c}\rvert\leq\lvert\mathbf{p}(S)\cdot\mathbf{c}\rvert$ . In particular, $\mathbf{p}(S)\cdot\mathbf{c}=0$ implies $\mathbf{p}(S^{\prime})\cdot\mathbf{c}=0$ . Considering another expression of the difference, we deduce that for $\mathbf{d}\geq 0$ satisfying $\mathbf{r}(S)\cdot\mathbf{d}=0$ there exists some $S^{\prime}$ such that $\mathbf{r}(S^{\prime})\cdot\mathbf{d}=0$ . By regarding these expressions as inequalities for $\mathbf{d}$ , we obtain

\{\mathbf{d}\in\mathbb{Z}^{n}:\mathbf{r}(S)\cdot\mathbf{d}=0,\;\mathbf{d}\geq\mathbf{0}\}\subset\bigcup_{S^{\prime}\neq S,[n]\setminus S}\{\mathbf{d}\in\mathbb{Z}^{n}:\mathbf{r}(S^{\prime})\cdot\mathbf{d}=0,\;\mathbf{d}\geq\mathbf{0}\}.

We will denote the left-hand side and the set in the union on the right-hand side by $C_{S}$ and $C_{S^{\prime}}$ respectively. From the notation and the expression above, we can deduce that $C_{S}$ is equal to the union of the intersections of $C_{S}$ with each $C_{S^{\prime}}$ , that is,

C_{S}=\bigcup_{S^{\prime}\neq S,[n]\setminus S}(C_{S}\cap C_{S^{\prime}}).

Now choose a minimal decomposition

C_{S}=\bigcup_{i=1}^{m}(C_{S}\cap C_{S^{\prime}_{i}})

(4)

with $m$ minimal. Then $m\geq 2$ , since $\mathbf{r}(S)$ and $\mathbf{r}(S^{\prime}_{i})$ are linearly independent and $\mathbf{p}(S)$ and $\mathbf{p}(S^{\prime}_{i})$ are both in $Q(n)$ . By minimality, no $C_{S}\cap C_{S^{\prime}_{i}}$ is contained in the union of other $C_{S}\cap C_{S^{\prime}_{j}}$ ’s. Take vectors $\mathbf{d}_{1}$ and $\mathbf{d}_{2}$ such that $\mathbf{d}_{1}\in C_{S}\cap C_{S^{\prime}_{1}}$ but $\mathbf{d}_{1}\notin C_{S}\cap C_{S^{\prime}_{i}}$ for $i\neq 1$ and $\mathbf{d}_{2}\in C_{S}\cap C_{S^{\prime}_{2}}$ but $\mathbf{d}_{2}\notin C_{S}\cap C_{S^{\prime}_{i}}$ for $i\neq 2$ . Consider the intersection of $C_{S}\cap C_{S^{\prime}_{i}}$ and the infinite set $K=\{\alpha\mathbf{d}_{1}+\mathbf{d}_{2}:\alpha\in\mathbb{Z},\alpha\geq 0\}\subset C_{S}$ . If $i=1$ , then the intersection is empty since $\mathbf{r}(S^{\prime}_{i})\cdot\mathbf{d}_{1}=0$ and $\mathbf{r}(S^{\prime}_{i})\cdot\mathbf{d}_{2}\neq 0$ . If $i\neq 1$ , then the intersection is at most one point since $\mathbf{r}(S^{\prime}_{i})\cdot\mathbf{d}_{1}\neq 0$ . So $K$ intersects each $C_{S}\cap C_{S^{\prime}_{i}}$ in at most one point. Since (4) holds, $K$ is a finite set, a contradiction. ∎

We thus can prove Theorem 1.

Proof of Theorem 1.

This follows immediately from Lemmas 20 and 21. ∎

We will consider an instance of the partition problem, that is, we take a concrete $\mathbf{c}$ into account. We can reduce the candidate solutions by using the partial order.

Proposition 22.

Given an instance $\mathbf{c}$ of the partition problem, the following holds:

(1)

If $\mathbf{p}(S)\cdot\mathbf{c}\geq 0$ for some subset $S$ of $[n]$ , then $\lvert\mathbf{p}(S)\cdot\mathbf{c}\rvert\leq\lvert\mathbf{p}(S^{\prime})\cdot\mathbf{c}\rvert$ for any $S^{\prime}$ that satisfies $\mathbf{p}(S^{\prime})\preceq_{P}-\mathbf{p}(S)$ or $\mathbf{p}(S)\preceq_{P}\mathbf{p}(S^{\prime})$ .
(2)

If $\mathbf{p}(S)\cdot\mathbf{c}\leq 0$ for some subset $S$ of $[n]$ , then $\lvert\mathbf{p}(S)\cdot\mathbf{c}\rvert\leq\lvert\mathbf{p}(S^{\prime})\cdot\mathbf{c}\rvert$ for any $S^{\prime}$ that satisfies $\mathbf{p}(S^{\prime})\preceq_{P}\mathbf{p}(S)$ or $-\mathbf{p}(S)\preceq_{P}\mathbf{p}(S^{\prime})$ .

Proof.

We show the first statement. From Proposition 18 it follows that $\mathbf{p}(S^{\prime})\cdot\mathbf{c}\leq-\mathbf{p}(S)\cdot\mathbf{c}$ or $\mathbf{p}(S)\cdot\mathbf{c}\leq\mathbf{p}(S^{\prime})\cdot\mathbf{c}$ . Hence, $\mathbf{p}(S^{\prime})\cdot\mathbf{c}\leq-\mathbf{p}(S)\cdot\mathbf{c}\leq 0$ or $0\leq\mathbf{p}(S)\cdot\mathbf{c}\leq\mathbf{p}(S^{\prime})\cdot\mathbf{c}$ . Either case implies that $\lvert\mathbf{p}(S)\cdot\mathbf{c}\rvert\leq\lvert\mathbf{p}(S^{\prime})\cdot\mathbf{c}\rvert$ .

In the same manner, we can prove the second. ∎

Proof of Theorem 2.

It immediately follows from Proposition 22. ∎

If the height of $Q(n)$ is large, we can reduce efficiently the candidate solutions by using Theorem 2. However, this is not the case; its height is $O(n^{2})$ , while its width is $O(2^{n}/n^{3/2})$ for $n$ congruent to 0 or 3 (mod 4). The large width indicates the hardness of the partition problem.

We will give some polynomially solvable cases by considering the minimal elements of $Q(n)$ . To this end, we show an interesting property of the minimal elements of $Q(n)$ .

Lemma 23.

Given a subset $S$ of $[n]$ , any minimal element of $Q(n)$ is less than or equal to either $\mathbf{p}(S)$ or $-\mathbf{p}(S)$ .

Proof.

Let $-\mathbf{m}_{k}$ be a minimal element of $Q(n)$ , where $k\in\{0,1,\dots\ell\}$ . We prove that there are $2^{n-1}$ subsets $S^{\prime}$ such that $-\mathbf{m}_{k}\preceq_{P}\mathbf{p}(S^{\prime})$ . Now $-\mathbf{m}_{k}$ is

(\underbrace{-1,\ldots,-1}_{k},\underbrace{1,\ldots,1}_{k+1},\underbrace{-1,\ldots,-1}_{n-2k-1}).

By Proposition 7, $\mathbf{p}(S^{\prime})$ is obtained from $-\mathbf{m}_{k}$ by applying addition and/or swap operators. We denote $\mathbf{p}(S^{\prime})$ by $(\mathbf{p}_{1},\mathbf{p}_{2})$ , where $\mathbf{p}_{1}\in P(2k+1),\,\mathbf{p}_{2}\in P(n-2k-1)$ . For a nonnegative integer $m\leq k$ , any $\mathbf{p}_{1}$ containing $m$ $-1$ ’s is greater than or equal to

(\underbrace{-1,\ldots,-1}_{k},\underbrace{1,\ldots,1}_{k+1})\in P(2k+1).

The number of elements $\mathbf{p}_{1}$ containing $m$ $-1$ ’s is $\binom{2k+1}{m}$ and the total number is as follows:

\binom{2k+1}{0}+\cdots+\binom{2k+1}{k}=2^{2k}.

On the other hand, any $\mathbf{p}_{2}\in P(n-2k-1)$ , the number of which is $2^{n-2k-1}$ , is obviously greater than or equal to $(-1,\ldots,-1)\in P(n-2k-1)$ . Therefore, we can obtain $2^{2k}\times 2^{n-2k-1}$ distinct subsets satisfying the condition, which contain no complementary pair, because otherwise $\mathbf{m}_{k}$ and $-\mathbf{m}_{k}$ are comparable by symmetry and this contradicts $\mathbf{m}_{k}\in Q(n)$

Consequently, for each subset $S$ of $[n]$ , either $-\mathbf{m}_{k}\preceq_{P}\mathbf{p}(S)$ or $-\mathbf{m}_{k}\preceq_{P}-\mathbf{p}(S)$ holds. ∎

In some cases, we can easily solve the partition problem.

Proof of Theorem 3.

Let $\mathbf{v}=-\mathbf{m}_{k}$ . It follows from Lemma 23 that $-\mathbf{m}_{k}\preceq_{Q}\mathbf{p}(S)$ or $-\mathbf{m}_{k}\preceq_{Q}-\mathbf{p}(S)$ for any $\mathbf{p}(S)\in Q(n)$ . Either way, using Theorem 2 (1) we have $|\mathbf{m}_{k}\cdot\mathbf{c}|\leq|\mathbf{p}(S)\cdot\mathbf{c}|$ . The left-hand side, the optimal value, is equal to $-\mathbf{m}_{k}\cdot\mathbf{c}$ . ∎

We obtain the following statement for the maximal element $\mathbf{m}_{k}$ of $Q(n)$ .

Corollary 24.

If $\mathbf{m}_{k}\cdot\mathbf{c}\geq 0$ , $\left(\mathbf{m}_{k}-\mathcal{S}^{(k,k+1)}(-\mathbf{m}_{k})\right)\cdot\mathbf{c}\leq 0$ (applicable for $k\neq 0$ ), and $\left(\mathbf{m}_{k}-\mathcal{A}^{(n)}(-\mathbf{m}_{k})\right)\cdot\mathbf{c}\leq 0$ (applicable for $k\neq(n-1)/2$ ) for some $k\in\{0,1,\dots\ell\}$ , then the subset $S$ such that $\mathbf{p}(S)=\mathbf{m}_{k}$ is a solution and the optimal value is $\mathbf{m}_{k}\cdot\mathbf{c}$ .

Proof.

Rewriting the three inequalities, we have

0\leq\mathbf{m}_{k}\cdot\mathbf{c}\leq\mathcal{S}^{(k,k+1)}(-\mathbf{m}_{k})\cdot\mathbf{c},\quad 0\leq\mathbf{m}_{k}\cdot\mathbf{c}\leq\mathcal{A}^{(n)}(-\mathbf{m}_{k})\cdot\mathbf{c}.

(5)

Since $\mathcal{S}^{(k,k+1)}(-\mathbf{m}_{k})\cdot\mathbf{c}\geq 0$ , $\mathcal{A}^{(n)}(-\mathbf{m}_{k})\cdot\mathbf{c}\geq 0$ and the elements covering the minimal element $-\mathbf{m}_{k}$ are only $\mathcal{S}^{(k,k+1)}(-\mathbf{m}_{k})$ for $k\neq 0$ and $\mathcal{A}^{(n)}(-\mathbf{m}_{k})$ for $k\neq(n-1)/2$ , it follows from Theorem 2 (1) and Lemma 23 that the candidate solutions are reduced to six elements: $\pm\mathbf{m}_{k},\pm\mathcal{S}^{(k,k+1)}(-\mathbf{m}_{k})$ , and $\pm\mathcal{A}^{(n)}(-\mathbf{m}_{k})$ . The inequalities (5) imply that the subsets $S$ such that $\mathbf{p}(S)=\pm\mathbf{m}_{k}$ are solutions and the optimal value is $\mathbf{m}_{k}\cdot\mathbf{c}$ . ∎

It is possible that these conditions could be written down for other elements as well. It is a future problem.

References

[1] B. Alidaee, F. Glover, G. A. Kochenberger, and C. Rego. A new modeling and solution approach for the number partitioning problem. Journal of Applied Mathematics and Decision Sciences, 2:113–121, 2005.
[2] C. Borgs, J. Chayes, and B. Pittel. Phase transition and finete-size scaling for the integer partitioning problem. Random Structures & Algorithms, 19:247–288, 2001.
[3] E. G. Coffman Jr. and G. S. Lueker. Probabilistic Analysis of Packing and Partitioning Algorithms. Wiley, Chichester, 1991.
[4] L. Fuksz and P. C. Pop. A hybrid genetic algorithm with variable neighborhood search approach to the number partitioning problem. In 8th International Conference on Hybrid Artificial Intelligence Systems, pages 649–658, 2013.
[5] M. R. Garey and D. S. Johnson. Computers and intractability: A guide to the theory of NP-completeness. W. H. Freeman, New York, 1979.
[6] I. P. Gent and T. Walsh. Phase transitions and annealed theories: Number partitioning as a case study. In W. Wahlster, editor, ECAI 96 : 12th European Conference on Artificial Intelligence, pages 170–174, Chichester, 1996. Wiley.
[7] A. K. Hartmann, A. Mann, and W. Radenbach. Solution-space structure of (some) optimization problems. Journal of Physics: Conference Series, 95:012011, 2008.
[8] E. Horowitz and S. Sahni. Computing partitions with applications to the knapsack problem. Journal of the ACM, 21:277–292, 1974.
[9] D. S. Johnson, C. R. Aragon, L. A. McGeoch, and C. Schevon. Optimization by simulated annealing: An experimental evaluation; part II, graph coloring and number partitioning. Operations Research, 39:378–406, 1991.
[10] N. Karmarkar and R. M. Karp. The differencing method of set partitioning. Technical Report, Computer Science Division, University of California, Berkeley, 82/113, 1982.
[11] R. M. Karp. Reducibility among combinatorial problems. In R. E. Miller, J. W. Thatcher, and J. Bohlinger, editors, Complexity of Computer Computations, pages 85–103, Boston, 1972. Springer.
[12] R. E. Korf. A complete anytime algorithm for number partitioning. Artificial Intelligence, 106:181–203, 1998.
[13] S. Kubo and K. Nishinari. An algebraic expression of the number partitioning problem. Discrete Applied Mathematics, 285:283–296, 10 2020.
[14] Lindström. Conjecture on a theorem similar to Sperner’s. In R. Guy, H. Hanani, N. Sauer, and J. Schönheim, editors, Combinatorial Structures and Their Applications, page 241, New York, 1970. Gordon and Breach.
[15] S. Mertens. Phase transition in the number partitioning problem. Physical Review Letters, 81:4281–4284, 1998.
[16] W. Ruml, J. T. Ngo, J. Marks, and S. M. Shieber. Easily searched encodings for number partitioning. Journal of Optimization Theory and Applications, 89:251–291, 1996.
[17] R. Schroeppels and A. Shamir. A ${T}={O}(2^{n/2})$ , ${S}={O}(2^{n/4})$ algorithm for certain NP-complete problems. SIAM Journal on computing, 10:456–464, 1981.
[18] R. P. Stanley. Weyl groups, the hard Lefschetz theorem, and the Sperner property. SIAM Journal on Algebraic and Discrete Methods, 1:168–184, 1980.
[19] R. P. Stanley. Some applications of algebra to combinatorics. Discrete Applied Mathematics, 34:241–277, 1991.
[20] B. D. Sullivan. On a conjecture of Andrica and Tomescu. Journal of Integer Sequences, 16:Article 13.3.1, 2013.
[21] L.-H. Tsai. Asymptotic analysis of an algorithm for balanced processor scheduling. SIAM Journal on Computing, 21:59–64, 1992.
[22] D. W. Wilson. Sequence A025591. The On-Line Encyclopedia of Integer Sequences, 2023.