Part-aware Shape Generation with Latent 3D Diffusion of Neural Voxel Fields
Abstract
This paper introduces a novel latent 3D diffusion model for generating neural voxel fields with precise part-aware structures and high-quality textures. In comparison to existing methods, this approach incorporates two key designs to guarantee high-quality and accurate part-aware generation. On one hand, we introduce a latent 3D diffusion process for neural voxel fields, allowing generation at significantly higher resolutions to capture rich textural and geometric details accurately. On the other hand, a part-aware shape decoder is introduced to integrate the part codes into the neural voxel fields, guiding accurate part decomposition and producing high-quality rendering results. Importantly, part-aware learning establishes structural relationships to generate texture information for similar regions, thereby facilitating high-quality rendering results. We evaluate our approach across eight different data classes through extensive experimentation and comparisons with state-of-the-art methods. The results demonstrate that our proposed method has superior generative capabilities in part-aware shape generation, outperforming existing state-of-the-art methods. Moreover, we have conducted image- and text-guided shape generation via the conditioned diffusion process, showcasing the advanced potential in multi-modal guided shape generation.
Index Terms:
3D diffusion models, shape generation, part-aware generation.I Introduction
Recent generative models have emerged for generating 3D shapes with different representations [1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11], among which neural field representation [12, 13, 14, 15] receives increasing attention due to many advantages such as integrated texture and shape generation. Despite the fast and notable progress made along this line of research, what has been largely missed is part/structure awareness. Most existing generative models based on neural fields are part-oblivious. They tend to generate 3D shapes in a holistic manner, without comprehending their compositional parts explicitly.
Generating 3D shapes with part information facilitates several downstream processing/tasks, such as editing, mix-and-match modeling, and segmentation learning. SPAGHETTI [16] and Part-NeRF [17] are two excellent part-aware generative models for 3D shape synthesis with neural field representation. Despite their strengths, there is still potential for enhancing the generative ability. SPAGHETTI relies on 3D supervision and mainly considers the geometry, ignoring the textured shape generation. On the other hand, Part-NeRF requires only 2D supervision but adopts a complex architecture with multiple neural radiance fields, leading to increased complexity in learning and subpar rendering outcomes. Moreover, both models perform object segmentation in an unsupervised manner, resulting in structurally insignificant information.
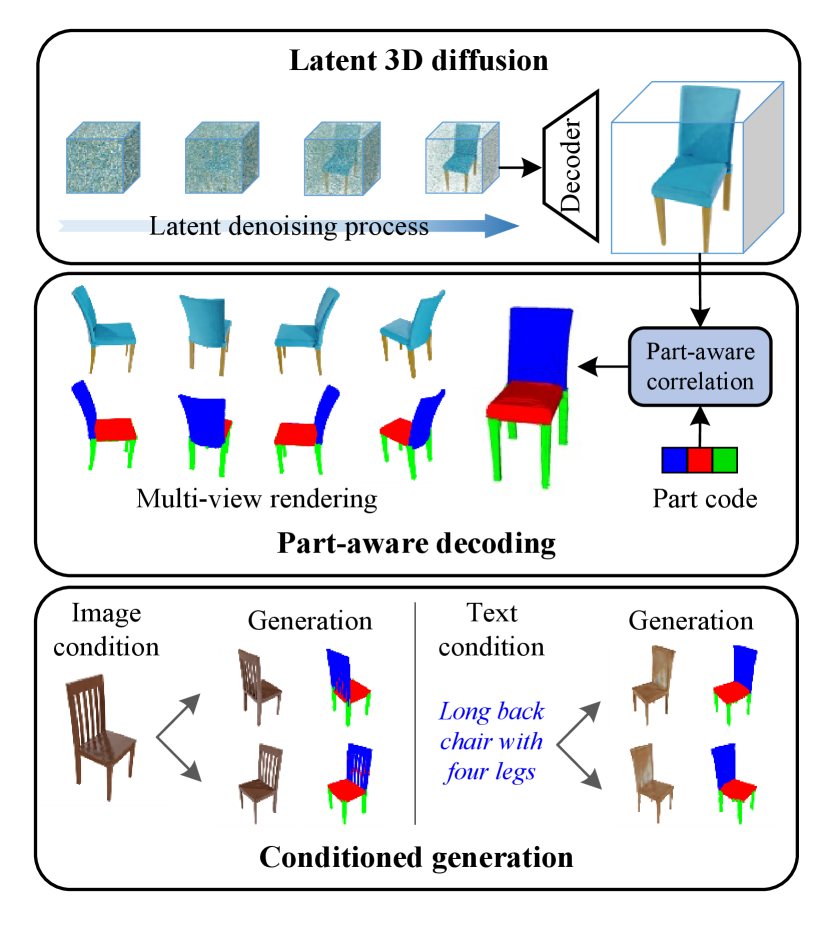
We propose a latent 3D diffusion model to generate neural voxel fields with accurate structural details in this paper. As shown in Fig 1, our network is composed of two parts, a latent 3D diffusion model of neural voxel fields and a part-aware shape decoder. Specifically, the latent 3D diffusion model utilizes the advantage of 3D convolution and employs the 3D denoising process in a latent space with a much lower resolution. On the other hand, the part-aware shape decoder incorporates the part code with the neural voxel field to learn part-aware relationships, guiding the precise generation of part-aware shapes and synthesizing high-quality rendering results.
Benefiting from the latent diffusion design, our model allows for shape generation with a much higher resolution than previous work (e.g., Matthias [18] and [19]). In particular, our method achieves resolution which is sufficient for representing rich geometric details of most common-seen objects. Furthermore, we integrate cross- and self-attention mechanisms into the part-aware decoder to establish robust dependencies between the part code and the voxel field. This integration aids in modeling the inherent relationships among various parts, significantly enhancing the precision of part segmentation. More importantly, learning part-aware information enhance the correlations between different regions, facilitating the geometry reconstruction and texture modeling in similar parts.
Our method adopts full volume learning part-learning and decoder-based part decomposition. This avoids the design of per-part neural fields which makes the decomposition and rendering overly complicated. Our architecture makes rendering rather simplistic and allows for high-quality rendering and hence accurate training.
The diffusion model admits multi-modal prompt for shape generation. For example, we have implemented image-conditioned diffusion enabling single-image guided generation. Concretely, a convolutional encoder is employed to extract features from the reference image. Subsequently, these obtained features are combined with the multi-scale features of the denoising UNet. As a result, the image information can effectively guide the shape generation. Moreover, we perform text-conditioned diffusion for text-guided shape generation. We utilize the general language model CLIP [20] to extract embedding for the text input, and perform cross-attention between the text embedding and the multi-scale features of the denoising UNet.
To make a fair comparison, we have implemented a supervised version of Part-NeRF. Similar to acquiring color, we use MLP layers to implicitly learn the part class probability of 3D position, obtaining the semantic part map via volume rendering. We conduct extensive experiments and compare to the state-of-the-art methods on eight classes of common-seen objects. The results show that our method achieves the best metrics (FID, MMD, COV) on all classes of data and higher-quality part-aware generation.
II Related Work
Diffusion Models for Shape Generation. Recent developments in diffusion models [21] have enabled the synthesis of 3D shapes through a variety of representations, including point cloud [22, 23], SDF [24], mesh [1], and neural field [12, 25, 26, 27, 28]. [29] proposes to utilize diffusion models to generate a compact wavelet representation with a pair of coarse and detail coefficient volumes. 3DShape2VecSet [30] introduces a novel representation for neural fields designed for generative diffusion models, which can encode 3D meshes or point clouds as neural fields. DiffFacto [31] learns the distribution of point clouds with part-level control including part-level sampling, mixing and interpolation. EXIM [32] use the text prompt as guidance, generating corresponding truncated signed distance field with diffusion models. However, most of above methods must adopt 3D input data as supervision, which is not available easily. Differently, this paper focus on generating neural voxel fields with differentiable rendering, enabling multi-view image as supervision.
Diffusion Models for Generating Neural Fields. Recently, the diffusion models [33, 21] have outperformed GANs in various 2D tasks [34, 35], which has inspired several diffusion-based methods to generate neural fields. DreamFusion [36] utilizes the 2D pretrained diffusion model as the distillation model to guide the generation of neural fields for the first time. Following this idea, a series of researches [37, 38, 39] can edit and generate neural fields via text prompt. However, they need to retrain the model for each generation, leading to a time-consuming generation process. Differently, another line of work directly applies the diffusion model to synthesize the neural fields without 2D pretrained diffusion models. DiffRF [18] applies the diffusion model to generate neural voxel fields, however, the 3D convolutional network takes up too much memory cost, limiting the generated resolution. SSD-NeRF [40] proposes a single-stage training paradigm to generate tri-plain fields with 2D convolutional network. In this paper, we propose a 3D latent diffusion model to directly generate neural voxel fields, enabling high-resolution and high-quality generation.
Part-aware Shape Generation. Previous methods [41, 42, 43, 16, 44, 45, 46] usually generate part-aware shapes with point cloud representation, however, they typically rely on 3D supervision. Recent PartNeRF [17] proposes to represent the different parts of a shape with different neural radiance fields, however, the divided parts are meaningless and multiple neural fields require much high computational resources. Differently, we carefully design the part relation module and supervise the model with 2D part mask, achieving precise and high-quality part-aware shape generation.
III Proposed Method
In this section, we introduce a latent 3D diffusion model to generate high-resolution part-aware neural voxel fields. As illustrated in Fig. 2, our approach consists of a latent 3D diffusion model and a part-aware shape decoder. Specifically, the latent 3D diffusion model compresses the object fields into the latent space with a much smaller spatial resolution, and then adopts the 3D UNet to conduct the diffusion process. This implementation facilitates the high resolution of the voxel field, allowing the high-quality rendering results. On the other hand, the part-aware shape decoder integrates the part codes into the voxel field, establishing relationships between different parts of the voxel field, and produces RGB images and semantic part maps through ray casting.
III-A Preliminary
III-A1 Neural Voxel Fields
Neural radiance fields (NeRFs) [47] represent 3D object implicitly and map the 3D position and view direction to the density and color emission , obtaining the novel view image via volume rendering. Based on NeRFs, DVGO [48] learns neural voxel fields to represent the object’s density and color. Specifically, there are a density voxel field and a feature voxel field, which are represented by and . We can acquire the density and color feature of position by querying from and directly, and the color feature and view direction are feed into multilayer perceptron (MLP) layers to get the color emission .
| (1) | ||||
Here, query() denotes the function querying the value of position from the voxel field , is the dimension of the modality, and is the spatial size of . With the ray casting, the RGB color of a given ray can be rendered by the following equation:
| (2) | ||||
where is the number of sampled points along the ray, is the probability of the termination at point , and is the distance between the sampled point and its adjacent point. In this way, the neural voxel field can be optimized by minimizing the mean square error of the rendered RGB and the ground truth color . After the optimization, we can represent the object with and . To simplify the formulation, we concatenate and along the first dimension, resulting in as the representation of the neural voxel field.
III-A2 Decoupled Diffusion Models
Diffusion models have shown great potential in generative tasks, however, they usually suffer from prolonged inference time. Recent decoupled diffusion models [49] propose to decouple the diffusion process to speed up the sampling process. The decoupled forward diffusion process is controlled by the analytic data attenuation and the standard Wiener process:
| (3) |
where is the time step, is the original voxel field and is the noisy field at time . is the analytic attenuation function describing the process of the original voxel field to zero field, and is the identity matrix. According to the derivation of [49], the corresponding reversed process is written as:
| (4) | ||||
where is the time interval, is the standard normal noise. Benefiting from the analytic attenuation function, we can solve the reversed process with arbitrary time intervals via analytic integration, improving the sampling efficiency greatly. In practice, we choose the particular constant form of : . In this way, the model is supervised by and simultaneously, and the training objective is formulated by:
| (5) |
where , and are the parameter and two outputs of the diffusion model respectively.
III-B Latent 3D Diffusion Model
Inspired by the preliminary work, we introduce a latent 3D diffusion model for the generation of high-resolution neural voxel fields. Our model offers two key advantages in comparison to previous diffusion-based methods. Unlike conventional 2D diffusion models [21, 50, 34, 51], we utilize 3D convolution to directly denoise the voxel field in 3D space, which enhances our modeling capabilities in terms of 3D geometry and consistency. On the other hand, due to the substantial computational demands of 3D convolution, training a 3D diffusion model with high-resolution voxel fields proves challenging, thereby constraining the generative quality. To address this limitation, we shift the denoising process to a latent space with reduced resolution, effectively eliminating constraints on voxel field resolution.
As shown in Fig. 2, the proposed latent 3D diffusion model comprises a 3D autoencoder and a 3D denoising UNet. The 3D autoencoder has an encoder for compressing the voxel field to the latent code and a decoder for recovering the original voxel field from , i.e. . Here, and represent the encoder and decoder of the 3D autoencoder; is the reconstructed voxel field. In practice, the resolution of is 64 lower than . After obtaining the latent code, we adopt a 3D UNet architecture to conduct the diffusion process in the latent space. Similar to Eq. 3, we sample the noisy code by adding the normal noise to . Then, the noisy code is fed into the 3D UNet with the time together, outputting the estimations of and . This process is formulated by:
| (6) | ||||
where is the parameter of 3D UNet, and are the predictions of and . Note that we use the special form of the attenuation function: .
For conditioned generation, we utilize the classifier-free [52] manner to synthesize shapes corresponding to the conditioned input. Specifically, the conditioned input is fed into a feature extractor, resulting in a feature embedding. We adopt the feature embedding as an additional input of the 3D UNet, thus we obtain the and by: , where is the feature embedding of the conditioned input.
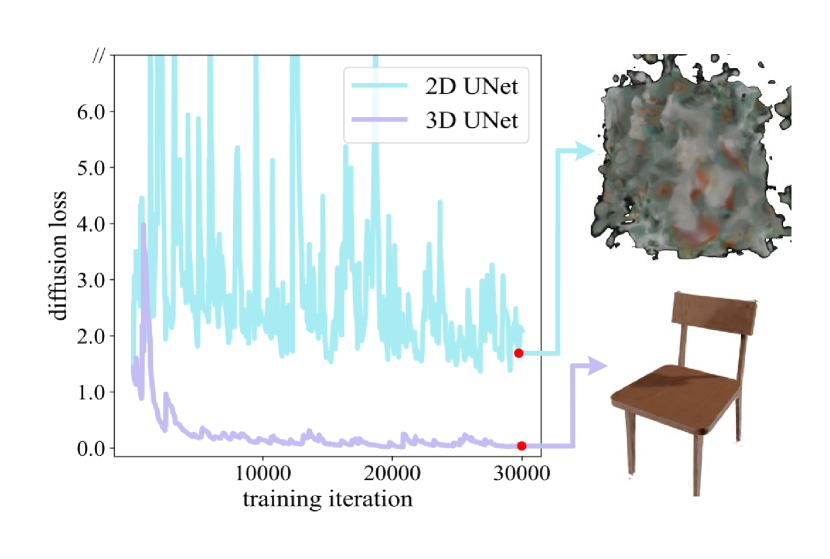
3D UNet vs. 2D UNet. Actually, though the latent code is a 4D tensor, it is possible to apply the 2D convolutional operator to this type of data. In practice, we can reshape into a 3D tensor, i.e. , thus adopting 2D UNet to model the denoising process. However, we found that the loss curve did not converge and it failed to obtain satisfactory results (details can be found in Sec. IV-C). We assume that the 2D UNet architecture hardly learns the 3D consistency of the voxel field, resulting in a perturbed result. In contrast, the 3D UNet architecture provides reasonable performance, demonstrating the necessity of adopting 3D UNet for denoising the neural voxel field.
| Method | Chair | Table | Airplane | Car | Guitar | Lamp | Laptop | Pistol | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| FID | KID | FID | KID | FID | KID | FID | KID | FID | KID | FID | KID | FID | KID | FID | KID | |
| Part-NeRF | 69.44 | 14.29 | 75.78 | 26.91 | 83.84 | 42.10 | 133.2 | 77.73 | 123.16 | 79.78 | 106.44 | 71.09 | 237.02 | 203.34 | 137.4 | 90.57 |
| EG3D | 104.24 | 36.71 | 116.88 | 76.47 | 108.82 | 64.77 | 162.79 | 128.52 | 111.83 | 67.85 | 131.52 | 70.24 | 232.65 | 198.93 | 126.33 | 80.00 |
| DiffRF | 43.92 | 7.25 | 56.28 | 22.61 | 53.33 | 19.85 | 88.33 | 26.65 | 80.55 | 49.25 | 99.77 | 43.48 | 198.32 | 81.59 | 65.83 | 45.19 |
| Ours | 27.70 | 5.19 | 44.27 | 21.74 | 36.01 | 21.10 | 62.27 | 29.66 | 62.79 | 30.70 | 75.31 | 17.43 | 146.17 | 107.64 | 60.58 | 34.23 |
III-C Part-aware Shape Decoder
After the denoising process of the latent 3D diffusion model, we can have a neural voxel field containing the density and color features. However, it can not provide the structural information and rendering results. Therefore, we propose a part-aware shape decoder to generate part-aware details and rendering results.
As shown in Fig. 2, to model the part-aware information, the shape decoder integrates the part code into the voxel field and utilizes the part attention to build the relations between different parts of the voxel field. Specifically, the part code is a learnable embedding and can be represented by , where is the number of parts, is the dimension of the embedding. To incorporate the part code into the neural field, we first project the reconstructed voxel field to have the same dimension as , and then flatten to be a 2D tensor like . Thus, we can utilize the multi-head cross-attention [53] to build a strong dependency between the part code and the voxel field. Moreover, to divide the voxel field accurately, we employ a self-attention to model the long-range relations between the different parts of the voxel field. After the cross-attention and self-attention, we reshape the tensor back to be a 4D voxel field. We formulate this process by the following equation:
| (7) |
where MHSA and MHCA represent the multi-head self-attention and cross-attention.
Incorporated with the part code, the refined voxel field contains both the color and structural information. In this way, we can utilize volume rendering to generate images and part maps of arbitrary views. Given a 3D position , we can query the point feature of the voxel field, and acquire the color emission and part class probability with MLP layers.
| (8) | ||||
where is the part class probability. In contrast to Eq. 3, we incorporate the part code into the MLP layers collectively to encode the structural information into individual points, thereby enhancing the generative intricacies. Subsequently, we derive the RGB image and semantic part map via ray casting following Eq. 2.

III-D End-to-end Training with Gradient Skip
Several methods [54, 55] in the literature have combined the diffusion model with the neural field decoder, typically training these two components independently. However, independent training neglects the consideration of noise in the prior term during the training of the neural field decoder, leading to biased learning of the decoder. In contrast, we propose an end-to-end training approach for the latent 3D diffusion model and the part-aware shape decoder, thereby avoiding noisy generation.
Gradient Skip. The diffusion model is trained on the latent space while the part-aware shape decoder is applied to the voxel field directly. Besides, there is the decoder of the 3D autoencoder between the two modules connecting the latent space and the voxel field space. Obviously, training the two modules jointly needs the backward propagation of the gradient of . However, this implementation incurs significant computational costs and hinders the effective feedback of gradients. To mitigate this problem, we propose to skip the gradient of , allowing the gradient of the part-aware shape decoder to directly propagate back to the latent space. Concretely, according to the Chain Rule, we have:
| (9) |
where is the rendering loss. We ignore the term to skip the gradient of the decoder in the 3D autoencoder, resulting in an efficient formulation of gradient calculation:
| (10) |
The main training objective is the summation of the diffusion loss and the rendering loss.
| (11) | ||||
where and are the rendered RGB image and part map from ray , and and are the corresponding ground truths; CE means the cross-entropy loss function. Since the predicted voxel field of the diffusion model is reasonable only with the time close to zero, we attach a time-dependent weight to the rendering loss: .
Except for the main training objective, we adopt two additional regularization loss functions. First, we conduct the total variation on the neural voxel fields to restrain the noise generating:
| (12) |
where denotes the squared difference between the value of -th channel in voxel: and the -th value in voxel , which can be extended to and . Moreover, we constrain the value of part code via its L2 norm attached with the weight 0.0001.
IV Experiments
IV-A Experimental Setup
IV-A1 Dataset
We collect eight categories of 3D objects from ShapeNet [56], including Chair, Table, Airplane, Car, Lamp, Guitar, Laptop, and Pistol. For each category, we random sample 500 objects, with a split of 450 for training and 50 for testing purposes. Utilizing BlenderProc [57], we render 100 views of each object at a resolution of 800800 resolution. With the posed images, we use the public code base [48] to generate neural voxel fields. For text-guided shape generation, we get the text labels of Chair and Table from [58].
| Method | Chair | Table | Airplane | Car | Guitar | Lamp | Laptop | Pistol | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MMD | COV | MMD | COV | MMD | COV | MMD | COV | MMD | COV | MMD | COV | MMD | COV | MMD | COV | |
| Part-NeRF | 1.17 | 60.4 | 1.26 | 56.4 | 0.48 | 39.6 | 0.64 | 23.8 | 0.26 | 31.7 | 1.57 | 59.4 | 0.86 | 31.7 | 0.34 | 48.5 |
| EG3D | 2.79 | 52.4 | 2.08 | 49.9 | 1.45 | 40.9 | 0.81 | 24.0 | 0.97 | 30.0 | 1.76 | 55.6 | 1.18 | 31.1 | 0.45 | 48.9 |
| DiffRF | 1.10 | 58.9 | 1.28 | 55.7 | 0.35 | 60.3 | 0.60 | 25.9 | 0.30 | 35.6 | 1.61 | 56.3 | 0.92 | 33.5 | 0.38 | 50.0 |
| Ours | 1.03 | 60.6 | 1.14 | 59.4 | 0.18 | 82.1 | 0.45 | 40.6 | 0.14 | 44.6 | 1.50 | 59.4 | 0.80 | 37.6 | 0.31 | 50.1 |
| Method | Chair | Table | Airplane | Car | Guitar | Lamp | Laptop | Pistol | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MMD | COV | MMD | COV | MMD | COV | MMD | COV | MMD | COV | MMD | COV | MMD | COV | MMD | COV | |
| Part-NeRF | 13.2 | 52.5 | 13.1 | 52.5 | 10.3 | 27.7 | 10.0 | 23.7 | 7.78 | 26.7 | 17.4 | 54.5 | 11.4 | 31.8 | 9.96 | 32.7 |
| EG3D | 20.2 | 38.5 | 18.5 | 47.6 | 9.39 | 42.0 | 14.2 | 22.1 | 10.5 | 30.3 | 21.9 | 43.9 | 16.0 | 31.9 | 9.98 | 34.1 |
| DiffRF | 13.5 | 50.8 | 13.4 | 54.3 | 9.95 | 30.3 | 9.41 | 28.8 | 7.01 | 30.5 | 17.8 | 53.9 | 13.4 | 32.0 | 9.52 | 36.1 |
| Ours | 12.3 | 53.1 | 12.4 | 57.4 | 6.99 | 51.5 | 8.78 | 36.6 | 6.49 | 36.5 | 16.2 | 55.5 | 11.0 | 37.8 | 9.34 | 36.7 |

IV-A2 Implementation Details
The resolution of the voxel field is 963, and the resolution of the latent code is 64 lower than the voxel field. We train the model for 100,000 iterations and we do not train the part-aware shape decoder for the first 20,000 iterations to warm up the latent 3D diffusion model. We set and for the part code. For each iteration, we sample 8192 rays of 5 random views to calculate the rendering loss. For the architecture of 3D UNet, we set the base channel to 96 and the channel multiplier is [1, 2, 4], resulting in 144M parameters of the whole model. We train the model in a single RTX 3090 GPU with batch size 2, taking up around 15,000M GPU memory cost.
IV-A3 Conditioned Generation
We performed two types of modality for conditioned generation: image and text. For image condition, we use Swin-S [59] as the image feature extractor to process the single image, and then concatenate the obtained features with the multi-scale features of the denoising UNet. For text condition, we utilize CLIP [20] to extract the text embedding and correlate it with the multi-scale features of the denoising UNet via the cross-attention mechanism.
IV-A4 Evaluation
We report the Frechet Inception Distance (FID) and Kernel Inception Distance (KID) to evaluate the quality of rendered images. We evaluate the two metrics at a resolution of 800800. In practice, we generate 200 objects and 10 views for each object to calculate metrics. We also report the Coverage (COV) and the Minimum Matching Distance (MMD) [60] using Chamfer distance and Earth Mover’s distance. MMD measures how likely it is that a generated shape looks like a test shape. COV measures how many shape variations are covered by the generated shapes.

IV-B Shape Generation
Quantitative comparison against state of the art. In Tab. I, Tab. II and Tab. III, We have conducted a quantitative comparison between our proposed method and state-of-the-art approaches. Tab. I reports the metrics of generated image quality, while Tab. II and Tab. III report the geometry metrics calculated by Chamfer distance and Earth Mover’s distance. EG3D [13] presents a GAN-based framework that introduces a sophisticated hybrid explicit-implicit network architecture for synthesizing the triplane representation. Despite its lightweight nature, the triplane representation struggles to encompass intricate details, resulting in unsatisfied rendering quality and geometry. Part-NeRF [17] employs multiple neural radiance fields to represent a single object, but the complex and redundant architecture increases the learning difficulty, ultimately yielding lower-quality results. DiffRF [18] also utilizes the diffusion model in 3D space; however, it directly applies the 3D UNet to the voxel field. This implementation imposes significant computational demands, constraining the resolution of the voxel fields and leading to sub-optimal performances. Leveraging the 3D latent diffusion design enables the generation of 3D shapes with enhanced geometric details, leading to the attainment of the highest MMD and COV metrics across all classes. Additionally, the part-aware shape decoder facilitates the establishment of relationships between distinct parts, thereby improving the rendering of different components and resulting in the best FID metric across all classes.
Qualitative comparison against state of the art. As depicted in Fig. 3, we plot the visual generations of various state-of-the-art methods. Leveraging the latent 3D diffusion model, we can generate high-resolution voxel fields, resulting in superior rendering quality. Similar to ours, Part-NeRF also produces part-aware rendering results. However, it employs an unsupervised approach that leads to the synthesis of meaningless structures. To ensure a fair comparison, we employ semantic part maps to supervise Part-NeRF, denoting this as Part-NeRF-S. As shown in Fig. 3, benefiting from the design of latent diffusion and part-aware shape decoder, our approach still outperforms Part-NeRF-S in both texture and part quality. Both quantitative and qualitative results indicate that the proposed method can generate accurate part-aware shapes and render high-quality images.
| Method | Chair | Airplane | ||||
|---|---|---|---|---|---|---|
| FID | MMD | COV | FID | MMD | COV | |
| with LD | 27.70 | 1.03 | 60.6 | 36.01 | 0.18 | 82.1 |
| without LD | 47.19 | 1.39 | 55.7 | 57.65 | 0.41 | 70.7 |
IV-C Ablation Studies
We ablate different components of the proposed method to show their importance.
| Method | Chair | Airplane | ||||
|---|---|---|---|---|---|---|
| FID | MMD | COV | FID | MMD | COV | |
| with PASD | 27.70 | 1.03 | 60.6 | 36.01 | 0.18 | 82.1 |
| without PASD | 29.18 | 1.05 | 59.5 | 38.23 | 0.21 | 79.3 |
Importance of the latent 3D diffusion. Different from previous methods, this paper proposes the latent 3D diffusion that transfers the diffusion process into latent space, increasing the generative resolution significantly and preserving the high-quality generation. We further apply the diffusion process to the voxel field directly to observe the performance change. Due to the limitation of computational cost, we set the resolution of voxel fields to 323232. Tab. IV reports the performance comparison. Without the latent diffusion, the FID drops a lot, and the geometry metric of MMD and COV drop 0.36 and 4.9, which shows the importance of latent diffusion. Moreover, we visualize the qualitative results of the two different settings in Fig. 5, and the results reveal that the latent 3D diffusion brings high-quality geometry and rendering details.
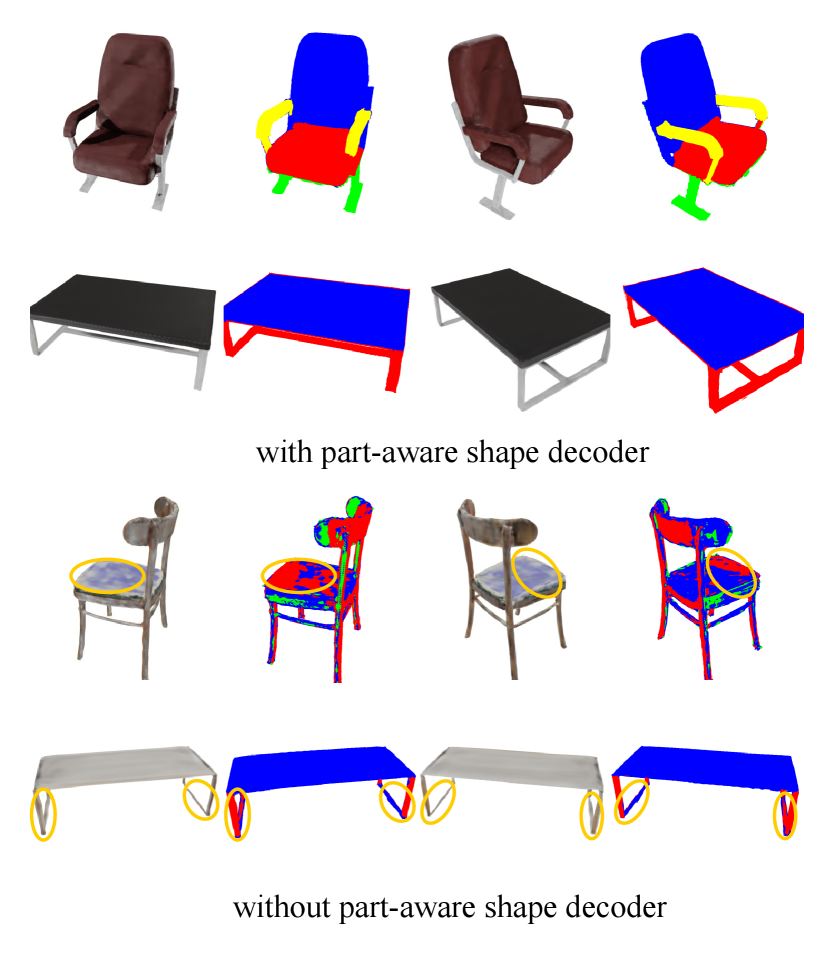
Importance of the part-aware shape decoder. The part-aware shape decoder incorporates the part code into the neural voxel field, generating the structural shape with accurate rendering results. To demonstrate its importance, we replace it with two independent MLPs, rendering the color and part maps from the voxel field directly. Tab. V shows that the part-aware shape decoder can bring more improvements in rendering quality. As depicted in Fig. 4, the part-aware shape decoder helps the model learn the accurate structural information, which allows for consistent rendering results of the local region.
Importance of the gradient skip. The gradient skip technique aims to reduce redundant gradient calculations and computational costs by jointly learning the latent 3D diffusion model and the part-aware shape decoder. In Fig. 11, we compare our method with the split training strategy, which does not utilize the gradient skip technique. It is evident from the comparison that the split training strategy lacking gradient skipping leads to the learning of a biased neural voxel field, consequently yielding inferior rendered images.

Importance of 3D UNet. We employ a 3D UNet as the network architecture to conduct the denoising process, and we have analyzed that the denoising network can be replaced by a 2D UNet possibly. However, we found that the 2D UNet failed to generate meaningful results as shown in Fig. 9. Compared to 3D UNet, the training loss curve of 2D UNet is not converged, culminating in a noisy generation. This observation indicates that it is necessary to utilize the 3D convolutional operator to extract features for the 3D voxel fields.
Effect of sampling steps. By leveraging rapid sampling from the decoupled diffusion model, we achieve satisfactory results in just 30 steps. Tab. VI presents a comparison of performance based on various sampling steps for chair generation. With an increase in the sampling step, performance shows a gradual improvement. Further increasing the sampling steps results in only a marginal improvement, suggesting that the generation quality is nearing saturation. It is observed that the sampling step has a greater impact on FID and KID metrics, highlighting its influence on image quality rather than geometry.
| Step | 10 | 20 | 30 | 40 | 50 |
|---|---|---|---|---|---|
| FID | 38.49 | 30.70 | 27.70 | 26.68 | 26.01 |
| KID | 7.25 | 6.15 | 5.19 | 5.08 | 5.01 |
| MMD | 1.10 | 1.05 | 1.03 | 1.03 | 1.01 |
| COV | 60.1 | 60.4 | 60.6 | 60.7 | 60.7 |
IV-D Shape Interpolation
Following the 2D diffusion model [50], we can utilize two different voxel fields to generate intermediate shapes with spherical linear interpolation [61]. As shown in Fig. 7, our model can achieve relatively smooth interpolation between the two shapes. In contrast, the model without the part-aware shape decoder generates unreasonable contents, which further indicates the effectiveness of the part-aware shape decoder. With the part-aware shape decoder, the generated intermediate shapes consistently maintain a precise structure, suggesting that the decoder effectively learns to decompose the neural voxel fields with the guidance of the part code.
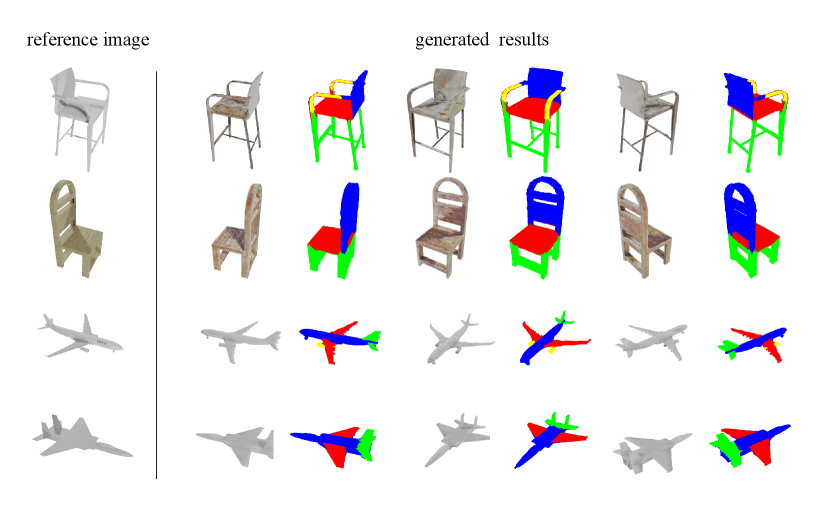
IV-E Single Image to Shape
Single image to shape can be seen as a conditional generation task in which we use an image as conditional input and generate a shape related to the image. In practice, we extract the multi-scale image features via the Swin backbone network, and then concatenate the obtained features with the multi-scale features of the denoising UNet. As shown in Fig. 6, given a reference image as a condition, our model can generate reasonable shapes with consistent geometry and accurate structure.
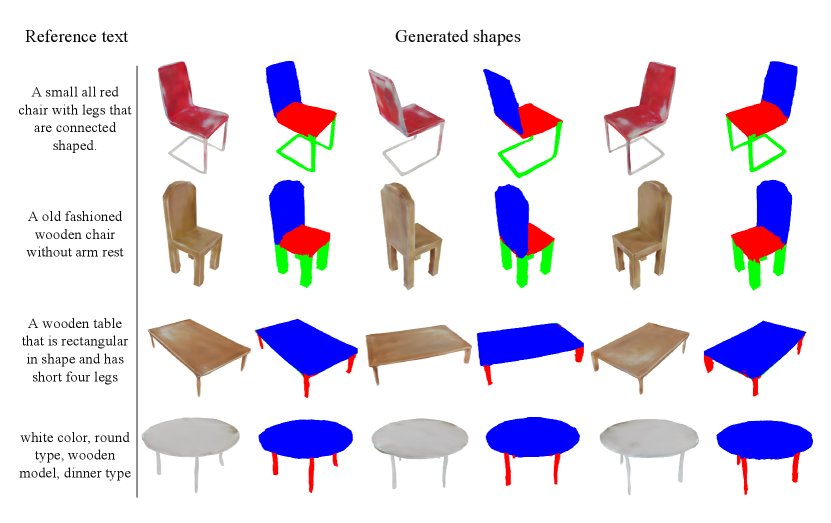
IV-F Text-guided Shape Generation
Text-guided shape generation is a form of conditioned generative method, where the text is embedded into a feature to control the generation process. We perform text-guided shape generation on Chairs and Tables. As shown in Fig. 8, our model is capable of generating reasonable shapes based on the provided texts. In fact, the textual condition provides a relatively coarse level of control for generation, resulting in better geometric accuracy compared to texture detail.
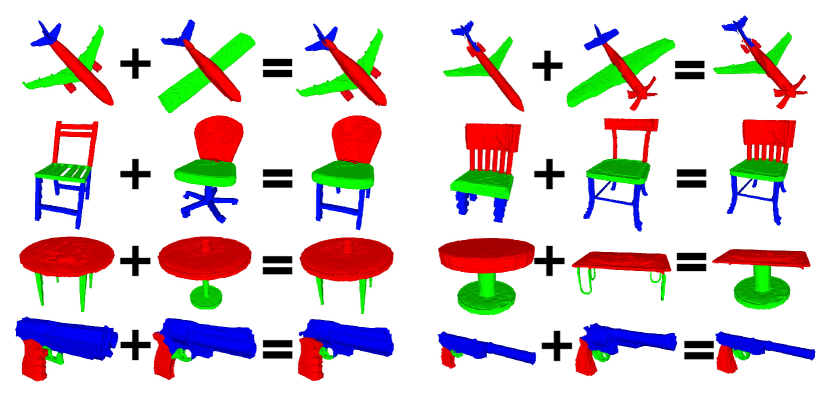
IV-G Shape Mixing
Due to the part-aware nature of the generated shapes, it becomes feasible to combine parts from different shapes to create new designs. Notably, these shapes conform to a shared coordinate system, enabling the direct integration of disparate parts to create a cohesive and compact shape. Fig. 10 illustrates the visual results of shape mixing on four different object categories. Our approach excels in producing clear part shapes, facilitating the composition of diverse shapes.
V Conclusion
In this paper, we introduce a method for generating part-aware neural voxel fields using latent 3D diffusion models. The proposed method consists of a latent 3D diffusion model and a part-aware shape decoder. On one hand, the latent 3D diffusion model enhances the high resolution of the neural voxel fields, thereby improving the geometric details and the quality of rendered images. On the other hand, the part-aware shape decoder integrates part codes into voxel fields to generate part-aware shapes with high-quality rendered images. We evaluate the effectiveness of our method on four classes by comparing it against state-of-the-art diffusion-based approaches, demonstrating its efficacy in generating precise part-aware shapes.
References
- [1] J. Gao, T. Shen, Z. Wang, W. Chen, K. Yin, D. Li, O. Litany, Z. Gojcic, and S. Fidler, “Get3d: A generative model of high quality 3d textured shapes learned from images,” Advances In Neural Information Processing Systems, 2022.
- [2] J. Wu, C. Zhang, T. Xue, B. Freeman, and J. Tenenbaum, “Learning a probabilistic latent space of object shapes via 3d generative-adversarial modeling,” Advances in neural information processing systems, 2016.
- [3] Y. Siddiqui, J. Thies, F. Ma, Q. Shan, M. Nießner, and A. Dai, “Texturify: Generating textures on 3d shape surfaces,” in European Conference on Computer Vision, 2022.
- [4] P. Henzler, N. J. Mitra, and T. Ritschel, “Escaping plato’s cave: 3d shape from adversarial rendering,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 2019.
- [5] B. Leng, C. Zhang, X. Zhou, C. Xu, and K. Xu, “Learning discriminative 3d shape representations by view discerning networks,” IEEE transactions on visualization and computer graphics, 2018.
- [6] Y. Guan, H. Liu, K. Liu, K. Yin, R. Hu, O. van Kaick, Y. Zhang, E. Yumer, N. Carr, R. Mech et al., “Fame: 3d shape generation via functionality-aware model evolution,” IEEE Transactions on Visualization and Computer Graphics, 2020.
- [7] Z. Ye, M. Xia, Y. Sun, R. Yi, M. Yu, J. Zhang, Y.-K. Lai, and Y.-J. Liu, “3d-carigan: an end-to-end solution to 3d caricature generation from normal face photos,” IEEE Transactions on Visualization and Computer Graphics, 2021.
- [8] Q. Deng, L. Ma, A. Jin, H. Bi, B. H. Le, and Z. Deng, “Plausible 3d face wrinkle generation using variational autoencoders,” IEEE Transactions on Visualization and Computer Graphics, 2021.
- [9] A. Mao, C. Dai, Q. Liu, J. Yang, L. Gao, Y. He, and Y.-J. Liu, “Std-net: Structure-preserving and topology-adaptive deformation network for single-view 3d reconstruction,” IEEE Transactions on Visualization and Computer Graphics, pp. 1785–1798, 2021.
- [10] K. Mo, S. Zhu, A. X. Chang, L. Yi, S. Tripathi, L. J. Guibas, and H. Su, “Partnet: A large-scale benchmark for fine-grained and hierarchical part-level 3d object understanding,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2019.
- [11] X. Wang, Y. Xu, K. Xu, A. Tagliasacchi, B. Zhou, A. Mahdavi-Amiri, and H. Zhang, “Pie-net: Parametric inference of point cloud edges,” Advances in neural information processing systems, 2020.
- [12] E. R. Chan, M. Monteiro, P. Kellnhofer, J. Wu, and G. Wetzstein, “pi-gan: Periodic implicit generative adversarial networks for 3d-aware image synthesis,” in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2021.
- [13] E. R. Chan, C. Z. Lin, M. A. Chan, K. Nagano, B. Pan, S. De Mello, O. Gallo, L. J. Guibas, J. Tremblay, S. Khamis et al., “Efficient geometry-aware 3d generative adversarial networks,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022.
- [14] J. Gu, L. Liu, P. Wang, and C. Theobalt, “Stylenerf: A style-based 3d aware generator for high-resolution image synthesis,” in The Tenth International Conference on Learning Representations, 2022.
- [15] P. Zhou, L. Xie, B. Ni, and Q. Tian, “CIPS-3D: A 3d-aware generator of gans based on conditionally-independent pixel synthesis,” CoRR, 2021.
- [16] A. Hertz, O. Perel, R. Giryes, O. Sorkine-Hornung, and D. Cohen-Or, “Spaghetti: Editing implicit shapes through part aware generation,” ACM Transactions on Graphics, 2022.
- [17] K. Tertikas, P. Despoina, B. Pan, J. J. Park, M. A. Uy, I. Emiris, Y. Avrithis, and L. Guibas, “Partnerf: Generating part-aware editable 3d shapes without 3d supervision,” in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2023.
- [18] N. Müller, Y. Siddiqui, L. Porzi, S. R. Bulo, P. Kontschieder, and M. Nießner, “Diffrf: Rendering-guided 3d radiance field diffusion,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2023.
- [19] A. Karnewar, N. J. Mitra, A. Vedaldi, and D. Novotny, “Holofusion: Towards photo-realistic 3d generative modeling,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 2023.
- [20] A. Radford, J. W. Kim, C. Hallacy, A. Ramesh, G. Goh, S. Agarwal, G. Sastry, A. Askell, P. Mishkin, J. Clark et al., “Learning transferable visual models from natural language supervision,” in International conference on machine learning, 2021.
- [21] J. Ho, A. Jain, and P. Abbeel, “Denoising diffusion probabilistic models,” Advances in neural information processing systems, 2020.
- [22] P. Achlioptas, O. Diamanti, I. Mitliagkas, and L. Guibas, “Learning representations and generative models for 3d point clouds,” in International conference on machine learning, 2018.
- [23] G. Sharma, D. Liu, S. Maji, E. Kalogerakis, S. Chaudhuri, and R. Měch, “Parsenet: A parametric surface fitting network for 3d point clouds,” in European conference on computer vision, 2020.
- [24] G. Chou, Y. Bahat, and F. Heide, “Diffusion-sdf: Conditional generative modeling of signed distance functions,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 2023.
- [25] I. Skorokhodov, S. Tulyakov, Y. Wang, and P. Wonka, “Epigraf: Rethinking training of 3d gans,” Advances in Neural Information Processing Systems, 2022.
- [26] K. Schwarz, A. Sauer, M. Niemeyer, Y. Liao, and A. Geiger, “Voxgraf: Fast 3d-aware image synthesis with sparse voxel grids,” Advances in Neural Information Processing Systems, 2022.
- [27] T. DeVries, M. A. Bautista, N. Srivastava, G. W. Taylor, and J. M. Susskind, “Unconstrained scene generation with locally conditioned radiance fields,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021.
- [28] Y. Liao, K. Schwarz, L. Mescheder, and A. Geiger, “Towards unsupervised learning of generative models for 3d controllable image synthesis,” in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2020.
- [29] J. Hu, K.-H. Hui, Z. Liu, R. Li, and C.-W. Fu, “Neural wavelet-domain diffusion for 3d shape generation, inversion, and manipulation,” ACM Transactions on Graphics, 2024.
- [30] B. Zhang, J. Tang, M. Niessner, and P. Wonka, “3dshape2vecset: A 3d shape representation for neural fields and generative diffusion models,” ACM Transactions on Graphics, 2023.
- [31] G. K. Nakayama, M. A. Uy, J. Huang, S.-M. Hu, K. Li, and L. Guibas, “Difffacto: Controllable part-based 3d point cloud generation with cross diffusion,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 2023.
- [32] Z. Liu, J. Hu, K.-H. Hui, X. Qi, D. Cohen-Or, and C.-W. Fu, “Exim: A hybrid explicit-implicit representation for text-guided 3d shape generation,” ACM Transactions on Graphics, 2023.
- [33] J. Sohl-Dickstein, E. Weiss, N. Maheswaranathan, and S. Ganguli, “Deep unsupervised learning using nonequilibrium thermodynamics,” in International conference on machine learning, 2015.
- [34] P. Dhariwal and A. Nichol, “Diffusion models beat gans on image synthesis,” Advances in neural information processing systems, 2021.
- [35] Y. Cao, X. Meng, P. Mok, T.-Y. Lee, X. Liu, and P. Li, “Animediffusion: Anime diffusion colorization,” IEEE Transactions on Visualization and Computer Graphics, 2024.
- [36] B. Poole, A. Jain, J. T. Barron, and B. Mildenhall, “Dreamfusion: Text-to-3d using 2d diffusion,” in The Eleventh International Conference on Learning Representations, 2023.
- [37] G. Qian, J. Mai, A. Hamdi, J. Ren, A. Siarohin, B. Li, H.-Y. Lee, I. Skorokhodov, P. Wonka, S. Tulyakov et al., “Magic123: One image to high-quality 3d object generation using both 2d and 3d diffusion priors,” arXiv preprint arXiv:2306.17843, 2023.
- [38] X. Long, Y.-C. Guo, C. Lin, Y. Liu, Z. Dou, L. Liu, Y. Ma, S.-H. Zhang, M. Habermann, C. Theobalt et al., “Wonder3d: Single image to 3d using cross-domain diffusion,” arXiv preprint arXiv:2310.15008, 2023.
- [39] Z. Zhou and S. Tulsiani, “Sparsefusion: Distilling view-conditioned diffusion for 3d reconstruction,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2023.
- [40] H. Chen, J. Gu, A. Chen, W. Tian, Z. Tu, L. Liu, and H. Su, “Single-stage diffusion nerf: A unified approach to 3d generation and reconstruction,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 2023.
- [41] R. Li, X. Li, K.-H. Hui, and C.-W. Fu, “Sp-gan: Sphere-guided 3d shape generation and manipulation,” ACM Transactions on Graphics (TOG), 2021.
- [42] D. Petrov, M. Gadelha, R. Měch, and E. Kalogerakis, “Anise: Assembly-based neural implicit surface reconstruction,” IEEE Transactions on Visualization and Computer Graphics, 2023.
- [43] R. Wu, Y. Zhuang, K. Xu, H. Zhang, and B. Chen, “Pq-net: A generative part seq2seq network for 3d shapes,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020.
- [44] Z. Hao, H. Averbuch-Elor, N. Snavely, and S. Belongie, “Dualsdf: Semantic shape manipulation using a two-level representation,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020.
- [45] J. Koo, S. Yoo, M. H. Nguyen, and M. Sung, “Salad: Part-level latent diffusion for 3d shape generation and manipulation,” in Proceedings of the IEEE/CVF International Conference on Computer Vision, 2023.
- [46] C. Zhu, K. Xu, S. Chaudhuri, L. Yi, L. J. Guibas, and H. Zhang, “Adacoseg: Adaptive shape co-segmentation with group consistency loss,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020.
- [47] B. Mildenhall, P. Srinivasan, M. Tancik, J. Barron, R. Ramamoorthi, and R. Ng, “Nerf: Representing scenes as neural radiance fields for view synthesis,” in European conference on computer vision, 2020.
- [48] C. Sun, M. Sun, and H.-T. Chen, “Direct voxel grid optimization: Super-fast convergence for radiance fields reconstruction,” in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2022.
- [49] Y. Huang, Z. Qin, X. Liu, and K. Xu, “Decoupled diffusion models: Simultaneous image to zero and zero to noise,” arXiv preprint arXiv:2306.13720, 2023.
- [50] J. Song, C. Meng, and S. Ermon, “Denoising diffusion implicit models,” in ICLR, 2021.
- [51] R. Rombach, A. Blattmann, D. Lorenz, P. Esser, and B. Ommer, “High-resolution image synthesis with latent diffusion models,” in Proceedings of the IEEE/CVF conference on computer vision and pattern recognition, 2022.
- [52] J. Ho and T. Salimans, “Classifier-free diffusion guidance,” arXiv preprint arXiv:2207.12598, 2022.
- [53] A. Vaswani, N. Shazeer, N. Parmar, J. Uszkoreit, L. Jones, A. N. Gomez, Ł. Kaiser, and I. Polosukhin, “Attention is all you need,” Advances in neural information processing systems, 2017.
- [54] E. Dupont, H. Kim, S. M. A. Eslami, D. J. Rezende, and D. Rosenbaum, “From data to functa: Your data point is a function and you can treat it like one,” in International Conference on Machine Learning, 2022.
- [55] M. A. Bautista, P. Guo, S. Abnar, W. Talbott, A. Toshev, Z. Chen, L. Dinh, S. Zhai, H. Goh, D. Ulbricht et al., “Gaudi: A neural architect for immersive 3d scene generation,” Advances in Neural Information Processing Systems, 2022.
- [56] A. X. Chang, T. Funkhouser, L. Guibas, P. Hanrahan, Q. Huang, Z. Li, S. Savarese, M. Savva, S. Song, H. Su et al., “Shapenet: An information-rich 3d model repository,” arXiv preprint arXiv:1512.03012, 2015.
- [57] M. Denninger, M. Sundermeyer, D. Winkelbauer, D. Olefir, T. Hodan, Y. Zidan, M. Elbadrawy, M. Knauer, H. Katam, and A. Lodhi, “Blenderproc: Reducing the reality gap with photorealistic rendering,” in International Conference on Robotics: Sciene and Systems, RSS 2020, 2020.
- [58] K. Chen, C. B. Choy, M. Savva, A. X. Chang, T. Funkhouser, and S. Savarese, “Text2shape: Generating shapes from natural language by learning joint embeddings,” in Asian Conference on Computer Vision, 2019.
- [59] Z. Liu, Y. Lin, Y. Cao, H. Hu, Y. Wei, Z. Zhang, S. Lin, and B. Guo, “Swin transformer: Hierarchical vision transformer using shifted windows,” in Proceedings of the IEEE/CVF international conference on computer vision, 2021.
- [60] P. Achlioptas, O. Diamanti, I. Mitliagkas, and L. J. Guibas, “Learning representations and generative models for 3d point clouds,” in Proceedings of the 35th International Conference on Machine Learning, 2018.
- [61] K. Shoemake, “Animating rotation with quaternion curves,” in Proceedings of the 12th annual conference on Computer graphics and interactive techniques, 1985.
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/6ce71764-5fb9-42d7-8853-d8c8ebcbeb9c/hyx.jpg) |
Yuhang Huang received the bachelor’s degree from the University of Shanghai for Science and Technology, Shanghai, China, in 2019, and the master’s degree from Shanghai University, Shanghai, China, in 2022. He is currently pursuing the Ph.D. degree at the National University of Defense Technology, Changsha, China. His research interests include computer vision, graphics, and generative models. |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/6ce71764-5fb9-42d7-8853-d8c8ebcbeb9c/zsl.jpg) |
Shilong Zou received the bachelor’s degree from the University of Dalian Maritime University, Dalian, 2023. He is currently pursuing the master’s degree at the National University of Defense Technology, Changsha, China. His research interests include computer vision and generative models. |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/6ce71764-5fb9-42d7-8853-d8c8ebcbeb9c/lxw.png) |
Xinwang Liu received his PhD degree from National University of Defense Technology (NUDT), China. He is now Professor of School of Computer, NUDT. His current research interests include kernel learning and unsupervised feature learning. Dr. Liu has published 60+ peer-reviewed papers, including those in highly regarded journals and conferences such as IEEE T-PAMI, IEEE T-KDE, IEEE T-IP, IEEE T-NNLS, IEEE T-MM, IEEE T-IFS, ICML, NeurIPS, ICCV, CVPR, AAAI, IJCAI, etc. He serves as the associated editor of Information Fusion Journal. More information can be found at https://xinwangliu.github.io/. |
![[Uncaptioned image]](https://cdn.awesomepapers.org/papers/6ce71764-5fb9-42d7-8853-d8c8ebcbeb9c/kevinxu.jpg) |
Kai Xu (Senior Member, IEEE) received the Ph.D. degree in computer science from the National University of Defense Technology (NUDT), Changsha, China, in 2011. From 2008 to 2010, he worked as a Visiting Ph.D. degree with the GrUVi Laboratory, Simon Fraser University, Burnaby, BC, Canada. He is currently a Professor with the School of Computer Science, NUDT. He is also an Adjunct Professor with Simon Fraser University. His current research interests include data-driven shape analysis and modeling, and 3-D vision and robot perception and navigation. |