Parameterized Multi-observable Sum Uncertainty Relations

The uncertainty principle is one of the cornerstones of quantum mechanics, which reveals the intrinsic differences between classical and quantum world. The uncertainty principle was firstly introduced by Heisenberg in 1927 Heisenberg (1927). It shows that if one measures the momentum of a particle with certainty, one can not measure its position with certainty at the same time. Since then a lot of research works have been dedicated to interpret the uncertainty relations via different forms, such as in terms of quantum variance Nielsen and Chuang (2002); Robertson (1929a); Schrödinger (1930); Maccone and Pati (2014); Kennard (1927); Schrödinger (1930); Robertson (1929b); Mondal et al. (2017); Chiew and Gessner (2022); Tóth and Fröwis (2022), entropy Maassen and Uffink (1988); Wu et al. (2009); Coles et al. (2017), noise and disturbance Busch et al. (2013), successive measurement Deutsch (1983); Distler and Paban (2013), majorization technique Puchała et al. (2013); Friedland et al. (2013), skew information Luo (2003); Zhang et al. (2021a); Zhang and Fei (2021); Ma et al. (2022) etc. These uncertainty relations play an important role in a wide range of applications such as entanglement detection Gühne (2004); Zhang and Fei (2020); Zhang et al. (2021b), quantum metrology Giovannetti et al. (2006), quantum steering Schneeloch et al. (2013), quantum gravity Hall (2005) and quantum cryptography Fuchs and Peres (1996).

Robertson Robertson (1929a) generalized the variance-based uncertainty relation for position and momentum to any two observables $A$ and $B$,

$$\Delta A\Delta B\geq\frac{1}{2}|\langle\psi|[A,B]|\psi\rangle|,$$

(1)

where $\Delta$ stands for the standard deviation of the observable with respect to a fixed state $|\psi\rangle$ and $[A,B]$ represents the commutator of the observables $A$ and $B$. Eq. (1) was later improved by Schrödinger Schrödinger (1930),

$$\Delta A\Delta B\geq\frac{1}{2}\sqrt{|\langle\{A,B\}\rangle-\langle A\rangle\langle B\rangle|^{2}+|\langle[A,B]\rangle|^{2}}.$$

(2)

Here, the lower bounds of the inequalities (1) and (2) may vanish even if the observables $A$ and $B$ are not commutative. For instance, when the measured state $|\psi\rangle$ is an eigenvector of either $A$ or $B$, the right hands of the inequality (1) and (2) are trivially zero. To overcome the flaw, uncertainty relations with respect to the sum of variances have been presented by Maccone and Pati Maccone and Pati (2014),

	$\displaystyle\Delta^{2}A+\Delta^{2}B$	$\displaystyle\geq\pm i\langle\psi|[A,B]|\psi\rangle+|\langle\psi|A\pm iB|\psi^{\perp}\rangle|^{2},$		(3)
	$\displaystyle\Delta^{2}$	$\displaystyle A+\Delta^{2}B\geq\frac{1}{2}\Delta^{2}(A+B),$		(4)

where the signs $\pm$ on the right-hand side of (3) are taken so that the $\pm i\langle\psi|[A,B]|\psi\rangle$ is positive, $|\psi^{\perp}\rangle$ satisfies $\langle\psi|\psi^{\perp}\rangle=0$. The lower bound in (3) is nonzero for most choices of $|\psi^{\perp}\rangle$ if $A$ and $B$ are not commutative.

Besides the variance-based uncertainty relations with respect to pairs of non-commutative observables, the uncertainty relations related to three non-commutative observables such as the three components of spins and angular momentums Kechrimparis and Weigert (2014); Dammeier et al. (2015); Ma et al. (2017) have been also investigated. The variance-based uncertainty relations for general multiple observables have been further studied either in summation form Chen et al. (2016); Chen and Fei (2015); Chen et al. (2019) or in product form Qin et al. (2016); Xiao and Jing (2016). For instance, Song $et\ al.$ derived an elegant variance-based uncertainty relation in Song et al. (2017),

$$\sum_{i=1}^{N}\Delta_{\rho}^{2}(A_{i})\geq\frac{1}{N}\Delta_{\rho}^{2}(\sum_{i=1}^{N}A_{i})+\frac{2}{N^{2}(N-1)}\Big{[}\sum_{1\leq i<j\leq N}\Delta_{\rho}(A_{i}-A_{j})\Big{]}^{2}.$$

(5)

Recently, based on the inequalities of vector norm, Zhang $et\ al.$ Zhang et al. (2023) proposed an improved variance-based sum uncertainty relation for $N$ arbitrary incompatible observables,

	$\displaystyle\sum_{i=1}^{N}\Delta_{\rho}^{2}(A_{i})\geq\max_{x\in\{0,1\}}$	$\displaystyle\frac{1}{2N-2}\bigg{\{}\frac{2}{N(N-1)}\Big{[}\sum_{1\leq i<j\leq N}\Delta_{\rho}(A_{i}+(-1)^{x}A_{j})\Big{]}^{2}$		(6)
		$\displaystyle+\sum_{1\leq i<j\leq N}\Delta_{\rho}^{2}(A_{i}+(-1)^{x+1}A_{j})\bigg{\}}.$

This paper is aimed to improve these uncertainty relations for $N$ arbitrary observables. Motivated by the skew information-based uncertainty relations proposed in Zhang et al. (2023) and Li et al. (2022), we combine the parameterized parallelogram law of vector norm with Cauchy-Schwarz inequality to improve the lower bounds of uncertainty relations for $N$ observables.

Denote $H_{d}$ the Hilbert space with $d$ dimension. Let $G=(g_{ij})_{l\times p}$ be a rectangular matrix with entries $g_{ij}$. The vectorization of $G$ is given by the vector $|G\rangle=(g_{11},\dots,g_{l1},\dots,g_{1p},\dots,g_{lp})^{t}$ with $t$ denoting the transpose. It is verified that $|GT\rangle=(I\otimes G)|T\rangle$ for any matrix $T$ and identity $I$ in suitable size. The quantum variance of any quantum state $\rho$ on $H_{d}$ with respect to an observable $M$ is defined by

	$\displaystyle\Delta^{2}_{\rho}(M)$	$\displaystyle={\rm Tr}(\rho M^{2})-[{\rm Tr}(\rho M)]^{2}={\rm Tr}(\sqrt{\rho}(\delta M)^{2}\sqrt{\rho})$		(7)
		$\displaystyle=\langle\delta M\sqrt{\rho}|\delta M\sqrt{\rho}\rangle=\langle\sqrt{\rho}|I_{d}\otimes(\delta M)^{2}|\sqrt{\rho}\rangle$
		$\displaystyle=\|I_{d}\otimes\delta M|\sqrt{\rho}\rangle\|^{2},$

where $I_{d}$ is the identity operator in $H_{d}$, $\delta M=M-{\rm Tr}(\rho M)$, $|\sqrt{\rho}\rangle$ denotes the vectorization of $\sqrt{\rho}$ and $\|\cdot\|$ the $2$-norm of a vector. Especially, when the quantum state $\rho$ is pure, that is $\rho=|\psi\rangle\langle\psi|$, one has $\Delta^{2}_{\rho}(M)=\|\delta M|\psi\rangle\|^{2}$. By using the parallelogram law of vector $2$-norm,

$$(2N-2)\sum_{i=1}^{N}\|a_{i}\|^{2}=\sum_{1\leq i<j\leq N}\|a_{i}+a_{j}\|^{2}+\sum_{1\leq i<j\leq N}\|a_{i}-a_{j}\|^{2}$$

(8)

for a set of vectors $a_{i}$, $i=1,...,N$, we have the following uncertainty relation.

[Proof] For all $x\in\{0,1\}$ and $y\in\{0,1\}$, the following parameterized parallelogram equality holds for $2$-norm of any vectors $a_{i}$,

	$\displaystyle\sum_{i=1}^{N}\|a_{i}\|^{2}=$	$\displaystyle\frac{1}{(1+\alpha^{2})(N-1)}\Big{[}\sum_{1\leq i<j\leq N}\|\alpha^{1-x}a_{i}+(-1)^{y}\alpha^{x}a_{j}\|^{2}$		(10)
		$\displaystyle+\sum_{1\leq i<j\leq N}\|\alpha^{x}a_{i}+(-1)^{1-y}\alpha^{1-x}a_{j}\|^{2}\Big{]}.$

Using the Cauchy-Schwarz inequality,

$$\sum_{1\leq i<j\leq N}\|\alpha^{1-x}a_{i}+(-1)^{y}\alpha^{x}a_{j}\|^{2}\geq\frac{2}{N(N-1)}\Big{[}\sum_{1\leq i<j\leq N}\|\alpha^{1-x}a_{i}+(-1)^{y}\alpha^{x}a_{j}\|\Big{]}^{2},$$

(11)

we obtain

	$\displaystyle\sum_{i=1}^{N}\|a_{i}\|^{2}\geq$	$\displaystyle\frac{1}{(1+\alpha^{2})(N-1)}\bigg{\{}\frac{2}{N(N-1)}\Big{[}\sum_{1\leq i<j\leq N}\|\alpha^{1-x}a_{i}+(-1)^{y}\alpha^{x}a_{j}\|\Big{]}^{2}$		(12)
		$\displaystyle+\sum_{1\leq i<j\leq N}\|\alpha^{x}a_{i}+(-1)^{1-y}\alpha^{1-x}a_{j}\|^{2}\bigg{\}}.$

Set $\|a_{i}\|=\|I_{d}\otimes\delta A_{i}|\sqrt{\rho}\rangle\|=\Delta_{\rho}A_{i}$ and $\|\alpha^{1-x}a_{i}+(-1)^{y}\alpha^{x}a_{j}\|=\Delta_{\rho}(\alpha^{1-x}A_{i}+(-1)^{y}\alpha^{x}A_{j})$. We have

	$\displaystyle\sum_{i=1}^{N}\Delta_{\rho}^{2}(A_{i})\geq$	$\displaystyle\frac{1}{(1+\alpha^{2})(N-1)}\bigg{\{}\frac{2}{N(N-1)}\Big{[}\sum_{1\leq i<j\leq N}\Delta_{\rho}(\alpha^{1-x}A_{i}+(-1)^{y}\alpha^{x}A_{j})\Big{]}^{2}$		(13)
		$\displaystyle+\sum_{1\leq i<j\leq N}\Delta_{\rho}^{2}(\alpha^{x}A_{i}+(-1)^{1-y}\alpha^{1-x}A_{j})\bigg{\}}.$

Namely, $\sum_{i=1}^{N}\Delta_{\rho}^{2}(A_{i})\geq\rm{LB1}$. $\Box$

Theorem 1 provides a series of uncertainty relations depending on the values of the parameter $\alpha$. We can obtain more stringent bound on the uncertainty relations by selecting the optimal parameters $\alpha$. The uncertainty relations (6) is a special case of Theorem 1 corresponding to $\alpha=1$. Note that the lower bound of Theorem 1 is non-zero unless the measured state $|\psi\rangle$ is a common eigenvector of all $A_{i}$. That is to say, no matter whether the observables are commutable or not, the lower bound of Theorem 1 does not vanish if $|\psi\rangle$ is not a common eigenvector of all observables.

In fact, the lower bound in Theorem 1 should be understood under the permutation of the observables. Let $\pi\in S(N)$ be an arbitrary $N$-element permutation. Define

	$\displaystyle{\rm LB1}_{\pi}=\mathop{\max_{{x\in\{0,1\}}\atop{y\in\{0,1\}}}}$	$\displaystyle\frac{1}{(1+\alpha^{2})(N-1)}\bigg{\{}\frac{2}{N(N-1)}\Big{[}\sum_{1\leq i<j\leq N}\Delta_{\rho}(\alpha^{1-x}A_{\pi(i)}+(-1)^{y}\alpha^{x}A_{\pi(j)})\Big{]}^{2}$		(14)
		$\displaystyle+\sum_{1\leq i<j\leq N}\Delta_{\rho}^{2}(\alpha^{x}A_{\pi(i)}+(-1)^{1-y}\alpha^{1-x}A_{\pi(j)})\bigg{\}}.$

The following variance-based uncertainty relation under the element permutation of all observables holds,

$$\sum_{i=1}^{N}\Delta_{\rho}^{2}(A_{i})\geq\max_{\pi\in S(N)}{\rm LB1}_{\pi}.$$

(15)

According to the following equalities,

$$\sum_{1\leq i<j\leq N}\|a_{i}+a_{j}\|^{2}=\|\sum_{i=1}^{N}a_{i}\|^{2}+(N-2)\sum_{i=1}^{N}\|a_{i}\|^{2}$$

(16)

and

$$\sum_{1\leq i<j\leq N}\|a_{i}-a_{j}\|^{2}=N\sum_{i=1}^{N}\|a_{i}\|^{2}-\|\sum_{i=1}^{N}a_{i}\|^{2},$$

(17)

one has Li et al. (2022),

	$\displaystyle\left[\alpha N+(N-2)\beta\right]\sum_{i=1}^{N}\|a_{i}\|^{2}=$	$\displaystyle\beta\sum_{1\leq i<j\leq N}\|a_{i}+a_{j}\|^{2}+\alpha\sum_{1\leq i<j\leq N}\|a_{i}-a_{j}\|^{2}$		(18)
		$\displaystyle+(\alpha-\beta)\|\sum_{i=1}^{N}a_{i}\|^{2},$

where both $\alpha,\beta$ are arbitrary real numbers.

[Proof] For all $\alpha,\beta>0$, by using (18) and the Cauchy-Schwarz inequality (11), we get

	$\displaystyle\sum_{i=1}^{N}\|a_{i}\|^{2}\geq$	$\displaystyle\frac{1}{\alpha N+(N-2)\beta}\Big{[}\frac{2\beta}{N(N-1)}(\sum_{1\leq i<j\leq N}\|a_{i}+a_{j}\|)^{2}$		(23)
		$\displaystyle+\alpha\sum_{1\leq i<j\leq N}\|a_{i}-a_{j}\|^{2}+(\alpha-\beta)\|\sum_{i=1}^{N}a_{i}\|^{2}\Big{]}$

and

	$\displaystyle\sum_{i=1}^{N}\|a_{i}\|^{2}\geq$	$\displaystyle\frac{1}{\alpha N+(N-2)\beta}\Big{[}\beta\sum_{1\leq i<j\leq N}\|a_{i}+a_{j}\|^{2}$		(24)
		$\displaystyle+\frac{2\alpha}{N(N-1)}(\sum_{1\leq i<j\leq N}\|a_{i}-a_{j}\|)^{2}+(\alpha-\beta)\|\sum_{i=1}^{N}a_{i}\|^{2}\Big{]}.$

When $\beta>\alpha>0$, due to $\|\sum\limits_{i=1}^{N}a_{i}\|^{2}\leq\frac{1}{(N-1)^{2}}(\sum\limits_{1\leq i<j\leq N}\|a_{i}+a_{j}\|)^{2}$, we obtain

	$\displaystyle\sum_{i=1}^{N}\|a_{i}\|^{2}\geq$	$\displaystyle\frac{1}{\alpha N+(N-2)\beta}\Big{[}\beta\sum_{1\leq i<j\leq N}\|a_{i}+a_{j}\|^{2}+\alpha\sum_{1\leq i<j\leq N}\|a_{i}-a_{j}\|^{2}$		(25)
		$\displaystyle+\frac{(\alpha-\beta)}{(N-1)^{2}}(\sum_{1\leq i<j\leq N}\|a_{i}+a_{j}\|)^{2}\Big{]}.$

Substituting $\|a_{i}\|=\Delta_{\rho}(A_{i})$ and $\|a_{i}\pm a_{j}\|=\Delta_{\rho}(A_{i}\pm A_{j})$ into the inequalities (23)-(25), we complete the proof. $\Box$

In Theorem 2 we note that, for a given amount of observables $N$, the larger $\alpha$ and the smaller $\beta$ mean larger $X$ and $Z$ given by (20) and (22), respectively. Nevertheless, the larger $\beta$ and the smaller $\alpha$ correspond to larger $Y$ given by (21). If one takes $\alpha=\beta$ in Theorem 2, the lower bound of Theorem 2 is coincident to that of (6). If one respectively takes $\beta<\alpha$ for X and $\beta>\alpha$ for Y, the lower bound of Theorem 2 is tighter than that of (6). In Li et al. (2022), Li $et\ al.$ proved that (23) and (24) are strictly tighter than those of norm inequalities related to (5) and (6) for appropriate $\alpha$ and $\beta$.

In particular, when one takes $\alpha=2$ and $\beta=1$ for (20), $\alpha=1$ and $\beta=2$ for (21) and (22), then $\rm{X}$, $\rm{Y}$ and $\rm{Z}$ respectively reduce to

	$\displaystyle\rm{X}=$	$\displaystyle\frac{1}{3N-2}\bigg{\{}\frac{2}{N(N-1)}\Big{[}\sum_{1\leq i<j\leq N}\Delta_{\rho}(A_{i}+A_{j})\Big{]}^{2}$		(26)
		$\displaystyle+2\sum_{1\leq i<j\leq N}\Delta_{\rho}^{2}(A_{i}-A_{j})+\Delta_{\rho}^{2}(\sum_{i=1}^{N}A_{i})\bigg{\}},$

	$\displaystyle\rm{Y}=$	$\displaystyle\frac{1}{3N-4}\bigg{\{}\frac{2}{N(N-1)}\Big{[}\sum_{1\leq i<j\leq N}\Delta_{\rho}(A_{i}-A_{j})\Big{]}^{2}$		(27)
		$\displaystyle+2\sum_{1\leq i<j\leq N}\Delta_{\rho}^{2}(A_{i}+A_{j})-\Delta_{\rho}^{2}(\sum_{i=1}^{N}A_{i})\bigg{\}},$

	$\displaystyle\rm{Z}=$	$\displaystyle\frac{1}{3N-4}\bigg{\{}2\sum_{1\leq i<j\leq N}\Delta_{\rho}^{2}(A_{i}+A_{j})+\sum_{1\leq i<j\leq N}\Delta_{\rho}^{2}(A_{i}-A_{j})$		(28)
		$\displaystyle-\frac{1}{(N-1)^{2}}\Big{[}\sum_{1\leq i<j\leq N}\Delta_{\rho}(A_{i}+A_{j})\Big{]}^{2}\bigg{\}}.$

For convenience, we consider the above special scenario of Theorem 2 in following concrete examples. We compare the lower bounds $\rm{LB1}$ and $\rm{LB2}$ respectively given in Theorem 1 and 2 with the ones given in (5) and (6).

Example 1 Consider the qubit mixed state given by Bloch vector $\vec{r}=(\frac{\sqrt{3}}{2}\cos\theta,\frac{\sqrt{3}}{2}\sin\theta,0)$,

$$\rho=\frac{1}{2}(I_{2}+\vec{r}\cdot\vec{\sigma}),$$

(29)

where the components of the vector $\vec{\sigma}=(\sigma_{x},\sigma_{y},\sigma_{z})$ are the standard Pauli matrices, $I_{2}$ is $2\times 2$ identity matrix. We choose Pauli matrices $\sigma_{x}-\sigma_{z}$, $\sigma_{y}+\sigma_{z}$ and $\sigma_{z}$ as the observables $A_{1}$, $A_{2}$ and $A_{3}$, respectively.

As shown in Fig. 1, we can obtain more stringent bound on the uncertainty relations in most choices of parameter $\alpha$. Especially, set $\alpha=1/2$ in Theorem 1, the results are shown in Fig. 1. Obviously, the lower bounds LB1 and LB2 are strictly tighter than the bounds of (5) and (6) in this case. In fact, our lower bonds depend on both the parameter $\alpha$ and the given set of observables. Generally it is difficult to find an analytical relation among the optimal lower bonds, the parameter $\alpha$ and the arbitrary set of observables. To illustrate their relationships, we consider two fixed states with $\theta=\pi/4$ and $\theta=\pi/2$ to show how our lower bounds change with the $\alpha$, see Fig. 1 and Fig. 1.

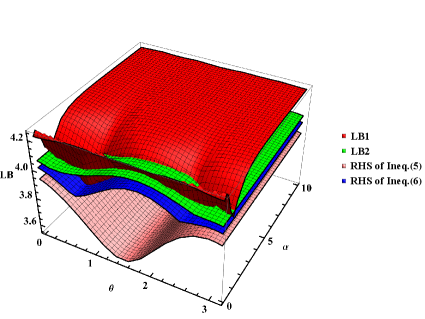
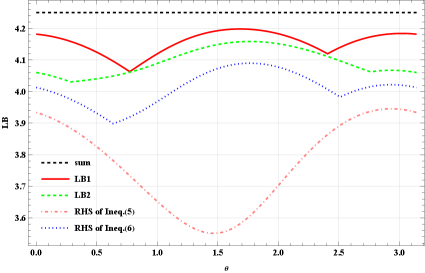
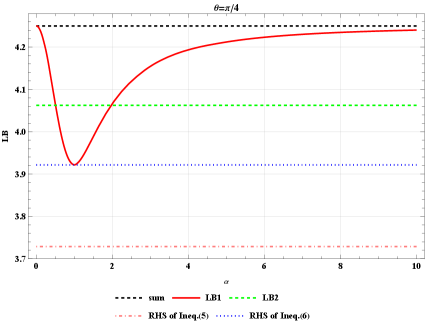
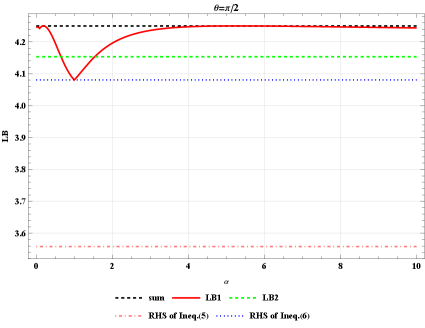
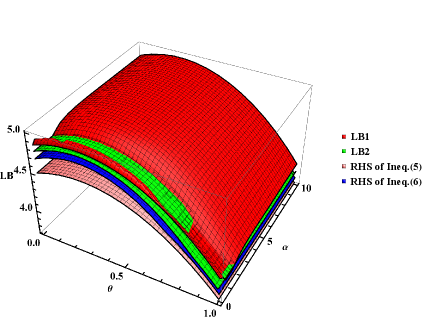
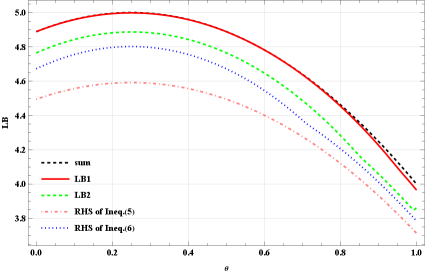
Example 2 Consider the following class of quantum states given by convex combination of the maximally entangled state and the maximally mixed state,

$$\rho_{\theta}=\frac{1-\theta}{d^{2}-1}(I_{d^{2}}-|\Psi^{+}\rangle\langle\Psi^{+}|)+\theta|\Psi^{+}\rangle\langle\Psi^{+}|,$$

(30)

with $0\leq\theta\leq 1$ and $|\Psi^{+}\rangle=\frac{1}{\sqrt{d}}\sum_{i=1}^{d}|ii\rangle$. Consider two-qubit case ($d=2$) and take $\sigma_{3}\otimes\sigma_{1}+\sigma_{3}\otimes\sigma_{2}$, $\sigma_{3}\otimes\sigma_{2}$ and $\sigma_{3}\otimes\sigma_{3}-\sigma_{3}\otimes\sigma_{2}$ as the observables $A_{1}$, $A_{2}$ and $A_{3}$, respectively.

As shown in Fig. 2, we can obtain more stringent bound on the uncertainty relations by selecting the appropriate parameter $\alpha$. For comparison, set $\alpha=5$ in Theorem 1, the results are shown in Fig. 2, the comparison among our bounds, Song $et\ al.$ and Zhang $et\ al.$’s lower bounds is depicted in Fig. 2.

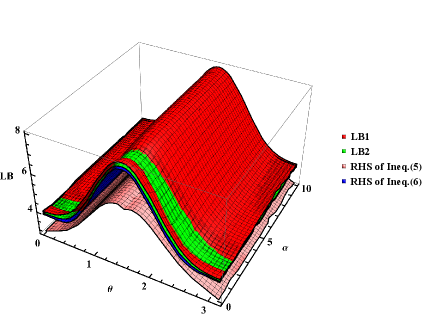
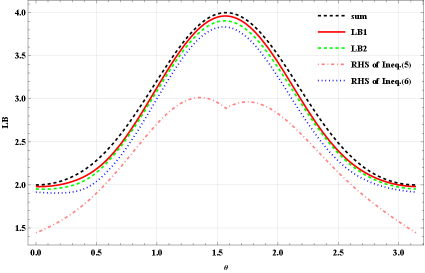
Example 3 Consider the following pure state of spin-1 system,

$$|\psi\rangle=\sin\theta\cos\phi|1\rangle+\sin\theta\sin\phi|0\rangle+\cos\theta|-1\rangle,$$

(31)

where $\theta\in[0,\pi]$ and $\phi\in[0,2\pi]$. We respectively take $L_{x}-L_{y}$, $L_{y}$ and $L_{z}+L_{y}$ as the observables $A_{1},A_{2}$ and $A_{3}$, where $L_{x},L_{y}$ and $L_{z}$ are the angular momentum operators ($\hbar=1$):

$$L_{x}=\frac{1}{\sqrt{2}}\begin{pmatrix}0&1&0\\ 1&0&1\\ 0&1&0\end{pmatrix},~{}~{}~{}L_{y}=\frac{1}{\sqrt{2}}\begin{pmatrix}0&-i&0\\ i&0&-i\\ 0&i&0\end{pmatrix},~{}~{}~{}L_{z}=\begin{pmatrix}1&0&0\\ 0&0&0\\ 0&0&-1\end{pmatrix}.$$

(32)

Set $\phi=\frac{\pi}{2}$. We show in Fig. 3 the comparison among our lower bounds of Theorem 1 and Theorem 2, and those of (5) and (6). In this scenario, it is easily seen that our bounds are tighter than others by selecting the appropriate parameter $\alpha$.

We have studied tighter variance-based sum uncertainty relations for $N$ arbitrary observables. By employing the parameterized norm identities and Cauchy-Schwarz inequalities we have derived more general and tighter sum uncertainty relations. Furthermore, we have showed that the bounds of our uncertainty relations are tighter than the existing variance-based uncertainty ones. These results and the simple approaches used in this article may highlight further investigations on related uncertainty relations.