Parameterized Bipartite Entanglement Measure
Abstract
We propose a novel parameterized entanglement measure -concurrence for bipartite systems. By employing positive partial transposition and realignment criteria, we derive analytical lower bounds for the -concurrence. Moreover, we calculate explicitly the analytic expressions of the -concurrence for isotropic states and Werner states.
I introduction
As a distinguishing feature of quantum mechanics, quantum entanglement is an important resource schrodinger1935gegenwartige ; PhysRev.47.777 ; PhysPhys195 in quantum computation and quantum information processing nielsen2002quantum such as quantum dense coding PhysRevLett.69.2881 , clock synchronization PRL852010 , quantum teleportation PhysRevLett.70.1895 , quantum secret sharing PhysRevA.59.1829 and quantum cryptography PRL67661 . One of the problems in quantum entanglement theory is to quantify the entanglement of a bipartite system. A reasonable entanglement measure should fulfill PhysRevLett.78.2275 ; PhysRevA.57.1619 ; PhysRevA.56.R3319 ; PhysRevA.59.141 ; PRL842014 : (E1) , with the equality holding iff is separable; (E2) is convex, i.e., for any states and , where ; (E3) does not increase under local operation and classical communication (LOCC), i.e., for any completely positive and trace preserving (CPTP) LOCC ; (E4) does not increase on average under stochastic LOCC, i.e., , where , and are the Kraus operators such that with the identity.
Several reasonable entanglement measures have been presented in the past few years, such as concurrence PhysRevLett.78.5022 ; PhysRevA.64.042315 , entanglement of formation PhysRevA.54.3824 ; PhysRevLett.80.2245 ; horodecki2001entanglement , negativity PhysRevA.65.032314 ; PhysRevLett.95.090503 and Rényi- entropy of entanglement gour2007dual ; Kim_2010 . Generally it is formidably difficult to calculate analytically the degree of entanglement for arbitrary given states. Analytical results are often available for two-qubit states PhysRevLett.80.2245 or special higher-dimensional mixed states PhysRevLett.85.2625 ; PhysRevA.64.062307 ; PhysRevA.67.012307 for several entanglement measures PhysRevA.68.062304 ; buchholz2016evaluating . Efforts have been also made towards the analytical lower bounds of entanglement measures like the concurrence PhysRevLett.95.210501 ; Li_Guo_2009 . In PhysRevLett.95.040504 analytical lower bound of the concurrence has been derived by employing the positive partial transpose (PPT) and realignment criteria PhysRevLett.77.1413 ; PhysRevA.59.4206 ; rudolph2004computable ; rudolph2005further ; chen2003matrix . In this paper, inspired by Tsallis- entropy of entanglement raggio1995properties ; PhysRevA.81.062328 and parameterized entanglement monotone -concurrence PhysRevA.103.052423 , we propose a novel parameterized entanglement measure -concurrence for any . Based on PPT and realignment criteria, we also obtain an analytic lower bound of the -concurrence for general bipartite systems. Finally, we calculate the -concurrence of isotropic states and Werner states analytically.
II -concurrence
Let be an arbitrary dimensional bipartite Hilbert space associated with subsystems and . Any pure state on the can be written as in the Schmidt form,
| (1) |
where with , is the Schmidt rank, . and are the local bases associated with the subsystems and , respectively nielsen2002quantum .
From (2), for a pure state given by (1) one has
| (3) |
where satisfies . It is obvious that the lower bound is attained if and only if is a separable state, that is, for some and . While the upper bound is achieved for the maximally entangled pure states .
For a general mixed state on the Hilbert space , the -concurrence is given by the convex-roof extension,
| (4) |
where the infimum is taken over all possible pure-state decompositions of , with and . Before showing that defined in (4) is indeed a bona fide entanglement measure, we first present the following lemma, see proof in Appendix A.
. The function is concave, that is,
| (5) |
for any , where is a probability distribution and are density matrices. The equality holds if and only if all are the same for all .
By using the above Lemma 1, we have the following theorem.
. The -concurrence given in (4) is a well defined parameterized entanglement measure.
. We need to verify that fulfills the following four requirements.
(E1) If is an entangled state, then there is at least one entangled pure state in any pure state decomposition of . Thus . Otherwise, for separable states.
(E2) Consider . Let () be the optimal pure state decomposition of () with () and (). We have
| (6) |
where the first inequality is due to that is also a pure state decomposition of .
(E3) We adopt the approach given in MINTERT2005207 to show that our entanglement measure does not increase under LOCC. Denote () the Schmidt vector given by the squared Schmidt coefficients of the state () in the decreasing order. It has been shown that the state can be prepared starting from the state under LOCC if and only if is majorized by PhysRevLett.83.436 , , where the majorization means that the components () of (), listed in nonincreasing order, satisfy for , with equality for .
Since the entanglement cannot increase under LOCC, any entanglement measure has to satisfy that whenever . This condition, known as the , is satisfied if and only if , given as a function of the squared Schmidt coefficients ’s ANDO1989163 , is invariant under the permutations of any two arguments and satisfies
| (7) |
for any two components and of .
For any pure state given by (1), the -concurrence is obviously invariant under the permutations of the Schmidt coefficients for any . Since
for any two components and of the squared Schmidt coefficients of , we have for any LOCC and .
Next let be the optimal pure state decomposition of with and . We obtain
for any , where the last inequality is from the definition (4).
(E4) Let be the optimal pure state decomposition of with and . Consider stochastic LOCC protocol given by Kraus operators with . We have
| (8) |
where is the probability of obtaining the outcome with , and is the probability of obtaining the outcome with . The first inequality is due to the concavity of the Lemma 1, since . The last inequality is from the definition of (4), since .
In PhysRevA.103.052423 the parameterized entanglement monotone -concurrence for any pure state defined in (1) has been introduced, , where . It seems that our -concurrence defined by (2), , is in some sense dual to the -concurrence as the parameter , while the parameter . Nevertheless, these two concurrences characterize the quantum entanglement in different aspects, even though they are both derived from the Tsallis- of entanglement PhysRevA.81.062328 . For large enough , the -concurrence converges to the constant for any entangled state , while the -concurrence not for any . Particularly, for , the measure for any pure state given in (1), where is the Schmidt rank of the state , which is solely determined by the Schmidt rank of the bipartite pure state . Therefore, the -concurrences with different provide different characterizations of the feature of entanglement.
III bounds on -concurrence
Owing to the optimization in the calculation of the entanglement measures, it is generally difficult to obtain analytical expressions of the entanglement measures for general mixed states. In this section, we derive analytical lower bounds for the -concurrence based on PPT and realignment criteria PhysRevLett.77.1413 ; HORODECKI19961 ; PhysRevA.59.4206 ; rudolph2004computable ; rudolph2005further ; chen2003matrix .
A bipartite state can be written as , where the subscripts and are the row and column indices for the subsystem , respectively, while and are such indices for the subsystem . The PPT criterion says that if the state is separable, then the partial transposed matrix with respect to the subsystem is non-negative, . While the realignment criterion says that the realigned matrix of , , satisfies that if is separable, where denotes the trace norm of matrix , .
For a pure state given by (1), it is straightforward to obtain that PhysRevLett.95.040504
| (9) |
where . In particular, for , the -concurrence becomes . One has then
| (10) |
for any pure state on the .
. For any mixed state on the , the -concurrence satisfies
| (11) |
. For a pure state given in (1), let us analyze the monotonicity of the following function,
| (12) |
for any , where . The first derivative of with respect to is given by
| (13) |
where
| (14) |
Employing the Lagrange multiplies PhysRevA.67.012307 under constraints and , one has that there is only one stable point for every , for which for any . Since the second derivative at this point,
| (15) |
for any , the maximum extreme value point is just the maximum value point. is a decreasing function for any , since .
IV -concurrence for Isotropic and Werner states
In this section, we compute the -concurrence for isotropic states and Werner states. Let be a convex-roof extended quantum entanglement measure. Denote the set of states and the set all pure states in . Let be a compact group acting on by . Assume that the measure defined on is invariant under the operations of . One can define the projection : by with the standard (normalized) Haar measure on , and the function on by
| (19) |
Then for , we have
| (20) |
where is the convex-roof extension of a function . In other words, it is the convex hull of .
IV.1 Isotropic states
The isotropic states are given by PhysRevA.59.4206 ,
| (21) |
where and . is separable if and only if PhysRevLett.85.2625 . Inspired by the techniques adopted in PhysRevLett.85.2625 ; PhysRevA.67.012307 ; PhysRevA.64.062307 ; PhysRevA.68.062304 , we have, see Appendix B,
| (22) |
for any , where .
Obviously, the second derivative of (22) with respect to is non-positive for any . Hence, is concave in the whole regime . The is the largest convex function that is upper bounded by , which is constructed in the following way. Find the line that passes through the points and of for any . Thus, we have the following analytical formula of the -concurrence for isotropic states.
. The -concurrence for isotropic states is given by
| (23) |
where and .
Since for rudolph2005further ; PhysRevA.65.032314 , surprisingly the lower bound of (11) is just exactly the (23) for every with .
The concurrence of isotropic states has been derived in PhysRevA.67.012307 , for any . Fig. 1 exhibits the relations between the concurrence and the -concurrence of isotropic states for and .
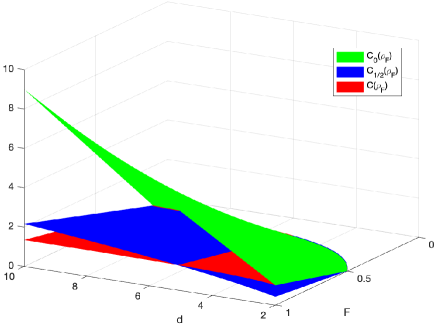
Especially, it shows that the with , and the concurrence of isotropic states is less than the -concurrence with . Moreover, we notice that the -concurrence is bigger than the concurrence with .
IV.2 Werner states
The Werner states are of the form,
| (24) |
where and PhysRevA.68.062304 . is separable if and only if PhysRevA.64.062307 ; PhysRevA.40.4277 . For , we have, see Appendix C,
| (25) |
for any .
It is direct to verify that the second derivative of (25) with respect to is non-positive, namely, is concave. Similar to (23), we have
. The -concurrence for Werner states is given by
| (26) |
where .
We remark that for , the lower bound of (11) for Werner states is given by
| (27) |
Accounting to (26), we obtain
| (28) |
where equality holds if , and the inequality holds strictly for higher dimensional quantum systems.
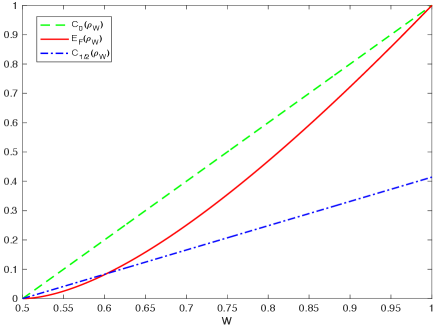
The concurrence of Werner states has been obtained in PhysRevA62044302 , for . It is direct to find that for any . Moreover, the entanglement of formation for Werner states is given by PhysRevA.64.062307 , . In Fig. 2 we illustrate the relations among the concurrence, entanglement of formation and -concurrence of Werner states for and . The entanglement of formation for Werner states is always upper bounded by the , and larger than the -concurrence for .
V summary
We have introduced the concept of -concurrence and shown that the -concurrence is a well defined entanglement measure. Analytical lower bounds of the -concurrence for general mixed states have been derived based on PPT and realignment criterion. Specifically, we have derived explicit formulae for the -concurrence of isotropic states and Werner states. Interestingly our lower bounds are exact for isotropic states and Werner states with . Our parameterized entanglement measure -concurrence gives a family of entanglement measures and enriches the theory of quantum entanglement, which may highlight further researches on the study of quantifying quantum entanglement and the related investigations like monogamy and polygamy relations in entanglement distribution, as well as the physical understanding of quantum correlations.
Acknowledgments
This work is supported by the National Natural Science Foundation of China (NSFC) under Grant Nos. 12075159 and 12171044; Beijing Natural Science Foundation (Grant No. Z190005); Academy for Multidisciplinary Studies, Capital Normal University; Shenzhen Institute for Quantum Science and Engineering, Southern University of Science and Technology (No. SIQSE202001), the Academician Innovation Platform of Hainan Province.
Appendix A Proof of Lemma 1
We only need to prove that for any . Since for any concave function , the is also concave RevModPhys.50.221 , with is concave for any . Let , and be corresponding eigendecompositions. We have
| (29) |
where the two inequalities follow from the concavity of . The equality holds if and are identical.
Appendix B for Isotropic states
Let be the -twirling operator defined by , where denotes the standard Haar measure on the group of all unitary operations. Then the operator satisfies that with . One has PhysRevA.64.062307 ; PhysRevA.59.4206 ; PhysRevA.68.062304 . Applying to the pure state given in (1), with and , we have
| (30) |
where and
| (31) |
with , and is the Schmidt vector of (1). Then the function defined in (19) becomes
| (32) |
It has been proved that the minimum above is attained for PhysRevA.68.062304 . Therefore, we have
| (33) |
For , one can always chose suitable and such that , and hence . For , similar to PhysRevA.103.052423 ; PhysRevLett.85.2625 , by using the Lagrange multipliers PhysRevA.67.012307 one can minimize (33) subject to the constraints
| (34) |
with . An extremum is attained when
| (35) |
where and denote the Lagrange multipliers.
It is evident that is a convex function of for any . Since a convex function and a linear function cross at most two points, equation (35) has at most two possible nonzero solutions for . Let and be these two positive solutions with . The Schmidt vector has the form,
| (36) |
where and . The minimization problem of (33) has been reduced to the following minimum problem,
| (37) |
with
| (38) |
subject to the constraints
| (39) |
By solving Eq. (39), we obtain
| (40) |
| (41) |
The relation suggests that we only need to consider the cases and , which are real for . On the other hand, since should be non-negative, we must have . Therefore, we see that , in consistent with the assumption . Here, as is ill defined.
We seek is the minimum of over all possible and , by minimizing on the parallelogram defined by and . Note that the parallelogram collapses to a line when , i.e., the separable boundary. We have in the parallelogram. Moreover, if and only if ; while if and only if .
When , we see from Eqs. (38) and (39) that Eq. (22) holds without any optimization. When , and Eq. (22) satisfied with the constraint conditions. From Eq.(39) the derivatives of and with respect to and are given by,
| (42) |
Hence, using Eq. (38) we have the partial derivatives of with respect to and ,
| (43) |
| (44) |
By lengthy calculations, we have
| (45) |
Denote . One has . Let
| (46) |
We have and
| (47) |
Set with . We obtain
| (48) |
From Eqs. (48) and (47), combining with Eq.(46) we have
| (49) |
Now corresponding to moving perpendicularly to and parallel to the constant boundaries of the parallelogram, we make a parameter transformation, and . The derivative of with respect to is given by
Set with . Let
| (50) |
with . We have the derivative of respect to ,
| (51) |
Again let
| (52) |
with . Then
| (53) |
where
| (54) |
We have and
| (55) |
From Eqs. (55) and (53), combining Eq. (51) we obtain . Then for any we have . Therefore,
| (56) |
From Eqs. (49) and (56), the minimum of is obtained when is the minimum and is the maximum. These results imply that the minimum of occurs at the vertex of and . Specifically, since on the boundary where Eqs. (49) and (56) are both hold, we have and . In this way, we derive an analytical expression of the function as follows,
| (57) |
Appendix C for Werner states
Let be the -twirling transformations PhysRevA.64.062307 . Then the Werner states defined in (IV.2) satisfy that, in analogous to the isotropic states, , where and PhysRevA.59.4206 ; PhysRevA.68.062304 . Applying to the pure state defined in (1), , we have
| (58) |
where and
| (59) |
with . Then the function defined in (19) becomes
| (60) |
By we have
| (61) |
where is the real part of .
Note that the equalities in (C) hold if only the two nozero components and , and , which give rise to the optimal minimum of (60) PhysRevA.64.062307 . Therefore, (60) becomes
| (62) |
For , we can always chose suitable and to have that , which results in . For , one minimizes (62) subject to the constraints
| (63) |
with . The rest of the calculation is the similar to the one in Appendix B. We only need to set and . In this way, we can obtain
| (64) |
References
- (1) Schrödinger E 1935 Naturwissenschaften 23 807
- (2) Einstein A, Podolsky B and Rosen N 1935 Phys. Rev. 47 777
- (3) Bell J S 1964 Phys. Phys. Fiz. 1 195
- (4) Nielsen M A and Chuang I L 2010 Quantum Computation and Quantum Information 10th edn (Cambridge: Cambridge University Press)
- (5) Bennett C H and Wiesner S J 1992 Phys. Rev. Lett. 69 2881
- (6) Jozsa R, Abrams D S, Dowling J P and Williams C P 2000 Phys. Rev. Lett. 85 2010
- (7) Bennett C H, Brassard G, Crépeau C, Jozsa R, Peres A and Wootters W K 1993 Phys. Rev. Lett. 70 1895
- (8) Hillery M, Bužek V and Berthiaume A 1999 Phys. Rev. A 59 1829
- (9) Ekert A K 1991 Phys. Rev. Lett. 67 661
- (10) Vedral V, Plenio M B, Rippin M A and Knight P L 1997 Phys. Rev. Lett. 78 2275
- (11) Vedral V and Plenio M B 1998 Phys. Rev. A 57 1619
- (12) Popescu S and Rohrlich D 1997 Phys. Rev. A 56 R3319
- (13) Vidal G and Tarrach R 1999 Phys. Rev. A 59 141
- (14) Horodecki M, Horodecki P and Horodecki R 2000 Phys. Rev. Lett. 84 2014
- (15) Hill S and Wootters W K 1997 Phys. Rev. Lett. 78 5022
- (16) Rungta P, Bužek V, Caves C M, Hillery M and Milburn G J 2001 Phys. Rev. A 64 042315
- (17) Bennett C H, DiVincenzo D P, Smolin J A and Wootters W K 1996 Phys. Rev. A 54 3824
- (18) Wootters W K 1998 Phys. Rev. Lett. 80 2245
- (19) Horodecki M 2001 Quantum Inf. Comput. 1 3
- (20) Vidal G and Werner R F 2002 Phys. Rev. A 65 032314
- (21) Plenio M B 2005 Phys. Rev. Lett. 95 090503
- (22) Gour G, Bandyopadhyay S and Sanders B C 2007 J. Math. Phys. 48 012108
- (23) Kim J S and Sanders B C 2010 J. Phys. A 43 445305
- (24) Terhal B M and Vollbrecht K G H 2000 Phys. Rev. Lett. 85 2625
- (25) Vollbrecht K G H and Werner R F 2001 Phys. Rev. A 64 062307
- (26) Rungta P and Caves C M 2003 Phys. Rev. A 67 012307
- (27) Lee S, Chi D P, Oh S D and Kim J 2003 Phys. Rev. A 68 062304
- (28) Buchholz L E, Moroder T and Gühne O 2016 Ann. Phys. (NY) 528 278
- (29) Chen K, Albeverio S and Fei S-M 2005 Phys. Rev. Lett. 95 210501
- (30) L. Li-Guo, T. Cheng-Lin, C. Ping-Xing and Y. Nai-Chang 2009 Chin. Phys. Lett. 26 060306
- (31) Chen K, Albeverio S and Fei S-M 2005 Phys. Rev. Lett. 95 040504
- (32) Peres A 1996 Phys. Rev. Lett. 77 1413
- (33) Horodecki M and Horodecki P 1999 Phys. Rev. A 59 4206
- (34) Rudolph O 2004 Lett. Math. Phys. 70 57
- (35) Rudolph O 2005 Quantum Inf. Process. 4 219
- (36) Chen K and Wu L-A 2003 Quantum Info. Comput. 3 193
- (37) Raggio G A 1995 J. Math. Phys. 36 4785
- (38) Kim J S 2010 Phys. Rev. A 81 062328
- (39) Yang X, Luo M-X, Yang Y-H and Fei S-M 2021 Phys. Rev. A 103 052423
- (40) Mintert F, Carvalho A R, Kuś M and Buchleitner A 2005 Phys. Rep. 415 207
- (41) Nielsen M A 1999 Phys. Rev. Lett. 83 436
- (42) Ando T 1989 Linear Algebra Appl. 118 163
- (43) Horodecki M, Horodecki P and Horodecki R 1996 Phys. Lett. A 223 1
- (44) Werner R F 1989 Phys. Rev. A 40 4277
- (45) Hiroshima T and Ishizaka S 2000 Phys. Rev. A 62 044302
- (46) Wehrl A 1978 Rev. Mod. Phys. 50 221