Parameter-free analytic continuation for quantum many-body calculations

The analytic continuation finds a spectral function $A(x)$ which satisfies Eq. (1) for given $G(i\omega_{n})$. Numerical implementation of this procedure requires a continuous description of $A(x)$ using a finite number of values. For this, we used the natural cubic spline [33, 34] interpolation, where $A(x)$ is represented as $A(x)=C_{i,0}+C_{i,1}(x-x_{i})+C_{i,2}(x-x_{i})^{2}+C_{i,3}(x-x_{i})^{3}$ in the $i$th interval of $x_{i}{\leq}x{\leq}x_{i+1}$ for $i=1,2,\cdots,n_{x}-1$, with $A^{\prime\prime}(x_{1})=A^{\prime\prime}(x_{n_{x}})=0$. Here $n_{x}$ is the number of grid points and $A^{\prime\prime}(x)$ is the second derivative of $A$. For appropriate grid points, we develop a kernel grid which depends only on the temperature $k_{B}T$, the real-frequency cutoff $x_{\textrm{max}}$, and the number of grid points $n_{x}$. The accurate analytic continuation requires the real-frequency grid which describes $G(i\omega_{n})$ of Eq. (1) accurately, so the grid should be dense near $x$ where $A(x)$ contributes greatly to $G(i\omega_{n})$. Thus, for a single $i\omega_{n}$, the appropriate grid density should be proportional to $\left|{\delta G(i\omega_{n})}/{\delta A(x)}\right|^{2}={1}/(\omega_{n}^{2}+x^{2})$. Hence, to describe $G(i\omega_{n})$ for all $i\omega_{n}$, we use the grid density $\rho(x)$ such that

where $\omega_{n}=(2n+1)\pi k_{B}T$ for the fermionic Green’s function. Then, grid points are determined by the equidistribution principle [34], $\int_{x_{i}}^{x_{i+1}}\rho(x)dx=C/(n_{x}-1)$ with $x_{1}=-x_{\textrm{max}}$, $x_{n_{x}}=x_{\textrm{max}}$, and $C=\int_{-x_{\textrm{max}}}^{x_{\textrm{max}}}\rho(x)dx$. Here $x_{\textrm{max}}$ and $n_{x}$ are determined to be large enough to make the obtained spectral function converge.

We compare the performance of our kernel grid with that of a uniform grid in Fig. 1. Figures 1(a) and 1(c) show two different spectral functions $A(x)$. The spectral function $A(x)$ shown in Fig. 1(a) has a sharp peak at the Fermi level ($x=0$), while that shown in Fig. 1(c) has no peak at the Fermi level. Figures 1(b) and 1(d) show $G(i\omega_{n})$ corresponding to $A(x)$ shown in Figs. 1(a) and 1(c), respectively. In the case that $A(x)$ has a sharp peak at the Fermi level ($x=0$), our kernel grid describes $A(x)$ accurately enough to produce $G(i\omega_{n})$ correctly, while the uniform grid does not [Fig. 1(b)]. In the case that $A(x)$ does not have a sharp peak, both our kernel grid and the uniform grid describe $A(x)$ accurately enough to produce $G(i\omega_{n})$ correctly [Fig. 1(d)].

Finding the spectral function $A(x)$ from $G(i\omega_{n})$ by minimizing $\chi^{2}[A]=\sum_{i\omega_{n}}|G(i\omega_{n})-\int\frac{A(x)}{i\omega_{n}-x}dx|^{2}$ is extremely ill-posed [5]. This ill-posedness can be significantly weakened by imposing the causality condition $A(x)\geq 0$ [35]. Since $A(x_{i})\geq 0$, $i=1,\cdots,n_{x}$, satisfies the causality only at the grid points ${x_{i}}$, we develop conditions that impose the causality for all $x$ as follows. The cubic spline can be expressed as a linear combination of cubic B-splines which are non-negative functions [36]. Thus, $A(x)\geq 0$ for all $x$ if expansion coefficients are non-negative [36]:

Here $A^{\prime}(x)$ is the derivative of $A$. The cubic spline constrained by Eq. (3) satisfies $A(x)\geq 0$ not only at grid points but also throughout intervals between grid points. This cubic spline, which we call the causal cubic spline, weakens the ill-posedness of the analytic continuation significantly, but it does not resolve the ill-posedness completely so minimization of $\chi^{2}[A]$ with the constraint Eq. (3) produces $A(x)$ still having spiky behavior due to overfitting to numerical errors [35]. To obtain smooth and physically meaningful $A(x)$, we employ an appropriate roughness penalty and the L-curve criterion.

To avoid the spiky behavior in $A(x)$ caused by overfitting to numerical errors, we use the second-derivative roughness penalty [30]. The roughness penalty $R[A]$ is defined as

Then, we obtain $A(x)$ by minimizing a regularized functional

with a regularization parameter $\lambda$. We use the interior-point method [37, 38] to implement this minimization. Then, the optimal $\lambda$ that balances $\chi^{2}[A]$ and $R[A]$ is found by the L-curve criterion [31, 32], which is a popular approach to determine the regularization parameter in various cases as follows. For each $\lambda$, one finds $A_{\lambda}$ that minimizes $Q_{\lambda}[A]$ in Eq. (5). Then, let $\chi^{2}(\lambda)=\chi^{2}[A_{\lambda}]$ and $R(\lambda)=R[A_{\lambda}]$. The L-curve is the plot of $\operatorname{log}_{10}[R(\lambda)]$ versus $\operatorname{log}_{10}[\chi^{2}(\lambda)]$. The L-curve criterion is to choose $\lambda$ that corresponds to the corner of the L-curve as the optimal value, $\lambda_{\textrm{opt}}$ as illustrated in Fig. 2(a). This procedure can be performed stably and efficiently by using a recently developed algorithm [39] which typically requires minimizations of $Q_{\lambda}[A]$ at about $20$ different values of $\lambda$. For a very small $\lambda$, $\chi^{2}[A]$ dominates $Q_{\lambda}[A]$ in Eq. (5), resulting in unphysical peaks in $A_{\lambda}(x)$, as shown in Fig. 2(b). For a very large $\lambda$, $R[A]$ dominates $Q_{\lambda}[A]$ in Eq. (5), resulting in too much broadening in $A_{\lambda}(x)$, as shown in Fig. 2(d). On the other hand, the spectral function computed with $\lambda_{\textrm{opt}}$ matches excellently the exact one, as shown in Fig. 2(c). With this criterion for $\lambda$ and with large enough values of $n_{x}$ and $x_{\textrm{max}}$ (see Appendix A for the convergence test with respect to $n_{x}$ and $x_{\textrm{max}}$), our analytic continuation does not have any arbitrarily chosen parameter that can affect the real-frequency result significantly, so we call our method a parameter-free method. Our analytic continuation method can be applied to the self-energy or other Matsubara frequency quantities which can be represented in a way similar to Eq. (1).

We can use the L-curve to estimate the precision of the analytic continuation as well. In the L-curve, $\lambda<\lambda_{\textrm{opt}}$ produces $A_{\lambda}(x)$ which is more fitted to $G(i\omega_{n})$, so the precision of $A_{\lambda_{\textrm{opt}}}(x)$ can be estimated by comparing it with $A_{\lambda}(x)$. In this regard, we define the L-curve averaged deviation (LAD),

where $C$ is the L-curve from $\lambda=0$ to $\lambda=\lambda_{opt}$, and we use it as an error estimator.

The Monte Carlo approach [22, 23, 24, 25, 26] is often used to calculate the imaginary-frequency Green’s function $G(i\omega_{n})$. As a result, the calculated $G(i\omega_{n})$ has statistical errors. The spectral function calculated by the analytic continuation of such data can exhibit artifacts from statistical errors in $G(i\omega_{n})$ [see Fig. 3(a) for an example]. Here we devise a bootstrap-averaged analytic continuation method. The bootstrap approach [28, 29] is a widely used resampling method in statistics. Suppose we have $N$ independent data $G(i\omega_{n})_{j}$, where ${j=1,\cdots,N}$, and we repeat the bootstrap sampling $N_{\textrm{B}}$ times. For the $k$th bootstrap sampling, we randomly sample $N$ data from $G(i\omega_{n})_{j}$ with replacement and calculate their average $g_{k}^{\textrm{B}}(i\omega_{n})=\frac{1}{N}\sum_{j=1}^{N}n_{kj}G(i\omega_{n})_{j}$, where $n_{kj}$ is the number of repetitions of $G(i\omega_{n})_{j}$ in the $k$th bootstrap sampling. Then, we obtain the analytically continued spectral function $A[g_{k}^{\textrm{B}}]$ for $g_{k}^{\textrm{B}}$. Finally, the spectral function $A(x)$ is calculated by $A(x)=\frac{1}{N_{\textrm{B}}}\sum_{k=1}^{N_{\textrm{B}}}A[g_{k}^{\textrm{B}}](x)$, which converges as $N_{\textrm{B}}$ increases. In our present work, we used $N_{\textrm{B}}=256$, which is large enough to obtain converged results. Similarly, we can also obtain bootstrap-averaged $\textrm{LAD}(x)$ for the error estimation of bootstrap-averaged $A(x)$.

Figure 3 compares the results of our analytic continuation without and with the bootstrap average. We consider an exact spectral function $A_{\textrm{exact}}(x)$ which has a narrow peak at $x=0$ and a broad peak at $x=-4$ and another broad peak at $x=5$, as shown by the black line in Fig. 3. We obtain the exact Green’s function $G_{\textrm{exact}}(i\omega_{n})$ from $A_{\textrm{exact}}(x)$. We used a temperature of $0.01$ and the first $100$ Matsubara frequencies. The kernel grid is generated with $x_{\textrm{max}}=10$ and $n_{x}=101$. To perform our analytic continuation without bootstrap average, we obtain the Green’s function $G(i\omega_{n})$ by adding a Gaussian error of the standard deviation of $10^{-6}$ to $G_{\textrm{exact}}(i\omega_{n})$. Then we obtain the spectral function $A(x)$ by applying our analytic continuation method to $G(i\omega_{n})$. Figure 3(a) shows the obtained $A(x)$, which deviates slightly from $A_{\textrm{exact}}(x)$ at around $x=5$. Next, to perform our bootstrap-averaged analytic continuation, we obtain $N=100$ independent values of $G(i\omega_{n})$ by adding a Gaussian error of the standard deviation of $10^{-5}$ to $G_{\textrm{exact}}(i\omega_{n})$. Then, we obtain the spectral function $A(x)$ by applying our bootstrap-averaged analytic continuation method with $N_{\textrm{B}}=256$. Figure 3(b) shows the obtained $A(x)$, which agrees excellently with $A_{\textrm{exact}}(x)$. The deviation of $A(x)$ from $A_{\textrm{exact}}(x)$ at around $x=5$ in Fig. 3(a) is due to overfitting of $A(x)$ to $G(i\omega_{n})$ with statistical errors, and it is avoided by the bootstrap average, as shown in Fig. 3(b). So the bootstrap average is useful for avoiding the overfitting to data with statistical errors. This bootstrap average can be used with any analytic continuation method.

Figure 4 demonstrates the statistical-error dependence of the spectral function $A(x)$ and $\textrm{LAD}(x)$ obtained with our method. We consider an exact $A(x)$ consisting of three peaks, from which we obtain the exact $G(i\omega_{n})$. Then, we add statistical errors to the exact $G(i\omega_{n})$ and apply our method to obtain $A(x)$ and $\textrm{LAD}(x)$. Here the standard deviation $\delta$ of the statistical errors is independent of $\omega_{n}$. (See Appendix B for $\delta$ varying with $\omega_{n}$.) As shown in Fig. 4(a), when statistical errors in $G(i\omega_{n})$ are large, the obtained $A(x)$ is broader than the exact one, and $\textrm{LAD}(x)$ is large. As the statistical errors are reduced, $A(x)$ converges to the exact one, and $\textrm{LAD}(x)$ diminishes [Figs. 4(b)–(d)]. These results show that our method behaves well with respect to the statistical errors, reproducing the exact spectral function if the statistical errors are small enough.

For a more detailed analysis, we fit the obtained $A(x)$ in Fig. 4 with three Gaussian functions. Table 1 shows the obtained peak centers and peak widths. These results show explicitly that peak centers and peak widths converge to the corresponding exact values as statistical errors in $G(i\omega_{n})$ decrease and show that peak centers converge faster than peak widths.

In addition, we tested our analytic continuation method with various spectral functions (Fig. 5). Here we performed the bootstrap average with $N_{\textrm{B}}=256$, using $N=100$ independent values of $G(i\omega_{n})$. Each independent value of $G(i\omega_{n})$ was obtained by adding a Gaussian error of the standard deviation of $10^{-5}$ to the exact Green’s function $G_{\textrm{exact}}(i\omega_{n})$ obtained from the exact spectral function $A_{\textrm{exact}}(x)$. Figure 5 confirms analytically continued spectral functions $A(x)$ agree excellently with corresponding $A_{\textrm{exact}}(x)$. We also compared our method with the maximum entropy method (Appendix C).

As an application of our method, we consider the two-orbital Hubbard model [40] described by the Hamiltonian

in the infinite-dimensional Bethe lattice with a semicircular noninteracting density of states. Here $d_{ia\sigma}$($d^{\dagger}_{ia\sigma}$) is the annihilation (creation) operator of an electron of spin $\sigma$ in the $a$th ($a=1,2$) orbital at the $i$th site, $n_{ia\sigma}=d^{\dagger}_{ia\sigma}d_{ia\sigma}$, $t^{ab}_{ij}$ is the nearest-neighbor hopping energy, $\mu$ is the chemical potential, $U$ is the local Coulomb interaction, and $J$ is the Hund’s coupling. With the Padé approximant, the imaginary part of the self-energy in this model shows a peak at around the Fermi level in the non-Fermi-liquid phase [41]. Our analytic continuation method makes it possible to analyze the existence and evolution of peaks in detail, as shown below.

We simulate the two-orbital Hubbard model of Eq. (7) with the dynamical mean field theory (DMFT) [42, 43, 44, 45, 46]. We implemented the hybridization-expansion continuous-time quantum Monte Carlo method [25] and used it as an impurity solver. Both orbitals have the same bandwidth of $4$ in our energy units. We simulated the case with $U=8,J=U/6,$ and temperature $T=0.02$ and considered the paramagnetic phase. We applied our analytic continuation method to obtain the real-frequency self-energy $\Sigma^{R}(x)$ from the first $100$ imaginary-frequency self-energies $\Sigma(i\omega_{n})$. We used $n_{x}=101$ and $x_{\textrm{max}}=30$ to form the kernel grid, which are large enough for converged results. For the bootstrap average, we used $1.28\times 10^{4}$ independent sets of $\Sigma(i\omega_{n})$ obtained with $2\times 10^{6}$ Monte Carlo steps. After obtaining $\Sigma^{R}(x)$, we computed the spectral function $A(x)=-\frac{1}{\pi}\operatorname{Im}[G(x+i\eta)]$ by using $G(x+i\eta)=\int_{-\infty}^{\infty}{D(\epsilon)}/(x+i\eta+\mu-\epsilon-\Sigma^{R}(x))d\epsilon$. Here $D(\epsilon)=\sqrt{4-x^{2}}/(2\pi)$.

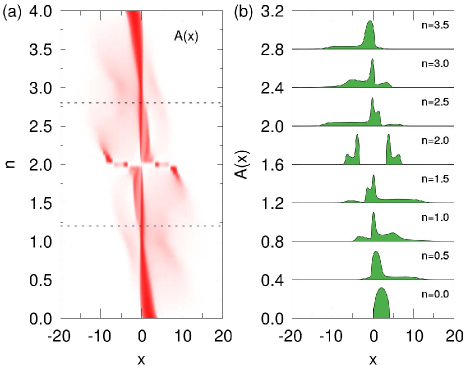
Figure 6 shows the spectral function as a function of the electron number $n$ per site, $A(x,n)$. The spectral function varies continuously except for the half filling ($n=2$), where the insulating phase appears. The particle-hole symmetry, $A(x,n)=A(-x,4-n)$, is clearly observed in Fig. 6, although it is not enforced. At $n\leq 1$ or $n\geq 3$, the spectral function shows a quasiparticle peak at the Fermi level and two Hubbard bands. As $n$ is increased from $1.2$ or decreased from $2.8$, a shoulder appears in the Fermi-level quasiparticle peak.

To investigate the origin of this shoulder, we plot $\operatorname{Im}[\Sigma^{R}(x,n)]$ in Fig. 7. At $n\leq 1$ or $n\geq 3$, $\operatorname{Im}[\Sigma^{R}(x)]$ shows two peaks corresponding to the lower and upper Hubbard bands, which we call the lower and upper Hubbard peaks. As $n$ is increased from $1.2$ (decreased from $2.8$), the lower (upper) Hubbard peak splits into two peaks, resulting in the shoulder of the quasiparticle peak in $A(x)$. These Hubbard-peak splittings induce non-Fermi-liquid behavior, as discussed below.

In Fig. 8, we compare the self-energies for $n=0.85$ and $n=1.55$. For $n=0.85$, $\operatorname{Im}[\Sigma(i\omega_{n})]$ is proportional to $\omega_{n}$ at small $\omega_{n}$, which indicates a Fermi-liquid behavior [47]. In the real frequency, the Fermi-liquid behavior, $\operatorname{Im}[\Sigma^{R}(x)]=C+\alpha x^{2}$ for small $x$ [48], is obtained from our analytic continuation [Fig. 8(b)]. On the other hand, for $n=1.55$, $\operatorname{Im}[\Sigma(i\omega_{n})]$ is almost proportional to $\sqrt{\omega_{n}}$, indicating a non-Fermi-liquid behavior [47]. This non-Fermi-liquid behavior appears in the real frequency $x$ as linear dependance of $\operatorname{Im}[\Sigma^{R}(x)]$ on $x$ near the Fermi level ($x=0$) [Fig. 8(d)]. This linear dependence comes from splitting of Hubbard peaks in $\operatorname{Im}[\Sigma^{R}(x)]$. Non-Fermi-liquid behavior in $\operatorname{Im}[\Sigma(i\omega_{n})]$ is known to appear at the spin-freezing crossover [47, 41, 49, 50]. Our results show that the spin-freezing crossover (or, equivalently, the spin-orbital separation [51]) occurs with the Hubbard-peak splitting in $\operatorname{Im}[\Sigma^{R}(x)]$.

To show the spin-freezing crossover, we obtain the local magnetic susceptibility $\chi_{\textrm{loc}}$ and the dynamic contribution $\Delta\chi_{\textrm{loc}}$ to the local magnetic susceptibility. With the operator $S_{z}=(1/2)\sum_{a=1}^{2}(n_{a\uparrow}-n_{a\downarrow})$, we define the local magnetic susceptibility as

and the dynamic contribution as

Here $\beta=1/k_{B}T$. Figure 9 shows $\chi_{\textrm{loc}}$ and $\Delta\chi_{\textrm{loc}}$ as functions of the electron number $n$ per site. As the electron number approaches the half filling ($n=2$), $\chi_{\textrm{loc}}$ increases monotonically. On the other hand, $\Delta\chi_{\textrm{loc}}$, which represents the fluctuation of the local spin moment, is maximal near $n=1.6$ and $2.4$. This indicates the spin-freezing crossover [47, 50].