Pairing effects on pure rotational energy of nuclei

The AMP is the method by which an intrinsic state is projected on angular-momentum eigenstates [3]. We consider an axially-symmetric intrinsic state, which is an eigenstate of $\hat{J}_{z}$ with the eigenvalue $M=0$. The intrinsic state $\ket{\Phi_{0}}$ is expanded by angular-momentum eigenstates $\ket{J0}$, $\ket*{\Phi_{0}}=\sum_{J}\ket*{J0}\innerproduct*{J0}{\Phi_{0}}$, where we omit indices other than $J$ and $M\,(=0)$ for simplicity. The Wigner (small) $d$ function [3, 40, 41] of the angle $\beta$, $d^{(J)}_{MK}(\beta):=\matrixelement*{JM}{e^{-i\hat{J}_{y}\beta}}{JK}$, takes a real number under the standard phase convention. The expectation values of the scalar operator $\hat{\mathcal{S}}$ on the angular-momentum eigenstates are obtained as follows [3, 23]:

$$\expectationvalue*{\hat{\mathcal{S}}}{J}=\,\frac{\displaystyle\int_{0}^{\pi/2}d\beta\sin\beta\,d^{(J)}_{00}(\beta)\expectationvalue*{\hat{\mathcal{S}}\,e^{-i\hat{J}_{y}\beta}}{\Phi_{0}}}{\displaystyle\int_{0}^{\pi/2}d\beta\sin\beta\,d^{(J)}_{00}(\beta)\expectationvalue*{e^{-i\hat{J}_{y}\beta}}{\Phi_{0}}}.$$

(1)

Equation (1) is the basic formula of the AMP. We here omit the index $M\,(=0)$ on the left-hand side (LHS) of Eq. (1). The energy difference $\expectationvalue*{\hat{H}}{J}-\expectationvalue*{\hat{H}}{0}$, where $\hat{H}$ is the Hamiltonian, is the pure rotational energy.

It has been pointed out in Ref. [23] that the cumulant expansion can straightforwardly be applied to the right-hand side (RHS) of Eq. (1). We expand $d^{(J)}_{00}(\beta)$ by the power series of $\beta$,

$$d^{(J)}_{00}(\beta)=\sum_{n=0}^{\infty}c_{2n}\beta^{2n};\,\quad c_{2n}=\,\frac{(-)^{n}}{(2n)!}\expectationvalue*{\hat{J}_{y}^{\,2n}}{J0}.$$

(2)

Note $c_{0}=1$, $c_{2}=-J(J+1)/(2!\,2)$ and $c_{2n}=\mathcal{O}(J^{2n})$. The function $\mathcal{S}^{01}(\beta)$ is defined and also expanded by the power series of $\beta$ as follows:

$$\mathcal{S}^{01}(\beta):=\,\frac{\expectationvalue*{\hat{\mathcal{S}}\,e^{-i\hat{J}_{y}\beta}}{\Phi_{0}}}{\expectationvalue*{e^{-i\hat{J}_{y}\beta}}{\Phi_{0}}}=\sum_{n=0}^{\infty}s_{2n}\beta^{2n};\quad s_{2n}=\,\frac{(-)^{n}}{(2n)!}\expectationvalue*{\hat{\mathcal{S}};\underbrace{\hat{J}_{y};\cdots;\hat{J}_{y}}_{2n}}{\Phi_{0}}_{\mathrm{cum}},$$

(3)

with the cumulant defined for a set of commutable operators $\{\hat{X}_{i};i=1,2,\cdots,n\}$ [42],

$$\expectationvalue*{\hat{X}_{1};\cdots;\hat{X}_{n}}_{\mathrm{cum}}:=\frac{\partial}{\partial t_{1}}\cdots\frac{\partial}{\partial t_{n}}\left.\ln\expectationvalue{\exp\left(\sum_{i=1}^{n}t_{i}{\hat{X}}_{i}\right)}\right|_{t_{1}=\cdots=t_{n}=0}.$$

(4)

The low-order cumulants are represented as

$$s_{0}=\expectationvalue*{\hat{\mathcal{S}}}{\Phi_{0}},\quad s_{2}=-\frac{1}{2!}\,C[\hat{\mathcal{S}},\hat{J}_{y}^{\,2}],\quad s_{4}=\,\frac{1}{4!}\left(C[\hat{\mathcal{S}},\hat{J}_{y}^{\,4}]-6\,C[\hat{\mathcal{S}},\hat{J}_{y}^{\,2}](\sigma[\hat{J}_{y}])^{2}\right).$$

(5)

Here $\sigma[\hat{A}]$ is the fluctuation of an operator $\hat{A}$, and $C[\hat{A},\hat{B}]$ is the correlation function of operators $\hat{A}$ and $\hat{B}$,

$$C[\hat{A},\hat{B}]:=\expectationvalue*{\hat{A}\hat{B}}{\Phi_{0}}-\expectationvalue*{\hat{A}}{\Phi_{0}}\expectationvalue*{\hat{B}}{\Phi_{0}},\quad\sigma[\hat{A}]:=\sqrt{C[\hat{A},\hat{A}]}.$$

(6)

Then Eq. (1) is exactly expressed in terms of the cumulants,

$$\expectationvalue*{\hat{\mathcal{S}}}{J}=\,\frac{\displaystyle\sum_{m,n=0}^{\infty}c_{2m}s_{2n}\varLambda_{2m+2n}}{\displaystyle\sum_{\ell=0}^{\infty}c_{2\ell}\varLambda_{2\ell}},$$

(7)

where

$$N_{2n}:=\int_{0}^{\pi/2}d\beta\sin\beta\,\beta^{2n}\expectationvalue*{e^{-i\hat{J}_{y}\beta}}{\Phi_{0}},\quad\varLambda_{2n}:=\frac{N_{2n}}{N_{0}},\quad(n=0,1,2,\cdots).$$

(8)

Expansion of Eq. (7) with respect to $c_{2n}$ yields the g.s. expectation value and the $J(J+1)$ rule for $\expectationvalue*{\hat{\mathcal{S}}}{J}$,

	$\displaystyle\expectationvalue*{\hat{\mathcal{S}}}{J}=$	$\displaystyle\,\expectationvalue*{\hat{\mathcal{S}}}{0}+\frac{J(J+1)}{2\,\mathcal{I}[\mathcal{S}]}+\cdots\,;$		(9a)
	$\displaystyle\expectationvalue*{\hat{\mathcal{S}}}{0}:=$	$\displaystyle\,\displaystyle\sum_{n=0}^{\infty}s_{2n}\varLambda_{2n},\quad\frac{1}{\mathcal{I}[\hat{\mathcal{S}}]}:=\,\sum_{n=1}^{\infty}s_{2n}\left[-\frac{1}{2}(\varLambda_{2n+2}-\varLambda_{2n}\varLambda_{2})\right].$		(9b)

The MoI of Peierls and Yoccoz [4, 7] is obtained by neglecting the $s_{2n}$ terms with $n\geq 2$ for $\hat{\mathcal{S}}=\hat{H}$. We shall call the approximation of Eq. (9) up to the $s_{2}$ terms Peierls-Yoccoz (PY) formula. It has been shown that the higher-order terms are not negligible in light nuclei or weakly-deformed intrinsic states [23].

The cumulant of Eq. (4) can be generalized as

$$\expectationvalue*{\hat{X}_{1};\cdots;\hat{X}_{n}}_{\mathrm{cum}}:=\frac{\partial}{\partial t_{1}}\cdots\frac{\partial}{\partial t_{n}}\left.\ln\expectationvalue{\prod_{i=1}^{n}\exp\Big(t_{i}\hat{X}_{i}\Big{missing})}\right|_{t_{1}=\cdots=t_{n}=0},$$

(10)

which distinguishes the ordering of the operators on the lhs and therefore is applicable even when the operators $\{\hat{X}_{i};i=1,2,\cdots,n\}$ are not commutable one another. The expansion is then extended to triaxially-deformed intrinsic states.

The nuclear effective Hamiltonian has translational, rotational, parity, and time-reversal symmetries, with the Galilean invariance and the number conservation. We assume that the individual terms of the Hamiltonian also have isospin symmetries except for the Coulomb force. The Hamiltonian is composed of the kinetic energy $\hat{K}=\sum_{i}\mathbb{p}_{i}^{2}/(2M)$, the effective nucleonic interaction $\hat{V}_{\mathrm{nucl}}=\sum_{i<j}\hat{v}_{ij}$, the Coulomb interaction between protons $\hat{V}_{\mathrm{Coul}}$, and the center-of-mass term $\hat{H}_{\mathrm{c.m.}}=\mathbb{P}^{2}/(2AM)$ with the total momentum $\mathbb{P}=\sum_{i}\mathbb{p}_{i}$ and the mass number $A=Z+N$,

$$\hat{H}=\hat{K}+\hat{V}_{\mathrm{nucl}}+\hat{V}_{\mathrm{Coul}}-\hat{H}_{\mathrm{c.m.}}.$$

(11)

The effective nucleonic interaction for the self-consistent MF calculations consists of the following terms [28, 43]:

$$\hat{V}_{\mathrm{nucl}}=\hat{V}^{(\mathrm{C})}+\hat{V}^{(\mathrm{LS})}+\hat{V}^{(\mathrm{TN})}+\hat{V}^{(\mathrm{C\rho})}\,;\quad\hat{V}^{(\mathrm{X})}=\sum_{i<j}\hat{v}_{ij}^{(\mathrm{X})},\quad(\mathrm{X}=\mathrm{C,LS,TN,C\rho}),$$

(12)

where $\hat{V}^{(\mathrm{C})}$, $\hat{V}^{(\mathrm{LS})}$ and $\hat{V}^{(\mathrm{TN})}$ are the central, LS and tensor forces. For the individual terms of Eq. (12), we consider the following forms:

$$\begin{split}\hat{v}_{ij}^{(\mathrm{C})}=&\sum_{n}\left(t^{\mathrm{(SE)}}_{n}P_{\mathrm{SE}}+t^{\mathrm{(TE)}}_{n}P_{\mathrm{TE}}+t^{\mathrm{(SO)}}_{n}P_{\mathrm{SO}}+t^{\mathrm{(TO)}}_{n}P_{\mathrm{TO}}\right)f^{\mathrm{(C)}}_{n}(r_{ij}),\\ \hat{v}_{ij}^{(\mathrm{LS})}=&\sum_{n}\left(t^{\mathrm{(LSE)}}_{n}P_{\mathrm{TE}}+t^{\mathrm{(LSO)}}_{n}P_{\mathrm{TO}}\right)f^{\mathrm{(LS)}}_{n}(r_{ij})\,\mathbb{L}_{ij}\cdot(\mathbb{s}_{i}+\mathbb{s}_{j}),\\ \hat{v}_{ij}^{(\mathrm{TN})}=&\sum_{n}\left(t^{\mathrm{(TNE)}}_{n}P_{\mathrm{TE}}+t^{\mathrm{(TNO)}}_{n}P_{\mathrm{TO}}\right)f^{\mathrm{(TN)}}_{n}(r_{ij})\,r^{2}_{ij}\,S_{ij},\\ \hat{v}_{ij}^{(\mathrm{C\rho})}=&\left(t^{\mathrm{(SE)}}_{\rho}P_{\mathrm{SE}}\cdot\left[\rho(\mathbb{r}_{i})\right]^{\alpha^{(\mathrm{SE})}}+t^{\mathrm{(TE)}}_{\rho}P_{\mathrm{TE}}\cdot\left[\rho(\mathbb{r}_{i})\right]^{\alpha^{(\mathrm{TE})}}\right)\delta(\mathbb{r}_{ij}),\end{split}$$

(13)

where $\mathbb{r}_{ij}:=\mathbb{r}_{i}-\mathbb{r}_{j}$, $r_{ij}:=|\mathbb{r}_{ij}|$, $\mathbb{\hat{r}}_{ij}:=\mathbb{r}_{ij}/r_{ij}$, $\mathbb{p}_{ij}:=(\mathbb{p}_{i}-\mathbb{p}_{j})/2$, $\mathbb{L}_{ij}:=\mathbb{r}_{ij}\times\mathbb{p}_{ij}$, $S_{ij}:=4\big{[}3(\mathbb{s}_{i}\cdot\mathbb{\hat{r}}_{ij})(\mathbb{s}_{j}\cdot\mathbb{\hat{r}}_{ij})-\mathbb{s}_{i}\cdot\mathbb{s}_{j}\big{]}$, and $\rho(\mathbf{r})$ is the nucleon density. The central density-dependent term is distinguished from $\hat{V}^{(\mathrm{C})}$ and represented by $\hat{V}^{(\mathrm{C\rho})}$. The projection operators on the singlet-even (SE), triplet-even (TE), singlet-odd (SO) and triplet-odd (TO) two-nucleon states are denoted by $P_{\mathrm{Y}}$ ($\mathrm{Y}=\mathrm{SE},\mathrm{TE},\mathrm{SO},\mathrm{TO}$).

We adopt the semi-realistic interaction M3Y-P6 [29, 30, 37, 38], in which the Yukawa function $f_{n}^{(\mathrm{X})}(r)=e^{-\mu_{n}^{(\mathrm{X})}r}/(\mu_{n}^{(\mathrm{X})}r)$ is used for the radial functions, except for $\hat{v}_{ij}^{(\mathrm{C\rho})}$. The longest-range term in $\hat{v}^{\mathrm{(C)}}_{ij}$ is fixed to be that of the one-pion exchange potential (OPEP). This central OPEP, denoted by $\hat{V}^{\mathrm{(OPEP)}}$, is an example of spin-dependent interactions. The values of the parameters for M3Y-P6 are given in Ref. [29].

The self-consistent MF calculations have been implemented via the Gaussian expansion method (GEM) [29, 30, 37, 38, 44]. The generalized Bogoliubov transformation in the HFB theory is given as [3, 45]

$$\alpha^{\dagger}_{i}:=\sum_{k}\left(c^{\dagger}_{k}\mathsf{U}_{ki}+c_{k}\mathsf{V}_{ki}\right).$$

(14)

We assume the axial, time-reversal, and parity symmetry on the MF state $\ket{\Phi_{0}}$, and then the variational parameters $\mathsf{U}_{ki}$ and $\mathsf{V}_{ki}$ are taken to be real numbers. Adding the terms constraining the particle numbers, we modify the Hamiltonian as

$$\hat{H}^{\prime}:=\hat{H}-\mu_{p}(\hat{N}_{p}-Z)-\mu_{n}(\hat{N}_{n}-N),$$

(15)

where $\mu_{p}$ ($\mu_{n}$) is the chemical potential for protons (neutrons), and $\hat{N}_{p}$ ($\hat{N}_{n}$) is the proton (neutron) number operator. The energy $\expectationvalue*{\hat{H}^{\prime}}{\Phi_{0}}$ is minimized in the HFB calculations. We do not consider the proton-neutron pairing in this paper.

The HFB handles the pairing effects self-consistently by taking into account the influences of the pairing on the particle-hole channel. However, in the HFB, the pairing may influence the particle-hole channel and alter the HF configuration. For clarifying the effects of the pairing, the HF+BCS (Bardeen-Cooper-Schrieffer) method is useful as well, in which the HF configuration is fixed. For analyzing the pairing effects on the pure rotational energy, we introduce a parameter $g$ as

$$\expectationvalue*{\hat{H}_{g}}=\expectationvalue*{\hat{H}_{\mathrm{dns}}}+g\expectationvalue*{\hat{H}_{\mathrm{pair}}},$$

(16)

where $\expectationvalue*{\hat{H}_{\mathrm{dns}}}$ consists of the terms including only the density matrix, while $\expectationvalue*{\hat{H}_{\mathrm{pair}}}$ is the pair energy containing the pairing tensor [3]. In the HF+BCS calculations, the axial-HF solution has been solved self-consistently, and the BCS equation is solved for $\expectationvalue*{\hat{H}_{g}}$ on top of the HF single-particle (s.p.) states. We denote its solution by $\ket{\Phi_{0}}_{g}$. The state $\ket{\Phi_{0}}_{g=0}$ corresponds to the HF state, and the state $\ket{\Phi_{0}}_{g=1}$ does to the HF+BCS state with the original Hamiltonian $\hat{H}^{\prime}$. Throughout this paper, the parameter $g$ is employed only in the HF+BCS scheme. We always apply $\hat{H}^{\prime}$ of Eq. (15) to the HFB calculation, not using $\expectationvalue*{\hat{H}_{g}}$.

In this work, the PAV has been applied for the AMP calculations of Eq. (1). The number projection is not applied. In reality, the intrinsic state could gradually change with increasing $J$, often accompanied by a breakdown of the axial and the time-reversal symmetry. While these effects can be handled in the cranking model [3, 6, 10] and in the VAP approaches [3], they are ignored in the present study, and we focus on the pure rotational energy, i.e., the rotational energy arising from a fixed intrinsic state, as stated in Introduction.

The overlap function $\expectationvalue*{e^{-i\hat{J}_{y}\beta}}{\Phi_{0}}$ has been calculated from the Onishi formula [3, 9, 11, 23]. Concerning the sign problem of the Onishi formula, solutions have been proposed [46, 47] and the non-negativity of the overlap function has been proven for the HF states under the time-reversal symmetry in Appendix C of Ref. [23]. We have here confirmed via the continuity with respect to $\beta$ that the sign of the overlap function is positive in all the cases under consideration.

There is a problem in the density-dependent coefficients in $\hat{v}_{ij}^{\mathrm{(C\rho)}}$ in the AMP calculations [19, 21, 22, 23]. In the present calculations, the standard treatment in Refs. [16, 23] has been adopted, replacing the density $\rho(\mathbf{r})$ in Eq. (13) with the “generalized density ” $\bar{\rho}(\mathbf{r};\beta)$,

$$\bar{\rho}(\mathbf{r};\beta):=\sum_{\tau}\sum_{\sigma}\frac{\expectationvalue*{\hat{\rho}(\mathbf{r}\sigma\tau)\,e^{-i\hat{J}_{y}\beta}}{\Phi_{0}}}{\expectationvalue*{e^{-i\hat{J}_{y}\beta}}{\Phi_{0}}};\quad\hat{\rho}(\mathbf{r}\sigma\tau):=\psi^{\dagger}(\mathbf{r}\sigma\tau)\psi(\mathbf{r}\sigma\tau),$$

(17)

where $\psi^{\dagger}(\mathbf{r}\sigma\tau)$ and $\psi(\mathbf{r}\sigma\tau)$ stand for the creation and annihilation operators for the spinor field [48], which satisfy the fermionic anticommutation relations:

$$\{\psi(x_{1}),\psi^{\dagger}(x_{2})\}=\delta(x_{1}-x_{2}),\quad\{\psi(x_{1}),\psi(x_{2})\}=\{\psi^{\dagger}(x_{1}),\psi^{\dagger}(x_{2})\}=0.$$

(18)

with the shorthand notation $x_{i}=(\mathbf{r}_{i}\sigma_{i}\tau_{i})$ ($i=1,2$) and $\delta(x_{1}-x_{2}):=\delta(\mathbf{r}_{1}-\mathbf{r}_{2})\delta_{\sigma_{1}\sigma_{2}}\delta_{\tau_{1}\tau_{2}}$. Although $\bar{\rho}(\mathbf{r};\beta)$ in Eq. (17) is a real number, owing to the time-reversal symmetry, $\bar{\rho}^{\,\alpha}(\mathbf{r};\beta)$ is multivalued unless the power $\alpha$ is an integer. In the M3Y-P6 interaction, $\alpha^{\mathrm{(SE)}}=1$ and $\alpha^{\mathrm{(TE)}}=1/3$ [29]. The phase of $\bar{\rho}^{\,\alpha^{\mathrm{(TE)}}}(\mathbf{r};\beta)$ has been chosen to be negative when $\bar{\rho}(\mathbf{r};\beta)$ is negative [23].

To investigate the relevance of the spatial correlations between nucleons to the rotational energy, we consider an operator comprised of the two-body delta function,

$$\hat{D}:=\sum_{i<j}\delta(\mathbf{r}_{ij}).$$

(19)

The expectation value $\expectationvalue*{\hat{D}}$ measures the degree how frequently two constituent nucleons sit at an equal position, representing the degree that two nucleons get spatially close to each other. We call $\expectationvalue*{\hat{D}}$ degree of proximity (DoP) in this paper.

The pair-distribution function has been employed to investigate the spatial correlation between two particles [49], such as the di-neutron correlation [39]. The pair-distribution function is defined as

$$\mathcal{G}(x_{1},x_{2}):=\,\frac{\expectationvalue*{\psi^{\dagger}(x_{1})\psi^{\dagger}(x_{2})\psi(x_{2})\psi(x_{1})}}{\expectationvalue*{\hat{\rho}(x_{1})}\expectationvalue*{\hat{\rho}(x_{2})}},$$

(20)

with $x_{i}=(\mathbf{r}_{i}\sigma_{i}\tau_{i})$. Notice $\mathcal{G}(x_{1},x_{2})=0$ for $x_{1}=x_{2}$, and $\mathcal{G}(x_{1},x_{2})\geq 0$. The DoP is regarded as a summation of the pair-distribution function at the same position, i.e.,

$$\begin{split}\expectationvalue*{\hat{D}}&=\frac{1}{2}\sum_{\tau_{1}\tau_{2}}\sum_{\sigma_{1}\sigma_{2}}\int d^{\,3}r\expectationvalue*{\psi^{\dagger}(\mathbf{r}\sigma_{1}\tau_{1})\psi^{\dagger}(\mathbf{r}\sigma_{2}\tau_{2})\psi(\mathbf{r}\sigma_{2}\tau_{2})\psi(\mathbf{r}\sigma_{1}\tau_{1})}\\ &=\frac{1}{2}\sum_{\tau_{1}\tau_{2}}\sum_{\sigma_{1}\sigma_{2}}\int d^{\,3}r\expectationvalue*{\hat{\rho}(\mathbf{r}\sigma_{1}\tau_{1})}\expectationvalue*{\hat{\rho}(\mathbf{r}\sigma_{2}\tau_{2})}\mathcal{G}(\mathbf{r}\sigma_{1}\tau_{1},\mathbf{r}\sigma_{2}\tau_{2}).\end{split}$$

(21)

Since $\hat{D}$ is a rotational scalar, the DoP for angular-momentum eigenstates $\expectationvalue*{\hat{D}}{J}$ is calculable via Eq. (1). By applying $\hat{D}P_{\mathrm{Y}}$ ($\mathrm{Y}=\mathrm{SE},\mathrm{TE}$) instead of $\hat{D}$ itself, the DoP can be separated between the SE and TE channels. Restricting $i$ and $j$ on the RHS of Eq. (19), we can calculate the DoP for individual isospin components.

We define the quadrupole deformation parameter $a_{20}$ as follows [1],

$$a_{20}:=\frac{q_{0}}{1.09A^{5/3}\,\mathrm{fm}^{2}},$$

(22)

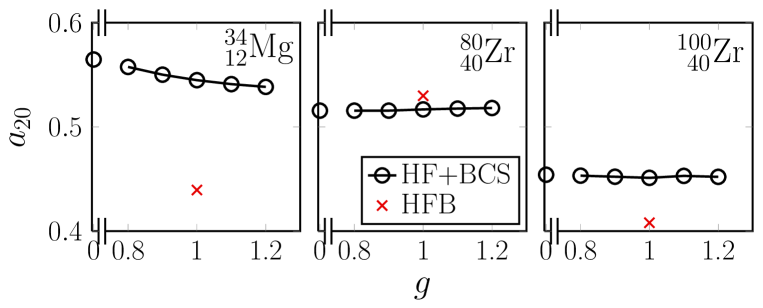
where $q_{0}$ is the mass quadrupole moment of the MF state [37]. In Fig.  1, the dependence of the deformation parameter $a_{20}$ on the pairing strength $g$ in the HF+BCS solutions [see Eq. (16)] is depicted for the ${}^{34}_{12}$Mg and ${}^{80,100}_{~{}~{}~{}~{}40}$Zr nuclei. The state $\ket{\Phi_{0}}_{g=0}$ corresponds with the HF state. As $g$ grows, the pair correlations arise at the critical values, corresponding with the normal-to-superfluid phase transition. The critical $g$ values for proton and neutron pairs are close, though not equal. While $a_{20}$ is insensitive to $g$ for the ${}^{80,100}_{~{}~{}~{}~{}40}$Zr nuclei, $a_{20}$ slightly decreases as $g$ grows for the ${}^{34}_{12}$Mg nucleus. The values of $a_{20}$ for the HFB minima are also shown. The $a_{20}$ values for the HF+BCS solutions are close to that of the HFB solution for the ${}^{80}_{40}$Zr nucleus, while they do not match well for the ${}^{34}_{12}$Mg and ${}^{100}_{~{}40}$Zr nuclei, indicating influence of the pairing on the HF configurations. Whereas the $a_{20}$ values for the HFB solutions are smaller than those for the HF solutions in ${}^{34}_{12}$Mg and ${}^{100}_{~{}40}$Zr, the opposite is realized at ${}^{80}_{40}$Zr. This enhancement of deformation at ${}^{80}_{40}$Zr takes place owing to the s.p. levels near the Fermi energy. The pairing moves a portion of neutrons at the highest occupied level with $\Omega^{\pi}=5/2^{+}$, which originates from the $0g_{9/2}$ spherical orbit, to the lowest unoccupied level with $\Omega^{\pi}=1/2^{+}$, by which the prolate deformation is slightly enhanced. Table 1 presents the $a_{20}$ values for the HF and HFB solutions at their lowest minima for ${}^{24}_{12}$Mg, ${}^{40}_{12}$Mg and ${}^{104}_{~{}40}$Zr.

Let us denote the expectation value of Eq. (1) measured from that of the g.s. by

$$\mathcal{S}_{\mathrm{x}}(J^{+}):=\expectationvalue*{\hat{\mathcal{S}}}{J}-\expectationvalue*{\hat{\mathcal{S}}}{0}.$$

(23)

We explicitly attach the parity quantum number ($+$) on the LHS. For $\mathcal{\hat{S}}=\hat{H}^{\prime}$, $\mathcal{S}_{\mathrm{x}}(J^{+})$ corresponds with the excitation energy (i.e., the pure rotational energy),

$$E_{\mathrm{x}}(J^{+})=\expectationvalue*{\hat{H}^{\prime}}{J}-\expectationvalue*{\hat{H}^{\prime}}{0}.$$

(24)

In Fig. 2, the $g$ dependence of the unprojected and the projected ($E(0^{+})=\expectationvalue*{\hat{H}^{\prime}}{0}$) g.s. energies is shown for the HF+BCS solutions of ${}^{34}_{12}$Mg and ${}^{80,100}_{~{}~{}~{}~{}40}$Zr. Up to the critical $g$ value where the pair correlations arise, the energies are equal to the HF case. As $g$ increases from the critical values, both the unprojected and projected energies decrease for the HF+BCS solutions. The unprojected and projected energies for the HFB minima are also shown. Irrespective of the unprojected or the projected energies, the energies for the HFB solutions are close to those for the HF+BCS ones in the region between $g=1.1$ and $1.2$.

As it is equal to $J(J+1)/6$ in the rigid-rotor model, the ratio $E_{\mathrm{x}}(J^{+})/E_{\mathrm{x}}(2^{+})$ can be a measure of how well the rotational band develops. The $g$ dependence of $E_{\mathrm{x}}(J^{+})/E_{\mathrm{x}}(2^{+})$ is shown for the ${}^{34}_{12}$Mg and ${}^{80,100}_{~{}~{}~{}~{}40}$Zr nuclei in Fig. 3. The ratios $E_{\mathrm{x}}(J^{+})/E_{\mathrm{x}}(2^{+})$ are insensitive to $g$ and close to the $J(J+1)/6$ lines except for high $J\,(\gtrsim 10)$ at ${}^{34}_{12}$Mg. For the ${}^{34}_{12}$Mg nucleus, the ratios $E_{\mathrm{x}}(J^{+})/E_{\mathrm{x}}(2^{+})$ decrease for high $J$ as $g$ increases. The deviation from the $J(J+1)/6$ lines indicates that the higher-$c_{2n}$ terms are not negligible in Eq. (7).

Figure 4 shows the $g$ dependence of the excitation energies $E_{\mathrm{x}}(2^{+})$ for the HF+BCS solutions of ${}^{34}_{12}$Mg and ${}^{80,100}_{~{}~{}~{}~{}40}$Zr. Those for the HFB solutions are also shown. As $g$ increases, $E_{\mathrm{x}}(2^{+})$ gets higher; the pair correlations reduce the MoI. The excitation energies $E_{\mathrm{x}}(2^{+})$ of the HF+BCS solutions between $g=1.0$ and $1.2$ are close to those of the HFB solutions. The $E_{\mathrm{x}}(2^{+})$ values for the HFB solutions in these nuclei are about 1.5 – 2 times higher than the rigid-rotor value [1],

$$E_{\mathrm{x}}^{(\mathrm{RR})}(J^{+})=\,\frac{J(J+1)}{2\,\mathcal{I}^{\mathrm{(RR)}}};\quad\mathcal{I}^{\mathrm{(RR)}}\approx\,0.0138\,A^{5/3}[\mathrm{MeV}^{-1}].$$

(25)

Compared to the experimental values, the $E_{\mathrm{x}}(2^{+})$ value is high in the HFB solution of the ${}^{34}_{12}$Mg nucleus, while slightly low in ${}^{80,100}_{~{}~{}~{}~{}40}$Zr.

We next investigate pairing effects on higher-order terms in Eq. (7). In Fig. 5, the $g$ dependence of $\varLambda_{2n}$ and $\varLambda_{2n+2}/\varLambda_{2n}$ in Eq. (8) is shown for the HF+BCS solutions of ${}^{34}_{12}$Mg and ${}^{80,100}_{~{}~{}~{}~{}40}$Zr. If $\varLambda_{2n+2}/\varLambda_{2n}$ stays small, both the $J(J+1)$ rule and the PY approximation are validated. For growing $g$, $\varLambda_{2n}$ and $\varLambda_{2n+2}/\varLambda_{2n}$ slightly increase for fixed $n$.

The g.s. correlation is defined and expanded by $s_{2n}$ for $\hat{\mathcal{S}}=\hat{H}^{\prime}$ as

$$\varDelta E_{\mathrm{g.s.c.}}:=\expectationvalue*{\hat{H}^{\prime}}{\Phi_{0}}-\expectationvalue*{\hat{H}^{\prime}}{0}=\displaystyle-\sum_{n=1}^{\infty}s_{2n}\varLambda_{2n}.$$

(26)

To view the influence of the higher-order terms, we have calculated the following quantities:

	$\displaystyle\varepsilon^{(k)}_{\mathrm{g.s.c.}}:=\,\frac{\displaystyle-\sum_{n=1}^{k}s_{2n}\varLambda_{2n}-\varDelta E_{\mathrm{g.s.c.}}}{\varDelta E_{\mathrm{g.s.c.}}},$		(27a)
	$\displaystyle\varepsilon^{(k)}_{\mathrm{x}}:=\,\frac{\displaystyle 3\sum_{n=1}^{k}s_{2n}\left[-\frac{1}{2}(\varLambda_{2n+2}-\varLambda_{2n}\varLambda_{2})\right]-E_{\mathrm{x}}(2^{+})}{E_{\mathrm{x}}(2^{+})}.$		(27b)

We calculate $s_{2}$ and $s_{4}$ from Eq. (3) via numerical differentiation. The values of $\varepsilon^{(k)}_{\mathrm{g.s.c.}}$ and $\varepsilon^{(k)}_{\mathrm{x}}$ ($k=1,2$) are shown for ${}^{34}_{12}$Mg and ${}^{80,100}_{~{}~{}~{}~{}40}$Zr in Fig. 6. Insensitive to $g$, $\varepsilon^{(1)}_{\mathrm{g.s.c.}}$ and $\varepsilon^{(1)}_{\mathrm{x}}$ almost vanish for ${}^{80,100}_{~{}~{}~{}~{}40}$Zr. Namely, the contributions of the higher-$s_{2n}$ terms to $\varDelta E_{\mathrm{g.s.c.}}$ and $E_{\mathrm{x}}(2^{+})$ are negligible, and the PY formula (Eq. (9b) truncated at $n=1$) is good. On the other hand, the $\varepsilon^{(1)}_{\mathrm{g.s.c.}}$ and $\varepsilon^{(1)}_{\mathrm{x}}$ values become larger as $g$ increases in the ${}^{34}_{12}$Mg nucleus. The pair correlations enhance the higher-$s_{2n}$ terms of the cumulant expansion, the terms including $s_{4}$ in practice, in the g.s. correlations and the MoI of this light nucleus. The $\varepsilon^{(2)}_{\mathrm{g.s.c.}}$ and $\varepsilon^{(2)}_{\mathrm{x}}$ values are vanishing.

In Fig. 6, the values of $\varepsilon^{(k)}_{\mathrm{g.s.c.}}$ and $\varepsilon^{(k)}_{\mathrm{x}}$ for $k=1,2$ are also shown for the HFB solutions of ${}^{34}_{12}$Mg and ${}^{80,100}_{~{}~{}~{}~{}40}$Zr. The results are similar to the HF+BCS cases. While the $\varepsilon^{(1)}_{\mathrm{g.s.c.}}$ and $\varepsilon^{(1)}_{\mathrm{x}}$ values are less than 10% for ${}^{80,100}_{~{}~{}~{}~{}40}$Zr, the $s_{4}$ terms are sizable for the ${}^{34}_{12}$Mg nucleus. This consequence is qualitatively similar also to the HF case in Ref. [23].

In Ref. [23], we analyzed the composition of the pure rotational energy of the axial-HF solutions. In this subsection, we present influences of the pairing on the composition of the pure rotational energy. By taking $\hat{\mathcal{S}}$ to be constituent terms of $\hat{H}^{\prime}$, the $\mathcal{S}_{\mathrm{x}}(J^{+})$ values of Eq. (23) yield their contributions to the rotational energy. In the following, $\hat{\mathcal{S}}$ is an element of the following set,

$$\hat{\mathcal{S}}\in\{\hat{H}^{\prime},\hat{K},\hat{V}^{\mathrm{(C)}},\hat{V}^{\mathrm{(LS)}},\hat{V}^{\mathrm{(TN)}},\hat{V}^{\mathrm{(C\rho)}},\hat{V}^{\mathrm{(OPEP)}},\hat{H}_{\mathrm{pair}}\}.$$

(28)

Each element has been defined in Sec. II. Since $\expectationvalue*{\hat{N}_{p}}{J}\neq Z$ and $\expectationvalue*{\hat{N}_{n}}{J}\neq N$, the chemical-potential terms in Eq. (15) have contributions to the rotational energy, which should be attributed to other terms of the Hamiltonian if the particle-number projection is simultaneously implemented. However, they are insignificant, staying within $-0.5-17\,\%$ for the MF states under investigation.

In Fig. 7, the $g$ dependence of $\mathcal{S}_{\mathrm{x}}(4^{+})/\mathcal{S}_{\mathrm{x}}(2^{+})$, the ratios given by the constituent terms of the effective Hamiltonian, is shown for the ${}^{34}_{12}$Mg and ${}^{80,100}_{~{}~{}~{}~{}40}$Zr nuclei. Contributions of the pairing tensors are excluded except for $\hat{H}_{\mathrm{pair}}$. The ratios are close to $10/3$ for ${}^{80,100}_{~{}~{}~{}~{}40}$Zr, almost independent of $g$ and $\hat{\mathcal{S}}$. In ${}^{34}_{12}$Mg, the ratios $\mathcal{S}_{\mathrm{x}}(4^{+})/\mathcal{S}_{\mathrm{x}}(2^{+})$ for $\hat{\mathcal{S}}=\hat{K}$, $\hat{V}^{\mathrm{(TN)}}$ and $\hat{H}_{\mathrm{pair}}$ are also almost independent of $g$, while those for $\hat{V}^{\mathrm{(C)}}$, $\hat{V}^{\mathrm{(LS)}}$, $\hat{V}^{\mathrm{(C\rho)}}$ and $\hat{V}^{\mathrm{(OPEP)}}$ become deviating from $10/3$ as $g$ increases. The irregular behavior for $\hat{V}^{\mathrm{(C)}}$ and $\hat{V}^{\mathrm{(OPEP)}}$ observed at $g\approx 1.1$ in ${}^{34}_{12}$Mg happens because $\mathcal{S}_{\mathrm{x}}(2^{+})\approx 0$ in this region, with sign inversion (see Fig. 8).

As long as any $\mathcal{S}_{\mathrm{x}}(J^{+})/\mathcal{S}_{\mathrm{x}}(2^{+})$ is close to $J(J+1)/6$, $\mathcal{S}_{\mathrm{x}}(J^{+})$ is well described by $\mathcal{I}[\hat{\mathcal{S}}]$ in Eq. (9a), and it is sufficient to inspect $\mathcal{S}_{\mathrm{x}}(2^{+})$ in analyzing the rotational energy. The contributions of the constituent terms of the effective Hamiltonian to the total rotational energy are represented by $\mathcal{S}_{\mathrm{x}}(2^{+})/E_{\mathrm{x}}(2^{+})$. In Fig. 8, the $g$ dependence of $\mathcal{S}_{\mathrm{x}}(2^{+})/E_{\mathrm{x}}(2^{+})$ is shown for ${}^{34}_{12}$Mg and ${}^{80,100}_{~{}~{}~{}~{}40}$Zr. As $g$ increases from the critical points, the $\mathcal{S}_{\mathrm{x}}(2^{+})/E_{\mathrm{x}}(2^{+})$ values for $\hat{\mathcal{S}}=\hat{K}$, $\hat{V}^{\mathrm{(C)}}$ and $\hat{V}^{\mathrm{(C\rho)}}$ vary; decrease for $\hat{\mathcal{S}}=\hat{V}^{\mathrm{(C)}}$, while increase for $\hat{V}^{\mathrm{(C\rho)}}$. Even their signs are inverted near $g=1.1$. As $g$ increases, the contribution of $g\hat{H}_{\mathrm{pair}}$ to the rotational energy is enhanced, which is dominated by the central force. The contributions of $\hat{V}_{\mathrm{Coul}}$, $\hat{H}_{\mathrm{c.m.}}$ and $\hat{V}^{\mathrm{(OPEP)}}$ to $E_{\mathrm{x}}(2^{+})$ are $\pm 10\%$ at most.

Figure 9 shows the ratios $\mathcal{S}_{\mathrm{x}}(J^{+})/\mathcal{S}_{\mathrm{x}}(2^{+})$ for the HFB solutions of the ${}^{24,34,40}_{~{}~{}~{}~{}~{}\,\,12}$Mg and ${}^{80,100,104}_{~{}~{}~{}~{}~{}~{}~{}~{}40}$Zr nuclei, all of which have prolate shapes. The ratios $E_{\mathrm{x}}(4^{+})/E_{\mathrm{x}}(2^{+})$ obtained in the present work are close to those of the experiments and $10/3$ except at ${}^{40}_{12}$Mg. For the deformed ₄₀Zr nuclei, the ratios of the constituent terms $\mathcal{S}_{\mathrm{x}}(J^{+})/\mathcal{S}_{\mathrm{x}}(2^{+})$ are also close to $J(J+1)/6$, although less close than in the HF case. On the other hand, some ratios $\mathcal{S}_{\mathrm{x}}(J^{+})/\mathcal{S}_{\mathrm{x}}(2^{+})$ do not obey the $J(J+1)$ rule for the ₁₂Mg nuclei. We find several cases in which even $\expectationvalue*{\hat{\mathcal{S}}}{J}$ is not monotonic for $J$, e.g., with $\mathcal{S}_{\mathrm{x}}(4^{+})/\mathcal{S}_{\mathrm{x}}(2^{+})<1$.

In Fig. 10, $\mathcal{S}_{\mathrm{x}}(2^{+})/E_{\mathrm{x}}(2^{+})$ are shown for the HFB solutions of the ${}^{24,34,40}_{~{}~{}~{}~{}~{}\,\,12}$Mg and ${}^{80,100,104}_{~{}~{}~{}~{}~{}~{}~{}~{}40}$Zr nuclei. The results significantly depend on the nuclei. The contribution of the kinetic energy $\hat{\mathcal{S}}=\hat{K}$ is large. It is remarked that those of the interactions $\hat{V}^{\mathrm{(C)}}$ and $\hat{V}^{\mathrm{(C\rho)}}$ are scattered, in sharp contrast to the results for the deformed HF solutions in Fig. 3 of Ref. [23]. For the HF solutions, the composition of the pure rotational energy for the well-deformed heavy nuclei is insensitive to nuclides and deformation. However, as elucidated in Fig. 8, $\mathcal{S}_{\mathrm{x}}(2^{+})/E_{\mathrm{x}}(2^{+})$ is sensitive to the pairing. Since the degree of the pair correlations depends on nuclei, the components of the pure rotational energy of nuclei also do, even for the well-deformed heavy nuclei.

In Ref. [23], we showed that the overlap functions $\expectationvalue*{e^{-i\hat{J}_{y}\beta}}{\Phi_{0}}$ and $\mathcal{S}^{01}(\beta)$ in Eq. (3) are relevant to the $J(J+1)$ rule and the composition of the rotational energy. The dependence of the overlap functions on the angle $\beta$ will be instructive in the HF+BCS and HFB cases, as well.

Figure 11 shows the $g$ dependence of the overlap functions $\expectationvalue*{e^{-i\hat{J}_{y}\beta}}{\Phi_{0}}_{g}$ for the HF+BCS solutions of ${}^{34}_{12}$Mg and ${}^{80,100}_{~{}~{}~{}~{}40}$Zr. For ${}^{80,100}_{~{}~{}~{}~{}40}$Zr, $\expectationvalue*{e^{-i\hat{J}_{y}\beta}}{\Phi_{0}}_{g}$ have sharp peaks near $\beta=0$, and become slightly broader as $g$ increases. In contrast, $\expectationvalue*{e^{-i\hat{J}_{y}\beta}}{\Phi_{0}}_{g}$ have broad peaks near $\beta=0$ and getting much broader for increasing $g$ for the ${}^{34}_{12}$Mg nucleus.

Figure 11 also depicts $\expectationvalue*{e^{-i\hat{J}_{y}\beta}}{\Phi_{0}}$ for the HFB solutions of ${}^{34}_{12}$Mg and ${}^{80,100}_{~{}~{}~{}~{}40}$Zr. The overlap functions $\expectationvalue*{e^{-i\hat{J}_{y}\beta}}{\Phi_{0}}$ for ${}^{80,100}_{~{}~{}~{}~{}40}$Zr have sharper peaks near $\beta=0$ than those for ${}^{34}_{12}$Mg. The broad peak near $\beta=0$ makes the ratios $\mathcal{S}_{\mathrm{x}}(J^{+})/\mathcal{S}_{\mathrm{x}}(2^{+})$ deviate from $J(J+1)/6$ in Fig. 9, as analogous arguments given in Ref. [23]. The curvature of $\expectationvalue*{e^{-i\hat{J}_{y}\beta}}{\Phi_{0}}$ at $\beta=0$ is equal to the variance $(\sigma[\hat{J}_{y}])^{2}$ apart from the sign (see Eq. (6)),

$$-\left.\frac{d^{\,2}}{d\beta^{\,2}}\,\expectationvalue*{e^{-i\hat{J}_{y}\beta}}{\Phi_{0}}\,\right|_{\beta=0}=(\sigma[\hat{J}_{y}])^{2}.$$

(29)

In Fig. 12, we show $(\sigma[\hat{J}_{y}])^{2}$ for ${}^{34}_{12}$Mg and ${}^{80,100}_{~{}~{}~{}~{}40}$Zr. Regardless of nuclei, the $(\sigma[\hat{J}_{y}])^{2}$ values decrease as $g$ increases, and $(\sigma[\hat{J}_{y}])^{2}$ of the HFB solutions are smaller than that of the HF solutions. The ${}^{100}_{~{}40}$Zr nucleus exemplifies that $a_{20}$ does not well correlate to $\sigma[\hat{J}_{y}]$ straightforwardly; $(\sigma[\hat{J}_{y}])^{2}$ substantially decreases as $g$ grows, while $a_{20}$ shown in Fig. 1 is insensitive to $g$.