PA-GM: Position-Aware Learning of Embedding Networks for Deep Graph Matching
Abstract
Graph matching can be formalized as a combinatorial optimization problem, where there are corresponding relationships between pairs of nodes that can be represented as edges. This problem becomes challenging when there are potential ambiguities present due to nodes and edges with high similarity, and there is a need to find accurate results for similar content matching. In this paper, we introduce a novel end-to-end neural network that can map the linear assignment problem into a high-dimensional space augmented with node-level relative position information, which is crucial for improving the method’s performance for similar content matching. Our model constructs the anchor set for the relative position of nodes and then aggregates the feature information of the target node and each anchor node based on a measure of relative position. It then learns the node feature representation by integrating the topological structure and the relative position information, thus realizing the linear assignment between the two graphs. To verify the effectiveness and generalizability of our method, we conduct graph matching experiments, including cross-category matching, on different real-world datasets. Comparisons with different baselines demonstrate the superiority of our method. Our source code is available under https://github.com/anonymous.
Index Terms— Graph Matching, Graph Embedding, Deep Neural Network
1 Introduction
Graph matching aims to establish the relationship between two or more graphs based on information derived from their nodes and edges [1]. Due to its ability to better express and encode data relationships, graph matching has gained considerable traction in computer vision and related fields. Applications of graph matching techniques include image registration in medical image analysis [2], link analysis in social networks [3] and image extrapolation in computer vision[4]. Current methods for solving the graph matching problem can be divided into two main classes: a) learning-free or b) learning-based [5, 6]. In the first case, the critical element is the mathematical method used for obtaining an approximate solution to an intrinsically NP-hard problem. On the other hand, learning-based methods aim to improve the solver with a number of methods including deep neural networks.
However, these methods can only compute a similarity score for the whole graph, or rely on inefficient global matching procedures[7]. For example, [8] only considers the embedding of local information for nodes in the graph, leading to a tendency to inconsistently match similar nodes from different regions of the graph, and thus resulted to have ambiguities. As is illustrated in Fig. 1, it shows that the node embedding representation, which relies only on local structural information and semantic node information, lacks sufficient discrimination to effectively resolve these ambiguities. As a result, it is difficult to distinguish the left and right ears of the dog in the example. From this, relative positional information is the key to the matching of diagrams, especially in cases where the graphs have similar semantic and structural content.
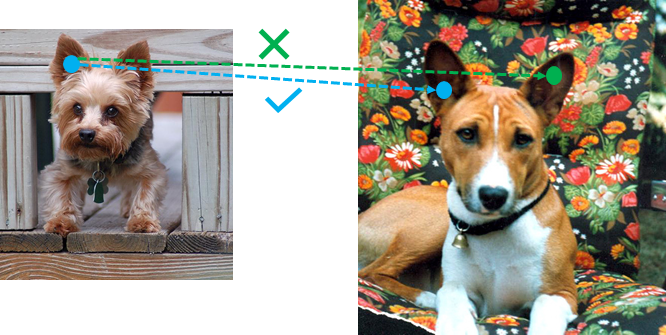
In this paper, we introduce the idea of position-awareness to solve the above-mentioned problem in graph matching. We first construct the graph as input to the model with node features extracted from an image, and then extract a collection of anchor points as reference coordinates for each node in the graph. We further propose a corresponding position-aware node embedding algorithm to capture the relative positional information of the nodes in the graph. With the node-wise graph embedding to hand, we identify a node permutation for node-to-node correspondence.

The main contributions of this paper are as follows:
-
•
We propose a novel Position-Aware Learning of Embedding Network for Deep Graph Matching (PA-GM). To the best of our knowledge, there are no methods that consider the learning of an embedding augmented with relative positional information in graph matching tasks. This restriction hampers their applications in terms of matching accuracy.
-
•
We extract the relative positional information for the nodes in constructing the node embedding instead of the traditional neighborhood aggregation approach. We fully consider the positional information relevant to the matching of keypoints, which is proved to be effective in our experiments.
-
•
The proposed framework is both scalable and flexible, and benefits from the use of a relative position coefficient together with an alignment loss. Experiments show that the model achieves state-of-the-art results on real-world datasets.
2 Methods
In this paper, we intend to resolve the graph matching problem based on the supervised matching of graphs. Specifically, we aim to learn an end-to-end model which can extract graph information and their matches through given pair-wise ground-truth correspondences for a set of graphs, and which can be further generalized to unseen graph pairs. The overall pipeline for graph matching using the position-aware embedding network is presented in Fig. 2.
2.1 Problem Definition
In this paper, we denote a graph by the triple which consists of a finite set of nodes , an adjacency matrix , and a set of node attributes extracted from images using CNN-based models[9, 10]. We construct a vector to indicate the match of vertices in the source graph and the target graph . The vector has elements if vertex is matched to vertex , and if otherwise. It is worth noting that all the vertex matches are subject to one-to-one mapping constraints and . Furthermore, we construct a square symmetric positive matrix as the affinity matrix, to encode the edge-to-edge affinity between two graphs in the off-diagonal elements. In this way, the two-graph matching between and can be formulated as an edge-preserving, quadratic assignment programming (QAP) problem [11]:
| (1) | ||||
where and . The goal of graph matching is to establish a correspondence between two attributed graphs, which minimizes the sum of local and geometric costs of assignment between the vertices of the two graphs.
2.2 Position-Aware Node Embedding
Pixels at neighboring positions in the image convey similar semantic information, therefore we need to distinguish them to resolve matching ambiguities. Here, we refer to the nodes used as reference positions named as anchors and propose an effective strategy to construct an anchor set consisting of all nodes in the graph, denoted by , serving as a stable reference for all nodes. To combine information from the nodes and the anchors, we design the information aggregation mechanism as is shown in Fig.3.

Considering that the amount of effective information transmission to the nodes by the anchors with different relative distances is different, we first compute a relative position coefficient between a pair of nodes and as:
| (2) |
where is the shortest path distance between the two nodes. In practice, to effectively reduce the time complexity of calculating the shortest path and also to reduce interference from those anchor points that are distant from the node under consideration, we demand that the maximum shortest path distance does not exceed the ceiling value . Otherwise, the value of the coefficient is set to infinity. We continue to compute the information aggregation function for the -th layer between node and as:
| (3) |
where and are the feature representation and position representation in the -th layer, and are combined through the message aggregation function. We further aggregate the information from all node-anchor pairs to obtaining a new representation in a high dimensional space using the non-linear variation. This hidden representation can be computed using the update
| (4) |
where AGG is typically a permutation-invariant function (e.g., sum), and is a learnable weight vector for the -th layer.
2.3 Graph Feature Matching
Utilizing the proposed position-aware node embedding, the proposed scheme encodes each node with position information into a high-level embedding space. In this way, we can simplify the second-order affinity matrix of paired graphs to a be a linear one with position-aware learning of the embedding. With the final hidden representation of the source graph and the target graph to hand, we can obtain a soft correspondence between these graphs with a node-wise affinity matrix through the inner product of the embeddings of the two graphs being matched. Specifically, to satisfy the condition that the original graph maps injectively onto the target graph, we apply the Sinkhorn normalization [12] to obtain rectangular doubly-stochastic correspondence matrices.
| (5) |
We further employ the cross-entropy loss function as the permutation loss between the predicted permutation matrix and the ground truth:
| (6) |
where is the ground truth permutation matrix. Consequently, the cross-entropy loss based on linear allocations can be learned end-to-end no matter the number of nodes and edges in the graph.

3 Experiments
3.1 Experimental Setting
Dataset. We use the Willow Object Class [13], consisting of 9963 images in total and is used as a benchmark by many methods to measure the accuracy of image classification and recognition algorithms. And IMC-PT-SparseGM [14] datasets, containing 16 object categories and 25061 images, which gather from 16 tourist attractions around the world. https://www.di.ens.fr/willow/research/graphlearning/.
Implementation Details. The experiments are conducted using two GeForce GTX 1080 Ti GPUs. We employ a batch size of 8 in training and evaluate the results of our method after 2000 epochs for each iteration. We employ the Adam [15] optimizer to train our models with a learning rate of . To overcome the over-smoothing problem common to graph neural network models, we adopt a two-layer graph embedding and restrict the degree of smoothing in our experiments.
Metrics. We evaluate the graph matching capacity of the proposed method using the matching accuracy, which is defined by from [8, 16]. Note that is the element of the predicted permutation matrix representing the correspondence matching of node and node from two different graphs. Similarly, is the correspondence of the ground truth between two nodes, and is the number of matching node pairs.
| Method | Car | Duck | Face | M-bike | W-bottle | Mean |
|---|---|---|---|---|---|---|
| GMN[17] | 67.90 | 76.70 | 99.80 | 69.20 | 83.10 | 79.34 |
| NHGM[18] | 86.50 | 72.20 | 99.90 | 79.30 | 89.40 | 85.50 |
| CIE-H[19] | 82.20 | 81.20 | 100.00 | 90.00 | 97.60 | 90.20 |
| PIA-GM[8] | 88.60 | 87.00 | 100.00 | 70.30 | 87.80 | 86.74 |
| PCA-GM[8] | 87.60 | 83.60 | 100.00 | 77.60 | 88.40 | 87.44 |
| IPCA-GM[16] | 90.40 | 88.60 | 100.00 | 83.00 | 88.30 | 90.06 |
| PA-GM (ours) | 92.70 | 91.30 | 100.00 | 84.50 | 93.80 | 92.46 |
3.2 Graph Matching Results on Real-world Datasets
Table 1 and Table 2 report the overall comparison of the performance results for graph matching accuracy. The CIE-H method excels on the M-bike and W-bottle classes of the Willow ObjectClass dataset, while our method scores highest in the two categories of accuracy, and the average accuracy. By successfully incorporating the position information, our model achieves excellent results in the average accuracy of Willow ObjectClass and IMC-PT-SparseGM datasets. Based on these results, it can be concluded that our method performs well on graph matching compared with existing methods.
3.3 Cross-category Generalization Study
To assess the robustness and generalization ability of our method on the different object categories, we further conduct the cross-category generalization study. Specifically, we train each of the five classes separately, and then test the generalization ability of the validation model for all five classes with the separate training classes. Comparing the elements of Fig. 4, it is clear that the generalization ability of the model framework that incorporates position information is superior to the alternative methods. In addition, the matching accuracy for face data is generally rather large. This may be related to the relatively simple background of the data and less interference from noise.
4 Conclusion
In this paper, we propose a novel deep learning method for graph matching based on node-wise embeddings between graphs that combine position-aware node embeddings. During the experiments, the proposed method is compared with alternative methods to demonstrate its robustness and effectiveness. Comparing our methodology to existing methods on real-world datasets demonstrates its state-of-the-art performance. Further improvements of graph matching will be achieved with the use of different relative positions strategies in future work.
References
- [1] Steven Gold and Anand Rangarajan, “A graduated assignment algorithm for graph matching,” IEEE Transactions on pattern analysis and machine intelligence, vol. 18, no. 4, pp. 377–388, 1996.
- [2] Kexin Deng, Jie Tian, Jian Zheng, Xing Zhang, Xiaoqian Dai, and Min Xu, “Retinal fundus image registration via vascular structure graph matching,” International Journal of Biomedical Imaging, vol. 2010, 2010.
- [3] Jiawei Zhang and S Yu Philip, “Multiple anonymized social networks alignment,” in 2015 IEEE International Conference on Data Mining. IEEE, 2015, pp. 599–608.
- [4] Miao Wang, Yu-Kun Lai, Yuan Liang, Ralph R Martin, and Shi-Min Hu, “Biggerpicture: data-driven image extrapolation using graph matching,” ACM Transactions on Graphics, vol. 33, no. 6, 2014.
- [5] Deepti Pachauri, Risi Kondor, and Vikas Singh, “Solving the multi-way matching problem by permutation synchronization,” in Advances in neural information processing systems. Citeseer, 2013, pp. 1860–1868.
- [6] Junchi Yan, Shuang Yang, and Edwin R Hancock, “Learning for graph matching and related combinatorial optimization problems,” in Proceedings of the Twenty-Ninth International Joint Conference on Artificial Intelligence, IJCAI-20. International Joint Conferences on Artificial Intelligence Organization, 2020, pp. 4988–4996.
- [7] Kun Xu, Liwei Wang, Mo Yu, Yansong Feng, Yan Song, Zhiguo Wang, and Dong Yu, “Cross-lingual knowledge graph alignment via graph matching neural network,” Proceedings of the 57th Annual Meeting of the Association for Computational Linguistics, 2019.
- [8] Runzhong Wang, Junchi Yan, and Xiaokang Yang, “Learning combinatorial embedding networks for deep graph matching,” in IEEE International Conference on Computer Vision, 2019, pp. 3056–3065.
- [9] Karen Simonyan and Andrew Zisserman, “Very deep convolutional networks for large-scale image recognition,” 3rd International Conference on Learning Representations, 2015.
- [10] Hussam Qassim, Abhishek Verma, and David Feinzimer, “Compressed residual-vgg16 cnn model for big data places image recognition,” in 2018 IEEE 8th Annual Computing and Communication Workshop and Conference (CCWC). IEEE, 2018, pp. 169–175.
- [11] Feng Zhou and Fernando De la Torre, “Factorized graph matching,” in 2012 IEEE Conference on Computer Vision and Pattern Recognition. IEEE, 2012, pp. 127–134.
- [12] Richard Sinkhorn and Paul Knopp, “Concerning nonnegative matrices and doubly stochastic matrices,” Pacific Journal of Mathematics, vol. 21, no. 2, pp. 343–348, 1967.
- [13] Minsu Cho, Karteek Alahari, and Jean Ponce, “Learning graphs to match,” in International Conference on Computer Vision, 2013, pp. 25–32.
- [14] Yuhe Jin, Dmytro Mishkin, Anastasiia Mishchuk, Jiri Matas, Pascal Fua, Kwang Moo Yi, and Eduard Trulls, “Image matching across wide baselines: From paper to practice,” International Journal of Computer Vision, pp. 517–547, 2021.
- [15] Diederik P Kingma and Jimmy Ba, “Adam: A method for stochastic optimization,” International Conference on Learning Representations, 2015.
- [16] Wang, Runzhong and Yan, Junchi and Yang, Xiaokang, “Combinatorial learning of robust deep graph matching: an embedding based approach,” IEEE Transactions on Pattern Analysis and Machine Intelligence, 2020.
- [17] A. Zanfir and C. Sminchisescu, “Deep learning of graph matching,” in IEEE Conference on Computer Vision and Pattern Recognition, 2018, pp. 2684–2693.
- [18] Runzhong Wang, Junchi Yan, and Xiaokang Yang, “Neural graph matching network: Learning lawler’s quadratic assignment problem with extension to hypergraph and multiple-graph matching,” IEEE Transactions on Pattern Analysis and Machine Intelligence, 2021.
- [19] Tianshu Yu, Runzhong Wang, Junchi Yan, and Baoxin Li, “Learning deep graph matching with channel-independent embedding and hungarian attention,” in International Conference on Learning Representations, 2020.
- [20] Runzhong Wang, Junchi Yan, and Xiaokang Yang, “Graduated assignment for joint multi-graph matching and clustering with application to unsupervised graph matching network learning.,” in NeurIPS, 2020.