Overdamped Phase Diffusion in hBN Encapsulated Graphene Josephson Junctions

Graphene-based superconductor-normal metal-superconductor (SNS) Josephson junctions have been a popular medium of choice for studying the fundamentals(Heersche et al., 2007; Miao et al., 2007; Du et al., 2008; Ojeda-Aristizabal et al., 2009; Borzenets et al., 2011; Ke et al., 2016; Lee et al., 2011; Coskun et al., 2012; Borzenets et al., 2016a; Shalom et al., 2015; Larson et al., 2020) as well as applications(Borzenets et al., 2016b, 2013; Amet et al., 2016; Wei et al., 2019; Lee et al., 2017; Park et al., 2017) of superconducting devices for more than a decade. However, the full spectrum and consequences of the interactions between the graphene Josephson junction and the environment have not been fully mapped. For example, the observed critical current $I_{C}$ of graphene Josephson junctions is consistently suppressed compared to theoretical predictions; leading to postulations that the junctions are severely underdamped(Tinkham, 2004; Borzenets et al., 2011; Ke et al., 2016; Borzenets et al., 2016a; Shalom et al., 2015), despite the relatively low hysteresis between the switching $I_{S}$ and the retrapping $I_{R}$ currents. The effect of a junction’s environment on its dynamics can be directly investigated by looking at the statistical distribution of the switching current $I_{S}$ (Borzenets et al., 2016a; Coskun et al., 2012; Lee et al., 2011; Fulton and Dunkleberger, 1974; Clarke et al., 1988), or via the measurement of zero-bias resistance arising from the phase diffusion mechanism(Tinkham, 2004; Borzenets et al., 2011; Ingold et al., 1994; Martinis and Kautz, 1989; Kautz and Martinis, 1990; Ivanchenko and Zil’berman, 1968, 1969). Indeed, often attributed to the large capacitance generated by the bonding pads and leads, previous works have shown that the vast majority of graphene-based JJs are underdamped(Borzenets et al., 2011; Ke et al., 2016; Shalom et al., 2015; Borzenets et al., 2016a).

In this work we report on Josephson junctions made from hexagonal boron-nitride (hBN) encapsulated graphene with Molybdenum-Rhenium (MoRe) alloy superconducting contacts (Wang et al., 2013; Wei et al., 2019; Amet et al., 2016). These devices are governed by ballistic electron transport and have been found to be in the intermediate to long-junction regime(Borzenets et al., 2016a) (see supplementary). Here, the MoRe contacts terminate shortly after the active region and are connected to the bonding pads via thin Gold leads. Moreover, the MoRe-Au interface seems to exhibit a significant contact resistance. The junctions were measured at temperatures between $2.7$ and $7$K, where a clear phase diffusion governed, zero-bias resistance can be observed(Tinkham, 2004; Borzenets et al., 2011; Ingold et al., 1994; Martinis and Kautz, 1989; Kautz and Martinis, 1990; Ivanchenko and Zil’berman, 1968, 1969). However, for these devices, when changing the carrier concentration via the back gate, the zero-bias resistance follows the trend expected for overdamped junctions(Borzenets et al., 2011; Ivanchenko and Zil’berman, 1969; Ambegaokar and Halperin, 1969). Thus, we conclude that we have demonstrated ballistic graphene Josephson junction in the overdamped regime.

Graphene is made using the exfoliation method(Novoselov et al., 2005) and is encapsulated in hexagonal boron-nitride (hBN) using the “pick-up” method (Wang et al., 2013). Using CHF₃/O₂ plasma, the hBN-Grahpene-hBN stack is etched thorough in order to make quasi-one dimensional electrical contacts with superconducting electrodes(Amet et al., 2016). Molybdenum-Rhenium(MoRe) alloy electrodes are deposited onto the device using DC sputtering with the approximate thickness of $100-120$nm. The bonding pads and thin metal leads making contact to MoRe are made of Cr/Au ($5$nm/$110$nm). Here, we present data on the device of length $L=500\mathrm{nm}$ (the distance between MoRe contacts), and the width $W=3\mu\mathrm{m}$ (see supplementary).

The device is measured in a home-made cryocooler with a base temperature of  2.5K, which is isolated via both a heat shield and RC filters placed at the low temperature stage. Josephson junction resistance is measured using the lockin method with a four-probe geometry. The junction is biased by a variable DC current with a small AC excitation of $5$nA. The voltage across the junction is amplified using a custom differential pre-amp prior to being fed into the lockin. The gate voltage applied to the back of the 300nm SiO₂ oxide layer is used to control the carrier density of graphene. Figure 1 presents the differential resistance $dV/dI$ as a function of applied DC bias current $I_{Bias}$. All the curves show two transition points, as the bias current is swept from a large negative value to a large positive value. The absolute value of the current on the negative side below which the junction becomes superconducting is the retrapping current $I_{R}$, i.e. $|I_{Bias}|=I_{R}$. On the positive side, the junction transitions from the superconducting to the normal state at the switching current $I_{S}$(Tinkham, 2004). Figure 1(a) shows resistance versus $I_{Bias}$ for different temperatures with the backgate voltage set to 35V. Figure 1(b) shows the resistance versus bias current for different gate voltages taken at 3K. In both cases, the switching and retrapping currents $I_{S}$ and $I_{R}$ follow the expected trends: falling exponentially with increasing temperature, and increasing with gate voltage away from the Dirac point with the hole conduction regime exhibiting a suppressed critical current due to the effects of contact doping(Borzenets et al., 2011; Ke et al., 2016; Borzenets et al., 2016a). Moreover, the trend of $I_{S}$ with respect to temperature $T$ follows that expected for ballistic Josephson junctions in the long junction regime (See Supplementary)(Borzenets et al., 2016a).

The vast majority of previously reported graphene Josephson junctions, exhibit hysteresis between the switching and retrapping currents, with $I_{S}>I_{R}$ even for temperatures above 3K. While certain works attribute this hysteresis to self-heating of the junction(Borzenets et al., 2013; Courtois et al., 2008), it has also been shown that most of the graphene Josephson junctions exhibit underdamped behavior(Borzenets et al., 2011; Ke et al., 2016; Shalom et al., 2015; Borzenets et al., 2016a). (Graphene-based Josephson junctions a typically overdamped due to the large capacitance caused by the presence of the backgate.) Here, however, for all tested gates and temperatures, we do not observe a difference between $I_{S}$ and $I_{R}$. This leads to an initial indication that the device may be overdamped.

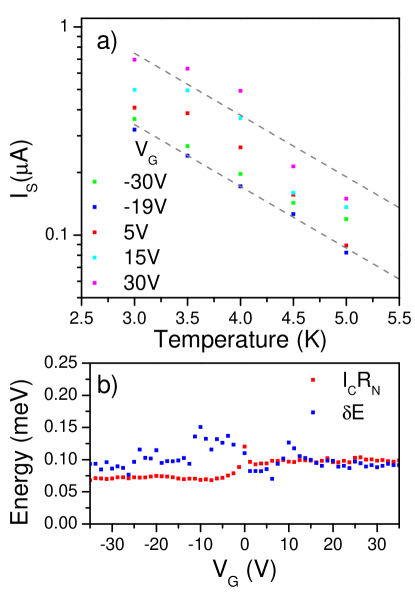
We now further investigate the junction dynamics via the characterization of device behavior in the phase diffusion regime. Phase diffusion manifests itself as an observable non-zero resistance below the critical current (even at $I_{Bias}=0$), arising from phase slips that are caused by thermal noise. The rate of these phase slips down the prototypical titled washboard potential, and therefore, the measured zero-bias resistance is governed by the junction dynamics which dictate the energy dissipation rate(Tinkham, 2004). Indeed, we are able to observe a measurable resistance in our devices, even at zero bias, and down to 3K in temperature. We define the measured zero-bias differential resistance as R₀. In order to confirm that $R_{0}$ arises from the phase diffusion mechanism, we study the evolution of this resistance with respect to temperature. Regardless of the junction damping dynamics the trend behavior of $R_{0}$ with respect to temperature should have the following dependence: (Tinkham, 2004; Borzenets et al., 2011; Ingold et al., 1994; Martinis and Kautz, 1989; Kautz and Martinis, 1990; Ivanchenko and Zil’berman, 1968, 1969; Ambegaokar and Halperin, 1969):

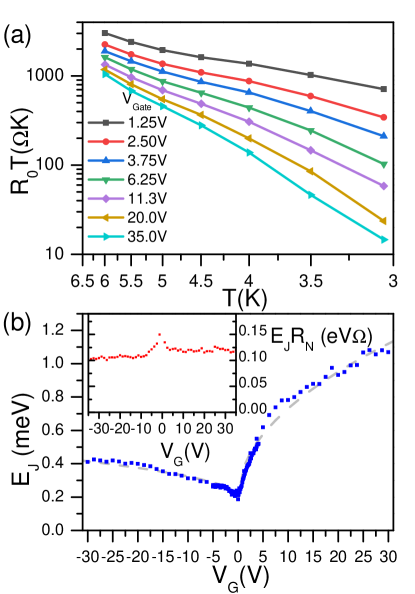
Here, $E_{J}=\hbar I_{C}/2e$ is the Josephson energy. (The above exponential dependence holds when $2E_{J}/k_{B}T>1$ (Tinkham, 2004).) Reworking equation (1), we can arrive at the proportionality relationship: $\log{(R_{0}(T)\cdot T)}\propto-2E_{J}/k_{B}T$. In Figure 2a we plot the value $R_{0}\cdot T$ versus inverse temperature $T$ on a semi-log scale. Indeed, we find that the relationship is nearly linear, consistent with theory. From here, knowing the temperature, we can extract $E_{J}$ from the slope of the curves. The fitted Josephson energy versus gate voltage is plotted in Figure 2b. For single layer graphene Josephson junctions governed by ballistic transport it is expected that value $E_{J}\cdot R_{N}$ is constant with respect to $V_{G}$(Borzenets et al., 2016a); and we find not only that indeed this is the case (see Figure 2 inset), but that this value matched well with the expected energy scale extracted from the trend of $I_{S}$ vs $T$ (see supplementary). Here $R_{N}$ is the normal resistance, i.e. the resistance of the junction when it is in normal state.

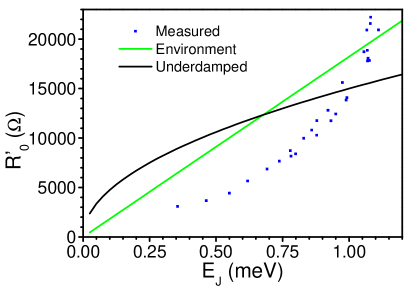
Having found the Josephson energy, we can determine the last parameter governing $R_{0}$. This final parameter is different depending on the damping dynamics of the junction. Previous theoretical works have defined three different regimes: For overdamped junctions, the governing parameter is $R_{N}$, the normal resistance(Ivanchenko and Zil’berman, 1969; Ambegaokar and Halperin, 1969). For underdamped junctions, $R_{0}$ depends on the plasma frequency $\omega_{p}\propto\sqrt{E_{J}/C}$(Kautz and Martinis, 1990). (Here $C$ is the capacitance of the junction.) Finally, if the junction is underdamped at low frequencies, but becomes overdamped at the plasma frequency (due to being shorted by the environment), we have $R_{0}\propto Z_{0}$(Ingold et al., 1994). Here $Z_{0}$ is the real part of the high frequency impedance caused by the junction’s environment (Ingold et al., 1994). We find that analyzing our devices as if they were underdamped, or damped by the environment does not produce a good match between measured data and theoretical expectation. (See supplementary).

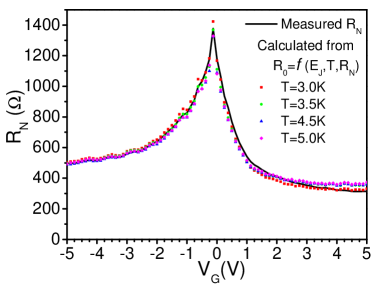
Now, we confirm that our devices are indeed in the overdamped regime by comparing the measured normal resistance $R_{N}$ with that back calculated from the the zero-bias resistance $R_{0}$. Following the full expression in Ref. (Ambegaokar and Halperin, 1969) we have:

Here, I₀ is the modified Bessel function, and $\gamma=I_{c}\hbar/ek_{B}T$. ($V$ is the voltage measured accross the junction.) For $I_{Bias}$ approaching zero, the equation simplifies to $R_{N}=R_{0}/[I_{0}(E_{J}/k_{B}T)]^{-2}$. Figure 3 shows the measured normal resistance $R_{N}$ versus gate voltage $V_{G}$ plotted together with the resistance calculated from Equation 2 for different temperatures. It can be seen that we have a good match between the measured and the theoretical result, in particular for high values of $R_{N}$.

The damping of the junction is typically determined by the quality factor $Q$, with $Q=R_{N}(2eI_{C}C/\hbar)^{1/2}=\frac{2e}{\hbar}R_{N}\sqrt{E_{J}C}$. ($C$ being the capacitance of the junction.) A $Q<0.85$ results in an overdamped junction(Likharev, 1991). However, the difficulty in calculating an accurate quality factor $Q$ is two fold: One, the measured critical current $I_{C}$ has been consistently less than the value predicted by theory, leading to the question of whether the true critical current is being measured. Two, it is unclear which areas of the device play an active role in the junction capacitance $C$. (Previous works have suggested that the capacitance all the way up to the capacitive coupling between the device bonding pads plays a significant role. Thus the junction capacitance is always several orders of magnitude larger compared to that expected from the dimensions of the SNS region itself.) Assuming that the junction capacitance includes the contribution of the $100\times 100\mu\mathrm{m}$ bonding pads that couple to each other via the backgate below the $300\mathrm{nm}$ thick $\mathrm{SiO_{2}}$ layer, we arrive at $C\approx 600\mathrm{fF}$. Taking $E_{J}=0.3\mathrm{meV}$ and $R_{N}=100\Omega$, we calculate a quality factor $Q=1.6$: the underdamped regime. Hence, we are led to conclude that the tested junction has been sufficiently isolated from the capacitive contribution of the bonding pads. Indeed, we estimate that the interface between MoRe superconducting contacts and the gold leads suffers from a contact resistance in the order of tens of $\Omega$, which is sufficient to reduce the quality factor below $1$Vion et al. (1996); Borzenets et al. (2013).

In conclusion, we have investigated the phase diffusion regime in hBN encapsulated graphene Josephson junction governed by ballistic electron transport. The observed trend of the measured zero-bias resistance $R_{0}$ with respect to carrier concentration conforms well to theory describing phase diffusion in an overdamped junction regime. This is the first conclusive confirmation of overdamped behavior in graphene-based Josephson junction. We attribute this behavior to effective isolation of the Josephson junction from the capacitive contribution of the bonding pads. The isolation arises from a resistive connection with the device layout.

Supplementary to: Overdamped Phase Diffusion in hBN Encapsulated Graphene Josephson Junctions