Out-of-distribution generalization under random, dense distributional shifts
Abstract
Many existing approaches for estimating parameters in settings with distributional shifts operate under an invariance assumption. For example, under covariate shift, it is assumed that remains invariant. We refer to such distribution shifts as sparse, since they may be substantial but affect only a part of the data generating system. In contrast, in various real-world settings, shifts might be dense. More specifically, these dense distributional shifts may arise through numerous small and random changes in the population and environment. First, we discuss empirical evidence for such random dense distributional shifts. Then, we develop tools to infer parameters and make predictions for partially observed, shifted distributions. Finally, we apply the framework to several real-world datasets and discuss diagnostics to evaluate the fit of the distributional uncertainty model.
1 Introduction
Distribution shift is a persistent challenge in statistics and machine learning. For example, we might be interested in understanding the determinants of positive outcomes in early childhood education. However, the relationships among learning outcomes and other variables can shift over time and across locations. This makes it challenging to gain actionable knowledge that can be used in different situations. As a result, there has been a surge of interest in robust and generalizable machine learning. Existing approaches can be classified as invariance-based approaches and adversarial approaches.
Invariance-based methods assume that the shifts only affect a sub-space of the data distribution [Pan and Yang, 2010, Baktashmotlagh et al., 2013]. For example, under covariate shift [Quinonero-Candela et al., 2009], the distribution of the covariates changes while the conditional distribution of the outcomes given the covariates stays invariant. In causal representation learning [Schölkopf et al., 2021], the goal is to disentangle the distribution into independent causal factors; based on the assumption that spurious associations can be separated from invariant associations. Both approaches assume the shift affects only a sub-space of the data. We call such shifts sparse distribution shifts.
Adversarial methods in robust machine learning consider worst-case perturbations. The idea is that some adversary can perturb the data either at the training [Huber, 1981] or deployment stage [Szegedy et al., 2014, Duchi and Namkoong, 2021]; and the goal is to learn a model that is robust to such deviations. While developing robust procedures is important, worst-case perturbations might be too conservative in many real-world applications.
Motivated by an empirical observation, in this paper we consider distributional shifts due to random and dense perturbations. As an example, consider replication studies. In replication studies, different research teams try to replicate results by following the same research protocol. Therefore, any distribution shift between the data may arise from the superposition of many unintended, subtle errors that affect every part of the distribution, which might be modeled as random. We call such shifts dense distributional shifts. The random, dense distributional shift model has recently been used to quantify distributional uncertainty in parameter estimation problems [Jeong and Rothenhäusler, 2023, Rothenhäusler and Bühlmann, 2023] and has shown success in modelling real-world temporal shifts in refugee placement [Bansak et al., 2024]. We will develop tools to measure the similarity between randomly perturbed distributions, infer parameters and predict outcomes for partially observed and shifted distributions.
1.1 Summary of contributions
In this subsection, we preview and summarize our contributions.
First, we discuss an intriguing phenomenon on a real-world dataset, in which means of arbitrary functions seem to be correlated across multiple distributions. To the best of our knowledge, existing distribution shift models do not imply this phenomenon.
To address this gap, we introduce a random distribution shift model for multiple datasets, where likelihood ratios exhibit random fluctuations. This builds on the perturbation model introduced in Jeong and Rothenhäusler [2023], which considers a single perturbed distribution. We generalize the model to handle multiple perturbed distributions that are possibly correlated. We then demonstrate the extended random perturbation model can explain the empirical distribution shift phenomenon.
Next, we consider the following domain adaptation problem. Our goal is to predict outcomes based on covariates . Specifically, we seek to estimate for some loss function , where denotes the expectation under the unknown target distribution. While we have access to complete datasets from multiple training distributions, the target dataset contains only covariates without corresponding outcomes . We adopt a weighted Empirical Risk Minimization (ERM) approach, where the parameters are estimated as
where denotes the empirical mean computed on the -th training dataset.
Under the random distribution shift model, we derive optimal weights for weighted ERM and expressions for the corresponding out-of-distribution error. Based on this expression, we derive prediction intervals for parameters of the target distribution.


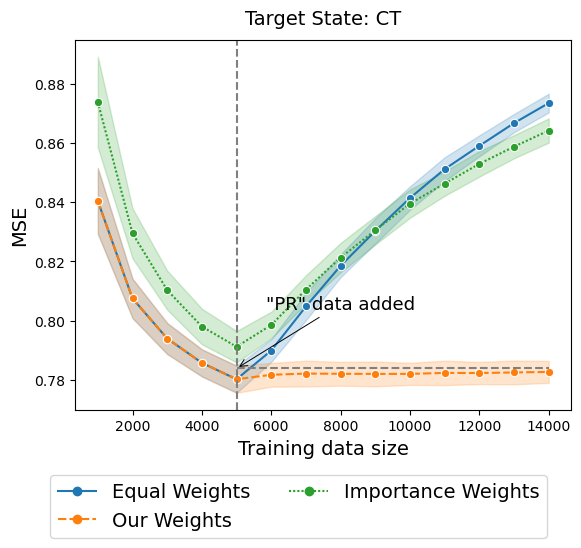
The effectiveness of our approach is illustrated in Figure 1, which shows the out-of-distribution error for income prediction task (see Section 4 for details) when the target state is either Texas (TX) or Washington (WA) state, and training datasets are from California (CA) and Puerto Rico (PR). We simulate a scenario where CA data is initially available, followed by additional data from PR. We optimize the weighted empirical risk under three different weighting schemes: (1) equal weighting of all samples, (2) sample-specific importance weighting under the assumption of covariate shifts, and (3) distribution-specific weighting based on our approach. Compared to equal weighting and importance weighting methods, our approach demonstrates remarkable robustness, maintaining consistently low out-of-distribution error even after including the PR dataset by optimally weighting two data sources.
The remainder of paper is outlined as follows. In Section 2, we present empirical evidence for random and dense distributional shifts and introduce the random distributional perturbation model. In Section 3, we establish the foundations for domain adaptation under random and dense distributional shifts. In particular, we derive out-of-distribution risk for weighted empirical risk minimization and conduct statistical inference for parameters of the target distribution. In Section 4 and Section 5, we apply our framework to several real-world datasets and demonstrate the robustness of our method. We conclude in Section 6.
1.2 Related work
This work addresses domain adaptation problems under a specific class of random distributional shifts. Domain adaptation methods generally fall into two main categories [Pan and Yang, 2010]. The first type involves re-weighing, where training samples are assigned weights that take the distributional change into account [Long et al., 2014, Li et al., 2016]. For example, under covariate shift, training samples can be re-weighted via importance sampling [Gretton et al., 2009, Shimodaira, 2000, Sugiyama et al., 2008]. Another type aims to learn invariant representations of features [Argyriou et al., 2007, Baktashmotlagh et al., 2013]. Under dense distributional shifts, as we will see in Section 2, instance-specific weights can be unstable or even be undefined due to overlap violations. Furthermore, under dense distributional shifts there might be no invariant representation. Thus, from a classical domain adaptation perspective, dense distribution shifts are a challenging setting.
The proposed method approximates the target distribution as a weighted combination of source distributions. Therefore, the proposed method shares methodological similarities with synthetic controls, which search for a linear combination of untreated units to represent treated units [Abadie and Gardeazabal, 2003]. Synthetic controls are applied to panel data and often assume a linear factor model for a continuous outcome of interest [Doudchenko and Imbens, 2016, Abadie et al., 2007, Bai, 2009, Xu, 2017, Athey et al., 2021]. Our framework can be seen as a justification for synthetic control methods under random distributional shifts. In addition, our procedure can be applied to model distribution shifts with or without time structure for any type of data (discrete, continuous, ordinal). Furthermore, our framework allows for straightforward generalizations to empirical risk minimization, which includes many modern machine learning tools.
The approach of weighting a combination of source distributions to approximate a target distribution also appears in the distributionally robust optimization (DRO) framework [Xiong et al., 2023, Zhan et al., 2024]. While there is some similarity in the prediction procedures, the random distribution shift model enables diagnostics and inference that are markedly different from a worst-case approach. One can think about the random shift model as a potential justification for a very particular type of distribution weighting, with additional inferential consequences.
Our procedure is also loosely related to meta-analysis and hierarchical modeling. Meta-analysis is a statistical procedure for combining data from multiple studies [Higgins et al., 2009]. Traditional meta-analysis relies on the assumption that the effect size estimates from different studies are independent. However, in real-world applications, this independence assumption often does not hold true. There are different strategies to handle dependencies. These include averaging the dependent effect sizes within studies into a single effect [Wood, 2008], incorporating dependencies into models through robust variance estimation [Hedges et al., 2010], or through multilevel meta-analysis where they assume a cluster structure and model dependence within and between clusters [Cheung, 2014]. In meta-regression, the effect sizes are expressed as linear functions of study characteristics, and they are independent conditional on these study characteristics [Borenstein et al., 2009, Hartung et al., 2008]. Bayesian hierarchical models with prior on model parameters can also be used to model dependency [Higgins et al., 2009, Lunn et al., 2013]. Compared to these procedures, our approach allows for correlations between studies and can be applied even when there is no hierarchical structure and no summary study characteristics are available. Furthermore, our approach is frequentist, so it does not require choosing a prior distribution.
In this paper, we model multiple correlated distributions using random distributional perturbation model introduced in Jeong and Rothenhäusler [2023], where dense distributional shifts emerge as the superposition of numerous small random changes. In Jeong and Rothenhäusler [2023], a single perturbed distribution is considered. In our paper, we extend this model to address multiple perturbed distributions that are possibly correlated.
2 Distributional Uncertainty
Due to a superposition of many random, small changes, a data scientist might not draw samples from the target distribution but from several randomly perturbed distributions . More specifically, we assume that a data scientist has datasets, with the -th dataset being an i.i.d. sample from a perturbed distribution . Intuitively speaking, some of these distributions might be similar to each other, while others might be very different. For instance, one replication study might closely resemble another due to collaboration among investigators. Additionally, a dataset obtained from California might be more similar to one from Washington than to one from Wyoming.
We illustrate the scenario where multiple datasets exhibit distributional correlations using the GTEx111The Genotype-Tissue Expression (GTEx) Project was supported by the Common Fund of the Office of the Director of the National Institutes of Health, and by NCI, NHGRI, NHLBI, NIDA, NIMH, and NINDS. The dataset used for the analyses described in this manuscript is version 6 and can be downloaded in the GTEx Portal: www.gtexportal.org. data. The GTEx V6 data offers pre-processed RNA-seq gene-expression levels collected from 450 donors across 44 tissues. Treating each tissue as an individual study, we have 44 datasets. Each dataset from tissue is considered as an independent sample from a perturbed distribution , where represents a joint distribution of all gene-expression levels. Some of these datasets are likely to be correlated due to factors such as an overlap of donors and the proximity between tissues. Empirical evidence of this correlation is presented in the left side of Figure 2, where each row and column corresponds to a tissue, and each dot represents a standardized covariance between gene expression levels of a randomly selected gene-pair, among the observations in the tissue. We randomly sample 1000 gene-pairs. We can see that some tissues exhibit a clear linear relationship. In the following, we will introduce a distribution shift model that implies this linear relationship.


To model the relatedness of multiple datasets, we will assume that each is a random perturbation of a common target distribution . Then, we adopt the random distributional perturbation model in Jeong and Rothenhäusler [2023], where dense distributional shifts emerge as the superposition of numerous small random changes, to construct perturbed distributions . In this random perturbation model, probabilities of events from a random probability measure are slightly up-weighted or down-weighted compared to the target distribution .
Without loss of generality, we construct distributional perturbations for uniform distributions on . A result from probability theory shows that any random variable on a finite or countably infinite dimensional probability space can be written as a measurable function , where is a uniform random variable on .222For any Borel-measurable random variable on a Polish (separable and completely metrizable) space , there exists a Borel-measurable function such that where follows the uniform distribution on [Dudley, 2018]. With the transformation , the construction of distributional perturbations for uniform variables can be generalized to the general cases by using
Let us now construct the perturbed distribution for a random variable that follows a uniform distribution under . Take bins for . Let be i.i.d. positive random variables with finite variance. We define the randomly perturbed distribution by setting
Then the datasets are generated as follows:
1. Generate perturbed distributions: Start with the target distribution and generate perturbed distributions using random weights .
2. Draw samples: For each , draw i.i.d. samples, , from the perturbed distribution (), conditioned on the weights .
Further, let such that converges to 0. This is the regime where the distributional uncertainty is of higher order than the sampling uncertainty.
Notation.
Let be the target distribution on , and be the perturbed distribution on conditioned on . We draw an i.i.d. sample from , conditioned on . Let be the marginal distribution of . We denote as the expectation under , as the expectation under , and as the expectation under . Specifically, is the mean of for a random variable and is the mean of for a random variable conditioned on . Moreover, we denote as the sample average in . For example, where . We write for the variance under and for the variance under . Specifically, is the variance of for a random variable .
Theorem 1 (Distributional CLT).
Under the assumptions we mentioned above, for any Borel measurable square-integrable function for , we have
| (1) |
where , and has
Here, denotes element-wise multiplication (Hadamard product).
Remark 1 (Random shift in ).
As an example, let us study how conditional expectations shift under this model. We consider the case where the data consists of both covariates and target , that is . Let be some subset of the sample space of with . Using a Taylor approximation,
where . Thus, by the CLT,
Hence, the conditional expectation is randomly shifted based on three factors: 1) it is proportional to the distribution shift strength, ; 2) it is proportional to the conditional noise, ; and 3) it is inversely proportional to the probability . This random shift in needs to be accounted for both estimation and inference.
Remark 2 (Distributional covariance).
We call the covariance between distributional perturbations. Two perturbed distributions and are positively correlated if . This means that when one perturbation slightly increases the probability of a certain event , the other distribution tends to slightly increase the probability of this event as well. This can be seen by choosing the test function :
However, if two perturbed distributions are negatively correlated, a (random) increase in the probability of an event under one distribution would often coincide with a (random) decrease in the probability of this event under the other distribution, compared to .
Remark 3 (Estimation of variance).
The variance under the target distribution can be estimated via the empirical variance of on the pooled data . Then, if has a finite fourth moment, we have . The details can be found in the Appendix 8.5.
An extended version of Theorem 1 where for some and the proof of Theorem 1 can be found in the Appendix, Section 8. In this paper, we consider the target distribution as fixed. In the Appendix 8.4, we discuss a version of Theorem 1 that allows for a randomly shifted target distribution. In Section 9 of the Appendix, we discuss several special cases of the random perturbation model, including random shift across time, i.i.d. shifts, and random shifts between locations.
Theorem 1 tells us that is the asymptotic covariance of and for any Borel-measurable square-integrable function with unit variance under . Remarkably, under our random distributional perturbation model, a -dimensional parameter quantifies the similarity of multiple distributions and captures all possible correlations of all square-integrable functions.
The random shift model explains the linear patterns in the GTEx scatterplot.
Consider two perturbed distributions and , and uncorrelated test functions with unit variances, . In the GTEx example, is a standardized product between gene expression levels of a randomly selected -th gene pair. Moreover, in Appendix 13, we see that these test functions are approximately uncorrelated. From Theorem 1, we have
where
Therefore, for , can be viewed as independent draws from a bivariate Gaussian distribution with distributional covariance . This explains the linear patterns observed in the left plot of Figure 2. Gaussianity can be evaluated by QQ plots of the statistic:
| (2) |
The QQ-plots of the statistic in (2) are presented on the right-hand side of Figure 2, when the target tissue is set to be brain cortex. These plots indicate that statistics in (2) indeed follow a Gaussian distribution.
3 Out-of-distribution generalization
In this section, we demonstrate how, under the random distributional perturbation model, we can share information across datasets from different times and locations, and infer parameters of a partially observed target distribution. Specifically, we show how the distributional CLT from the previous section allows us to identify the optimal convex combination of source distributions to best approximate the target distribution.
We consider the following domain adaptation setting throughout the section. We aim to predict a target based on some covariates , that is the data is . We want to estimate for some loss function . We consider the setting where we observe full only on the source distributions . More specifically, for the -th source data (), we observe i.i.d. samples drawn from the source distribution . Furthermore, there are i.i.d. samples from the target distribution , but we only observe a subset and have .
For any fixed non-negative weights with , one can consider weighted empirical risk minimization, that is, one can set
In the following, we want to study the excess risk
This will give us insights into how to choose the weights in an optimal fashion, and allow us to conduct statistical inference.
Lemma 1 (Out-of-distribution error of weighted ERM).
For each in an open subset of , let be twice continuously differentiable in for every . Assume that the matrix exists and is nonsingular. Assume that the third partial derivatives of are dominated by a fixed function for every in a neighborhood of . We assume that , and are square-integrable under . Assume that . Then,
for some random variable , with
The proof of Lemma 1 is provided in Appendix 10, along with the additional regularity assumptions under which the consistency assumption stated in Lemma 1 holds.
By this lemma, the optimal in terms of out-of-distribution error is
A priori, is unknown to the researcher. In the following, we will describe estimation and inference for . Our estimation strategy is based on the following observation. Using the distributional CLT, for any function and any ,
| (3) |
We can use this fact that the covariance term of the limiting distribution is inflated by the factor regardless of the test functions to estimate . Consider different test functions of , that is , . For example, we may use individual covariates as test functions, . Then, we can estimate by solving
| (4) |
and set the final estimate of as
We will discuss the accuracy of this estimate in the following section. More specifically, we will derive confidence intervals for and .
Remark 4.
In practice, one might wonder how to choose different test functions . From a theoretical standpoint, under the distributional uncertainty model, one can technically choose any function with finite variance. However, for actual applications, we suggest the following guideline. Our method considers a distribution to be “close” to if the averaged values of test functions on closely align with the corresponding averaged values on . Therefore, these test functions should be chosen to capture the dimensions of the problem where a close match is important. For example, in the numerical experiments in Section 4, the target function of interest is the logarithmic value of income and using the means of covariates that are well-known to be related to the income variable as test functions demonstrates good performance. We also provide simple diagnostics, presented in Figure 3 as standard residual plots and normal QQ-plots, that allow one to assess the fit of the distributional perturbation model and the choice of test functions.
3.1 Inference for and
In the following, we discuss how to form asymptotically valid confidence intervals for and when and are allowed to have negative weights. As discussed earlier, we choose different test functions . For now we assume that test functions are uncorrelated and have unit variances under . Later we will discuss cases where test functions are correlated and have different variances. In the previous section, we saw that can be estimated via a least-squares problem with a linear constraint on the weights. To remove the linear constraint in equation (4), we perform the following reparametrization,
We can obtain via . We can re-write this as the following linear regression problem
where the feature matrix in the linear regression is defined as
and the outcome vector in the linear regression is defined as
Since test functions were assumed to be uncorrelated and have unit variances under , using Theorem 1, rows of the feature matrix and the outcome vector are asymptotically i.i.d., with each row drawn from a centered Gaussian distribution. Therefore, the problem may be viewed as a standard multiple linear regression problem where the variance of the coefficient is estimated as
and the residual variance is calculated as
Different from standard linear regression, in our setting each column represents a data distribution and each row represents a test function, and Gaussianity does not hold exactly in finite samples. Therefore, a priori it is unclear whether standard statistical tests in linear regression (such as -test and -test) carry over to the distributional case. The following theorem tells us that the standard linear regression results still hold. Therefore, we can conduct statistical inference for the optimal weights in the same manner as we conduct t-tests and F-tests in a standard linear regression. The proof of Theorem 2 can be found in Appendix, Section 11. Note that these results assume a finite number of test functions and datasets but are asymptotic in terms of as they rely on the distributional CLT.
Theorem 2.
Assume that test functions are uncorrelated and have unit variances under . Let and be defined as above. Then, we have
where follows the -dimensional multivariate t-distribution with degrees of freedom.
Remark 5 (Distributional t-test).
For this test, the null hypothesis is that the dataset should have weight zero in the weighted empirical risk minimization. Mathematically, this corresponds to testing the null hypothesis . Thus, we consider the following hypotheses:
The test statistic is defined as
From Theorem 2, under the null hypothesis,
where is a univariate -distribution with degrees of freedom.
Remark 6 (Distributional F-test).
For this test, the null hypothesis is that each dataset is equally informative for the target distribution. Mathematically, this corresponds to testing the null hypothesis for . Thus, we consider the following hypotheses:
The test statistic is defined as
From Theorem 2, under the null hypothesis,
where is a F-distribution with degrees of freedom and .
Remark 7 (Distributional confidence intervals for parameters of the target distribution).
We will now discuss how to form asymptotically valid confidence intervals for when and . Here we assume that the influence function has a finite fourth moment under . Then, we can form -confidence intervals for with as follows:
Here, denotes the empirical variance of
on the pooled donor data . The proof of this result can be found in the Appendix, Section 12.
Remark 8 (Distributional sample size and degrees of freedom).
Note that the asymptotic variance of “distributional” regression parameters has the same algebraic form as the asymptotic variance for regression parameters in a standard Gaussian linear model. In the classical setting, the test statistics of regression parameters follow -distributions with degrees of freedom, where is the sample size and is the number of covariates. In our setting, we have degrees of freedom, where corresponds to the number of test functions and corresponds to the number of donor distributions.
Remark 9 (Correlated test functions).
We assumed that the are uncorrelated and have unit variances under . In practice, this might not be the case. In such cases, we can apply a linear transformation to the test functions in a pre-processing step to obtain uncorrelated test functions with unit variances. We define the transformation matrix , where is an estimate of the covariance matrix of on the pooled data. From Remark 3, if have finite fourth moments, we have .
4 ACS Income Data
In this section, we demonstrate the effectiveness and robustness of our method when the training dataset is obtained from multiple sources. We focus on the ACS Income dataset [Ding et al., 2021] where the goal is to predict the logarithmic value of individual income based on tabular census data.
Similar as in Shen et al. [2023], we consider a scenario where we initially have a limited training dataset from California (CA), and subsequently, we obtain additional training dataset from Puerto Rico (PR). We iterate through the target state among the rest of 49 states. Note that there are substantial economic, job market, and cost-of-living disparities between CA and PR. Most of the states are more similar to CA than PR. Therefore, increasing the training dataset with data sourced from PR will lead to substantial performance degradation of the prediction algorithm on the target state.
We compare three methods in our study. In the first method, we fit the XGBoost on the training dataset in the usual manner, with all samples assigned equal weights. In the second method, we employ sample-specific importance weights. The importance weights are calculated as follows. First, pool the covariates of the training dataset (CA + PR) and the target dataset. Let be the label which is 1 if the -th sample is from the target dataset and 0 otherwise. Then, the importance weight for the -th sample is obtained as
where we estimate using XGBoost on the pooled covariates data and estimate as the ratio of the sample size of the target data to the sample size of the pooled data.
In the third method, based on our approach, the XGBoost is fitted on the training dataset, but this time samples receive different weights depending on whether they originate from CA or PR. We utilize the occupation-code feature to construct test functions. The test function is defined as whether -th sample has the -th occupation code. The occupation code is a categorical variable representing around 500 different occupation categories. The data dictionary at ACS PUMS documentation333https://www.census.gov/programs-surveys/acs/microdata/documentation.2018.html provides the full list of occupation codes. The number of test functions in total is therefore around 500. Then, we estimate distribution-specific-weights by running
Note that is the proportion of samples of the srtate with the -th occupation code.
The results with the target states of Texas (TX) and Washington (WA) are given in Figure 1. Similar patterns are observed for other target states, aligning with either TX or WA behaviors. Results for other target states can be found in the Appendix 13.
For the target TX, as we include the PR data, the Mean Squared Error (MSE) initially drops for all the methods. However, as more data from PR is added, the MSE starts to increase for both methods with equal weights and importance weights. In contrast, our method demonstrates robustness, with the MSE decreasing after including PR data and staying consistently low, even when the PR source becomes dominant in the training dataset. Turning to the target WA, for both methods with equal weights and importance weights, adding data sourced from PR results in a straightforward increase in MSE. In contrast, our method assigns weights close to 0 for samples originating from PR, preventing significant performance degradation.
5 GTEx Data
In this section, we illustrate our methods using the GTEx data. We will also run model diagnostics to evaluate model fit. The GTEx V6 dataset provides RNA-seq gene-expression levels collected from 450 donors across 44 tissues.
Treating each tissue as a separate study, we have 44 different datasets. As shown in Figure 2, some tissues exhibit higher correlations than others. To demonstrate our method, we select 5 different tissues (same as in Figure 2): Adipose subcutaneous, Adipose visceral omentum, Brain cortex, Brain frontal cortex, and Brain cerebellum. Let brain cortex be our target tissue (the third tissue in Figure 2). The code and the data are available as R package dlm at https://github.com/yujinj/dlm.
For our test functions, we randomly sample 1000 gene-pairs and define a test function as the standardized product of gene-expression levels of a pair. In total, we have 1000 test functions. Most genes are known to be uncorrelated with each other, with the 90th percentile range of correlations between two different test functions being about . We employ group Lasso to estimate the sparse inverse covariance matrix. As the estimated inverse covariance matrix is close to a diagonal matrix (details provided in the Appendix 13), we do not perform a whitening transformation.
The R package dlm (https://github.com/yujinj/dlm) contains a function dlm that performs distributional linear regressions:
dlm(formula, test.function, data, whitening)
Here, the formula parameter specifies which model we want to fit. The test.function parameter represents considered test functions. The data parameter passes a list of datasets. The whitening parameter is a boolean indicating whether one wants to perform a whitening transformation. Additional details and descriptions of the function can be found on the GitHub page.
Below is the summary output of the dlm function with a model formula “Brain cortex Adipose subcutaneuous + Adipose visceral omentum + Brain frontal cortex + Brain cerebellum” with 1000 test functions defined as standardized products of randomly selected gene-pairs. Note that the summary output of the dlm function closely resembles that of the commonly used lm function.
Call:dlm(formula = Brain_Cortex ~ Adipose_Subcutaneous + Adipose_Visceral_Omentum + Brain_Frontal_Cortex_BA9 + Brain_Cerebellum, test.function = phi, data = GTEx_data, whitening = FALSE)Residuals: Min 1Q Median 3Q Max-0.56838 -0.09436 -0.00604 0.08739 0.40917Coefficients: Estimate Std. Error t value Pr(>|t|)Adipose_Subcutaneous -0.0001295 0.0304036 -0.004 0.9966Adipose_Visceral_Omentum 0.0462641 0.0250888 1.844 0.0655 .Brain_Frontal_Cortex_BA9 0.7846112 0.0184325 42.567 < 2e-16 ***Brain_Cerebellum 0.1692543 0.0217128 7.795 1.61e-14 ***---Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1Residual standard error: 0.1377 on 997 degrees of freedomMultiple R-squared: 0.5088,Adjusted R-squared: 0.5073F-statistic: 344.3 on 3 and 997 DF, p-value: < 2.2e-16
The coefficient represents the estimated weight for each perturbed dataset. The sum of coefficients equals to one. The estimated weight for the brain-frontal-cortex dataset is close to 1: 0.7846112. On the other hand, the estimated weights for adipose-subcutaneous and adipose-visceral-omentum datasets are close to 0: -0.0001295 and 0.0462641. This supports the observations made in Figure 2, where the brain-cortex dataset (target) exhibits a higher correlation with the brain-frontal-cortex dataset than others.
Let us discuss the summary output in more detail. All tests have in common that the probability statements are with respect to distributional uncertainty, that is, the uncertainty induced by the random distributional perturbations.
-
1.
(Distributional t-test). The summary output provides a t-statistic and a p-value for each estimated weight. Based on the output, the estimated weight for the brain-frontal-cortex dataset is highly significant (with a t-statistic 42.567 and a p-value less than ). We have enough evidence to believe that the true optimal weight for the brain-frontal-cortex dataset is nonzero, and thus we conclude that the brain-frontal-cortex dataset is important for predicting the target dataset. On the other hand, the estimated weights for the adipose-subcutaneous and adipose-visceral-omentum datasets are not statistically significant (with t-statistics -0.004 and 1.844 and p-values 0.9966 and 0.0655). We conclude those datasets are not as important as the brain-frontal-cortex dataset for predicting the target dataset.
-
2.
(Distributional F-test). The summary output provides a F-statistic and a corresponding p-value for a null hypothesis: the optimal weights are uniform ( in our example). This means that different datasets are equally informative in explaining the target dataset. The F-statistic is given as 344.3, which follows the F-distribution with degrees of freedom 3 and 997 under the null hypothesis. The resulting p-value is less than . Therefore, we reject the null hypothesis. From Figure 2 and the estimated weights, we can see that the brain-frontal-cortex and brain-cerebellum datasets are more informative in explaining the target dataset than the adipose-subcutaneous and adipose-visceral-omentum datasets.
-
3.
(R-squared). Usually, the coefficient of determination (R-squared) measures how much of the variation of a target variable is explained by other explanatory variables in a regression model. In our output, R-squared measures how much of the unexplained variance of a target dataset, compared to considering uniform weights, is explained by considering our proposed weights. Specifically, it is calculated as
R-squared is close to 0 if the estimated weights are close to uniform weights.
Finally, we should consider diagnostic plots to evaluate the appropriateness of the fitted distribution shift model. This can be evaluated using a distributional Tukey-Anscombe and a distributional QQ-Plot. In contrast to conventional residual plots and QQ-Plots, each point in these plot corresponds to a mean of a test function instead of a single observation. Figure 3 shows that neither the QQ-Plot nor the TA plot indicate a deviation from the modelling assumptions.


6 Discussion
In many practical settings, there is a distribution shift between the training and the target distribution. Existing distribution shift models fall into two categories. One category, which we term “sparse distribution shift”, assumes that the shift affects specific parts of the data generation process while leaving other parts invariant. Existing methods attempt to re-weight training samples to match the target distribution or learn invariant representations of features. The second category considers worst-case distributional shifts. More specifically, they consider the worst-case behavior of a statistical functional over a fixed neighborhood of the model based on the distributional distance. This often requires knowledge of the strength and shape of the perturbations.
In contrast, we consider random dense distributional shifts, where the shift arises as the superposition of many small random changes. We have found that the random perturbation model can be useful in modeling empirical phenomena observed in Figure 2. Moreover, we see that even when the overlap assumptions seem to be violated (when the reweighing approach fails), or when the distribution shift appears large in Kullback-Leibler divergence, the random perturbation model may still be appropriate and useful. Under the random distributional perturbation model, we establish foundations for transfer learning and generalization.
Our method shares methodological similarities with synthetic controls. While synthetic controls are typically applied to panel data under the assumption of a linear factor model, our procedure can be applied to model distribution shifts of any type of data (discrete, continuous, ordinal) with or without time structure. Furthermore, our method justifies the linearity in synthetic control methods under random distributional shifts, rather than assuming a linear factor model. The random distributional shift assumption can be evaluated based on plots in Figure 3. Additionally, we propose a generalization of our procedure to empirical risk minimization.
In practice, perturbations may involve a combination of sparse and dense shifts. In such cases, hybrid approaches (sparse + dense) may be appropriate. We view hybrid models as an important generalization and leave it for future work.
A companion R package, dlm, is available at https://github.com/yujinj/dlm. Our package performs distributional generalization under the random perturbation model. Users can replicate the results in Section 5 with the data and code provided in the package.
7 Acknowledgments
The authors are grateful for insightful discussions with Naoki Egami, Kevin Guo, Ying Jin, Hongseok Namkoong, and Elizabeth Tipton. This work was supported by Stanford University’s Human-Centered Artificial Intelligence (HAI) Hoffman-Yee Grant, and by the Dieter Schwarz Foundation.
References
- Abadie and Gardeazabal [2003] A. Abadie and J. Gardeazabal. The economic costs of conflict: A case study of the basque country. American Economic Review, 93(1):113–132, 2003.
- Abadie et al. [2007] A. Abadie, A. Diamond, and J. Hainmueller. Synthetic control methods for comparative case studies: Estimating the effect of california’s tobacco control program. Journal of the American Statistical Association, 105:493–505, 2007.
- Argyriou et al. [2007] A. Argyriou, T. Evgeniou, and M. Pontil. Multi-task feature learning. In Advances in Neural Information Processing Systems 19 (NIPS), pages 41–48, 2007.
- Athey et al. [2021] S. Athey, M. Bayati, N. Doudchenko, G. Imbens, and K. Khosravi. Matrix completion methods for causal panel data models. Journal of the American Statistical Association, pages 1–41, 2021.
- Bai [2009] J. Bai. Panel data models with interactive fixed effects. Econometrica, 77(4):1229–1279, 2009.
- Baktashmotlagh et al. [2013] M. Baktashmotlagh, M. T. Harandi, B. C. Lovell, and M. Salzmann. Unsupervised domain adaptation by domain invariant projection. Proceedings of the IEEE International Conference on Computer Vision, pages 769–776, 2013.
- Bansak et al. [2024] K. Bansak, E. Paulson, and D. Rothenhäusler. Learning under random distributional shifts. International Conference on Artificial Intelligence and Statistics, 2024.
- Bodnar and Okhrin [2008] T. Bodnar and Y. Okhrin. Properties of the singular, inverse and generalized inverse partitioned wishart distributions. Journal of Multivariate Analysis, 99(10):2389–2405, 2008.
- Borenstein et al. [2009] M. Borenstein, L. V. Hedges, J. P. Higgins, and H. R. Rothstein. Introduction to Meta-Analysis. John Wiley & Sons, New York, NY, 2009.
- Cheung [2014] M. W. Cheung. Modeling dependent effect sizes with three-level meta-analyses: a structural equation modeling approach. Psychological Methods, 19(2):211–229, 2014.
- Ding et al. [2021] F. Ding, M. Hardt, J. Miller, and L. Schmidt. Retiring adult: New datasets for fair machine learning. In Advances in Neural Information Processing Systems, volume 34, pages 6478–6490, 2021.
- Doudchenko and Imbens [2016] N. Doudchenko and G. W. Imbens. Balancing, regression, difference-in-differences and synthetic control methods: A synthesis. Technical report, National Bureau of Economic Research, 2016.
- Duchi and Namkoong [2021] J. C. Duchi and H. Namkoong. Learning models with uniform performance via distributionally robust optimization. The Annals of Statistics, 49(3):1378–1406, 2021.
- Dudley [2018] R. M. Dudley. Real analysis and probability. CRC Press, 2018.
- Gretton et al. [2009] A. Gretton, J. Smola, M. Huang, K. Schmittfull, K. Borgwardt, and B. Schölkopf. Covariate shift by kernel mean matching. Dataset shift in machine learning, 3:131–160, 2009.
- Hartung et al. [2008] J. Hartung, G. Knapp, and B. K. Sinha. Statistical Meta-Analysis With Applications. John Wiley & Sons, New York, NY, 2008.
- Hedges et al. [2010] L. V. Hedges, E. Tipton, and M. C. Johnson. Robust variance estimation in meta-regression with dependent effect size estimates. Research Synthesis Methods, 1(1):39–65, 2010.
- Higgins et al. [2009] J. Higgins, S. G. Thompson, and D. J. Spiegelhalter. A re-evaluation of random-effects meta-analysis. Journal of the Royal Statistical Society: Series A (Statistics in Society), 172(1):137–159, 2009.
- Huber [1981] P. Huber. Robust Statistics. Wiley, New York, 1981.
- Jeong and Rothenhäusler [2023] Y. Jeong and D. Rothenhäusler. Calibrated inference: statistical inference that accounts for both sampling uncertainty and distributional uncertainty. arXiv preprint arXiv:2202.11886, 2023.
- Li et al. [2016] S. Li, S. Song, and G. Huang. Prediction reweighting for domain adaptation. IEEE Transactions on Neural Networks and Learning Systems, 28(7):1682–1695, 2016.
- Long et al. [2014] M. Long, J. Wang, G. Ding, J. Sun, and P. S. Yu. Transfer joint matching for unsupervised domain adaptation. Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, pages 1410–1417, 2014.
- Lunn et al. [2013] D. Lunn, J. Barrett, M. Sweeting, and S. Thompson. Fully bayesian hierarchical modelling in two stages, with application to meta-analysis. Journal of the Royal Statistical Society. Series C (Applied Statistics), 62(4):551–572, 2013.
- Muirhead [1982] R. J. Muirhead. Aspects of Multivariate Statistical Theory. Wiley Series in Probability and Statistics. John Wiley & Sons, Inc., 1982.
- Pan and Yang [2010] S. J. Pan and Q. Yang. A survey on transfer learning. IEEE Transactions on Knowledge and Data Engineering, 22(10):1345–1359, 2010.
- Quinonero-Candela et al. [2009] J. Quinonero-Candela, M. Sugiyama, A. Schwaighofer, and N. D. Lawrence. Dataset shift in machine learning. Mit Press, 2009.
- Rothenhäusler and Bühlmann [2023] D. Rothenhäusler and P. Bühlmann. Distributionally robust and generalizable inference. Statistical Science, 38(4):527–542, 2023.
- Schölkopf et al. [2021] B. Schölkopf, F. Locatello, S. Bauer, N. R. Ke, N. Kalchbrenner, A. Goyal, and Y. Bengio. Toward causal representation learning. Proceedings of the IEEE, 109(5):612–634, 2021.
- Shen et al. [2023] J. H. Shen, I. D. Raji, and I. Y. Chen. Mo’data mo’problems: How data composition compromises scaling properties. 2023.
- Shimodaira [2000] H. Shimodaira. Improving predictive inference under covariate shift by weighting the log-likelihood function. Journal of Statistical Planning and Inference, 90(2):227–244, 2000.
- Sugiyama et al. [2008] M. Sugiyama, S. Nakajima, H. Kashima, P. Buenau, and M. Kawanabe. Direct importance estimation with model selection and its application to covariate shift adaptation. In Advances in Neural Information Processing Systems 21 (NIPS), pages 1433–1440, 2008.
- Szegedy et al. [2014] C. Szegedy, W. Zaremba, I. Sutskever, J. Bruna, D. Erhan, I. Goodfellow, and R. Fergus. Intriguing properties of neural networks. In International Conference on Learning Representations (ICLR), 2014.
- Van der Vaart [2000] A. Van der Vaart. Asymptotic Statistics, volume 3. Cambridge university press, 2000.
- Wood [2008] A. Wood. Methodology for dealing with duplicate study effects in a meta-analysis. Organizational Research Methods, 11:79–95, 01 2008.
- Xiong et al. [2023] X. Xiong, Z. Guo, and T. Cai. Distributionally robust transfer learning. arXiv preprint arXiv:2309.06534, 2023.
- Xu [2017] Y. Xu. Generalized synthetic control method: Causal inference with interactive fixed effects models. Political Analysis, 25(1):57–76, 2017.
- Zhan et al. [2024] K. Zhan, X. Xiong, Z. Guo, T. Cai, and M. Liu. Transfer learning targeting mixed population: A distributional robust perspective. arXiv preprint arXiv:2407.20073, 2024.
Appendix
8 Proof of Theorem 1
8.1 Extended Theorem 1
In the following, we present the extended version of Theorem 1. Note that we get Theorem 1 in the main text by defining .
Extended Theorem 1.
Under the assumptions of Theorem 1, for any Borel measurable square-integrable function , we have
| (5) |
where is
Here, denotes a kronecker product. Note that can be written as
8.2 Auxiliary Lemma for Theorem 1
Let us first state an auxiliary lemma that will turn out helpful for proving Theorem 1.
Lemma 2.
Proof.
Let . Without loss of generality, assume that for . Note that
Let
First, note that
| (6) |
for all . As the second step, we want to show that
| (7) |
where , , and is an element-wise multiplication. For any , define as
Then, we have
for as goes to infinity. This is because any bounded function can be approximated by a sequence of step functions of the form . Next we will show that for any ,
| (8) |
Let . Then this is implied by the dominated convergence theorem as
| (9) |
Combining equations (6), (7), and (8), we can apply multivariate Lindeberg’s CLT. Together with Slutsky’s theorem, we have
where . This completes the proof. ∎
8.3 Proof of Theorem 1
Proof.
For any and for any given , there exits a bounded function such that and for . Then,
| (a) | |||
| (b) | |||
| (c) |
Note that for any and for ,
as the distributional uncertainty is of higher order than the sampling uncertainty. Therefore, (a) . Next let us investigate (b). Recall that with ,
The variance of the numerator is bounded as
where the first inequality holds by Jensen’s inequality with . The denominator converges in probability to . Therefore, we can write
where is . Combining results, for , we have that and
From Lemma 2, we know that
Let . Note that for any ,
Therefore,
Combining results, we have
Note that all the results hold for arbitrary . This completes the proof. ∎
8.4 Random target distribution
From Extended Theorem 1 with datasets and , and considering that the sampling uncertainty is of low order than distributional uncertainty, for any Borel measurable square-integrable function , we have
| (10) |
where
Therefore, with as a new target distribution, we still have Extended Theorem 1 but with a different distributional covariance matrix .
8.5 Proof of Remark 3
Note that is an empirical variance of on the pooled donor data and can be written as
where . As has a finite fourth moment, by Theorem 1, we have that
9 Special cases of the random perturbation model.
We present special cases of the random perturbation model to help develop some intuition about potential applications.
Example 1 (Random shift across time).
Consider the case where , where the have mean zero and are uncorrelated for . This can be used to model random distributional shifts across time. For example, at some time point, we might see (randomly) higher or lower percentage of old patients at a hospital. Similarly, one could also have an auto-regressive model . Please note that these auto-regressive models are defined on the weights of the distribution and not the data itself. This allows us to model random distributional shift for different data modalities such as discrete, ordinal, or continuous sample spaces, with a single framework.
Example 2 (Independent shifts and meta analysis).
If the distributional perturbations are i.i.d. across , then is a diagonal matrix. Thus, for any , are asymptotically Gaussian and uncorrelated across . This implies a meta-analytic model
| (11) |
where and . Thus, in this special case, the random perturbation model justifies a random effect meta-analysis.
Example 3 (Random shift between locations).
In general, the meta-analytic model might not hold since the distributional perturbations might not be independent or identically distributed across . As an example, data from California might be similar to data from Washington, but very different from data from Pennsylvania. In the synthetic control literature, it is popular to model data distributions from different locations as (approximate) mixtures of each other. For example, data from California might be well approximated by a mixture of Washington and Nevada. In our framework, this can be expressed as
| (12) |
where is mean-zero noise.
10 Proof of Lemma 1
Proof.
The first part of proof follows Van der Vaart [2000], Theorem 5.41 with
By Taylor’s theorem there exists a (random vector) on the line segment between and such that
By Extended Theorem 1 with , we have
| (13) |
By assumption, there exists a ball around such that is dominated by a fixed function for every . The probability of the event tends to 1. On this event,
Using Extended Theorem 1 with , we get
| (14) |
Combining (13) and (14) gives us
The probability that the matrix is invertible tends to 1. Multiplying the preceding equation by and applying left and right gives us that
where . By Extended Theorem 1, we have
| (15) |
Now let . By Taylor’s theorem, there exist , on the line segment between and such that
as and with probability approaching 1. Then the rescaled excess risk can be written as
| (16) |
Using (15), asymptotically (16) follows a distribution with asymptotic mean
This completes the proof.
In the following, we add regularity conditions that lead to the consistency of M-estimators, .
Lemma 3 (Consistency of M-estimators).
Consider the M-estimator
and the target , where is a compact subset of . Assume that is continuous and that is square-integrable under for every and and that is square-integrable. We assume that has a unique minimum. Then, .
Proof.
The proof follows Van der Vaart [2000], Theorem 5.14 with .
Fix some and let be a decreasing sequence of open balls around of diameter converging to zero. Write for . The sequence is decreasing and greater than for every . As is continuous, by monotone convergence theorem, we have .
For , we have . Combine this with the preceding paragraph to see that for every there exits an open ball around with . For any given , let the set . The set is compact and is covered by the balls . Let be a finite sub-cover. Then,
| (17) |
where for the equality we apply Theorem 1 with for all .
∎
11 Proof of Theorem 2
Define the feature matrix before reparametrization as
where the -th row is defined as .
By Theorem 1 and using that the sampling uncertainty is of low order than distributional uncertainty, we have
where are i.i.d Gaussian random variables following . Let be a matrix in which the -th row is .
Note that
The closed form of is known as
We write . Moreover, the closed form of is
Let be a non-random matrix with . Let where
Note that the . Define where
Similarly, let where and .
Results from Multivariate Statistical Theory.
Note that which is the Wishart distribution with a degree of freedom and a scale matrix . By Theorem 3.2.11 and 3.6 in Muirhead [1982], we have
which is the inverse-Wishart distribution with a degree of freedom and a scale matrix . By Theorem 3 (b) and (d) of Bodnar and Okhrin [2008], we have that
Therefore, we get
The right hand side does not depend on anymore. Therefore, we have
| (18) |
By Theorem 3.2.12 in Muirhead [1982], we have
By Theorem 3 (e) of Bodnar and Okhrin [2008], is independent of and . Hence, we get
where is -dimensional (centered) -distribution with degrees of freedom. Now using from Theorem 1, we get
| (19) | |||
| (20) |
where
Connection with Reparametrized Linear Regression.
In this part, we will show that
| (21) |
Using the closed form of , we have that
| (22) |
Then combining (20), (21), and (22), we have
Note that this is a more general version of Theorem 2. By letting be an identity matrix, we have Theorem 2. For the simplicity of notation, let . Note that
where and . Then, by applying Sherman-Morrison lemma, we have
By using the inverse of block matrix as
we also get
Then, we can easily check that . This completes the proof.
12 Confidence Intervals for Target Parameters
First, we will discuss how to form asymptotically valid confidence intervals for . Assume that test functions are uncorrelated and have unit variances under .
Let’s say in (4) is consistent as follows,
Then, we have for ,
since and . By Theorem 1,
Therefore,
| (23) |
Then, we can construct confidence interval for as
How can we obtain a consistent estimator for ? By Theorem 1,
where for are independent standard Gaussian variables. Then,
Therefore, we may estimate as
| (24) |
where is a chi-squared random variable with degrees of freedom .
Finally, as , we have the consistency of and . Suppose we have as in Remark 3. Combining all the results, we have asymptotically valid () confidence interval as and :
Now let’s consider the case in Remark 7 where
Assume the regularity conditions of Lemma 1 and the consistency of and (, ). Then, from the proof of Lemma 1, we have
where . Then, from the results above, we only need to show that . Note that
Similarly as in the proof of Lemma 1, we have that
Moreover, with the consistency of and Theorem 1, we have
Therefore,
Note that
where . The inequality is from the Cauchy-Schwarz inequality. Similarly as in the proof of Lemma 1 with Taylor expansion, we have
and we have from Thereom 1. Then, we get
By using Cauchy-Schwarz inequality in other direction as well, we get
Similarly, we can derive
Then, the variance estimate on the pooled donor data can be written as
Then, by the proof in the Appendix, 8.5, we have . Finally, as , we have the consistency of and under the regularity conditions of Lemma 3, we have the consistency of by following the proof of Lemma 3. This completes the proof.
13 Additional Details in Data Analysis
13.1 Covariance of Test Functions in GTEx Data Analysis
We estimate the sparse inverse covariance matrix of test functions defined in Section 5, using group Lasso with a Python package sklearn.covariance.GraphicalLassoCV. The heatmap of fitted precision matrix is given in Figure 4. As the estimated inverse covariance matrix was close to a diagonal matrix, we did not perform a whitening transformation for the 1000 test functions.

13.2 Additional Results for ACS Income Data Analysis
In this section, we provide additional results for ACS income data analysis in Section 4 for 6 randomly selected target states. The results are presented in Figure 5.