¹¹institutetext: NLPR, Institute of Automation, Chinese Academy of Sciences, China ²²institutetext: School of Artificial Intelligence, University of Chinese Academy of Sciences, China ³³institutetext: CAIR, HK Institute of Science and Innovation, China⁴⁴institutetext: University of Science and Technology Beijing, China

Out-of-distribution Detection with
Boundary Aware Learning

Sen Pei 11 Xin Zhang 11 Bin Fan 44 Gaofeng Meng Corresponding author112233

Abstract

There is an increasing need to determine whether inputs are out-of-distribution (OOD) for safely deploying machine learning models in the open world scenario. Typical neural classifiers are based on the closed world assumption, where the training data and the test data are drawn i.i.d. from the same distribution, and as a result, give over-confident predictions even faced with OOD inputs. For tackling this problem, previous studies either use real outliers for training or generate synthetic OOD data under strong assumptions, which are either costly or intractable to generalize. In this paper, we propose boundary aware learning (BAL), a novel framework that can learn the distribution of OOD features adaptively. The key idea of BAL is to generate OOD features from trivial to hard progressively with a generator, meanwhile, a discriminator is trained for distinguishing these synthetic OOD features and in-distribution (ID) features. Benefiting from the adversarial training scheme, the discriminator can well separate ID and OOD features, allowing more robust OOD detection. The proposed BAL achieves state-of-the-art performance on classification benchmarks, reducing up to 13.9% FPR95 compared with previous methods.

Keywords:

OOD detection, Boundary aware learning, GAN

1 Introduction

Deep convolutional neural networks are one of the basic architectures in deep learning, and they have achieved great success in modern computer vision tasks. However, the over-confidence issue of OOD data has always been with CNN which harms its generalization performance seriously. In previous researches, neural networks have been proved to generalize well when the test data is drawn i.i.d. from the same distribution as the training data, i.e., the ID data. However, when deep learning models are deployed in an open world scenario, the input samples can be OOD data and therefore should be handled cautiously.

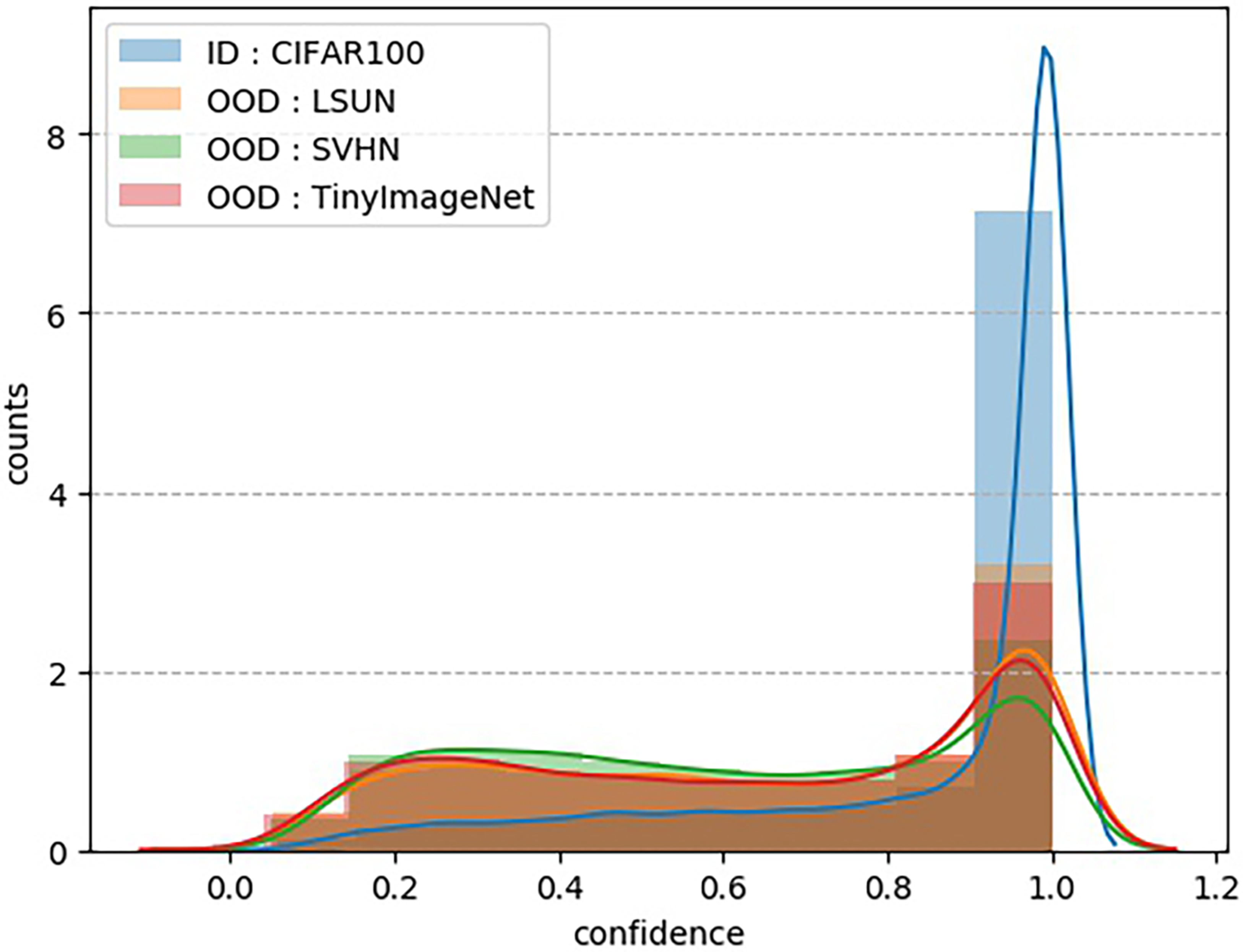
Generally, there are two major challenges for improving the robustness of models: adversarial examples and OOD examples. As pointed out in [10], adding very small perturbations to the input can fool a well-trained classification net, and these modified inputs are the so-called adversarial examples. Another problem is how to detect OOD examples that are drawn far away from the training data. The trained neural networks often produce very high confidence to these OOD samples which has raised concerns for AI Safety [4] in many applications, which is the so-called over-confidence issue [28]. As shown in Figure 1 (a), a trained ResNet18 is used for extracting features from the MNIST dataset, and the blue points indicate feature representations of ID data. It can be found that almost the whole feature space is assigned with high confidence score but the ID data only concentrates in some narrow regions densely.

Previous studies have proposed different approaches for detecting OOD samples to improve the robustness of classifiers. In [12], a max-softmax method is proposed for identifying OOD samples. Further, in ODIN [25], temperature scaling and input pre-processing are introduced for improving the confidence scores of ID samples. In [38], convolutional prototype learning is proposed for image classification which shows effectiveness in OOD detection and class-incremental learning. In [7], it points out that the outputs of softmax can not represent the confidence of neural net actually, and thus, a new branch is separated for confidence estimation independently. All these previous works have brought many different perspectives and inspirations for solving the open world recognition tasks. However, these methods pay limited attention to the learning of OOD features which is a key factor in OOD detection. The neural networks can better detect OOD samples if they are supervised by the trivial and hard OOD information, and that’s why we argue OOD feature learning is important for OOD uncertainty estimation.

In this paper, we attribute the reason of poor OOD detection performance to the fact that the traditional classification networks can not perceive the boundary of ID data due to lack of OOD supervision, as illustrated in Figure 1 (a) and (b). Consequently, this paper focuses on how to generate synthetic OOD information that supervises the learning of classifiers. The key idea of our proposed boundary aware learning (BAL) is to generate synthetic OOD features from trivial to hard gradually via a generator. At the same time, a discriminator is trained to distinguish ID and OOD features. Powered by this adversarial training phase, the discriminator can well separate ID and OOD features. The key contributions of this work can be summarized as follows:

•

A boundary aware learning framework is proposed for improving the rejection ability of neural networks while maintaining the classification performance. This framework can be combined with mainstream neural net architectures.
•

We use a GAN to learn the distribution of OOD features adaptively step by step without introducing any assumptions about the distribution of ID features. Alongside, we propose an efficient method called RSM (Representation Sampling Module) to sample synthetic hard OOD features.
•

We test the proposed BAL on several datasets with different neural net architectures, the results suggest that BAL significantly improves the performance of OOD detection, achieving state-of-the-art performance and allowing more robust classification in the open world scenario.

2 Related Works

OOD detection with softmax-based scores. In [12], a baseline approach to detect OOD inputs named max-softmax is proposed, and the metrics of evaluating OOD detectors are defined properly. Following this, inspired by [10], ODIN [25] and generalized ODIN [15] are proposed for improving the detection ability of max-softmax using temperature scaling, input pre-processing and confidence decomposition. In [3, 24], these studies argue that the feature maps from the penultimate layer of neural networks are not suitable for detecting outliers, and thus, they use the features from a well-chosen layer and adopt some metrics such as Euclidean distance, Mahalanobis distance and OSVM [34]. In [7], a branch is separated out for confidence regression since the outputs of softmax can not well represent the confidence of neural networks. More recently, GradNorm [17] finds that the magnitude of gradients is higher in ID than that of OOD, making it informative for OOD detection. In [26], energy score derived from discriminative models is used for OOD detection which also brings some improvement.

OOD detection with synthetic data. These kinds of methods usually use the ID samples to generate fake OOD samples, and then, train a $(C+1)$ classifier which can improve the rejection ability of neural nets. [35] treats the OOD samples as two types, one indicates these samples that are close to but outside the ID manifold, and the other is these samples which lie on the ID boundary. This work uses Variational AutoEncoder [33] to generate such data for training. In [23], the authors argue that samples lie on the boundary of ID manifold can be treated as OOD samples, and they use GAN [9] to generate these data. The proposed joint training method of confident classifier and adversarial generator inspire our work. It can not be ignored that the methods mentioned above are only suitable for small toy datasets, and the joint training method harms the classification performance of neural nets. Further, in [6], the study points out that AutoEncoder can reconstruct the ID samples with much less error than OOD examples, allowing more effective detection with taking reconstruction error into consideration. Very recently, a newly proposed VOS [8] introduces the OOD detection into object detection tasks, and its main focus is still the OOD feature generation. In these previous works, the features of each category from penultimate layer of CNN are assumed to follow a multivariate gaussian distribution. We argue and verify that this assumption is not reasonable. Our proposed BAL uses a GAN to learn the OOD distribution adaptively without making assumptions, and the experimental results show that BAL outperforms gaussian assumption based methods significantly.

Improving detection robustness with model ensembles. These kinds of methods are similar to bagging in machine learning. In [21], the authors initialize different parameters for neural networks randomly, and the bagging sampling method is used for generating training data. Similarly, in [31], the features from different layers of neural network are used for identifying OOD samples. The defined higher order Gram Matrices in this work yield better OOD detection performance. More recently, [32] converts the labels of training data into different word embeddings using GloVe [29] and FastText [18] as the supervision to gain diversity and redundancy, the semantic structure improves the robustness of neural networks.

OOD detection with auxiliary supervision. In [30], the authors argue that the likelihood score is heavily affected by the population level background statistics, and thus, they propose a likelihood ratio method to deal with background and semantic targets in image data. In [14], the study finds that self-supervision can benefit the robustness of recognition tasks in a variety of ways. In [40], a residual flow method is proposed for learning the distribution of feature space of a pre-trained deep neural network which can help to detect OOD examples. The latest work in [36] treats ood samples as near-OOD and far-OOD samples, it argues that contrastive learning can capture much richer features which improve the performance in detecting near-OOD samples. In [13], the author uses auxiliary datasets served as OOD data for improving the anomaly detection ability of neural networks. Generally, these kinds of methods use some prior information to supervise the learning of OOD detector.

3 Preliminaries

3.0.1 Problem Statement

This work considers the problem of separating ID and OOD samples. Suppose $P_{in}$ and $P_{out}$ are distributions of ID and OOD data, $X=\{x_{1},x_{2},...,x_{N}\}$ are images randomly sampled from these two distributions. This task aims to give lower confidence of image $x_{i}$ sampled from $P_{out}$ while higher to that of $P_{in}$ . Typically, OOD detection can be formulated as a binary classification problem. With a chosen threshold $\gamma$ and confidence score $S(x)$ , input is judged as OOD data if $S(x)<\gamma$ otherwise ID. Figure 2 (a) shows the traditional classifiers can not capture the OOD uncertainty, and as a result, produce over-confident predictions on OOD data. Figure 2 (b) shows an ideal case where ID data gets higher score than OOD. Methods that aim to boost the performance of OOD detection should use no data labeled as OOD explicitly.

3.0.2 Methodology

For a given image $x$ , its corresponding feature representation $f$ can be got from the penultimate layer of a pre-trained classification net, and based on the total probability theorem, we have:

\begin{split}P(w|f)=P(w|f\in\mathcal{M}_{f})\cdot P(f\in\mathcal{M}_{f}|f)\\ +P(w|f\notin\mathcal{M}_{f})\cdot P(f\notin\mathcal{M}_{f}|f)\end{split}

(1)

where $w$ is the category label of ID data, and $\mathcal{M}_{f}$ represents the manifold of ID features. Typical neural networks have no access to OOD data, therefore its softmax output is actually the conditional probability assuming the inputs are ID data, i.e., $P(w|f\in\mathcal{M}_{f})$ . Empirically, since the OOD data has quite different semantic meanings compared with ID data, it is reasonable to approximate $P(w|f\notin\mathcal{M}_{f})$ to 0. Then, we have:

P(w|f)\approx P(w|f\in\mathcal{M}_{f})\cdot P(f\in\mathcal{M}_{f}|f)

(2)

It tells that the approximation of posterior can be formulated as the product of outputs from pre-trained classifiers and the probability $f$ belongs to $\mathcal{M}_{f}$ . The proposed BAL aims to estimate $P(f\in\mathcal{M}_{f}|f)$ with features from the penultimate layer of pre-trained CNN.

4 Boundary Aware Learning

The proposed boundary aware learning framework contains three modules as illustrated in Figure 3. These modules handle the following problems: (I) Representation Extraction Module (REM) : how to generate trivial OOD features to supervise the learning of conditional discriminator; (II) Representation Sampling Module (RSM) : how to generate synthetic hard OOD features to enhance the discrimination ability of conditional discriminator step by step; (III) Representation Discrimination Module (RDM) : how to make the conditional discriminator aware the boundary of ID features.

4.1 Representation Extraction Module (REM)

This module handles the problem of how to generate trivial synthetic OOD features. As in prior works, we use the outputs of penultimate layer in CNN to represent the input images. In the following parts, $\mathcal{H}$ and $h$ are used to indicate the pre-trained classification net with and without the top classification layer, and $\theta$ is the pre-trained weights. Formally, the feature $f$ of an input image $x$ is described as:

f=h(x;\theta)

(3)

During training, image $x$ and its corresponding label $c$ are sampled from dataset $\mathcal{X}$ . We get an ID feature-label pair $\left\langle f,c\right\rangle$ with Eq.(3). For generating trivial synthetic OOD features, we sample data in feature space uniformly. Given a batch features $\{f_{1},f_{2},f_{3},...,f_{k}\}$ , the length of each feature vector $f_{i}$ is $m$ . We first calculate the minimal and maximal bound in $m$ -dimensional space that contains all features within this batch. For $j\in\{1,2,3,...,m\}$ , we have:

	$\displaystyle R_{\min}^{(j)}$	$\displaystyle=\min_{1\leq i\leq k}f_{i}^{(j)}$		(4)
	$\displaystyle R_{\max}^{(j)}$	$\displaystyle=\max_{1\leq i\leq k}f_{i}^{(j)}$		(5)

therefore, the lower and upper bound of feature vectors are obtained as follows:

	$\displaystyle a$	$\displaystyle=(R_{\min}^{(1)},R_{\min}^{(2)},...,R_{\min}^{(m)})^{T}$		(6)
	$\displaystyle b$	$\displaystyle=(R_{\max}^{(1)},R_{\max}^{(2)},...,R_{\max}^{(m)})^{T}$		(7)

We use $\mathbb{U}(a,b)$ to indicate a batch-wise uniform distribution in feature space. Randomly sampled feature $\hat{f}$ from $\mathbb{U}(a,b)$ is treated as negative sample with a randomly generated label $\hat{c}$ . The negative pair is expressed as $\left\langle\hat{f},\hat{c}\right\rangle$ . We give the reasons of uniform sampling : (a) It can not be guaranteed that features from the penultimate layer of CNN follow a multivariate gaussian distribution no matter in low dimensional space or higher feature space. For verifying this idea, we set the penultimate layer of CNN to have two and three neurons for feature visualization, the results shown in Figure 4 indicate the unreasonableness of this assumption. (b) ID features densely distribute in some narrow regions which means the most samples from uniform sampling are OOD data. Conflicts may happen when $\hat{f}$ is close to ID and $\hat{c}$ does match with $\hat{f}$ , the RDM deals with these conflicts.

4.2 Representation Sampling Module (RSM)

This module is used for generating hard OOD features. For noise $z$ sampled from normal distribution $P_{z}$ , its corresponding synthetic ID feature $f$ can be got by $G(z,c)$ where $c$ is a conditional label. Since the generator $G$ is trained for generating ID data, the feature $f$ is much closer to ID instead of OOD. With Fast Gradient Sign Method [10], we push the feature $f$ towards the boundary of ID manifold which gets a much lower score from discriminator.

	$\displaystyle\tilde{f}$	$\displaystyle=f-\epsilon\frac{\partial D(f;c)}{\partial f}\approx f-\epsilon\,\mathrm{sgn}(\frac{\partial D(f;c)}{\partial f})$		(8)
	$\displaystyle\tilde{z}$	$\displaystyle=z-\epsilon\frac{\partial D(f;c)}{\partial z}=z-\epsilon\frac{\partial D(G(z;c);c)}{\partial G(z;c)}\frac{\partial G(z;c)}{\partial z}$		(9)

where $\tilde{f}$ represents the calibrated feature which scatters at the low density area of ID feature distribution $P_{f}$ . $\tilde{z}$ can be used for generating OOD features by $G(\tilde{z};c)$ . In particular, we set $\epsilon$ a random variable which follows a gaussian distribution for improving the diversity of sampling. $\left\langle\tilde{f},\tilde{c}\right\rangle$ is treated as hard OOD feature pair because its quality is growing with the adversarial training process.

4.3 Representation Discrimination Module (RDM)

This module aims to make the discriminator aware the boundary of ID features. The generator with FGSM is used for generating hard OOD representations while the discriminator is used for separating ID and OOD features. The noise vector $z$ is sampled from a normal distribution $P_{z}$ . The features of training images from REM follow a distribution $P_{f}$ . For learning the boundary of ID data via discriminator, we propose shuffle loss and uniform loss. The shuffle loss makes the discriminator aware the category of each ID cluster in feature space, and the uniform loss makes the discriminator aware the boundary of each ID feature cluster.

4.3.1 Shuffle loss.

In each batch of the training data, we get feature-label pairs like $\left\langle f,c\right\rangle$ . In a conditional GAN, these $\left\langle f,c\right\rangle$ pairs are treated as positive samples. With a shuffle function $T(\cdot)$ , the positive pair $\left\langle f,c\right\rangle$ is transformed to a negative pair $\left\langle f,\tilde{c}\right\rangle$ where $\tilde{c}=T(c)\neq c$ is a mismatched label with feature $f$ . The discriminator is expected to identify these mismatch pairs as OOD data for awareness of category label, and the classification loss is the so called shuffle loss as below:

L_{s}=\mathbb{E}_{P_{f}}(\log D(f;T(c))-\log D(f;c))

(10)

4.3.2 Uniform loss.

We get positive pair $\left\langle f,c\right\rangle$ and negative pair $\left\langle\hat{f},\hat{c}\right\rangle$ from REM. It is mentioned before that conflicts may happen when $\hat{f}$ is close to some ID feature clusters and the randomly generated label $\hat{c}$ dose match with them. For tackling this issue, we strengthen the memory of discriminator about positive pair $\left\langle f,c\right\rangle$ while weaken that about negative pair $\left\langle\hat{f},\hat{c}\right\rangle$ . We force the discriminator to maximize $D(f;c)$ for remembering positive pairs, meanwhile, a hyperparameter $\lambda_{c}$ is used to mitigate the negative effects of conflicts. The uniform loss is defined as follows:

L_{u}=\lambda_{c}\cdot\mathbb{E}_{P_{\mathbb{U}}}\log D(\hat{f};\hat{c})-\mathbb{E}_{P_{f}}\log D(f;c)

(11)

Alongside, the hard OOD features from RSM introduce no conflicts, and they are treated as negative OOD pairs for calculating uniform loss when training discriminator. Formally, the loss function $L_{d}$ for conditional discriminator can be formulated as below:

	$\displaystyle L_{t}$	$\displaystyle=-\mathbb{E}_{P_{f}}\log D(f;c)-\mathbb{E}_{P_{z}}\log(1-D(G(z);c))$		(12)
	$\displaystyle L_{d}$	$\displaystyle=L_{t}+L_{s}+L_{u}$		(13)

where $L_{t}$ is the loss of discriminator in a vanilla conditional GAN. A well trained discriminator is a binary classifier for separating ID and OOD features. In the process of training generator, we add a regularization term to accelerate the convergence. The loss function of generator is written as:

L_{g}=\mathbb{E}_{P_{z}}\log(1-D(G(z;c);c))+\lambda(\min_{f_{c}\in\mathcal{M}_{c}}||f_{c}-G(z;c)||_{1})

(14)

where $||\cdot||_{1}$ indicates the L1 norm, $\mathcal{M}_{c}$ is the set of ID features with label $c$ , and $\lambda$ is a balance hyperparameter. The regularization term reduces the difference between synthetic features and the real. We set $\lambda$ to 0.01 in our experiments. In the process of training generator, the label $c$ is generated randomly.

Generally, the BAL framework only trains the conditional GAN while keeps the pre-trained classification net unchanged. The confidence score outputted by a trained discriminator is treated as $P(f\in\mathcal{M}_{f}|f)$ . Based on Eq.(2), the approximation of posteriori is formulated as the product of outputs from pre-trained classification net and discriminator. The whole training and inference pipeline is shown in Algorithm 1.

Input: pre-trained network

\mathcal{H}

(backbone

h

) on ID data with parameter

\theta

, initial generator

G

, initial discriminator

D

, ID dataset

\mathcal{X}

Output: OOD discriminator

D

, synthetic ID generator

G

1 while Training do

2 for iter = 1 to M do

3 # Discriminator training;

4 Sample a batch data

x

from

\mathcal{X}

;

5 Get the corresponding feature vectors :

f=h(x;\theta)

;

6 Calculate the lower and upper bound of

f

with Eqs.(4,5,6,7);

7 Transform the positive pairs

\left\langle f,c\right\rangle

into negative pairs

\left\langle f,T(c)\right\rangle

;

8 Sample trivial OOD and hard OOD feature pairs

\left\langle\hat{f},\hat{c}\right\rangle

via uniform sampling and RSM;

9 Calculate the shuffle loss

L_{s}

, the uniform loss

L_{u}

, and the vanilla loss

L_{t}

with Eqs.(10,11,12);

10 Update the parameters of

D

with gradient descent method.

11 # Generator training;

12 Sample noise

z

from normal distribution;

13 Get the features conditioned by random labels :

G(z;c)

;

14 Calculate the loss function of generator with Eq.(14);

15 Update the parameters of

G

with gradient descent method.

18while Inference do

19 Get feature vector :

\hat{f}=h(\hat{x};\theta)

;

20 Get predict label and corresponding confidence:

p_{1},\hat{c}=\mathcal{H}(\hat{x};\theta)

;

21 Get ID confidence score :

p_{2}=D(\hat{f},\hat{c})

;

22 Perform OOD detection with

p_{1}\cdot p_{2}

under a chosen threshold.

Algorithm 1 OOD Detection with Boundary Aware Learning

5 Experiments

In this section, we validate the proposed BAL framework on several image classification datasets and neural net architectures. Experimental setup is described from Section 5.1 to Section 5.3, ablation study is described in Section 5.4. We report the main results and metrics in Section 5.5. Visualization of synthetic OOD data is given in Section 5.6.

5.1 Dataset

MNIST [22] : A database of handwritten digits in total 10 categories, has a training set of 60k examples, and a test set of 10k examples.

Fashion-MNIST [37] : A dataset contains grayscale images of fashion products from 10 categories, has a training set of 60k images, and a test set of 10k images.

Omniglot [20] : A dataset that contains 1623 different handwritten characters from 50 different alphabets. In this work, we treat Omniglot as OOD data.

CIFAR-10 and CIFAR-100 [19] : The former one contains 60k colour images in 10 classes, with 6k images per class. The latter one also contains 60k images but in 100 classes, with 600 images per class.

TinyImageNet [5] : A dataset contains 120k colour images in 200 classes, with 600 images per class.

SVHN [27] and LSUN [39] : The former one contains colour images of street view house number. The latter one is a large-scale scene understanding dataset.

5.2 Evaluation metrics

We report the following metrics to measure the performance of OOD detection. The quantity of ID and OOD examples are strictly kept same in evaluation. FPR at 95% TPR (FPR95) is the probability of an OOD example being misclassified as ID examples when the True Positive Rate is 95%. True positive Rate and False Positive Rate are the same as defined in ROC curve.

Detection Error measures the misclassification probability when True Positive Rate is 95%. It is defined as $0.5(1-\mathrm{TPR})+0.5\mathrm{FPR}$ .

AUROC represents the area under ROC curve. Greater AUROC indicates that the neural network is more confident to assign higher score to ID data than OOD data. An ideal classifier has an AUROC score of 100%.

AUPR represents the area under Precision-Recall curve. AUPR_in indicates the ability of detecting ID data while AUPR_out indicates that of OOD data.

5.3 Experimental setup

Softmax baseline. ResNet [11] and DenseNet [16] are used as backbones, and they are trained with an Adam optimizer using cross-entropy loss in total of 300 epochs. Images from MNIST, Fashion-MNIST and Omniglot are resized to 28 $\times$ 28 with only one channel. Other datasets are resized to 32 $\times$ 32 with RGB channels. For MNIST, Fashion-MNIST and Omniglot, ResNet18 is used as the feature extractor. For any other datasets, ResNet34 and DenseNet-BC with 100 layers are used for feature extraction.

GCPL. We use distance-based cross-entropy loss and prototype loss as mentioned in [38] for generalized convolutional prototype learning. The hyperparameter $\lambda$ that controls the weight of prototype loss is set to 0.01.

ODIN and Generalized ODIN. For ODIN, parameters ( $T$ , $\epsilon$ ) are (10, 2e-3), (100, 5e-4) and (10, 5e-4) for CIFAR-10, CIFAR-100 and SVHN respectively.

AEC. This method uses reconstruction error to detect outliers. The architectures and experimental details can be found in [6], we use the same pipeline to reproduce it.

5.4 Ablation study

5.4.1 Ablation on proposed loss functions.

We compare different loss functions proposed in BAL. Specifically, we use DenseNet-BC as the feature extractor. CIFAR-10 is set as ID data while TinyImageNet is set as OOD data. We consider four combinations of proposed loss functions: $L_{t}$ , $L_{t}+L_{s}$ , $L_{t}+L_{u}$ and $L_{t}+L_{s}+L_{u}$ . The details of pre-mentioned loss functions can be found in Eqs.(10-12). For uniform loss $L_{u}$ , we set the hyperparameter $\lambda_{c}$ to 0.7. The results are summarized in Table 1, where BAL with shuffle loss and uniform loss outperforms the alternative combinations. Compared to max-softmax, BAL reduces FPR95 up to 36.1%.

Table 1: Ablation on different combinations of loss functions. All networks are trained with the training set of CIFAR-10, and no OOD data is used.

\lambda_{c}

in uniform loss

L_{u}

is set to 0.7. It can be seen that the proposed shuffle loss and uniform loss enhance the ability for detecting outliers.

	$\uparrow$ AUPR_in	$\uparrow$ AUPR_out	$\uparrow$ AUROC	$\downarrow$ FPR 95
Softmax baseline	95.3	92.2	94.1	41.1
BAL ( $L_{t}$ )	97.0	96.0	96.6	17.9
BAL ( $L_{t}+L_{s}$ )	97.1	96.2	96.6	9.3
BAL ( $L_{t}+L_{u}$ )	97.2	96.3	96.7	8.1
BAL ( $L_{t}+L_{s}+L_{u}$ )	98.2	98.0	97.0	5.0

5.4.2 Ablation on $\lambda_{c}$ in uniform loss.

We consider different value settings to test the sensitivity of $\lambda_{c}$ in Eq.(11). CIFAR-10 and TinyImageNet are set as ID and OOD respectively. DenseNet-BC is used as the backbone. The ablation results shown in Table 2 demonstrate that with the increasing of $\lambda_{c}$ , AUPR_out of neural networks increases synchronously which means the classifier can aware more OOD data. In particular, using $\lambda_{c}$ as 0.7 yields both better ID and OOD detection performance.

Table 2: Ablation on parameter

\lambda_{c}

. All networks are trained with the training set of CIFAR-10, and no OOD data is used. In the following experiments, if not specified,

\lambda_{c}

is set to 0.7 throughout.

$\lambda_{c}$	0.1	0.3	0.5	0.7	0.9
AUROC	94.8	95.2	96.7	97.0	96.2
AUPR_in	95.3	95.3	97.1	98.2	96.3
AUPR_out	92.1	93.4	96.9	98.0	97.1

5.4.3 Ablation on OOD synthesis sampling methods.

We consider different trivial OOD feature sampling methods. As described in Section 4.1, the distribution of features in convolutional layer are usually assumed to follow a multivariate gaussian distribution. Therefore, the low density area of each category is treated as OOD region. We argue this assumption is not reasonable enough because : (I) From Figure 1 (a) and Figure 4, we can see that in low dimensional feature space, the conditional distribution of each category has a great deviation with multivariate gaussian distribution; (II) In high dimensional space, the distribution of ID features is extremely sparse, therefore it is hard to estimate the probability density of assumed gaussian distribution accurately; (III) It is costly to calculate the mean vector $\mu$ and covariance matrix $\Sigma$ of multivariate gaussian distribution in feature space with high dimensionality; (IV) Inefficient sampling. It is in low efficiency since the probability density need to be calculated for each synthetic sample.

Without introducing any strong assumptions about the ID features, we verify that the naive uniform sampling together with a GAN framework can model the OOD feature distribution effectively. We still use CIFAR-10 and TinyImageNet as ID and OOD data. We compare uniform sampling and gaussian sampling in feature space. The dimensionality of features is controlled by setting different number of neurons in the penultimate fully connected layer. The ablation results are shown in Table 3. It is clear that BAL with uniform sampling outperforms gaussian sampling in both low and high dimensional feature space.

Table 3: Ablation on BAL with different sampling methods. The values in the table are AUROC. Both uniform sampling and gaussian sampling are performed within BAL framework.

feature dim	2	64	256	512	1024
BAL (Gaussian)	94.3	96.4	96.9	98.1	98.5
BAL (Uniform)	96.5	97.0	97.3	98.1	98.8

5.5 Detection results

We detail the main experimental results on several datasets with ResNet18, ResNet34 and DenseNet-BC. For CIFAR-10, CIFAR-100 and SVHN, we use the pre-trained ResNet-34 and DenseNet-BC, and for MNIST, Fashion-MNIST and Omniglot, we train the ResNet18 from scratch.

5.5.1 Results on MNIST, Fashion-MNIST and Omniglot.

We observe the effects of BAL in two groups. In the first group, MNIST is ID data, and the mixture of Fashion-MNIST and Omniglot is OOD data. In the second group, Fashion-MNIST is ID data while MNIST and Omniglot are OOD data. For simplicity, Cls Acc and Det Err are used to represent Classification Accuracy and Detection Error. For ODIN, temperature ( $T$ ) and magnitude ( $\epsilon$ ) are 10 and 5e-4 respectively. The results summarized in Table 4 tell that BAL is effective on image classification benchmark, particularly, BAL reduces FPR95 up to 24.1% compared with ODIN in the second group.

Table 4: Detecting OOD samples on MNIST, Fashion-MNIST and Omniglot with ResNet18. We use the mixture of two datasets as OOD samples.

ID	MNIST				F-MNIST
OOD	F-MNIST & Omniglot				MNIST & Omniglot
Methods	Softmax baseline[12] / ODIN[25] / GCPL[38] / BAL(ours)
$\uparrow$ Cls Acc	99.43	99.43	99.23	99.43	91.51	91.51	90.93	91.51
$\downarrow$ Det Err	4.14	5.01	4.77	3.06	32.42	19.14	30.73	7.10
$\downarrow$ FPR 95	3.29	5.03	4.54	1.11	59.84	33.27	56.45	9.20
$\uparrow$ AUROC	97.66	97.94	97.96	99.32	89.44	93.45	81.79	97.82
$\uparrow$ AUPR_in	97.22	97.42	98.14	99.46	90.80	94.28	72.40	98.31
$\uparrow$ AUPR_out	97.24	97.64	97.35	99.09	86.20	91.36	82.38	96.95

Table 5: Main OOD detection results. We use C-10, C-100, TIN, D-BC and R-34 to represent CIFAR-10, CIFAR-100, TinyImageNet, DenseNet-BC and ResNet-34.

ID	OOD	$\downarrow$ FPR at 95% TPR					$\uparrow$ AUPR in					$\uparrow$ AUPR out
		Softmax baseline[12] / AEC[6] / ODIN[25] / Generalized ODIN[15] / BAL(ours)
C-10 D-BC	SVHN	59.8	57.2	63.6	44.2	32.6	91.9	92.3	89.1	94.6	99.7	87.0	92.5	83.9	88.7	99.7
	LSUN	33.4	27.6	5.6	5.2	4.7	96.4	97.3	98.9	99.0	99.5	94.0	96.3	98.7	98.9	98.9
	TIN	41.1	35.1	10.5	9.3	5.0	95.3	96.2	98.1	97.9	98.2	92.2	94.0	97.8	97.4	98.0
C-10 R-34	SVHN	67.5	57.2	64.4	12.7	11.3	92.2	93.4	85.8	94.5	95.5	84.9	84.5	81.8	93.4	97.4
	LSUN	54.6	34.6	26.2	21.3	15.8	92.3	91.8	93.7	94.0	93.9	88.5	92.1	93.8	93.9	94.1
	TIN	55.3	28.7	28.0	27.4	21.6	92.4	93.1	94.0	94.3	93.9	88.3	90.1	92.9	92.7	93.8
C-100 D-BC	SVHN	73.3	63.2	60.9	31.9	21.5	85.9	89.3	90.2	90.7	91.5	78.5	86.7	85.2	89.5	92.8
	LSUN	83.3	66.0	58.4	23.9	11.3	72.4	87.4	85.0	88.1	89.3	65.4	84.9	82.0	87.6	88.7
	TIN	82.4	59.7	56.9	22.7	12.0	73.0	83.7	84.7	86.5	91.5	67.4	82.9	83.0	84.3	90.6
C-100 R-34	SVHN	79.7	76.5	76.5	31.2	17.3	81.5	82.5	73.8	85.3	87.1	74.5	79.6	74.2	85.1	89.3
	LSUN	81.2	52.1	54.6	27.1	18.7	76.0	80.0	82.4	89.0	91.5	70.1	78.4	84.1	89.0	88.7
	TIN	79.6	55.3	50.6	29.7	22.5	79.2	87.1	86.8	89.3	91.6	72.3	85.6	87.0	88.0	89.8
SVHN D-BC	LSUN	22.9	22.7	22.1	18.7	16.4	96.7	95.4	95.3	97.2	98.5	88.0	88.7	89.3	86.3	89.3
	C-10	30.7	20.1	24.7	20.3	12.1	95.4	93.2	92.5	96.0	97.3	88.5	84.7	81.7	84.2	89.9
	TIN	21.2	18.6	19.9	15.2	11.7	97.0	96.1	95.5	97.3	98.5	88.9	90.7	90.1	91.6	90.6
SVHN R-34	LSUN	25.7	21.0	22.2	18.1	13.5	93.8	91.3	91.3	96.4	97.8	84.6	86.5	85.9	89.4	92.1
	C-10	21.7	19.5	20.0	16.7	14.8	94.8	92.0	91.9	97.0	97.6	86.4	87.3	87.1	88.2	89.0
	TIN	21.0	19.3	18.0	15.4	14.3	95.4	93.4	93.5	96.8	98.2	86.9	88.5	88.6	89.4	89.4

5.5.2 Results on CIFAR-10, CIFAR-100 and SVHN.

We consider sufficient experimental settings in this part for testing the generalization ability of BAL. The pre-trained ResNet-34 and DenseNet-BC on CIFAR-10, CIFAR-100 and SVHN come from [1]. The main results on image classification tasks are summarized in Table 5, where BAL demonstrates superior performance compared with the mainstream methods under different experimental settings. Optimal temperature ( $T$ ) and magnitude ( $\epsilon$ ) are searched for ODIN in each group. Specifically, BAL reports a decline of FPR95 up to 13.9% compared with Generalized ODIN.

5.6 Visualization of trivial and hard OOD features

We show the visualization results of trivial OOD features from uniform sampling and the hard OOD features from generator via FGSM. We set the training data as two gaussian distribution with dimensionality $m=2$ . We use a MLP with three layers as the classifier. The discriminator and generator only use fully connected layers. In the adversarial training process, we sample data in raw data space uniformly since the dimensionality of raw data is fairly low. The other training details are the same as pipeline shown in Algorithm 1.

We also report the classification results on dogs vs. cats [2]. The top-1 classification results of BAL and Softmax baseline are given in Figure 6.

6 Conclusions

In this paper, we propose BAL to learn the distribution of OOD features adaptively. No strong assumptions about the ID features are introduced. We use a simple uniform sampling method combined with a GAN framework can generate OOD features in very high quality step by step. BAL has been proved to generalized well across different datasets and architectures. Experimental results on common image classification benchmarks promise the state-of-the-art performance of BAL. The ablation study also shows BAL is stable with different parameter settings. We also report the visualization results of synthetic OOD features and open world scenario detection.

Acknowledgement

This research was supported in part by the National Key Research and Development Program of China under Grant No. 2020AAA0109702, and the National Natural Science Foundation of China under Grants 61976208, and the InnoHK project.

References

[1] https://github.com/facebookresearch/odin
[2] https://www.kaggle.com/c/dogs-vs-cats
[3] Abdelzad, V., Czarnecki, K., Salay, R., Denouden, T., Vernekar, S., Phan, B.: Detecting out-of-distribution inputs in deep neural networks using an early-layer output. CoRR abs/1910.10307 (2019), http://arxiv.org/abs/1910.10307
[4] Amodei, D., Olah, C., Steinhardt, J., Christiano, P.F., Schulman, J., Mané, D.: Concrete problems in AI safety. CoRR abs/1606.06565 (2016), http://arxiv.org/abs/1606.06565
[5] Deng, J., Dong, W., Socher, R., Li, L.J., Li, K., Fei-Fei, L.: Imagenet: A large-scale hierarchical image database. In: 2009 IEEE conference on computer vision and pattern recognition. pp. 248–255. Ieee (2009)
[6] Denouden, T., Salay, R., Czarnecki, K., Abdelzad, V., Phan, B., Vernekar, S.: Improving reconstruction autoencoder out-of-distribution detection with mahalanobis distance. CoRR abs/1812.02765 (2018), http://arxiv.org/abs/1812.02765
[7] DeVries, T., Taylor, G.W.: Learning confidence for out-of-distribution detection in neural networks. stat 1050, 13 (2018)
[8] Du, X., Wang, Z., Cai, M., Li, Y.: Vos: Learning what you don’t know by virtual outlier synthesis. Proceedings of the International Conference on Learning Representations (2022)
[9] Goodfellow, I., Pouget-Abadie, J., Mirza, M., Xu, B., Warde-Farley, D., Ozair, S., Courville, A., Bengio, Y.: Generative adversarial nets. Advances in neural information processing systems 27 (2014)
[10] Goodfellow, I.J., Shlens, J., Szegedy, C.: Explaining and harnessing adversarial examples. In: Bengio, Y., LeCun, Y. (eds.) 3rd International Conference on Learning Representations, ICLR 2015, San Diego, CA, USA, May 7-9, 2015, Conference Track Proceedings (2015), http://arxiv.org/abs/1412.6572
[11] He, K., Zhang, X., Ren, S., Sun, J.: Deep residual learning for image recognition. In: Proceedings of the IEEE conference on computer vision and pattern recognition. pp. 770–778 (2016)
[12] Hendrycks, D., Gimpel, K.: A baseline for detecting misclassified and out-of-distribution examples in neural networks. Proceedings of International Conference on Learning Representations (2017)
[13] Hendrycks, D., Mazeika, M., Dietterich, T.: Deep anomaly detection with outlier exposure. Proceedings of the International Conference on Learning Representations (2019)
[14] Hendrycks, D., Mazeika, M., Kadavath, S., Song, D.: Using self-supervised learning can improve model robustness and uncertainty. Advances in Neural Information Processing Systems (NeurIPS) (2019)
[15] Hsu, Y.C., Shen, Y., Jin, H., Kira, Z.: Generalized odin: Detecting out-of-distribution image without learning from out-of-distribution data. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 10951–10960 (2020)
[16] Huang, G., Liu, Z., Van Der Maaten, L., Weinberger, K.Q.: Densely connected convolutional networks. In: Proceedings of the IEEE conference on computer vision and pattern recognition. pp. 4700–4708 (2017)
[17] Huang, R., Geng, A., Li, Y.: On the importance of gradients for detecting distributional shifts in the wild. Advances in Neural Information Processing Systems 34 (2021)
[18] Joulin, A., Grave, E., Bojanowski, P., Douze, M., Jégou, H., Mikolov, T.: Fasttext.zip: Compressing text classification models. arXiv preprint arXiv:1612.03651 (2016)
[19] Krizhevsky, A., Hinton, G., et al.: Learning multiple layers of features from tiny images (2009)
[20] Lake, B.M., Salakhutdinov, R., Tenenbaum, J.B.: Human-level concept learning through probabilistic program induction. Science 350(6266), 1332–1338 (2015)
[21] Lakshminarayanan, B., Pritzel, A., Blundell, C.: Simple and scalable predictive uncertainty estimation using deep ensembles. Advances in neural information processing systems 30 (2017)
[22] LeCun, Y.: The mnist database of handwritten digits. http://yann. lecun. com/exdb/mnist/ (1998)
[23] Lee, K., Lee, H., Lee, K., Shin, J.: Training confidence-calibrated classifiers for detecting out-of-distribution samples. In: 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, April 30 - May 3, 2018, Conference Track Proceedings. OpenReview.net (2018), https://openreview.net/forum?id=ryiAv2xAZ
[24] Lee, K., Lee, K., Lee, H., Shin, J.: A simple unified framework for detecting out-of-distribution samples and adversarial attacks. Advances in neural information processing systems 31 (2018)
[25] Liang, S., Li, Y., Srikant, R.: Enhancing the reliability of out-of-distribution image detection in neural networks. In: 6th International Conference on Learning Representations, ICLR 2018, Vancouver, BC, Canada, April 30 - May 3, 2018, Conference Track Proceedings. OpenReview.net (2018), https://openreview.net/forum?id=H1VGkIxRZ
[26] Liu, W., Wang, X., Owens, J., Li, Y.: Energy-based out-of-distribution detection. Advances in Neural Information Processing Systems 33, 21464–21475 (2020)
[27] Netzer, Y., Wang, T., Coates, A., Bissacco, A., Wu, B., Ng, A.: Reading digits in natural images with unsupervised feature learning. NIPS (01 2011)
[28] Nguyen, A., Yosinski, J., Clune, J.: Deep neural networks are easily fooled: High confidence predictions for unrecognizable images. In: Proceedings of the IEEE conference on computer vision and pattern recognition. pp. 427–436 (2015)
[29] Pennington, J., Socher, R., Manning, C.: Glove: Global vectors for word representation. vol. 14, pp. 1532–1543 (01 2014). https://doi.org/10.3115/v1/D14-1162
[30] Ren, J., Liu, P.J., Fertig, E., Snoek, J., Poplin, R., Depristo, M., Dillon, J., Lakshminarayanan, B.: Likelihood ratios for out-of-distribution detection. Advances in Neural Information Processing Systems 32 (2019)
[31] Sastry, C.S., Oore, S.: Detecting out-of-distribution examples with in-distribution examples and gram matrices. CoRR abs/1912.12510 (2019), http://arxiv.org/abs/1912.12510
[32] Shalev, G., Adi, Y., Keshet, J.: Out-of-distribution detection using multiple semantic label representations. Advances in Neural Information Processing Systems 31 (2018)
[33] Sohn, K., Lee, H., Yan, X.: Learning structured output representation using deep conditional generative models. In: Cortes, C., Lawrence, N., Lee, D., Sugiyama, M., Garnett, R. (eds.) Advances in Neural Information Processing Systems. vol. 28. Curran Associates, Inc. (2015), https://proceedings.neurips.cc/paper/2015/file/8d55a249e6baa5c06772297520da2051-Paper.pdf
[34] Tax, D.M.J., Duin, R.P.W.: Support vector domain description. Support vector domain description (1999)
[35] Vernekar, S., Gaurav, A., Abdelzad, V., Denouden, T., Salay, R., Czarnecki, K.: Out-of-distribution detection in classifiers via generation. CoRR abs/1910.04241 (2019), http://arxiv.org/abs/1910.04241
[36] Winkens, J., Bunel, R.: Contrastive training for improved out-of-distribution detection. CoRR abs/2007.05566 (2020), https://arxiv.org/abs/2007.05566
[37] Xiao, H., Rasul, K., Vollgraf, R.: Fashion-mnist: a novel image dataset for benchmarking machine learning algorithms. CoRR abs/1708.07747 (2017), http://arxiv.org/abs/1708.07747
[38] Yang, H., Zhang, X., Yin, F., Liu, C.: Robust classification with convolutional prototype learning. In: 2018 IEEE Conference on Computer Vision and Pattern Recognition, CVPR 2018, Salt Lake City, UT, USA, June 18-22, 2018. pp. 3474–3482. Computer Vision Foundation / IEEE Computer Society (2018). https://doi.org/10.1109/CVPR.2018.00366, http://openaccess.thecvf.com/content_cvpr_2018/html/Yang_Robust_Classification_With_CVPR_2018_paper.html
[39] Yu, F., Zhang, Y., Song, S., Seff, A., Xiao, J.: LSUN: construction of a large-scale image dataset using deep learning with humans in the loop. CoRR abs/1506.03365 (2015), http://arxiv.org/abs/1506.03365
[40] Zisselman, E., Tamar, A.: Deep residual flow for out of distribution detection. In: Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition. pp. 13994–14003 (2020)

Out-of-distribution Detection with Boundary Aware Learning