Oscillations of a quasi-one-dimensional dipolar supersolid
Abstract
The properties of a supersolid state (SS) in quasi-one-dimensional dipolar Bose-Einstein condensate is studied, considering two possible mechanisms of realization - due to repulsive three-body atomic interactions and quantum fluctuations in the framework of the Lee-Huang-Yang (LHY) theory. The role of both mechanisms in the formation of SS properties has been emphasized. The proposed theoretical model, based on minimization of the energy functional, allows evaluating the amplitude of the SS for an arbitrary set of parameters in the extended Gross-Pitaevskii equation (eGPE). To explore the dynamics of the SS first we numerically construct its ground state in different settings, including periodic boundary conditions, box-like trap and parabolic potential, then impose a perturbation. In oscillations of the perturbed supersolid we observe the key manifestation of SS, namely the free flow of the superfluid fraction through the crystalline component of the system. Two distinct oscillation frequencies of the supersolid associated with the superfluid fraction and crystalline components of the wave function are identified from numerical simulations of the eGPE.
keywords:
Dipolar condensate , quantum fluctuations , supersolid , oscillations1 Introduction
The existence of an unusual state of matter, called supersolid, was theoretically predicted more than half a century ago (see review articles [1, 2]). In this state, matter exhibits both the crystalline order and superfluidity at the same time. More definitely, some fraction of the total mass is rigid as a crystal, while the rest flows through the system freely, without dissipation. The last property is considered to be the key signature of the supersolid state (SS) and its experimental observation has been the main objective pursued over the years of research. To date, there are some experimental pieces of evidence for this phenomenon in solid He, but the theoretical interpretation of observed properties remains inconclusive, as summarized in [3, 4]. Recent studies have discovered, that quantum gases with strong dipole-dipole atomic interactions can be another medium, where the SS clearly shows up [5, 6, 7, 8]. The advantage here is that the quantum gases appear to be a highly controllable coherent system. The physical mechanism behind the emerging SS in this system is the delicate balance between the long-range dipolar and short-range contact interactions among the atoms of the gas. The stabilizing effect of quantum fluctuations is essential for the existence of quantum droplets and dipolar supersolids (see review articles [9, 10, 11]). The short-range interactions originate from two-body and three-body atomic collisions, characterized by the -wave scattering length , while the quantum fluctuation effects are described in the local density approximation by the Lee-Huang-Yang (LHY) theory [12, 13]. The quantum fluctuations and elastic three-body atomic interactions were shown to play similar roles in the process of stabilization of self-bound quantum droplets [14]. It is natural to suggest, that they play similar roles in stabilizing the supersolids as well. Formation of an array of quantum droplets in dipolar Bose-Einstein condensates (BEC), stabilized solely by the conservative three-body atomic interactions, was theoretically demonstrated [15, 16]. The model was able to reproduce experimental observations, confirming the insignificance of the three-body losses for the relevant time scales. A new kind of dipolar quantum droplets, which can be made of strongly interacting bosons, was reported in [17]. In the strongly interacting Tonks-Girardeau regime, the governing equation of Ref. [17] reduces to the nonlocal Gross-Pitaevskii equation (GPE) with quintic nonlinearity, previously studied in the context of flat-top localized states in quasi-1D dipolar condensates [18, 19], while in the weakly interacting limit it reduces to usual nonlocal GPE with cubic nonlinearity [20, 21]. In a recent study [22], the authors have derived the modified GPE, taking into account the next order (beyond LHY) quantum fluctuation effects. The additional term in the energy functional has a cubic dependence on the gas density, i.e. formally similar to the effect of attractive three-body atomic interactions. A conservative quintic nonlinear term whose contribution may be of the same order as of the LHY effect, may arise also from the expansion of the well known quasi-1D nonpolynomial Schrödinger equation (NPSE) [23, 24]. It follows from the above arguments that the extended Gross-Pitaevskii equation (eGPE) with cubic-quintic nonlinearity and usual LHY term can be a more adequate framework for describing the SS in dipolar quantum gases, therefore it is adopted in the present study.
The basic properties of condensed matter systems can be revealed from the analysis of their excitation spectra. The spectrum of elementary excitations in dipolar quantum gases of 162Dy and 166Er, confined to a harmonic trap, was studied in [8, 25]. It was experimentally demonstrated, that in the regime of BEC the system exhibits ordinary quadrupole oscillations with a single frequency, while in the supersolid regime two distinct frequencies arise, corresponding to oscillations of the superfluid and crystalline phases. An important result of these works is that the two-frequency response of a supersolid, originally predicted for infinite-size systems, was confirmed for finite-size trapped quantum gases. The possibility of dynamical and simultaneous excitation of the roton and maxon modes in Rydberg-dressed condensates through interaction quenches was reported [26]. Supersolid behavior of a dipolar BEC was addressed through numerical simulations of the Bogolyubov - de Gennes equations in a tubular periodic confinement [27]. In this work, the coherence of the system across the phase transitions BEC - supersolid - isolated quantum droplets was analyzed. Description of the ground state and collective excitations of a supersolid in dipolar quantum gases, based on the variational approach, was presented in [28, 29]. A comprehensive introduction to the nonlocal GPE with the contribution of quantum fluctuation effects in a quasi-one-dimensional setting can be found in [30]. Despite impressive experimental and theoretical progress in exploring the SS in dipolar quantum gases, some static and dynamic aspects of trapped supersolids remain less studied.
Our objective in this work consists in exploring the conditions, which can support a robust SS in a quasi-one-dimensional dipolar Bose-Einstein condensate with competing long-range dipole-dipole and short-range contact atomic interactions, in the presence of quantum fluctuation effects. A theoretical model will be developed to estimate the amplitude of the emerging SS. It should be noted that the amplitude of the SS is directly linked to the experimentally measurable quantity, called density contrast [31, 32]. Therefore the proposed model can be useful for the analysis and interpretation of experimental results. Besides, we numerically investigate the dynamics of a supersolid, subject to a weak perturbation, to demonstrate its key property, namely the free flow of the superfluid fraction of the quantum gas through its crystalline fraction. When perturbed, the crystalline and superfluid components of the system perform undamped oscillations with different frequencies [8, 25, 33], which is the hallmark property of supersolids. In our numerical simulations by recording the time-dependence of the width of the oscillating supersolid, and Fourier-analyzing the obtained data, we identify these two distinct frequencies.
The paper is structured as follows. In the next Sec. II we present the main equations, the spectrum of elementary excitations, and the variational approach for the amplitude of the supersolid. Sec. III is devoted to SS dynamics subject to perturbation. In Sec. IV we summarize our findings.
2 The model and main equations
The model is based on a normalized quasi-1D eGPE, derived from its full three-dimensional version (for details of 3D to 1D reduction see [30, 34])
| (1) |
where is the mean-field wave function of the condensate,
is the trap potential, are the coefficients of
two-body, three-body and dipole-dipole atomic interactions,
respectively. The parameter quantifies the contribution of
quantum fluctuations,
is
the response function which characterizes the degree of nonlocality
of the medium [35]. The Eq. (2) is obtained for
the condensate, which is tightly confined in the radial direction,
with the transverse and axial trap frequencies satisfying the
condition . Under such confinement, the
condensate acquires a highly elongated form in the axial direction
commonly termed as cigar-shaped condensate. Below we consider
different types of confinement, namely a tubular geometry with
periodic boundary conditions, mimicking the infinite system,
box-like potential with soft walls, and parabolic trap potential.
The dimensionless time, space, and wave function in Eq. (2)
are linked to corresponding physical quantities as follows , , , with being the
background value of the -wave scattering length, is the radial harmonic oscillator
length, is the atomic mass. The dimensionless coefficients of
Eq. (2) are expressed through the actual parameters of the
system as follows ,
, , where characterizes the
strength of three-body atomic interactions, are the
permeability of vacuum and atomic magnetic moment, respectively. In
these notations and , corresponds to
attractive contact interactions competing with the repulsive dipolar
and three-body terms. The contribution of quantum fluctuations is
characterized by , where
is the ratio
between the dipolar and -wave scattering lengths. The LHY energy
correction in dipolar condensates leads to a repulsive term in the eGPE (2) provided that the
one-dimensional density of the gas is sufficiently large
() [36]. It is relevant to mention
that the coefficient in Eq. (2) may also be associated
with the term of quintic nonlinearity arising from expansion of the
NPSE [23, 24], or the beyond LHY
description of quantum fluctuation effects [22].
2.1 Dispersion relation for elementary excitations
The spatial period of emerging density modulations in a dipolar condensate, which can transform in suitable conditions into SS, can be defined from the dispersion curve of elementary excitations. To derive the dispersion relation we consider the ground state wave function of the form
| (2) |
where is the constant background density, is the uniform phase
| (3) |
Next, we introduce weak perturbation to the ground state , assuming and . Substituting into Eq. (2) and linearizing around one obtains
| (4) |
Splitting the perturbation field into real and imaginary parts , and taking the Fourier transform of the resulting equation, yields the following coupled system for the transformed components
| (5) | |||
where the overdot denotes the derivative with respect to time, while the tilde stands for the Fourier transform , and is given by
| (6) |
with being the exponential integral function [37]. Notice that the above equations are equivalent to a single harmonic oscillator equation
| (7) |
with the frequency
| (8) |
For small values of the wave vector the above frequency defines the energy spectrum of the elementary excitations obtained from the Bogoliubov-de Gennes analysis with a sound velocity
| (9) |
For larger values of and suitable parameters the dispersion relation (8) features a local minimum at , corresponding to quasi-particles known as rotons, whose existence in dipolar condensates was theoretically predicted [38] and experimentally confirmed [39, 40]. Although initially the roton was linked to local vorticity in superfluid 4He [41], nowadays it is viewed as the precursor of a crystallization instability [42].
Figure 1 illustrates the dispersion relation (8) for different sets of parameter values. The real and positive values of the frequency (blue dashed and brown dot-dashed lines in Fig. 1) signify that the density modulations in the condensate are of standing wave type. A small energy gap near implies that the roton quasi-particles are more effectively generated in the condensate compared to other types of excitations [34]. The supersolid emerges as the frequency (8) becomes imaginary (red and black solid lines in Fig. 1) and roton instability sets in [43]. The steady growth of the amplitude of density waves, caused by the roton instability, is counterbalanced by the repulsive LHY term and/or three-body atomic scattering effects. It should be stressed that the balance solely between the attractive two-body () and repulsive dipolar () interactions is unstable (corresponding to the curve (a) in Fig. 1). Therefore, the presence of repulsive LHY and/or three-body interaction terms is essential for the existence of stable SS in dipolar condensates. Either of these two higher-order nonlinear terms or a combination of them can stabilize the supersolid, producing very similar stationary density profiles. The spatial period of the supersolid represents its most important characteristic which is defined by the wave vector of rotons . Another important parameter is the amplitude of the SS, expressed through its field contrast as , where () denotes the maximum (minimum) over the space.
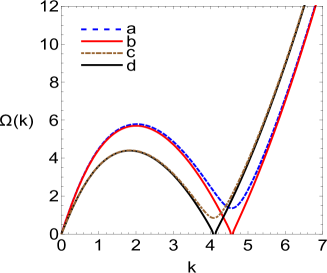
Below we study the existence of SS in dipolar quantum gases and its dynamics employing the variational approach and numerical integrations of the eGPE (2).
2.2 Variational approach for supersolids in dipolar quantum gases
It was pointed out earlier that supersolids in dipolar condensates can exist due to the stabilizing effect of repulsive quantum fluctuations and/or three-body atomic interactions. The existence conditions and some characteristics of the supersolid can be evaluated using the variational approach. A variational theory based on minimization of the GPE energy functional was developed for the former [28, 29] and latter [44] cases, using the cosine modulated trial function , with being the average linear density of the condensate. The variational parameters and characterize the amplitude and period of the density modulations, respectively. This ansatz is valid for weakly modulated density waves in the absence of trapping potential.
Below we develop a variational approach for supersolids in dipolar quantum gases using an alternative trial function
| (10) |
where the variational parameters () are introduced, meaning the amplitude of the background, amplitude and wave vector of density modulations, respectively. The normalization to the average linear density of the condensate
| (11) |
is adopted. Similar (sine-modulated) trial function was previously employed in Ref. [32]. These trial functions are suitable when the axial confinement is absent (). By substitution of the ansatz (10) into the energy density, corresponding to Eq. (2) without the harmonic trap
| (12) |
and integration over the space variable , one obtains the following GP energy functional
| (13) |
The response function in the Fourier space , defined by Eq. (6), has the following properties
| (14) |
where the prime stands for the derivative with respect to . Using these relations the expression for the amplitude of density modulations can be derived from minimization of the energy ()
| (15) |
and the vanishing of the roton gap () at some . The supersolid amplitude Eq. (15) implicitly depends on the system parameters through . Calculations according to Eq. (8) and Eq. (15) for parameter values specified for the black line (d) in Fig. 1 gives for the roton minimum , and SS amplitude at average linear density , which is in good agreement with the results of eGPE ().
3 Dynamics of the perturbed supersolid
The basic properties of a supersolid can be studied by observing its collective dynamics. Oscillations of the supersolid can be induced in different ways, such as changing the atomic interactions or variations of the trapping potential. Below we present the results of numerical simulations where the oscillations of the supersolid in three different configurations have been recorded and Fourier analyzed. The first case belongs to periodic boundary conditions, emulating the infinite system. The second and third cases correspond to box-like and parabolic traps respectively.
The starting point is the ground state of a SS, which is numerically obtained by the method of Pitaevskii phenomenological damping [45, 46], applied to eGPE(2). The governing Eq. (2) has been solved by combination of the fast Fourier transform and fourth order Runge-Kutta procedures, using the phenomenological damping parameter [46]. The number of Fourier modes and time step were and , respectively. The length of the integration domain is selected to accommodate nine periods of the supersolid , with , being the roton wave number. The parameter values for in Eq. (2) correspond to situation, when the roton minimum of the dispersion curve (8) touches the zero axis (see Fig. 1). The oscillations of the supersolid can be induced either by a slight variation of the coefficient of atomic interactions, or modification of the trap potential. The main parameter of interest for trapped supersolid will be its time dependent average width
| (16) |
where is the norm of the wave function, which is linked to the number of atoms in the condensate through . For a uniform condensate with amplitude , confined to a ring trap .
3.1 Supersolid with periodic boundary conditions
The majority of theoretical research concerns the infinite supersolid, which can be emulated in numerical simulations using periodic boundary conditions. Figure 2 illustrates the ground state of the supersolid and its oscillations induced by slight variation of the strength of dipolar interactions.
a) b)


It should be pointed out, that in case of periodic boundary conditions, variation of the strength of atomic interactions leads to excitation of the amplitude mode only, leaving the width Eq.(16) unaffected. Owing to a superfluid nature of the system and equal heights of density peaks, the SS performs undamped oscillations of its amplitude with a single frequency (see Fig. 2b).
Oscillations of the effective width can be induced using the external potential providing a small shift of the density peaks from their equilibrium positions, meantime not violating the periodic boundary conditions. In numerical simulations we employ the following potential
| (17) |
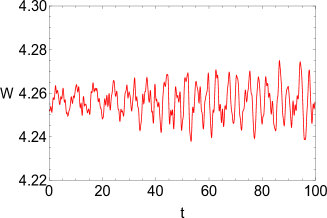
with parameter values , , . In addition to the displacement of the peak positions, their heights also become unequal. In Fig. 3 we show the ground state of the supersolid in presence of the potential (17), and its dynamics caused by subsequent elimination of the potential. The excitation of both the superfluid and crystalline modes is evident. The Fourier analysis of the time dependent width Eq. (16) reveals two distinct frequencies, associated with the superfluid () and crystalline () components of the system.
a) b)


c) d)

If the density peaks of the supersolid become unequal due to the external potential, a notable mixing of oscillations occurs. As a consequence, additional small peaks arise in the Fourier spectrum (Fig. 3d).
3.2 Supersolid in a box-like potential
Supersolids in confined geometries exhibit more complex dynamics. Below we consider the SS confined to a soft-wall box potential
| (18) |
where the parameters characterize its strength, spatial extent, and width of the transition region.
In experiments the potential (18) can be created by laser beams [47, 48]. To study oscillations of the supersolid first we create its ground state in the box potential, as shown in Fig. 4. The peculiarity of this case is the existence of density spikes near the trap edges [49]. The ground state with a density peak (drop) at emerges if the trap can accommodate an odd (even) number of supersolid periods .
a) b)


c) d)

Sudden reduction of the repulsive dipolar interactions gives rise to flow of superfluid matter into the central region of the trap, which shows up as raising (and subsequent oscillations) of the central density peaks (see Fig. 4b). This is a clear manifestation of the key property of supersolids, namely free flow of the superfluid component through its crystalline phase.
To identify the frequencies of particular modes we perform Fourier analysis of the time-dependent width calculated according to Eq.(16), with being the numerical solution of the eGPE (2). The Fourier transform reveals three frequencies (see Fig. 4d). The lower frequency is associated with the superfluid component, while other two higher frequencies are linked to the crystalline component of the SS. The additional frequency originates from two pronounced density peaks (edge states) of dipolar BEC confined to a box-potential (see Fig. 4a). These density peaks can be viewed as a separate crystal component, oscillating at a different frequency than the main crystalline phase, occupying the central part of the box-trap.
3.3 Supersolid in a parabolic potential
The parabolic potential is a frequently used setting in experiments with ultra-cold quantum gases. The ground state of the supersolid confined to a parabolic trap, numerically produced by the Pitaevskii phenomenological damping procedure, is depicted in Fig. 5. The figure gives evidence that the stronger is the parabolic trap, the more amount of superfluid matter is expelled to the trap periphery. A similar effect was noticed for the box trap where the edge states with increased matter density emerge even for parameter regimes, where the SS phase is absent. As a consequence, the lateral density peaks in the parabolic trap become less pronounced.
a) b)


c) d)


To study the collective dynamics of the SS in a parabolic trap we introduce its ground state (red solid line in Fig. 5a) into the eGPE as initial condition and reduce the trap strength from to . The resulting collective dynamics of the supersolid is shown through the density plot in Fig. 5b. Notable periodic variation of the inter-peak separation can be seen. The average width of the supersolid also shows complex dynamics, giving evidence of the superposition of few oscillations (Fig. 5c). The Fourier transform of the effective width reveals two main frequencies (Fig. 5d), corresponding to oscillations of the superfluid component () and crystalline phase (), respectively.
Figure 5 represents the example of SS with dominating crystalline component, which shows a stronger peak in the Fourier spectrum than that of the superfluid component. Now we consider the opposite situation with dominating superfluid phase, which is shown in Fig. 6. The ground state is numerically obtained by the Pitaevskii phenomenological damping procedure starting from the uniform condensate with linear density . For selected parameter values the density modulations are less pronounced in the central region of the trap, while notable density peaks show up near the borders, similar to edge states in the box-trap (see Fig. 4a).
a) b)


c) d)


To induce oscillations of the condensate initially residing in the ground state of the parabolic trap, we slightly change its strength . Figure 6 c illustrates the variation of the effective width of the condensate caused by a 5 % reduction of the parameter . Here a superposition of two frequencies can be noticed. The Fourier transform shown in Fig. 6 d reveals these two frequencies, associated with the superfluid and crystalline components. The crystalline phase, although quite weakly, shows up through the density peaks near trap edges. By comparing the results shown in figures 5 and 6 we conclude that when the SS is perturbed, its crystalline (superfluid) component oscillates with higher (lower) frequency, in accordance with experimental findings [8].
3.4 Estimation of parameter values
Now we estimate the parameters of our model using the quantities relevant to experiments [8, 33]. Consider 162Dy atoms, whose magnetic dipole moment, background -wave scattering length and atomic mass are , , kg, respectively, with , being the Bohr magneton and Bohr radius. The roton instability sets in, thus supersolid phase emerges, when the -wave scattering length is tuned to m. The condensate of atoms is held in a tight quasi-1D trap with radial confinement frequency Hz. The corresponding radial harmonic oscillator length, which is the adopted length scale in this work, is m. The unit of time is s. The ratio between the strengths of dipolar and contact interactions, computed with above defined parameters, is found to be , therefore we have the dipolar interaction dominated regime. The coefficients of two-body contact interactions and long-range dipolar interactions in physical units are and , yielding the dimensionless parameter . The strength of three-body atomic interactions in dysprosium condensate was reported to be in the range for real conservative part and for imaginary part, characterizing the three-body recombination rate [15]. Since the imaginary part of this parameter is smaller than its real part by three orders of magnitude, we have omitted it in the eGPE (2), leaving only the conservative part . The coefficient of quintic nonlinearity, computed using this value and above defined parameters is found to be in the range . The coefficient of quantum fluctuations corresponding to above mentioned parameter values is estimated as .
Numerical simulations are performed using the integration domain of length m. The amplitude of the background wave in dimensionless units is defined as , where stands for the number of atoms in the condensate. The linear density of the condensate is .
The above estimates for dimensionless parameters obtained from experimentally possible quantities are in the range of values used in our numerical simulations. Since the radial confinement length is much greater than the atomic scattering length (), usage of parameter values relevant to 3D geometry for numerical simulations in quasi-1D setting is justified. Some deviations can be adjusted by changing the tunable parameters of the system, such as the -wave scattering length, frequency of radial confinement, and the strength of dipolar interactions. As for the roles of the repulsive three-body atomic collisions and quantum fluctuations, these are two possible factors responsible for the existence of stable supersolids [44, 8], and for a complete description of the problem, both terms should be taken into account.
4 Conclusions
We have explored the static and dynamic properties of a supersolid state in quasi-one-dimensional dipolar quantum gases in three different settings, including the periodic boundary conditions, box-like confinement, and parabolic potential. The model is based on the extended Gross-Pitaevskii equation involving the effect of quantum fluctuations and three-body atomic interactions, which correspond to quartic and quintic nonlinearities, respectively. The dipolar interatomic repulsion gives rise to density peaks near the edges of the confining potential, which is shown for the box-like and parabolic traps. The analytic approach, based on minimization of the Gross-Pitaevskii energy functional is developed to estimate the amplitude of the supersolid, which is linked to the experimentally relevant quantity called the density contrast. The supersolid states with weak and strong modulation of the condensate density are produced by numerical methods. The amplitude of the weakly modulated supersolid well agrees with the theoretical prediction. The oscillations of the supersolid residing in the ground state are induced by changing the strength of atomic interactions, and variation of the confining potential. By recording the time-dependent effective width of the perturbed condensate and subsequent Fourier analysis of the obtained data we identify two distinct oscillation frequencies, associated with the superfluid and crystalline components. These frequencies depend on the type and strength of the external potential. The edge states of a dipolar condensate in the confining potential can produce additional frequency in the Fourier spectrum. In numerical simulations we observed the key property of the supersolid - free flow of the superfluid fraction through the crystalline component of the condensate.
Acknowledgments
We thank Dr. E. N. Tsoy for valuable discussions. The work of BBB is partially supported by the Ministry of Innovative Development of Uzbekistan through International Uzbekistan-Turkey Project UT-A-2020-3.
References
- [1] M. Boninsegni and N. V. Prokof’ev, Colloquium: Supersolids: What and where are they?, Rev. Mod. Phys. 84, 759 (2012).
- [2] S. Balibar, The enigma of supersolidity, Nature 464, 176 (2010).
- [3] N. Prokof’ev, What makes a crystal supersolid? Adv. Phys. 56, 381 (2007).
- [4] V.I. Yukalov, Saga of superfluid solids, Physics, 2, 49 (2020).
- [5] L. Tanzi, E. Lucioni, F. Famá, J. Catani, A. Fioretti, C. Gabbanini, R. N. Bisset, L. Santos, and G. Modugno, Observation of a dipolar quantum gas with metastable supersolid properties, Phys. Rev. Lett. 122, 130405 (2019).
- [6] F. Böttcher, J. N. Schmidt, M. Wenzel, J. Hertkorn, M. Guo, T. Langen, and T. Pfau, Transient supersolid properties in an array of dipolar quantum droplets, Phys. Rev. X 9, 011051 (2019).
- [7] L. Chomaz, D. Petter, P. Ilzhöfer, G. Natale, A. Trautmann, C. Politi, G. Durastante, R. M. W. van Bijnen, A. Patscheider, M. Sohmen, M. J. Mark, and F. Ferlaino, Long-lived and transient supersolid behaviors in dipolar quantum gases, Phys. Rev. X 9, 021012 (2019).
- [8] L. Tanzi, S. M. Roccuzzo, E. Lucioni, F. Famá, A. Fioretti, C. Gabbanini, G. Modugno, A. Recati, and S. Stringari, Supersolid symmetry breaking from compressional oscillations in a dipolar quantum gas, Nature 574, 382 (2019).
- [9] Z. Luo, W. Pang, B. Liu, Y. Li, and B. A. Malomed, A new form of liquid matter: quantum droplets, Front. Phys. 16, 32201 (2021).
- [10] M. Guo, T. Pfau, A new state of matter of quantum droplets, Front. Phys. 16, 32202 (2021).
- [11] F. Böttcher, J. -N. Schmidt, J. Hertkorn, K. S. H. Ng, S. D. Graham, M. Guo, T. Langen and T. Pfau, New states of matter with fine-tuned interactions: quantum droplets and dipolar supersolids, Rep. Prog. Phys. 84, 012403 (2021).
- [12] T. D. Lee, K. Huang, and C. N. Yang, Eigenvalues and eigenfunctions of a Bose system of hard spheres and its low-temperature properties, Phys. Rev. 106, 1135 (1957).
- [13] D. S. Petrov, Quantum mechanical stabilization of a collapsing Bose-Bose mixture, Phys. Rev. Lett. 115, 155302 (2015).
- [14] S. Gautam and S. K. Adhikari, Self-trapped quantum balls in binary Bose-Einstein condensates, J. Phys. B: At. Mol. Opt. Phys. 52, 055302 (2019).
- [15] R. N. Bisset and P. B. Blakie, Crystallization of a dilute atomic dipolar condensate, Phys. Rev. A 92, 061603(R) (2015).
- [16] Kui-Tian Xi and Hiroki Saito, Droplet formation in a Bose-Einstein condensate with strong dipole-dipole interaction, Phys. Rev. A 93, 011604(R) (2016).
- [17] R. Oldziejewski, W. Gorecki, K. Pawlowski, and K. Rzazewski, Strongly correlated quantum droplets in quasi-1D dipolar Bose gas, Phys. Rev. Lett. 124, 090401 (2020).
- [18] E. B. Kolomeisky, T. J. Newman, J. P. Straley, and X. Qi, Low-dimensional Bose liquids: Beyond the Gross-Pitaevskii approximation, Phys. Rev. Lett. 85, 1146 (2000).
- [19] B. B. Baizakov, F. K. Abdullaev, B. A. Malomed, and M. Salerno, Solitons in the Tonks-Girardeau gas with dipolar interactions, J. Phys. B: At. Mol. Opt. Phys. 42, 175302 (2009).
- [20] J. Cuevas, B. A. Malomed, P. G. Kevrekidis, D. J. Frantzeskakis, Solitons in quasi-one-dimensional Bose-Einstein condensates with competing dipolar and local interactions, Phys. Rev. A 79, 053608 (2009).
- [21] B. B. Baizakov, S. M. Al-Marzoug, U. Al Khawaja and H. Bahlouli, Weakly bound solitons and two-soliton molecules in dipolar Bose-Einstein condensates, J. Phys. B: At. Mol. Opt. Phys. 52, 095301 (2019).
- [22] M. Ota, G. E. Astrakharchik, Beyond Lee-Huang-Yang description of self-bound Bose mixtures, SciPost Phys. 9, 020 (2020).
- [23] L. Salasnich, A. Parola and L. Reatto, Effective wave equations for the dynamics of cigar-shaped and disk-shaped Bose condensates, Phys. Rev. A 65, 043614 (2002).
- [24] G. Gligoric, A Maluckov, L. Hadzievski and B. A. Malomed, Collapse instability of solitons in the nonpolynomial Schrödinger equation with dipolevdipole interactions, J. Phys. B: At. Mol. Opt. Phys. 42, 145302 (2009).
- [25] G. Natale, R. M. W. van Bijnen, A. Patscheider, D. Petter, M. J. Mark, L. Chomaz, and F. Ferlaino, Excitation spectrum of a trapped dipolar supersolid and its experimental evidence, Phys. Rev. Lett. 123, 050402 (2019).
- [26] G. McCormack, R. Nath, and W. Li, Dynamical excitation of maxon and roton modes in a Rydberg-dressed Bose-Einstein condensate, Phys. Rev. A 102, 023319 (2020).
- [27] S. M. Roccuzzo and F. Ancilotto, Supersolid behavior of a dipolar Bose-Einstein condensate confined in a tube, Phys. Rev. A 99, 041601 (2019).
- [28] P. B. Blakie, D. Baillie, and S. Pal, Variational theory for the ground state and collective excitations of an elongated dipolar condensate, Commun. Theor. Phys. 72, 085501 (2020).
- [29] P. B. Blakie, D. Baillie, L. Chomaz, and F. Ferlaino, Supersolidity in an elongated dipolar condensate, Phys. Rev. Research 2, 043318 (2020).
- [30] M. J. Edmonds, T. Bland, and N. G. Parker, Quantum droplets of quasi-one-dimensional dipolar Bose-Einstein condensates, J. Phys. Commun. 4 125008 (2020).
- [31] D. Petter, A. Patscheider, G. Natale, M. J. Mark, M. A. Baranov, R. v. Bijnen, S. M. Roccuzzo, A. Recati, B. Blakie, D. Baillie, L. Chomaz, and F. Ferlaino, High-energy Bragg scattering measurements of a dipolar supersolid, Preprint arXiv: 2005.02213.
- [32] L. Chomaz, Probing the supersolid order via high-energy scattering: Analytical relations among the response, density modulation, and superfluid fraction, Phys. Rev. A 102, 023333 (2020).
- [33] M. Guo, F. Böttcher, J. Hertkorn, J. N. Schmidt, M. Wenzel, H. P. Büchler, T. Langen and T. Pfau, The low-energy Goldstone mode in a trapped dipolar supersolid, Nature 574, 386 (2019).
- [34] B. Kh. Turmanov, B. B. Baizakov, F. Kh. Abdullaev, Generation of density waves in dipolar quantum gases by time-periodic modulation of atomic interactions, Phys. Rev. A 101, 053616 (2020).
- [35] S. Sinha and L. Santos, Cold dipolar gases in quasi-one-dimensional geometries, Phys. Rev. Lett. 99, 140406 (2007).
- [36] D. Edler, C. Mishra, F. Wächtler, R. Nath, S. Sinha, and L. Santos, Quantum fluctuations in quasi-one-dimensional dipolar Bose-Einstein condensates, Phys. Rev. Lett. 119, 050403 (2017).
- [37] M. Abramowitz and I. A. Stegun, Handbook of mathematical functions, (National Bureau of Standards, Washington, 1964).
- [38] L. Santos, G. V. Shlyapnikov, and M. Lewenstein, Roton-maxon spectrum and stability of trapped dipolar Bose-Einstein condensates, Phys. Rev. Lett. 90, 250403 (2003).
- [39] L. Chomaz, R. M.W. van Bijnen, D. Petter, G. Faraoni, S. Baier, J. H. Becher,M. J.Mark, F.Wachtler, L. Santos, and F. Ferlaino, Observation of roton mode population in a dipolar quantum gas, Nat. Phys. 14, 442 (2018).
- [40] D. Petter, G. Natale, R. M.W. van Bijnen, A. Patscheider, M. J. Mark, L. Chomaz, and F. Ferlaino, Probing the roton excitation spectrum of a stable dipolar Bose gas, Phys. Rev. Lett. 122, 183401 (2019).
- [41] L. D. Landau, The theory of superfluidity of helium II, Phys. Rev. 60, 356 (1941).
- [42] P. Nozieres, Is the roton in superfluid 4 He the ghost of a Bragg spot?, J. Low Temp. Phys. 137, 45 (2004).
- [43] S. Giovanazzi and D. H. J. O’Dell, Instabilities and the roton spectrum of a quasi-1D Bose-Einstein condensed gas with dipole-dipole interactions, Eur. Phys. J. D 31, 439 (2004).
- [44] Zhen-Kai Lu, Yun Li, D. S. Petrov, and G. V. Shlyapnikov, Stable dilute supersolid of two-dimensional dipolar bosons, Phys. Rev. Lett. 115, 075303 (2015).
- [45] L. P. Pitaevskii, Phenomenological theory of superfluidity near the point, Zh. Eksp. Teor. Fiz. 35, 408 (1958)[Sov. Phys. JETP 35, 282 (1959)].
- [46] S. Choi, S. A. Morgan, and K. Burnett, Phenomenological damping in trapped atomic Bose-Einstein condensates, Phys. Rev. A 57, 4057 (1998).
- [47] T. P. Meyrath, F. Schreck, J. L. Hanssen, C.-S. Chuu, and M. G. Raizen, Bose-Einstein condensate in a box, Phys. Rev. A 71, 041604(R) (2005).
- [48] N. Navon, R. P. Smith, Z.. Hadzibabic, Quantum gases in optical boxes, Preprint arXiv: 2106.09716.
- [49] S. M. Roccuzzo, S. Stringari, and A. Recati, Supersolid edge and bulk phases of a dipolar quantum gas in a box, Preprint: arXiv:2104.01068.