Origin of Interstitial Doping Induced Coercive Field Reduction in Ferroelectric Hafnia
Abstract
Hafnia-based ferroelectrics hold promise for nonvolatile ferroelectric memory devices. However, the high coercive field required for polarization switching remains a prime obstacle to their practical applications. A notable reduction in coercive field has been achieved in ferroelectric Hf(Zr)1+xO2 films with interstitial Hf(Zr) dopants [Science 381, 558 (2023)], suggesting a less-explored strategy for coercive field optimization. Supported by density functional theory calculations, we demonstrate the phase, with a moderate concentration of interstitial Hf dopants, serves as a minimal model to explain the experimental observations, rather than the originally assumed rhombohedral phase. Large-scale deep potential molecular dynamics simulations suggest that interstitial defects promote the polarization reversal by facilitating -like mobile 180 domain walls. A simple pre-poling treatment could reduce the switching field to less than 1 MV/cm and enable switching on a subnanosecond timescale. High-throughput calculations reveal a negative correlation between the switching barrier and dopant size and identify a few promising interstitial dopants for coercive field reduction.
Ferroelectric hafnia (HfO2) has emerged as a promising candidate for integrating ferroelectric functionalities into integrated circuits, enabled by its robust nanoscale ferroelectricity and exceptional silicon compatibility [1, 2, 3]. However, the high coercive field () required to switch the polarization in HfO2-based thin films remains a critical issue, impeding the commercialization of this silicon-compatible ferroelectric [3, 4]. Typically, polycrystalline thin films of hafnia fabricated through atomic-layer deposition display an exceeding 1 MV/cm [5]. High-quality epitaxial thin films, obtained by pulsed laser deposition, can show even higher values of 2–5 MV/cm [6, 7, 8, 9]. The need for applying high electric fields, close to the material’s breakdown strength, for polarization reversal seriously limits its field cycling endurance. Reducing without sacrificing the nanoscale ferroelectricity of hafnia is a pressing challenge for the wider adoption of HfO2-based ferroelectrics.
Various strategies such as doping [10, 11], strain [12, 13], and superlattices [14] have been theoretically explored to lower the barrier for polarization switching, aiming to reduce . Investigations based on density functional theory (DFT) revealed that the polarization switching process in the ferroelectric othorhombic () phase often involves an intermediate tetragonal () phase, and the energy difference between these two phases could serve as a measure of the switching barrier [11, 15]. Substitutional Si has been suggested as an effective dopant for reducing due to its intrinsic bonding with oxygen, which helps stabilize the intermediate phase [11, 16]. Conversely, most other substitutional dopants have shown limited effectiveness in influencing based on DFT calculations [11]. Recently, a substantial reduction in , down to 0.65 MV/cm, has been achieved in thin films of Hf(Zr)1+xO2, a composition rich in hafnium-zirconium [Hf(Zr)] [17]. This reduction was attributed to the interstitial doping of Hf and Zr atoms into a polar rhombohedral () phase. DFT calculations show that a 7%-strained -phase Hf1.08O2 exhibits a switching barrier of 7.6 meV/atom, significantly lower than that of 20 meV/atom in stoichiometric -HfO2.
However, assuming a polar phase in Hf1.08O2 films grown via magnetron sputtering leads to notable discrepancies between theory and experiment [18, 19]. The unstrained phase is actually a nonpolar cubic phase [3, 20]; the polar symmetry only emerges under an equibiaxial compressive strain within the (111) crystallographic plane. Although the relative stability between the and phases can be reversed with 8% interstitial doping [17], highly-doped -Hf1.08O2 without strain remains nonpolar; a giant compressive strain of 7% is nevertheless required to induce a polarization of 15 C/cm2, still below the experimental value of 22 C/cm2 in polycrystalline films [17]. Moreover, X-ray diffraction (XRD) patterns of Hf(Zr)1+xO2 thin films show only a slight offset from both unstrained and phases [21], indicating the absence of high strains.
In this work, we combine DFT and deep potential molecular dynamics (DPMD) simulations [22] to investigate how interstitial Hf doping reduces the coercive field in ferroelectric HfO2. We find that interstitial Hf dopants diminish the energy difference between the polar orthorhombic phase and the intermediate tetragonal phase, lowering the switching barrier and coercive field. Unlike the phase, which demands additional compressive strains for polarization, the phase of Hf1.03O2, with a moderate doping concentration of 3%, already exhibits a low switching barrier and a high polarization. We propose that the phase of HfO2 with interstitial Hf defects better explains experimental observations. Large-scale MD simulations at finite temperatures with a DFT-derived machine learning force field demonstrate that 0.5% interstitial doping in HfO2 is enough to reduce the switching field significantly. Moreover, after a pre-poling treatment during which interstitial dopants induce the formation of mobile domain walls, the switching field can drop below 1 MV/cm, comparable to experimental results. Further DFT calculations covering various interstitial dopants reveal a negative correlation between the switching barrier and dopant size.
All DFT calculations are carried out using the Vienna ab initio simulation package (VASP) [23] with the projector augmented-wave (PAW) method [24, 25] and the Perdew-Burke-Ernzerhof (PBE) exchange correlation functional [26]. The cut-off energy for the plane-wave basis is set to 600 eV. The Brillouin zones of the 12-atom pseudocubic unit cell and the 222 supercell for doped systems are sampled by -centered 444 and 222 Monkhorst-Pack [27] -point meshes, respectively. All the structures are fully optimized until the atomic forces converge to 0.01 eV/Å. The polarization values are determined using the Berry phase method [28, 29]. The polarization switching pathway is determined using the nudged elastic band (NEB) method [30]. The bond order analysis is performed with the crystal orbital Hamilton population (COHP) method [31] implemented in LOBSTER [32]. To investigate the ferroelectric switching in Hf1+xO2 at finite temperatures, we perform isobaric-isothermal ensemble () MD simulations using a deep neural network-based force field [33, 34], with model accuracy verification and sample inputs available via an online notebook [35]. The electric fields are included in MD simulations using the “force method” [36, 37, 15], where an additional force is added on the ion according to , with being the Born effective charge (BEC) tensor of ion .
We start with an analysis of the phase stability of Hf1+xO2 with interstitial Hf dopants (Hfi), considering the monoclinic () , polar orthorhombic () , tetragonal () , rhombohedral () , and cubic () phases. Two doping concentrations, 3.125% and 6.25% (abbreviated as 3% and 6%), are modeled by intercalating one and two excess Hf atom within the hollow sites in a 96-atom 222 supercell, respectively. As shown in Fig. 1(a), pristine HfO2 polymorphs exhibit an inverse correlation between the thermodynamic stability and crystal symmetry.With increasing Hfi concentration, the energies of these phases become closer, suggesting higher Hfi formation energy in lower-symmetry and phases but lower in higher-symmetry and phases. This dependence is due to different effective void sizes in each phase [see the inset of Fig. 1(a)]. Specifically, the and phases have smaller voids due to alternating fourfold-coordinated (4C) and threefold-coordinated (3C) oxygen atoms, hindering Hfi integration and resulting in higher formation energy.
Consistent with previous DFT results [17], our calculations show that, compared to the phase, Hfi doping destabilizes the lower-symmetry and phases while imposing minimal impact on the relative stability of the phase. This suggests that the phase would become energetically more favorable than the phase above a critical Hfi concentration, if it remains stable. However, the Hfi-doped phase is nonpolar, requiring a (111) in-plane compressive strain to achieve a polarized phase. Using a 36-atom hexagonal supercell with a 7% in-plane compressive strain and an excess Hf atom, Wang et al. reported a polarized -Hf1.08O2 with a low switching barrier of 7.6 meV/atom [17]. Notably, such a high strain state should correspond to a large out-of-plane interplanar spacing, Å. This does not align with the experimental XRD data of Hf1+xO2 films, which shows a (111) peak at , indicating only a 0.1 shift compared to the stoichiometric phase (with 2.96 Å, see Fig. S1).
In contrast to the phase, the phase is inherently polar and does not depend on applied strain for polarization. The ferroelectric switching barrier in the phase can be estimated from the energy difference between the phase and phase () [11]. As illustrated in Fig. 1(a), interstitial doping elevates the energy of the phase relative to the phase, thereby reducing . Figure 1(b) plots the NEB energy variation along the switching pathway in the phase for different doping concentrations. The switching barrier decreases drastically from 28 meV/atom in pristine HfO2 to 12.3 meV/atom in Hf1.03O2, and further drops to 7.5 meV/atom in Hf1.06O2.
As summarized in Fig. 1(c), for the phase, both the switching barrier and polarization decrease with increasing Hfi concentration. This reduction in polarization is attributed to the diminished local displacements of polar oxygen atoms surrounding Hfi. Further increasing Hfi concentration destabilizes the phase, causing it to transform into a -like structure during DFT geometry relaxation (see Fig. S2). Importantly, -Hf1.06O2, with a lower Hfi concentration, exhibits a switching barrier (7.5 meV/atom) comparable to that of 7%-strained -Hf1.08O2. It also features a higher spontaneous polarization along the [111] direction, matching closely to the experimental value. Although large local strains in polycrystalline thin films cannot be ruled out, the phase with moderate interstitial Hf doping serves as a minimal model to explain experimental observations. We note that Hfi exhibits a negative BEC of , indicating that its slight movement induces a change in polarization equivalent to the displacement of two negative elementary charges. This counterintuitive result is likely due to the crowding effect of the confining cage around Hfi. Nevertheless, since the Hfi is strongly confined, it does not change the polarization switching mechanism identified with DFT-based NEB calculations.
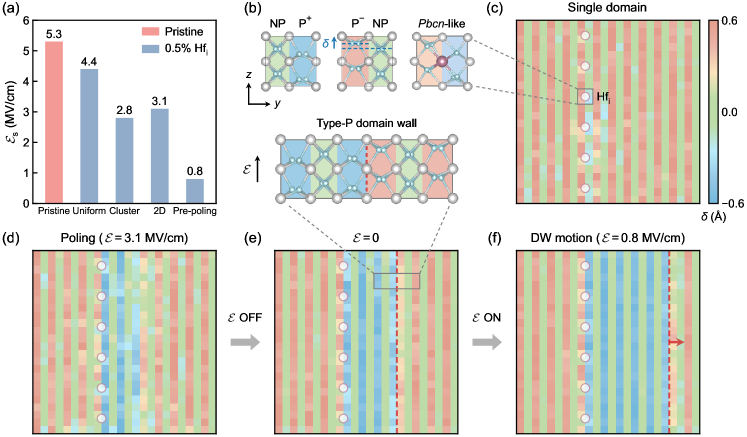
Limited by computational cost, our DFT investigations focused on small supercells. This raises a legitimate question: how does the reduced energy difference between the and phases, seen in zero-Kelvin DFT calculations, manifest in larger supercells at elevated temperatures that better represent the experimental sample conditions? To address this, we perform large-scale MD simulations at finite temperatures for an -Hf1.005O2 supercell of 20,772 atoms, considering different Hfi dopant distributions. The force field is a deep neural network-based model potential [15], which accurately reproduces various properties including the energy variation along the switching pathway in Hf1+xO2 (see Fig. S3). All simulations are conducted at 400 K to facilitate the switching process on (sub)nanosecond time scales, thereby mitigating computational cost. We gauge the ease of switching by determining the lowest field strength () that triggers polarization switching within 200 ps in MD simulations. As shown in Fig. 2(a), the switching field is 5.3 MV/cm for pristine single-domain HfO2. Introducing uniformly distributed 0.5% Hfi dopants decreases to 4.4 MV/cm. The local enrichment of Hfi dopants further reduce : the cluster-like and two-dimensional (2D) distributions of Hfi lead to of 2.8 and 3.1 MV/cm, respectively (see dopant distributions in Fig. S4).
We discover that a simple pre-poling treatment can bring to an even lower value of 0.8 MV/cm. The switching process extracted from MD simulations is presented in Fig. 2(c-f), with the color scheme explained in Fig. 2(b). The starting configuration has 3C oxygen atoms displaced upward (P-) relative to 4C oxygen atom (NP). The 2D-confined Hfi dopants are distributed randomly within the plane between P- and NP layers. A main impact of Hfi is the slight downward displacement of 4C atoms [left inset of Fig. 2(c)]. Upon poling under an electric field of MV/cm, the Hfi enriched layer facilitates the nucleation of 180 domain walls characterized by oppositely polarized 3C atoms, called type-P walls [see Fig. 2(d)]. Locally, the type-P wall resembles a unit cell, consistent with DFT calculations showing a spontaneous transformation of the phase to a -like structure at high Hfi concentration (see Fig. S2). We confirm that Hfi dopants reduce the type-P domain-wall energy (see Fig. S5). Consequently, polarization switching is driven by the motion of a type-P wall, while the other type-P wall is pinned by Hfi dopants. When the external field is turned off, the mobile type-P wall remains stable. After pre-poling, a much lower electric field of 0.8 MV/cm is sufficient to drive the domain-wall motion again.
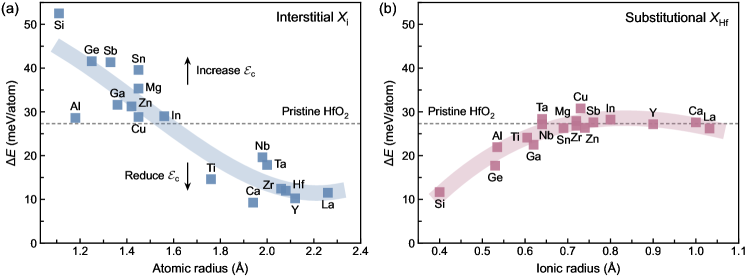
Above results show that the value of , easily accessible through DFT calculations at the unit cell level, can indeed serve as a useful descriptor for . To identify more types of dopants for regulating in ferroelectric HfO2, we perform high-throughput DFT calculations covering diverse dopant atoms, Hf, Zr, Ti, La, Ta, Y, Nb, Sn, Ge, Si, Al, Ga, In, Sb, Mg, Ca, Cu, Zn, with a fixed concentration of 3%. As shown in Fig. 3(a), between the and phases with interstitial dopants () is plotted against the dopant atomic radius, revealing a clear negative correlation. Interstitial dopants with large atomic radii, such as Hf, Zr, and Ti, tend to reduce the , while smaller interstitial atoms such as Si, Ge, and Sn tend to increase , potentially leading to higher .
This negative correlation between and dopant size for interstitial doping contrasts sharply with substitutional doping, where a volcano-like dependence (mostly a positive correlation) of on the ionic radius of the substitutional dopant was observed [11]. We further examine substitutional doping with atom () and plot as a function of the ionic radius of [see Fig.3(b)]. Different from interstitial doping, the of HfO2 under substitutional doping increases with dopant size, consistent with previous DFT results [11]. Notably, only a few small substitutional dopants, like SiHf, effectively lower . This has been attributed to the formation of stable bonds between the substitutional Si dopant and neighboring oxygen atoms in the phase [11].
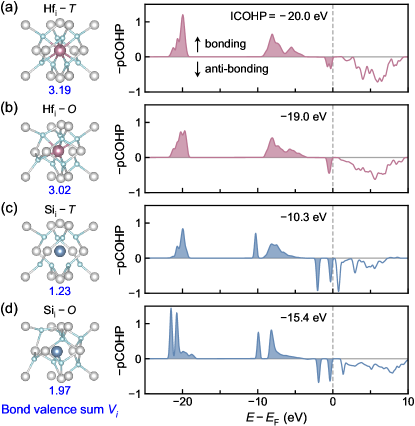
To comprehend the diametrically opposing effects of Hfi and Sii on and , we analyze the bonding of interstitial atoms in the and phases of HfO2. As depicted in Fig. 4, the intercalated atom is surrounded by eight oxygen atoms. We quantify the bonding strength of an interstitial dopant based on the bond-valence conservation principle [38, 39]. According to this principle, each atom has a preferred atomic valence , which is often the nominal oxidation state of the atom (e. g., for Hf). The actual atomic valence, , is obtained by summing the individual bond valence () for bonds between the atom and its neighbors (), . A smaller deviation of from reflects stronger overall bonding strength. The bond valence for each oxygen-dopant pair is calculated as , where is the bond length, and are Brown’s empirical parameters [40]. The calculated for Hfi is 3.19 in the phase and 3.02 in the phase, indicating stronger bonding of Hfi in the phase. This is further supported by the projected COHP analysis. As shown in the right panel of Fig. 4, the total integration of COHP (ICOHP) for HfiO pairs is 20.0 and 19.0 eV in the and phases, respectively. The higher magnitude of ICOHP in the phase confirms stronger bonding between Hfi and oxygen atoms.
The difference between the energy of the and phases containing Hfi ( and ) can be directly related to the differences in the formation energy of Hfi () as follows:
where is the chemical potential of Hf and is the energy of the pristine crystal. The relatively stronger HfiO bonding in the phase suggests a lower formation energy of Hfi than that in the phase () [41], which is responsible for the reduced compared to the undoped value (). In the case of Sii, the pCOHP curve reveals a stronger anti-bonding character, which is corroborated by the small values of . Importantly, both the magnitudes of ICOHP and are larger in the phase than those in the phase. This points to a lower formation energy of Sii in the low-energy phase, which will further increases the energy difference between and phases.
In summary, our investigations combining both zero-Kelvin DFT calculations and large-scale MD simulations at finite temperatures establish the link between interstitial doping and coercive field in ferroelectric HfO2. Unit-cell-level DFT calculations act as a mean-field-like analysis, demonstrating that the coercive field reduction from interstitial Hf doping is due to the lower defect formation energy in the intermediate phase. MD simulations, better representing experimental conditions, suggest that interstitial Hf dopants likely promote switching by forming mobile -like domain walls. With pre-poling, a switching field of 1.0 MV/cm can drive polarization reversal within subnanoseconds. Finally, high-throughput DFT calculations reveal a negative correlation between the switching barrier and the size of the interstitial dopant. The comprehensive understanding of interstitial doping effects in hafnia offers useful guidelines for optimizing the coercive field in this silicon-compatible ferroelectric oxide.
Acknowledgements.
T.Z., L.M. and S.L. acknowledge the supports from National Key R&D Program of China (2021YFA1202100), National Natural Science Foundation of China (12361141821, 12074319), and Westlake Education Foundation. The computational resource is provided by Westlake HPC Center.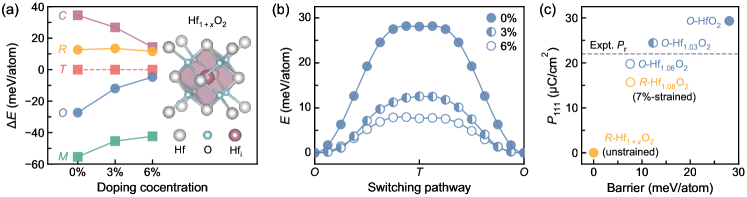
References
- Böscke et al. [2011] T. S. Böscke, J. Müller, D. Bräuhaus, U. Schröder, and U. Böttger, Ferroelectricity in hafnium oxide thin films, Appl. Phys. Lett. 99, 102903 (2011).
- Cheema et al. [2020] S. S. Cheema, D. Kwon, N. Shanker, R. dos Reis, S.-L. Hsu, J. Xiao, H. Zhang, R. Wagner, A. Datar, M. R. McCarter, C. R. Serrao, A. K. Yadav, G. Karbasian, C.-H. Hsu, A. J. Tan, L.-C. Wang, V. Thakare, X. Zhang, A. Mehta, E. Karapetrova, R. V. Chopdekar, P. Shafer, E. Arenholz, C. Hu, R. Proksch, R. Ramesh, J. Ciston, and S. Salahuddin, Enhanced ferroelectricity in ultrathin films grown directly on silicon, Naure 580, 478 (2020).
- Schroeder et al. [2022] U. Schroeder, M. H. Park, T. Mikolajick, and C. S. Hwang, The fundamentals and applications of ferroelectric HfO2, Nat. Rev. Mater. 7, 653 (2022).
- Noheda et al. [2023] B. Noheda, P. Nukala, and M. Acuautla, Lessons from hafnium dioxide-based ferroelectrics, Nat. Mater. 22, 562 (2023).
- Schroeder et al. [2014] U. Schroeder, E. Yurchuk, J. Müller, D. Martin, T. Schenk, P. Polakowski, C. Adelmann, M. I. Popovici, S. V. Kalinin, and T. Mikolajick, Impact of different dopants on the switching properties of ferroelectric hafnium oxide, Jpn. J. Appl. Phys. 53, 08LE02 (2014).
- Wei et al. [2018] Y. Wei, P. Nukala, M. Salverda, S. Matzen, H. J. Zhao, J. Momand, A. S. Everhardt, G. Agnus, G. R. Blake, P. Lecoeur, B. J. Kooi, J. Íñiguez, B. Dkhil, and B. Noheda, A rhombohedral ferroelectric phase in epitaxially strained Hf0.5Zr0.5O2 thin films, Nat. Mater. 17, 1095 (2018).
- Lyu et al. [2019] J. Lyu, I. Fina, R. Solanas, J. Fontcuberta, and F. Sánchez, Growth window of ferroelectric epitaxial Hf0.5Zr0.5O2 thin films, ACS Appl. Electron. Mater. 1, 220 (2019).
- Estandía et al. [2019] S. Estandía, N. Dix, J. Gazquez, I. Fina, J. Lyu, M. F. Chisholm, J. Fontcuberta, and F. Sánchez, Engineering ferroelectric Hf0.5Zr0.5O2 thin films by epitaxial stress, ACS Appl. Electron. Mater. 1, 1449 (2019).
- Song et al. [2020] T. Song, R. Bachelet, G. Saint-Girons, R. Solanas, I. Fina, and F. Sánchez, Epitaxial ferroelectric La-doped Hf0.5Zr0.5O2 thin films, ACS Appl. Electron. Mater. 2, 3221 (2020).
- Qi and Rabe [2020] Y. Qi and K. M. Rabe, Phase competition in with applied electric field from first principles, Phys. Rev. B 102, 214108 (2020).
- Yang et al. [2020] H. Yang, H.-J. Lee, J. Jo, C. H. Kim, and J. H. Lee, Role of Si doping in reducing coercive fields for ferroelectric switching in HfO2, Phys. Rev. Appl. 14, 064012 (2020).
- Wei et al. [2022] W. Wei, G. Zhao, X. Zhan, W. Zhang, P. Sang, Q. Wang, L. Tai, Q. Luo, Y. Li, C. Li, and J. Chen, Switching pathway-dependent strain-effects on the ferroelectric properties and structural deformations in orthorhombic HfO2, J. Appl. Phys. 131, 154101 (2022).
- Zhou et al. [2022] S. Zhou, J. Zhang, and A. M. Rappe, Strain-induced antipolar phase in hafnia stabilizes robust thin-film ferroelectricity, Sci. Adv. 8, eadd5953 (2022).
- Zhao et al. [2024] H. J. Zhao, Y. Fu, L. Yu, Y. Wang, Y. Yang, L. Bellaiche, and Y. Ma, Creating ferroelectricity in monoclinic (HfO2)1/(CeO2)1 superlattices, Phys. Rev. Lett. 132, 256801 (2024).
- Ma et al. [2023] L. Ma, J. Wu, T. Zhu, Y. Huang, Q. Lu, and S. Liu, Ultrahigh oxygen ion mobility in ferroelectric hafnia, Phys. Rev. Lett. 131, 256801 (2023).
- Falkowski et al. [2018] M. Falkowski, C. Künneth, R. Materlik, and A. Kersch, Unexpectedly large energy variations from dopant interactions in ferroelectric HfO2 from high-throughput ab initio calculations, npj Comput. Mater. 4, 73 (2018).
- Wang et al. [2023] Y. Wang, L. Tao, R. Guzman, Q. Luo, W. Zhou, Y. Yang, Y. Wei, Y. Liu, P. Jiang, Y. Chen, S. Lv, Y. Ding, W. Wei, T. Gong, Y. Wang, Q. Liu, S. Du, and M. Liu, A stable rhombohedral phase in ferroelectric Hf(Zr)1+xO2 capacitor with ultralow coercive field, Science 381, 558 (2023).
- Fina and Sánchez [2021] I. Fina and F. Sánchez, Epitaxial ferroelectric HfO2 films: Growth, properties, and devices, ACS Appl. Electron. Mater. 3, 1530 (2021).
- Wei et al. [2023] J. Wei, G. Xu, M. Huang, Y. Wu, W. Li, H. Xiang, and S. Chen, Intrinsic instability of rhombohedral (Hf,Zr)O2 phases and endurance crisis of Hf-based ferroelectric devices, Preprint at Research Square 10.21203/rs.3.rs-2634489/v1 (2023).
- Zhu et al. [2023] T. Zhu, S. Deng, and S. Liu, Epitaxial ferroelectric hafnia stabilized by symmetry constraints, Phys. Rev. B 108, L060102 (2023).
- Qi et al. [2020] Y. Qi, S. Singh, C. Lau, F.-T. Huang, X. Xu, F. J. Walker, C. H. Ahn, S.-W. Cheong, and K. M. Rabe, Stabilization of competing ferroelectric phases of HfO2 under epitaxial strain, Phys. Rev. Lett. 125, 257603 (2020).
- Zhang et al. [2018] L. Zhang, J. Han, H. Wang, R. Car, and W. E, Deep potential molecular dynamics: A scalable model with the accuracy of quantum mechanics, Phys. Rev. Lett. 120, 143001 (2018).
- Kresse and Furthmüller [1996] G. Kresse and J. Furthmüller, Efficient iterative schemes for ab initio total-energy calculations using a plane-wave basis set, Phys. Rev. B 54, 11169 (1996).
- Blöchl [1994] P. E. Blöchl, Projector augmented-wave method, Phys. Rev. B 50, 17953 (1994).
- Kresse and Joubert [1999] G. Kresse and D. Joubert, From ultrasoft pseudopotentials to the projector augmented-wave method, Phys. Rev. B 59, 1758 (1999).
- Perdew et al. [1996] J. P. Perdew, K. Burke, and M. Ernzerhof, Generalized gradient approximation made simple, Phys. Rev. Lett. 77, 3865 (1996).
- Monkhorst and Pack [1976] H. J. Monkhorst and J. D. Pack, Special points for Brillouin-zone integrations, Phys. Rev. B 13, 5188 (1976).
- King-Smith and Vanderbilt [1993] R. D. King-Smith and D. Vanderbilt, Theory of polarization of crystalline solids, Phys. Rev. B 47, 1651 (1993).
- Vanderbilt and King-Smith [1993] D. Vanderbilt and R. D. King-Smith, Electric polarization as a bulk quantity and its relation to surface charge, Phys. Rev. B 48, 4442 (1993).
- Sheppard et al. [2012] D. Sheppard, P. Xiao, W. Chemelewski, D. D. Johnson, and G. Henkelman, A generalized solid-state nudged elastic band method, J. Chem. Phys. 136, 074103 (2012).
- Dronskowski and Bloechl [1993] R. Dronskowski and P. E. Bloechl, Crystal orbital Hamilton populations (COHP): Energy-resolved visualization of chemical bonding in solids based on density-functional calculations, J. Phys. Chem. 97, 8617 (1993).
- Maintz et al. [2016] S. Maintz, V. Deringer, A. Tchougréeff, and R. Dronskowski, Lobster: A tool to extract chemical bonding from plane-wave based DFT, J. Comput. Chem. 37, 1030 (2016).
- Wu et al. [2021] J. Wu, Y. Zhang, L. Zhang, and S. Liu, Deep learning of accurate force field of ferroelectric HfO2, Phys. Rev. B 103, 024108 (2021).
- Wu et al. [2023] J. Wu, J. Yang, L. Ma, L. Zhang, and S. Liu, Modular development of deep potential for complex solid solutions, Phys. Rev. B 107, 144102 (2023).
- [35] Ultrahigh oxygen ion mobility in ferroelectric hafnia, https://nb.bohrium.dp.tech/detail/1034100470.
- Umari and Pasquarello [2002] P. Umari and A. Pasquarello, Ab initio molecular dynamics in a finite homogeneous electric field, Phys. Rev. Lett. 89, 157602 (2002).
- Liu et al. [2016] S. Liu, I. Grinberg, and A. M. Rappe, Intrinsic ferroelectric switching from first principles, Nature 534, 360 (2016).
- Brown [2009] I. D. Brown, Recent developments in the methods and applications of the bond valence model, Chem. Rev. 109, 6858 (2009).
- Liu et al. [2013] S. Liu, I. Grinberg, H. Takenaka, and A. M. Rappe, Reinterpretation of the bond-valence model with bond-order formalism: An improved bond-valence-based interatomic potential for PbTiO3, Phys. Rev. B 88, 104102 (2013).
- Gagné and Hawthorne [2015] O. C. Gagné and F. C. Hawthorne, Comprehensive derivation of bond-valence parameters for ion pairs involving oxygen, Acta Cryst. B71, 562 (2015).
- Wei et al. [2021] J. Wei, L. Jiang, M. Huang, Y. Wu, and S. Chen, Intrinsic defect limit to the growth of orthorhombic HfO2 and (Hf, Zr)O2 with strong ferroelectricity: First-principles insights, Adv. Funct. Mater. 31, 2104913 (2021).
- Wu et al. [2024] J. Wu, J. Yang, Y. Sun, and S. Liu, Low-coercive-field ferroelectric hafnia with mobile domain walls, Preprint at arXiv 10.48550/arXiv.2403.09426 (2024).