\pdfximage

supplement.pdf

In recent years, interfacing two-dimensional (2D) materials with different layers or substrates [1] has revealed fascinating properties that are difficult to achieve with individual layers. For example, interlayer electron-electron interactions, can give rise to diverse phenomena such as moiré excitons [2], superconducting phases [3], and Mott insulating states [4]. Likewise, interlayer electron-phonon interactions can affect the mobilities [5] and superconducting temperatures [6] of 2D materials.

Similarly, recent optical scattering measurements on 2D heterostructures have shed light on the coupling of excitons in one layer with phonons of the adjacent layer [7, 8, 9, 10, 11, 12]. This remarkable interlayer exciton-phonon coupling was first demonstrated in monolayer WSe₂ encapsulated in hexagonal boron nitride ($h$BN) using Raman spectroscopy [7]. Subsequent Raman and photoluminescence measurements have confirmed its existence in various other heterostructures [12, 9, 13, 14]. This interlayer exciton-phonon coupling can play a key role in exciton lifetimes and decoherence times [15], and the study of phonon polaritons in neighbouring layers [16].

Albeit the experimental evidence for interlayer exciton-phonon coupling, the microscopic mechanism responsible for this phenomenon still remains a mystery. In this Letter, we use WSe₂@$h$BN as an example to unveil the microscopic mechanism of exciton-phonon coupling across layers. Using ab initio methods, we compute resonant Raman intensities, which provide a detailed atomistic view of the interlayer exciton-phonon scattering process. We demonstrate the selection rules in interlayer exciton-phonon scattering, which are responsible for the anomalous resonant Raman intensities: when in resonance with the A exciton of WSe₂, the out-of-plane $h$BN phonon mode (which is Raman forbidden in pure $h$BN) exhibits a much higher intensity in the heterostructure than the Raman-allowed in-plane mode [7]. Our main findings reveal that the deformation potential of the $h$BN phonon scatters the hybridized part of the WSe₂ exciton-hole in the vicinity of the $h$BN layer, giving rise to interlayer exciton-phonon coupling. We show that this coupling is extremely sensitive to the interlayer distance and bond polarity of the phonon layer and is not required at all to observe this effect [9, 10, 11, 12].

We start our discussion by looking at the resonant Raman scattering in a monolayer WSe₂@$h$BN heterostructure. We follow Refs. [17, 18] and calculate the differential cross section for Stokes Raman scattering mediated by one phonon:

$$\frac{\mathrm{d}\sigma}{\mathrm{d}\Omega}\propto\frac{\omega_{\mathrm{L}}-\omega_{\lambda}}{\omega_{\mathrm{L}}}|\mathcal{M}_{\mu\nu}^{\lambda}(\omega_{L},\omega_{\lambda})|^{2}.$$

(1)

Here, $\mu$ and $\nu$ denote the polarization of the incoming and outgoing light, respectively, while $\omega_{\mathrm{L}}$ and $\omega_{\lambda}$ denote the frequencies of the incoming light and the created phonon of branch $\lambda$, respectively. Within the Tamm-Dancoff approximation [19], the Raman scattering matrix element $\mathcal{M}^{\lambda}_{\mu\nu}$ takes on the simple form

$$\begin{split}\mathcal{M}_{\mu\nu}^{\lambda}\left(\omega_{L},\omega_{\lambda}\right)=\sum_{S,S^{\prime}}\frac{\left(d^{\nu}_{S^{\prime}}\right)^{*}(g_{SS^{\prime}}^{\lambda})^{*}d_{S}^{\mu}}{\left(\hbar\omega_{\mathrm{L}}-E_{S}+i\gamma\right)\left(\hbar\omega_{\mathrm{L}}-\hbar\omega_{\lambda}-E_{S^{\prime}}+i\gamma\right)}\\ +\sum_{S,S^{\prime}}\frac{\left(d_{S}^{\mu}\right)^{*}g_{SS^{\prime}}^{\lambda}d^{\nu}_{S^{\prime}}}{\left(\hbar\omega_{\mathrm{L}}+E_{S}-i\gamma\right)\left(\hbar\omega_{\mathrm{L}}-\hbar\omega_{\lambda}+E_{S^{\prime}}-i\gamma\right)}.\end{split}$$

(2)

The sums run over all excitonic states $S$ and $S^{\prime}$ with energies $E_{S{(\prime)}}$ and decay constant $\gamma$. The quantity $d^{\mu}_{S}$ is the coupling matrix element between an exciton $S$ and a photon of polarization $\mu$, while $(g^{\lambda}_{SS^{\prime}})^{*}$ represents the exciton-phonon coupling matrix element related to the scattering of an exciton $S$ to an exciton $S^{\prime}$ via emission of one phonon of branch $\lambda$ [18]. We obtain all needed quantities for an evaluation of Eq. 2 for a hetereostructure of one layer hBN and one layer of WSe₂ from first principles using the GW-BSE [20, 21] formalism on top of density functional theory (see supplementary information (SM) [22] for details of the ab initio methods [23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37]).

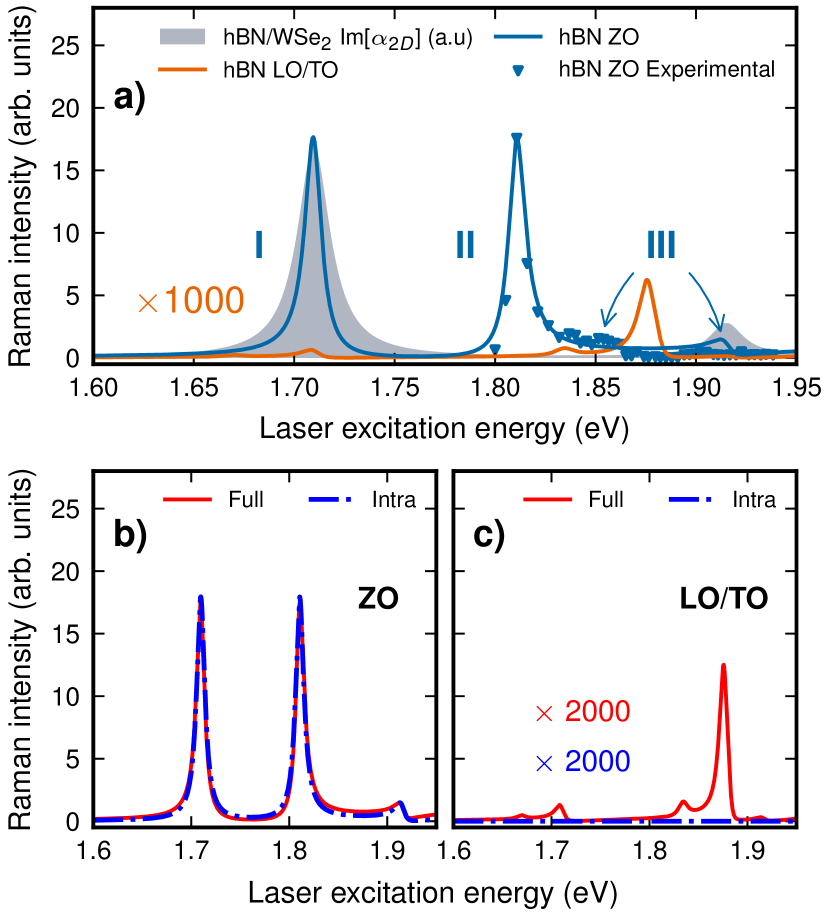
In Fig. 1a, we show the calculated, phonon branch-dependent Raman intensities, as a function of the energy of the incoming photon. The blue line denotes the Raman intensity for the out-of-plane optical (ZO) phonon of the hBN layer. We compare the Raman intensity profiles to the imaginary part of the in-plane polarizability (absorption coefficient) of the heterostructure (shaded area) and to experimental Raman intensities from McDonnell et al. [38](blue triangles, see SM [22] for further details). The most striking features of the ZO-mode intensity profile are the two strong resonances at $\omega_{\mathrm{L}}\approx 1.72$ eV and $\omega_{\mathrm{L}}\approx 1.82$ eV, labeled “I” and “II” in Fig. 1a. The first of these two peaks coincides with a resonance in the absorption coefficient which corresponds to the well-known $1s$ state of the “A”-exciton [39] of WSe₂ and can thus be interpreted as the resonant excitation of the $1s$ A-exciton in WSe₂, which then couples to the $h$BN ZO mode. The second peak, in contrast, has no such counterpart in the absorption spectrum. It is the quantum of one ZO mode away from the first resonance peak and corresponds to the resonant recombination of the $1s$ exciton under phonon emission (when $\omega_{\mathrm{L}}=E_{1s}+\omega_{\mathrm{ZO}}$), compare Eq. (2). Finally, Peak III coincides with the $2s$-A-exciton of the absorption coefficient and is due to the resonant excitation of the $2s$ state. The results of our calculation match the the experimental data of McDonnell et al. [38] well in terms of the local peak intensities. We note that the $2s$ exciton is blue-shifted in our calculation with respect to experiment, as we consider a heterostructure of one layer WSe₂ on top of one layer of $h$BN vs. a system of monolayer WSe₂ sandwiched in bulk $h$BN in experiment (where screening is stronger and, thus, the energy difference between $1s$ and $2s$ excitons reduced) [39].

Compared to the ZO mode of $h$BN, its in-plane LO/TO mode displays a Raman intensity three orders of magnitude lower, yet with a qualitatively similar resonance structure as a function of $\omega_{\mathrm{L}}$. This remarkable, anomalous behavior of two different allowed phonon modes coupling so differently when the incident light is in resonance with a neighboring layer has been reported in Ref. [7], which provided a speculative interpretation of the underlying Raman scattering process. Using our atomistic first-principles approach, we can now scrutinize the Raman scattering pathways and understand them in terms of symmetry and involved scattering events.

From Eq. (2), it is clear that any contributing scattering pathway must feature non-zero optical matrix elements $d^{\mu}_{S}$ and $d^{\nu}_{S^{\prime}}$ as well as a non-vanishing exciton-phonon coupling matrix element $g^{\lambda}_{S,S^{\prime}}$. In order to infer the corresponding selection rules, we note that the underlying $C_{3}$ point group symmetry of the $h$BN@WSe₂ heterostructure allows the classification of zero-momentum phonons and excitons by their total angular momentum component in the out-of-plane direction, with corresponding quantum number $m=+1$, 0, or -1. A finite optical strength $d^{\mu}_{S}$ for light polarized parallel to the heterostructure is only possible for excitons $S$ with $m_{S}=\pm 1$. Meanwhile, the exciton-phonon matrix elements $g^{\lambda}_{S,S^{\prime}}$ are non-zero only if total angular momentum (modulo 3) is conserved (see SM [22] for derivation):

$$m_{S}-m_{S^{\prime}}-m_{\lambda}\equiv 0\text{ (mod 3)}.$$

(3)

For the ZO-phonon ($m_{\mathrm{ZO}}=0$), this implies that active scattering pathways necessarily have $m_{S}=m_{S^{\prime}}$. By contrast, for the LO/TO-phonon ($m_{\mathrm{LO/TO}}=\pm 1$), we need to have $m_{S}=m_{S^{\prime}}\pm 1$ (mod 3).

The combination of the optical and phonon-specific selection rules allows us then to understand the nature of the resonance features I, II, and III in Fig. 1a. As the $1s$ exciton of WSe₂ is the only optically active low-energy exciton available, resonance I and II are associated with the scattering process $1s\to 1s$, which gives rise to resonances for both the incoming (I) and the outgoing (II) light. However, while this resonance structure is seen in both the ZO and the LO/TO mode, the latter is three orders of magnitude less intense, although formerly allowed by symmetry. To understand this enormous difference between the phonon modes, we first note that the $1s$ exciton of WSe₂ is in fact doubly degenerate due to time reversal symmetry [40]. The two members of the doublet are localized at different, inequivalent corners K and K’ of the first Brillouin zone and carry opposite total angular momentum $m_{1s,K^{(\prime)}}=+(-)1$. For the ZO mode, this implies that $1s\to 1s$ scattering is allowed within a valley (intra-valley scattering), while for the LO/TO mode with finite angular momentum, $1s\to 1s$ scattering is only allowed between $1s$ states in opposite valleys (inter-valley scattering). However, due to the strong localization of the $1s$-exciton wave function in momentum space (see Fig. S4 of SM [22]), there is only a miniscule overlap between wave functions centered in different valleys and, as a result, the inter-valley scattering required for the LO/TO mode is strongly suppressed and so is consequently the Raman intensity.

In order to substantiate this, we re-calculate the Raman intensities by considering only intra-exciton scattering channels, i.e., by restricting the double sum in Eq. (2) to $S=S^{\prime}$. As shown in Fig. 1b and c, we can indeed numerically confirm that intra-exciton scattering is absent for the LO/TO mode while being the dominant scattering process for the ZO mode. In terms of the three most prominent resonances in the ZO mode Raman intensities, we can thus conclude that resonances I and II stem from $1s$-to-$1s$ intra-valley exciton scattering and III from $2s$-to-$2s$ intra-valley scattering. We note that this finding is in contrast to previous assumptions [7] that identified peaks II and III to the two resonances associated with the inter-exciton scattering process $1s\to 2s$. For the LO/TO mode, however, we can confirm that intra-valley scattering plays no role and that the suppressed finite Raman intensity around the $1s$ exciton can only stem from weak inter-exciton scattering.

While these symmetry considerations explain the difference between Raman intensities of the LO/TO- and the ZO-mode, a complimentary analysis is required to understand the precise mechanism for the interlayer exciton-phonon coupling. In order to elucidate the microscopic mechanism, we consider the $1s\to 1s$ scattering pathway for the ZO mode, which is the dominant Raman scattering channel in the region $\omega_{\mathrm{L}}\lesssim$1.8 eV. The $1s$ exciton is mostly composed of one conduction and one valence band state [22], therefore we can approximate the $1s\to 1s$ exciton-phonon matrix element as (see SM [22] for details)

$$g_{1s,1s}^{\mathrm{ZO}}\approx\sum_{\mathbf{k}}\left|A^{1s}_{\mathbf{k}cv}\right|^{2}\left(g^{ZO}_{\mathbf{k}c}-g^{ZO}_{\mathbf{k}v}\right),$$

(4)

where $A^{1s}_{\mathbf{k}cv}$ is the exciton envelope wave function for the single-electron transition $|\mathbf{k},v\rangle\to|\mathbf{k},c\rangle$. The diagonal electron-phonon matrix elements $g^{\mathrm{ZO}}_{\mathbf{k}n}$ for a single-electron state $|\mathbf{k}n\rangle$ within the framework of DFT are given by [41]

$$g^{\mathrm{ZO}}_{\mathbf{k}n}=\int\mathrm{d}^{3}\mathbf{r}\,|\psi_{\mathbf{k}n}(\mathbf{r})|^{2}\partial_{{}_{\mathrm{ZO}}}V_{\text{KS}}(\mathbf{r}).$$

(5)

Here, $\psi_{\mathbf{k}n}(\mathbf{r})$ denotes the one-electron wave function for state $|\mathbf{k}n\rangle$, $V_{\mathrm{KS}}(\mathbf{r})$ corresponds to the total self-consistent Kohn-Sham (KS) potential, and $\partial_{\mathrm{ZO}}$ represents the directional derivative along the ZO phonon mode displacement vector [41]. Combining Eqs. (4) and (5), we obtain

$$g_{1s,1s}^{\mathrm{ZO}}\approx\int\mathrm{d}^{3}\mathbf{r}\,\left[n^{1s}_{c}(\mathbf{r})-n^{1s}_{v}(\mathbf{r})\right]\partial_{{}_{\mathrm{ZO}}}V_{\mathrm{KS}}(\mathbf{r}),$$

(6)

where $n^{1s}_{c(v)}(\mathbf{r})=\sum_{\mathbf{k},v(c)}|A^{1s}_{\mathbf{k}cv}|^{2}|\psi_{\mathbf{k}c(v)}(\mathbf{r})|^{2}$ denotes an “exciton-averaged” electron ($c$) or hole ($v$) density for the $1s$ exciton.

Previous studies [9, 10, 11, 12] have suggested that the polar nature of the ZO phonon is responsible for the origin of the interlayer exciton-phonon coupling. In order to verify this claim, we separate the total perturbed potential in Eq. (6) into macroscopic and microscopic components [42]: $\partial_{{}_{\mathrm{ZO}}}V_{\mathrm{KS}}(\mathbf{r})=\partial_{{}_{\mathrm{ZO}}}V_{\mathrm{micro}}(\mathbf{r})+\partial_{{}_{\mathrm{ZO}}}V_{\mathrm{macro}}(\mathbf{r})$. The macroscopic part is the dipole field resulting from the polar nature of $h$BN, i.e., from its Born effective charges, and in the literature is often referred to as the Fröhlich field [42]. The microscopic part of the perturbed potential is then calculated by subtracting the macroscopic part from the total perturbed potential.

In Figure 2, we illustrate the different components of the $1s\to 1s$ exciton-phonon matrix element, as described by Eq. (6). We plot the in-plane average of the change in KS potential (divided into microscopic and macroscopic part) and the integrated electron and hole densities as a function of the out-of-plane spatial coordinate ($z$). We distinguish between the region close to the $h$BN layer, the near field (grey shading), and the remaining area, the far field.

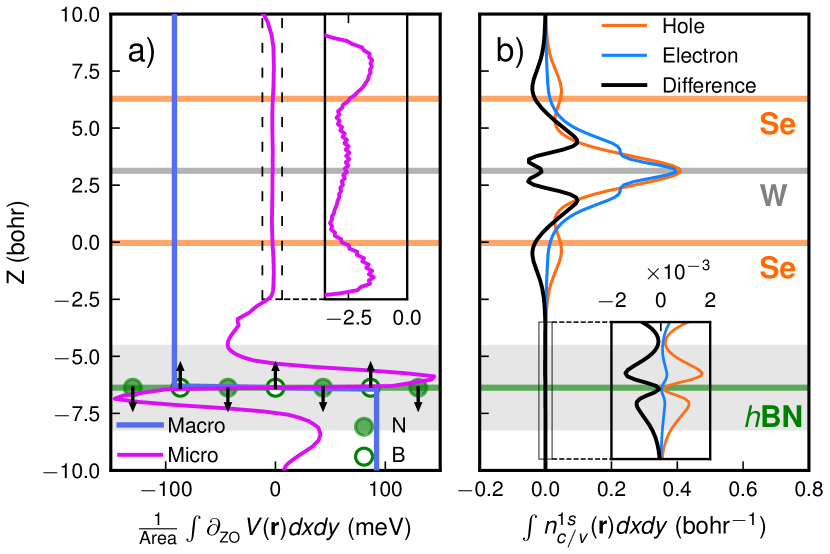
Figure 2a shows the in-plane average of the microscopic (magenta line) and macroscopic (blue line) components of the total field (refer to SM [22] for computational details). The macroscopic component attains a constant value on both sides of the $h$BN layer and extends entirely along the out-of-plane direction, resembling the field generated by a uniformly charged plate. Conversely, the microscopic component vanishes asymptotically due to the charge neutrality of the system. Interestingly, the microscopic part exhibits two prominent features: (i) a large and rapidly varying part in the near field, and (ii) a tiny part in the far field that is localized within the WSe₂ layer, as depicted in the inset of Fig. 2b. The former arises from the change in lattice potential due to the displacement of nuclei and the induced field of the $h$BN electron density; the latter is due to the induced field generated by the WSe₂ electron density [41].

The different components of the total field are felt by the $1s$ exciton charge density of the WSe₂ layer. In Fig. 2b, we depict the in-plane integrated electron and hole densities ($n^{1s}_{c/v}(\mathbf{r})$) of the $1s$ exciton. Both the electron and hole densities of the $1s$ exciton are mostly made up of tungsten $d$ orbitals [43]. However, while the electron density of the $1s$ exciton is completely localized within the WSe₂ layer, the hole density also has a small, but finite component in the $h$BN layer (see inset of Fig. 2c). This component corresponds to the hybridization of the $p_{z}$ orbitals of the $h$BN layer with the $d$ orbitals of the WSe₂ layer, i.e., to the weak chemical bond between the two layers. It is noteworthy that the hybridization only occurs for the valence, i.e., bonding orbitals, and not for the conduction band orbitals, owing to the favourable or unfavorable band alignment between the $h$BN and WSe₂ valence and conduction bands, respectively. This hybridization has been experimentally observed and reported in Ref. [44].

Finally, we consider the interaction of the electron and hole densities of the $1s$ exciton with the total field to gain atomistic insight on the exciton-phonon interaction across layers. The $1s\rightarrow 1s$ exciton-phonon matrix element can a priori receive contributions from three different channels: (i) the constant, macroscopic part interacting with the electron and hole densities over all space (ii) the large near field interacting with the small hybridized hole density in the near-field, and (iii) The small far field in the WSe₂ layer interacting with the large electron and hole densities.

To quantify the contribution of each channel to the overall exciton-phonon interaction, we define the cumulative work $W(z)$ along the z axis for a field $\partial V(\mathbf{r})$ as

$$W(z)=\int_{-\infty}^{z}\mathrm{d}^{3}\mathbf{r}\,\big{(}n^{1s}_{c}(\mathbf{r})-n^{1s}_{v}(\mathbf{r})\big{)}(\partial V(\mathbf{r})-\partial V(\mathbf{r}\rightarrow\infty)).$$

(7)

The cumulative work for the total field asymptotically reaches the diagonal exciton-phonon matrix of the $1s$ exciton as given in Eq. 6.

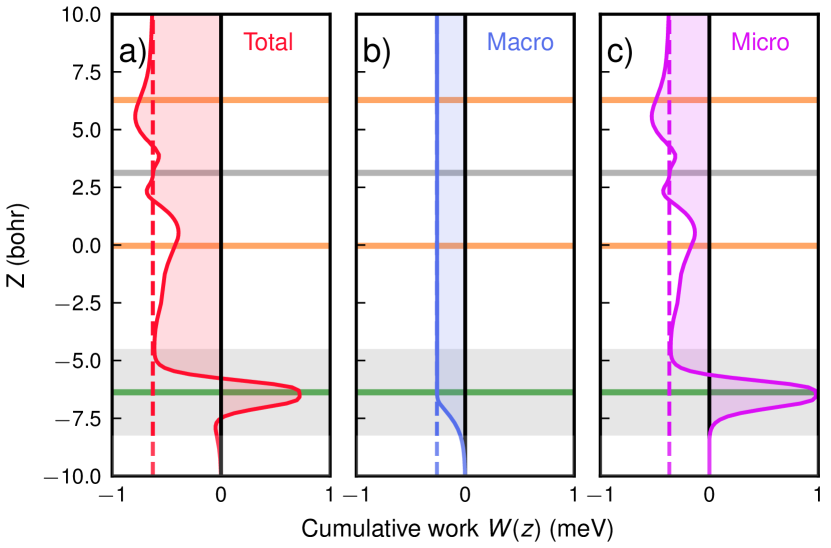
In Fig. 3, we depict the cumulative work done by the total field and its constituents, denoting their asymptotic values with dashed, vertical lines. The cumulative work for all component fields starts from zero and reaches the asymptotic value by the end of the near-field volume. This implies that the coupling of the $1s$ exciton to the ZO phonon arises almost entirely from the electric fields in the near-field region and their interaction with the hybridized part of the charge density of the $1s$ exciton. Given that only the hole of the $1s$ exciton hybridizes with the $h$BN orbitals, the $1s\rightarrow 1s$ exciton-phonon scattering can be interpreted as being primarily due to the scattering of the hole by the ZO phonon.

We further examine the contributions of each individual field to the total exciton-phonon coupling by considering the cumulative work of the macroscopic and microscopic components separately. Although the macroscopic part interacts with the entire electron and hole densities, the cumulative work reaches its asymptotic value already at the interface of the $h$BN layer and the region around the WSe₂ layer does not yield a net contribution. Given that the macroscopic component is nearly constant, the work done by the electron and by the hole compensate each other almost perfectly, as a consequence of the exciton being a charge neutral excitation. However, the macroscopic part does contribute a finite amount of work to the exciton-phonon coupling through its interaction with the hybridized part of the hole density. Due to the local horizontal mirror symmetry of the ZO phonon, the macroscopic part flips its sign at the $h$BN layer and consequently does a finite amount of work to the hole (Fig. 3a and b).

At the same time, due to lowering of symmetry in the heterostructure, the hybridized hole density around the $h$BN layer is not mirror symmetric with respect to the $h$BN plane. In combination with the large microscopic field, this asymmetry leads to a finite amount of work in the near-field region, see Fig. 3c. By contrast, in the far-field regime, the electron and hole distribution are mirror symmetric with respect to the W-layer and in consequence, the net work done by the ZO mode to the exciton cancels out.

It is worthwhile to stress that, unlike the interlayer electron-phonon coupling, which is very strong and is predominantly caused by the macroscopic component in the far-field region [45], the interlayer exciton-phonon coupling is much weaker and originates in the near-field region, with nearly equal contributions coming from both macroscopic and microscopic components. Remarkably, exciton-phonon scattering takes place even in the absence of the macroscopic component. This implies that bond polarity is not a prerequisite for the occurrence of the interlayer exciton-phonon scattering, contrary to current speculations [9, 10, 11, 12], which hypothesized a macroscopic dipole-dipole coupling mechanism. Furthermore, in Fig. S5 of the SM [22], we show that the Raman intensities decreases rapidly with increasing inter-layer distance, as observed experimentally in Ref. [8], confirming the near-field effect of this phenomenon.

In summary, we theoretically and computationally investigated the coupling of excitons and phonons across layers and its signature in resonant Raman scattering. Using symmetries, we identified the main exciton-phonon scattering channel in the Raman process of a prototypical WSe₂@$h$BN heterostructures. We find that the exciton-phonon coupling is due to the scattering of the hybridized part of the WSe₂ exciton hole with the deformation potential of the $h$BN phonon. This finding sheds light on the nature of the exciton-phonon coupling, which previously was hypothesized to be due to a macroscopic, polar dipole-dipole interaction, but which we find to actually be a near-field effect. This understanding of the interlayer exciton-phonon coupling in two-dimensional heterostructures can be a valuable guide for tailoring inter-layer interactions in such systems.

Acknowledgements– We acknowledge the use of the HPC facilities of the University of Luxembourg [46]. S.R. acknowledges funding from the National Research Fund (FNR) Luxembourg, project C20/MS/14802965/RESRAMAN. L.W. acknowledges funding by the FNR through project C22/MS/17415967/ExcPhon. We thank Aseem Rajan Kshirsagar and Henry Fried for helpful discussions.

\foreach\x

in 1,…,0 See pages \x, of supplement.pdf