Orbital Selective Superconductivity in a Two-band Model of Infinite-Layer Nickelates
Abstract
In the present study, we explore superconductivity in NdNiO2 and LaNiO2 employing a first-principles derived low-energy model Hamiltonian, consisting of two orbitals: Ni -, and an axial orbital. The axial orbital is constructed out of Nd/La , Ni 3- and Ni characters. Calculation of the superconducting pairing symmetry and pairing eigenvalue of the spin-fluctuation mediated pairing interaction underlines the crucial role of inter-orbital Hubbard interaction in superconductivity, which turns out to be orbital-selective. The axial orbital brings in materials dependence in the problem, making NdNiO2 different from LaNiO2, thereby controlling the inter-orbital Hubbard interaction assisted superconductivity.
Introduction.– The discovery of high Tc superconductivity in cuprate family,cuprate has kept the researchers busy over the last two decades or so, in understanding the mechanism of its superconductivity. While the mechanism of superconductivity in cuprates still remains debated, attempt has been made in search of superconductivity in transition-metal oxides other than cuprates. Nickelates, Ni being neighboring element to Cu, turns out to be most promising in this respect. Towards this goal, a number of attempts has been made. For example, LaAlO3/LaNiO3 superlatticelao-lno with theoretically predicted singly occupied Ni - band,oka ; millis bilayer and trilayer reduced La3Ni2O6 and La4Ni3O8martha ; tsd ; pickett-multi have been studied. Unfortunately, experimental realization of superconductivity in these systems remained elusive. In this connection, stabilization of unusual Ni1+ valence in LaNiO2 and NdNiO2, having the same 3d9 configuration as Cu2+ in cuprates, in the isostructural infinite-layer CaCuO2 structure,lno ; nno therefore generated interest. Recent reporthwang of superconductivity in 20 Sr doped NdNiO2 with Tc of 9-15 K has reignited this interest with reports of several theoretical studies aoki ; rony ; millis-nno ; karsten ; JiangDFT ; GuDFT ; AritaDFT ; pickett ; Devereaux ; Changdwave ; ZhangKondo ; Vishwanath ; SavrasovDMFT devoted to understand this.
The most sought after issue, in this respect, has been whether Nd/LaNiO2 (N/LNO) can be described within the same theoretical framework as cuprates. It is noteworthy that while the undoped cuprates are antiferromagnetic with strong insulating properties,cuprate-afm undoped N/LNO is reported to be nonmagnetic with bad metallic properties.lno ; hwang Comparing the electronic structure with that of cuprates, the most obvious difference is the large O 2 - Ni 3 charge transfer energy for Ni1+ compared to small O 2- Cu 3 charge transfer energy for Cu2+, resulting in a significantly weaker hybridization with O 2 compared to cuprates. This fact has been evidenced in electronic structure calculationsmillis-nno ; pickett as well as in terms of the absence of pre-peak in x-ray absorption spectroscopy (XAS) near the O K-edge.sawatzky This also provides justification for weak super-exchange in NNO compared to strong antiferromagnetism in undoped cuprates, the super exchange energy scale being estimated to be a factor of 10 smaller compared to cuprates.J-scale The large charge transfer energy puts the Ni 3 levels higher up in energy compared to Cu 3, which facilitates their hybridization with usually empty Nd/La bands. While the hybridization of in-plane Ni - with out-of-plane Nd/La orbitals is negligible, they can hybridize via the Ni - and Ni .pickett ; SIT This creates two three-dimensional (3D) Fermi surface (FS) pockets in N/LNO, one centered around and another around A point of the 3D BZ.rony ; pickett The Nd/La-Ni hybridization has been signaled in additional low energy shoulder features in XAS and resonant inelastic x-ray scattering (RIXS) spectra of N/LNO.sawatzky Fitting of the XAS and RIXS spectra, through exact diagonalization calculation produced a mixing from rare-earths as large as 44 .sawatzky Thus while in case of cuprates, the intercalated non-copper-oxide layers act as spectators, playing the role of simple “charge reservoir”, in case of N/LNO the rare-earth layer may provide active electronic degrees of freedom. This prompted Hepting et al.sawatzky to suggest a two-band model, consisting of a 3D rare-earth band coupled to a Ni -y2 derived 2D Mott system. Interestingly, a more recent report shows a sign reversal of Hall resistivity with doping and temperature,hwang-new which may further evince the two band scenario.
Given this background, a natural question would be, can doped carriers give rise to superconductivity in such a two-band model description of NNO and LNO, and if so, is there any difference between NNO and LNO. This, to the best of our knowledge, has remained unexplored so far, though superconductivity in nickelates has been explored within the framework of one-band, and three-band model with onsite correlations,rony one band Hubbard model,karsten and multi-band Ni - Nd Hubbard model within fluctuation-exchange approximation,aoki as well as from strong coupling starting points.Vishwanath ; Changdwave ; ZhangKondo
In the present study, we first construct a two-band model, starting from the self-consistent-field density functional theory (DFT) and by retaining Ni - and Ni orbitals in the basis, and downfolding the rest. Here, our main finding is that the Ni basis forms an axial orbital, resulting from the hybridization of Nd/La 3-, Nd/La , Ni 3- and Ni . Moreover, while the downfolded Ni-- Wannier orbital is very similar in the La and Nd compounds, the detailed nature of the axial orbital set these two materials apart, giving clue to its possible role on the materials dependent superconductivity.
We next solve the pairing eigenvalue and pairing eigenfunctions of the spin-fluctuation mediated pairing interaction, computed within the DFT-derived two Wannier orbital Hubbard model. We find that (i) in the Nd compound, the superconducting (SC) coupling constant grows almost exponentially with the inter-orbital interaction , while the intra-orbital interactions alone is not conducive for superconductivity. In a crude analogy with the renormalization theory, we can say that intra-orbital interactions are ‘marginal’ do not directly mediate superconductivity, while the inter-orbital interaction is a ‘relevant’ parameter for superconductivity. (ii) Secondly, in NNO, we find that the pairing eigenfunction turns out to be orbital selective: being a 2D --type for the Ni orbital, and a 3D 3--type symmetry for the axial orbital. The results are consistent with the corresponding orbital weight distributions on the 3D FS topology, and the corresponding FS features. The same study in LNO results in a single - wave pairing symmetry, but with SC coupling constant significantly smaller than that of NNO. Our findings emphasize the importance of axial orbital and a two-band model in which orbital selective pairing symmetry is augmented by the inter-orbital interaction.
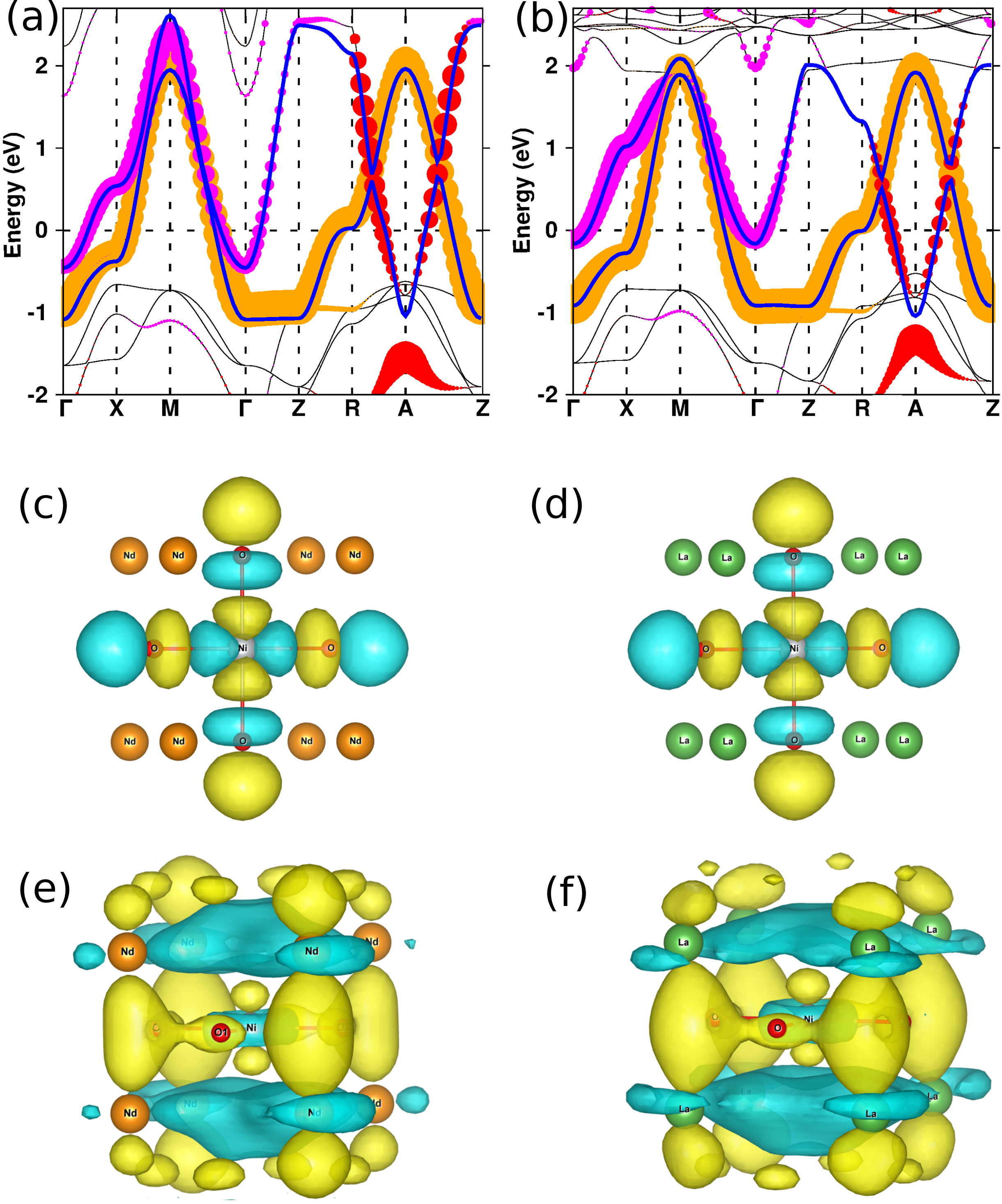
DFT band-structure and two-band model.– The DFT band structure is computed in plane wave basis, as implemented in Vienna Ab-initio Simulation Package (VASP)vasp with projected augmented wave (PAW) potentialpaw and choice of generalized gradient approximationpbe (GGA) for exchange-correlation functional. For details of the calculation, see supplementary materials (SM).suppl The resuts for undoped N/LNO is shown in Fig. 1(a)-(b). The band structure of N/LNO, which is well studied in literature,rony ; pickett ; arita ; botana primarily consists of O-2 dominated bands ranging from about -8 eV to about -3 eV, Ni-3 dominated bands ranging from about -3 eV to 2 eV, and Nd/La-5 dominated bands ranging from about -1 eV to 8 eV. The low-energy electronic structure has two bands crossing the Fermi level: one canonical Ni - band creating a hole pocket centered around M (A) point, bearing strong resemblance with cuprates, and the other one is derived out of Nd/La mixed with Ni characters creating electron pockets at and A points. While the generic features are found to be similar in the band structures of NNO [(a)] and LNO [(b)], there are subtle differences. Comparing the Ni - bands in the two compounds, while it extends from -1.1 eV to 2 eV for NNO, it extends from -0.9 eV to about 2 eV for LNO, making the band width of Ni - in LNO band smaller by about 0.2 eV as compared to NNO. The corresponding dispersion is also smaller for LNO compared to NNO. The saddle point at R is positioned about 0.2 eV higher compared to that at X in LNO, whereas R saddle point is about 0.5 eV higher compared to that at X for NNO. This dispersion highlights the mixing with the axial orbital, making the Ni - band deviating from its 2D nature, as emphasized by Lee and Pickett.pickett Comparing the second band, we find that firstly the Nd -Ni derived electron pocket centered around is about -0.4 eV lower in energy in NNO as compared to LNO, making the self-doping effect more pronounced in the Nd compound compared to the La compound. Secondly, the width of the second band is about 1 eV smaller in LNO compared to NNO.
These subtle but important material-specific differences of the electronic structure of nickelate compounds get reflected in Wannier functionsWAN defining the downfolded two-band structure, designed to reproduce the two low energy bands of the DFT band structure. In order to construct the low energy two-band structure, we retain Ni - and Ni degrees of freedom, and downfold the rest. This choice is guided by the four band model of cuprates,our ; our1 consisting of Cu , Cu -, O and O , the material dependence being included in the Cu in downfolded basis, which forms the axial orbital by combining Cu , Cu 3-, apical oxygen and orbitals of farther axial cations. In the present case, we downfold O and O , as the larger charge transfer energy between Nd and O in nickelates, compared to cuprates, makes their mixing with - much smaller than in cuprates. The resultant Wannier functions corresponding to downfolded two-band structure are shown in Fig. 1(c)-(f) for N/LNO. The - Wannier function which forms antibonding combination [(c)-(d)] is found to be identical between Nd and La compounds. We note that the -like tail of - Wannier functions sitting at O sites show asymmetry between the positive and negative lobes, which signifies the mixing with diffuse Ni . The material dependence, however, shows up in the Wannier function which forms the axial orbital [(e)-(f)]. We find this axial orbital is a hybrid between Ni , Ni 3 - , Nd/La 3 - and Nd/La . Inspecting this orbital, we find that starting from the central Ni atom, Ni 3 - which bonds to Ni , and antibonds to O , bonds strongly with predominant feature of Nd/La 3 - and , highlighting the hybridization between Ni and Nd/La . We find that the Ni 3 - /Ni character is more in La compound [(f)] compared to Nd compound [(e)], while Nd 3 - /Nd character is less in La compound compared to Nd compound. This makes the axial orbital much more cylindrical in NNO [(e)] and more spherical in LNO [(f)]. This differential nature of the axial orbital is reflected in both in-plane and out-of-plane hopping interactions within the two-band description (see SM) as well as the energy of the axial orbital () measured from energy of - () lying 0.25 eV higher in NNO compared to that in LNO. The in-plane hopping is found to be 30-20 larger in NNO compared to LNO. The out-plane hopping, especially the hopping connecting axial orbital to axial orbital show significantly larger values for NNO compared to LNO (1.2 to 7 times), accounting for about 1 eV larger band width of the axial band in NNO compared to LNO.
Calculation of superconducting properties.– In analogy with cuprates,SCcuprates pnictides,SCpnictides and heavy-fermion superconductors,SCHF we assume superconductivity in the present compound is spin-fluctuation mediated. The estimated electron-phonon interaction turns out to be too small to support observed Tc.arita Based on a two-band Hubbard model, we obtain the pairing potential by considering the bubble and ladder diagrams:SCcuprates ; SCpnictides ; SCHF ; SCrepulsive
| (1) |
The symbol ‘tilde’ denotes a tensor in the orbital basis. The subscripts ‘s’ and ‘c’ denote spin and charge fluctuation channels, respectively. are the onsite interaction tensors for spin and charge fluctuations, respectively whose non-vanishing components are for intra-orbital - and axial, and the inter-orbital component is ( are orbital indices).footnote1 are the spin and charge density-density correlation functions (tensors in the same orbital basis), computed within the random-phase-approximation (RPA). The details of the formalism is given in SM.suppl Application of a weak coupling theory may be justified by the fact that exchange-scale in nickelates are smaller than cuprates.
We compute the eigenvalue and eigenfunctions of the pairing interaction on the 3D Fermi momenta, by solving the following equation:
| (2) |
Here , denote band indices, and is the pairing interaction, projected onto the band basis. is the pairing eigenvalue (proportional to the SC coupling strength), and is the corresponding pairing eigenfunction. Since the pairing potential is repulsive here, the highest positive eigenvalue , and the corresponding pairing symmetry can be shown to govern the lowest Free energy value in the SC state.SCrepulsive
The origin of the unconventional pairing symmetry, and the role of FS nesting can be understood as follows. For and in Eq. 2, the pairing symmetry must change sign over the FS to compensate for the negative sign in the left hand side of Eq. 2. changes sign between the two -points, and either between different or same bands which are connected by the momentum at which acquires strong peaks. The locii of the peaks in are primarily dictated by the FS nesting, while the overall amplitude is determined by and . We fix the hole doping level at , which is about the optimal doping for NNO.hwang ; hwang-new
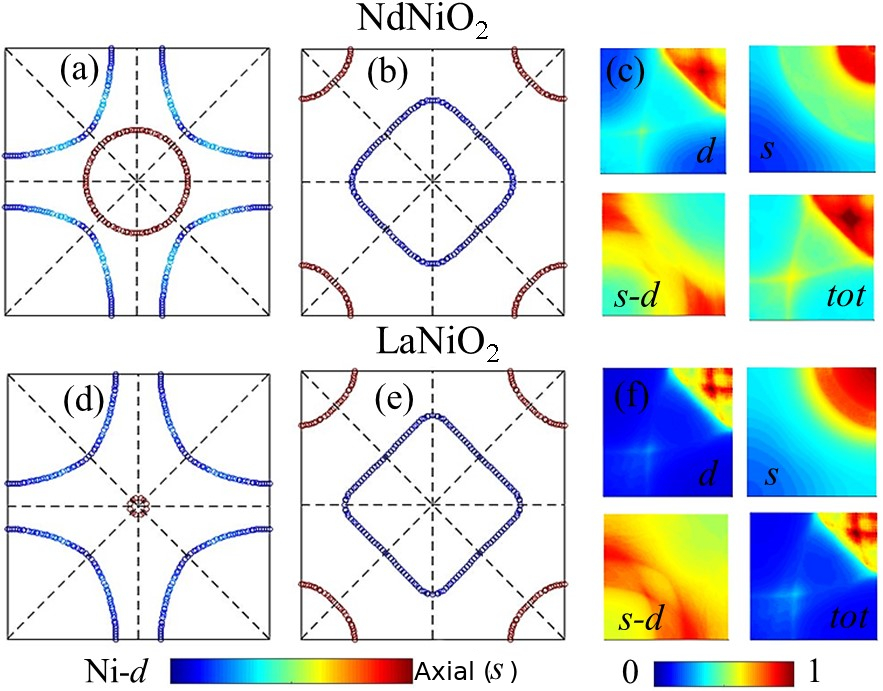
In Fig. 2, we show the FS topology for NNO [(a)-(b)] and LNO [(d)-(e)] at two cuts, with the corresponding orbital weight indicated by red to blue color map. The FS-s are seen to be strongly 3D, which is typically detrimental for FS nesting strength. However, owing to the particular orbital weight distributions, there arise dominant nesting channels, which are highly orbital resolved. Interestingly, there is a complete orbital inversion among two FS sheets between = 0 and . While the large hole pocket centering the zone boundary, and electron pocket in zone center of NNO BZ is of Ni (-) and axial character (), respectively in = 0, they reverse their roles in = . The Ni orbital enjoys a FS topology similar to the cuprates case in the low region, giving a nearly 2D FS nesting feature around and hence a -pairing symmetry. On the other hand, the axial orbital acquires a FS nesting, considerably weaker in strength compared to the Ni orbital case, at , which is responsible for the 3- type pairing symmetry. The FS for LNO, shown in Fig. 2(d)-(e) is topologically similar to NNO, except it almost looses its FS pocket at the -point. Since this heavily weakened FS pocket is dominated by axial orbital in NNO, the multiband picture is less prominent in LNO. This is also reflected in the far weaker contribution of the inter-orbital susceptibility to be discussed in the following.
The orbital resolved spin susceptibility for NNO is shown in Fig. 2(c), which highlights the importance of inter-orbital contribution. The relative contributions from axial orbital () and inter-orbital (-), compared to Ni- are found to be 1/10-th and 1/5-th, respectively. In comparison, in LNO, they are 1/100-th and 1/20-th, respectively. This makes the total susceptibility dominated almost entirely by the -orbital contribution for LNO, while the significant inter-orbital orbital contribution makes the total susceptibility in NNO appreciably different from the -orbital contribution (cf. Fig. 2(c) and (f)).
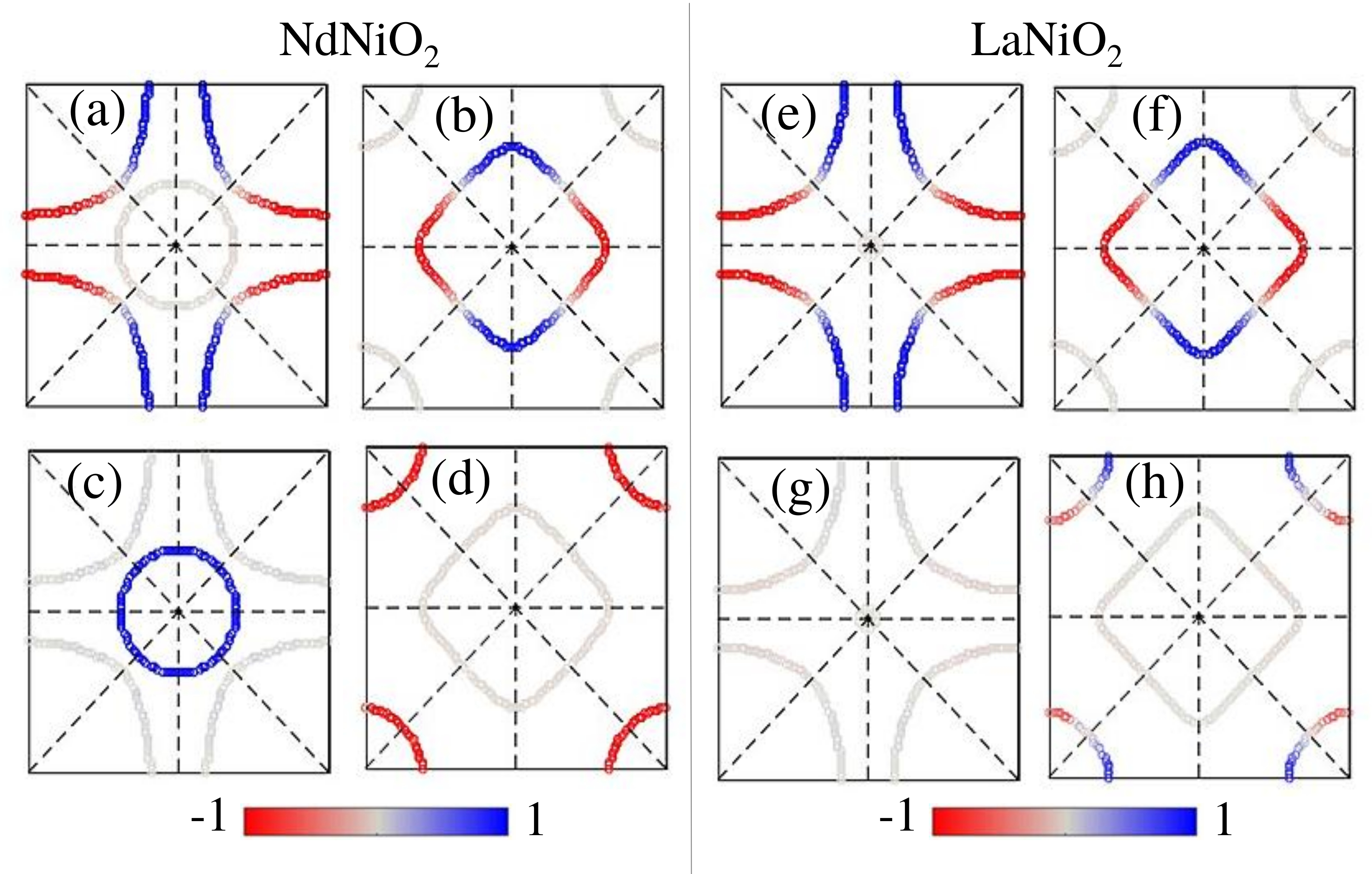
In Fig. 3 we plot the pairing eigenfunction for the highest eigenvalue , but projected onto the different orbital channels as ( dependence is suppressed for simplicity), where , are orbital indices, and is the band index. is the eigenvector of the two-band Hamiltonian. In NNO, we clearly observe that the pairing symmetry of the Ni orbital onto the FS is a pure type, with very little or no three dimensional component. On the other hand, the projected pairing symmetry on the axial orbital can be described by a simple dispersion as , with no signature of the basal plane anisotropy. In contrast, in LNO compound, the axial orbital’s contribution on the FS is drastically reduced, and hence the calculated pairing symmetry changes to a simple . This result implies that the axial orbital, although seemingly has reduced weight on the FS, can play important role to determine the pairing symmetry.
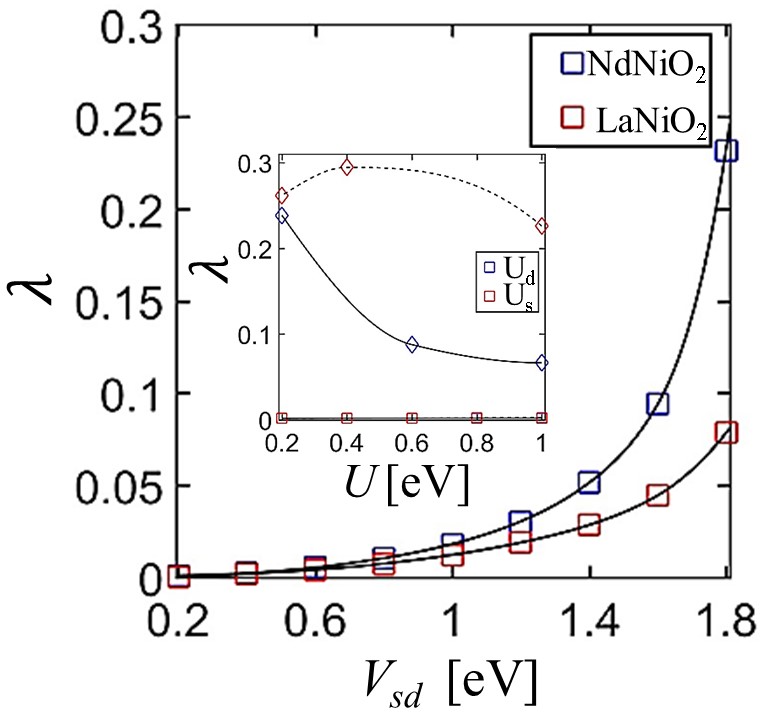
Finally, we study how the pairing strength depends on the choice of Hubbard interaction parameters, , and , which unravels as interesting scenario. Firstly, focusing on NNO, we find that increases almost exponentially with (cf. Fig. 4), while neither or is effective in enhancing . Thus, an appreciable is obtained only when becomes appreciable. Secondly, relative to NNO, the pairing strength grows much more slowly with in LNO. Thus even for appreciable value of , the the pairing strength in LNO is much smaller than NNO. This in turn highlights the important role of the inter-orbital interaction for superconductivity in nickelate compounds under discussion, and their material dependence.
Conclusion.– In summary, motivated by the two band scenario,sawatzky ; Vishwanath ; hwang-new proposed for NiO2 ( = La, Nd), we derived a two band Hamiltonian out of DFT calculations, keeping the Ni - and Ni degrees of freedom active, and integrating the rest. The latter forms an axial orbital from a combination of Nd/La , Ni 3- and Ni , and encodes the materials dependence. Calculation of superconducting properties in such a two orbital picture, shows an orbital selective pairing for the Nd compound, while it is found to be only of - symmetry in La compound. Most importantly, we find while the SC pairing grows almost in an exponential fashion with inter-orbital Hubbard interaction for the Nd compound, it is not helped by the choice of intra-orbital Hubbard interactions. Though the same holds good for La compound, the growth of pair interaction with the strength of inter-orbital Hubbard interaction is much weaker than in Nd compound, presumably justifying the fact that superconductivity has been so far observed only for the Nd compound.hwang ; hwang-new
Acknowledgements.
T.S-D acknowledges financial support from Department of Science and Technology, India. T.S-D and I.D acknowledge support from the National Science Foundation under Grant No. NSF PHY-1748958 and hospitality from KITP where part of this work was performed. TD acknowledges supports from the MHRD, Govt. of India under STARS research funding. Equal contribution.References
- (1) Patrick A. Lee, Naoto Nagaosa, and Xiao-Gang Wen, Rev. Mod. Phys. 78, 17 (2006).
- (2) Ankit S. Disa, Divine P. Kumah, Andrei Malashevich, Hanghui Chen, Dario A. Arena, Eliot D. Specht, Sohrab Ismail-Beigi, F. J. Walker, and Charles H. Ahn, Phys. Rev. Lett. 114, 026801 (2015).
- (3) P. Hansmann, Xiaoping Yang, A. Toschi, G. Khaliullin, O. K. Andersen, and K. Held, Phys. Rev. Lett. 103, 016401 (2009).
- (4) M. J. Han, Xin Wang, C. A. Marianetti, and A. J. Millis Phys. Rev. Lett. 107, 206804 (2011).
- (5) Viktor V. Poltavets, Martha Greenblatt, Gerhard H. Fecher, and Claudia Felser Phys. Rev. Lett. 102, 046405 (2009); Viktor V. Poltavets, Konstantin A. Lokshin, Sibel Dikmen, Mark Croft, Takeshi Egami, Martha Greenblatt, J. Am. Chem. Soc. 128, 9050 (2006).; Ph.Lacorre, J. Solid State Chem. 97, 495 (1992).
- (6) Soumyajit Sarkar, I. Dasgupta, Martha Greenblatt, and T. Saha-Dasgupta Phys. Rev. B 84, 180411(R) (2011).
- (7) V. Pardo and W. E. Pickett, Phys. Rev. Lett. 105, 266402 (2010); V. Pardo and W. E. Pickett, Phys. Rev. B 83, 245128 (2011).
- (8) M. A. HaywardM. A. GreenM. J. RosseinskyJ. Sloan, J. Am. Chem. Soc. 121, 8843 (1999).
- (9) M.A.Hayward and M.J.Rosseinsky, Solid State Sci. 5, 839 (2003).
- (10) D. Li, K. Lee, B. Y. Wang, M. Osada, S. Crossley, H. R. Lee, Y. Cui, Y. Hikita, H. Y. Hwang, Nature 572, 624 (2019).
- (11) H. Sakakibara, H. Usui, K. Suzuki, T. Kotani, H. Aoki, K. Kuroki, arXiv;1909.00060
- (12) X. Wu, D. D. Sante, T. Schwemmer, W. Hanke, H. Y. Hwang, S. Raghu, R. Thomale, Phys. Rev. B 101, 060504(R) (2020).
- (13) J. Karp, A. S. Botana, M. R. Norman, H. Park, M. Zingl, A. Millis, arXiv:2001.06441
- (14) M. Kitatani, L. Si, O. Janson, R. Arita, Z. Zhong, K. Held, arXiv:2002.12230
- (15) P. Jiang, et al arXiv:1909.13634.
- (16) Y. Gu, et al. arXiv:1911.00814
- (17) Y. Nomura et al. arXiv:1909.03942.
- (18) K.-W. Lee and W. E. Pickett, Phys. Rev. B 70, 165109 (2004).
- (19) E. Been, it et al. arXiv:2002.12300.
- (20) J. Chang, J. Zhao, and Y. DIng, arXiv:1911.12731.
- (21) G.-M. Zhang, et al. arXiv: 1909.11845.
- (22) Y.-H. Zhang, and A. Vishwanath, arXiv:1909.12865.
- (23) I. Leonov, S. L. Skornyakov, and S. Y. Savrasov, arXiv:200304368.
- (24) E. A. Stepanov, L. Peters, I. S. Krivenko, A. I. Lichtenstein, M. I. Katsnelson, A. N. Rubtsov, npj Quantum Mater. 3, 54 (2018)
- (25) M. Hepting, D. Li, C. J. Jia, H. Lu, E. Paris, Y. Tseng, X. Feng, M. Osada, E. Been, Y. Hikita, Y.-D. Chuang, Z. Hussain, K. J. Zhou, A. Nag, M. Garcia-Fernandez, M. Rossi, H. Y. Huang, D. J. Huang, Z. X. Shen, T. Schmitt, H. Y. Hwang, B. Moritz, J. Zaanen, T. P. Devereaux, W. S. Lee, Nature Mater. 19, 381 (2020).
- (26) G. A. Sawatzky, Nature 572, 592 (2019); M. Jiang, M. Berciu, G. A. Sawatzky, arXiv:1909.02557.
- (27) A. Fujimori, Electronic structure, magnetism, and supercon-ductivity in infinite-layer nickelates, J. Club Condensed Matter Phys. (2019), doi:10.36471/JCCM.
- (28) D. Li, B. Y. Wang, K. Lee, S. P. Harvey, M. Osada, B. H. Goodge, L. F. Kourkoutis, H. Y. Hwang, arXiv:2003.08506.
- (29) G. Kresse and J. Hafner, Phys. Rev. B 47, R558 (1993), G. Kresse and J. Furthmueller, Phys. Rev. B 54, 11169 (1996).
- (30) P. E. Blöchl, Phys. Rev. B 50, 17953 (1994).
- (31) J. P. Perdew et. al., Phys. Rev. B 48, 4978(E) (1993).
- (32) Supplementary material contains DFT computational details and details of superconductivity calculation.
- (33) Yusuke Nomura, Motoaki Hirayama, Terumasa Tadano, Yoshihide Yoshimoto, Kazuma Nakamura, and Ryotaro Arita Phys. Rev. B 100, 205138 (2019).
- (34) A. S. Botana and M. R. Norman, Phys. Rev. X 10, 011024 (2020).
- (35) A. A. Mostofi, J. R. Yates, Y.-S. Lee, I. Souza, D. Vanderbilt and N. Marzari Comput. Phys. Commun. 178, 685 (2008).
- (36) E. Pavarini, I. Dasgupta, T. Saha-Dasgupta, O. Jepsen, and O. K. Andersen, Phys. Rev. Lett. 87, 047003 (2001).
- (37) E. Pavarini, I. Dasgupta, T. Saha-Dasgupta, and O. K. Andersen Phys. Rev. Lett. 124, 109701 (2020).
- (38) D. J. Scalapino, E. Loh, Jr., and J. E. Hirsch, Phys. Rev. B 34, 8190 (R) (1986); ibid Phys. Rev. B 34, 6420 (1986); J. R. Schrieffer, Theory of Superconductivity (W. A. Benjamin, New York) (1964); J. R. Schrieffer, X. G. Wen, and S. C. Zhang, Phys. Rev. B 39, 11663 (1989); P. Monthoux, A. V. Balatsky, and D. Pines, Phys. Rev. Lett. 67, 3448 (1991); M. Sigrist, and Kazuo Ueda, Rev. Mod. Phys. 63, 239 (1991); D. J. Scalapino, Rev. Mod. Phys. 84, 1383 (2012); J. C. Seamus Davis and Dung-Hai Lee, PNAS 110, 17623-17630 (2013); T Das, RS Markiewicz, A Bansil, Adv. Phys. 63, 151 (2014).
- (39) I. I. Mazin, D. J. Singh, M. D. Johannes, and M. H. Du, Phys. Rev. Lett. 101, 057003S (2008); S. Graser, T. A. Maier, P. J. Hirschfeld, D. J. Scalapino, New J. Phys. 11, 025016 (2009); Zi-Jian Yao, Jian-Xin Li, and Z D Wang, New J. Phys. 11, 025009 (2009); T. Das, A. V. Balatsky, Phys. Rev. B 84, 014521 (2011); A. Chubukov, Ann. Rev. Conden. Mat. Phys. 3, 57-92 (2012).
- (40) Tetsuya Takimoto, Takashi Hotta, and Kazuo Ueda, Phys. Rev. B 69, 104504 (2004); K. Kubo, Phys. Rev. B 69, 104504 (2004); T. Das, J.-X. Zhu, M. J. Graf, Sci. Rep. 5, 8632 (2015); Hiroaki Ikeda, Michi-To Suzuki, Ryotaro Arita, Phys. Rev. Lett. 114, 147003 (2015); T. Nomoto, H. Ikeda, Phys. Rev. Lett. 117, 217002 (2016); T. Nomoto, H. Ikeda, J. Phys. Soc. Jpn. 86, 023703 (2017).
- (41) D. J. Scalapino, Rev. Mod. Phys. 84, 1383 (2012); A. V. Chubukov, D. Pines, J. Schmalian, In: Bennemann K.H., Ketterson J.B. (eds) The Physics of Superconductors. Springer, Berlin, Heidelberg; T Das, RS Markiewicz, A Bansil, Adv. Phys. 63, 151 (2014).
- (42) Since the weigth of the axial orbital largely belongs to La/Nd , the Hunds coupling is not included.