Orbital Magnetization as the Origin of the Nonlinear Hall Effect and Its Implications
Abstract
The nonlinear Hall effect is a new type of Hall effect that has recently attracted significant attention. For the physical origin of the nonlinear Hall effect, while orbital magnetization has long been hypothesized to underpin the nonlinear Hall effect, quantitative connections between the two remain elusive. Here, we resolve the problem by deriving the first explicit formula connecting the electric field induced orbital magnetization to the second order nonlinear Hall conductivity. Our theory reveals that the applied electric field plays dual roles in generating the nonlinear Hall effect: it first generates nonequlibrium orbital magnetization and subsequently perturbs the circulating edge states to produce transverse Hall voltage. Based on this scenario, we point out that in isotropic chiral metals of T and O point groups, although the nonlinear Hall response of a monochromatic linear polarized electric field is forced to vanish due to the crystalline symmetry, applying a non-collinear bichromatic electric field can give rise to a nonvanishing nonlinear Hall current that directly manifests the chiral correlation of the applied electric field. This discovery in isotropic chiral crystals enables us to incoporate both the nonlinear Hall effect and the circulat photo-galvanic effect into the framework of orbital magnetization.
Introduction.— The nonlinear Hall effect is a Hall phenomenon where a nonlinear voltage transverse to the applied electric field is generated in materials Intisodeman ; Qiongma ; Fai01 ; Haizhou01 ; Ortix ; Narayan ; YuewenFang . As a new member of the Hall effect family, the nonlinear Hall effect has sparked active investigations due to its broad application prospect and deep connection to quantum geometry Qiongma ; Fai01 ; Kumar ; Ortix02 ; Yugui ; Meizhen01 ; NingWang ; ZhiqiangMAO ; Zhimin01 ; Changgan ; GaoAn ; WeiboGao ; WeiboGao2 ; Sankar ; YangGao01 ; DiXiao ; Shengyuan ; Kalan ; Haizhou2 ; YangZhang01 ; Isobe ; Cano ; Liangfu02 . Recent studies have ascribed the intrinsic mechanism of the nonlinear Hall effect to a series of quantum geometric quantities including Berry curvature dipole Intisodeman ; Qiongma ; Fai01 , quantum metric dipole YangGao01 ; DiXiao ; Shengyuan ; Kalan ; GaoAn ; WeiboGao , and other gauge invariant terms Chengping ; Longjun ; Agarwal ; Wenyu01 . Those Berry curvature related quantum geometric quantities underlie many current studies of the nonlinear Hall effect.
Yet, a pivotal question persists: what is the microscopic origin of the nonlinear Hall effect? In the linear regime, the Berry curvature is intimately tied to both the Hall conductivity Thouless ; Nagaosa ; QianNiu and orbital magnetization QianNiu ; QianNiu02 ; Thonhauser ; Ceresoli ; Resta01 . It is known that the Berry curvature induced Hall conductivity originates from the edge current that simultaneously causes orbital magnetization Halperin ; Yoshioka . Such intrinsic connection between the Hall conductivity and the orbital magnetization is speculated to also apply to the nonlinear Hall effect Fai01 ; ZhiminLiao ; Manchon . Recent experimental observations in the few layer WTe2 Qiongma ; Fai01 ; Zhimin01 ; Ralph , TaIrTe4 Kumar ; Zhimin03 , strained monolayer MoS2 JieunLee ; JieunLee2 and WSe2 ZhiminLiao show that the nonlinear Hall effect and the current induced orbital magnetization are companion phenomenon, which further supports the orbital magnetization as the origin of the nonlinear Hall effect. However, current understanding of the nonlinear Hall effect in terms of the orbital magnetization remains phenomenological, as the quantitative relation between the two effects has yet been established.
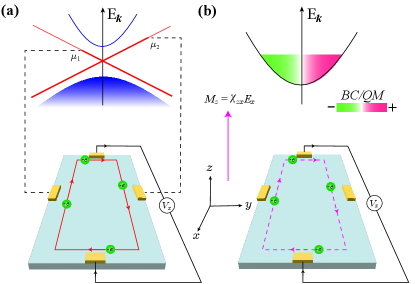
In this work, we resolve the problem by showing explicitly how the second order nonlinear Hall effect observed in metals arises from the electric field induced nonequilibrium orbital magnetization at the linear order. Past studies have demonstrated that the quadratic coupling of electric field components via dipoles of Berry curvature and quantum metric gives rise to second order nonlinear Hall current Intisodeman ; YangGao01 ; DiXiao ; Shengyuan . Here, we reveal that in generating the nonlinear Hall effect, the two electric field components in the quadratic coupling are individually involved in two successive processes: one component firstly creates net orbital magnetization and the other one subsequently acts as a perturbation to induce the transverse Hall voltage (see Fig.1). When the two successive processes are combined, the nonlinear Hall effect naturally occurs.
After clarifying the orbital magnetization as the physical origin of the nonlinear Hall effect, we get inspired to predict that isotropic chiral metals of T and O point groups can host a unique nonlinear Hall effect driven by a non-collinear bichromatic electric field. Here the non-collinear bichromatic electric field means that the non-collinear components of the electric field have different oscillation frequencies. We show that the non-collinear components of the bichromatic electric field mutually act as perturbations to their induced orbital magnetizations, giving rise to the sum frequency generation Boyd in the direction perpendicular to the polarization plane of the non-collinear bichromatic electric field. Moreover, we identify the circular photo-galvanic effect in isotropic chiral metals as a special case of the nonlinear Hall effect and find that the nonlinear Hall current directly manifests the chiral correlation of the applied electric field. In this way, both the nonlinear Hall effect and the circular photo-galvanic effect in isotropic chiral metals are incorporated into a unified description of the electric field induced orbital magnetization. Finally, we propose a series of B20 transition metal monosilicides Burkov of T point group as the candidate materials that can exhibit the unique nonlinear Hall effect driven by the non-collinear bichromatic electric field.
Orbital magnetization and Hall effect.— The intrinsic connection between the Hall effect and orbital magnetization can be traced back to the classical scenario of Lorentz force induced electrons’ cyclotron motion, which leads to the Hall effect and orbital magnetization simultaneously. In the classical picture, the cyclotron orbits of electrons bounce off the edge, forming chiral edge states circulating around the sample Kane . The picture of chiral edge states plays a central role in the modern theory of Hall effect. The electronic chiral edge states are known to induce an orbital magnetization QianNiu ; QianNiu02 ; Thonhauser ; Ceresoli ; Resta01
| (1) |
with , , being the Berry curvature and denoting the band dispersion. Here the subscript labels the band index and is the dimension. When an electric field is applied in the sample plane, the chemical potential of the electronic states in the sample starts to become spatially inhomogeneous. According to the standard definition of orbital magnetization Jackson , the Hall current density at the linear order is derived to take the form
| (2) |
In the electric dipole approximation Sipe , the linear gradient of the chemical potential is approximately equal to the applied electric field: , so Eq. 2 can be rearranged into the form of . By combining Eq. 1 and Eq. 2, we recover the Berry curvature induced linear Hall conductivity to be Resta01
| (3) |
where is the Levi-Civita symbol, is the Fermi Dirac distribution function, and the superscript in denotes the spatial component of . Comparing Eq. 1 and Eq. 2, we find that the Berry curvature acts as the central hub connecting the orbital magnetization and the Hall conductivity.
The above derivations clearly demonstrate that the linear Hall conductivity arises from the coupling between orbital magnetization and an external electric field. In the linear Hall effect that requires broken time reversal symmetry, the orbital magnetization in Eq. 1 is a ground state property that reflects the edge currents circulating around the sample. As can be seen in Fig. 1 (a), applying an electric field in the sample plane unbalances the edge currents at opposite edges, so the electrons in opposite propagating channels have different chemical potentials Halperin ; Yoshioka . When electrodes are attached to measure the voltage transverse to the edge current direction, the chemical potential difference at opposite edges gives the Hall voltage. The scenario of orbital magnetization with the associated edge currents applies well to the interpretation of the Hall effect at linear order, and it also inspires an insightful understanding of the second order nonlinear Hall effect as presented in the below.
Second order nonlinear Hall conductivity derived from orbital magnetization.— At linear order, the prerequisite for obtaining a nonzero Hall conductivity in Eq. 3 is to have a finite orbital magnetization in the material. In the linear Hall effect, the finite orbital magnetization can result from either an external magnetic field or a spontaneous time reversal symmetry breaking. Apart from them, orbital magnetization can also be induced by applying an electric field, which is known as the orbital magnetoelectric effect Moore ; Wenyu02 . In a material that exhibits active orbital magnetoelectric response, it is conceivable that the orbital magnetization induced by the first order electric field can be further perturbed by the second order electric field. Following the the mechanism of Hall voltage generation from the orbital magnetization in the linear Hall effect, we find that the second order nonlinear Hall conductivity can be similarly derived from the linear orbital magnetoelectric susceptibility.
Through a Taylor expansion of the edge current induced orbital magnetization in Eq. 1, we can obtain the orbital magnetization resulting from an external electric field: . Here the orbital magnetization is assumed to be zero before applying the electric field. The corresponding orbital magnetoelectric susceptibility is found to have the form Supp
| (4) |
with and being the band resolved quantum metric tensor Supp ; KamalDas . Similar to the linear Hall effect, the electric field induced nonequilibrium orbital magnetization is also accompanied by a Hall current. Substituting and Eq. 4 back to Eq. 2, we obtain the Hall current density , where the second order nonlinear Hall conductivity takes the form
| (5) |
It is clear that the nonlinear Hall conductivity derived in Eq. Orbital Magnetization as the Origin of the Nonlinear Hall Effect and Its Implications captures the intrinsic contribution from both the Berry curvature dipole Intisodeman and the quantum metric dipole YangGao01 ; DiXiao ; Shengyuan .
The closely related Eq. 4 and Eq. Orbital Magnetization as the Origin of the Nonlinear Hall Effect and Its Implications demonstrate that the generation of second order nonlinear Hall voltage response undergoes a nonequilibrium process. In the process, the first order effect of the applied electric field is to induce a nonequilibrium orbital magnetization associated with an edge current, as is shown in Fig. 1 (b). Then the second order electric field introduces spatial inhomogeneity to the chemical potentials of the states at opposite edges. Eventually, the coupling between the second order electric field and the orbital magnetization through the edge states gives rise to the second order nonlinear Hall response. Our analysis indicates that the intrinsic connection between the nonlinear Hall effect and the orbital magnetization is based on the conjecture that the applied electric field plays two distinct roles. To further investigate the roles of the applied electric field in the nonlinear process, we focus on the second order nonlinear Hall effect in isotropic chiral metals of T and O point groups.
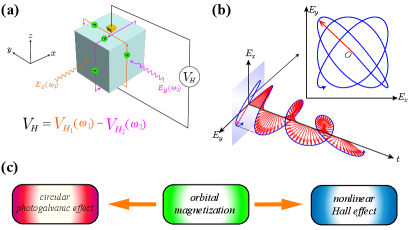
Nonlinear Hall effect in chiral metals.— Isotropic chiral metals of T and O point groups, according to symmetry, allow finite magnetoelectric response Wenyu03 ; Wenyu04 . Specifically, in isotropic chiral metals with Fermi surfaces, applying an electric current along arbitrary direction generates an orbital magnetization parallel to the current direction itself Wenyu04 . It seems that such longitudinal orbital magnetoelectric effect should bring about a finite second order nonlinear Hall effect in those isotropic chiral metals. However, as long as the driving electric field is linear polarized with a single constant frequency, the symmetry of T and O point groups always forces the second order nonlinear Hall conductivity to vanish Wenyu01 ; Nandy .
In isotropic chiral metals with a monochromatic linear polarized electric field applied, although a finite current induced orbital magnetization can arise, the isotropic chiral crystalline symmetry smears the two distinctive roles of the applied electric field, which vanishes the second order nonlinear Hall response. As schematically shown in Fig. 2 (a), the applied electric field can always be decomposed along two perpendicular directions. The two electric field components individually induce mutually perpendicular orbital magnetizations associated with edge currents. Simultaneously, each electric field component introduces a perturbation to the edge current circulating in the same plane, similar to that shown in Fig. 1 (a). Since the two electric field components are in phase with the same frequency, the Hall voltages arising from the two edge currents have opposite signs and therefore get canceled out. The monochromaticity and in phase property of the decomposed two electric field components are the key reasons why the second order Hall response gets eliminated in isotropic chiral metals. If the frequency and phase of one electric field component deviate from those of the other, the above cancellation of the Hall voltages becomes no longer valid.
In fact, two perpendicular electric field components with generally different frequencies and phases correspond to a non-collinear bichromatic electric field. Such a non-collinear bichromatic electric field, when applied to an isotropic chiral metal with time reversal symmetry, can lead to a finite second order nonlinear Hall current response. Incorporating the frequency dependence into the Berry curvature dipole term in Eq. Orbital Magnetization as the Origin of the Nonlinear Hall Effect and Its Implications, we find that the second order nonlinear Hall current density has the form Supp
| (6) |
with being the relaxation time. Here the isotropic chiral crystalline symmetry makes the Berry curvature dipole take the form while the quantum metric dipole vanishes due to the time reversal symmetry. It can be seen from Eq. 6 that the Hall current density is driven by the dynamical chirality Smirnova of the non-collinear bichromatic electric field. As the chirality of the chiral metal determines the sign of HongDing , the nonlinear Hall current direction reflects the crystal’s chirality. Consistent with the symmetry constraint put by the T and O point groups, as when , the Hall current density in the linear polarized monochromatic limit.
It is worth noting that the driving non-collinear bichromatic electric fields in Eq. 6 can be manifested by a Lissajous curve as plotted in Fig. 2 (b). In the general case of , the Lissajous curve indicates that the superposition of the non-collinear electric field ocillates and rotates at the same time, which resembles the precession of a circularly polarized electric field Supp . As a result, the two perpendicular electric fields with different frequencies exhibit a chirality evolving over time. When the driving frequencies approach , the dynamical chirality tends to become the static circular polarizability of the total applied electric field. In the limit of , it is clear that Eq. 6 gives the circular photo-galvanic current density Orenstein . From this perspective, the circular photo-galvanic effect in isotropic chiral metals corresponds to a special case of the nonlinear Hall effect and also originates from orbital magnetization (see Fig. 2 (c)).
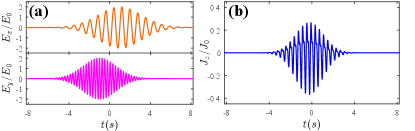
To further clarify the role of the applied electric field in generating nonlinear Hall current in isotropic chiral metals, we apply the Fourier transformation to Eq. 6 and obtain the nonlinear Hall current density in the time domain to be Supp
| (7) |
where is the Heaviside step function. It is clear to see that the two perpendicular components of the applied electric field act in sequence to generate . In Fig. 3, we present the simulation of induced by a Gaussian pulse field . Here the electric field components take the form with . Along with more simulations of in the Supplemental Materials Supp , we find that a finite of Gaussian-like envelope can always arise as long as the applied pulse field is not purely linear polarized, namely that vanishes only when all the conditions , , and with are met. This is consistent with the previous analysis that the nonlinear Hall response in isotropic chiral metals is intrinsically related to the circular polarizability of the applied electric field. In fact, Eq. 7 shows that the chiral correlator of the applied electric field acts as the kernel to generate the finite Supp , which means that in isotropic chiral metals of T and O point groups, the nonlinear Hall current current directly manifests the chiral correlation of the applied electric fields.
Among the 18 gyrotropic point groups that allow finite orbital magnetoelectric effect Wenyu03 , the T and O point groups are the only two exceptions where the Berry curvature dipole couples to a non-collinear bichromatic electric field, rather than a linear polarized monochromatic electric field, to generate the nonlinear Hall effect. As shown in Fig. 3, the resulting nonlinear Hall effect is sensitive to the frequency and phase difference between the non-collinear electric field components. According to our analysis above, identifying such nonlinear Hall effect in chiral metals of T and O point groups in turn verifies the orbital magnetization origin of the nonlinear Hall effect. Recently, a series of B20 transition metal monosillicides Burkov including RhSi, CoSi, AlPt, PtGa and PdGa have been identified to be isotropic chiral metals of T point group. Importantly, those materials are observed to host multi-fold Weyl point degeneracies at time reversal invariant momenta HongDing ; Hasan ; HongDing2 ; Sato ; Yulin ; Claudia01 ; Claudia02 , which act as source of Berry curvature in the momentum space. As a result, those Weyl semimetals of B20 chiral cubic structure are considered to be good candiates to exhibit the non-collinear bichromatic electric field driven nonlinear Hall effect. In Fig. S2, RhSi is taken as an example to show its electronic band dispersions and the Berry curvature dipole distribution. At eV, the Berry curvature dipole density mainly concentrates at (see Fig. S2 (b)), and the resulting Berry curvature dipole reaches 0.04, which is in the same order as that in WTe2 YangZhang02 . Since RhSi has been observed to exhibit a giant circular photo-galvanic effect Rees ; LiangWu2 , the related non-collinear bichromatic electric field driven nonlinear Hall effect is also expected to be observable in RhSi.
Discussions.— In this work, we formulate the origin of the nonlinear Hall effect in terms of orbital magnetization. The current scenario of orbital magnetization origin deals with the low frequency limit that accounts for the intra-band contribution to the second order nonlinear Hall effect. A generalization of the scenario is to take into account inter-band processes where the driving frequency of the applied electric field approaches resonance. In that case, the nonlinear Hall effect bypasses the constraint of Fermi surfaces so that insultors can also exhibit finite nonlinear Hall response Wenyu01 . As the orbital magnetization occurs naturally in quantum Hall insulators, an extension of our scenario of the second order Hall response to the third order one is expected to provide a possible interpretation to the recently observed third order nonlinear Hall effect in the graphene quantum Hall system PanHe . It is important to note that our current scenario of orbital magnetization origin applies only to the nonlinear Hall effect arising from intrinsic band properties. For the disorder scattering induced nonlinear Hall phenomenon Haizhou2 ; ZZDu03 , its relation to the orbital magnetization needs further exploration.
Starting from the scenario of orbital magnetization origin, we have pointed out that isotropic chiral metals of T and O point groups host a unique nonlinear Hall effect driven by a non-collinear bichromatic electric field. Such nonlinear Hall current response in isotropic chiral metals has been shown to manifest the chiral correlation of the applied electric fields. If the two non-collinear electric field components are in phase with the same frequency, the nonlinear Hall response will vanish due to the isotropic chiral crystalline symmetry of T and O point groups. From this perspective, applying a non-collinear bichromatic electric field to measure the sum-frequency generation in the transverse direction can serve as a powerful chiral spectroscopy Hache ; YRShen to accurately identify the chiral structure of the crystals in T and O point groups. Our discovery also lays the foundation to develop the chiral coherent spectroscopy, which can serves as a two-pump nonlinear probe to the electronic states with chiral structure. In the other way, since isotropic chiral crystals can enable the circular polarized part of the applied electric field to undergo the sum-frequency generation in the transverse direction, one can utilize isotropic chiral crystals to quantify the chiral correlation of the applied electric field.
Acknowledgements.— W.-Y.H. acknowledges the support from the National Natural Science Foundation of China (No. 12304200), the BHYJRC Program from the Ministry of Education of China (No. SPST-RC-10), the Shanghai Rising-Star Program (24QA2705400), and the start-up funding from ShanghaiTech University.
References
- (1) I. Sodemann and L. Fu, Phys. Rev. Lett. 115, 216806 (2015).
- (2) Z. Z. Du, H.-Z. Lu, and X. C. Xie, Nat. Rev. Phys. 3, 744 (2021).
- (3) C. Ortix, Quantum Technol. 4, 2100056 (2021).
- (4) A. Bandyopadhyay, N. B. Joseph, and A. Narayan, Mater. Today Electro. 8, 100101 (2024).
- (5) S. Wang, W. Niu, and Y.-W. Fang, arXiv: 2412.09298
- (6) Q. Ma et al., Nature 565, 337 (2019).
- (7) K. Kang, T. Li, E. Sohn, J. Shan, and K. F. Mak, Nat. Mater. 18, 324 (2019).
- (8) D. Kumar, C.-H. Hsu, R. Sharma, T.-R. Chang, P. Yu, J. Wang, G. Eda, G. Liang, and H. Yang, Nat. Nanotechnol. 16, 421 (2021).
- (9) S.-C. Ho, C.-H. Chang, Y.-C. Hsieh, S.-T. Lo, B. Huang, T.-H.-Y. Vu, C. Ortix, and T.-M. Chen, Nat. Electron. 4, 116 (2021).
- (10) J. Duan, Y. Jian, Y. Gao, H. Peng, J. Zhong, Q. Feng, J. Mao, and Y. Yao, Phys. Rev. Lett. 129, 186801 (2022).
- (11) M. Huang et al., Natl. Sci. Rev. nwac232 (2022).
- (12) M. Huang, Z. Wu, X. Zhang, X. Feng, Z. Zhou, S. Wang, Y. Chen, C. Chen, K. Sun, Z. Y. Meng, and N. Wang, Phys. Rev. Lett. 131, 066301 (2023).
- (13) L. Min, H. Tan, Z. Xie, L. Miao, R. Zhang, S. H. Lee, V. Gopalan, C.-X. Liu, N. Alem, B. Yan, and Z. Mao, Nat. Commun. 14, 364 (2023).
- (14) X.-G. Ye, H. Liu, P.-F. Zhu, W.-Z. Xu, S. A. Yang, N. Shang, K. Liu, and Z.-M. Liao, Phys. Rev. Lett. 130, 016301 (2023).
- (15) B. Chen, Y. Cao, Z. Zheng, S. Chen, Z. Liu, L. Zhang, Q. Zhu, H. Li, L. Li, and C. Zeng, Nat. Commun. 15, 5513 (2024).
- (16) S. Lai, H. Liu, Z. Zhang, J. Zhao, X. Feng, N. Wang, C. Tang, Y. Liu, K. S. Novoselov, S. A. Yang, and W. Gao, Nat. Nanotechnol. 16, 869 (2021).
- (17) S. Sankar et al., Phys. Rev. X 14, 021046 (2024).
- (18) A. Gao, Y.-F. Liu, J.-X. Qiu, B. Ghosh, T. V. Trevisan, Y. Onishi, C. Hu, T. Qian, H.-J. Tien, and S.-W. Chen et al., Science 381, 181 (2023).
- (19) N. Wang, D. Kaplan, Z. Zhang, T. Holder, N. Gao, A. Wang, X. Zhou, F. Zhou, Z. Jiang, and C. Zhang et al., Nature 621, 487 (2023).
- (20) Y. Gao, S. A. Yang, and Q. Niu, Phys. Rev. Lett. 112, 166601 (2014).
- (21) C. Wang, Y. Gao, and D. Xiao, Phys. Rev. Lett. 127, 277201 (2021).
- (22) H. Liu, J. Zhao, Y.-X. Huang, W. Wu, X.-L. Sheng, C. Xiao, and S. A. Yang, Phys. Rev. Lett. 127, 277202 (2021).
- (23) D. Kaplan, T. Holder, and B. Yan, Phys. Rev. Lett. 132, 026301 (2024).
- (24) Z. Z. Du, C. M. Wang, H.-P. Sun, H.-Z. Lu, and X. C. Xie, Nat. Commun. 12, 5038 (2021).
- (25) Y. Zhang and L. Fu, Proc. Natl. Acad. Sci. U.S.A. 118, e2100736118 (2021).
- (26) H. Isobe, S. Y. Xu, and L. Fu, Sci. Adv. 6, eaay2497 (2020).
- (27) Y. Fang, J. Cano, and S. A. A. Ghorashi, Phys. Rev. Lett. 133, 106701 (2024).
- (28) Y. Onishi and L. Fu, Phys. Rev. B 110, 075122 (2024).
- (29) C.-P. Zhang, X.-J. Gao, Y.-M. Xie, H. C. Po, and K. T. Law, Phys. Rev. B 107, 115142 (2023).
- (30) L. Xiang, C. Zhang, L. Wang, and J. Wang, Phys. Rev. B 107, 075411 (2023).
- (31) D. Mandal, S. Sarkar, K. Das, and A. Agarwal, Phys. Rev. B 110, 195131 (2024).
- (32) W.-Y. He and K. T. Law, arXiv: 2411.07456.
- (33) D. J. Thouless, M. Kohmoto, M. P. Nightingale, and M. den Nijs, Phys. Rev. Lett. 49, 405 (1982).
- (34) N. Nagaosa, J. Sinova, S. Onoda, A. H. Macdonald, and N. P. Ong, Rev. Mod. Phys. 82, 1539 (2010).
- (35) D. Xiao, M.-C. Chang, Q. Niu, Rev. Mod. Phys. 82, 1959 (2010).
- (36) D. Xiao, J. Shi, and Q. Niu, Phys. Rev. Lett. 95, 137204 (2005).
- (37) T. Thonhauser, D. Ceresoli, D. Vanderbilt, and R. Resta, Phys. Rev. Lett. 95, 137205 (2005).
- (38) D. Ceresoli, T. Thonhauser, D. Vanderbilt, and R. Resta, Phys. Rev. B 74, 024408 (2006).
- (39) R. Resta, J. Phys. Condens. Matter 22, 123201 (2010).
- (40) B. I. Halperin, Phys. Rev. B 25, 2185 (1982).
- (41) D. Yoshioka, The Quantum Hall Effect (Springer-Verlag Berlin Heidelberg 2002).
- (42) M.-S. Qin, P.-F. Zhu, X.-G. Ye, W.-Z. Xu, Z.-H. Song, J. Liang, K. Liu, and Z.-M. Liao, Chin. Phys. Lett. 38, 017301 (2021).
- (43) D. G. Ovalle, A. Pezo, A. Manchon, Phys. Rev. B 110, 094439 (2024).
- (44) D. MacNeill, G. M. Stiehl, M. H. D. Guimaraes, R. A. Buhrman, J. Park, and D. C. Ralph, Nat. Phys. 13, 300 (2017).
- (45) A.-Q. Wang, D. Li, T.-Y. Zhao, X.-Y. Liu, J. Zhang, X. Liao, Q. Yin, Z.-C. Pan, P. Yu et al., Phys .Rev. B 110, 155434 (2024).
- (46) J. Lee, Z. Wang, H. Xie, K. F. Mak, and J. Shan, Nat. Mater. 16, 887 (2017).
- (47) J. Son, K.-H. Kim, Y. H. Ahn, H.-W. Lee, and J. Lee, Phys. Rev. Lett. 123, 036806 (2019).
- (48) R. Boyd, Nonliear Optics (Academic Press, 2020).
- (49) D. A. P. Severin and A. T. Burkov, Materials 12, 2710 (2019).
- (50) M. Z. Hasan and C. L. Kane, Rev. Mod. Phys. 82, 3045 (2010).
- (51) J. D. Jackson, Classical Electrodynamics (John Wiley & Sons, New York, 2021).
- (52) C. Aversa and J. E. Sipe, Phys. Rev. B 52, 14636 (1995).
- (53) S. Zhong, J. E. Moore, and I. Souva, Phys. Rev. Lett. 116, 077201 (2016).
- (54) W.-Y. He, D. G. Gordon, and K. T. Law, Nat. Commun. 11, 1650 (2020).
- (55) See Supplemental Materials for details on 1) the derivation of the linear orbital magnetoelectric susceptbility, 2) the non-collinear bichromatic electric field induced nonlinear Hall effect in chiral metals of T and O point groups, 3) the calculation of the Berry curvature dipole in RhSi, 4) the nonlinear Hall current in the time domain and the chiral correlation function, 5) the calculation of the nonlinear Hall current in Gaussian wave packet. Two supplemental videos are attached to demonstrate the Lissajous curve of the Gaussian pulse field and the nonlinear Hall current in different parameters.
- (56) K. Das, S. Lahiri, R. B. Atencia, D. Culcer, and A. Agarwal, Phys. Rev. B 108, L201405 (2023).
- (57) W.-Y. He and K. T. Law, Phys. Rev. Research 2, 012073 (R) (2020).
- (58) W.-Y. He, X. Y. Xu, and K. T. Law, Commun. Phys. 4, 66 (2021).
- (59) S. Nandy and I. Sodemann, Phys. Rev. B 100, 195117 (2019).
- (60) D. Ayuso, O. Neufeld, A. F. Ordonez, P. Decleva, G. Lerner, O. Cohen, M. Ivanov, and O. Smirnova, Nat. Photonics 13, 866 (2019).
- (61) H. Li, S. Xu, Z.-C. Rao, L.-Q. Zhou, Z.-J. Wang, S.-M. Zhou, S.-J. Tian, S.-Y. Gao, J.-J. Li, Y.-B. Huang, H.-C. Lei, H.-M. Weng, Y.-J. Sun, T.-L. Xia, T. Qian, and H. Ding, Nat. Commun. 10, 5505 (2019).
- (62) J. E. Moore and J. Orenstein, Phys. Rev. Lett. 105, 026805 (2010).
- (63) D. S. Sanchez, L. Belopolski, T. A. Cochran, X. Xu, J.-X. Yin, G. Chang, W. Xie et al., Nature 567, 500 (2019).
- (64) Z. Rao, H. Li, T. Zhang, S. Tian, C. Li, B. Fu, C. Tang, L. Wang et al., Nature 567, 486 (2019).
- (65) D. Takane, Z. Wang, S. Souma, K. Nakayama, T. Nakamura, H. Oinuma, Y. Nakata, H. Iwasa, C. Cacho et al., Phys. Rev. Lett. 122, 076402 (2019).
- (66) N. B. M. Schröter, D. Pei, M. G. Vergniory, Y. Sun, K. Manna, F. Juan, J. A. Krieger et al., Nat. Phys. 15, 759 (2019).
- (67) M. Yao, K. Manna, Q. Yang, A. Fedorov, V. Voroshnin, B. V. Schwarze et al., Nat. Commun. 11, 2033 (2020).
- (68) N. B. N. Schröter, S. Stolz, K. Manna, F. Juan, M. G. Vergniory, J. A. Krieger, D. Pei et al., Science 369, 179 (2020).
- (69) Y. Zhang, Y. Sun, and B. Yan, Phys. Rev. B 97, 041101 (R) (2018).
- (70) D. Rees, K. Manna, B. Lu, T. Morimoto, H. Borrmann, C. Felser, J. E. Moore, D. H. Torchinsky, and J. Orenstein, Sci. Adv. 6, eaba0509 (2020).
- (71) Z. Ni, B. Xu, M.-A. Sánchez-Martínez, Y. Zhang, K. Manna, C. Bernhard, J. W. F. Venderbos, F. de Juan, C. Felser, A. G. Grushin, and L. Wu, Npj Quantum Mater. 5, 96 (2020).
- (72) P. He, H. Isobe, G. K. W. Koon, J. Y. Tan, J. Hu, J. Li, N. Nagaosa, and J. Shen, Nat. Nanotechbnol. 19, 1460 (2024).
- (73) Z. Z. Du, C. M. Wang, S. Li, H.-Z. Lu, and X. C. Xie, Nat. Commun. 10, 3047 (2019).
- (74) P. Fischer and F. Hache, Chirality 17, 421 (2005).
- (75) Y.-R. Shen, Fundamentals of Sum-Frequency Spectroscopy (Cambridge University Press, Cambridge, England, 2016).