remarkRemark \newsiamremarkhypothesisHypothesis \newsiamthmclaimClaim \headersOptimization of MFPT in Near-Disk and Elliptical Domains S. Iyaniwura, T. Wong, C. B. Macdonald, M. J. Ward
Optimization of the Mean First Passage Time in Near-Disk and Elliptical Domains in 2-D with Small Absorbing Traps
Abstract
The determination of the mean first passage time (MFPT) for a Brownian particle in a bounded 2-D domain containing small absorbing traps is a fundamental problem with biophysical applications. The average MFPT is the expected capture time assuming a uniform distribution of starting points for the random walk. We develop a hybrid asymptotic-numerical approach to predict optimal configurations of small stationary circular absorbing traps that minimize the average MFPT in near-disk and elliptical domains. For a general class of near-disk domains, we illustrate through several specific examples how simple, but yet highly accurate, numerical methods can be used to implement the asymptotic theory. From the derivation of a new explicit formula for the Neumann Green’s function and its regular part for the ellipse, a numerical approach based on our asymptotic theory is used to investigate how the spatial distribution of the optimal trap locations changes as the aspect ratio of an ellipse of fixed area is varied. The results from the hybrid theory for the ellipse are compared with full PDE numerical results computed from the closest point method [10]. For long and thin ellipses, it is shown that the optimal trap pattern for identical traps is collinear along the semi-major axis of the ellipse. For such essentially 1-D patterns, a thin-domain asymptotic analysis is formulated and implemented to accurately predict the optimal locations of collinear trap patterns and the corresponding optimal average MFPT.
1 Introduction
The concept of first passage time arises in various applications in biology, biochemistry, ecology, physics, and biophysics (see [6], [7], [20], [15] [23], [21], and the references therein). Narrow escape or capture problems are first passage time problems that characterize the expected time it takes for a Brownian “particle” to reach some absorbing set of small measure. These problems are of singular perturbation type as they involve two spatial scales: the spatial scale of the confining domain and the asymptotically small scale of the absorbing set. Narrow escape and capture problems arise in various applications, including estimating the time it takes for a receptor to hit a certain target binding site, the time it takes for a diffusing surface-bound molecules to reach a localized signaling region on the cell membrane, or the time it takes for a predator to locate its prey, among others (cf. [1], [2], [4], [3], [9], [16], [24], [19], [15]). A comprehensive overview of the applications of narrow escape and capture problems in cellular biology is given in [8].
In this paper, we consider a narrow capture problem that involves determining the MFPT for a Brownian particle, confined in a bounded two-dimensional domain, to reach one of small stationary circular absorbing traps located inside the domain. The average MFPT for this diffusion process is the expected time for capture given a uniform distribution of starting points for the random walk. In the limit of small trap radius, this narrow capture problem can be analyzed by techniques in strong localized perturbation theory (cf. [26], [27]). For a disk-shaped domain spatial configurations of small absorbing traps that minimize the average MFPT domain were identified in [12]. However, the problem of identifying optimal trap configurations in other geometries is largely open. In this direction, the specific goal of this paper is to develop and implement a hybrid asymptotic-numerical theory to identify optimal trap configurations in near-disk domains and in the ellipse.
In § 2, we use a perturbation approach to derive a two-term approximation for the average MFPT in a class of near-disk domains in terms of a boundary deformation parameter . In our analysis, we allow for a smooth, but otherwise arbitrary, star-shaped perturbation of the unit disk that preserves the domain area. At each order in , an approximate solution is derived for the MFPT that is accurate to all orders in , where is the common radius of the circular absorbing traps contained in the domain. To leading-order in , this small-trap singular perturbation analysis is formulated in the unit disk and leads to a linear algebraic system for the leading-order average MFPT involving the Neumann Green’s matrix. At order , a further linear algebraic system that sums all logarithmic terms in is derived that involves the Neumann Green’s matrix and certain weighted integrals of the boundary profile characterizing the domain perturbation. In § 3, we show how to numerically implement this asymptotic theory by using the analytical expression for the Neumann Green’s function for the unit disk together with the trapezoidal rule to compute certain weighted integrals of the boundary profile with high precision. From this numerical implementation of our asymptotic theory, and combined with either a simple gradient descent procedure or a particle swarming approach [11], we can numerically identify optimal trap configurations that minimize the average MFPT in near-disk domains. In § 3.1, we illustrate our hybrid asymptotic-numerical framework by determining some optimal trap configurations in various specific near-disk domains.
For a general 2-D domain containing small absorbing traps, a singular perturbation analysis in the limit of small trap radii, related to that in [15], [4], [12], and [26], shows that the average MFPT is closely approximated by the solution to a linear algebraic system involving the Neumann Green’s matrix. The challenge in implementing this analytical theory is that, for an arbitrary 2-D domain, a full PDE numerical solution of the Neumann Green’s function and its regular part is typically required to calculate this matrix. However, for an elliptical domain, in (4.36) and (4.37) below, we provide a new explicit representation of this Neumann Green’s function and its regular part. These explicit formulae allow for a rapid numerical evaluation of the Neumann Green’s interaction matrix for a given spatial distribution of the centers of the circular traps in the ellipse. The linear algebraic system determining the average MFPT is then coupled to a gradient descent numerical procedure in order to readily identify optimal trap configurations that minimize the average MFPT in an ellipse. Although, a similar formula for the Neumann Green’s function has been derived previously for a rectangular domain (cf. [17], [18], [14]), and an explicit and simple formula exists for the disk [12], to our knowledge there has been no prior derivation of a rapidly converging infinite series representation for the Neumann Green’s function in an ellipse. The derivation of this Neumann Green’s function using elliptic cylindrical coordinates is deferred until § 5.
With this explicit approach to determine the Neumann Green’s matrix, in § 4 we develop a hybrid asymptotic-numerical framework to approximate optimal trap configurations that minimize the average MFPT in an ellipse of a fixed area. In § 4.1 we implement our hybrid method to investigate how the optimal trap patterns change as the aspect ratio of the ellipse is varied. The results from the hybrid theory for the ellipse are favorably compared with full PDE numerical results computed from a computationally intensive numerical procedure of using the closest point method [10] to compute the average MFPT and a particle swarming approach [11] to numerically identify the optimum trap configuration. As the ellipse becomes thinner, our hybrid theory shows that the optimal trap pattern for identical traps becomes collinear along the semi-major axis of the ellipse. In the limit of a long and thin ellipse, in § 4.2 a thin-domain asymptotic analysis is formulated and implemented to accurately predict the optimal locations of collinear trap configurations and the corresponding optimal average MFPT.
In § 6, we show that the optimal trap configurations that minimize the average MFPT also correspond to trap patterns that maximize the coefficient of order in the asymptotic expansion of the fundamental Neumann eigenvalue of the Laplacian in the perforated domain. This fundamental eigenvalue characterizes the rate of capture of the Brownian particle by the traps. Eigenvalue optimization problems for the fundamental Neumann eigenvalue in a domain with small absorbing traps have been studied in [12] for the unit disk. The results herein extend this previous analysis to the ellipse and to near-disk domains.
2 Asymptotics of the MFPT in Near-Disk Domains
We derive an asymptotic approximation for the MFPT for a class of near-disk 2-D domains that are defined in polar coordinates by
| (2.1) |
where the boundary profile, , is assumed to be an , smooth periodic function with . Observe that as , where is the unit disk. Since , the domain area for is .
Inside the perturbed disk , we assume that there are circular traps of a common radius that are centered at arbitrary locations with and as . The -th trap, centered at some , is labelled by . The near-disk domain with the union of the trap regions deleted is denoted by . In , it is well-known that the mean first passage time (MFPT) for a Brownian particle starting at a point to be absorbed by one of the traps satisfies (cf. [20])
| (2.2) |
In terms of polar coordinates, the Neumann boundary condition in (2.2) becomes
| (2.3) |
For an arbitrary arrangement of the centers of the traps, and for and , we will derive a reduced problem consisting of two linear algebraic systems that provide an asymptotic approximation to the MFPT that has an error . These linear algebraic systems involve the Neumann Green’s matrix and certain weighted integrals of the boundary profile .
To analyze (2.2), we use a regular perturbation series to approximate (2.2) for the near-disk domain to problems involving a unit disk. We expand the MFPT as
| (2.4) |
and substitute it into (2.2) and (2.3). This yields the leading-order problem
| (2.5) |
together with the following problem for the next order correction :
| (2.6) |
Observe that (2.5) and (2.6) are formulated on the unit disk and not on the perturbed disk. Assuming , we use (2.4) and to derive an expansion for the average MFPT, defined by , in the form
| (2.7) |
where and is the leading-order solution evaluated on .
Since the asymptotic calculation of the leading-order solution by the method of matched asymptotic expansions in the limit of small trap radius was done previously in [4] (see also [15] and [26]), we only briefly summarize the analysis here. In the inner region near the -th trap, we define the inner variables and with , for . Upon writing (2.5) in terms of these inner variables, we have for and for each that
| (2.8) |
where . This admits the radially symmetric solution , where is an unknown constant. From an asymptotic matching of the inner and outer solutions we obtain the required singularity condition for the outer solution as for . In this way, we obtain that satisfies
| (2.9a) | ||||
| (2.9b) | ||||
where . In terms of the Delta distribution, (2.9) implies that
| (2.10) |
By applying the divergence theorem to (2.10) over the unit disk we obtain that . The solution to (2.10) is represented as
| (2.11) |
where is the Neumann Green’s function for the unit disk, which satisfies
| (2.12a) | |||
| (2.12b) | |||
Here, is the regular part of the Green’s function at . Expanding (2.11) as , and using the singularity behaviour of given in (2.12b), together with the far-field behavior (2.9b) for , we obtain the matching conditon:
| (2.13) |
This yields a linear algebraic system for and , given by
| (2.14) |
Here, , , is the identity matrix, and is the symmetric Green’s matrix with matrix entries given by
| (2.15) |
We left-multiply the equation for in (2.14) by , which isolates . By using this expression in (2.14), and defining the matrix by , we get
| (2.16) |
Remark 2.1.
The result (2.16) effectively sums all the logarithmic terms in powers of . To estimate the error with this approximation with regards to the leading-order in problem (2.5), we calculate using (2.11) the refined local behavior
| (2.17) |
where . To account for this gradient term, near the -th trap we must modify the inner expansion as . Here in , with on and as . The solution is . The far field behavior for implies that in the outer region we must have that , where as . This shows that the -error estimate for is , as claimed in (2.7).
Next, we study the problem for given in (2.6). We construct an inner region near each of the traps by introducing the inner variables and with . From (2.6), this yields the same leading-order inner problem (2.8) with replaced by . The radially symmetric solution is , where is a constant to be found. By matching this far-field behavior of the inner solution to the outer solution we obtain the singularity behavior for as for . In this way, we find from (2.6) that satisfies
| (2.18a) | ||||
| (2.18b) | ||||
| where and is defined by | ||||
| (2.18c) | ||||
| In deriving (2.18c) we used at , as obtained from (2.5). | ||||
Next, we introduce the Dirac distribution and write the problem (2.18) for as
| (2.19) |
Since , the divergence theorem yields . We decompose
| (2.20) |
where is the unknown average of over the unit disk, and is the Neumann Green’s function satisfying (2.12). Here, is taken to be the unique solution to
| (2.21) |
Next, by expanding (2.20) as , we use the singularity behaviour of as given in (2.12b) to obtain the local behavior of as , for each . The asymptotic matching condition is that this behavior must agree with that given in (2.18b). In this way, we obtain a linear algebraic system for the constant and the vector , which is given in matrix form by
| (2.22) |
Here, is the identity, , and . Next, we left multiply the equation for by . This determines , which is then re-substituted into (2.22) to obtain the uncoupled problem
| (2.23) |
where . Since , we observe from (2.23) that , as required. Equation (2.23) gives a linear system for the average MFPT in terms of the Neumann Green’s matrix , and the vector .
To determine , we use Green’s second identity on (2.21) and (2.12) to obtain a line integral over the boundary of the unit disk. Then, by using (2.18c) for , integrating by parts and using periodicity we get
| (2.24) |
Then, by setting (2.11) for into (2.24), we obtain in terms of the of (2.16) that
| (2.25a) | |||
| Here, is defined by the following boundary integral with : | |||
| (2.25b) | |||
¿From a numerical evaluation of the boundary integrals in (2.25), we can calculate , which specifies the right-hand side of the linear system (2.23) for . After determining , we obtain from the second relation in (2.23). Finally, by substituting (2.11) for into (2.7), and recalling that , we obtain a two-term expansion for the average MFPT given by
| (2.26) |
Here, and is determined from (2.16).
3 Optimizing Trap Configurations for the MFPT in the Near-Disk
To numerically evaluate the boundary integrals in (2.25) and (2.26), we need explicit formulae for and on the boundary of the unit disk where . For the unit disk, we obtain from equation (4.3) of [12] that
| (3.27a) | |||
| (3.27b) | |||
For an arbitrary configuration of traps, these expressions can be used to evaluate the Neumann Green’s matrix of (2.15) as needed in (2.16) and (2.23).
Next, by setting we can evaluate on , and then calculate its tangential boundary derivative . By using (3.27a), we obtain
| (3.28a) | ||||
| (3.28b) | ||||
where and . Then, since , we can write the two boundary integrals appearing in (2.25) and (2.26) explicitly as
| (3.29a) | |||
| (3.29b) | |||
Although for an arbitrary the integrals in (3.29) cannot be evaluated in closed form, they can be computed to a high degree of accuracy with relatively few grid points using the trapezoidal rule since this quadrature rule is exponentially convergent for smooth periodic functions [25]. When , the logarithmic singularities off of the axis of integration for in (3.29) are mild and pose no particular problem. In this way, we can numerically calculate the two-term expansion (2.26) for the average MFPT with high precision.
Then, to determine the optimal trap configuration we can either use the particle swarming approach [11], or the ODE relaxation dynamics scheme
| (3.30) |
and is given in (2.26). Starting from an admissible initial state , where at for , the gradient flow dynamics (3.30) converges to a local minimum of . Because of our high precision in calculating , a centered difference scheme with mesh spacing was used to estimate the gradient in (3.30).
3.1 Examples of the Theory




We first set and consider the boundary profile , where is a positive integer representing the number of boundary folds. In [10], an explicit two-term expansion for the average MFPT was derived for the special case where traps are equidistantly spaced on a ring of radius , concentric within the unperturbed disk. For such a ring pattern, in Proposition 1 of [10] it was proved that when , then , as the correction at order vanishes identically. Therefore, in order to determine the optimal trap pattern when we must consider arbitrary trap configurations, and not just ring patterns of traps. By minimizing (2.26) using the ODE relaxation scheme (3.30), in the left panel of Fig. 1 we show our asymptotic prediction for the optimal trap configuration for folds and traps of a common radius . The optimal pattern is not of ring-type. The corresponding results computed from the closest point method of [10], shown in Fig. 2, are very close to the asymptotic result.
In the left-middle panel of Fig. 1, we show the optimal trap pattern computed from our asymptotic theory (2.26) and (3.30) for the boundary profile with traps and . The optimal pattern is now a ring pattern of traps. In this case, as predicted by Proposition 1 of [10], the optimal pattern has traps on the rays through the origin that coincide with the maxima of the domain boundary. By applying Proposition 2 of [10], the optimal perturbed ring radius has the expansion . When , this gives , and compares well with the value calculated from (2.26) and (3.30).
In the two rightmost panels of Fig. 1, we show for and , that there are two seven-trap patterns that give local minima for the average MFPT . The minimum values of for these patterns are very similar.
Next, we construct a boundary profile with a localized protrusion, or bulge, near . To this end, we define . By using the Taylor expansion of , combined with a simple identity for , we conclude that when is related to by
| (3.31) |
As increases, the boundary deformation becomes increasingly localized near .

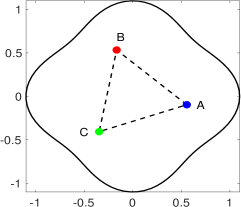




For , for which , in Fig. 3 we show optimal trap patterns for and traps for both an outward domain bulge, where , and an inward domain bulge, were , with . For the three-trap case, by comparing the two leftmost plots in Fig. 3, we observe that an inward domain bulge will displace the trap locations to the left, as expected intuitively. Alternatively, for an outward bulge, the location of the optimal trap on the line of symmetry becomes closer to the domain protrusion. An intuitive, but as we will see below in Fig. 4, naïve interpretation of the qualitative effect of this domain bulge is that it acts to confine or pin a Brownian particle in this region, and so in order to reduce the mean capture time of such a pinned particle, the best location for a trap is to move closer to the region of protrusion. For the case of four traps, a similar qualitative comparison of the optimal trap configuration for an inward and outward domain bulge is seen in the two rightmost plots in Fig. 3.
In Fig. 4, we show optimal trap patterns from our hybrid theory for circular traps of radius in a domain with boundary profile , where and . This boundary profile perturbs the unit disk inwards near and outwards near . For , in Fig. 5 we show a favorable comparison between the full numerical PDE results and the hybrid results for the optimal average MFPT and trap locations. Moreover, from the two rightmost plots in Fig. 4, we observe that there are two five-trap patterns that give local minima for . The pattern that has a trap on the line of symmetry near the outward bulge at is, in this case, not a global minimum of the average MFPT. This indicates that hard-to-assess global effects, rather than simply the local geometry near a protrusion, play a central role for characterizing the optimal trap pattern.





4 Optimizing Trap Configurations for the MFPT in an Ellipse
Next, we consider the trap optimization problem in an ellipse of arbitrary aspect ratio, but with fixed area . Our analysis uses a new explicit analytical formula, as derived in § 5, for the Neumann Green’s function and its regular part of (5.54).
For circular traps each of radius , the average MFPT satisfies (see (2.16))
| (4.32) |
Here , , , and the Green’s matrix depends on the trap locations . To determine optimal trap configurations that are minimizers of the average MFPT, given in (4.32), we use the ODE relaxation scheme
| (4.33) |
In our implementation of (4.33), the gradient was approximated using a centered difference scheme with mesh spacing . The results shown below for the optimal trap patterns are confirmed from using a particle swarm approach [11].
The derivation of the Neumann Green’s function and its regular part in § 5 is based on mapping the elliptical domain to a rectangular domain using
| (4.34a) | |||
| With these elliptic cylindrical coordinates, the ellipse is mapped to the rectangle and , where and , so that | |||
| (4.34b) | |||
To determine , given a pair , we invert the transformation (4.34a) using
| (4.35a) | |||
| To recover , we define and use | |||
| (4.35b) | |||
As derived in § 5, the matrix entries in are obtained from the explicit result
| (4.36a) | |||
| where , , and the complex constants are defined in terms of , and by | |||
| (4.36b) | |||
Observe that the Dirac point at is mapped to . The transformation (4.34) and its inverse (4.35), determines explicitly in terms of .
Moreover, as shown in § 5, the regular part of the Neumann Green’s function, , satisfying as , is given by
| (4.37a) | |||
| Here, is the limiting value of , defined in (4.36b), as , given by | |||
| (4.37b) | |||
4.1 Examples of the Theory
In this subsection, we will apply our hybrid analytical-numerical approach based on (4.32), (4.36), (4.37) and the ODE relaxation scheme (4.33), to compute optimal trap configurations in an elliptical domain of area with either circular traps of a common radius . In our examples below, we set and we study how the optimal pattern of traps changes as the aspect ratio of the ellipse is varied. We will compare our results from this hybrid theory with the near-disk asymptotic results of (2.26), with full PDE numerical results computed from the closest point method [10], and with the asymptotic approximations derived below in § 4.2, which are valid for a long and thin ellipse.


For traps, in the right panel of Fig. 6 we show results for the optimal average MFPT versus the semi-minor axis of the ellipse. The hybrid theory is seen to compare very favorably with full numerical PDE results for all . For near unity and for small, the near-disk theory of (2.26) and (3.30), and the thin-domain asymptotic result in (4.45) are seen to provide, respectively, good predictions for the optimal MFPT. Our hybrid theory shows that the optimal trap locations are on the semi-major axis for all . In the left panel of Fig. 6, the optimal trap locations found from the steady-state of our ODE relaxation (4.33) are seen to compare very favorably with full PDE results. Remarkably, we observe that the thin-domain asymptotics prediction in (4.45) agrees well with the optimal locations from our hybrid theory for .
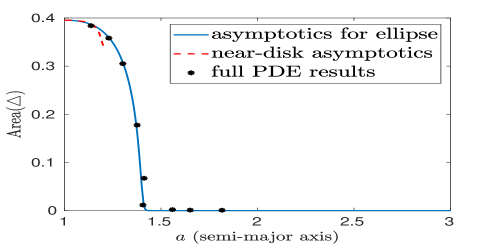


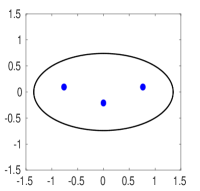



Next, we consider the case . To clearly illustrate how the optimal trap configuration changes as the aspect ratio of the ellipse is varied, we use the hybrid theory to compute the area of the triangle formed by the three optimally located traps. The results shown in Fig. 7 are seen to compare favorably with full PDE results. These results show that that the optimal traps become colinear on the semi-major axis when . In Fig. 8 we show snapshots, at certain values of the semi-major axis, of the optimal trap locations in the ellipse. In the right panel of Fig. 9, we show that the optimal average MFPT from the hybrid theory compares very well with full numerical PDE results for all , and that the thin domain asymptotics (4.48) provides a good approximation when . In the left panel of Fig. 9 we plot the optimal trap locations on the semi-major axis when the trap pattern is collinear. We observe that results for the optimal trap locations from the hybrid theory, the thin domain asymptotics (4.48), and the full PDE simulations, essentially coincide on the full range .





For the case of four traps, where , in Fig. 10 we use the hybrid theory to plot the area of the quadrilateral formed by the four optimally located traps versus the semi-major axis . The full PDE results, also shown in Fig. 10, compare well with the hybrid results. This figure shows that as the aspect ratio of the ellipse increases the traps eventually become collinear on the semi-major axis when . This feature is further illustrated by the snapshots of the optimal trap locations shown in Fig. 11 at representative values of . In the right panel of Fig. 12, we show that the hybrid and full numerical PDE results for the optimal average MFPT agree very closely for all , but that the thin-domain asymptotic result (4.51) agrees well only when . However, as similar to the three-trap case, on the range of where the trap pattern is collinear, in the left panel of Fig. 12 we show that the hybrid theory, the full PDE simulations, and the thin-domain asymptotics all provide essentially indistinguishable predictions for the optimal trap locations on the semi-major axis.










Finally, we show similar results for the case of five traps. In Fig. 13, we plot the optimal trap locations in the ellipse as the semi-major axis of the ellipse is varied. This plot shows that the optimal pattern becomes collinear when (roughly) . In the right panel of Fig. 14, we show a close agreement between the hybrid and full numerical PDE results for the optimal average MFPT. However, as seen in Fig. 14, the thin-domain asymptotic result (4.53) accurately predicts the optimal MFPT only for rather small . As for the four-trap case, in the left panel of Fig. 14 we show that the hybrid theory, the full PDE simulations, and the thin-domain asymptotics all yield similar predictions for the optimal trap locations on the semi-major axis.
4.2 Thin-Domain Asymptotics
For a long and thin ellipse, where and but with , we now derive simple approximations for the optimal trap locations and the optimal average MFPT using an approach based on thin-domain asymptotics. For the optimal trap locations are on the semi-major axis (cf. Fig. 6), while for the optimal trap locations become collinear when the semi-minor axis decreases below a threshold (see Fig. 8, Fig. 11, and Fig. 13).
As derived in Appendix A, the leading-order approximation for the MFPT satisfying (2.2) in a thin elliptical with is
| (4.38) |
where the one-dimensional profile , with , satisfies the ODE
| (4.39) |
with and bounded as . In terms of , the average MFPT for the thin ellipse is estimated for as
| (4.40) |
In the thin domain limit, the circular traps of a common radius centered on the semi-major axis are approximated by zero point constraints for at locations on the interval . In this way, (4.39) becomes a multi-point BVP problem, whose solution depends on the locations of the zero point constraints. Optimal values for the location of these constraints are obtained by minimizing the 1-D integral in (4.40) approximating . We now apply this approach for collinear traps.
For traps centered at with , the multi-point BVP for on satisfies
| (4.41) |
with and bounded as . A particular solution for (4.41) is , while the homogeneous solution is . By combining these solutions, we readily calculate that
| (4.42a) | |||
| where and are given by | |||
| (4.42b) | |||
Upon substituting (4.42a) into (4.40), we obtain that
| (4.43a) | ||||
| where the two integrals and are given by | ||||
| (4.43b) | ||||
| (4.43c) | ||||
where . By performing a few quadratures, and using (4.42b) for and , we obtain an explicit expression for :
| (4.44) |
To estimate the optimal average MFPT we simply maximize in (4.44) on . We compute that , and correspondingly . Then, by setting and , we obtain the following estimate for the optimal trap location and minimum average MFPT for traps in the thin domain limit:
| (4.45) |
These estimates are favorably compared in Fig. 6 with full PDE solutions computed using the closest point method [10] and with the full asymptotic theory based on (4.32).
Next, suppose that . Since there is an additional trap at the origin, we simply replace the condition in (4.41) with . In place of (4.42a),
| (4.46a) | |||
| where and are given by | |||
| (4.46b) | |||
The average MFPT is given by (4.43a), where is now defined by
| (4.47) |
with . By maximizing on , we obtain , so that . In this way, the optimal trap location and the minimum of the average MFPT satisfies
| (4.48) |
In Fig. 9 these scaling laws are seen to compare well with full PDE solutions and with the full asymptotic theory of (4.32), even when is only moderately small.
Next, we consider the case , with two symmetrically placed traps on either side of the origin. Therefore, we solve (4.41) with , , and , where . In place of (4.42a), we get
| (4.49a) | |||
| where and are given by | |||
| (4.49b) | |||
The average MFPT is given by (4.43a), where is now given by
| (4.50) |
where . By using a grid search to maximize on , we obtain that and . This yields that the optimal trap locations and the minimum of the average MFPT, given by , have the scaling law
| (4.51) |
These scaling laws are shown in Fig. 12 to agree well with the full PDE solutions and with the full asymptotic theory of (4.32) when is small.
Finally, we consider the case , where we need only modify the analysis by adding a trap at the origin. Setting , , and we obtain that is again given by (4.49a), except that now in (4.49a) is replaced by , with as defined in (4.46b). The average MFPT satisfies (4.43a), where in place of (4.50) we obtain that is given by
| (4.52) |
with . A grid search yields that is maximized on when and . In this way, the corresponding optimal trap locations and minimum average MFPT have the scaling law
| (4.53) |
Fig. 14 shows that (4.53) compares well with the full PDE solutions and with the full asymptotic theory of (4.32) when is small.
5 An Explicit Neumann Green’s Function for the Ellipse
We derive the new explicit formula (4.36) for the Neumann Green’s function and its regular part in (4.37) in terms of rapidly converging infinite series. This Green’s function for the ellipse is the unique solution to
| (5.54a) | ||||
| (5.54b) | ||||
where is the area of and is the regular part of the Green’s function. Here is the outward normal derivative to the boundary of the ellipse. To remove the term in (5.54a), we introduce defined by
| (5.55) |
We readily derive that satisfies
| (5.56a) | ||||
| (5.56b) | ||||
We assume that , so that the semi-major axis is on the -axis. To solve (5.56) we introduce the elliptic cylindrical coordinates defined by (4.34) and its inverse mapping (4.35). We set and seek to convert (5.56) to a problem for defined in a rectangular domain. It is well-known that
| (5.57) |
Moreover, by computing the scale factors and of the transformation, we obtain that
| (5.58) |
where we used . By using (5.57) and (5.58), we obtain that the PDE in (5.56a) transforms to
| (5.59) |
To determine how the normal derivative in (5.56a) transforms, we calculate
| (5.60) |
where from (4.34a) we calculate
| (5.61) |
Now using and on , we calculate on that
| (5.62) |
By using (5.61), we calculate on that . With this expression, we obtain after some algebra that (5.62) becomes
| (5.63) |
Next, we discuss the other boundary conditions in the transformed plane. We require that and are periodic in . The boundary condition imposed on , which corresponds to the line segment and between the two foci, is chosen to ensure that and the normal derivative are continuous across this segment. Recall from (4.35b) that the top of this segment and corresponds to , while the bottom of this segment and corresponds to . To ensure that is continuous across this segment, we require that satisfies for any . Moreover, since on , and , we must have on .
Finally, we examine the normalization condition in (5.56b) by using
| (5.64) |
Since , we obtain from (5.64) that (5.56b) becomes
| (5.65) |
In summary, from (5.59), (5.65), and the condition on , satisfies
| (5.66a) | |||
| (5.66b) | |||
| (5.66c) | |||
| (5.66d) | |||
The solution to (5.66) is expanded in terms of the eigenfunctions in the direction:
| (5.67) |
The boundary condition (5.66b) is satisfied with and , for . To satisfy , we require for . Finally, to satisfy , we require that and for . In the usual way, we can derive ODE boundary value problems for , , and . We obtain that
| (5.68a) | |||
| while on , and for each , we have | |||
| (5.68b) | |||
| (5.68c) | |||
We observe from (5.68a) that is specified only up to an arbitrary constant.
We determine this constant from the normalization condition (5.66d). By substituting (5.67) into (5.66d), we readily derive the identity that
| (5.69) |
We will use (5.69) to derive a point constraint on . To do so, we define , which satisfies and . We integrate by parts and use and to get
| (5.70) |
Next, set in (5.68b) and integrate over . Using the no-flux boundary conditions we get . We substitute this result, together with (5.70), into (5.69) and solve the resulting equation for to get
| (5.71) |
To simplify this expression we use to calculate and , while from (4.34a) we get
Upon substituting these results into (5.71), we conclude that
| (5.72) |
where is the area of the ellipse. With this explicit value for , the normalization condition (5.66d), or equivalently the constraint , is satisfied.
Next, we solve the ODEs (5.68) for , , and , for , to obtain
| (5.73a) | |||
| (5.73b) | |||
where we have defined and .
To determine an explicit expression for , as given in (5.55), we substitute (5.72) and (5.73) into the eigenfunction expansion (5.67) for . In this way, we get
| (5.74a) | |||
| where the infinite sum is defined by | |||
| (5.74b) | |||
Next, from the product to sum formulas for and we get
| (5.75) |
Then, by using product to sum formulas for , the identity , , and , some algebra yields that
| (5.76) |
The next step in the analysis is to convert the hyperbolic functions in (5.76) into pure exponentials. A simple calculation yields that
| (5.77a) | |||
| where and are defined by | |||
| (5.77b) | |||
Then, for any with and integer , we use the identity for the choice , which converts and into infinite sums. This leads to a doubly-infinite sum representation for in (5.77a) given by
| (5.78) |
where the complex constants are defined by (4.36b). From these formulae, we readily observe that on for any . Since , we can then switch the order of the sums in (5.78) when and use the identity , where denotes modulus. In this way, upon setting for , we obtain a compact representation for . Finally, by using this result in (5.74) we obtain for , or equivalently , the result given explicitly in (4.36) of § 4.
Next, to determine the regular part of the Neumann Green’s function we must identify the singular term in (4.36a) at . Since , while for , at , the singular contribution arises only from the term in . As such, we add and subtract the fundamental singularity in (4.36a) to get
| (5.79a) | |||
| (5.79b) |
To identify , we must find . To do so, we use a Taylor approximation on (4.34a) to derive at that
| (5.80) |
By calculating the partial derivatives in (5.80) using (5.61), and then noting from (4.36b) that as , we readily derive that
| (5.81) |
Finally, we substitute (5.81) into (5.79b) and let . This yields the formula for the regular part of the Neumann Green’s function as given in (4.37) of § 4. In Appendix B we show that the Neumann Green’s function (4.36) for the ellipse reduces to the expression given in (3.27) for the unit disk when .
6 Discussion
Here we discuss the relationship between our problem of optimal trap patterns and a related optimization problem for the fundamental Neumann eigenvalue of the Laplacian in a bounded 2-D domain containing small circular absorbing traps of a common radius . That is, is the lowest eigenvalue of
| (6.82) |
Here is a circular disk of radius centered at . In the limit , a two-term asymptotic expansion for in powers of is (see [12, Corollary 2.3] and Appendix C)
| (6.83) |
where and is the Neumann Green’s matrix. To relate this result for with that for the average MFPT satisfying (4.32), we let in (4.32) and calculate that . ¿From (4.32), we conclude that
| (6.84) |
where is defined in (6.83). By comparing (6.84) and (6.83) we conclude, up to terms of , that the trap configurations that provide local minima for the average MFPT also provide local maxima for the first Neumann eigenvalue for (6.82). Qualitatively, this implies that, up to terms of order , the trap configuration that maximizes the rate at which a Brownian particle is captured also provides the best configuration to minimize the average mean first capture time of the particle. In this way, our optimal trap configurations for the average MFPT for the ellipse identified in § 4.1 also correspond to trap patterns that maximize up to terms of order . Moreover, we remark that for the special case of a ring-pattern of traps, the first two-terms in (6.84) provide an exact solution of (4.32). As such, for these special patterns, the trap configuration that maximizes the term in provides the optimal trap locations that minimize the average MFPT to all orders in .
Finally, we discuss two possible extensions of this study. Firstly, in near-disk domains and in the ellipse it would be worthwhile to use a more refined gradient descent procedure such as in [22] and [5] to numerically identify globally optimum trap configurations for a much larger number of identical traps than considered herein. One key challenge in upscaling the optimization procedure to a larger number of traps is that the energy landscape can be rather flat or else have many local minima, and so identifying the true optimum pattern is delicate. Locally optimum trap patterns with very similar minimum values for the average MFPT already occurs in certain near-disk domains at a rather small number of traps (see Fig. 1 and Fig. 4). One advantage of our asymptotic theory leading to (2.26) for the near-disk and (4.32) for the ellipse, is that it can be implemented numerically with very high precision. As a result, small differences in the average MFPT between two distinct locally optimal trap patterns are not due to discretization errors arising from either numerical quadratures or evaluations of the Neumann Green’s function. As such, combining our hybrid theory with a refined global optimization procedure should lead to the reliable identification of globally optimal trap configurations for these domains.
Another open direction is to investigate whether there are computationally useful analytical representations for the Neumann Green’s function in an arbitrary bounded 2-D domain. In this direction, in [13, Theorem 4.1] an explicit analytical result for the gradient of the regular part of the Neumann Green’s function was derived in terms of the mapping function for a general class of mappings of the unit disk. It is worthwhile to study whether this analysis can be extended to provide a simple and accurate approach to compute the Neumann Green’s matrix for an arbitrary domain. This matrix could then be used in the linear algebraic system (4.32) to calculate the average MFPT, and a gradient descent scheme implemented to identify optimal patterns.
7 Acknowledgements
Colin Macdonald and Michael Ward were supported by NSERC Discovery grants. Tony Wong was partially supported by a UBC Four-Year Graduate Fellowship.
Appendix A Derivation of the Thin Domain ODE
In the asymptotic limit of a long thin domain, we use a perturbation approach on the MFPT PDE (2.2) for in order to derive the limiting problem (4.39). We introduce the stretched variables and by and , and set . Then the PDE in (2.2) becomes . By expanding in this PDE, we collect powers of to get
| (A.1) |
On the boundary , or equivalently , where , the unit outward normal is , where . The condition for the vanishing of the outward normal derivative in (2.2) becomes
This is equivalent to the condition that on . Upon substituting into this expression, and equating powers of , we obtain on that
| (A.2) |
From (A.1) and (A.2) we conclude that and . Assuming that the trap radius is comparable to the domain width , we will approximate the zero Dirichlet boundary condition on the three traps as zero point constraints for .
The ODE for is derived from a solvability condition on the problem:
| (A.3) |
We multiply this problem for by and integrate in over . Upon using Lagrange’s identity and the boundary conditions in (A.3) we get
| (A.4) | ||||
Thus, satisfies the ODE , with , as given in (4.39) of § 4.2. This gives the leading-order asymptotics .
Appendix B Limiting Case of the Unit Disk
We now show how to recover the well-known Neumann Green’s function and its regular part for the unit disk by letting in (4.36) and (4.37), respectively. In the limit only the terms in the infinite sums in (4.36) and (4.37) are non-vanishing. In addition, as , we obtain from (4.34) that and , and , where . This yields that
| (B.5) |
As such, only the and terms in the infinite sums in (4.36a) with persist as , and so (4.36a) reduces in this limit to
| (B.6) |
where and . Since and , where and are the polar angles for and , we get from (4.36b) that as . We then calculate that
| (B.7) |
Next, with regards to the term we calculate for that
| (B.8) |
From (4.36b) this yields for that
| (B.9) |
By using (B.9), we calculate for that
| (B.10) |
Next, we estimate the remaining term in (B.6) as using
| (B.11) |
Finally, by using (B.7), (B.10), and (B.11) into (B.6), we obtain for that
| (B.12) |
where . This result agrees with that in (3.27a) for the Neumann Green’s function in the unit disk. Similarly, we can show that the regular part for the ellipse given in (4.37) tends as to that given in (3.27b) for the unit disk.
Appendix C Asymptotics of the Fundamental Neumann Eigenvalue
For , it was shown in [12], by using a matched asymptotic expansion analysis in the limit of small trap radii similar to that leading to (4.32), that the fundamental Neumann eigenvalue for (6.82) is the smallest positive root of
| (C.13) |
Here and is the Helmholtz Green’s matrix with matrix entries
| (C.14) |
where the Helmholtz Green’s function and its regular part satisfy
| (C.15a) | ||||
| (C.15b) | ||||
For , we estimate by expanding , for some to be found. From (C.15), we derive in terms of the Neumann Green’s matrix that
| (C.16) |
for . From (C.16) and (C.13), the fundamental Neumann eigenvalue is the smallest for which there is a nontrivial solution to
| (C.17) |
Since this occurs when , we define by , so that (C.17) can be written in equivalent form as
| (C.18) |
Since , while for any with , we conclude for that the only non-zero eigenvalue of (C.18) satisfies with . To determine the correction to this leading-order result, in (C.18) we expand and . From collecting terms in (C.18), we get
| (C.19) |
Since is symmetric with the 1-D nullspace , the solvability condition for (C.19) is that . Since , this yields the two-term expansion
| (C.20) |
Finally, using , we obtain the two-term expansion as given in (6.83).
References
- [1] O. Bénichou and R. Voituriez. From first-passage times of random walks in confinement to geometry-controlled kinetics. Physics Reports, 539(4):225–284, 2014.
- [2] P. Bressloff and S. D. Lawley. Stochastically gated diffusion-limited reactions for a small target in a bounded domain. Phys. Rev. E., 92:062117, 2015.
- [3] A. F Cheviakov, M. J Ward, and R. Straube. An asymptotic analysis of the mean first passage time for narrow escape problems: Part II: The sphere. SIAM J. Multiscale Model. Simul., 8(3), 2010.
- [4] D. Coombs, R. Straube, and M. J. Ward. Diffusion on a sphere with localized traps: Mean first passage time, eigenvalue asymptotics, and Fekete points. SIAM J. Appl. Math., 70(1), 2009.
- [5] J. Gilbert and A. Cheviakov. Globally optimal volume-trap arrangements for the narrow-capture problem inside a unit sphere. Phys. Rev. E., 99(012109), 2019.
- [6] I. V Grigoriev, Y. A Makhnovskii, A. M Berezhkovskii, and V. Yu Zitserman. Kinetics of escape through a small hole. J. Chem. Phys., 116(22):9574–9577, 2002.
- [7] D. Holcman and Z. Schuss. Escape through a small opening: receptor trafficking in a synaptic membrane. J. Stat. Phys., 117(5-6):975–1014, 2004.
- [8] D. Holcman and Z. Schuss. The narrow escape problem. SIAM Review, 56(2):213–257, 2014.
- [9] D. Holcman and Z. Schuss. Time scale of diffusion in molecular and cellular biology. J. of Physics A: Math. and Theor., 47(17):173001, 2014.
- [10] S. Iyaniwura, T. Wong, M. J. Ward, and C. B. Macdonald. Simulation and optimization of mean first passage time problems in 2-d using numerical embedded methods and perturbation theory. submitted, SIAM J. Multiscale Model. Simul., 2019.
- [11] J. Kennedy. Particle swarm optimization. Encyclopedia of machine learning, pages 760–766, 2010.
- [12] T. Kolokolnikov, M. S Titcombe, and M. J. Ward. Optimizing the fundamental Neumann eigenvalue for the Laplacian in a domain with small traps. Europ. J. Appl. Math., 16(2):161–200, 2005.
- [13] T. Kolokolnikov and M. J. Ward. Reduced wave Green’s functions and their effect on the dynamics of a spike for the Gierer-Meinhardt model. Europ. J. Appl. Math, 14(5):513–545, 2003.
- [14] T. Kolokolnikov, M. J. Ward, and J. Wei. Spot self-replication and dynamics for the Schnakenburg model in a two-dimensional domain. J. Nonl. Science, 19(1):1–56, 2009.
- [15] V. Kurella, J. C Tzou, D. Coombs, and M. J Ward. Asymptotic analysis of first passage time problems inspired by ecology. Bull. Math. Biol., 77(1), 2015.
- [16] A. E. Lindsay, A. J. Bernoff, and M. J. Ward. First passage statistics for the capture of a Brownian particle by a structured spherical target with multiple surface traps. SIAM J. Multiscale Model. Simul., 15(1):74–109, 2017.
- [17] S. L. Marshall. A rapidly convergent modified Green’s function for Laplace’s equation in a rectangular domain. Proc. Roy. Soc. London A, 455:1739–1766, 1999.
- [18] R. C. McCann, R. D. Hazlett, and D. K. Babu. Highly accurate approximations of Green’s and Neumann functions on rectangular domains. Proc. Roy. Soc. Lond. A, 457:767–772, 2001.
- [19] S. Pillay, M. J Ward, A. Peirce, and T. Kolokolnikov. An asymptotic analysis of the mean first passage time for narrow escape problems: Part I: Two-dimensional domains. SIAM J. Multiscale Model. Simul., 8(3), 2010.
- [20] S. Redner. A guide to first-passage processes. Cambridge University Press, 2001.
- [21] L. M Ricciardi. Diffusion approximations and first passage time problems in population biology and neurobiology. In Mathematics in Biology and Medicine, pages 455–468. Springer, 1985.
- [22] W. J. M. Ridgway and A. Cheviakov. Locally and globally optimal configurations of n particles on the sphere with applications in the narrow escape and narrow capture problems. Phys. Rev. E., 100(042413), 2019.
- [23] Z. Schuss, A. Singer, and D. Holcman. The narrow escape problem for diffusion in cellular microdomains. Proc. Natl. Acad. Sci., 104(41):16098–16103, 2007.
- [24] A. Singer, Z. Schuss, and D. Holcman. Narrow escape, Part II: The circular disk. J. Stat. Phys., 122(3):465–489, 2006.
- [25] L. N. Trefethen and J. A. C. Weideman. The exponentially convergent trapezoidal rule. SIAM Review, 56(3):28–51, 2014.
- [26] M. J. Ward, W. D. Henshaw, and J. B. Keller. Summing logarithmic expansions for singularly perturbed eigenvalue problems. SIAM J. Appl. Math., 53(3):799–828, 1993.
- [27] M. J. Ward and J. B. Keller. Strong localized perturbations of eigenvalue problems. SIAM J. App. Math., 53(3):770–798, 1993.