nameyeardelim,
Optimal Delegation in a Multidimensional World
We study a model of delegation in which a principal takes a multidimensional action and an agent has private information about a multidimensional state of the world. The principal can design any direct mechanism, including stochastic ones. We provide necessary and sufficient conditions for an arbitrary mechanism to maximize the principal’s expected payoff. We also discuss simple conditions which ensure that some convex delegation set is optimal. A key step of our analysis shows that a mechanism is incentive compatible if and only if its induced indirect utility is convex and lies below the agent’s first-best payoff.
1 Introduction
In many economic and political environments, a principal delegates decisions to a better-informed agent: a firm appoints a manager to choose investment levels in different projects; US Congress delegates power to federal agencies; a legislative forms a committee to draft bills; a regulator lets a monopolist choose prices. Following [18], an extensive literature models such delegation problems by assuming that both the action and the state of the world lie in a one-dimensional space. A main result of this literature characterizes when it is optimal for the principal to constrain the agent’s choice to lie in an interval, and this conclusion has been used to explain why managers face spending caps, regulators impose price ceilings, and trade agreements specify maximum tariff levels.
The assumption that the action and state space are one-dimensional is made for tractability. In many applications, the underlying states and actions are more complex and more realistically modeled as multidimensional: managers invest in several projects, Congress delegates many decisions to the EPA, and committees draft multiple bills. What mechanisms are optimal in such multidimensional settings? How robust are conclusions obtained for one-dimensional models? And can we still expect that relatively simple mechanisms are often optimal?
To study these questions, we consider a principal that takes a multidimensional action and faces an agent with private information about a multidimensional state of the world (the agent’s type). Payoffs depend on the action and the state of the world, and transfers are infeasible. The principal can design arbitrary mechanisms, including stochastic ones, to maximize her expected payoff. Our main result characterizes, for an arbitrary mechanism, when this mechanism is optimal. Often, it is optimal to delegate the decision to the agent but to constrain the agent by requiring that her action lies in some set. For convex delegation sets, we provide a simple characterization, which is a direct analog of conditions characterizing when interval delegation is optimal in one-dimensional models. Our results illustrate how a principal can benefit from optimally bundling independent decisions. Even for one-dimensional models, our approach provides new insights: Our main result characterizes for arbitrary mechanisms—not just interval delegation sets—when this mechanism is optimal. And as corollaries, we obtain a novel condition under which some interval delegation set will be optimal and a comparative statics result showing when the agent will get more discretion.
A key step to deriving our results lies in obtaining a simple characterization of the set of feasible mechanisms. Given a mechanism, the corresponding indirect utility assigns to any type the payoff this type would get by choosing his report optimally. This payoff must be less than the first-best payoff, i.e., the payoff this type would get if he could choose the action without any constraints. Moreover, the indirect utility must be a convex function since it is the maximum of a family of affine functions. Lemma 1 shows that any function satisfying these two properties is the indirect utility of an incentive-compatible mechanism.
This characterization is easy to use and already helpful for one-dimensional delegation models. Our formulation differs from the previous literature, which often considered only deterministic mechanisms. Since the convex combination of two incentive-compatible mechanisms is not necessarily incentive compatible, the set of deterministic mechanisms is not even convex.111Some earlier papers also consider stochastic mechanisms (or allow for money burning/restricted transfer) and obtain a convex set of mechanisms; see, for example, [2, 25, 5, 3, 21, 22]. Moreover, a common approach is to first treat the model as one with transfers and then impose that these transfers are zero (or negative). Compared to this approach, formulating the problem via indirect utilities is more direct and provides valuable geometric insights into which mechanisms can be optimal. For the multidimensional problem, the approach via indirect utilities provides additional benefits because it circumvents intricate characterizations of incentive compatibility [33, see].
To find the optimal mechanism, we formulate the principal’s problem in terms of indirect utilities. In this formulation, the problem becomes a linear program, and we use linear programming duality to derive necessary and sufficient conditions for a given mechanism to be optimal. Typically, optimal mechanisms pool certain types, and our main result shows that a mechanism is optimal if conditional on any pooling region, a stochastic dominance condition (using the convex order) is satisfied. Intuitively, this condition requires that restricted to the pooling region (where the indirect utility function is affine), any convex indirect utility yields a lower payoff. If the pooling regions are at most one-dimensional, the stochastic dominance condition has a simple formulation in terms of majorization. Using this observation, we provide necessary and sufficient conditions for a convex delegation set with a smooth boundary to be optimal. These conditions are easy to check and are straightforward extensions of conditions that ensure the optimality of interval delegation sets in one-dimensional models [2, see].
Related Literature
The literature on delegation has focused mainly on problems in which the principal delegates a single one-dimensional decision and therefore assumed that both the action and state spaces are one-dimensional; see, for example, [18, 19, 30, 1, 2, 24].
A few delegation papers do consider richer action and/or type spaces. [6] considers an agent with two-dimensional private information and discusses several applications. Since the principal’s action is assumed to be one-dimensional (and only interval delegation sets are considered), there is only limited scope to screen two-dimensional types in his analysis. [23] characterize the optimal mechanism in a setting where two decisions depend on a single-dimensional underlying state. [15] considers multidimensional information and actions but restricts the principal’s choice to a particular class of “budgeting mechanisms”. The closest paper to ours is [14], which studies the delegation of several independent decisions, which yield multidimensional action and state spaces. For quadratic preferences with a constant bias, he shows that if the states are independently and identically distributed according to normal distributions then it is optimal to delegate a ‘half space’. Without the normality assumption, he shows that the principal’s payoff from such a mechanism converges to the first-best as the number of independent decision problems grows. [13] also considers multidimensional delegation problems and characterizes the max-min optimal mechanism, which maximizes the principal’s payoff against the worst-case preference type of the agent.
The elicitation of information about multiple independent decisions from a biased agent has been studied in general mechanism design [20, e.g.,] and cheap talk environments [9, 26]. [20] show that by linking independent decisions, the principal’s payoff converges to the first-best as the number of decisions grows. Our results can be used to show how the principal should optimally link decisions, which can be important if there is a limited number of decisions.
2 Model
A principal chooses an action . An agent is privately informed about the state of the world , where is compact and convex. The agent’s and principal’s payoffs depend on both the action and the state of the world, and are given by
respectively, where is strictly concave, differentiable with a Lipschitz-continuous gradient mapping, and satisfies ,222Since we do not artificially constrain the set of actions, some assumptions are needed to ensure that for every type there is an optimal action. The current assumptions ensure this and simplify some arguments, but weaker conditions on could be imposed. is continuous, and .
We assume that the state is distributed according to a probability distribution with differentiable density and support . The principal aims to maximize her expected payoff and can design arbitrary mechanisms.
The revelation principle applies and we define a mechanism to be a function such that expected payoffs are integrable.333We denote by the Borel -algebra on . To simplify notation, we extend the domain of and linearly to include probability distributions over , so that and analogously for . A mechanism is incentive compatible if for all and in ,
3 Characterizing incentive-compatible mechanisms
We characterize the set of incentive-compatible mechanisms in terms of their indirect utilities. To any incentive-compatible mechanism corresponds an indirect utility defined by
Which indirect utilities correspond to some incentive-compatible mechanism? First, any indirect utility is convex as the supremum of a family of functions that are affine in the state . Second, in the absence of transfers the agent’s utility cannot be higher than if he was free to choose his action. Defining the first-best payoff by
is clearly necessary.444We denote the pointwise order by , so means for all in the common domain of and . The following result shows that these two conditions characterize the set of feasible indirect utilities.
Lemma 1.
An indirect utility corresponds to an incentive-compatible mechanism if and only if is convex and lies below the first-best payoff: .
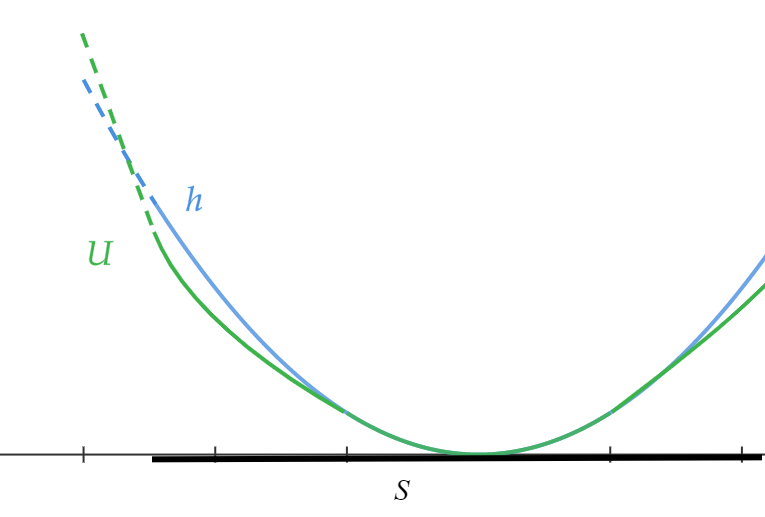
Intuitively, if is convex then it would correspond to an incentive-compatible mechanism if transfers were available and the agent had quasi-linear preferences. If the required transfers are all negative then we can use the agent’s risk aversion (coming from the strict concavity of ) to simulate these transfers via stochastic actions. One can show that implies that the required transfers are negative. This last step relies on the domain of and being large enough and it would not suffice to require only that for all . Figure 1 illustrates a convex function which lies below on all of , but which does not correspond to a mechanism because the lotteries assigned to low types would yield a strictly higher payoff than the first-best payoffs for some hypothetical types, an impossibility.
-
Proof.
Let us first state three basic observations from convex analysis. The convex conjugate of a function is denoted by and defined by . We will use the following facts, which follow immediately from this definition: (i) , (ii) implies , and (iii) implies .555Here, denotes the subdifferential of at . To see (iii), note that the definition of implies . Conversely, convexity of implies that for all , . Taking the supremum of the right-hand side with respect to yields .
Suppose is convex and satisfies . Let the mechanism assign to any type a lottery with expected value that yields the payoff . Such a lottery exists because would be the payoff for type from always getting action , because fact (ii) implies that the agents payoff is lower, and because is strictly concave.666More formally, strict concavity of implies that for any and nonzero there is such that . It follows that for any , Therefore, by choosing arbitrarily large, one can design lotteries with expected value that yield arbitrarily low payoff to the agent. Then facts (i) and (iii) imply that the payoff of a truthful type is :
It remains to show that is incentive compatible. For all and ,
where the first inequality follows since . ∎
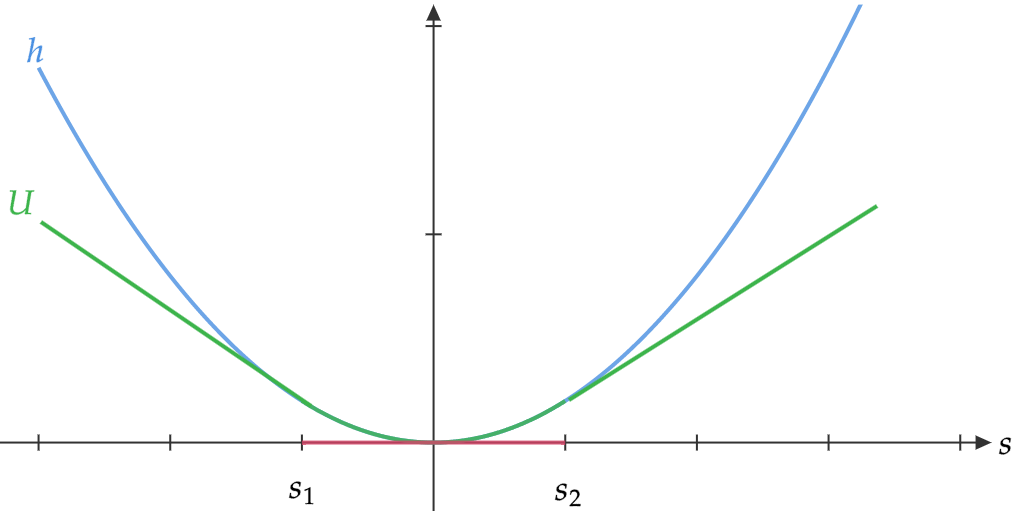
Figure 2 illustrates the result for one-dimensional types and quadratic payoffs. It shows four indirect utilities that, according to Lemma 1, correspond to incentive-compatible mechanisms. In 2(a), all types between and obtain their first-best utility and is affine below and above . This indirect utility can be obtained by letting types choose their preferred action from the interval of deterministic actions . In 2(b), the menu of actions from which the agent can choose contains an additional deterministic action above . The indirect utility in 2(c) contains an affine piece that lies strictly below the graph of . This part of the indirect utility corresponds to types that obtain a (nondegenerate) stochastic action, which yields no type its first-best payoff. Finally, 2(d) illustrates an indirect utility corresponding to a mechanism in which types in two adjacent regions obtain a stochastic action.

4 Characterizing optimal mechanisms
We characterize the optimal mechanisms in this section. To do so, we first formulate the principal’s problem in terms of indirect utilities (Section 4.1). We then state the main characterization of optimal mechanisms in Section 4.2 and illustrate the result for particular mechanisms. Finally, we outline the proof of the main result in Section 4.3.
4.1 Formulating the principal’s problem
Consider an indirect utility that corresponds to some incentive-compatible mechanism. In general, there are many incentive-compatible mechanisms that induce the same indirect utility; however, all such mechanism induce the same payoff for the principal. To see this, let be an incentive-compatible mechanism with corresponding indirect utility . Using (by an Envelope theorem) and , the principal’s payoff from mechanism in state is completely determined by :
This observation implies that the principal’s payoff is a linear function of . Therefore, a solution to the principal’s problem can be found at an extreme point of the feasible set. Returning to Figure 2, it is easy to see that the indirect utilities in Figures 2(a)–2(c) are extremal in that they cannot be written as a nontrivial convex combination of two feasible indirect utilities. In contrast, the indirect utility in 2(d) can be written as such a convex combination. This implies that whenever this mechanism is optimal, there is another (and simpler) mechanism which is also optimal. Intuively, one can write this indirect utility as a convex combination because two adjacent regions obtain distinct stochastic actions. This insight shows how, without loss of optimality, one can restrict attention to a smaller class of mechanism.777[22] develop this point more formally in the context of one-dimensional types/actions and quadratic utilities and characterize the set of extremal mechanisms. Formulating the problem in terms of indirect utilities and using our Lemma 1, one can obtain this characterization more directly. It would be interesting to extend this characterization of extremal mechanisms to the multidimensional setting. For multidimensional settings, analogous arguments show that many complicated mechanisms are not extremal and therefore the principal need not consider these mechanisms.
As is standard in multidimensional mechanism design [[, see, for example,]]rochet1998ironing, we can use the divergence theorem to reformulate the objective function as follows:
where denotes the divergence of a function, for any set , denotes the boundary of , denotes the -dimensional Hausdorff measure on the boundary of , and denotes the outward normal vector to the convex set at .
This allows us to write the principal’s problem as888The existence of a maximizer follows from standard arguments.
where the measure is defined by
is the Lebesgue measure on plus the Hausdorff measure on the boundary of , and
Cearly, plays an important role in determining which mechanisms are optimal. Heuristically, measures how much the prinicipal’s payoff increases if the indirect utility of type is increased, but where types on the boundary get extra weight.
To illustrate and for later use, let use compute for a one-dimensional type space :
| (1) |
Example 1.
Suppose and is the uniform distribution on . Let us assume payoffs are quadratic and that for some ; this implies that the principal is biased towards the ex-ante optimal action . In that case, simplifies to
| (2) |
4.2 Optimal mechanisms
Given an indirect utility , we let denote a coarsest partition of such that is affine on each partition element. We denote by a conditional measure of given .
Theorem 1.
Let be a feasible indirect utility. Then is optimal if for all , and , where is a point mass of mass at if there is satisfying and is the zero-measure otherwise.
Moreover, this condition is necessary for to be optimal if is differentiable -almost everywhere.
Two comments on the conditions in Theorem 1 are in order. First, if there is such that then it is unique because is affine on and is strictly convex. Second, for the necessity result, observe that is differentiable Lebesgue-almost everywhere since it is a convex function. Since is absolutely continuous with respect to the Lebesgue measure on the interior of , is differentiable -almost everywhere if, for example, the density is zero on the boundary of or if is differentiable -almost everywhere on the boundary of . In the one-dimensional case, this last condition can always be satisfied.
Why are the conditions in Theorem 1 sufficient for to be optimal? Consider a partition element and suppose is a point mass at . Then any feasible indirect utility will be convex and lie below at . Also, implies . Moreover, if is an affine function that coincides with at the barycenter of then we get . Since restricted to is affine, lies above at , and , this implies that conditional on the type belonging to , the principal’s expected payoff under is higher than under . And if is the zero measure then might lie above but the same conclusion follows since and conditional on , adding a constant to the indirect utility does not change the principal’s payoff. The conclusion that these conditions are also essentially necessary shows that the problem can in some sense be decomposed: whenever the principal can improve conditional on , she can extend this improved version to a feasible indirect utility that yields unconditionally a higher payoff.
A particularly simple mechanism is if the principal delegates the decision to the agent, potentially restricting the agents action to belong to some set . Note that any deterministic mechanism can be implemented as an indirect mechanism in this way. For a closed set , we say that delegating to is optimal if an optimal mechanism takes the form that any type in gets her first-best action, and any other type gets her most preferred action among the first-best actions of types in . For example, if and then delegating to is optimal if there is an optimal mechanism in which any type below gets the first-best action of type , any type in gets her first best action, and any type above gets the first-best action of type . In the following we will specialize Theorem 1 and discuss under what conditions such a mechanism is optimal.
We can simplify the conditions in Theorem 1 by recalling that the convex order has a simple structure for one-dimensional spaces. A cdf on a one-dimensional interval dominates a cdf in the convex order if and only if majorizes :
for all with equality for [[]Theorem 3.A.1]shaked2007stochastic. This observation simplifies the characterization in Theorem 1 whenever is affine on at most one-dimensional sets. As we will see, this is useful even if the type space is multidimensional. To illustrate the simpler conditions, we first consider when interval delegation is optimal with one-dimensional types [[, for earlier characterizations, see]]AM:08,AB:13.
Corollary 1.
Suppose and with . Delegating to the interval is optimal if and only if
-
(i)
for all ,
-
(ii)
for all with equality for , and
-
(iii)
for all with equality for .
-
Proof.
Note that the partition induced by has elements , , and for all . For all , is equivalent to and for .999For , if then follows because is continuous on the interior of . And if , there is with and hence implies . Now consider and let denote the conditional distribution of conditional on . Since is a point mass of mass at , we can use majorization to rewrite as
for all with equality for . Integrating by parts, this becomes condition (ii). Moreover, since the derivative with respect to of the left-hand side evaluated at is negative, we obtain . The argument for is analogous. ∎
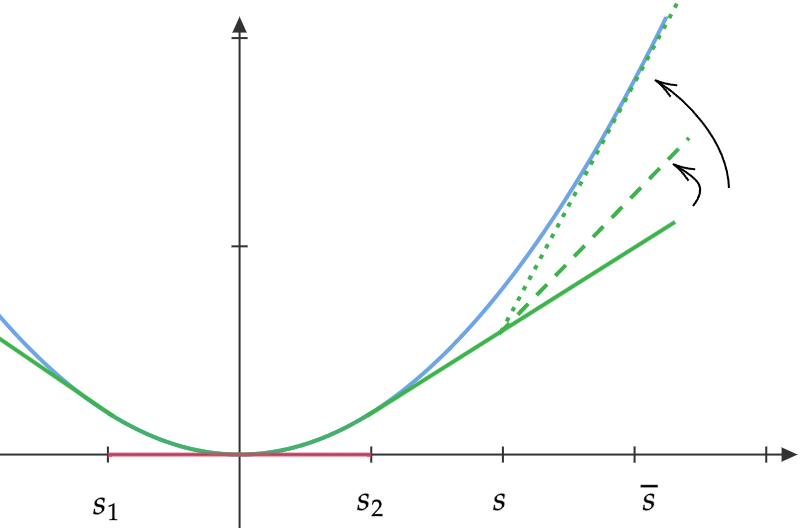
Figure 3 illustrates condition (ii). Suppose that starting with interval delegation (represented by the solid indirect utility), the principal changes the mechanism and assigns a lottery with expected value strictly above to all types above . This tilts the indirect utility starting at upwards (see the dashed indirect utility) and therefore increases the indirect utility for every type in proportion to . The change in the principal’s expected payoff is therefore proportional to . Consequently, condition (ii) ensures that such changes are not profitable. Equality for implies, in addition, that it would not be profitable to marginally reduce the action for all types above either.
Interestingly, the conditions identified in Corollary 1 are in our setting equivalent to the ones obtained in [2, Proposition 2a ]. This might initially be surprising since we characterize optimality of interval delegation in the class of stochastic mechanisms and [2] characterize optimality in the class of deterministic mechanisms (and stochastic mechanisms can do strictly better in general). Figure 3 illustrates why the conditions are the same: Suppose the principal strictly benefits from deviating to the dashed indirect utility, which represents a stochastic mechanism. Since her payoff is linear in , the arguments in the previous paragraph imply that she also benefits from deviating to the dotted indirect utility. Since the dotted linear utility corresponds to a deterministic mechanism, we conclude that conditions (ii) in (iii) in Corollary 1 are necessary for interval delegation to be optimal in the class of deterministic mechanisms (and necessity of condition (i) can be shown easily). Later, it will become clear that this equivalence is specific to the one-dimensional setting.
Corollary 2.
If and is an interval, then delegating to an interval is optimal.
The key insight for this result is that any pooling region (i.e., any such that is not a singleton) must contain types with (since ) and types with (since no point measure can dominate a distinct positive measure in the convex order). If is positive on an interval, it follows that there can be at most two pooling regions. A simple argument then shows that delegating to an interval is an optimal mechanism.
Corollary 2 extends Proposition 2(a) in [4], which in our notation requires to be positive on . An simple implication of our result is the following, which can be useful for applications.
Corollary 3.
Suppose the type space is one-dimensional (i.e., ), , and the agent has a constant bias (i.e., for some ). If is logconcave then delegating to an interval is optimal.
As another illustration, let us return to Example 1 specializing to a one-dimensional type space.
Example 1 (continued).
For and , the objective function simplifies to for , , and . Since is positive on an interval, Corollary 2 implies that delegating to an interval is optimal, and it only remains to find the best interval.
The optimal interval must satisfy Condition (ii) as an equality for , which requires
and simple algebra yields . Using symmetry, it follows that it is optimal to delegate to the interval .
For a one-dimensional type space, the approach used in Corollary 1 can be used to simplify the conditions in Theorem 1 for any mechanism, not just interval delegation. More generally, this approach is useful even with multidimensional types. To see this, let be a closed and convex set and, for , let denote the normal cone to at . With quadratic payoffs, if the principal delegates and , then all types in will choose action . Moreover, if the boundary of is differentiable then is a (one-dimensional) ray and we can again use majorization to simplify the convex dominance conditions in Theorem 1.
Corollary 4.
Suppose payoffs are quadratic and is closed, convex, has nonempty interior and a differentiable boundary. Delegating to is optimal if and only if
-
(i)
for all and
-
(ii)
for all and ,
with equality for .
The conditions in Corollary 4 closely resemble those in Corollary 1. Indeed, Condition (i) in either case requires that is positive on the set of types that obtain their first-best payoffs, and Condition (ii) (and Conditions (ii) and (iii), respectively) impose that for each point on the boundary the analogous stochastic dominance condition holds.
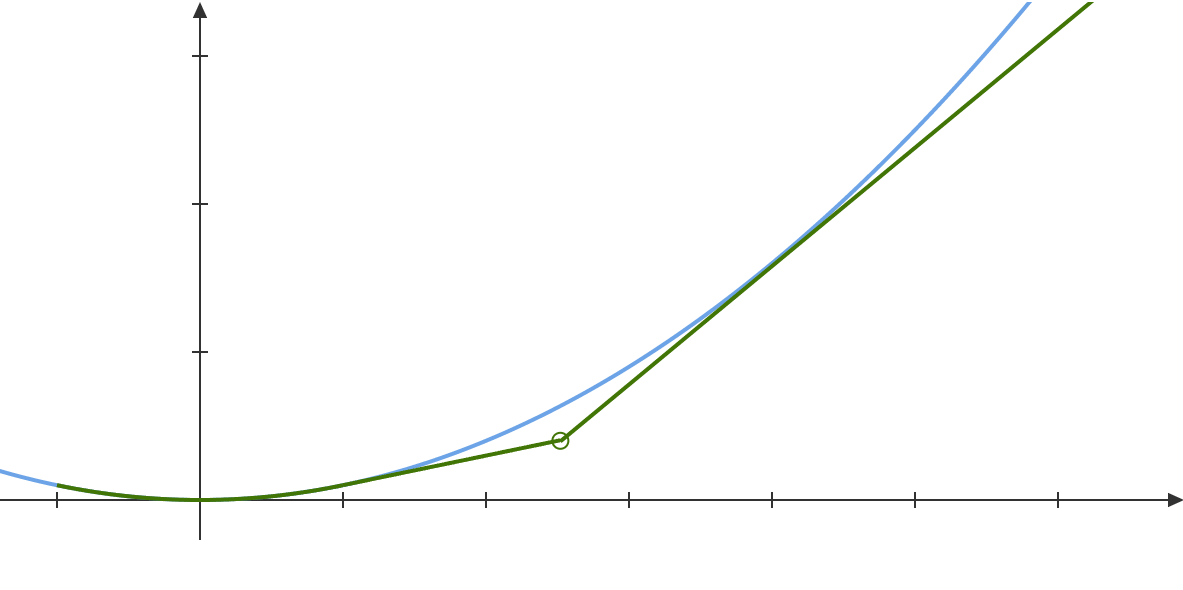
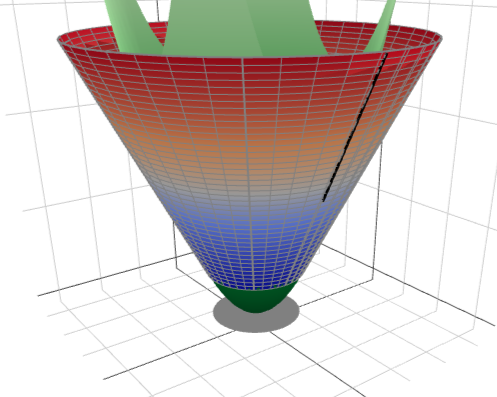
The economic interpretation of Condition (ii) is analogous to how we interpreted Condition (ii) in Corollary 1. This condition ensures that the principal does not benefit from marginally tilting the indirect utility along line segments that are orthogonal to the boundary of , e.g., the solid line segment in Figure 4. Observe that there is a stochastic mechanism in which the indirect utility is increased only in a small neighborhood of the solid line segment (by Lemma 1). On the other hand, there is no deterministic mechanism achieving this because for any deterministic action the indirect utility would have to increase significantly along the solid line segment (in order to reach the first-best payoff for some type) and convexity then requires that all types in a neighborhood of the line segment obtain higher indirect utilities. This indicates that our characterization relies in the multidimensional setting on stochastic mechanisms being feasible.
Example 1 (continued).
Consider a two-dimensional example and recall that is the uniform distribution and for some . We assume quadratic payoffs; in that case, the problem is separable across dimensions: the principal’s optimal action in dimension 1 depends only on the first component of the state and is independent of the action in dimension 2.
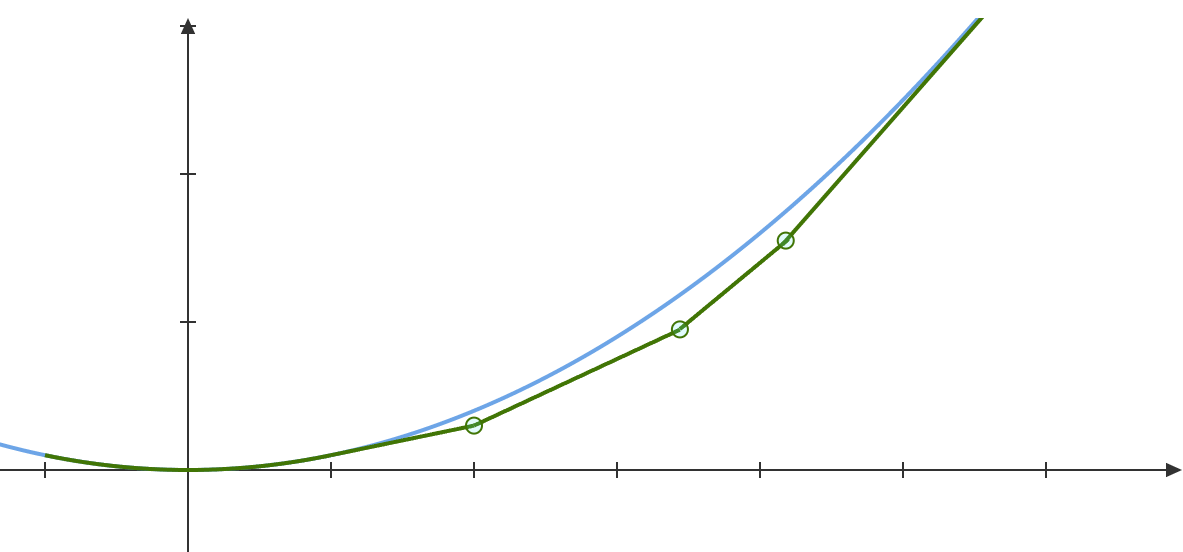
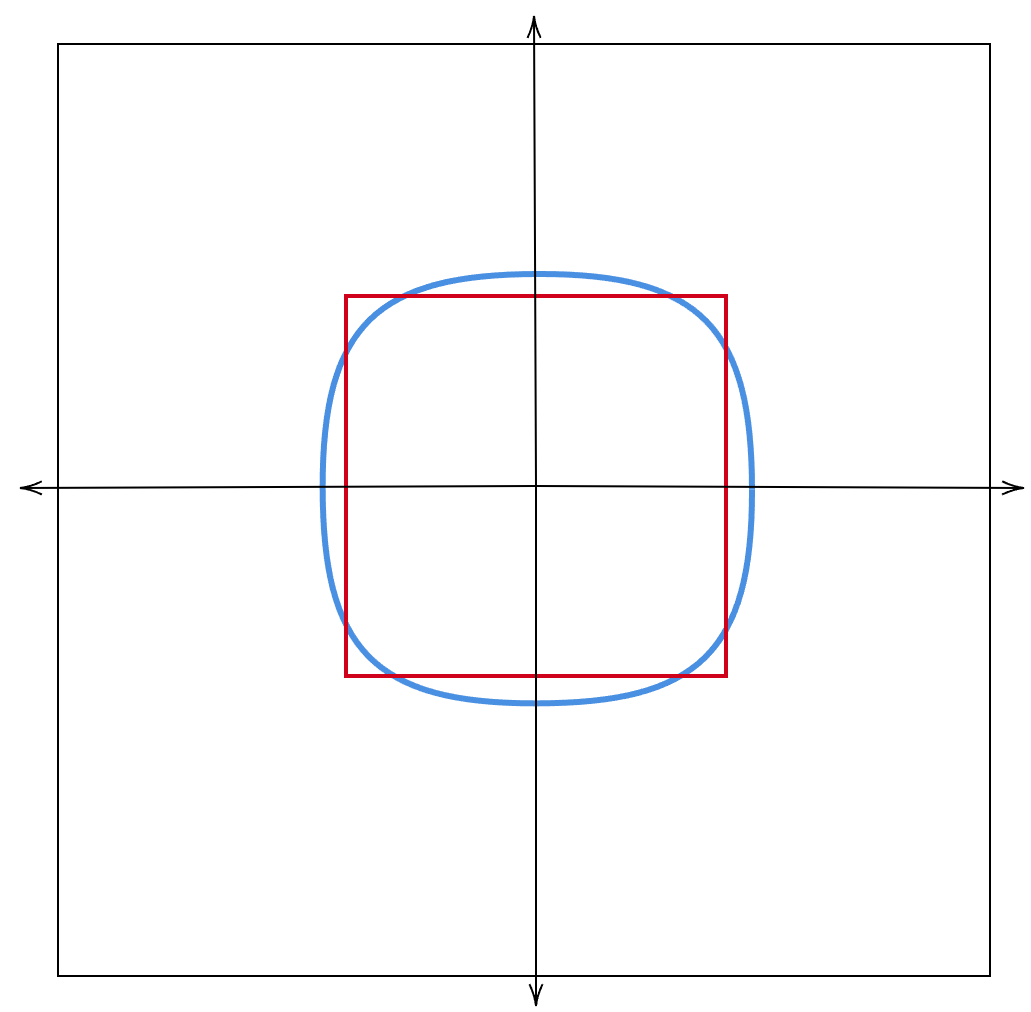
Suppose first that there are two agents: For , agent has private information about (but not for ) and cares only about the action and state in dimension . It follows that the principal faces two independent delegation problems, and our earlier analysis implies that it is optimal to let each agent choose any action in . In effect, the agents’ choice will be the action in the red square in Figure 5 that is closed to the realized state.
Now compare this to the situation where there is only one agent. This agent has private information about both dimensions of the state and cares about both dimensions of the action. How can the principal improve her expected payoff? Intuitively, she could offer the agent to take more extreme actions in one dimension if he moderates his action in the other dimension. How can the principal optimally bundle the two decision problems?
Corollary 4 provides insights into how to solve the problem: if one can find a satisfying the conditions stated there, delegating to this set will be an optimal mechanism. Since is positive on the interior of and strictly negative on the boundary of , Condition (i) will be satisfied if and Condition (ii) will be satisfied if, for every , equality holds in Condition (ii) for . This yields a second-order differential equation, whose solution describes the boundary of the optimal delegation set, see the blue curve in Figure 5 for an illustration.
4.3 Proof Sketch
To proof Theorem 1, we use duality in linear programming. To formulate the dual program, it is more convenient to work with indirect utilities that are defined on a compact domain. But recall that it is not enough to only require that for all . The following technical result ensures that we can restrict the indirect utilities to have a compact domain as long as this domain is chosen large enough.
Lemma 2.
There is a compact such that the principal’s problem can be written as .
Formally, we show that if is chosen large enough then for any solution to the above problem there is a corresponding solution to the original problem. For a convex function defined on , we consider the smallest convex function defined on that extends . If this extension lies below on a large set then for some is possible only if is large for some , i.e., the expected action for some type is large. We show that this implies that the principal’s expected payoff is low, contradicting that is a solution.
Now let be as in the above lemma and denote by the set of convex continuous functions that map to and by the set of positive measures on . We can formulate the principal’s problem as follows (and call this formulation the primal problem):
| (P) | ||||
The dual problem
We will show that the following problem is the dual problem:
| (D) | ||||
where denotes the convex order on the space of measures.
Note that is a convex function; therefore, if was a positive measure, this would be a trivial problem with solution . However, since is a signed measure and has to be a positive measure, is not feasible in general.
It is easy to see that weak duality holds, that is, the value of the primal problem (P) is always below the value of the dual problem (D). Indeed, for any feasible and ,
| (3) |
since (i) is convex and and (ii) is a positive measure and . The following result shows that strong duality holds, that is the optimal values of both problems are equal and the dual problem has a solution.
Lemma 3 (Strong duality).
A feasible mechanism is optimal if and only if there exists a positive measure such that
| (4) | ||||
| (5) |
This result is an analogue of a result in the revenue-maximization problem of a multiproduct monopolist [[, see Theorem 2 in]]daskalakis-etal2017. Our formulation of the delegation problem allows us to easily deduce strong duality. Note that there is a convex function such that for all . Therefore, Slater’s condition is satisfied and standard results from linear programming imply that the dual problem has a solution and that the optimal solutions of the primal and dual problems achieve the same value. Since both inequalities in (3) have to hold as equalities, Lemma 3 follows.
Proof idea for Theorem 1.
It is easy to show that the conditions in Theorem 1 imply that is optimal: by aggregating the measures , one obtains a positive measure satisfying the complementary slackness conditions (4) and (5) and . Lemma 3 then implies that is optimal.
For the converse direction, suppose is optimal. By Lemma 3, there is a positive measure such that the complementary slackness conditions (4) and (5) hold and . Letting () denote the positive (negative) part of , this last condition is equivalent to . Strassen’s theorem then implies that is a mean-preserving spread of : one can obtain the measure by taking, for every , the mass puts on and spreading it according to a probability measure with expected value . Since is convex, Jensen’s inequality implies that and equality holds only if is affine on the convex hull of the support of . Since equality must hold by (5), we obtain that for all and , the support of is contained in the closure of . To simplify this informal discussion, suppose that for all and , the support of is actually contained in (and not just the closure of ) and consider a partition element of positive measure. Then the conditional measure is positive (since is positive) and satisfies (since the left-hand side is a mean-preserving spread of the right-hand side). Moreover, by (5) we get for every in the support of . Since is strictly convex and is affine on , there is at most one with and therefore is a point mass at this or the zero measure. It follows that , where is a point mass at or is the zero measure. The proof in the Appendix follows this sketch but uses the additional assumption in Theorem 1 and additional arguments to deal with the case where the support of is a subset of the closure of but not a subset of .101010If lies in the closure of and , then is not differentiable at and, therefore, . If follows from (4) that such points have measure zero under . The additional assumption ensures that such points also have measure zero under and , and hence play no role.
References
- [1] Ricardo Alonso and Niko Matouschek “Optimal Delegation” In Review of Economic Studies 75.1, 2008, pp. 259–293.
- [2] Manuel Amador and Kyle Bagwell “The Theory of Optimal Delegation with an Application to Tariff Caps” In Econometrica 81.4, 2013, pp. 1541–1599
- [3] Manuel Amador and Kyle Bagwell “Money burning in the theory of delegation” In Games and Economic Behavior 121, 2020, pp. 382–412 DOI: https://doi.org/10.1016/j.geb.2020.02.010
- [4] Manuel Amador, Kyle Bagwell and Alex Frankel “A Note on Interval Delegation” In Economic Theory Bulletin 6.2, 2018, pp. 239–249 DOI: 10.1007/s40505-017-0133-4
- [5] Attila Ambrus and Georgy Egorov “Delegation and Nonmonetary Incentives” In Journal of Economic Theory 171, 2017, pp. 101–135
- [6] Mark Armstrong “Delegating Decision-Making to an Agent with Unknown Preferences” unpublished, 1995
- [7] Vladimir Igorevich Bogachev “Measure theory” Springer, 2007
- [8] Vladimir Igorevich Bogachev “Measure theory” Springer, 2007
- [9] Archishman Chakraborty and Rick Harbaugh “Comparative cheap talk” In Journal of Economic Theory 132.1 Elsevier, 2007, pp. 70–94
- [10] Constantinos Daskalakis, Alan Deckelbaum and Christos Tzamos “Strong Duality for a Multiple-Good Monopolist” In Econometrica 85.3 Blackwell Publishing Ltd, 2017, pp. 735–767 DOI: 10.3982/ECTA12618
- [11] F Dragomirescu and C Ivan “The smallest convex extensions of a convex function” In Optimization 24.3-4 Taylor & Francis, 1992, pp. 193–206
- [12] Nelson Dunford and Jacob T. Schwartz “Linear Operators, Part 1: General Theory” John WileySons, 1988
- [13] Alex Frankel “Aligned delegation” In American Economic Review 104.1, 2014, pp. 66–83
- [14] Alex Frankel “Delegating multiple decisions” In American Economic Journal: Microeconomics 8.4, 2016, pp. 16–53
- [15] Simone Galperti “A theory of personal budgeting” In Theoretical Economics 14.1 Wiley Online Library, 2019, pp. 173–210
- [16] Nima Haghpanah and Jason Hartline “When is pure bundling optimal?” In The Review of Economic Studies 88.3 Oxford University Press, 2021, pp. 1127–1156
- [17] Jean-Baptiste Hiriart-Urruty and Claude Lemaréchal “Fundamentals of convex analysis” Springer Science & Business Media, 2004
- [18] Bengt Holmström “On Incentives and Control in Organizations” Ph.D. Thesis, Stanford University, 1977
- [19] Bengt Holmström “On the Theory of Delegation” In Bayesian Models in Economic Theory North Holland, 1984, pp. 115–141
- [20] Matthew O Jackson and Hugo F Sonnenschein “Overcoming incentive constraints by linking decisions” In Econometrica 75.1 Wiley Online Library, 2007, pp. 241–257
- [21] Navin Kartik, Andreas Kleiner and Richard Van Weelden “Delegation in veto bargaining” In American Economic Review 111.12, 2021, pp. 4046–87
- [22] Andreas Kleiner, Benny Moldovanu and Philipp Strack “Extreme points and majorization: Economic applications” In Econometrica 89.4 Wiley Online Library, 2021, pp. 1557–1593
- [23] Frédéric Koessler and David Martimort “Optimal delegation with multi-dimensional decisions” In Journal of Economic Theory 147.5 Elsevier, 2012, pp. 1850–1881
- [24] Anton Kolotilin and Andriy Zapechelnyuk “Persuasion meets Delegation” unpublished, 2019
- [25] Eugen Kováč and Tymofiy Mylovanov “Stochastic Mechanisms in Settings Without Monetary Transfers: The Regular Case” In Journal of Economic Theory 144.4, 2009, pp. 1373–1395
- [26] Elliot Lipnowski and Doron Ravid “Cheap talk with transparent motives” In Econometrica 88.4 Wiley Online Library, 2020, pp. 1631–1660
- [27] Alejandro M Manelli and Daniel R Vincent “Bundling as an optimal selling mechanism for a multiple-good monopolist” In Journal of Economic Theory 127.1 Elsevier, 2006, pp. 1–35
- [28] Alejandro M Manelli and Daniel R Vincent “Multidimensional mechanism design: Revenue maximization and the multiple-good monopoly” In Journal of Economic theory 137.1 Elsevier, 2007, pp. 153–185
- [29] Albert W Marshall, Ingram Olkin and Barry C Arnold “Inequalities: theory of majorization and its applications” Springer, 2010
- [30] Nahum Melumad and Toshiyuki Shibano “Communication in Settings with No Transfers” In RAND Journal of Economics 22.2, 1991, pp. 173–198
- [31] Robert R Phelps “Lectures on Choquet’s theorem” Springer, 2001
- [32] Chris Preston “Some Notes on Standard Borel and Related Spaces” arXiv, 2008 DOI: 10.48550/ARXIV.0809.3066
- [33] Jean-Charles Rochet “A necessary and sufficient condition for rationalizability in a quasi-linear context” In Journal of Mathematical Economics 16.2 Elsevier, 1987, pp. 191–200
- [34] Jean-Charles Rochet and Philippe Choné “Ironing, sweeping, and multidimensional screening” In Econometrica JSTOR, 1998, pp. 783–826
- [35] Moshe Shaked and J George Shanthikumar “Stochastic orders” Springer, 2007
- [36] Alexander Shapiro “On duality theory of conic linear problems” In Semi-Infinite Programming: Recent Advances Springer, U.S.A., 2010
Appendix A Omitted Proofs
-
Proof of Lemma 2.
Let denote a ball of radius around and let be a solution to . We will show that can be extended to a solution to the principal’s original problem. Let denote the smallest convex extension to of the restriction of to [[, see]]dragomirescu92. If is not feasible for the original problem then there is such that and there is such that (since is the smallest convex extension). Using strong convexity of (which follows since has Lipschitz-continuous gradients, see Theorem E.4.2.2 in [17]), one can show that , where as .111111 Let denote modulus of convexity of . Then, for all that lie on the line segment from to x, and all , Since and the first two terms of the RHS are positive, the claim follows. Then either for all or, on a set of positive Lebesgue-measure, for some constant independent of and . Since by assumption, this implies that in either case for large enough, the principals payoff from will be less than her payoff from taking the ex-ante optimal action. This contradicts our assumption that was optimal. Hence, any solution can be extended to a solution of the original problem. ∎
-
Proof of Lemma 3.
Let denote the vector space of continuous functions on with the supremum norm and recall that its dual space is the space of (Radon) measures on , which we denote by . Let ; the polar cones of and are defined by
The principal’s problem can be written as subject to . This is a conical linear program and its dual is subject to [[, e.g.,]]shapiro10. Since by the Riesz representation theorem [[]p. 65]dunford-schwartz88a and is equivalent to , (D) is the dual problem.
Since there is such that is in the interior of , Slater’s condition is satisfied and standard results imply that strong duality holds [[, e.g.,]Proposition 2.8]shapiro10. Therefore, is optimal if and only if there is a positive measure such that , which implies the result. ∎
-
Proof of Theorem 1.
Given , we denote by the partition element of that contains .
“”: Let . Given the properties of , we conclude that and . Moreover, for all ,
and equality holds for because (i) is affine on each and (ii) implies for any affine function . Therefore, is feasible for the dual problem and satisfies the complementary slackness conditions (4) and (5). We conclude that is optimal.
“”: By Lemma 3, is optimal if and only if there is satisfying (4), (5), and . Letting and denote the positive and negative parts of , respectively, the last condition becomes . Since both sides of the inequality are positive measures, Strassen’s theorem [[, see, for example,]p. 93-94]phelps01 implies that there is a dilation (that is, for each , is a probability measure with barycenter ) satisfying .
Let be a (regular, proper) system of conditional measures (such conditional measures exist by Example 10.4.11 in [8]), which by definition satisfies
for all . Letting , we claim that there is such that has -measure 0 and, for all , is a positive measure that has support on .
Before proving this claim, we show that it implies the result: From the definition of it follows that if is a positive measure then . Also, since is a dilation; therefore, if has support in then , where is a point mass at or the zero measure if for all . For each , we let be the zero measure and observe that is still a conditional measure for since has measure 0. This proves the result.
First, suppose there is with strictly positive -measure such that, for all , the support of is not a subset of the closure of . Fix arbitrary . Since the support of is not contained in the closure of , there is a set of strictly positive -measure such that, for all , the support of is not contained in the closure of . Since Jensen’s inequality is strict whenever the convex function is not affine on the convex hull of the support [[]Proposition 16.C.1]marshall79, we obtain
This yields
which contradicts (5). We conclude that, except possibly on a -Null set, the support of is a subset of the closure of .
Second, we show that is a positive measure for -almost every : Let
and note that for any , is not differentiable at and therefore . Since by (4), . Moreover, because is continuously differentiable -almost everywhere by assumption. Let denote the -algebra generated by and note that the Borel -algebra on is generated by some countable algebra [[]Propositions 3.1 and 3.3]preston08. For each and ,
The bracketed term equals and is therefore positive. The last term is zero since
(recall that ). Since is -measurable in , it follows that there is a -Null set such that for all . Letting , for all and Borel sets , by Caratheodory’s extension theorem [[, see]Theorem 1.5.6 and the comment afterward]bogachev07a.
Finally, if it is not true that for -almost every , the support of is a subset of , then , contradicting (4). Moreover, for any , is not differentiable at and therefore (because and is differentiable). We conclude that there is a collection with -measure 0 such that, for all , is a positive measure that has support on . ∎
-
Proof of Corollary 2.
Let be an optimal indirect utility and a corresponding partition. Since and , any pooling region121212That is, any such that contains strictly more than one element. must contain types with and types with .
If and , is positive everywhere and the claim follows. So suppose ; then there is a pooling region which contains and some with . If , then must hold and the claim follows. Therefore, assume . The measure from Theorem 1 must be a point mass at some with (if were the zero measure or a point mass at with , then whenever , which contradicts ). It follows that .
If then for all and delegating to is optimal. If , repeating our previous argument implies that there is an interval which contains and some with and . Since for all , delegating to is optimal. If and , a symmetric argument applies. ∎
-
Proof of Corollary 3.
It follows from (1) that for . If then is singlecrossing from below on (since is logconcave) and . The claim then follows from Corollary 2. ∎
-
Proof of Corollary 4.
The corresponding indirect utility induces the partition with the following elements: for any in the interior of , , and for any , the normal cone , which is a ray through and orthogonal to . For any such normal ray , condition (ii) is equivalent to by the same argument as in Corollary 1.
“”: Condition (i) ensures that is positive for all in the interior of . Since it has singleton support, . For any normal ray , by condition (ii) and since follows from condition (ii). It follows from Theorem 1 that is optimal.
“”: If for some in the interior of then there is a subset of with positive -measure on which is strictly negative, which implies on a set of positive measure, which contradicts optimality of . Similarly, if for some then it can be shown that on a set of positive measure, which contradicts optimality of by Theorem 1.
If condition (ii) is violated, on a set of positive measure, which again contradicts optimality of by Theorem 1. ∎