Optimal Control of Multi-Agent Systems
with Processing Delays

Mruganka Kashyap M. Kashyap is with the Department of Electrical and Computer Engineering at
Northeastern University, Boston, MA 02115, USA. (e-mail: [email protected]). Laurent Lessard L. Lessard is with the Department of Mechanical and Industrial Engineering at
Northeastern University, Boston, MA 02115, USA. (e-mail: [email protected]).

Abstract

In this article, we consider a cooperative control problem involving a heterogeneous network of dynamically decoupled continuous-time linear plants. The (output-feedback) controllers for each plant may communicate with each other according to a fixed and known transitively closed directed graph. Each transmission incurs a fixed and known time delay. We provide an explicit closed-form expression for the optimal decentralized controller and its associated cost under these communication constraints and standard linear quadratic Gaussian (LQG) assumptions for the plants and cost function. We find the exact solution without discretizing or otherwise approximating the delays. We also present an implementation of each sub-controller that is efficiently computable, and is composed of standard finite-dimensional linear time-invariant (LTI) and finite impulse response (FIR) components, and has an intuitive observer-regulator architecture reminiscent of the classical separation principle.

1 Introduction

In multi-agent systems such as swarms of unmanned aerial vehicles, it may be desirable for agents to cooperate in a decentralized fashion without receiving instructions from a central coordinating entity. Each agent takes local measurements, performs computations, and may communicate its measurements with a given subset of the other agents, with a time delay. In this article, we investigate the problem of optimal control under the aforementioned communication constraints.

We model each agent as a continuous-time linear time-invariant (LTI) system. We make no assumption of homogeneity across agents; each agent may have different dynamics. We assume the aggregate dynamics of all agents are described by the state-space equations

\begin{bmatrix}\dot{x}\\ z\\ y\end{bmatrix}=\begin{bmatrix}A&B_{1}&B_{2}\\ C_{1}&0&D_{12}\\ C_{2}&D_{21}&0\end{bmatrix}\begin{bmatrix}x\\ w\\ u\end{bmatrix},

(1)

where $x$ is the global state, $z$ is the regulated output, $y$ is the measured output, $w$ is the exogenous disturbance, and $u$ is the controlled input. The decoupled nature of the agents imposes a sparsity structure on the plant. Namely, if we partition $x$ , $y$ , $w$ , $u$ each into $N$ pieces corresponding to the $N$ agents, the conformally partitioned state space matrices $A$ , $B_{1}$ , $B_{2}$ , $C_{2}$ , $D_{21}$ are block-diagonal. The regulated output $z$ , however, couples all agents’ states and inputs, so in general $C_{1}$ and $D_{12}$ will be dense. The matrix transfer function $(w,u)\to(z,y)$ is a standard four-block plant that takes the form¹¹1In a slight abuse of notation, the vectors $z$ , $y$ , $w$ , and $u$ now refer to the Laplace transforms of the corresponding time-domain signals in (1).

\begin{bmatrix}z\\ y\end{bmatrix}=\begin{bmatrix}\mathcal{P}_{11}(s)&\mathcal{P}_{12}(s)\\ \mathcal{P}_{21}(s)&\mathcal{P}_{22}(s)\end{bmatrix}\begin{bmatrix}w\\ u\end{bmatrix},

(2)

where $\mathcal{P}_{21}$ and $\mathcal{P}_{22}$ are block-diagonal.

We assume information sharing is mediated by a fixed and known directed graph. Specifically, if there is a (possibly multi-hop) directed path from Agent $i$ to Agent $j$ , then Agent $j$ can observe the local measurements of Agent $i$ with a delay $\tau$ . We further assume there are no self-delays, so agents can observe their local measurements instantaneously.

In practice, our setting corresponds to a network where the chief source of latency is due to processing and transmission delays [12, §1.4] (the encoding, decoding, and transmission of information). Therefore, we neglect propagation delays (proportional to distance traveled) and queuing delays (related to network traffic and hops required to reach the destination).

We assume $\tau$ is fixed and known and homogeneous across all communication paths, as it is determined by the physical capabilities (e.g., underlying hardware and software) of the individual agents rather than external factors. Thus, Agent $i$ ’s feedback policy (in the Laplace domain) is of the form²²2There is no loss of generality in assuming a linear control policy; see Section 1.1 for details.

u_{i}=\mathcal{K}_{ii}(s)y_{i}+\sum_{j\to i}e^{-s\tau}\mathcal{K}_{ij}(s)y_{j},

(3)

where the sum is over all agents $j$ for which there is a directed path from $j$ to $i$ in the underlying communication graph.

Given the four-block plant (2), the directed communication graph, and the processing delay $\tau$ , we study the problem of finding a structured controller that is internally stabilizing and minimizes the $\mathcal{H}_{2}$ norm of the closed-loop map $w\to z$ .

In spite of the non-classical information structure present in this problem, it is known that there is a convex Youla-like parameterization of the set of stabilizing structured controllers, and the associated $\mathcal{H}_{2}$ synthesis problem is a convex, albeit infinite-dimensional, optimization problem.

Main contribution. We provide a complete solution to this structured cooperative control problem that is computationally tractable and intuitively understandable. Specifically, the optimal controller can be implemented with a finite memory and transmission bandwidth that does not grow over time. Moreover, the controller implementations at the level of individual agents have separation structures between the observer and regulator reminiscent of classical $\mathcal{H}_{2}$ synthesis theory.

In the remainder of this section, we give context to this problem and relate it to works in optimal control, delayed control, and decentralized control. In Section 2, we cover some mathematical preliminaries and give a formal statement of the problem. In Section 3, we give a convex parameterization of all structured suboptimal controllers, and present the $\mathcal{H}_{2}$ -optimal controller for the non-delayed ( $\tau=0$ ) and delayed ( $\tau>0$ ) cases. In Section 4, we describe the optimal controller architecture at the level of the individual agents, and give intuitive interpretations of the controller architecture. In Section 5, we present case studies that highlight the trade-offs between processing delay, connectivity of the agents, and optimal control cost. Finally, we conclude in Section 6 and discuss future directions.

1.1 Literature review

If we remove the structural constraint (3) and allow each $u_{i}$ to have an arbitrary causal dependence on all $y_{j}$ with no delays, the optimal controller is linear and admits an observer–regulator separation structure [34]. This is the classical $\mathcal{H}_{2}$ (LQG) synthesis problem, solved for example in [37].

The presence of structural constraints generally leads to an intractable problem [1]. For example, linear compensators can be strictly suboptimal, even under LQG assumptions [33]. Moreover, finding the best linear compensator also leads to a non-convex infinite-dimensional optimization problem.

However, not all structural constraints lead to intractable synthesis problems. For LQG problems with partially nested information, there is a linear optimal controller [4]. If the information constraint is quadratically invariant with respect to the plant, the problem of finding the optimal LTI controller can be convexified [27, 26]. The problem considered in this article is both partially nested and quadratically invariant, so there is no loss in assuming a linear policy as we do in (3).

Once the problem is convexified, the optimal controller can be computed exactly using approaches like vectorization [28, 32], or approximated to arbitrary accuracy using Galerkin-style numerical approaches [25, 29]. However, these approaches lead to realizations of the solution that are neither minimal nor easily interpreted. For example, a numerical solution will not reveal a separation structure in the optimal controller, nor will it provide an interpretation of controller states or the signals communicated between agents’ controllers. Indeed, the optimal controller may have a rich structure, reminiscent of the centralized separation principle. Such explicit solutions were found for broadcast [15], triangular [31, 18], and dynamically decoupled [9, 8, 6] cases.

The previously mentioned works do not consider time delays. In the presence of delays, we distinguish between discrete and continuous time. In discrete time, the delay transfer function $z^{-1}$ is rational. Therefore, the problem may be reduced to the non-delayed case by absorbing each delay into the plant [14]. However, this reduction is not possible in continuous time because the continuous-time delay transfer function $e^{-s\tau}$ is irrational. A Padé approximation may be used for the delays [35], but this leads to approximation error and a larger state dimension.

Although the inclusion of continuous-time delays renders the state space representation infinite-dimensional, the optimal controller may still have a rich structure. For systems with a dead-time delay (the entire control loop is subject to the same delay), a loop-shifting approach using finite impulse response (FIR) blocks can transform the problem into an equivalent delay-free LQG problem with a finite-dimensional LTI plant [24, 20]. A similar idea was used in the discrete-time case to decompose the structure into dead-time and FIR components, which can be optimized separately [13].

The loop-shifting technique can be extended to the adobe delay case, where the feedback path contains both a delayed and a non-delayed path [21, 22, 23]. The loop-shifting technique was also extended to specific cases like bilateral teleoperation problems that involve two stable plants whose controllers communicate across a delayed channel [10, 2], and haptic interfaces that have two-way communication with a shared virtual environment [11]. Another example is the case of homogeneous agents coupled via a diagonal-plus-low-rank cost [19]. All three of these examples are special cases of the information structure (3).

In the present work, we solve a general structured $\mathcal{H}_{2}$ synthesis problem with $N$ agents that communicate using a structure of the form (3). We present explicit solutions that show an intuitive observer-regulator structure at the level of each individual sub-controller. Preliminary versions of these results that only considered stable or non-delayed plants were reported in [6, 7]. In this article, we consider the general case of an unstable plant, we find an agent-level parameterization of all stabilizing controllers, and we obtain explicit closed-form expressions for the optimal cost.

2 Preliminaries

Transfer matrices.

Let $\mathbb{C}_{\alpha}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\left\{s\in\mathbb{C}\;|\;\operatorname{Re}(s)>\alpha\right\}$ and $\bar{\mathbb{C}}_{\alpha}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\left\{s\in\mathbb{C}\;|\;\operatorname{Re}(s)\geq\alpha\right\}$ . A transfer matrix $\mathcal{G}(s)$ is said to be proper if there exists an $\alpha>0$ such that $\sup_{s\in\mathbb{C}_{\alpha}}\lVert{\mathcal{G}(s)}\rVert<\infty$ . We call this set $\mathcal{L}_{\textup{prop}}$ . Similarly, a transfer matrix $\mathcal{G}(s)$ is said to be strictly proper if this supremum vanishes as $\alpha\rightarrow\infty$ . The Hilbert space $\mathcal{L}_{2}$ consists of analytic functions $\mathcal{F}:i\mathbb{R}\to\mathbb{C}^{m\times n}$ equipped with the inner product $\langle\mathcal{F},\mathcal{G}\rangle\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\frac{1}{2\pi}\int_{\mathbb{R}}\operatorname{\mathrm{tr}}\bigl{(}\mathcal{F}(i\omega)^{*}\mathcal{G}(i\omega)\bigr{)}\,\mathrm{d}\omega$ , where the inner product induced norm $\lVert{\mathcal{F}}\rVert_{2}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}{\langle\mathcal{F},\mathcal{F}\rangle}^{1/2}$ is bounded. A function $\mathcal{F}:\bar{\mathbb{C}}_{0}\to\mathbb{C}^{m\times n}$ is in $\mathcal{H}_{2}$ if $\mathcal{F}(s)$ is analytic in $\mathbb{C}_{0}$ , $\textup{lim}_{\sigma\rightarrow 0^{+}}\mathcal{F}\left(\sigma+i\omega\right)=\mathcal{F}\left(i\omega\right)$ for almost every $\omega\in\mathbb{R}$ , and $\sup_{\sigma\geq 0}\frac{1}{2\pi}\int_{-\infty}^{\infty}\operatorname{\mathrm{tr}}\bigl{(}\mathcal{F}(\sigma+i\omega)^{*}\mathcal{F}(\sigma+i\omega)\bigr{)}\,\mathrm{d}\omega<\infty$ . This supremum is always achieved at $\sigma=0$ when $\mathcal{F}\in\mathcal{H}_{2}$ . The set $\mathcal{H}_{2}^{\perp}$ is the orthogonal complement of $\mathcal{H}_{2}$ in $\mathcal{L}_{2}$ . The set $\mathcal{RH}_{2}$ refers to the subspace of strictly proper rational transfer functions with no poles in $\bar{\mathbb{C}}_{0}$ . Similarly, the set $\mathcal{RH}_{2}^{\perp}$ refers to the subspace of strictly proper rational transfer functions with all poles in $\mathbb{C}_{0}$ . The set $\mathcal{L}_{\infty}$ consists of matrix-valued functions $\mathcal{F}:i\mathbb{R}\to\mathbb{C}^{m\times n}$ for which $\sup_{\omega\in\mathbb{R}}\lVert{\mathcal{F}(i\omega)}\rVert<\infty$ . $\mathcal{H}_{\infty}$ and $\mathcal{RH}_{\infty}$ are defined analogously to $\mathcal{H}_{2}$ and $\mathcal{RH}_{2}$ .

The state-space notation for transfer functions is

\displaystyle\mathcal{G}(s)=\left[\begin{array}[]{c|c}A&B\\ \hline\cr\rule{0.0pt}{9.90276pt}C&D\end{array}\right]\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}D+C(sI-A)^{-1}B.

(6)

A square matrix $A$ is Hurwitz if none of its eigenvalues belong to $\mathbb{C}_{0}$ . If $A$ is Hurwitz in (6), then $\mathcal{G}\in\mathcal{RH}_{\infty}$ . If $A$ is Hurwitz and $D=0$ , then $\mathcal{G}\in\mathcal{RH}_{2}$ . The conjugate of $\mathcal{G}$ is

\displaystyle\mathcal{G}^{\sim}(s)=\mathcal{G}^{\mathsf{T}}(-s)=\left[\begin{array}[]{c|c}-A^{\mathsf{T}}&C^{\mathsf{T}}\\ \hline\cr\rule{0.0pt}{9.90276pt}{-B^{\mathsf{T}}}&D^{\mathsf{T}}\end{array}\right].

The dynamics (1) and four-block plant $\mathcal{P}$ from (2) satisfy

\mathcal{P}(s)\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\begin{bmatrix}\mathcal{P}_{11}(s)&\mathcal{P}_{12}(s)\\ \mathcal{P}_{21}(s)&\mathcal{P}_{22}(s)\end{bmatrix}=\left[\begin{array}[]{c|cc}A&B_{1}&B_{2}\\ \hline\cr\rule{0.0pt}{9.90276pt}C_{1}&0&D_{12}\\ C_{2}&D_{21}&0\end{array}\right].

(7)

If we use the feedback policy $u=\mathcal{K}y$ , then we can eliminate $u$ and $y$ from (2) to obtain the closed-loop map $w\to z$ , which is given by the lower linear fractional transformation (LFT) defined as $\mathcal{F}_{l}(\mathcal{P},\mathcal{K})\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\mathcal{P}_{11}+\mathcal{P}_{12}\mathcal{K}(I-\mathcal{P}_{22}\mathcal{K})^{-1}\mathcal{P}_{21}$ . LFTs can be inverted: if $\mathcal{K}=\mathcal{F}_{l}(\mathcal{J},\mathcal{Q})$ and $\mathcal{J}$ has a proper inverse, then $\mathcal{Q}=\mathcal{F}_{u}(\mathcal{J}^{-1},\mathcal{K})$ , where $\mathcal{F}_{u}$ is the upper linear fractional transformation: $\mathcal{F}_{u}(\mathcal{P},\mathcal{K})\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\mathcal{P}_{22}+\mathcal{P}_{21}\mathcal{K}(I-\mathcal{P}_{11}\mathcal{K})^{-1}\mathcal{P}_{12}$ .

Block indexing.

Ordered lists of indices are denoted using $\{\ldots\}$ . The total number of agents is $N$ and $[N]\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\{1,\dots,N\}$ . The $i^{\text{th}}$ subsystem has state dimension $n_{i}$ , input dimension $m_{i}$ , and measurement dimension $p_{i}$ . The global state dimension is $n\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}n_{1}+\cdots+n_{N}$ and similarly for $m$ and $p$ . The matrix $I_{k}$ is the identity of size $k$ and $\operatorname{\mathrm{blkd}}(\{X_{i}\})$ is the block-diagonal matrix formed by the blocks $\{X_{1},\dots,X_{n}\}$ . The zeros used throughout are matrix or vector zeros and their sizes are dependent on the context.

We write $\underline{i}$ to denote the descendants of node $i$ , i.e., the set of nodes $j$ such that there is a directed path from $i$ to $j$ for all $i\in[N]$ . By convention, we list $i$ first, and then the remaining indices in increasing order. The directed path represents the direction of information transfer between the agents. Similarly, $\bar{i}$ denotes the ancestors of node $i$ (again listing $i$ first). We also use $\bar{\bar{i}}$ and $\underline{\underline{i}}$ to denote the strict ancestors and descendants, respectively, which excludes $i$ . For example, in Fig. 1, we have $\underline{2}=\{2,5\}$ and $\bar{\bar{3}}=\{1,4\}$ .

Refer to caption — Figure 1: Directed graph representing five interconnected systems.

We also use this notation to index matrices. For example, if $X$ is a $5\times 5$ block matrix, then $X_{1\underline{2}}=\begin{bmatrix}X_{12}&X_{15}\end{bmatrix}$ . We will use specific partitions of the identity matrix throughout: $I_{n}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{blkd}}(\{I_{n_{i}}\})$ , and for each agent $i\in[N]$ , we define $E_{n_{i}}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}(I_{n})_{:i}$ (the $i^{\textup{th}}$ block column of $I_{n}$ ). We have $n_{\underline{i}}=\sum_{k\in\underline{i}}n_{k}$ and $n_{\bar{i}}=\sum_{k\in\bar{i}}n_{k}$ , akin to the descendant and ancestor definitions above. The dimensions of $E_{{n_{\bar{i}}}}$ and $E_{{n_{\underline{i}}}}$ are determined by the context of use. We also use the notations $X_{:i}$ and $X_{\bar{i}:}$ to indicate the $i^{\textup{th}}$ block column and $\bar{i}^{\textup{th}}$ block rows respectively for a matrix $X$ . Similar notations $1_{n}$ is the $n\times 1$ matrix of $1$ ’s. Further notations are defined at their points of first use.

2.1 Delay

We follow the notation conventions set in [23]. The adobe delay matrix $\Lambda_{m}^{i}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{blkd}}(I_{m_{i}},e^{-s\tau}I_{m_{\underline{\underline{i}}}})$ leaves block $i$ unchanged and imposes a delay of $\tau$ on all strict descendants of $i$ . We define $\Gamma:(\mathcal{P},\Lambda_{m}^{i})\mapsto(\tilde{\mathcal{P}},\Pi_{u},\Pi_{b})$ that maps the plant $\mathcal{P}$ in (7) and adobe delay matrix $\Lambda_{m}^{i}$ to a modified plant $\tilde{\mathcal{P}}$ and FIR systems $\Pi_{u}$ and $\Pi_{b}$ . This loop-shifting transformation reported in [21, 23, 22] shown in Fig. 2 transforms a loop with adobe input delay into a modified system involving a rational plant $\tilde{\mathcal{P}}$ . See Section A for details on the definition of $\Gamma$ .

In this decomposition, $\langle\Delta,\Psi\rangle=0$ and $\Psi$ is inner (if $\Psi\in\mathcal{RH}_{\infty}$ and $\Psi^{\sim}\Psi=I$ ), so the closed-loop map satisfies $\lVert{\mathcal{F}_{l}(\mathcal{P},\Lambda_{m}^{i}\mathcal{K})}\rVert^{2}=\lVert{\Delta}\rVert^{2}+\lVert{\mathcal{F}_{l}(\tilde{\mathcal{P}},\tilde{\mathcal{K}})}\rVert^{2}$ . Thus, we can find the $\mathcal{H}_{2}$ -optimal $\mathcal{K}$ by first solving a standard $\mathcal{H}_{2}$ problem with $\tilde{\mathcal{P}}$ to obtain $\tilde{\mathcal{K}}$ , and then transforming back using $\mathcal{K}=\Pi_{u}\tilde{\mathcal{K}}(I-\Pi_{b}\tilde{\mathcal{K}})^{-1}$ . This transformation, illustrated in the bottom left panel of Fig. 2, has the form of a modified Smith predictor, where the FIR blocks $\Pi_{u}$ and $\Pi_{b}$ compensate for the effect of the adobe delay in the original loop. See [22, §III.C] for further detail.

2.2 Problem statement

Consider a four-block plant (7) representing the aggregated dynamics of $N$ agents as described in Section 1, which we label using indices $i\in[N]$ . Suppose $x\in\mathbb{R}^{n}$ , $u\in\mathbb{R}^{m}$ , and $y\in\mathbb{R}^{p}$ , partitioned conformally with the $N$ subsystems as $n=n_{1}+\cdots+n_{N}$ and similarly for $m$ and $p$ .

Consider a directed graph on the nodes $[N]$ , and let $\mathcal{S}_{\tau}$ be the set of compensators of the form (3). For example, for the directed graph of Fig. 1, every controller takes the form

\begin{bmatrix}\mathcal{K}_{11}&0&0&0&0\\ e^{-s\tau}\mathcal{K}_{21}&\mathcal{K}_{22}&0&0&0\\ e^{-s\tau}\mathcal{K}_{31}&0&\mathcal{K}_{33}&e^{-s\tau}\mathcal{K}_{34}&0\\ e^{-s\tau}\mathcal{K}_{41}&0&e^{-s\tau}\mathcal{K}_{43}&\mathcal{K}_{44}&0\\ e^{-s\tau}\mathcal{K}_{51}&e^{-s\tau}\mathcal{K}_{52}&e^{-s\tau}\mathcal{K}_{53}&e^{-s\tau}\mathcal{K}_{54}&\mathcal{K}_{55}\end{bmatrix}

where $\mathcal{K}_{ij}\in\mathcal{L}_{\textup{prop}}$ . So each agent may use its local measurements with no delay, and measurements from its ancestors with a delay of $\tau$ . An output-feedback policy $u=\mathcal{K}y$ (internally) stabilizes $\mathcal{P}$ if

\begin{bmatrix}I&-\mathcal{P}_{22}\\ -\mathcal{K}&I\end{bmatrix}^{-1}\in\mathcal{H}_{\infty}.

For further background on stabilization, we refer the reader to [37, 3]. We consider the problem of finding a structured controller that is stabilizing and minimizes the $\mathcal{H}_{2}$ norm of the closed-loop map. Specifically, we seek to

	$\displaystyle\underset{\mathcal{K}}{\text{minimize}}$	$\displaystyle\bigl{\lVert}{\mathcal{F}_{l}(\mathcal{P},\mathcal{K})}\bigr{\rVert}_{2}^{2}$		(8)
	subject to	$\displaystyle\mathcal{K}\in\mathcal{S}_{\tau}\text{ and $\mathcal{K}$ stabilizes $\mathcal{P}$.}$		(8)

In the remainder of this section, we list our technical assumptions and define control and estimation gains that will appear in our solution. The assumptions we make ensure that relevant estimation and control subproblems are non-degenerate. We make no assumptions regarding the open-loop stability of $\mathcal{P}$ .

Assumption 1 (System assumptions).

For the $N$ interacting agents, the Riccati assumptions defined in Definition 2 hold for $(A,B_{2},C_{1},D_{12})$ and for $(A_{ii}^{\mathsf{T}},C_{2_{ii}}^{\mathsf{T}},B_{1_{ii}}^{\mathsf{T}},D_{{21}_{ii}}^{\mathsf{T}})$ for all $i\in[N]$ .

Definition 2 (Riccati assumptions).

Matrices $(A,B,C,D)$ satisfy the Riccati assumptions [8, 23] if:

R1.

$D^{\mathsf{T}}D\succ 0$ .
R2.

$(A,B)$ is stabilizable.
R3.

$\begin{bmatrix}A-j\omega I&B\\ C&D\end{bmatrix}$ has full column rank for all $\omega\in\mathbb{R}$ .

If the Riccati assumptions hold, there is a unique stabilizing solution for the corresponding algebraic Riccati equation. We write this as $(X,F)=\operatorname{\mathrm{Ric}}(A,B,C,D)$ . Thus, $X\succ 0$ satisfies

A^{\mathsf{T}}X+XA+C^{\mathsf{T}}C-(XB+C^{\mathsf{T}}D)(D^{\mathsf{T}}D)^{-1}(B^{\mathsf{T}}X+D^{\mathsf{T}}C)=0,

with $A+BF$ Hurwitz and $F\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}-(D^{\mathsf{T}}D)^{-1}(B^{\mathsf{T}}X+D^{\mathsf{T}}C)$ .

2.2.1 Riccati equations

The algebraic Riccati equations (AREs) corresponding to the centralized linear quadratic regulator (LQR) and Kalman filtering are


$\displaystyle(X_{\textup{cen}},F_{\textup{cen}})$	$\displaystyle\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{Ric}}(A,B_{2},C_{1},D_{12}),$	(9a)
$\displaystyle(Y_{\textup{cen}},L_{\textup{cen}}^{\mathsf{T}})$	$\displaystyle\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{Ric}}(A^{\mathsf{T}},C_{2}^{\mathsf{T}},B_{1}^{\mathsf{T}},D_{21}^{\mathsf{T}}).$	(9b)

Consider controlling the descendants of Agent $i$ using only measurements $y_{i}$ . The associated four-block plant is

\displaystyle{\mathcal{P}}_{i}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\left[\begin{array}[]{c c}{\mathcal{P}}_{11_{:i}}&{\mathcal{P}}_{12_{:\underline{i}}}\\ {\mathcal{P}}_{21_{ii}}&{\mathcal{P}}_{22_{i\underline{i}}}\end{array}\right]\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\left[\begin{array}[]{c|cc}A_{\underline{ii}}&B_{1_{\underline{i}i}}&B_{2_{\underline{ii}}}\\[2.0pt] \hline\cr\rule{0.0pt}{9.90276pt}{C}_{1_{:\underline{i}}}&0&D_{12_{:\underline{i}}}\\ C_{2_{i\underline{i}}}&D_{21_{ii}}&0\end{array}\right],

(15)

and we define the corresponding ARE solutions as


$\displaystyle(X^{i},F^{i})$	$\displaystyle\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{Ric}}(A_{\underline{ii}},B_{2_{\underline{ii}}},C_{1_{:\underline{i}}},D_{12_{:\underline{i}}}),$	(16a)
$\displaystyle(Y^{i},{L^{i}}^{\mathsf{T}})$	$\displaystyle\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{Ric}}(A_{ii}^{\mathsf{T}},C_{2_{ii}}^{\mathsf{T}},B_{1_{ii}}^{\mathsf{T}},D_{{21}_{ii}}^{\mathsf{T}}).$	(16b)

Note that the block-diagonal structure of the estimation subproblems implies $Y_{\textup{cen}}=\operatorname{\mathrm{blkd}}(\{Y^{i}\})$ and $L_{\textup{cen}}=\operatorname{\mathrm{blkd}}(\{L^{i}\})$ . Existence of the matrices defined in (9) and (16) follows from Assumption 1 and the fact that $A$ , $B_{1}$ , $B_{2}$ , $C_{2}$ , and $D_{21}$ are block-diagonal. If we apply the loop-shifting transformation $\Gamma$ described in Section 2.1 and Fig. 2, we obtain the modified plant

\displaystyle\tilde{\mathcal{P}}_{i}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\left[\begin{array}[]{c c}\tilde{\mathcal{P}}_{11_{:i}}&\tilde{\mathcal{P}}_{12_{:\underline{i}}}\\ {\mathcal{P}}_{21_{ii}}&\tilde{\mathcal{P}}_{22_{i\underline{i}}}\end{array}\right]\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\left[\begin{array}[]{c|cc}A_{\underline{ii}}&B_{1_{\underline{i}i}}&\tilde{B}_{2_{\underline{ii}}}\\[2.0pt] \hline\cr\rule{0.0pt}{9.90276pt}\tilde{C}_{1_{:\underline{i}}}&0&D_{12_{:\underline{i}}}\\ C_{2_{i\underline{i}}}&D_{21_{ii}}&0\end{array}\right].

This modified plant has the same estimation ARE as in (16b), but a new control ARE, which we denote

\displaystyle(\tilde{X}^{i},\tilde{F}^{i})

\displaystyle\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{Ric}}(A_{\underline{ii}},\tilde{B}_{2_{\underline{ii}}},\tilde{C}_{1_{:\underline{i}}},D_{12_{:\underline{i}}}),

(17)

Existence of the matrices defined in (17) also follows from Assumption 1 [23, Lem. 4 and Rem. 1].

3 Optimal Controller

We now present our solution to the structured optimal control problem described in Section 2.2. We begin with a convex parameterization of all structured stabilizing controllers.

3.1 Parameterization of stabilizing controllers

This parameterization is similar to the familiar state-space parameterization of all stabilizing controllers [37, 3], but with an additional constraint on the parameter $\mathcal{Q}$ to enforce the required controller structure.

Lemma 3.

Consider the structured optimal control problem described in Section 2.2with $\mathcal{P}$ given by (7) and suppose Assumption 1 holds. Pick $F_{d}$ and $L_{d}$ block-diagonal such that $A+B_{2}F_{d}$ and $A+L_{d}C_{2}$ are Hurwitz. The following are equivalent:

(i)

$\mathcal{K}\in\mathcal{S}_{\tau}$ and $\mathcal{K}$ stabilizes $\mathcal{P}$ .

(ii)

$\mathcal{K}=\mathcal{F}_{l}(\mathcal{J},\mathcal{Q})$ for some $\mathcal{Q}\in\mathcal{H}_{\infty}\cap\mathcal{S}_{\tau}$ , where

\displaystyle\mathcal{J}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\left[\begin{array}[]{c|cc}A+B_{2}F_{d}+L_{d}C_{2}&-L_{d}&B_{2}\\ \hline\cr\rule{0.0pt}{9.90276pt}F_{d}&0&I\\ -C_{2}&I&0\end{array}\right].

(21)

Proof.

A similar approach was used in [16, Thm. 11] to parameterize the set of stabilizing controllers when $\mathcal{K}\in\mathcal{S}_{0}$ (no delays). In the absence of the constraint $\mathcal{K}\in\mathcal{S}_{\tau}$ , the set of stabilizing controllers is given by $\left\{\mathcal{F}_{l}(\mathcal{J},\mathcal{Q})\;|\;\mathcal{Q}\in\mathcal{H}_{\infty}\right\}$ [37, Thm. 12.8]. It remains to show that $\mathcal{K}\in\mathcal{S}_{\tau}$ if and only if $\mathcal{Q}\in\mathcal{S}_{\tau}$ . Expanding the definition of the lower LFT, we have

\mathcal{K}=\mathcal{J}_{11}+\mathcal{J}_{12}\mathcal{Q}\left(I-\mathcal{J}_{22}\mathcal{Q}\right)^{-1}\mathcal{J}_{21}.

(22)

The matrices $A$ , $B_{2}$ , $C_{2}$ , $F_{d}$ , $L_{d}$ are block-diagonal, so $\mathcal{J}_{ij}$ is block-diagonal and therefore $\mathcal{J}_{ij}\in\mathcal{S}_{\tau}$ . The delays in our graph satisfy the triangle inequality, so $\mathcal{S}_{\tau}$ is closed under multiplication (whenever the matrix partitions are compatible). Moreover, $\mathcal{S}_{\tau}$ is quadratically invariant with respect to $\mathcal{J}_{22}$ [26]. Therefore, if $\mathcal{Q}\in\mathcal{S}_{\tau}$ , then $\mathcal{Q}\left(I-\mathcal{J}_{22}\mathcal{Q}\right)^{-1}\in\mathcal{S}_{\tau}$ [26, 17], and we conclude from (22) that $\mathcal{K}\in\mathcal{S}_{\tau}$ . Applying the inversion property of LFTs, we have $\mathcal{Q}=\mathcal{F}_{u}(\mathcal{J}^{-1},\mathcal{K})$ . Now

\mathcal{J}^{-1}=\left[\begin{array}[]{c|cc}A&B_{2}&-L_{d}\\[2.0pt] \hline\cr\rule{0.0pt}{9.90276pt}C_{2}&0&I\\ -F_{d}&I&0\end{array}\right],

so we can apply a similar argument to the above to conclude that $(\mathcal{J}^{-1})_{ij}\in\mathcal{S}_{\tau}$ and $\mathcal{K}\in\mathcal{S}_{\tau}\implies\mathcal{Q}\in\mathcal{S}_{\tau}$ .

We refer to $\mathcal{Q}$ in Lemma 3 as the Youla parameter, due to its similar role as in the classical Youla parameterization [36].

Remark 4.

Although the problem we consider is quadratically invariant (QI), the existing approaches for convexifying a general QI problem [27] or even a QI problem involving sparsity and delays [26] require strong assumptions, such as $\mathcal{P}_{22}$ being stable or strongly stabilizable. Due to the particular delay structure of our problem, the parameterization presented in Lemma 3 does not require any special assumptions and holds for arbitrary (possibly unstable) $\mathcal{P}$ .

Remark 5.

In the special case where $A$ is Hurwitz (so $\mathcal{P}$ is stable), we can substitute $F_{d}=0$ and $L_{d}=0$ in (21) to obtain a simpler parameterization of stabilizing controllers.

Using the parameterization of Lemma 3, we can rewrite the synthesis problem (8) in terms of the Youla parameter $\mathcal{Q}$ . After simplification, we obtain the convex optimization problem

	$\displaystyle\underset{\mathcal{Q}}{\text{minimize}}$	$\displaystyle\bigl{\lVert}{\mathcal{T}_{11}+\mathcal{T}_{12}\mathcal{Q}\mathcal{T}_{21}}\bigr{\rVert}_{2}^{2}$		(23)
	subject to	$\displaystyle\mathcal{Q}\in\mathcal{H}_{\infty}\cap\mathcal{S}_{\tau}.$		(23)

where $\mathcal{T}=\begin{bmatrix}\mathcal{T}_{11}&\mathcal{T}_{12}\\ \mathcal{T}_{21}&0\end{bmatrix}$

\displaystyle={\left[\begin{array}[]{cc|cc}A+B_{2}F_{d}&-B_{2}F_{d}&B_{1}&B_{2}\\ 0&A+L_{d}C_{2}&B_{1}+L_{d}D_{21}&0\\ \hline\cr\rule{0.0pt}{9.90276pt}C_{1}+D_{12}F_{d}&-D_{12}F_{d}&0&D_{12}\\ 0&C_{2}&D_{21}&0\end{array}\right]}.

(28)

Remark 6.

The convex problem (23)–(28) is similar to its unstructured counterpart [37, Thm. 12.16], except we have the additional constraint $\mathcal{Q}\in\mathcal{S}_{\tau}$ on the Youla parameter.

Remark 7.

We use $L\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}L_{\textup{cen}}=L_{d}=\operatorname{\mathrm{blkd}}(\{L^{i}\})$ throughout the rest of the article. This choice of $L$ yields a $\mathcal{Q}_{\textup{opt}}$ with reduced state dimension and simplifies our exposition.

3.2 Optimal controller without delays

When there are no processing delays ( $\tau=0$ ), the optimal structured controller is rational. We now provide an explicit state-space formula for this optimal $\mathcal{K}$ .

Theorem 8.

Consider the structured optimal control problem described in Section 2.2 and suppose Assumption 1 holds. Choose a block-diagonal $F_{d}$ such that $A+B_{2}F_{d}$ is Hurwitz. A realization of the $\mathcal{Q}_{\textup{opt}}$ that solves (23) in the case $\tau=0$ is

\displaystyle\mathcal{Q}_{\textup{opt}}={\left[\begin{array}[]{c|c}\bar{A}+\bar{B}\bar{F}&-\bar{L}\bar{\mathbf{1}}_{p}\\ \hline\cr\rule{0.0pt}{9.90276pt}\bar{\mathbf{1}}_{m}^{\mathsf{T}}(\bar{F}-\bar{F}_{d})&0\end{array}\right]}

(31)

and a corresponding $\mathcal{K}_{\textup{opt}}$ that solves (8) is

\displaystyle\mathcal{K}_{\textup{opt}}=\left[\begin{array}[]{c|c}\bar{A}+\bar{B}\bar{F}+\bar{L}\bar{C}\bar{\mathbf{1}}_{n}\bar{\mathbf{1}}_{n}^{\mathsf{T}}&-\bar{L}\bar{\mathbf{1}}_{p}\\ \hline\cr\rule{0.0pt}{9.90276pt}\bar{\mathbf{1}}_{m}^{\mathsf{T}}\bar{F}&0\end{array}\right].

(34)

In (31)–(34), we defined the new symbols

	$\displaystyle\bar{A}\!\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\!I_{N}\!\otimes\!A,\hskip 8.0pt\bar{B}\!\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\!I_{N}\!\otimes\!B_{2},\hskip 8.0pt\bar{C}\!\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\!I_{N}\!\otimes\!C_{2},\hskip 8.0pt\bar{F}_{d}\!\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\!I_{N}\!\otimes\!F_{d},$
	$\displaystyle\bar{\mathbf{1}}_{n}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}1_{N}\otimes I_{n},\qquad\bar{\mathbf{1}}_{m}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}1_{N}\otimes I_{m},\qquad\bar{\mathbf{1}}_{p}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}1_{N}\otimes I_{p}.$

Matrices $\bar{L}$ and $\bar{F}$ are block-diagonal concatenations of zero-padded LQR and Kalman gains for each agent. Specifically, $\bar{F}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{blkd}}(\{E_{m_{\underline{i}}}F^{i}E_{n_{\underline{i}}}^{\mathsf{T}}\})$ and $\bar{L}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{blkd}}(\{E_{n_{i}}L^{i}E_{p_{i}}^{\mathsf{T}}\})$ for all $i\in[N]$ , where $F^{i}$ and $L^{i}$ are defined in (16).

Proof.

See Section C.

Remark 9.

The optimal controller (34) can also be expressed explicitly in terms of the adjacency matrix; see for example [30, 6]. We opt for the realization (34) as this expression generalizes more readily to the case with delays.

Remark 10.

Since agents can act as relays, any cycles in the communication graph can be collapsed and the associated nodes can be aggregated when there are no delays. For example, the graph of Fig. 1 would become the four-node diamond graph $\{1\}\to\{3,4\}\to\{5\}$ , and $\{1\}\to\{2\}\to\{5\}$ . So in the delay-free setting, there is no loss of generality in assuming the communication graph is acyclic.

Remark 11.

Although the optimal $\mathcal{Q}_{\textup{opt}}$ (31) and associated $\mathcal{J}$ (21) depend explicitly on $F_{d}$ , the optimal $\mathcal{K}_{\textup{opt}}$ (34) does not.

3.3 Optimal controller with delays

In this section, we generalize Theorem 8 to include an arbitrary but fixed processing delay $\tau>0$ . To this end, we introduce a slight abuse of notation to aid in representing non-rational transfer functions. We generalize the notation of (6) to allow for $A,B,C,D$ that depend on $s$ . So we write:

\left[\begin{array}[]{c|c}A(s)&B(s)\\ \hline\cr\rule{0.0pt}{9.90276pt}C(s)&D(s)\end{array}\right]\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}D(s)+C(s)\left(sI-A(s)\right)^{-1}B(s).

Theorem 12.

Consider the setting of Theorem 8. The transfer function of $\mathcal{Q}_{\textup{opt}}\in\mathcal{H}_{\infty}\cap\mathcal{S}_{\tau}$ that solves (23) for any $\tau\geq 0$ is

\mathcal{Q}_{\textup{opt}}=\left[\begin{array}[]{cc|c}\bar{A}\!+\!\bar{L}\bar{C}&\tilde{B}\tilde{F}\!-\!\bar{L}\bar{\Pi}_{b}\tilde{F}\!-\!\bar{B}\bar{\Pi}_{u}\tilde{F}&0\\ \bar{L}\bar{C}&\bar{A}\!+\!\tilde{B}\tilde{F}\!-\!\bar{L}\bar{\Pi}_{b}\tilde{F}&-\bar{L}\bar{\mathbf{1}}_{p}\\ \hline\cr\rule{0.0pt}{9.90276pt}\bar{\mathbf{1}}_{m}^{\mathsf{T}}\bar{\Lambda}_{m}\bar{F}_{d}&\bar{\mathbf{1}}_{m}^{\mathsf{T}}\bar{\Lambda}_{m}(\bar{\Pi}_{u}\tilde{F}\!-\!\bar{F}_{d})&0\end{array}\right]

(35)

and a corresponding $\mathcal{K}_{\textup{opt}}$ that solves (8) is

\mathcal{K}_{\textup{opt}}=\left[\begin{array}[]{c|c}\bar{A}\!+\!\tilde{B}\tilde{F}\!+\!\bar{L}\bar{C}\bar{\mathbf{1}}_{n}\bar{\mathbf{1}}_{n}^{\mathsf{T}}\bar{\Lambda}_{n}\!-\!\bar{L}\bar{\Pi}_{b}\tilde{F}&-\bar{L}\bar{\mathbf{1}}_{p}\\ \hline\cr\rule{0.0pt}{9.90276pt}\bar{\mathbf{1}}_{m}^{\mathsf{T}}\bar{\Lambda}_{m}\bar{\Pi}_{u}\tilde{F}&0\end{array}\right],

(36)

where $\bar{A}$ , $\bar{L}$ , $\bar{F}_{d}$ , $\bar{\mathbf{1}}_{n}$ , $\bar{\mathbf{1}}_{m}$ , $\bar{\mathbf{1}}_{p}$ , are defined in Theorem 8. The remainder of the symbols are defined as follows. We apply the loop-shifting transformation $(\tilde{\mathcal{P}}_{i},\Pi_{u_{i}},\Pi_{b_{i}})=\Gamma(\mathcal{P}_{i},\Lambda_{m}^{i})$ , where $\mathcal{P}_{i}$ , $\tilde{\mathcal{P}}_{i}$ , $\tilde{F}^{i}$ are defined in Section 2.2.1, and

	$\displaystyle\tilde{F}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{blkd}}(\{E_{m_{\underline{i}}}\tilde{F}^{i}E_{n_{\underline{i}}}^{\mathsf{T}}\}),\quad\bar{\Pi}_{b}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{blkd}}(\{E_{p_{\underline{i}}}\Pi_{b_{i}}E_{m_{\underline{i}}}^{\mathsf{T}}\}),$
	$\displaystyle\tilde{B}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{blkd}}(\{E_{n_{\underline{i}}}\tilde{B}_{2_{\underline{ii}}}E_{m_{\underline{i}}}^{\mathsf{T}}\}),\quad\bar{\Pi}_{u}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{blkd}}(\{E_{m_{\underline{i}}}\Pi_{u_{i}}E_{m_{\underline{i}}}^{\mathsf{T}}\}),$
	$\displaystyle\bar{\Lambda}_{k}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{blkd}}(\{E_{k_{\underline{i}}}\Lambda_{k}^{i}E_{k_{\underline{i}}}^{\mathsf{T}}\}),\quad\textit{for}\;k\in\{m,n\}.$

Proof.

See Section D.

The transfer matrices $\mathcal{Q}_{\textup{opt}}$ in (35) and $\mathcal{K}_{\textup{opt}}$ in (36) are not rational, due to the presence of the FIR blocks $\bar{\Pi}_{u}$ , $\bar{\Pi}_{b}$ , and delay blocks $\bar{\Lambda}_{m}$ and $\bar{\Lambda}_{n}$ . Consequently, we cannot write standard state-space realizations as in Theorem 8. When $\tau=0$ , we have $\bar{\Pi}_{u}=I$ , $\bar{\Pi}_{b}=0$ , $\bar{\Lambda}_{m}=I$ , $\tilde{F}=\bar{F}$ , and $\tilde{B}=\bar{B}$ , and we recover the results of Theorem 8.

4 Agent-level controllers

The optimal controller presented in Theorem 8 is generally not minimal. For example, $\mathcal{K}_{\textup{opt}}$ in (34) has a state dimension of $Nn$ , which means a copy of the global plant state for each agent. However, if we extract the part of $\mathcal{K}_{\textup{opt}}$ associated with a particular agent, there is a dramatic reduction in state dimension. So in a distributed implementation of this controller, each agent would only need to store a small subset of the controller’s state. A similar reduction exists for the optimal controller for the delayed problem presented in Theorem 12.

Our next result presents reduced implementations for these agent-level controllers and characterizes the information each agent should store and communicate with their neighbors. We find that Agent $i$ simulates its descendants’ dynamics, and so has dimension $n_{\underline{i}}$ , which is at least $N$ times smaller than the dimension $Nn$ of the aggregate optimal controller from Theorem 8.

Theorem 13.

Consider the setting of Theorem 8 with $\tau\geq 0$ . The agent-level implementation of all structured stabilizing controllers, parameterized by $\hat{\mathcal{Q}}\in\mathcal{H}_{\infty}\cap\mathcal{S}_{0}$ , is shown in Fig. 3. Here, the optimal controller is achieved when $\hat{\mathcal{Q}}=0$ . In this case, we obtain the simpler structure of Fig. 4. All symbols used are defined in Theorems 8 and 12.

Proof.

See Section E.

4.1 Interpretation of optimal controller

Fig. 3 shows that Agent $i$ transmits the same signal $v_{i}$ to each of its strict descendants. When an agent receives the signals $v_{\bar{\bar{i}}}$ from its strict ancestors $\bar{\bar{i}}$ , it selectively extracts and sums together certain components of the signals. To implement the optimal controller, each agent only needs to know the dynamics and topology of its descendants.

If the network has the additional property that there is at most one directed path connecting any two nodes³³3Also known as a multitree or a diamond-free poset., then the communication scheme can be further simplified. Since Agent $i$ ’s decision $u_{i}$ is a sum of terms from all ancestors, but each ancestor has exactly one path that leads to $i$ , the optimal controller can be implemented by transmitting all information to immediate descendants only and performing recursive summations. This scheme is illustrated for a four-node chain graph in Fig. 5.

Remark 14.

The agent-level controller from Fig. 4 can be represented as the combination of an observer with transfer matrix $\mathcal{T}_{\underline{ii}}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}(sI-A_{\underline{ii}}-E_{n_{\underline{i}}}^{\mathsf{T}}E_{n_{i}}L^{i}C_{2_{i\underline{i}}})^{-1}$ , and a regulator with an LQR gain $\tilde{F}^{i}$ in Fig. 6. This yields a separation structure reminiscent of standard LQG theory [37].

Remark 15.

Compared to the architecture proposed in [7, Fig. 4], the agent-level optimal controller in Fig. 4 is more efficient because each agent transmits a single vector $v_{i}$ to its descendants, instead of two.

Remark 16.

The controller in Fig. 4 has the form of a feed-forward Smith predictor, similar to Fig. 2 (bottom left). The FIR block $\Pi_{u_{i}}$ compensates for the effect of adobe delay. Similarly, the FIR block $\Pi_{b_{i}}$ resembles the internal feedback in traditional dead-time controllers.

5 Characterizing the cost

In this section, we characterize the cost of any structured stabilizing controller. The cost is defined as $J\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\bigl{\lVert}{\mathcal{F}_{l}(\mathcal{P},\mathcal{K})}\bigr{\rVert}_{2}^{2}=\bigl{\lVert}{\mathcal{T}_{11}+\mathcal{T}_{12}\mathcal{Q}\mathcal{T}_{21}}\bigr{\rVert}_{2}^{2}$ , where $\mathcal{K}$ is feasible for (8) or equivalently, $\mathcal{Q}=\mathcal{F}_{u}(\mathcal{J}^{-1},\mathcal{K})$ is feasible for (23) (see Lemma 3). We show how to interpret the cost in different ways, and how to compute it efficiently. We illustrate our result using an example with $N=4$ agents.

Theorem 17.

Consider the setting of Theorem 8. The optimal (minimal) costs for the cases: a fully connected graph with no delays, a decentralized graph with no delays, a fully connected graph with delays, and a decentralized graph with delays are:


$\displaystyle J_{\textup{cen}}$	$\displaystyle=\operatorname{\mathrm{tr}}(Y_{\textup{cen}}C_{1}^{\mathsf{T}}C_{1})+\operatorname{\mathrm{tr}}(X_{\textup{cen}}LD_{21}D_{21}^{\mathsf{T}}L^{\mathsf{T}}),$	(37a)
$\displaystyle J_{\textup{dec}}$	$\displaystyle=\operatorname{\mathrm{tr}}(Y_{\textup{cen}}C_{1}^{\mathsf{T}}C_{1})+\operatorname{\mathrm{tr}}(X_{\textup{dec}}LD_{21}D_{21}^{\mathsf{T}}L^{\mathsf{T}}),$	(37b)
$\displaystyle J_{\textup{del}}$	$\displaystyle=\operatorname{\mathrm{tr}}(Y_{\textup{cen}}C_{1}^{\mathsf{T}}C_{1})+\operatorname{\mathrm{tr}}(X_{\textup{del}}LD_{21}D_{21}^{\mathsf{T}}L^{\mathsf{T}}),$	(37c)
$\displaystyle J_{\textup{dec},\textup{del}}$	$\displaystyle=\operatorname{\mathrm{tr}}(Y_{\textup{cen}}C_{1}^{\mathsf{T}}C_{1})+\operatorname{\mathrm{tr}}(X_{\textup{dec,del}}LD_{21}D_{21}^{\mathsf{T}}L^{\mathsf{T}}),$	(37d)

respectively. If a feasible but sub-optimal $\mathcal{Q}$ is used in any of the above cases, write $\mathcal{Q}_{\Delta}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\mathcal{Q}-\mathcal{Q}_{\textup{opt}}$ . The cost of this sub-optimal $\mathcal{Q}$ is found by adding $J_{Q}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\bigl{\lVert}{\mathcal{T}_{12}\mathcal{Q}_{\Delta}D_{21}}\bigr{\rVert}_{2}^{2}$ to (37a)–(37d). The various symbols are defined as

	$\displaystyle X_{\textup{dec}}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{blkd}}(\{X^{i}(1,1)\}),\quad X_{\textup{del}}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{blkd}}(\{\Xi_{c_{\tau}}^{i}(1,1)\}),$
	$\displaystyle X_{\textup{dec,del}}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{blkd}}(\{\Xi_{\tau}^{i}(1,1)\}),\qquad\textit{and satisfy}$


$\displaystyle\operatorname{\mathrm{blkd}}(\{X_{\textup{cen}}(i,i)\})$	$\displaystyle\preceq X_{\textup{dec}}\preceq X_{\textup{dec,del}},$	(38a)
$\displaystyle\operatorname{\mathrm{blkd}}(\{X_{\textup{cen}}(i,i)\})$	$\displaystyle\preceq X_{\textup{del}}\preceq X_{\textup{dec,del}}.$	(38b)

$X_{\textup{cen}},Y_{\textup{cen}},F_{\textup{cen}}$ , and $L$ are defined in Section 2.2.1. $\Xi_{\tau}^{i}$ and $\Xi_{c_{\tau}}^{i}$ are defined in Sections F.6 and F.7, respectively.

Proof.

See Section F.

In (37a) we recognize $J_{\textup{cen}}$ as the standard LQG cost (fully connected graph with no delays). Further, there are two intuitive interpretations for Theorem 17 that are represented in Fig. 7 for a 3-agents system. The intermediate graph topologies are different, but the starting and ending topologies are equal for both. Along the upper path, $J_{\textup{dec}}-J_{\textup{cen}}$ is the additional cost incurred due to decentralization alone, and $J_{\textup{dec},\textup{del}}-J_{\textup{dec}}$ is the further additional cost due to delays. Likewise, along the lower path, $J_{\textup{del}}-J_{\textup{cen}}$ is the additional cost due to delays alone and $J_{\textup{dec},\textup{del}}-J_{\textup{del}}$ is the further additional cost due to decentralization. Finally, $J_{Q}$ is the additional cost incurred due to suboptimality. Theorem 17 unifies existing cost decomposition results for the centralized [37, §14.6], decentralized [18, Thm. 16], and delayed [23, Prop. 6] cases.

Remark 18.

Delay and decentralization do not contribute independently to the cost. Specifically, the marginal increase in cost due to adding processing delays depends on the graph topology. Likewise, the marginal increase in cost due to removing communication links depends on the processing delay. In other words, $J_{\textup{cen}}+J_{\textup{dec},\textup{del}}\neq J_{\textup{dec}}+J_{\textup{del}}$ .

Remark 19.

There is a dual expression for the cost $J_{\textup{cen}}$ in (37a):

J_{\textup{cen}}=\operatorname{\mathrm{tr}}(X_{\textup{cen}}B_{1}B_{1}^{\mathsf{T}})+\operatorname{\mathrm{tr}}(Y_{\textup{cen}}F_{\textup{cen}}^{\mathsf{T}}D_{12}^{\mathsf{T}}D_{12}F_{\textup{cen}}).

The corresponding dual expressions for (37b)–(37d) are unfortunately more complicated. See Section F.3 for details.

5.1 Synchronization example

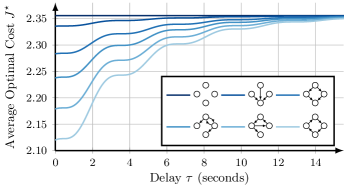
We demonstrate Theorem 8 via a simple structured LQG example. We consider $N=4$ identical lightly damped oscillators. The oscillators begin with different initial conditions and the goal is to achieve synchronization. The oscillators have identical dynamics defined by the differential equations in Figs. 8 and 9. Fig. 8 shows the open-loop zero-input response for the four oscillators with given initial conditions. Due to the light damping, the states slowly converge to zero as $t\rightarrow\infty$ .

Fig. 9 shows the closed-loop response using the optimal controller from Theorem 8 for a diamond-shaped communication network with no processing delay. The controller states are initialized to match the initial state of the plant. Since the observer is an unbiased estimator, the LQG controller replicates the behavior of full-state feedback LQR. Fig. 9 shows the four oscillators leveraging their shared information to achieve synchronization to a common oscillation pattern.

In Fig. 10, we use the same system as in Fig. 9, but we plot the total average cost as a function of time delay for various network topologies. The highest cost corresponds to a fully disconnected network, while the lowest cost corresponds to a fully connected network. In the limit as $\tau\to\infty$ (infinite processing delay), the cost tends to that of the fully disconnected case.

6 Conclusion

We studied a structured optimal control problem where multiple dynamically decoupled agents communicate over a delay network. Specifically, we characterized the structure and efficient implementation of optimal controllers at the individual agent level. We now propose some possible future applications for our work.

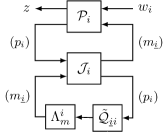
First, our approach can be readily generalized to treat cases with a combination of processing delays and network latency, where the various delays are heterogeneous but known [5]. Next, the observer-regulator architecture elucidated in Fig. 6 could also be used to develop heuristics for solving cooperative control problems where the agents’ dynamics are nonlinear or the noise distributions are non-Gaussian. Examples could include decentralized versions of the Extended Kalman Filter or Unscented Kalman Filter. Finally, our closed-form expressions for the optimal cost can serve as lower bounds to the cost of practical implementation that have additional memory, power, or bandwidth limitations.

Appendices

A Definition of the $\Gamma$ function

The $\Gamma$ function takes in a four-block plant $\mathcal{P}$ and adobe delay matrix $\Lambda_{m}^{i}$ and returns a transformed plant $\tilde{\mathcal{P}}$ and FIR systems $\Pi_{u}$ , $\Pi_{b}$ . As in [23], we first consider the special case where $D_{12}^{\mathsf{T}}D_{12}=I$ . The completion operator $\pi_{\tau}\{\cdot\}$ acts on a rational LTI system delayed by $\tau$ and returns the unique FIR system supported on $[0,\tau]$ that provides a rational completion:

\pi_{\tau}\Biggl{\{}\left[\begin{array}[]{c|c}A&B\\ \hline\cr\rule{0.0pt}{9.90276pt}C&0\end{array}\right]\!e^{-s\tau}\Biggr{\}}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\left[\begin{array}[]{c|c}A&e^{-A\tau}\!B\\ \hline\cr\rule{0.0pt}{9.90276pt}C&0\end{array}\right]-\left[\begin{array}[]{c|c}A&B\\ \hline\cr\rule{0.0pt}{9.90276pt}C&0\end{array}\right]e^{-s\tau}\!.

The input matrices $B_{2}$ and $D_{12}$ of $\mathcal{P}$ are partitioned according to the blocks of adobe delay matrix $\Lambda_{m}^{i}$ . So, ${B}_{2}=\begin{bmatrix}B_{2_{0}}&B_{2_{\tau}}\end{bmatrix}$ , where the two blocks correspond to inputs with delay $0$ and $\tau$ , respectively. $D_{12}$ is partitioned in a similar manner. Define the Hamiltonian matrix

H=\begin{bmatrix}H_{11}&H_{12}\\ H_{21}&H_{22}\end{bmatrix}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\begin{bmatrix}A\!-\!B_{2_{0}}D_{12_{0}}^{\mathsf{T}}C_{1}&-B_{2_{0}}B_{2_{0}}^{\mathsf{T}}\\ -C_{1}^{\mathsf{T}}P_{\tau}C_{1}&-A^{\mathsf{T}}\!+\!C_{1}^{\mathsf{T}}D_{12_{0}}B_{2_{0}}^{\mathsf{T}}\end{bmatrix}\!,

where $P_{0}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}D_{{12}_{0}}D_{{12}_{0}}^{\mathsf{T}}$ and $P_{\tau}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}I-P_{0}$ , and define its matrix exponential as $\Sigma\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}e^{H\tau}$ . Define the modified matrices

	$\displaystyle\tilde{B}_{2}$	$\displaystyle\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\begin{bmatrix}B_{2_{0}}&\Sigma_{12}^{\mathsf{T}}C_{1}^{\mathsf{T}}D_{{12}_{\tau}}+\Sigma_{22}^{\mathsf{T}}B_{2_{\tau}}\end{bmatrix}$
	$\displaystyle\tilde{C}_{1}$	$\displaystyle\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\left(P_{\tau}C_{1}+P_{0}C_{1}\Sigma_{22}^{\mathsf{T}}-D_{{12}_{0}}B_{2_{0}}^{\mathsf{T}}\Sigma_{21}^{\mathsf{T}}\right)\Sigma_{22}^{-\mathsf{T}},$

where the $\Sigma_{ij}$ are partitioned the same way as the $H_{ij}$ . The modified four-block plant output by $\Gamma$ is then

\tilde{\mathcal{P}}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\begin{bmatrix}\tilde{\mathcal{P}}_{11}&\tilde{\mathcal{P}}_{12}\\ \mathcal{P}_{21}&\tilde{\mathcal{P}}_{22}\end{bmatrix}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\left[\begin{array}[]{c|cc}A&B_{1}&\tilde{B}_{2}\\ \hline\cr\rule{0.0pt}{9.90276pt}\tilde{C}_{1}&0&D_{12}\\ C_{2}&D_{21}&0\end{array}\right],

Finally, define the FIR systems

\begin{bmatrix}\tilde{\Pi}_{u}\\ \tilde{\Pi}_{b}\end{bmatrix}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\pi_{\tau}\!\left\{\left[\begin{array}[]{cc|c}H_{11}&H_{12}&B_{2_{\tau}}\\ H_{21}&H_{22}&-C_{1}^{\mathsf{T}}D_{12_{\tau}}\\ \hline\cr\rule{0.0pt}{9.90276pt}D_{12_{0}}^{\mathsf{T}}{C}_{1}&B_{2_{0}}&0\\ C_{2}&0&0\end{array}\right]e^{-s\tau}\right\}.

FIR outputs of $\Gamma$ are $\Pi_{u}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\begin{bmatrix}I&\tilde{\Pi}_{u}\\ 0&I\end{bmatrix}$ and $\Pi_{b}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\begin{bmatrix}0&\tilde{\Pi}_{b}\end{bmatrix}$ .

In the general case $D_{12}^{\mathsf{T}}D_{12}\neq I$ , we can use a standard change of variables to transform back to the case $D_{12}^{\mathsf{T}}D_{12}=I$ . See [21, Rem. 2] for details.

B Gramian equations

Here we provide the set of Lyapunov equations that are uniquely associated with the multi-agent problem.

Lemma 20.

Suppose $(X_{\textup{cen}},F_{\textup{cen}})$ and $(X^{i},F^{i})$ are defined in (9a) and (16a) respectively. Then $W_{X}^{i}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}X^{i}-X_{\textup{cen}_{\underline{ii}}}\succeq 0$ is the unique solution to the Lyapunov equation

(A_{\underline{ii}}+B_{2_{\underline{ii}}}F^{i})^{\mathsf{T}}W_{X}^{i}+W_{X}^{i}(A_{\underline{ii}}+B_{2_{\underline{ii}}}F^{i})+(E_{m_{\underline{i}}}F^{i}-F_{\textup{cen}}E_{n_{\underline{i}}})^{\mathsf{T}}D_{12}^{\mathsf{T}}D_{12}(E_{m_{\underline{i}}}F^{i}-F_{\textup{cen}}E_{n_{\underline{i}}})=0.

(39)

Proof.

Left and right multiply the ARE for (9a) by $E_{n_{\underline{i}}}^{\mathsf{T}}$ and $E_{n_{\underline{i}}}$ respectively, and subtract it from (16a). The result follows from algebraic manipulation and applying the definitions of $F^{i}$ and $F_{\textup{cen}}$ . Since the final term in (39) is positive semidefinite and $A_{\underline{ii}}+B_{2_{\underline{ii}}}F^{i}$ is Hurwitz, it follows that $W_{X}^{i}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}X^{i}-X_{\textup{cen}_{\underline{ii}}}\succeq 0$ and is unique.

We also have a dual analog to Lemma 20, provided below.

Lemma 21.

Consider the setting of Lemma 20. There exists a unique $W_{Y}^{i}\succeq 0$ that satisfies the Lyapunov equation

(A_{\underline{ii}}+B_{2_{\underline{ii}}}F^{i})W_{Y}^{i}+W_{Y}^{i}(A_{\underline{ii}}+B_{2_{\underline{ii}}}F^{i})^{\mathsf{T}}+E_{n_{\underline{i}}}^{\mathsf{T}}\bar{L}\bar{\mathbf{1}}_{p}D_{21}D_{21}^{\mathsf{T}}\bar{\mathbf{1}}_{p}^{\mathsf{T}}\bar{L}^{\mathsf{T}}E_{n_{\underline{i}}}=0.

(40)

Proof.

Since $E_{n_{\underline{i}}}^{\mathsf{T}}\bar{L}\bar{\mathbf{1}}_{p}D_{21}D_{21}^{\mathsf{T}}\bar{\mathbf{1}}_{p}^{\mathsf{T}}\bar{L}^{\mathsf{T}}E_{n_{\underline{i}}}\succeq 0$ and the matrix $A_{\underline{ii}}+B_{2_{\underline{ii}}}F^{i}$ is Hurwitz, $W_{Y}^{i}\succeq 0$ and is unique.

C Proof of Theorem 8

For the case $\tau=0$ , we can replace $\mathcal{Q}\in\mathcal{H}_{\infty}\cap\mathcal{S}_{\tau}$ by $\mathcal{Q}\in\mathcal{H}_{2}\cap\mathcal{H}_{\infty}\cap\mathcal{S}_{0}$ in (23) because the closed-loop map must be strictly proper in order to have a finite $\mathcal{H}_{2}$ norm. Since $\mathcal{T}_{11}$ is strictly proper, this forces $\mathcal{Q}$ to be strictly proper as well, and hence $\mathcal{Q}\in\mathcal{H}_{2}\cap\mathcal{H}_{\infty}$ . Further, if $\mathcal{Q}$ is rational, we have $\mathcal{Q}\in\mathcal{RH}_{2}$ . The optimization problem (23) is a least squares problem with a subspace constraint, so the necessary and sufficient conditions for optimality are given by the normal equations $\mathcal{T}_{12}^{\sim}(\mathcal{T}_{11}+\mathcal{T}_{12}\mathcal{Q}\mathcal{T}_{21})\mathcal{T}_{21}^{\sim}\in\left(\mathcal{RH}_{2}\cap\mathcal{S}_{0}\right)^{\perp}$ with the constraint that $\mathcal{Q}\in\mathcal{RH}_{2}\cap\mathcal{S}_{0}$ .

We can check membership $\mathcal{F}\in(\mathcal{RH}_{2}\cap\mathcal{S}_{0})^{\perp}$ by checking if $\mathcal{F}_{ij}\in\mathcal{RH}_{2}^{\perp}$ whenever there is a path $j\to i$ . For example, consider the two-node graph $1\to 2$ . Then we have

\mathcal{RH}_{2}\cap\mathcal{S}_{0}=\begin{bmatrix}\mathcal{RH}_{2}&0\\ \mathcal{RH}_{2}&\mathcal{RH}_{2}\end{bmatrix}\quad\text{and}\quad(\mathcal{RH}_{2}\cap\mathcal{S}_{0})^{\perp}=\begin{bmatrix}\mathcal{RH}_{2}^{\perp}&\mathcal{L}_{2}\\ \mathcal{RH}_{2}^{\perp}&\mathcal{RH}_{2}^{\perp}\end{bmatrix}.

So here, $\mathcal{F}\in(\mathcal{RH}_{2}\cap\mathcal{S}_{0})^{\perp}$ if and only if $\mathcal{F}_{11},\mathcal{F}_{21},\mathcal{F}_{22}\in\mathcal{RH}_{2}^{\perp}$ . We will show that the proposed $\mathcal{Q}_{\textup{opt}}$ in (31) is optimal by directly verifying the normal equations.

Substituting $\mathcal{Q}_{\textup{opt}}$ from (31) into $\mathcal{T}_{11}+\mathcal{T}_{12}\mathcal{Q}_{\textup{opt}}\mathcal{T}_{21}$ with $\mathcal{T}_{ij}$ defined in (28), we obtain the closed-loop map

\mathcal{T}_{11}+\mathcal{T}_{12}\mathcal{Q}_{\textup{opt}}\mathcal{T}_{21}=\left[\begin{array}[]{c|c}A_{\textup{cl}}&B_{\textup{cl}}\\ \hline\cr\rule{0.0pt}{9.90276pt}C_{\textup{cl}}&0\end{array}\right]\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\left[\begin{array}[]{cc|c}\bar{A}+\bar{B}\bar{F}&-\bar{L}\bar{C}\bar{\mathbf{1}}_{n}&-\bar{L}\bar{\mathbf{1}}_{p}D_{21}\\ 0&A_{L}&B_{L}\\ \hline\cr\rule{0.0pt}{9.90276pt}C_{1}\bar{\mathbf{1}}_{n}^{\mathsf{T}}+D_{12}\bar{\mathbf{1}}_{m}^{\mathsf{T}}\bar{F}&C_{1}&0\end{array}\right],

(41)

where $A_{L}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}A+LC_{2}$ and $B_{L}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}B_{1}+LD_{21}$ . Next, we show that the controllability Gramian for the closed loop map is block-diagonal.

Lemma 22.

The controllability Gramian for the closed-loop map (41) is given by

\Theta\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{blkd}}(\{E_{n_{\underline{i}}}W_{Y}^{i}E_{n_{\underline{i}}}^{\mathsf{T}}\}_{i\in[N]},Y_{\textup{cen}}),

where $Y_{\textup{cen}}$ and $W_{Y}^{i}$ are defined in Eqs. 9b and 21, respectively. In other words, $\Theta\succeq 0$ is the unique solution to $A_{\textup{cl}}\Theta+\Theta A_{\textup{cl}}^{\mathsf{T}}+B_{\textup{cl}}B_{\textup{cl}}^{\mathsf{T}}=0$ .

Proof.

$A_{\textup{cl}}$ is Hurwitz and $B_{\textup{cl}}B_{\textup{cl}}^{\mathsf{T}}\succeq 0$ so the Lyapunov equation has a unique solution and $\Theta\succeq 0$ . We can verify the solution by direct substitution using Lemma 21 and the ARE associated with (9b).

Lemma 22 has the following statistical interpretation. If the controlled system (41) is driven by standard Gaussian noise, its state in these coordinates will have a steady-state covariance $\Theta$ , so each block component will be mutually independent.

C.1 Proof of optimality

Let $\Omega\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\mathcal{T}_{12}^{\sim}(\mathcal{T}_{11}+\mathcal{T}_{12}\mathcal{Q}_{\textup{opt}}\mathcal{T}_{21})\mathcal{T}_{21}^{\sim}$ . Substituting $\mathcal{Q}_{\textup{opt}}$ from (31) and using (41), we obtain

\displaystyle\Omega

\displaystyle={\left[\begin{array}[]{ccc|c}-A_{K}^{\mathsf{T}}&-C_{K}^{\mathsf{T}}C_{\textup{cl}}&0&0\\ 0&A_{\textup{cl}}&B_{\textup{cl}}B_{L}^{\mathsf{T}}&B_{\textup{cl}}D_{21}^{\mathsf{T}}\\ 0&0&-A_{L}^{\mathsf{T}}&-C_{2}^{\mathsf{T}}\\ \hline\cr\rule{0.0pt}{9.90276pt}B_{2}^{\mathsf{T}}&D_{12}^{\mathsf{T}}C_{\textup{cl}}&0&0\end{array}\right]},

(46)

where $A_{K}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}A+B_{2}F_{d}$ , $C_{K}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}C_{1}+D_{12}F_{d}$ , and $A_{\textup{cl}}$ , $B_{\textup{cl}}$ , $C_{\textup{cl}}$ , are defined in (41). Apply the state transformation

\displaystyle T=\begin{bmatrix}I&\begin{bmatrix}\bar{\mathbf{1}}_{n}^{\mathsf{T}}\bar{X}&0\end{bmatrix}&\bar{\mathbf{1}}_{n}^{\mathsf{T}}\bar{X}\bar{W}\bar{\mathbf{1}}_{p}\\ 0&I&\Theta\bar{\mathbf{1}}_{p}\\ 0&0&I\end{bmatrix}

to (46), where we defined $\bar{W}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{blkd}}(\{E_{n_{\underline{i}}}W_{Y}^{i}E_{n_{\underline{i}}}^{\mathsf{T}}\}_{i\in[N]})$ and $\bar{X}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{blkd}}(\{E_{n_{\underline{i}}}W_{X}^{i}E_{n_{\underline{i}}}^{\mathsf{T}}+X_{\textup{cen}}\}_{i\in[N]})$ , and $\Theta$ is defined in Lemma 22. The transformed $\Omega$ is

\displaystyle\Omega={\left[\begin{array}[]{cccc|c}-A_{K}^{\mathsf{T}}&{\star}_{1}&\star&\star&\star\\ 0&\bar{A}+\bar{B}\bar{F}&-\bar{L}\bar{C}\bar{\mathbf{1}}_{n}&{\star}_{2}&{\star}_{3}\\ 0&0&A_{L}&{\star}_{5}&{\star}_{6}\\ 0&0&0&-A_{L}^{\mathsf{T}}&-C_{2}^{\mathsf{T}}\\ \hline\cr\rule{0.0pt}{9.90276pt}B_{2}^{\mathsf{T}}&{\star}_{4}&D_{12}^{\mathsf{T}}C_{1}&\star&0\end{array}\right]},

where we have defined the symbols

	$\displaystyle{\star}_{1}$	$\displaystyle\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}-A_{K}^{\mathsf{T}}\bar{\mathbf{1}}_{n}^{\mathsf{T}}\bar{X}\!-\!C_{K}^{\mathsf{T}}(C_{1}\bar{\mathbf{1}}_{n}^{\mathsf{T}}\!+\!D_{12}\bar{\mathbf{1}}_{m}^{\mathsf{T}}\bar{F})\!-\!\bar{\mathbf{1}}_{n}^{\mathsf{T}}\bar{X}(\bar{A}\!+\!\bar{B}\bar{F})$
	$\displaystyle{\star}_{2}$	$\displaystyle\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}-\bar{L}\bar{\mathbf{1}}_{p}D_{21}B_{L}^{\mathsf{T}}\!-\!\bar{L}\bar{C}\bar{\mathbf{1}}_{n}Y_{\textup{cen}}\!+\!(\bar{A}\!+\!\bar{B}\bar{F})\bar{W}\bar{\mathbf{1}}_{p}\!+\!\bar{W}\bar{\mathbf{1}}_{p}A_{L}^{\mathsf{T}}$
	$\displaystyle{\star}_{3}$	$\displaystyle\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}-\bar{L}\bar{\mathbf{1}}_{p}D_{21}^{\mathsf{T}}+\bar{W}\bar{\mathbf{1}}_{p}C_{2}^{\mathsf{T}}$
	$\displaystyle{\star}_{4}$	$\displaystyle\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}D_{12}^{\mathsf{T}}(C_{1}\bar{\mathbf{1}}_{n}^{\mathsf{T}}+D_{12}\bar{\mathbf{1}}_{m}^{\mathsf{T}}\bar{F})+B_{2}^{\mathsf{T}}\bar{\mathbf{1}}_{n}^{\mathsf{T}}\bar{X}$
	$\displaystyle{\star}_{5}$	$\displaystyle\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}A_{L}Y_{\textup{cen}}+B_{L}B_{L}^{\mathsf{T}}+Y_{\textup{cen}}A_{L}^{\mathsf{T}}$
	$\displaystyle{\star}_{6}$	$\displaystyle\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}B_{L}D_{21}^{\mathsf{T}}+Y_{\textup{cen}}C_{2}^{\mathsf{T}}.$

A $\star$ without subscript denotes an unimportant block. Simplifying using Riccati and Lyapunov equations from Section 2.2.1 and Section B respectively, we get ${\star}_{5}={\star}_{6}=0$ ; the mode $A_{L}$ is uncontrollable. Removing it, we obtain

\displaystyle\Omega={\left[\begin{array}[]{ccc|c}-A_{K}^{\mathsf{T}}&\star_{1}&\star&\star\\ 0&\bar{A}+\bar{B}\bar{F}&{\star}_{2}&{\star}_{3}\\ 0&0&-A_{L}^{\mathsf{T}}&-C_{2}^{\mathsf{T}}\\ \hline\cr\rule{0.0pt}{9.90276pt}B_{2}^{\mathsf{T}}&{\star}_{4}&\star&0\end{array}\right]}.

(51)

Now consider a block $\Omega_{ij}$ for which there is a path $j\to i$ .

\displaystyle\Omega_{ij}

\displaystyle={\left[\begin{array}[]{ccc|c}-A_{K_{ii}}^{\mathsf{T}}&{\star}_{1_{i:}}&\star&\star\\[2.84526pt] 0&\bar{A}+\bar{B}\bar{F}&{\star}_{2_{:j}}&{\star}_{3_{:j}}\\[2.84526pt] 0&0&-A_{L_{jj}}^{\mathsf{T}}&-C_{2_{jj}}^{\mathsf{T}}\\[2.84526pt] \hline\cr\rule{0.0pt}{9.90276pt}B_{2_{ii}}^{\mathsf{T}}&{\star}_{4_{i:}}&\star&0\end{array}\right]}.

(56)

Let $\star_{1}^{k}$ and $\star_{4}^{k}$ denote the $k^{\text{th}}$ block column and let $\star_{2}^{k}$ and $\star_{3}^{k}$ denote the $k^{\text{th}}$ block row. Algebraic manipulation reveals that

(i)

If $i\in\underline{k}$ and $\ell\in\underline{k}$ , then $\star^{k}_{1_{i\ell}}=\star^{k}_{4_{i\ell}}=0$ .
(ii)

If $\ell\notin\underline{k}$ or $j\notin\underline{k}$ , then $\star^{k}_{2_{\ell j}}=\star^{k}_{3_{\ell j}}=0$ .

Consider the $k^{\text{th}}$ diagonal block of $\bar{A}+\bar{B}\bar{F}$ in (56), which is $A+E_{n_{\underline{k}}}B_{2_{\underline{k}\underline{k}}}F^{k}E_{n_{\underline{k}}}^{\mathsf{T}}$ . This block is itself block-diagonal; it contains the block $A_{\underline{k}\underline{k}}+B_{2_{\underline{k}\underline{k}}}F^{k}$ and smaller blocks $A_{\ell\ell}$ for all $\ell\notin\underline{k}$ . We have three cases.

1.

If $k\in\bar{i}$ , then for all $\ell\in\underline{k}$ , we have $\star^{k}_{1_{i\ell}}=\star^{k}_{4_{i\ell}}=0$ from Item (i) above, so the mode $A_{\underline{k}\underline{k}}+B_{2_{\underline{k}\underline{k}}}F^{k}$ is unobservable.
2.

If $k\in\bar{i}$ , but instead $\ell\notin\underline{k}$ , we have $\star^{k}_{2_{\ell j}}=\star^{k}_{3_{\ell j}}=0$ from Item (ii) above, so the modes $A_{\ell\ell}$ are uncontrollable.
3.

If $k\notin\bar{i}$ , then $k\notin\bar{j}$ because $j\to i$ by assumption. Then from Item (ii) above, all such modes are uncontrollable.

Consequently every block of $\bar{A}+\bar{B}\bar{F}$ is either uncontrollable or unobservable, leading us to the reduced realization

\displaystyle\Omega_{ij}

\displaystyle={\left[\begin{array}[]{cc|c}-A_{K_{ii}}^{\mathsf{T}}&\star&\star\\ 0&-A_{L_{jj}}^{\mathsf{T}}&-C_{2_{jj}}^{\mathsf{T}}\\ \hline\cr\rule{0.0pt}{9.90276pt}B_{2_{ii}}^{\mathsf{T}}&\star&0\end{array}\right]}.

(60)

Therefore, $\Omega_{ij}\in\mathcal{RH}_{2}^{\perp}$ whenever $j\to i$ , as required.

D Proof of Theorem 12

Start with the convexified optimization problem (23). Based on the structured realization (28), we see that $\mathcal{T}_{21}$ is block-diagonal. Therefore, the optimal cost can be split by columns:

\bigl{\lVert}{\mathcal{T}_{11}+\mathcal{T}_{12}\mathcal{Q}\mathcal{T}_{21}}\bigr{\rVert}_{2}^{2}=\sum_{i=1}^{N}\bigl{\lVert}{\mathcal{T}_{{11}_{:i}}+\mathcal{T}_{{12}_{:i}}\mathcal{Q}_{\underline{i}i}\mathcal{T}_{{21}_{ii}}}\bigr{\rVert}_{2}^{2}.

Since $\mathcal{Q}\in\mathcal{H}_{\infty}\cap\mathcal{S}_{\tau}$ , we can factor each block column of $\mathcal{Q}$ as $\mathcal{Q}_{\underline{i}i}=\Lambda_{m}^{i}\tilde{\mathcal{Q}}_{\underline{i}i}$ , where $\tilde{\mathcal{Q}}_{\underline{i}i}\in\mathcal{H}_{\infty}$ has no structure or delay, and $\Lambda_{m}^{i}$ is the adobe delay matrix (defined in Section 2.1). We can therefore optimize for each block column $\tilde{\mathcal{Q}}_{\underline{i}i}$ separately. Thus, each subproblem is to

\underset{\tilde{\mathcal{Q}}_{\underline{i}i}\in\mathcal{H}_{\infty}}{\text{minimize}}\qquad\bigl{\lVert}{\mathcal{T}_{{11}_{:i}}+\mathcal{T}_{{12}_{:i}}\Lambda_{m}^{i}\tilde{\mathcal{Q}}_{\underline{i}i}\mathcal{T}_{{21}_{ii}}}\bigr{\rVert}_{2}^{2},

(61)

Define $\mathcal{T}_{i}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\begin{bmatrix}\mathcal{T}_{{11}_{:i}}&\mathcal{T}_{{12}_{:\underline{i}}}\\ \mathcal{T}_{{21}_{ii}}&0\end{bmatrix}$ . Comparing to (23)–(28), we observe that (61) is a special case of the problem (23), subject to the transformations $\mathcal{P}\mapsto\mathcal{P}_{i}$ (defined in (15)) and $F_{d}\mapsto F_{d_{\underline{i}\underline{i}}}$ , $L_{d}\mapsto E^{\mathsf{T}}_{n_{\underline{i}}}E_{n_{i}}L^{i}$ , and $\mathcal{Q}\mapsto\Lambda_{m}^{i}\tilde{\mathcal{Q}}_{\underline{i}i}$ . If we define the associated $\mathcal{J}_{i}$ for this subproblem (according to (21)), we view the subproblem as that of finding the $\mathcal{H}_{2}$ -optimal controller for the plant $\mathcal{P}_{i}$ subject to an adobe input delay, as illustrated in the left panel of Fig. 11. The key difference between this problem and (8) is that we no longer have a sparsity constraint.

Figure 11: Equivalent subproblems via commuting

\Lambda_{m}^{i}

and

\mathcal{J}_{i}

. Dimensions of signals are indicated along the arrows.

The adobe delay $\Lambda_{m}^{i}$ can be shifted to the input channel, shown in the right panel of Fig. 11. This follows from leveraging state-space properties and the block structure of certain blocks of $\mathcal{J}_{i}$ . Examples include $B_{2_{\underline{i}\underline{i}}}\Lambda_{m}^{i}=\Lambda_{n}^{i}B_{2_{\underline{i}\underline{i}}}$ and $\Lambda_{n}^{i}E_{n_{\underline{i}}}^{\mathsf{T}}E_{n_{i}}L^{i}=E_{n_{\underline{i}}}^{\mathsf{T}}E_{n_{i}}L^{i}$ .

The remainder of the proof proceeds as follows: we define $\mathcal{K}_{i}$ to be the shaded system in Fig. 11 (right panel). This is a standard adobe delayed problem, so we can apply the $\Gamma$ transformation illustrated in Fig. 2. Specifically, we define $(\tilde{\mathcal{P}}_{i},\Pi_{u_{i}},\Pi_{b_{i}})=\Gamma(\mathcal{P}_{i},\Lambda_{m}^{i})$ , and obtain Fig. 12.

By the properties of the loop-shifting transformation discussed in Section 2.1, the optimal $\tilde{K}_{i}$ is found by solving a standard non-delayed LQG problem in the (rational) plant $\tilde{\mathcal{P}}_{i}$ , whose solution is

\displaystyle\tilde{\mathcal{K}}_{i}

\displaystyle=\left[\begin{array}[]{c|c}A_{\underline{ii}}+\tilde{B}_{2_{\underline{ii}}}\tilde{F}^{i}+E_{n_{\underline{i}}}^{\mathsf{T}}E_{n_{i}}L^{i}C_{2_{i\underline{i}}}&-E_{n_{\underline{i}}}^{\mathsf{T}}E_{n_{i}}L^{i}\\ \hline\cr\rule{0.0pt}{9.90276pt}\tilde{F}^{i}&0\end{array}\right]\!.

Inverting each transformation, $\mathcal{K}_{i}=\Pi_{u_{i}}\tilde{\mathcal{K}}_{i}(I-\Pi_{b_{i}}\tilde{\mathcal{K}}_{i})^{-1}$ , and we can recover the Youla parameter via $\tilde{\mathcal{Q}}_{\underline{i}i}=\mathcal{F}_{u}(\mathcal{J}_{i}^{-1},\mathcal{K}_{i})$ , which leads to (62).

\tilde{\mathcal{Q}}_{\underline{i}i}=\left[\begin{array}[]{cc|c}A_{\underline{ii}}&{B}_{2_{\underline{ii}}}\Pi_{u_{i}}\tilde{F}^{i}&-E_{n_{\underline{i}}}^{\mathsf{T}}E_{n_{i}}L^{i}\\ -E_{n_{\underline{i}}}^{\mathsf{T}}E_{n_{i}}L^{i}C_{2_{i\underline{i}}}&A_{\underline{ii}}+\tilde{B}_{2_{\underline{ii}}}\tilde{F}^{i}-E_{n_{\underline{i}}}^{\mathsf{T}}E_{n_{i}}L^{i}\Pi_{b_{i}}\tilde{F}^{i}+E_{n_{\underline{i}}}^{\mathsf{T}}E_{n_{i}}L^{i}C_{2_{i\underline{i}}}&-E_{n_{\underline{i}}}^{\mathsf{T}}E_{n_{i}}L^{i}\\ \hline\cr\rule{0.0pt}{9.90276pt}-F_{d_{\underline{ii}}}&\Pi_{u_{i}}\tilde{F}^{i}&0\end{array}\right].

(62)

Now zero-pad, reintroduce delays, and concatenate, to obtain the global Youla parameter (35) via $\mathcal{Q}_{\textup{opt}}=\sum_{i=1}^{N}E_{m_{\underline{i}}}\Lambda_{m}^{i}\tilde{\mathcal{Q}}_{\underline{i}i}E_{p_{i}}^{\mathsf{T}}$ and recover the optimal controller (36) via $\mathcal{K}_{\textup{opt}}=\mathcal{F}_{l}(\mathcal{J},\mathcal{Q}_{\textup{opt}})$ .

E Proof of Theorem 13

From Lemma 3, the set of sub-optimal controllers is parameterized as $\mathcal{K}=\mathcal{F}_{l}(\mathcal{J},\mathcal{Q})$ , where $\mathcal{Q}\in\mathcal{S}_{\tau}$ . Equivalently, write $\mathcal{K}=\mathcal{F}_{l}(\mathcal{J},\mathcal{Q}_{\textup{opt}}+\mathcal{Q}_{\Delta})$ , where $\mathcal{Q}_{\Delta}\in\mathcal{S}_{\tau}$ and $\mathcal{Q}_{\textup{opt}}$ is given in Theorem 12. The controller equation $u=\mathcal{K}y$ can be expanded using the LFT as $\left(\begin{smallmatrix}u\\ \eta\end{smallmatrix}\right)=\mathcal{J}\left(\begin{smallmatrix}y\\ v\end{smallmatrix}\right)$ with $v=\mathcal{Q}\eta$ . If $\mathcal{J}$ has state $\xi$ , the state-space equation for $\mathcal{J}$ decouples as

	$\displaystyle\dot{\xi}_{i}$	$\displaystyle=(A_{ii}+B_{2_{ii}}F_{d_{ii}}+L^{i}C_{2_{ii}})\xi_{i}-L^{i}y_{i}+B_{2_{ii}}v_{i},$
	$\displaystyle u_{i}$	$\displaystyle=F_{d_{ii}}\xi_{i}+v_{i},$
	$\displaystyle\eta_{i}$	$\displaystyle=-C_{2_{ii}}\xi_{i}+y_{i},\quad\text{for }i=1,\dots,N.$

Note that we replaced $L_{d_{ii}}$ by $L^{i}$ from (16b). This leads to simpler algebra, but is in principle not required. Meanwhile, the $\mathcal{Q}$ equation is coupled: $v=(\mathcal{Q}_{\textup{opt}}+\mathcal{Q}_{\Delta})\eta$ . Now consider Agent $i$ . Since we are interested in the agent-level implementation, we begin by extracting $u_{i}$ , which requires finding $v_{i}$ . Separate $\mathcal{Q}$ by columns as in Section D to obtain

$\displaystyle v_{i}$	$\displaystyle=E_{m_{i}}^{\mathsf{T}}\left(\mathcal{Q}_{\textup{opt}}+\mathcal{Q}_{\Delta}\right)\eta$
	$\displaystyle=\sum_{k\in[N]}E_{m_{i}}^{\mathsf{T}}E_{m_{\underline{k}}}\Lambda_{m}^{k}\left(\tilde{\mathcal{Q}}_{\underline{k}k}+\hat{\mathcal{Q}}_{\underline{k}k}\right)\eta_{k}$
	$\displaystyle=\left(\tilde{\mathcal{Q}}_{ii}+\hat{\mathcal{Q}}_{ii}\right)\eta_{i}+e^{-s\tau}\sum_{k\in\bar{\bar{i}}}\left(\tilde{\mathcal{Q}}_{ik}+\hat{\mathcal{Q}}_{ik}\right)\eta_{k},$	(63)

where $\tilde{\mathcal{Q}}_{\underline{i}i}$ is given in (62), and $\hat{\mathcal{Q}}\in\mathcal{S}_{0}$ is the delay-free component of $\mathcal{Q}_{\Delta}$ . A possible distributed implementation is to have Agent $i$ simulate $\xi_{i}$ locally. Since $y_{i}$ is available locally, then so is $\eta_{i}$ . We further suppose Agent $i$ computes $v_{i,\underline{i}}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}(\tilde{\mathcal{Q}}_{\underline{i}i}+\hat{\mathcal{Q}}_{\underline{i}i})\eta_{i}$ locally. Component $v_{i,i}$ is used locally, while component $v_{i,j}$ for $j\in\underline{\underline{i}}$ is transmitted to descendant $j$ . Each agent then computes $v_{i}$ by summing its local $v_{i,i}$ with the delayed $e^{-s\tau}v_{i,k}$ received from strict ancestors $k\in\bar{\bar{i}}$ . The complete agent-level implementation is shown in Fig. 3.

When $\hat{\mathcal{Q}}=0$ , we recover the optimal controller. In this case, the equations simplify considerably; standard state-space manipulations reduce Fig. 3 to the simpler Fig. 4. It is worth noting that the optimal controller does not depend on the choice of nominal gain $F_{d}$ .

F Proof of Theorem 17

All the estimation, control gains and Riccati solutions used here are defined in Section 2.2.1. The additional cost incurred due to suboptimality is $J_{Q}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\bigl{\lVert}{\mathcal{T}_{12}\mathcal{Q}_{\Delta}\mathcal{T}_{21}}\bigr{\rVert}_{2}^{2}$ [37, §14.6]. Using [37, Lem. 14.3], we have $J_{Q}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\bigl{\lVert}{\mathcal{T}_{12}\mathcal{Q}_{\Delta}D_{21}}\bigr{\rVert}_{2}^{2}$ .

F.1 $J_{\textup{cen}}$ (37a)

The optimal cost for a fully connected graph [37, Thm. 14.7] is

	$\displaystyle J_{\textup{cen}}$	$\displaystyle\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\Biggl{\lVert}{\left[\begin{array}[]{c\|c}A+B_{2}F_{\textup{cen}}&B_{1}\\ \hline\cr\rule{0.0pt}{9.90276pt}C_{1}+D_{12}F_{\textup{cen}}&0\end{array}\right]}\Biggr{\rVert}_{2}^{2}+\Biggl{\lVert}{\left[\begin{array}[]{c\|c}A_{\textit{L}}&B_{\textit{L}}\\ \hline\cr\rule{0.0pt}{9.90276pt}D_{12}F_{\textup{cen}}&0\end{array}\right]}\Biggr{\rVert}_{2}^{2},$
		$\displaystyle=\operatorname{\mathrm{tr}}(Y_{\textup{cen}}C_{1}^{\mathsf{T}}C_{1})+\operatorname{\mathrm{tr}}(X_{\textup{cen}}LD_{21}D_{21}^{\mathsf{T}}L^{\mathsf{T}}),$
		$\displaystyle=\operatorname{\mathrm{tr}}(X_{\textup{cen}}B_{1}B_{1}^{\mathsf{T}})+\operatorname{\mathrm{tr}}(Y_{\textup{cen}}F_{\textup{cen}}^{\mathsf{T}}D_{12}^{\mathsf{T}}D_{12}F_{\textup{cen}}),$

where $A_{\textit{L}}$ , $B_{\textit{L}}$ are defined in Section C for (41).

F.2 $J_{\textup{dec}}$ (37b)

Consider that $\mathcal{K}_{\textup{opt}}$ in (34) is a sub-optimal centralized controller for $\bigl{\lVert}{\mathcal{T}_{11}+\mathcal{T}_{12}\mathcal{Q}\mathcal{T}_{21}}\bigr{\rVert}_{2}^{2}$ , subject to $\mathcal{Q}\in\mathcal{RH}_{2}$ . Centralized $\mathcal{H}_{2}$ theory [37] implies that $J_{\textup{dec}}=J_{\textup{cen}}+\Delta$ , where $\Delta\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\bigl{\lVert}{D_{12}\mathcal{Q}_{\textup{you}}D_{21}}\bigr{\rVert}_{2}^{2}$ and $\mathcal{Q}_{\textup{you}}$ is the centralized Youla parameter. Here, $\mathcal{Q}_{\textup{you}}=\mathcal{F}_{u}(\mathcal{J}^{-1},\mathcal{K}_{\textup{opt}})$ , where

\displaystyle\mathcal{J}^{-1}=\left[\begin{array}[]{c|cc}A&B_{2}&-L\\[2.0pt] \hline\cr\rule{0.0pt}{9.90276pt}C_{2}&0&I\\ -F_{\textup{cen}}&I&0\end{array}\right].

After simplifications, we obtain

\displaystyle\mathcal{Q}_{\textup{you}}={\left[\begin{array}[]{c|c}\bar{A}+\bar{B}\bar{F}&-\bar{L}\bar{\mathbf{1}}_{p}\\ \hline\cr\rule{0.0pt}{9.90276pt}\bar{\mathbf{1}}_{m}^{\mathsf{T}}(\bar{F}-\bar{F}_{\textup{cen}})&0\end{array}\right]}.

We substitute $\mathcal{Q}_{\textup{you}}$ into the expression for $\Delta$ , using $\bigl{\lVert}{D_{s}+C_{s}(sI-A_{s})^{-1}B_{s}}\bigr{\rVert}_{2}^{2}=\operatorname{\mathrm{tr}}(C_{s}W_{c}C_{s}^{\mathsf{T}})$ , where $W_{c}$ is the controllability Gramian given by Lyapunov equation $A_{s}W_{c}+W_{c}A_{s}^{\mathsf{T}}+B_{s}B_{s}^{\mathsf{T}}=0$ . Based on the Lemma 20 and using the identity $L_{i}=E_{n_{i}}L^{i}E_{p_{i}}^{\mathsf{T}}$ , we evaluate

	$\displaystyle\Delta$	$\displaystyle=\sum_{i=1}^{N}\operatorname{\mathrm{tr}}(D_{21}^{\mathsf{T}}L_{i}^{\mathsf{T}}E_{n_{\underline{i}}}\{X^{i}-X_{\textup{cen}_{\underline{ii}}}\}E_{n_{\underline{i}}}^{\mathsf{T}}L_{i}D_{21})$
		$\displaystyle=\operatorname{\mathrm{tr}}((\operatorname{\mathrm{blkd}}(\{X^{i}(1,1)\})-X_{\textup{cen}})LD_{21}D_{21}^{\mathsf{T}}L^{\mathsf{T}}).$

We obtain (37b) by substituting $\Delta$ into $J_{\textup{dec}}=J_{\textup{cen}}+\Delta$ .

F.3 Alternative formulas for the cost

We obtained an alternative formula for $J_{\textup{cen}}$ in Section F.1. Similarly, in Section F.2 for $J_{\textup{dec}}$ , $\bigl{\lVert}{D_{s}+C_{s}(sI-A_{s})^{-1}B_{s}}\bigr{\rVert}_{2}^{2}$ is also equal to $\operatorname{\mathrm{tr}}(B_{s}B_{s}^{\mathsf{T}}W_{o})$ , where $W_{o}$ is the observability Gramian given by the dual Lyapunov equation $A_{s}^{\mathsf{T}}W_{o}+W_{o}A_{s}+C_{s}^{\mathsf{T}}C_{s}=0$ . Based on Lemma 21, we can evaluate $\Delta=\sum_{i=1}^{N}\operatorname{\mathrm{tr}}(D_{12}(E_{m_{\underline{i}}}F_{i}-F_{\textup{cen}}E_{n_{\underline{i}}})W_{Y}^{i}(E_{m_{\underline{i}}}F_{i}-F_{\textup{cen}}E_{n_{\underline{i}}})^{\mathsf{T}}D_{12}^{\mathsf{T}})$ . Similar alternative formulas exist for (37c), and (37d) as well.

F.4 $J_{\textup{dec},\textup{del}}$ (37c)

We can split the cost in (23) into a sum of $N$ separate terms because $\mathcal{T}_{21}$ is block-diagonal. Using [23, Prop. 6] on each of these $N$ problems, we write $J_{\textup{dec},\textup{del}}$ as a combination of a non-delayed cost $J_{\textup{dec}}$ and a $\Delta$ incurred by adding delays to that system: $J_{\textup{dec},\textup{del}}=J_{\textup{dec}}+\Delta$ , where $\Delta\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\sum_{i=1}^{N}\operatorname{\mathrm{tr}}(D_{{21}_{ii}}^{\mathsf{T}}L_{i}^{\mathsf{T}}E_{n_{\underline{i}}}^{\mathsf{T}}(\Xi_{\tau}^{i}-X^{i})E_{n_{\underline{i}}}L_{i}D_{{21}_{ii}})$ . Also, $\Delta=\operatorname{\mathrm{tr}}(\operatorname{\mathrm{blkd}}(\{\Xi_{\tau}^{i}(1,1)-X^{i}(1,1)\})LD_{21}D_{21}^{\mathsf{T}}L^{\mathsf{T}})$ since $L_{i}=E_{n_{i}}L^{i}E_{p_{i}}^{\mathsf{T}}$ . We obtain (37c) by substituting $\Delta$ into $J_{\textup{dec},\textup{del}}=J_{\textup{dec}}+\Delta$ . See Section F.6 below for explanation on $\Xi_{\tau}^{i}$ .

F.5 $J_{\textup{del}}$ (37d)

Derivation is analogous to that of $J_{\textup{dec},\textup{del}}$ . See Section F.7 below for explanation on $\Xi_{c_{\tau}}^{i}$ .

F.6 Proofs for (38a)

We have $X^{i}-X_{{\textup{cen}}_{\underline{ii}}}\succeq 0$ in Lemma 20 for all $i\in[N]$ . The properties of a positive semi-definite matrix give us $X^{i}(1,1)-X_{{\textup{cen}}_{\underline{ii}}}(1,1)\succeq 0$ , and hence $\operatorname{\mathrm{blkd}}(\{X_{\textup{cen}}(i,i)\})\preceq X_{\textup{dec}}$ .

Now we define $\Xi_{\tau}^{i}$ and establish that $\Xi_{\tau}^{i}-X^{i}\succeq 0$ . The Hamiltonian for the control Riccati equation (17) is

H^{i}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\begin{bmatrix}A_{\underline{ii}}-\tilde{B}_{2_{i\underline{i}}}M^{-1}D_{12_{:i}}^{\mathsf{T}}\tilde{C}_{1_{:\underline{i}}}&-\tilde{B}_{2_{i\underline{i}}}M^{-1}\tilde{B}_{2_{i\underline{i}}}^{\mathsf{T}}\\ -\tilde{C}_{1_{:\underline{i}}}^{\mathsf{T}}P_{\tau}\tilde{C}_{1_{:\underline{i}}}&-A_{\underline{ii}}^{\mathsf{T}}+\tilde{C}_{1_{:\underline{i}}}^{\mathsf{T}}D_{12_{:i}}M^{{-1}^{\mathsf{T}}}\tilde{B}_{2_{i\underline{i}}}^{\mathsf{T}}\end{bmatrix}\!,

where $M\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}D_{12_{:i}}^{\mathsf{T}}D_{12_{:i}}$ , $P_{0}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}D_{12_{:i}}M^{-1}D_{12_{:i}}^{\mathsf{T}}$ and $P_{\tau}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}I-P_{0}$ , and define the corresponding symplectic matrix exponential as $\Sigma^{i}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}e^{H^{i}\tau}$ . The elements $\Sigma_{22}^{i}$ , $\Sigma_{21}^{i}$ of this modified $\Sigma^{i}$ are used to define the $\Xi_{\tau}^{i}$ . For all $i\in[N]$ , we define $\Xi_{\tau}^{i}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\tilde{X}^{i}-(\Sigma_{22}^{i^{-1}}\Sigma_{21}^{i})^{\mathsf{T}}$ . By solving the associated Differential Riccati Equation (DRE) [23, Eq. 16], we show $\Xi_{\tau}^{i}-X^{i}\succeq 0$ [23, §4.3]. This gives us $X_{\textup{dec}}\preceq X_{\textup{dec,del}}$ .

F.7 Proofs for (38b)

Next we consider the case of a fully connected graph with delays. So Agent $i$ ’s feedback policy looks like $u_{i}=\mathcal{K}_{ii}(s)y_{i}+\sum_{j\in[N]\setminus i}e^{-s\tau}\mathcal{K}_{ij}(s)y_{j}$ . Since we solve for $\mathcal{Q}$ by solving for individual columns $\mathcal{Q}_{\underline{i}i}$ , we define the associated state transition matrix for each column as $A_{{\underline{ii}}}^{c}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{blkd}}(\{A_{ii},A_{\underline{\underline{ii}}}\})$ , where $\underline{\underline{i}}=[N]\setminus i$ . We define the corresponding $B_{1_{{\underline{i}i}}}^{c}$ , $B_{2_{{\underline{ii}}}}^{c}$ ${C}_{1_{{:\underline{i}}}}^{c}$ , $D_{12_{{:\underline{i}}}}^{c}$ , $C_{2_{{i\underline{i}}}}^{c}$ , and $D_{21_{{ii}}}^{c}$ in a similar manner. We also define a centralized $\Xi_{c_{\tau}}^{i}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\tilde{X}_{c}^{i}-(\Sigma_{{22}_{c}}^{i^{-1}}\Sigma_{{21}_{c}}^{i})^{\mathsf{T}}$ for each $\Gamma$ -modified plant

\displaystyle\tilde{\mathcal{P}}_{i}^{c}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\left[\begin{array}[]{c|cc}A_{{\underline{ii}}}^{c}&B_{1_{{\underline{i}i}}}^{c}&\tilde{B}_{2_{{\underline{ii}}}}^{c}\\[2.0pt] \hline\cr\rule{0.0pt}{9.90276pt}\tilde{C}_{1_{{:\underline{i}}}}^{c}&0&D_{12_{{:\underline{i}}}}^{c}\\ C_{2_{{i\underline{i}}}}^{c}&D_{21_{{ii}}}^{c}&0\end{array}\right].

Each individual column $\mathcal{Q}_{\underline{i}i}$ has its own $\tilde{\mathcal{P}}^{c}_{i}$ as the associated adobe delay matrix is different. We have a corresponding control ARE $(\tilde{X}_{c}^{i},\tilde{F}_{c}^{i})\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\operatorname{\mathrm{Ric}}(A_{\underline{ii}}^{c},\tilde{B}_{2_{\underline{ii}}}^{c},\tilde{C}_{1_{:\underline{i}}}^{c},D_{12_{:\underline{i}}}^{c}).$ We solve DREs for each $\Xi_{c_{\tau}}^{i}$ as in [23, §V.C] to obtain $\Xi_{c_{\tau}}^{i}-X_{{\text{cen}}_{\underline{ii}}}^{c}\succeq 0$ for all $i\in[N]$ , where $X_{{\text{cen}}_{\underline{ii}}}^{c}$ is a reshuffling of $X_{\text{cen}}$ to mirror the ordering of $\underline{i}=\{i,[N]\setminus i\}$ . This proves that $\operatorname{\mathrm{blkd}}(\{X_{\textup{cen}}(i,i)\})\preceq X_{\textup{cen,del}}$ for all $i\in[N]$ .

Lemma 23 proves that $X_{\textup{cen,del}}\preceq X_{\textup{dec,del}}$ for all $i\in[N]$ .

Lemma 23.

$\Xi_{c_{\tau}}^{i}$ and $\Xi_{{\tau}}^{i}$ are the solutions of the DREs for delayed fully connected and decentralized graphs respectively. Then, $W_{\Xi}^{i}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}\Xi_{\tau}^{i}-\Xi_{c_{\underline{ii}}}^{i}\succeq 0$ , where $\Xi_{c_{\underline{ii}}}^{i}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}E_{n_{\underline{i}}}^{\mathsf{T}}\Xi_{c_{\tau}}^{i}E_{n_{\underline{i}}}$ , and $\underline{i}$ corresponds to $\Xi_{\tau}^{i}$ .

Proof.

The DREs for $\Xi_{\tau}^{i}$ , and $\Xi_{c_{\tau}}^{i}$ are subtracted to obtain the differential Lyapunov equation

\dot{\Xi}_{c_{\underline{ii}}}^{i}-\dot{\Xi}_{\tau}^{i}=(A_{\underline{ii}}+B_{2_{\underline{i}i}}F_{\Xi}^{i})^{\mathsf{T}}W_{\Xi}^{i}+W_{\Xi}^{i}(A_{\underline{ii}}+B_{2_{\underline{i}i}}F_{\Xi}^{i})\\ +(E_{m_{\underline{i}}}F_{\Xi}^{i}-F_{\Xi_{c}}^{i}E_{n_{\underline{i}}})^{\mathsf{T}}D_{12}^{\mathsf{T}}D_{12}(E_{m_{\underline{i}}}F_{\Xi}^{i}-F_{\Xi_{c}}^{i}E_{n_{\underline{i}}}),

where $F_{\Xi}^{i}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}-(D_{12_{{:i}}}^{\mathsf{T}}D_{12_{{:i}}})^{-1}(\Xi_{\tau}^{i}B_{2_{{\underline{i}i}}}+C_{1_{:\underline{i}}}^{\mathsf{T}}D_{12_{{:i}}})^{\mathsf{T}}$ , and $F_{\Xi_{c}}^{i}\mathrel{\mathchoice{\vbox{\hbox{$\displaystyle:$}}}{\vbox{\hbox{$\textstyle:$}}}{\vbox{\hbox{$\scriptstyle:$}}}{\vbox{\hbox{$\scriptscriptstyle:$}}}{=}}-(D_{12_{{:i}}}^{c^{\mathsf{T}}}D_{12_{{:i}}}^{c})^{-1}(\Xi_{c_{\tau}}^{i}B_{2_{{\underline{i}i}}}^{c}+C_{1_{:\underline{i}}}^{c^{\mathsf{T}}}D_{12_{{:i}}}^{c})^{\mathsf{T}}$ . The rest is analogous to the proof of Lemma 20. Finally, we obtain $\Xi_{\tau}^{i}-\Xi_{c_{\underline{ii}}}^{i}-X^{i}+X_{{\textup{cen}}_{\underline{ii}}}\succeq 0$ . Using $X^{i}-X_{{\textup{cen}}_{\underline{ii}}}\succeq 0$ from Lemma 20, we obtain $\Xi_{\tau}^{i}-\Xi_{c_{\underline{ii}}}^{i}\succeq 0$ .

References

[1] V. D. Blondel and J. N. Tsitsiklis. A survey of computational complexity results in systems and control. Automatica, 36(9):1249–1274, 2000.
[2] J. H. Cho and M. Kristalny. On the ${H}^{2}$ decentralized controller synthesis for delayed bilateral teleoperation systems. IFAC Proceedings Volumes, 45(22):393–398, 2012.
[3] G. E. Dullerud and F. Paganini. A course in robust control theory: a convex approach, volume 36. Springer Science & Business Media, 2013.
[4] Y.-C. Ho and K.-C. Chu. Team decision theory and information structures in optimal control problems—Part I. IEEE Transactions on Automatic Control, 17(1):15–22, 1972.
[5] M. Kashyap. Optimal Decentralized Control with Delays. PhD thesis, Northeastern University, 2023.
[6] M. Kashyap and L. Lessard. Explicit agent-level optimal cooperative controllers for dynamically decoupled systems with output feedback. In IEEE Conference on Decision and Control, pages 8254–8259, 2019.
[7] M. Kashyap and L. Lessard. Agent-level optimal LQG control of dynamically decoupled systems with processing delays. In IEEE Conference on Decision and Control, pages 5980–5985, 2020.
[8] J.-H. Kim and S. Lall. Explicit solutions to separable problems in optimal cooperative control. IEEE Transactions on Automatic Control, 60(5):1304–1319, 2015.
[9] J.-H. Kim, S. Lall, and C.-K. Ryoo. Optimal cooperative control of dynamically decoupled systems. In IEEE Conference on Decision and Control, pages 4852–4857, 2012.
[10] M. Kristalny and J. H. Cho. On the decentralized $H^{2}$ optimal control of bilateral teleoperation systems with time delays. In IEEE Conference on Decision and Control, pages 6908–6914, 2012.
[11] M. Kristalny and J. H. Cho. Decentralized ${H}^{2}$ optimal control of haptic interfaces for a shared virtual environment. In IEEE Conference on Decision and Control, pages 5204–5209, 2013.
[12] J. F. Kurose and K. W. Ross. Computer Networking: A top-down approach. Pearson, 8 edition, 2021.
[13] A. Lamperski and J. C. Doyle. The $\mathcal{H}_{2}$ control problem for quadratically invariant systems with delays. IEEE Transactions on Automatic Control, 60(7):1945–1950, 2015.
[14] A. Lamperski and L. Lessard. Optimal decentralized state-feedback control with sparsity and delays. Automatica, 58:143–151, 2015.
[15] L. Lessard. Decentralized LQG control of systems with a broadcast architecture. In IEEE Conference on Decision and Control, pages 6241–6246, 2012.
[16] L. Lessard, M. Kristalny, and A. Rantzer. On structured realizability and stabilizability of linear systems. In American Control Conference, pages 5784–5790, 2013.
[17] L. Lessard and S. Lall. An algebraic approach to the control of decentralized systems. IEEE Transactions on Control of Network Systems, 1(4):308–317, 2014.
[18] L. Lessard and S. Lall. Optimal control of two-player systems with output feedback. IEEE Transactions on Automatic Control, 60(8):2129–2144, 2015.
[19] D. Madjidian and L. Mirkin. $H_{2}$ optimal cooperation of homogeneous agents subject to delyed information exchange. IFAC-PapersOnLine, 49(10):147–152, 2016.
[20] L. Mirkin. On the extraction of dead-time controllers and estimators from delay-free parametrizations. IEEE Transactions on Automatic Control, 48(4):543–553, 2003.
[21] L. Mirkin, Z. J. Palmor, and D. Shneiderman. Loop shifting for systems with adobe input delay. IFAC Proceedings Volumes, 42(6):307–312, 2009.
[22] L. Mirkin, Z. J. Palmor, and D. Shneiderman. Dead-time compensation for systems with multiple I/O delays: A loop-shifting approach. IEEE Transactions on Automatic Control, 56(11):2542–2554, 2011.
[23] L. Mirkin, Z. J. Palmor, and D. Shneiderman. ${H}^{2}$ optimization for systems with adobe input delays: A loop shifting approach. Automatica, 48(8):1722–1728, 2012.
[24] L. Mirkin and N. Raskin. Every stabilizing dead-time controller has an observer–predictor-based structure. Automatica, 39(10):1747–1754, 2003.
[25] X. Qi, M. V. Salapaka, P. G. Voulgaris, and M. Khammash. Structured optimal and robust control with multiple criteria: A convex solution. IEEE Transactions on Automatic Control, 49(10):1623–1640, 2004.
[26] M. Rotkowitz, R. Cogill, and S. Lall. Convexity of optimal control over networks with delays and arbitrary topology. International Journal of Systems, Control and Communications, 2(1-3):30–54, 2010.
[27] M. Rotkowitz and S. Lall. A characterization of convex problems in decentralized control. IEEE Transactions on Automatic Control, 50(12):1984–1996, 2005.
[28] M. Rotkowitz and S. Lall. Convexification of optimal decentralized control without a stabilizing controller. In International Symposium on Mathematical Theory of Networks and Systems, pages 1496–1499, 2006.
[29] C. W. Scherer. Structured finite-dimensional controller design by convex optimization. Linear Algebra and its Applications, 351–352:639–669, 2002.
[30] P. Shah and P. A. Parrilo. $\mathcal{H}_{2}$ -optimal decentralized control over posets: A state-space solution for state-feedback. IEEE Transactions on Automatic Control, 58(12):3084–3096, 2013.
[31] T. Tanaka and P. A. Parrilo. Optimal output feedback architecture for triangular LQG problems. In American Control Conference, pages 5730–5735, 2014.
[32] A. S. M. Vamsi and N. Elia. Optimal distributed controllers realizable over arbitrary networks. IEEE Transactions on Automatic Control, 61(1):129–144, 2016.
[33] H. S. Witsenhausen. A counterexample in stochastic optimum control. SIAM Journal on Control, 6(1):131–147, 1968.
[34] W. Wonham. On the separation theorem of stochastic control. SIAM Journal on Control, 6(2):312–326, 1968.
[35] J. Yan and S. E. Salcudean. Teleoperation controller design using ${H}_{\infty}$ -optimization with application to motion-scaling. IEEE Transactions on Control Systems Technology, 4(3):244–258, 1996.
[36] D. Youla, H. Jabr, and J. Bongiorno. Modern Wiener-Hopf design of optimal controllers–Part II: The multivariable case. IEEE Transactions on Automatic Control, 21(3):319–338, 1976.
[37] K. Zhou, J. C. Doyle, and K. Glover. Robust and optimal control, volume 40. Prentice Hall, New Jersey, 1996.

Optimal Control of Multi-Agent Systems with Processing Delays

Abstract

1 Introduction

1.1 Literature review

2 Preliminaries

Transfer matrices.

Block indexing.

2.1 Delay

2.2 Problem statement

Assumption 1 (System assumptions).

Definition 2 (Riccati assumptions).

2.2.1 Riccati equations

3 Optimal Controller

3.1 Parameterization of stabilizing controllers

Lemma 3.

Proof.

Remark 4.

Remark 5.

Remark 6.

Remark 7.

3.2 Optimal controller without delays

Theorem 8.

Proof.

Remark 9.

Remark 10.

Remark 11.

3.3 Optimal controller with delays

Theorem 12.

Proof.

4 Agent-level controllers

Theorem 13.

Proof.

4.1 Interpretation of optimal controller

Remark 14.

Remark 15.

Remark 16.

5 Characterizing the cost

Theorem 17.

Proof.

Remark 18.

Remark 19.

5.1 Synchronization example

6 Conclusion

Appendices

A Definition of the Γ\Gamma function

B Gramian equations

Lemma 20.

Proof.

Lemma 21.

Proof.

C Proof of Theorem 8

Lemma 22.

Proof.

C.1 Proof of optimality

D Proof of Theorem 12

E Proof of Theorem 13

F Proof of Theorem 17

F.1 JcenJ_{\textup{cen}} (37a)

F.2 JdecJ_{\textup{dec}} (37b)

F.3 Alternative formulas for the cost

F.4 Jdec,delJ_{\textup{dec},\textup{del}} (37c)

F.5 JdelJ_{\textup{del}} (37d)

F.6 Proofs for (38a)

F.7 Proofs for (38b)

Lemma 23.

Proof.

References

Optimal Control of Multi-Agent Systems
with Processing Delays

A Definition of the $\Gamma$ function

F.1 $J_{\textup{cen}}$ (37a)

F.2 $J_{\textup{dec}}$ (37b)

F.4 $J_{\textup{dec},\textup{del}}$ (37c)

F.5 $J_{\textup{del}}$ (37d)