Optimal collision energy for realizing macroscopic high baryon-density matter

Introduction.— Exploring the properties of matter at extremely high baryon densities that exceed several times the normal nuclear density $\rho_{0}\approx 0.17\;{\rm fm}^{-3}$ is one of the most exciting frontiers in current physics. Such a high density environment is realized in, for example, the core of neutron stars. Recent remarkable progress in the observation of neutron stars through gravitational waves from binary neutron-star mergers [1, *LIGOScientific:2017ync, *LIGOScientific:2018cki, *LIGOScientific:2018hze] and pulsar X-rays [5, *Miller:2021qha, *Riley:2019yda, *Riley:2021pdl] provides valuable information for constraining the equation of state of the dense matter [9]. The form of matter in such extreme conditions is determined by quantum chromodynamics (QCD) — the theory of strong interaction — and is expected to have rich phase structure [10]. Unveiling their properties is one of the ultimate goals of nuclear physics. Experimental inputs are crucial to achieve this, since the first-principle lattice-QCD calculation is difficult due to the notorious sign problem [11] and the low-energy effective models, such as the chiral effective theory, become invalid when the baryon density exceeds about $2\rho_{0}$ [12, 13, 14].

Relativistic heavy-ion collisions are the only terrestrial experiments to create such high baryon-density matter and to study their properties in laboratories [15]. In these experiments, dense and hot matter is created by colliding heavy nuclei accelerated up to almost the speed of light with a large accelerator. The experiments have been carried out at various facilities such as the LHC [16], RHIC [17], and SIS18 [18], for a wide range of collision energies with the center-of-mass energy per nucleon pair $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}$ up to $5\;{\rm TeV}$. In the past decades, the high energy region $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}\gtrsim 100\;{\rm GeV}$ has been extensively investigated at the LHC and RHIC. They are suitable for creating extremely hot but low baryon-density matter, and have succeeded in reproducing the primordial form of matter of the Universe just after the Big Bang — the quark-gluon plasma [19]. Recently, the lower energy range $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}\approx 3\,\mathchar 45\relax\,20\;{\rm GeV}$, which we call intermediate collision energies, is attracting renewed attention. The intermediate energies are expected to be suitable for exploring high baryon-density and low-temperature matter, which is crucial to understand the interiors of neutron stars and supernovae. This energy range is actively investigated in the Beam-Energy Scan (BES) program at RHIC [20] and NA61/SHINE at SPS [21], and will be further studied worldwide [22] in NICA [23], FAIR [24], HIAF [25], and J-PARC-HI [26], which will drastically improve the statistics.

Several experimental results support the formation of high baryon-density matter at the intermediate energy region. First, the rapidity distribution of net-proton number in collisions of gold (Au) nuclei at $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}=5\,\mathchar 45\relax\,200\;{\rm GeV}$ [27] implies strong stopping of baryon charges at mid-rapidity for the AGS energy $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}\approx 5\;{\rm GeV}$ and hence realization of high baryon density. Second, a more quantitative estimate is feasible with the thermal-statistical fit to the hadron yields. It has been estimated in Ref. [28] that the baryon density at the chemical freezeout is maximized at $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}\approx 8\;{\rm GeV}$. However, it is not the maximum baryon density for a whole heavy-ion reaction, since the chemical freezeout occurs at a late stage, where the baryon density is diluted by the expansion.

To investigate the maximum baryon density, one must resort to dynamical models of heavy-ion collisions, such as microscopic transport models [29, 30, 31, 32], hydrodynamic models [33, 34, 35, 36], and hybrid models [37, 38, 39, 40]. Previous microscopic transport-model calculations predicted that the maximum baryon density at the center of the collision system can exceed $8\rho_{0}$ for $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}\gtrsim 5\;{\rm GeV}$ [41, 42, 43, 44]. It has also been discussed that even higher densities over $10\rho_{0}$ can be reached in some collision events due to large event-by-event fluctuations [43]. However, these studies focus on the density at the center, and it is unclear how much the dense region extends in space and time. The large spatial and temporal sizes, besides the maximum baryon density, are crucial for the dense matter to leave observable signals in the final state. Despite its importance, to the best of our knowledge, quantitative studies on the volume and lifetime of the dense region and their dependence on $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}$ have not been performed.

The purpose of this letter is to examine the spacetime volume of the high baryon-density region in intermediate-energy heavy-ion collisions and to estimate the optimal collision energy that maximizes the spacetime volume.

Measures.— To quantify the volume and lifetime of the high-baryon-density region in heavy-ion collisions, we propose the following three measures. These measures are constructed from the baryon density in the local rest frame (Eckart frame) ¹¹1Equation (1) is ill-defined for $J^{2}<0$, which can happen when anti-baryon production occurs. However, anti-baryon production is well suppressed for $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}<20\;{\rm GeV}$. Hence, it is rare to have $J^{2}<0$, and even if it happens the value is very close to zero within the numerical accuracy. Therefore, in our simulation, we simply set $\rho(x)=0$ if $J^{2}(x)<0$. ,

$\displaystyle\rho(x):=\sqrt{J^{\mu}(x)J_{\mu}(x)}\;,$

(1)

where $J^{\mu}(x)$ is the baryon current at each spacetime point $x$ in the center-of-mass frame of a collision system.

The first measure is the spatial volume that exceeds a threshold density value $\rho_{\rm th}$,

$\displaystyle V_{3}(\rho_{\rm th};t):=\int_{\rho(x)>\rho_{\rm th}}{\rm d}^{3}{\bm{x}}\,\gamma[J(x)]\;.$

(2)

The Lorentz factor $\gamma[J(x)]:=1/\sqrt{1-({\bm{J}}(x)/J^{0}(x))^{2}}$ is inserted to define the volume in the local rest frame. Second, we introduce a Lorentz invariant four-volume $V_{4}(\rho_{\rm th})$ as ²²2The integral in Eq. (3) diverges for $\rho_{\rm th}\lesssim\rho_{0}$, since nuclear matter has the density $\rho_{0}$ for $t<0$ and also nuclear clusters can be formed during heavy-ion reactions, which can survive for a long time. We, thus, limit ourselves to $\rho_{\rm th}>2\rho_{0}$, where these effects are negligible.

$\displaystyle V_{4}(\rho_{\rm th}):=\int_{\rho(x)>\rho_{\rm th}}{\rm d}t{\rm d}^{3}\bm{x}\;.$

(3)

Finally, we define a measure of the typical lifetime of the dense region as

$\displaystyle\tau(\rho_{\rm th}):=\frac{V_{4}(\rho_{\rm th})}{\max[V_{3}(\rho_{\rm th};t)]}\;,$

(4)

where $\max[V_{3}(\rho_{\rm th};t)]$ is the maximum of $V_{3}(\rho_{\rm th};t)$ over time. We compute Eqs. (2)–(4) on an event-by-event basis, i.e., they are constructed from $J^{\mu}(x)$ for each event.

The advantages of the measures are their simplicity and the clarity of the physical meanings. They can be calculated straightforwardly in a given dynamical model without any further assumptions, once $J^{\mu}(x)$ is given. However, these measures are not concerned with the local equilibration, and hence the local temperature and/or the chemical potential. Whereas local equilibration has been studied within some microscopic transport models [47, 48, 49, 50, 51, 52], it must introduce criteria for equilibration in a finite and dynamical system, leaving ambiguities in the analysis/interpretation.

Nevertheless, we emphasize that these measures can constrain the spacetime profile of the equilibrated region, since $V_{3}(\rho_{\rm th},t)$ and $V_{4}(\rho_{\rm th})$ obviously give the upper limits for the spacetime volumes of the equilibrated region. Furthermore, the formation of the dense region is of interest even without equilibration because such a high density can induce intriguing phenomena, such as the chiral vortical effect [53] and the nucleation of deconfined regions.

Simulation method.— We investigate the $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}$ dependence of the measures (2)–(4) in central Au ​+ ​Au collisions. We employ a microscopic transport model JAM [54, 55] and generate 1000 collision events with the impact parameter less than $3\;{\rm fm}$, which roughly corresponds to the top 5% centrality cut. The simulations are performed with version 2.5743 in the default setting, unless otherwise stated. This version incorporates the recently implemented covariant cascade algorithm [56] and the Lorentz-vector version of the relativistic molecular dynamics (RQMDv) with the mean field of the soft momentum-dependent potential [57, 58]. As shown in Refs. [57, 58], RQMDv can successfully reproduce various experimental data, such as the collision energy dependencies of the directed flows of protons and $\Lambda$ over a wide range of collision energies.

To define the baryon current $J^{\mu}(x)$ as a continuous quantity, we smear the baryon density of particles at position $X_{b}$ and momentum $P^{\mu}_{b}$ as $J^{\mu}(x):=\sum_{b\in{\rm baryons}}V^{\mu}_{b}B_{b}g(x-X_{b};P_{b})$, where $B_{b}$ and $V^{\mu}_{b}=P^{\mu}_{b}/P_{b}^{0}$ are the baryon number and velocity of the $b$-th baryon ³³3In general, the velocity $V^{\mu}$ can receive correction from the mean field [92, 93]. However, we neglect it since we have checked that its effect is well suppressed., respectively, and $g(x;P):=\gamma[P]/(\sqrt{2\pi}r)^{3}\exp[-(|\bm{x}|^{2}+(\gamma[P]\bm{V}_{b}\cdot\bm{x})^{2})/(2r^{2})]$ is a relativistic Gaussian smearing function [60, 61]. We use the smearing width $r=1\;{\rm fm}$ for all baryons, which is almost the same size as the charge radius of protons [62]. The smearing can be interpreted as the intrinsic distribution of baryon density inside baryons or a technical coarse-graining for numerics. The maximum value of the smearing function $g(0;0)\approx 0.37\rho_{0}$ is much smaller than $\rho_{0}$, indicating that a considerable number of baryons must overlap to realize $\rho(x)\gg\rho_{0}$.

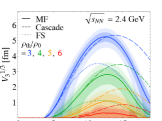
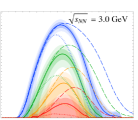
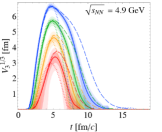
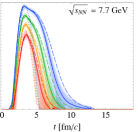
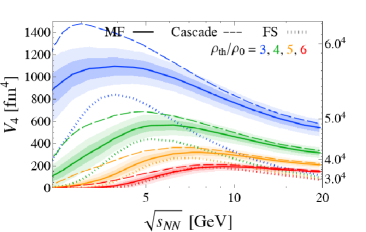
Simulation results.— Figure 1 shows the time dependence of $V_{3}(\rho_{\rm th};t)$ for various collision energies. The thick-solid, thin-dashed, and dotted lines show, respectively, the results from the full simulation with the mean field (MF), the cascade mode (Cascade), where the mean field is turned off, and the free streaming (FS) simulations, where all the interactions are switched off.

One observes that $V_{3}(\rho_{\rm th};t)$ for $\rho_{\rm th}/\rho_{0}=3$ has the maximum value $({\rm max}[V_{3}(\rho_{\rm th};t)])^{1/3}\approx 6\;{\rm fm}$ for all collision energies. We regard this length scale as “macroscopically” large, since it is much larger than the typical microscopic length scale of the system $\approx 1\;{\rm fm}$, determined by the interaction range and the sizes of hadrons. Additionally, the achieved length scale is comparable to the radius of the colliding gold ions $R_{\rm Au}\approx 6.4\;{\rm fm}$ and thus is “maximally” large in the sense that the overlap of two nuclei cannot result in a volume larger than $\approx R_{\rm Au}^{3}$. Regions with $\rho_{\rm th}/\rho_{0}>3$ are created with smaller $V_{3}(\rho_{\rm th};t)$, which increase with $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}$. It is also found that the dense region disappears more quickly for larger $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}$.

When comparing MF with Cascade, one finds that $V_{3}(\rho_{\rm th};t)$ is more suppressed in MF. This is because the repulsive mean field [57] makes the matter less compressed [63]. The mean-field effect becomes more important for lower collision energies, especially for $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}\lesssim 3.0\;{\rm GeV}$. The comparison between MF and FS shows that $V_{3}(\rho_{\rm th};t)$ is enhanced by the interaction. Due to the collisions, the particles are decelerated and gather around the collision point, forming a dense region.

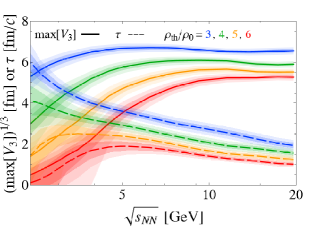
In order to examine the $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}$ dependence observed in Fig. 1 quantitatively, we show ${\rm max}[V_{3}(\rho_{\rm th};t)]$ and $\tau(\rho_{\rm th})$ as functions of $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}$ in Fig. 2. It shows that ${\rm max}[V_{3}(\rho_{\rm th};t)]$ grows and saturates with increasing $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}$. Meanwhile, $\tau(\rho_{\rm th})$ decreases except for $\rho_{\rm th}/\rho_{0}\geq 5$ at low collision energies, where the formation of the region with $\rho(x)>\rho_{\rm th}$ scarcely occurs.

To obtain an observable signal of dense matter, both the spatial volume and the lifetime must be large. The optimal $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}$ to maximize ${\rm max}[V_{3}(\rho_{\rm th};t)]$ and $\tau(\rho_{\rm th})$ simultaneously may be estimated from the crossing point of the solid- and dashed-blue lines in Fig. 2. Taking $\rho_{\rm th}/\rho_{0}=3$ as an example, it is located at $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}\approx 2.6\;{\rm GeV}$, where a macroscopically large spacetime volume, ${\rm max}[V_{3}(\rho_{\rm th};t)]^{1/3}=\tau(\rho_{\rm th})\approx 5.5\;{\rm fm}$, is realized. For $\rho_{\rm th}/\rho_{0}=4$, the crossing point is located at $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}\approx 2.8\;{\rm GeV}$ with ${\rm max}[V_{3}(\rho_{\rm th};t)]^{1/3}=\tau\approx 4\;{\rm fm}$, which is smaller than the result for $\rho_{\rm th}/\rho_{0}=3$, but still occupies a certain spacetime volume of the reaction zone. Similar arguments suggest that an experimental analysis of the matter with $\rho(x)/\rho_{0}\gtrsim 5$ is challenging, as ${\rm max}[V_{3}(\rho_{\rm th};t)]$ and $\tau(\rho_{\rm th})$ are suppressed and are no longer macroscopically large.

One can make a similar estimate of the optimal $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}$ from an analysis of the $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}$ dependence of $V_{4}(\rho_{\rm th})$, shown in Fig. 3. We estimate the optimal $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}$ with the maximum of $V_{4}(\rho_{\rm th})$, which is located around $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}=4$ and $5.5\;{\rm GeV}$ for $\rho_{\rm th}/\rho_{0}=3$ and $4$, respectively. These values are slightly higher than those estimated from the crossing points in Fig. 2. The corresponding maximum values are $(V_{4}(\rho_{\rm th}))^{1/4}=5.8\;{\rm fm}$ and $4.9\;{\rm fm}$, respectively, which are almost the same as the values of $(V_{3}(\rho_{\rm th},t))^{1/3}$ and $\tau(\rho_{\rm th})$ at the crossing points in Fig. 2.

Wrapping up these results, we conclude that the region with $\rho(x)/\rho_{0}\geq 3$ can be formed with macroscopically large spatial and temporal sizes in central Au ​+ ​Au collisions. The sweet spot of $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}$ to maximize the spatial and temporal sizes simultaneously starts from $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}\lesssim 3\;{\rm GeV}$ and extends up to $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}\gtrsim 4\;{\rm GeV}$. The optimal collision energy for $\rho(x)/\rho_{0}\geq 4$ is estimated to be slightly higher than that for $\rho(x)/\rho_{0}\geq 3$. Compared to the previous research, the estimated optimal $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}$ is considerably smaller [28, 43]. RemoveAlso, Although the maximum baryon density can locally exceed $\rho(x)/\rho_{0}=8$, as shown in Refs. [41, 42, 43, 44], the volume and lifetime of such high baryon-density regions are small.

Finally, we discuss the event-by-event fluctuations. In Figs. 1–3, the colored bands show the $1\sigma$ (dense) and $2\sigma$ (light) ranges of the event-by-event distribution of the individual quantities. The figures show that $V_{3}(\rho_{\rm th};t)$, $\tau$, and $V_{4}(\rho_{\rm th})$ can fluctuate significantly, which are driven by the positional fluctuation of nucleons on the colliding nuclei [63]. For example, the upper and lower bounds of the $2\sigma$ band of $V_{4}(\rho_{\rm th})$ at $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}\lesssim 3\;{\rm GeV}$ and $\rho_{\rm th}/\rho_{0}=3$ are $1250$ and $850\;{\rm fm}^{4}$, respectively. In other words, the values of $V_{4}(3\rho_{0})$ in the top and bottom $2.5\%$ collision events differ by a factor of more than $1250/850\approx 1.5$. This means that, if a selection of such large- and small-$V_{4}$ events is available, their comparison is used to investigate the properties of dense matter from the spacetime-volume dependence of experimental observables. As another example, for $\rho_{\rm th}/\rho_{0}=5$, the lower $2\sigma$-bound of ${\rm max}[V_{3}(5\rho_{0},t)]$ vanishes at $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}\approx 3\;{\rm GeV}$, whereas the upper bound is about $(3\;{\rm fm})^{3}$. Exploiting these large event-by-event fluctuations may allow us to explore even denser regions in the experiments.

Discussions.— We have shown that a high-density matter with $\rho(x)/\rho_{0}\gtrsim 3$ can be created with macroscopically large volume at intermediate collision energies. Since $\rho(x)/\rho_{0}\gtrsim 3$ is the density expected to be realized in the core of neutron stars [64, 9], it is an important next step to pursue the connection between the two realms. In heavy-ion collisions, observables, such as the directed flow [65, 66], dilepton yields [67, 68, 69, 70], and fluctuations of conserved charges [71, 72, 73], are expected to be sensitive to the equations of state and the phase transitions. Examining these observables based on our results on the spacetime density profile enables us to further constrain the properties of the matter at baryon densities relevant to neutron stars. In the present study, we have focused on the measures (2)–(4), which do not care about the equilibration of matter. Although this ignorance is the key to realizing the quantitative analysis of the spacetime profile, the consideration of equilibration, as well as the estimation of the resulting temperature and chemical potential, is another important extension of this study to approach the matter properties in equilibrium [63].

Let us discuss the validity of our JAM simulation, which (1) is based on the particular choice of the mean field, i.e., RQMDv with a soft momentum-dependent potential, and (2) is a hadronic model, containing no explicit quark and gluon degrees of freedom. Regarding the choice of the mean field (1), we have also executed JAM with other mean field parameters, such as a hard momentum-dependent potential and momentum-independent potentials [57], for comparison. We have found that the choice of the mean field for $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}>2.4\;{\rm GeV}$ only gives minor differences, which are smaller than that between the MF and Cascade results shown in Figs. 1 and 3 [63]. Thus, we expect that the estimated optimal $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}$ is robust against the choice of the mean field. Nevertheless, the above expectation is drawn from the analysis within JAM, and hence it is an interesting subject to study the spacetime volume and the optimal $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}$ with other transport models to reinforce our findings. Regarding (2), we note that recent experimental data on elliptic flow suggest that quark-number scaling [74], which is a possible signal of the formation of the quark-gluon plasma, is violated for $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}\lesssim 4\;{\rm GeV}$ [75, 76, 77]. Therefore, at least around the optimal $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}\approx 3\,\mathchar 45\relax\,4\;{\rm GeV}$, the quark-gluon plasma is unformed, and hence the hadronic treatment would suffice. One could, nonetheless, argue that the violation of the quark-number scaling does not fully exclude the possibility that the quark-gluon plasma is locally created in the matter. We expect that the inclusion of quark and gluon degrees of freedom will not significantly alter our conclusions, as the fraction of quark deconfinement phase at $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}\lesssim 10\;{\rm GeV}$ is not so large [78, 32]. Additionally, the phase transition can influence the spacetime evolution of the matter by softening the equations of state, whose impact on the density is found to be small [52]. Nevertheless, it is worthwhile to test those expectations using models that include explicit quark degrees of freedom such as AMPT [79, 80], PHSD [81, 82, 78], PHQMD [32], PACIAE [83], and hybrid models [84, 39, 85, 86, 40], and that incorporate the phase transition dynamics such as UrQMD [68, 87, 88, 89] and JAM with an advanced option [52].

We comment on the relation of this study with the event-by-event analysis of fluctuations in conserved charges [71, 72, 73]. The large fluctuations of the spacetime volume shown in Figs. 1–3 may fake signals of the fluctuation observables, which are important for the search for the QCD critical point. Taming the fluctuations of the spacetime volume, which would in part be regarded as the volume fluctuations [90, 91], may be crucial in this energy range.

Summary.— We have investigated the volume and lifetime of the high baryon-density matter created in central Au ​+ ​Au collisions by introducing the three measures (2)–(4) and estimated the optimal collision energy to realize the largest spacetime volume using a microscopic transport model JAM. The numerical results suggest that the dense region with $\rho(x)/\rho_{0}\gtrsim 3$ can be created with large volume and lifetime with the optimal collision energy around $\sqrt{s_{{}_{\;\!\!N\;\!\!\;\!\!N}}}\approx 3\,\mathchar 45\relax\,4\;{\rm GeV}$. These findings are crucial for further investigations of the dense matter with near-future facilities such as NICA, FAIR, HIAF, and J-PARC-HI, as well as the current RHIC BES program.

Acknowledgments.— The authors thank Akira Ohnishi and Toru Nishimura for the collaboration at the early stage of the present work. They also thank Takao Sakaguchi and Hiroyuki Sako for useful discussions. This work is supported by JSPS KAKENHI under grant Nos. 22K14045 and 24K17058 (HT), Nos. JP19H05598, JP22K03619, JP23H04507, and JP24K07049 (MK), No. JP21K03577 (YN), the RIKEN special postdoctoral researcher program (HT), JST SPRING, Grant Number JPMJSP2110 (AJ), the Center for Gravitational Physics and Quantum Information (CGPQI) at Yukawa Institute for Theoretical Physics (MK). A part of the numerical simulations have been carried out on Yukawa-21 at Yukawa Institute for Theoretical Physics (YITP), Kyoto University.