Optically Controlled Topological Phases in the Deformed $\alpha$-$T_{3}$ Lattice

Higher-order topological phases have revolutionized our understanding of quantum materials [1, 2], by extending the concept of topology beyond conventional edge or surface states to boundary modes localized at corners or hinges [3]-[6]. These phases represent a profound advancement in the study of topological phenomena, challenging traditional classifications based on symmetry and topology [7, 8]. This framework builds upon earlier discoveries such as the quantum Hall effect [9, 10], where quantized Hall conductivity is governed by topological invariants like the Chern number [11, 12]. Haldane’s seminal work on breaking time-reversal symmetry in honeycomb lattices provided a theoretical foundation for understanding these invariants and their role in phase transitions [13], inspiring experimental realizations in diverse geometries and materials including Lieb and Kagome lattices [15, 16], iron-based honeycomb ferromagnetic insulators [17], and electronic and photonic systems [18, 19, 20, 21].

Two-dimensional topological insulators are defined by time-reversal symmetry and a $\mathbb{Z}_{2}$ topological invariant [22, 23]. Breaking this symmetry triggers a topological phase transition, forming a Chern insulator characterized by chiral edge states and the quantized Hall effect [24]. The Chern number determines the system’s topological phase, with zero indicating a trivial phase. Additionally, circularly polarized off-resonant light can induce topological transitions [25], driving systems from trivial to non-trivial phases through Floquet theory [26, 27]. Second-order photon processes allow for band gap tuning, enabling effective Hamiltonians dependent on light frequency and intensity, as in the Haldane model. This framework explains transitions like the polarized light-induced transition of semi-metallic graphene into a Chern insulator [28]. Such prominent example under non-resonant polarized light involves a phenomenon corroborated by numerous analogous experiments on radiative systems [29, 30].

While most Chern insulators have a Chern number of 1, research is increasingly focused on higher Chern numbers, which have been observed experimentally in systems like thin film magnetic topological insulators and photonic crystals  [31]. It have been also predicted theoretically in the Dirac-Weyl semimetals on the $\alpha-T_{3}$ lattice [32]. Numerous studies have revealed remarkable properties of the $\alpha-T_{3}$ system, including enhanced Hall conductivity and unconventional Berry phase effects, which are closely tied to its unique electronic structure [33, 34]. For instance, the $\alpha-T_{3}$ lattice, characterized by a tunable parameter controlling the weight of its flat band, exhibits intriguing phenomena like Klein tunneling and Fabry-Perot resonances, which have been extensively studied in both single-layer and bilayer configurations [33, 34]. Additionally, the interplay between the flat band and the Berry phase in these systems leads to novel magneto-optical properties and phase transitions, such as the quantum spin Hall phase transition [35]. Further insights have been gained from detailed analyses of Floquet states in optically driven $\alpha-T_{3}$ lattices. Under resonant and circularly polarized light irradiation, these systems exhibit the opening of Berry phase-dependent optical gaps, revealing unique topological signatures and symmetry-driven phenomena [36]. Moreover, the dice lattice, a special case of the $\alpha-T_{3}$ model with a flat band parameter, has shown to exhibit higher Chern numbers, accompanied by a significant enhancement in unconventional Hall conductivity [37].

High Chern numbers have also been reported in decorated lattices, multi-orbital systems, and lattices with spin-orbit coupling or ultracold gases, broadening the understanding of topological materials. Introducing the Haldane model into a bilayer of the $\alpha-T_{3}$ lattice has resulted in observed Chern numbers of up to 5 [38], along with a substantial enhancement of the $6e^{2}/h$ Hall conductivity [38, 39]. Other lattice structures, such as the decorated honeycomb or starlike lattices [40], and multi-orbital triangular lattices [41], also exhibit high Chern numbers and larger jumps. High Chern numbers have also been reported in Dirac [42] and semi-Dirac [43] systems. Additionally, the presence of spin-orbit coupling in honeycomb lattices [44] and ultracold gases in triangular lattices [45] has been shown to give rise to high Chern numbers. These studies contribute to a deeper understanding of the topological properties of these advanced materials.

In this work, we explore the topological properties of the $\alpha-T_{3}$ lattice, a fascinating system that generalizes the honeycomb lattice. The $\alpha-T_{3}$ lattice consists of two sublattices, A and B, representing carbon atoms located at the vertices of a hexagonal structure, and a third site, C, positioned at the center of each hexagon, as illustrated in Fig. 1. Within this structure, quasiparticles can hop from site C to site A within the same hexagon. The hopping energy between sites A and B is described as $\gamma\cos\phi$, while that between sites A and C is $\gamma\sin\phi$. The parameter $\alpha$, defined by $\tan\phi=\alpha$, governs the lattice configuration. By varying $\alpha$ between 0 and 1, different lattice structures can be realized: when $\phi=0$ $(\alpha=0)$, the lattice corresponds to graphene, and when $\phi=\pi/4$ $(\alpha=1)$, it becomes the dice lattice. Further details about this lattice structure are provided in [46].

In this study, we investigate the topological properties of the $\alpha-T_{3}$ lattice under the influence of an external off-resonant electric field. This field induces a term analogous to the Haldane model, breaking time-reversal symmetry and modulating the band gap, which is pivotal in determining the system’s topological properties. The simultaneous tunability of the $\alpha$ parameter and the presence of a flat band create a distinctive energy dispersion. Additionally, we consider the effect of anisotropic deformations by altering the hopping energies of quasiparticles between nearest-neighbor bonds. Specifically, the hopping energy along the position vector $\delta_{1}$ changes to $\gamma_{1}\sin\phi$ for sites A and C, and $\gamma_{1}\cos\phi$ for sites A and B, while the hopping energies along vectors $\delta_{2}$ and $\delta_{3}$ remain unchanged. As the parameter $\gamma_{1}$ increases, the Dirac points approach each other and eventually merge at the M point in the Brillouin zone when $\gamma_{1}=2\gamma$, leading to band closure and the loss of topological properties. This critical point marks a topological phase transition. Beyond this point, the energy dispersion acquires a Dirac-like form along the $k_{x}$-axis, a phenomenon that has been previously observed in graphene [47], graphene bilayers [48], and the dice lattice [49]. Furthermore, this method has been applied to the single-layer honeycomb structure $Si_{2}O$, yielding a semi-Dirac dispersion [50].

To gain deeper insights, we study the effects of deformation on the topological properties by tuning the hopping energy $\gamma_{1}$ to specific values. We calculate the Berry curvature, which encapsulates key symmetries such as particle-hole symmetry, inversion symmetry, and $C_{3}$ symmetry in the standard case ($\gamma_{1}=\gamma$). As $\gamma_{1}$ deviates from $\gamma$, the $C_{3}$ symmetry is broken, leading to topological transitions. We also compute the Chern number, which indicates the system’s transition from a non-trivial to a trivial topological phase. To further confirm this transition, we analyze the evolution of the Wannier charge center along a closed loop in the Brillouin zone, representing the average charge position within the unit cell. This analysis is consistent with the behavior of surface energy bands [51, 52, 53]. Moreover, we investigate the quantum Hall conductivity and its response to the deformation of the energy spectrum as $\gamma_{1}$ varies. Our results provide valuable insights into the interplay between lattice deformation and topological phase transitions, shedding light on the tunable nature of topological properties in $\alpha-T_{3}$ lattices.
The originality of the present work lies in its comprehensive analysis of the interplay between lattice deformation, external electric fields, and topological properties in the $\alpha-T_{3}$ lattice. By exploring the combined effects of anisotropic hopping energies, Berry curvature, and quantum Hall conductivity, this study not only advances the understanding of topological materials but also paves the way for potential applications in quantum technologies.

This article is organized as follows: Section II presents the Hamiltonian describing quasiparticle dynamics in irradiated and deformed $\alpha-T_{3}$ lattices. Section III analyzes and discusses the quasi-energy spectrum. Section IV investigates the topological properties of this lattice, including the Berry curvature (Subsection IV.1), the Chern phase diagram (Subsection IV.2), and the evolution of the Wannier charge center (Subsection IV.3). Section V examines the anomalous Hall conductivity. Finally, Section VI provides a conclusion and summary of the work.

The rescaled tight-binding Hamiltonian describing the motion of a quasiparticle along a $p_{z}$ orbital in a $\alpha-T_{3}$ lattice between its nearest neighbours is given by [46]

$$H(\bm{k})=\begin{pmatrix}0&\cos(\varphi)\rho(\bm{k})&0\\ \cos(\varphi)\rho^{\ast}(\bm{k})&0&\sin(\varphi)\rho(\bm{k})\\ 0&\sin(\varphi)\rho^{\ast}(\bm{k})&0\end{pmatrix}$$

(1)

where $\rho(\bm{k})=\sum_{j=1}^{3}\gamma_{j}e^{i\bm{k}\bm{\delta_{i}}}$ and $\bm{\delta_{j}}$ are the vectors connecting the nearest neighbors, and $\gamma_{j}$ is the hopping energy. In our model, we consider $\gamma_{1}$ along the $\bm{\delta}_{1}=a(0,1)$ direction and $\gamma_{2}=\gamma$, $\gamma_{3}=\gamma$ along the $\bm{\delta}_{2}=a(-\sqrt{3}/2,-1/2)$ and $\bm{\delta}_{3}=a(\sqrt{3}/2,-1/2)$ directions where $a$ is the distance of the nearest neighbour, as shown in Fig.1. In this section we’ll study photon-electron interactions by applying a polarised electric field perpendicular to the plane of the $a-T_{3}$ lattice. The electric field is derived from the vector potential with respect to time $\partial_{t}A(t)$, and this vector potential depends on time, $\bm{A}(t)=A_{0}(\sin(\omega t),\cos(\omega t))$, where $\omega$ and $A_{0}$ are the radiation frequency and the vector potential amplitude, respectively. The intensity of light is characterized by a dimensionless parameter $\varsigma=eA_{0}a_{0}/\hbar$ and is much smaller than 1, where $a_{0}=\sqrt{3}a$ and $e$ is the electric charge.

when an electric field is applied to electrons moving from site $\bm{m}$ to the nearest site $\bm{m}+\mathbf{\delta}$, they gain energy, represented by the hopping energy $\gamma_{j}$, which is transformed into $\gamma_{j}e^{i\varpi}$, where $\varpi=e/\hbar\int_{\bm{m}}^{\mathbf{m}+\bm{\delta}}\bm{A}(t)d\mathbf{x}$ is the phase factor gained by the electron. The Hamiltonian then becomes

$$H(\bm{k},t)=\begin{pmatrix}0&\cos(\varphi)\rho(\bm{k},t)&0\\ \cos(\varphi)\rho^{\ast}(\bm{k},t)&0&\sin(\varphi)\rho(\bm{k},t)\\ 0&\sin(\varphi)\rho^{\ast}(\bm{k},t)&0\end{pmatrix},$$

(2)

with $\rho(\bm{k},t)=\sum_{j=1}^{3}\gamma_{j}e^{i(\mathbf{\bm{k}}+e\mathbf{A}(t))\mathbf{\delta_{j}}}=\sum_{n=0}^{\infty}J_{n}(\varsigma)\left[\gamma_{1}e^{inwt}e^{i\bm{k}\mathbf{\delta}_{1}}+\gamma e^{i\bm{k}\bm{\delta}_{2}}e^{-in(wt+\pi/3)}+\gamma e^{i\bm{k}\bm{\delta}_{3}}e^{in(\pi/3-wt)}\right]$, where $J_{n}(\varsigma)$ is a Bessel function of the first kind. We consider that the light incident on the $\alpha-T_{3}$ lattice has an off-resonance frequency, as explained in [25]. When an electron is subjected to an off-resonance frequency, it does not excite it directly but simply modifies the band structure in an effective way by absorbing and emitting virtual photons. An off-resonance state is reached when the frequency of the photons is well above the bandwidth, i.e. $\omega>>3\gamma_{1}$. We have a time-dependent and periodic Hamiltonian $H(T+t,k)=H(t,k)$. Floquet’s theorem is perhaps the most convenient solution to this problem, with $T=2\pi/\omega$. In this case, we can describe the properties of the off-resonance light effect by means of the effective Hamiltonian [25, 39].

$$H_{eff}(\bm{k})=H_{0}(\bm{k})+\dfrac{1}{\hbar\omega}\left[H_{-1}(\bm{k}),H_{+1}(\bm{k})\right]+\epsilon(1/\omega^{2}).$$

(3)

We express the time-dependent Fourier components of the Hamiltonian as follows:

$$H_{s}(\bm{k})=\dfrac{1}{T}\int_{0}^{T}H(\bm{k},t)e^{-iswt}dt.$$

(4)

The second term is responsible for the absorption of a virtual photon by an electron through $H_{1}H_{-1}$ and its emission through $H_{-1}H_{1}$. We give the explicit expression of the effective Hamiltonian considering terms up to $\epsilon(1/\omega)$.

$$H_{eff}(\bm{k})=\begin{pmatrix}\eta(\bm{k})\cos(\varphi)^{2}&J_{0}(\varsigma)\cos(\varphi)\rho(\bm{k})&0\\ J_{0}(\varsigma)\cos(\varphi)\rho^{\ast}(k)&-\eta(\bm{k})\cos(2\varphi)&J_{0}(\varsigma)\sin(\varphi)\rho(\bm{k})\\ 0&J_{0}(\varsigma)\sin(\varphi)\rho^{\ast}(\bm{k})&-\eta(\bm{k})\sin(\varphi)^{2}\end{pmatrix},$$

(5)

and $\eta(\bm{k})$ are defined as follows

$$\eta(\bm{k})=2\Delta(-\cos[\dfrac{\sqrt{3}k_{x}a}{2}]+\dfrac{\gamma_{1}}{\gamma}\cos(\dfrac{3k_{y}a}{2}))\sin(\dfrac{\sqrt{3}k_{x}a}{2}).$$

(6)

where $\Delta=\dfrac{\sqrt{3}\gamma^{2}\varsigma^{2}}{2\hbar\omega}$. We consider a weak conduit $\varsigma<<1$, which implies taking the approximation $J_{0}(\varsigma)\approx 1$ and $J_{1}(\varsigma)\approx\dfrac{\varsigma}{2}$. $\eta(\bm{k})$ is the light-induced term, identical to the near-second Haldane term with $\phi=\pi/2$ and $t_{2}=\Delta$, which satisfies the Haldane model for graphene and the dice lattice [37, 47]. This term is responsible for breaking the time reversal symmetry. This results in a gap in the Dirac points. Later we’ll discuss the $\gamma_{1}$-effect, which is a mesh distortion that changes the location of this gap.

As explained previously [32], if we take $\gamma_{1}=\gamma$, $H_{eff}(\bm{k})$ satisfies the anticommutation relations when $\alpha=0$ and $\alpha=1$.

$$\left\{H^{\alpha=0}_{eff}(\bm{k}),C^{\alpha=0}\right\}=0,\quad\left\{H^{\alpha=1}_{eff}(\bm{k}),C^{\alpha=1}\right\}=0.$$

(7)

where $C^{\alpha=0}$ is defined as the graphene operator and $C^{\alpha=1}$ as the dice operator, given as:

$$C^{\alpha=0}\begin{pmatrix}0&-1&0\\ 1&0&0\\ 0&0&1\end{pmatrix}\mathcal{K},\quad C^{\alpha=1}\begin{pmatrix}0&0&-1\\ 0&1&0\\ -1&0&0\end{pmatrix}\mathcal{K}.$$

(8)

with $\mathcal{K}$ as the complex conjugate, equation (7) implies the existence of a particle and a hole such that $\varepsilon(\bm{k})=-\varepsilon(-\bm{k})$, as well as a flat band at zero. However, when we take $\gamma_{1}=2\gamma$ and whatever $\alpha$ is, at point $\bm{M}$ (see Fig.2), $H_{eff}(\bm{k})$ satisfies the anticommutation relations.

$$\left\{H_{eff}(\bm{k}),C^{\alpha=0}\right\}=0,\quad\left\{H_{eff}(\bm{k}),C^{\alpha=1}\right\}=0.$$

(9)

In this case, we can conclude that the radiation does not affect the system in the same way as it would normally, because the system no longer depends on $\alpha$. We will later demonstrate the importance of modifying $\gamma_{1}$, as this results in the deformation of a lattice, a change $\gamma_{1}$, and an observation of its effect on topological properties.

In this section, we study the energy bands as $\gamma_{1}$ varies. The Hamiltonian will be diagonalized to obtain the eigenvalues. This diagonalization leads to the characteristic equation, known as the depressed cubic equation, $\lambda_{3}\varepsilon^{3}+\lambda_{1}\varepsilon+\lambda_{0}=0$, whose solutions can be expressed as follows:

$$\varepsilon_{\nu}(\bm{k})=2\sqrt{\dfrac{-\lambda_{1}}{3}}\cos\left[\dfrac{1}{3}\arccos\left[\dfrac{3\lambda_{0}}{2\lambda_{1}}\sqrt{\dfrac{-3}{\lambda_{1}}}\right]-\dfrac{2\nu\pi}{3}\right],$$

(10)

and

	$\displaystyle\lambda_{0}$	$\displaystyle=-\dfrac{1}{8}\eta^{3}(\bm{k})\sin(2\varphi)\sin(4\varphi),\quad$		(11)
	$\displaystyle\lambda_{1}$	$\displaystyle=-\dfrac{1}{8}\left(8|\rho(\bm{k})|^{2}+\eta^{2}(\bm{k})(5+3\cos(4\phi))\right),$		(12)
	$\displaystyle\lambda_{3}$	$\displaystyle=1.$		(13)

The quasi-energy associated with the conduction band is represented by the value $\nu=0$, while the flat band and the valence band are represented by the values $\nu=1$ and $\nu=2$, respectively. These quasienergies correspond to normalised pseudo-vectors.

$$\ket{\Upsilon_{\nu}(\bm{k})}=\mathcal{N}_{\nu}(\bm{k})\begin{pmatrix}-\frac{\cos(\phi)\rho(\bm{k})}{-\varepsilon_{\nu}(\bm{k})+\eta(\bm{k})}&1&\frac{\sin(\phi)\rho^{\ast}(\bm{k})}{\varepsilon_{\nu}(\bm{k})+\eta(\bm{k})}\end{pmatrix}^{T},$$

(14)

and

$$\mathcal{N}_{\nu}(\bm{k})=\left[1+|\rho(\bm{k})|^{2}\left(\frac{\cos^{2}(\phi)}{(-\varepsilon_{\nu}(\bm{k})+\eta(\bm{k}))^{2}}+\frac{\sin^{2}(\phi)}{(\varepsilon_{\nu}(\bm{k})+\eta(\bm{k}))^{2}}\right)\right]^{-1/2}.$$

(15)

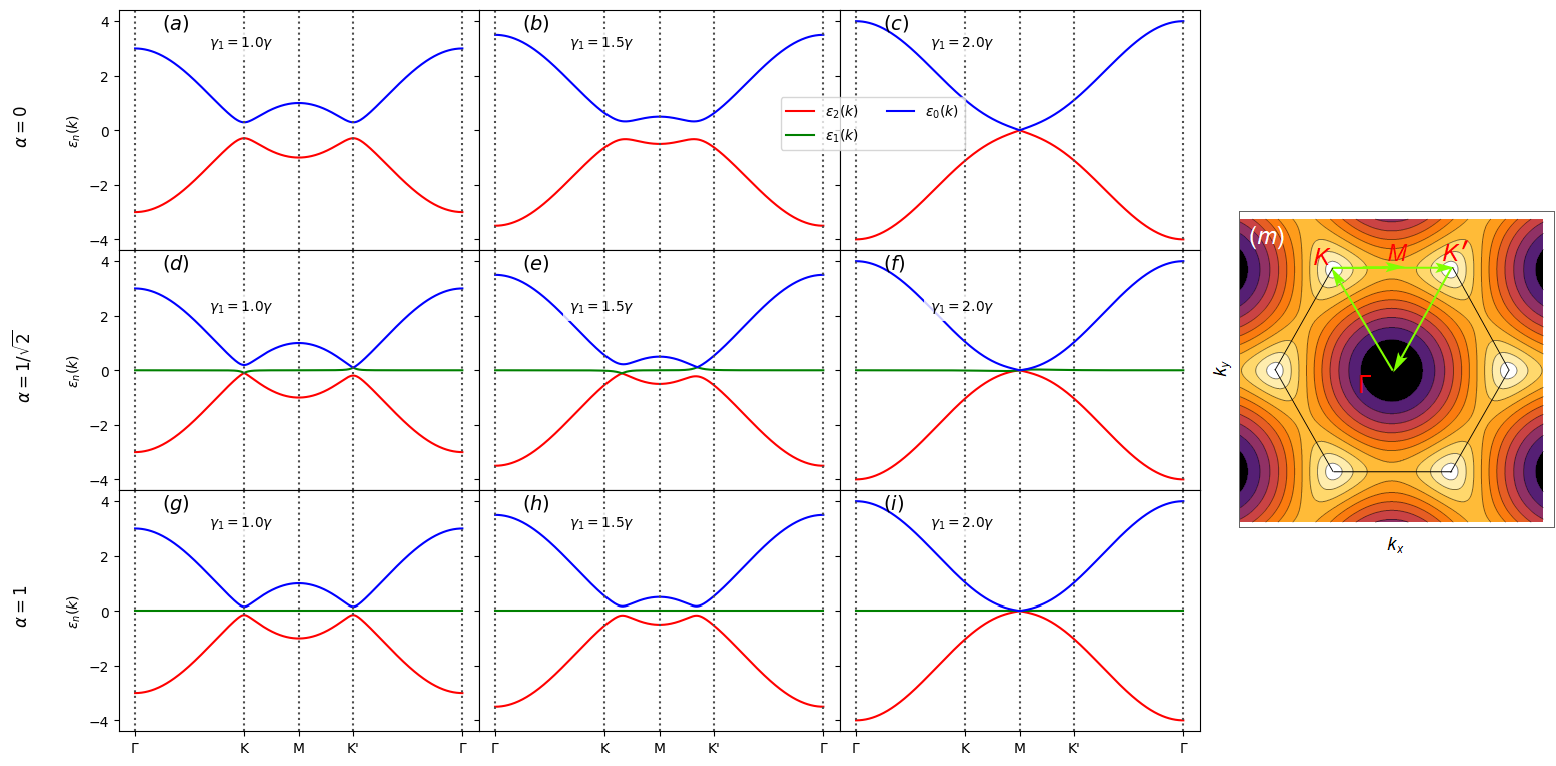
Before discussing the band structure, we determine the path of the first Brillouin zone in the reciprocal lattice, which is in the form of a hexagonal lattice, to construct the band structure path, as shown in Fig.2-(m). Now, we analyse and discuss the band structure by varying $\alpha$ for three values: 0, $1/\sqrt{2}$ and 1. In addition, for each fixed value of $\alpha$, we vary $\gamma_{1}$ while keeping $\Delta$ constant. It is known that when the $\alpha-T_{3}$ lattice is not exposed to radiation, the three bands touch at the Fermi level at points $\bm{K}\left(-\dfrac{2\pi}{3\sqrt{3}a},\dfrac{2\pi}{3a}\right)$ and $\bm{K}^{\prime}\left(\dfrac{2\pi}{3\sqrt{3}a},\dfrac{2\pi}{3a}\right)$, known as Dirac points. On the other hand, under the effect of active radiation, a gap opens that is in a quasi-energy sense dependent on $\alpha$. As $\gamma_{1}$ increases, we observe that for $\alpha=0$(see fig2(a)-2(c)), in the case of graphene, the gap progressively decreases, moving away from the Dirac points and adopting a behaviour similar to the deformed Haldane model. When $\gamma_{1}$ reaches a particular value, $\gamma_{1}=2\gamma$, the gap disappears at the point $\bm{M}(0,\dfrac{2\pi}{3a})$ (see figure 2(c)), where two bands degenerate. Similar behaviour is observed for dice lattices ($\alpha=1$), which also have a structure close to the deformed Haldane model. In this case the gap decreases with increasing g1 and the conduction ,flat, and valence bands become degenerate at the $\bm{M}$ point for $\gamma_{1}=2\gamma$(see fig2(d)). This happens despite the presence of radiation that breaks the time-reversal symmetry. The spectrum then exhibits a semi-Dirac-type dispersion, characterised by a quadratic dependence along $k_{x}$ and a linear dependence along $k_{y}$, in the absence of radiation. In the presence of radiation, for $\gamma_{1}=2\gamma$, electrons move with distinct and linear velocities in both directions, thereby revealing a linear anisotropy. When $\gamma$1 passes $2\gamma(\gamma_{1}>2\gamma)$, a gap opens at point $\bm{M}$. For $\alpha=1/\sqrt{2}$, the gap partially closes at points $\bm{K}$ and $\bm{K}^{\prime}$, as illustrated in Figure2(i)-(j). At points $\bm{K}$ and $\bm{K}^{\prime}$, the dispersion becomes kinetic, except in the interval $\gamma\leqslant\gamma_{1}<2\gamma$. Conversely, when $\gamma_{1}=2\gamma$, the gap disappears and the bands become degenerate at point $\bm{M}$. When $\gamma_{1}>2\gamma$, the effect of radiation is unable to control the gap adjustment, leading to a reopening of the gap.In summary, we can conclude that the effect of radiation is significant only in the interval $\gamma\leqslant\gamma_{1}<2\gamma$.

One aspect that merits attention is that, despite the system being subjected to radiation and $\gamma_{1}$ being fixed at 2$\gamma$, the gap closes and the time-reversal symmetry remains broken. This could indicate a change in the topological properties of the $\alpha-T_{3}$ lattice. This is precisely what we are going to examine in the study of topological properties as $\gamma_{1}$ varies.

In this section, we study the effect of deformation from $\gamma_{1}$ change on Berry curvature, Chern number, and Wannier charge center.

In this section, we calculate and discuss the anomalous Hall conductivity (AHC) for the $\alpha-T_{3}$ lattice exposed to irradiation and deformation. This conductivity is evaluated by examining the electron response to an external electric field in an anisotropic context, providing information about the system topology. To determine the AHC, we integrate the Berry curvature over all occupied states in the entire Brillouin zone (BZ), by Eq.(16). We use the following formula to perform this calculation [54].

$$\sigma_{xy}=\frac{\sigma_{0}}{2\pi}\sum_{\nu}\int_{BZ}d^{2}k\,\varOmega_{\nu}(\bm{k})f_{\nu}(\bm{k}).$$

Where $f_{\nu}(\bm{k})=\left[1+e^{(\varepsilon_{\nu}(\mathbf{k})-\mu)/k_{B}T}\right]^{-1}$ is the Fermi-Dirac distribution function, $\mu$ is the chemical potential, T is the temperature, $k_{B}$ is the Boltzmann constant and $\sigma_{0}=e^{2}/h$. The AHC can be calculated numerically as a function of the chemical potential $\mu$ at T=100 K by fixing $\Delta=0.35\gamma$ and $\alpha$ for four cases: $\alpha=0,0.45,0.8$ and 1, while varying $\gamma_{1}$, as shown in Fig.8.
We first examine the first two cases, $\alpha=0$ and $\alpha=1$, where the hopping energy $\gamma_{1}$ varies, as shown in Fig. 8(a) and (d). A quantised plateau is observed with $\sigma_{xy}=\sigma_{0}$ for $\alpha=0$ and $\sigma_{xy}=2\sigma_{0}$ for $\alpha=1$. When the chemical potential $\mu$ lies within the global gap, the width of the plateau corresponds to that of the gap in the dispersion spectrum and increases proportionally with increasing $\Delta$. It is noteworthy that $\sigma_{xy}$ for $\alpha=1$ is twice that for $\alpha=0$. In this case, the Berry curvature associated with the flat band ($\nu=1$) disappears and has no contribution to $\sigma_{xy}$. When $\mu$ intercepts the bands (whetherconduction $\varepsilon_{0}$ or valence $\varepsilon_{2}$), $\sigma_{xy}$ decreases. This decrease is explained by the fact that the integral isperformed on occupied states and $\mu$ has left the global band.
In addition, the width of the plateau decreases with increasing $\gamma_{1}$, as the overall gap between the dispersive bands narrows. At $\gamma_{1}=2\gamma$ the plateau disappears completely, as does the Hall conductivity.
For cases $\alpha\neq 0$ and 1, the flat band $\varepsilon_{1}$ becomes dispersive, which changes the behaviour of the Hall conductivity. In fact, due to this dispersive nature, there is no longer a smooth plateau in the Hall conductivity. Instead, $\sigma_{xy}$ exhibits a summit located at $\mu=0$, as observed for $\alpha=0.45$ (see Fig. 8(a)). In this scenario, two distinct plateaus of $\sigma_{xy}$ are observed when $\mu$ lies within two energy gaps: one between the flat band $\varepsilon_{1}$ and $\varepsilon_{2}$ at point K, and the other between $\varepsilon_{0}$ and $\varepsilon_{1}$ at point K’. In these cases, the value of $\sigma_{xy}$ for each plateau is $\sigma_{xy}=\sigma_{0}$.
For $\alpha=0.8$, two similar plateaus are also observed, but the value of $\sigma_{xy}$ reaches $\sigma_{xy}=2\sigma_{0}$. This increase in $\sigma_{xy}$ results from a phase transition when $\alpha=1/\sqrt{2}$. As discussed earlier, the Chern number remains constant in the $1/\sqrt{2}<\alpha\leq 1$ phase, which keeps $\sigma_{xy}$ at 2$\sigma_{0}$. However, in this regime, there are no smooth plateaus in the Hall conductivity. Instead, $\sigma_{xy}$ exhibits a dip near $\mu=0$, as shown in Fig. 8(d).
Here, for $\alpha=0.45$ and $\alpha=0.8$, the width of the plateaus in $\sigma_{xy}$ decreases with increasing $\gamma_{1}$ as long as $\gamma_{1}<2\gamma$ and disappears completely when $\gamma_{1}\geq 2\gamma$.

Finally, we find that the value of $\alpha$ plays a crucial role in increasing the Hall conductivity as well as in widening the corresponding plateaus. These plateaus are proportional to the Chern number, with $\sigma_{xy}=|C_{0,2}|\sigma_{0}$ as long as the system remains a non-trivial topological insulator. However, these plateaus are sensitive to the hopping energy $\gamma_{1}$, which leads to a progressive reduction in their width as $\gamma_{1}$ increases. Ultimately, these plateaus disappear when the band gap closes at the critical point $\gamma_{1}=2\gamma$, marking the system’s transition to a trivial topological insulator state.

In this work, we have investigated the effect of deformation on the topological properties induced by light polarisation in $\alpha-T_{3}$ lattices. We introduced this deformation by modifying the hopping energy in the $\alpha-T_{3}$ lattice, particularly by modifying $\gamma_{1}$ at the A-B and A-C sites along the $\delta_{1}$ direction, while remaining unchanged hopping energies along the $\delta_{2}$ and $\delta_{3}$ directions. This modification of $\gamma_{1}$ led to a change in the band structure for three specific cases: $\alpha=0$, $\alpha=1/\sqrt{2}$ and $\alpha=1$. In these cases, the Dirac cones at points $\bm{K}$ and $\bm{K}^{\prime}$ move towards point $\bm{M}$ when the system is subjected to off-resonance circular polarization. This polarisation induces a Haldane mass term at $\phi=\pi/2$, breaking the time-reversal symmetry. This term is responsible for the opening of a gap. However, in the case of $\alpha=1/\sqrt{2}$, the gap partially opens at points $\bm{K}$ and $\bm{K}^{\prime}$. Moreover, the gap size decreases with increasing $\gamma_{1}$ and disappears completely when $\gamma_{1}=2\gamma$, where the system adopts semi-Dirac behaviour. This deformation, which breaks the $C_{3}$ symmetry,leads to a shift in the concentration of Berry curvature in the Brillouin zone , from points $\bm{K}$ and $\bm{K}^{\prime}$ to point $\bm{M}$. In the standard case, $\gamma=\gamma_{1}$, we observe particle-hole symmetry for $\alpha=0$ and $\alpha=1$ and inversion symmetry. We have calculated the corresponding Chern numbers for the conduction ($C_{0}$), flat ($C_{1}$) and valence ($C_{2}$) bands: For $\alpha<1/\sqrt{2}$ the Chern numbers are $C_{0}=-1$, $C_{1}=0$ and $C_{2}=1$. For $\alpha\geq 1/\sqrt{2}$ the values change to $C_{0}=-2$, $C_{1}=0$ and $C_{2}=2$. This shows a phase transition. We then focused on the Chern number corresponding to $C_{2}$. Fixing $\alpha=1$, we plotted $C_{2}$ as a function of $\gamma_{1}$. It turned out that there is a phase transition with gap closure at $\gamma_{1}=2\gamma$. When $\gamma_{1}>2\gamma$, the system changes from a non-trivial topological insulator ($C_{2}=2$) to a trivial topological insulator ($C_{2}=0$). We have also plotted a phase diagram in the parameter space of $\Delta/\gamma$ and $\alpha$ by fixing $\gamma_{1}$. When $\gamma_{1}=2\gamma$, in the interval of $\Delta/\gamma_{1}$ and $\alpha$, the system transforms into a trivial topological insulator. This transition was confirmed by plotting the Wannier charge centre. Fixing $\gamma_{1}$, we observed that the system changes state from a non-trivial topological insulator to another trivial topological insulator state when $\gamma_{1}>2\gamma$. We have also calculated the anomalous Hall conductivity for four values of $\alpha$: 0, 0.45, 0.8, and 1. For $\alpha=0$ and $\alpha=0.45$, the conductivity shows quantized behaviour in the form of plateaus with a value of $\sigma_{xy}=1\sigma_{0}$. For $\alpha=0.8$ and $\alpha=1$, the conductivity value increases to $\sigma_{xy}=2\sigma_{0}$, characterized by a plateau at $\gamma_{1}=\gamma$. This plateau decreases with increasing $\gamma_{1}$ and disappears when $\gamma_{1}>2\gamma$. These plateaus correspond to the Chern number, where $\sigma_{xy}=|C_{0,2}|\sigma_{0}$. The disappearance of these plateaus indicates that the system is transitioning from a non-trivial topological insulator to a trivial topological state.

The authors would like to acknowledge the ” Hassan II Academy of Sciences and Techologies-Morocco for its financial support. The authors also thank the LPHE-MS, Faculty of Sciences, Mohammed V University in Rabat, Morocco for the technical support through facilities.