Optical absorptions activated by an ultrashort halfcycle pulse in metallic and superconducting states of the Hubbard model
Abstract
The development of high-intensity ultrashort laser pulses unlocks the potential of pump-probe spectroscopy in sub-femtosecond timescale. Notably, subcycle pump pulses can generate electronic states unreachable by conventional multicycle pulses, leading to a phenomenon that we refer to as subcycle-pulse engineering. In this study, we employ the time-dependent density-matrix renormalization group method to unveil the transient absorption spectra of superconducting and metallic states in nearly half-filled one-dimensional and two-dimensional Hubbard models excited by an ultrashort halfcycle pulse, which can induce a current with inversion-symmetry breaking. In a superconducting state realized in attractive on-site interactions, we find the transient activation of absorptions at energies corresponding to the amplitude modes of superconducting and charge-density-wave states. On the other hand, in a metallic state realized in the two-dimensional model with repulsive on-site interactions, we obtain another type of absorption enhancements, which are distributed broadly in spin excitation energies. These findings indicate that superconducting and metallic states are sensitive to an ultrashort halfcycle pulse, leading to the transient activations of optical absorptions with their respective mechanisms.
I Introduction
The development of strong ultrashort pulse lasers has enabled the observation of non-equilibrium electron dynamics on femtosecond and even attosecond timescales Krausz2009 ; Gallmann2012 . A novel technique called subcycle-pulse engineering has been proposed, involving the application of a subcycle pulse with less than one cycle oscillation within a pulse envelope Tsuji2012 ; Lenarcic2014 ; Shinjo2022 ; Shinjo2023 ; Tohyama2023 ; Shinjo2024 . This approach aims to generate electronic states that cannot be accessed using conventional multicycle pulses. It has been suggested that applying ultrashort subcycle pulses to metallic or superconducting states can induce current with inversion-symmetry breaking, which is detectable by second-harmonic generations Kawakami2020 ; Shinjo2023 .
In a current-induced state with a broken inversion symmetry, exotic phenomena are anticipated, including the Doppler shifts of quasi-particle excitations known as the Volovik effect Volovik1993 . Particularly in absorption spectra, supercurrents in a dirty superconductor with intermediate strength of disorder can activate absorptions at a Higgs-mode energy between quasiparticle excitations with a gap Moor2017 . This behavior has been observed in a superconductor NbN with a current generated by a DC bias Nakamura2019 ; Shimano2020 . While disorder effects are often essential in understanding absorptions in superconductors Mattis1958 ; Laplae1983 ; Zimmermann1991 , it has been pointed out that inversion-symmetry breaking due to supercurrent can change a selection rule, leading to a significant absorption at even in clean superconductors Seibold2020 ; Papaj2022 ; Crowley2022 .
In this paper, we investigate how ultrashort halfcycle pulses, which can induce a current with an inversion-symmetry breaking, contribute to transient absorption spectra of strongly correlated electron systems. Using the time-dependent density-matrix renormalization group (tDMRG) method, we demonstrate that the halfcycle pump pulse leads to the enhancement of optical absorptions in metallic and superconducting states of the Hubbard model.
In the one-dimensional (1D) and two-dimensional (2D) Hubbard models with attractive on-site interactions, we find the enhancement of absorptions at energies corresponding to amplitude modes associated with superconducting and charge-density-wave (CDW) orders. This behavior is the manifestation of a current-induced activation of absorptions at amplitude modes in a clean superconducting state. In a 2D system, we find that the amplitude-mode absorptions emerge in both parallel and perpendicular directions to the pump pulse for (in the unit of the electron hopping), but only in parallel for . This dependence comes from the difference in the localized nature of superconducting pairing at weak and strong couplings.
In a metallic state of the 2D Hubbard model at nearly half filling with repulsive on-site interactions, we find another type of absorption enhancement broadly distributed in the Mott gap. The mid-gap absorptions appear in both directions parallel and perpendicular to the pump pulse, whose nonlocal nature can be attributed to the effect of magnetic excitations.
The rest of this paper is organized as follows. We introduce the Hubbard model with a time-dependent electric field in Sec. II. We also show a method to obtain time-dependent optical conductivity by the tDMRG method. In Sec. III, we show transient absorption spectra of the Hubbard models with attractive interactions . We demonstrate that a halfcycle pulse activates absorptions at superconducting and CDW amplitude modes. In Sec. IV, we show transient absorption spectra of the Hubbard models with repulsive interactions . We show the enhancement of absorptions at energies corresponding to spin-exchange interactions. Finally in Sec. V, we give a summary of this paper. Additional results for the - model are provided in Appendix A.
II Model and Method
To investigate nonequilibrium properties of strongly correlated electron systems, we consider the Hubbard model on a ladder-shaped cluster of sites with a time () dependent vector potential , with () being the unit vector along the -axis (-axis) direction, described by the following Hamiltonian:
| (1) |
where , is the electron creation operator at site , located at in the cluster, with spin , and . is nearest-neighbor hopping and is on-site Coulomb interaction. Hereafter, we set as the energy unit. The sum indicated by runs over all pair of nearest-neighbor sites and , and . We impose open boundary conditions along the - and -axis directions. A spatially homogeneous electric field is incorporated via the Peierls substitution in the hopping terms Peierls1933 . Note that we set the light velocity , the elementary charge , the Dirac constant , and the lattice constant to 1.
The effect of a strong ultrashort pump pulse applied to the Hubbard model can be investigated with a vector potential introducing a phase shift Lenarcic2014 at in the -axis direction with
| (2) |
where we set the width of the pump pulse to . For , leads to a halfcycle pulse that can quench the flux of and twists the phase of many-body wavefunctions Shinjo2023 . As a result, the pump pulse can induce an inversion-symmetry breaking associated with a current in metallic and superconducting states.
To obtain transient absorptions of the Hubbard model parallel (perpendicular) to the pump pulse, we subsequently apply a probe pulse [] at time polarized in the -axis (-axis) direction with
| (3) |
We set , , and . Note that indicates the delay time between pump and probe pulses. We obtain a current
| (4) |
with a time-dependent many-body wave function evaluated by the tDMRG method implemented with the Legendre polynomial Shinjo2021 ; Shinjo2021b ; Shinjo2022 . Here, implies and the initial state of is the ground state of the Hubbard model with in Eq. (1). With the present methodology, we obtain both singular and regular parts of the optical conductivity in nonequilibrium Shao2016 ; Shinjo2018 ; Shinjo2022 by directly calculating
| (5) |
where and are the Fourier transform of and , respectively. Here, and are obtained by taking and , respectively, in Eq. (4). For the Fourier transformation, we evaluate for up to . We take a broadening factor in this paper. In a finite system with open boundary conditions, we obtain the singular part of at , where and are the diagonal components of along the - and -axis directions, respectively.
III Attractive Hubbard model
III.1 One dimensional systems
We first show transient absorption spectra for the attractive Hubbard model with on a 1D cluster . We set in Figs. 1(a)–1(c) and in Figs. 1(d)–1(f), which respectively lie on the Bardeen-Cooper-Schrieffer (BCS) and Bose-Einstein-condensation (BEC) sides across the BCS-BEC crossover Scalettar1989 ; Moreo1991 ; Fontenele2022 ; Hartke2023 . These results are obtained by doping electrons with density in a half-filled state, where is the total number of electrons. However, note that since we consider bipartite lattices in this study, a particle-hole transformation maps electron doping to hole doping.
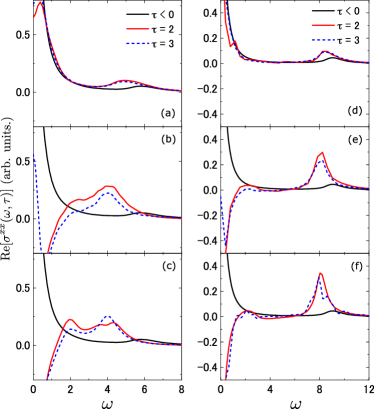
Before applying a pump pulse, i.e., , we find that most of spectral weights concentrate at due to the presence of a nonzero superfluid weight , as shown in the black lines in Fig. 1. In other words, most of contributions to Re comes from the diamagnetic term . Here, note that the peak structure has a finite width since a broadening factor is introduced in Eq. (5).
For delay times and 3 after pumping, indicated by red solid and blue dashed lines in Fig. 1, respectively, we find the suppression of and the enhancement of absorptions at , which become clearer with increasing notex . In particular at , we find the enhancement of a lower-energy mode at , as shown in Figs. 1(b) and 1(c). We consider that this structure corresponds to the amplitude mode of a superconducting order, i.e., the Higgs mode activated by the inversion-symmetry breaking induced by a halfcycle pulse notesc . The breaking of an inversion symmetry via a current in a superconducting state results in an absorption at in the optical conductivity, where is a superconducting gap Papaj2022 ; Crowley2022 . For , we can roughly estimate with the BCS mean-field model for half filling on a square lattice. Considering the suppression of by quantum fluctuations Gersch2008 to about 70%, it is reasonable for an activated Higgs mode to appear at . The Higgs-mode absorptions observed in the 1D system do not appear stable for long times and are captured by ultrafast transient absorption spectroscopy.
At strong coupling , there is no enhancement in absorption associated with the Higgs mode. This is likely associated with the fact that the Higgs mode becomes broadened and eventually disappears when the Cooper pairs turn into tightly bound pairs leading to BEC Varma2002 ; Pekker2015 ; Behrle2018 .
In addition to the Higgs-mode absorptions, we find another enhancement in absorptions at higher energies , as shown in Figs. 1(b) and 1(c) [Figs. 1(e) and 1(f)] for (). This is due to the activation of another amplitude mode, i.e., a CDW amplitude mode, by the halfcycle pulse, since corresponds to the energy required to dissolve a doublon.
We also find that the kinetic energy increases with and almost zero at for and Note1 . This behavior indicates that the total spectral weights proportional to is also almost zero after pumping at , although the amplitude-mode absorptions with positive spectral weights are enhanced. The enhanced contribution of the paramagnetic Van Vleck term with spectral weights is allowed because the decrease in total spectral weights is compensated by the emergence of a negative superfluid weight Stafford1991 ; Fye1991 ; Fye1992 .
III.2 Two dimensional systems
To examine the possibility of the emergence of amplitude-mode absorptions in 2D systems, we investigate Re and Re of the Hubbard model in Eq. (1) on a square lattice with excited by an ultrashort halfcycle pulse. We take the bond dimension in the tDMRG calculations, leading to a truncation error less than . We map a cluster onto a 1D system using tilted-z mapping, which makes the electronic state obtained with finite symmetrical in the - and -axis directions Shinjo2021b . The results for () are shown in Figs. 2(a)–(c) [Figs. 2(d)–(f)] with , , and . Before applying a pump pulse, most of spectral weights concentrate at due to the presence of , as indicated by the black lines in Fig. 2.
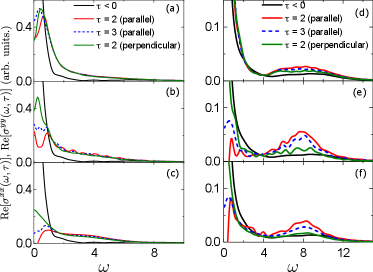
In Fig. 2, we show Re with red solid (blue dashed) lines for () and Re with green solid line for , which are probed in parallel and perpendicular to the pump pulse applied in the -axis direction, respectively. We find the enhancement of absorption at , which corresponds to a CDW amplitude mode also observed in the 1D Hubbard model with and . In 2D systems, however, the enhanced spectral weights are broader compared to those in the 1D systems. Thus, the Higgs-mode absorption is hidden by the CDW amplitude-mode absorption, making it difficult to distinguish between the two absorptions. To clearly differentiate these two amplitude modes, higher resolution is required, which necessitates longer time evolutions and larger clusters in the computation. This exceeds our current computational resource and is therefore left for future study.
We find that the nature of the amplitude-mode absorptions varies depending on the strength of . For , the amplitude-mode absorptions appear in both parallel and perpendicular directions to the pump pulse. In contrast, for , the amplitude-mode absorptions primarily appear in the direction parallel to the pump pulse. This is because the pairing is strongly coupled, i.e., BEC type with a localized nature, for and thus the effect of the pump pulse does not extend in the perpendicular direction. On the other hand, for , the pairing is weakly coupled, i.e., BCS type with a nonlocal nature, allowing the effect of the pump pulses to extend into the perpendicular direction as well. The nonlocal nature of pairing observed for is consistent with findings in an optical lattice for Hartke2023 .
Finally, we compare the experimental results for NbN Nakamura2019 with our study, although a direct comparison is challenging due to differences in the experimental setup. In the experiment, the activation of the Higgs mode is observed only in the direction parallel to the current. This behavior corresponds to the amplitude-mode absorptions obtained for in our study. However, is much larger than the attractive interaction present in NbN, where the superconducting state is considered to be of the BCS type. We speculate that the disorder effect in NbN makes the nature of the amplitude-mode absorptions to be localized.
IV Repulsive Hubbard model
In the 2D Hubbard models with noteu , we find another type of absorption induced by a halfcycle pulse. The results of Re for are shown in Fig. 3(a), while those of Re and Re for are shown in Fig. 3(b). In the tDMRG calculations, the bond dimensions are set to and for the and systems, respectively. Since we consider carrier densities of for the system and for the system, both of which are near half filling, there are absorptions above the remnant Mott gap at , as shown by the black lines in Fig. 3. At low energies, in addition to the Drude weight at , we find incoherent spectral weights in the ranges for and for . These incoherent weights originate from string-type antiferromagnetic excitations present in 2D Mott insulators Dagotto1992 ; Stephan1990 ; Inoue1990 ; Jaklic2000 ; Tohyama2005 ; Shinjo2021 , and have been experimentally observed in La2-xSrxCuO4 Uchida1991 and Sr14-xCaxCu24O41 Osafune1997 in the mid-infrared (MIR) region. The incoherent spectral weights in the MIR band extend to higher energies, up to in 2D systems Tohyama2005 , compared to in two-leg ladder systems. Furthermore, the Drude weight is larger in the system than in the system, since the 1D nature is retained in the two-leg ladder Osafune1997 .
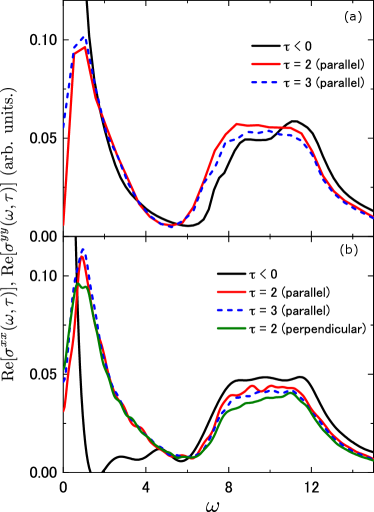
After pumping with a halfcycle pulse, we find a redshift of the remnant Mott gap in the two-leg ladder system with , as shown in Fig. 3(a), along with the suppression of the Drude weight. We attribute this redshift to the Stark shift, as a halfcycle pulse induces polarization Shinjo2023 . A similar redshift behavior of the remnant Mott gap is also observed in 1D systems (not shown). However, in contrast to quasi-1D systems, no redshift of the remnant Mott gap is observed in a square lattice, as shown in Fig. 3(b). This is because the induced polarization after pumping is smaller in a square lattice compared to quasi-1D systems (not shown).
In the mid-gap energy range , we find a slight enhancement in absorption. The mid-gap absorptions are attributed to magnetic excitations activated by a halfcycle pulse, with peak positions characterized by spin-exchange interactions (see Appendix A). This behavior suggests that antiferromagnetic order partially remains in the nearly half-filled Mott insulator, leading to spin excitations caused by charge motion. A similar mid-gap structure has been observed in pump-probe spectroscopy of Sr14-xCaxCu24O41 using a near-infrared laser Fukaya2015 ; Hashimoto2016 ; Shao2019 .
The mid-gap absorptions are more pronounced in the 2D system with , as shown by colored lines in Fig. 3(b), where they are broadly distributed in the range . A similar large and broad enhancement of mid-gap absorptions has also been observed in a carrier-doped Bi-based cuprate Peli2017 , excited by a near-infrared pulse. If we assume that the enhanced mid-gap absorption observed in this experiment shares the same origin as our results, we expect that the structure found in Fig. 3(b) can be reproduced not only by pumping with a halfcycle pulse but also with a near-infrared multicycle pulse, as investigated in Ref. Shinjo2017 .
Finally, we compare Re parallel to the pump pulse [the red line in Fig. 3(b)] with Re perpendicular to the pump pulse [the green line in Fig. 3(b)]. We find that the effect of the pump pulse extends to the perpendicular direction, causing changes in absorption both parallel and perpendicular to the pump pulse. This behavior can be attributed to spin-charge coupling in the square lattice. Indeed, it has been reported that charge dynamics in the direction parallel to the electric field is coupled with that in the perpendicular direction via magnetic excitations Tsutsui2021 .
V Summary
Using the tDMRG method, we investigated the transient absorption spectra of superconducting and metallic states in the Hubbard models excited by an ultrashort halfcycle pulse. In the superconducting state of the Hubbard model with attractive interactions, we found an enhancement of absorption induced by the halfcycle pump pulse. The energies of these induced absorptions correspond to the amplitude modes of superconducting and CDW orders, indicating the current-induced activation of amplitude-mode absorptions in a clean superconducting state. In the square lattice, we found that the behavior of amplitude-mode absorptions depends on the strength of . At in the strong coupling region, where pairing is formed locally, the amplitude-mode absorptions are activated only in the direction parallel to the pump pulse. In contrast, at , where pairing is formed nonlocally, absorptions are activated both in the parallel and perpendicular directions.
In the metallic state of the Hubbard model on a square lattice near half filling with repulsive interactions, we found a different behavior in the transient absorption spectra. A halfcycle pump pulse induces absorptions that are broadly distributed in the mid-gap region. These mid-gap absorptions appear in both directions parallel and perpendicular to the pump pulse, and their nonlocal nature can be attributed to the effect of magnetic excitations.
Acknowledgements.
This work was supported by Grant-in-Aid for Scientific Research (B) (Nos. 19H05825, 20H01849, 21H03455, 24K00560, and 24K02948) and Grant-in-Aid for Early-Career Scientists (No. 23K13066) from Ministry of Education, Culture, Sports, Science, and Technology (MEXT), Japan, and by JST PRESTO (Grant No. JPMJPR2013). This work was also supported in part by the COE research grant in computational science from Hyogo Prefecture and Kobe City through Foundation for Computational Science. Numerical calculation was carried out using the HOKUSAI supercomputer at RIKEN, computational resources of the facilities of the Supercomputer Center at Institute for Solid State Physics, the University of Tokyo, and the supercomputer system at the information initiative center, Hokkaido University through the HPCI System Research Project (Project IDs: hp230066 and hp240038).Appendix A Results for - model
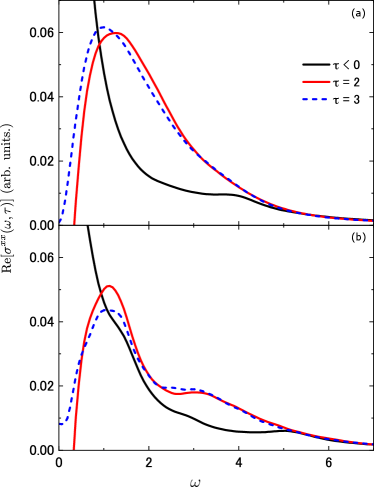
In this appendix, we show that the centroid energy of absorptions in the - model, excited by an ultrashort halfcycle pulse, shifts to higher energies as the spin-exchange interaction increases. The Hamiltonian of the - model without a vector potential is given by
| (6) |
where , , and represents the opposite spin to . is the -component of the spin-1/2 operator at site , where is the element of the -component of the Pauli matrix. The time dependent vector potential is introduced similarly as in Eq. (1). Figure 4 shows the results of Re for the - model with a hole density on a two-leg ladder of sites under open boundary conditions. As in the case of the Hubbard model, after pumping, we observe a suppression of the Drude weight and an enhancement of absorptions at finite energies in the range . Comparing the results for and 2 in Figs. 4(a) and 4(b), respectively, we find that the centroid energy of the induced absorptions shifts to higher values with increasing . Therefore, the induced absorptions can be attributed to spin-exchange interactions.
References
- (1) F. Krausz and M. Ivanov, Attosecond physics, Rev. Mod. Phys. 81, 163 (2009).
- (2) L. Gallmann, C. Cirelli, and U. Keller, Attosecond Science: Recent Highlights and Future Trends, Annu. Rev. Phys. Chem. 63, 447 (2012).
- (3) N. Tsuji, T. Oka, H. Aoki, and P. Werner, Repulsion-to-attraction transition in correlated electron systems triggered by a monocycle pulse, Phys. Rev. B 85, 155124 (2012).
- (4) Z. Lenarčič, D. Golež, J. Bonča, and P. Prelovšek, Optical response of highly excited particles in a strongly correlated system, Phys. Rev. B 89, 125123 (2014).
- (5) K. Shinjo, S. Sota, and T. Tohyama, Glassy dynamics of the one-dimensional Mott insulator excited by a strong terahertz pulse, Phys. Rev. Res. 4, L032019 (2022).
- (6) K. Shinjo, S. Sota, S. Yunoki, and T. Tohyama, Controlling inversion and time-reversal symmetries by subcycle pulses in the one-dimensional extended Hubbard model, Phys. Rev. B 107, 195103 (2023).
- (7) T. Tohyama, K. Shinjo, S. Sota, and S. Yunoki, Anomalous suppression of photo-induced in-gap weight in the optical conductivity of a two-leg Hubbard ladder, Phys. Rev. B 108, 035113 (2023).
- (8) K. Shinjo and T. Tohyama, Keldysh crossover in one-dimensional Mott insulators, APL Mater. 12, 041109 (2024).
- (9) Y. Kawakami, T. Amano, H. Ohashi, H. Itoh, Y. Nakamura, H. Kishida, T. Sasaki, H. M. Yamamoto, K. Yamamoto, S. Ishihara, K. Yonemitsu, and S. Iwai, Petahertz non-linear current in a centrosymmetric organic superconductor, Nat. Commun. 11, 4138 (2020).
- (10) G. Volovik, Superconductivity with lines of gap nodes-density-of-states in the vortex, Pis’ma Zh. Eksp. Teor. Fiz. 58, 457 (1993) [JETP Lett. 58, 457 (1993)].
- (11) A. Moor, A. F. Volkov, and K. B. Efetov, Amplitude Higgs Mode and Admittance in Superconductors with a Moving Condensate, Phys. Rev. Lett. 118, 047001 (2017).
- (12) S. Nakamura, Y. Iida, Y. Murotani, R. Matsunaga, H. Terai, and R. Shimano, Infrared Activation of the Higgs Mode by Supercurrent Injection in Superconducting NbN, Phys. Rev. Lett. 122, 257001 (2019).
- (13) R. Shimano and N. Tsuji, Higgs Mode in Superconductors, Annu. Rev. Condens. Matter Phys. 11, 103 (2020).
- (14) D. C. Mattis and J. Bardeen, Theory of the Anomalous Skin Effect in Normal and Superconducting Metals, Phys. Rev. 111, 412 (1958).
- (15) L. Leplae, Derivation of an expression for the conductivity of superconductors in terms of the normal-state conductivity, Phys. Rev. B 27, 1911 (1983).
- (16) W. Zimmermann, E. H. Brandt, M. Bauer, E. Seider, and L. Genzel, Optical conductivity of BCS superconductors with arbitrary purity, Physica C 183, 99 (1991).
- (17) G. Seibold and J. Lorenzana, Nonequilibrium dynamics from BCS to the bosonic limit, Phys. Rev. B 102, 144502 (2020).
- (18) M. Papaj and J. E. Moore, Current-enabled optical conductivity of superconductors, Phys. Rev. B 106, L220504 (2022).
- (19) P. J. D. Crowley and L. Fu, Supercurrent-induced resonant optical response, Phys. Rev. B 106, 214526 (2022).
- (20) R. Peierls, Zur Theorie des Diamagnetismus von Leitungselektronen, Z. Phys. 80, 763 (1933).
- (21) K. Shinjo, S. Sota, and T. Tohyama, Effect of phase string on single-hole dynamics in the two-leg Hubbard ladder, Phys. Rev. B 103, 035141 (2021).
- (22) K. Shinjo, Y. Tamaki, S. Sota, and T. Tohyama, Density-matrix renormalization group study of optical conductivity of the Mott insulator for two-dimensional clusters, Phys. Rev. B 104, 205123 (2021).
- (23) C. Shao, T. Tohyama, H.-G. Luo, and H. Lu, Numerical method to compute optical conductivity based on pump-probe simulations, Phys. Rev. B 93, 195144 (2016).
- (24) K. Shinjo and T. Tohyama, Ultrafast transient interference in pump-probe spectroscopy of band and Mott insulators, Phys. Rev. B 98, 165103 (2018).
- (25) R. T. Scalettar, E. Y. Loh, J. E. Gubernatis, A. Moreo, S. R. White, D. J. Scalapino, R. L. Sugar, and E. Dagotto, Phase diagram of the two-dimensional negative- Hubbard model. Phys. Rev. Lett. 62, 1407 (1989).
- (26) A. Moreo and D. J. Scalapino, Two-dimensional negative- Hubbard model. Phys. Rev. Lett. 66, 946 (1991).
- (27) R. A. Fontenele, N. C. Costa, R. R. dos Santos, and T. Paiva, Two-dimensional attractive Hubbard model and the BCS-BEC crossover, Phys. Rev. B 105, 184502 (2022).
- (28) T. Hartke, B. Oreg, C. Turnbaugh, N. Jia, and M. Zwierlein, Direct observation of nonlocal fermion pairing in an attractive Fermi-Hubbard gas, Science 381, 82 (2023).
- (29) A halfcycle pulse introduces a small amount of photo-doped carriers. In (), photo-doped doublon density evaluated immediately after pumping are 0.01, 0.03, and (0.004, 0.02, and ) for , , and , respectively. Here, .
- (30) We have confirmed that the long-range behavior of a superconducting pair correlation function is almost unchanged after pumping even with , where is a pair field.
- (31) R. Gersch, C. Honerkamp, and W. Metzner, Superconductivity in the attractive Hubbard model, New J. Phys. 10, 045003 (2008).
- (32) C. M. Varma, J. Low Temp. Phys. 126, 901 (2002).
- (33) D. Pekker and C. M. Varma, Amplitude/Higgs Modes in Condensed Matter Physics, Annu. Rev. Condens. Matter Phys. 6, 269 (2015).
- (34) A. Behrle, T. Harrison, J. Kombe, K. Gao, M. Link, J.-S. Bernier, C. Kollath, and M. Köhl, Nat. Phys. 14, 781 (2018).
- (35) In (), the kinetic energy after pumping is =, , and (, , and ) for , , and , respectively.
- (36) C. A. Stafford, A. J. Millis, and B. S. Shastry, Finite-size effects on the optical conductivity of a half-filled Hubbard ring, Phys. Rev. B 43, 13660 (1991).
- (37) R. M. Fye, M. J. Martins, D. J. Scalapino, J. Wagner, and W. Hanke, Drude weight, optical conductivity, and flux properties of one-dimensional Hubbard rings, Phys. Rev. B 44, 6909 (1991).
- (38) R. M. Fye, M. J. Martins, D. J. Scalapino, J. Wagner, and W. Hanke, Optical-conductivity properties of one-dimensional Hubbard rings: Repulsive- and attractive- cases, Phys. Rev. B 45, 7311 (1992).
- (39) Re in La2CuO4 is described with Shinjo2021b .
- (40) E. Dagotto, A. Moreo, F. Ortolani, J. Riera, and D. J. Scalapino, Optical conductivity of the two-dimensional Hubbard model, Phys. Rev. B 45, 10107 (1992).
- (41) W. Stephan and P. Horsch, Optical properties of one- and two-dimensional Hubbard and - models, Phys. Rev. B 42, 8736 (1990).
- (42) J. Inoue and S. Maekawa, Spin Correlations around Mobile Holes in an Antiferromagnet, J. Phys. Soc. Jpn. 59, 2110 (1990).
- (43) J. Jaklič and P. Prelovšek, Finite-temperature properties of doped antiferromagnets, Adv. Phys. 49, 1 (2000).
- (44) T. Tohyama, Y. Inoue, K. Tsutsui, and S. Maekawa, Exact diagonalization study of optical conductivity in the two-dimensional Hubbard model, Phys. Rev. B 72, 045113 (2005).
- (45) S. Uchida, T. Ido, H. Takagi, T. Arima, Y. Tokura, and S. Tajima, Optical spectra of : Effect of carrier doping on the electronic structure of the plane, Phys. Rev. B 43, 7942 (1991).
- (46) T. Osafune, N. Motoyama, H. Eisaki, and S. Uchida, Optical Study of the System: Evidence for Hole-Doped Ladders, Phys. Rev. Lett. 78, 1980 (1997).
- (47) R. Fukaya, Y. Okimoto, M. Kunitomo, K. Onda, T. Ishikawa, S. Koshihara, H. Hashimoto, S. Ishihara, A. Isayama, H. Yui, and T. Sasagawa, Nat. Commun. 6, 8519 (2015).
- (48) H. Hashimoto and S. Ishihara, Phys. Rev. B 93, 165133 (2016).
- (49) C. Shao, T. Tohyama, H.-G. Luo, and H. Lu, Phys. Rev. B 99, 035121 (2019).
- (50) S. Peli, S. Dal Conte, R. Comin, N. Nembrini, A. Ronchi, P. Abrami, F. Banfi, G. Ferrini, D. Brida, S. Lupi, M. Fabrizio, A. Damascelli, M. Capone, G. Cerullo, and C. Giannetti, Mottness at finite doping and charge instabilities in cuprates. Nat. Phys. 13, 806 (2017).
- (51) K. Shinjo and T. Tohyama, Photoinduced absorptions inside the Mott gap in the two-dimensional extended Hubbard model, Phys. Rev. B 96, 195141 (2017).
- (52) K. Tsutsui, K. Shinjo, and T. Tohyama, Antiphase oscillations in the time-resolved spin structure factor of a photoexcited Mott insulator, Phys. Rev. Lett. 126, 127404 (2021).