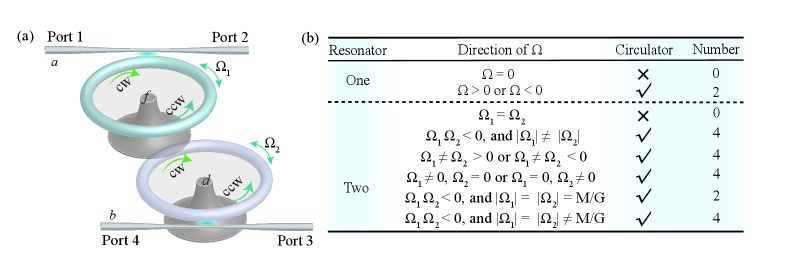
Operating Single-Photon Circulator by Spinning Optical Resonators

Nonreciprocal optical devices, such as isolators [1, 2, 3], circulators [4, 5, 6], and directional amplifiers [7], featuring different optical responses after exchanging positions between the input and output terminals, are not only important components in optical systems but also have important applications in constructing quantum networks and implementing quantum communication. One of the most basic requirements for achieving nonreciprocal transmission in optical systems is to break the symmetry of time inversion [8]. In recent years, in order to meet the requirements of chip integration, a large number of non-magnetic and nonreciprocal systems have begun to develop, which are generally based on dynamic spatiotemporal modulation structures [9], quantum Hall effects [10], Kerr-nonlinear microresonators [11, 12, 13, 14, 15], optomechanical resonator [16, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35, 36, 37, 38, 39, 40, 41, 42], non-Hermitian systems [43, 45, 44, 46, 47, 48, 49, 50, 51], moving atomic gases [52, 53, 54, 55, 56, 57, 58, 59], and spinning resonators [62, 60, 61].

Recent experimental studies [62, 63, 64, 65] have shown that spinning resonators can break the time reversal symmetry via Fizeau resistance to achieve nonreciprocal transmission of light. Afterwards, more and more researchers became interested in rotating resonators and proposed many nonreciprocal quantum devices, such as nonreciprocal photon blocking [66, 67, 68, 69, 70, 71], nonreciprocal phonon lasers [72, 73], nonreciprocal entanglement [74], nonreciprocal optical solitons [75], nonreciprocal optical bandwidth [76, 77], and photon circulators [78]. Circulator is typically a nonreciprocal device composed of three or four ports. They separate the paths of the sender and receiver by introducing non reciprocity between ports. The circulator has been experimentally proven by microwave [79, 80, 81, 82] and optical signals [83, 84], and can be applied in regions ranging from classical to quantum [84, 85, 86, 87]. Recently, a two-frequency point photon circulator based on a rotating resonator with two tapered fibers has been proposed [78]. However, the novel possibility of a four-frequency points single-photon circulator by utilizing two spinning resonators, as far as we know, has not been explored.

In this paper, we found that four frequency points can achieve photon circulator by utilizing two spinning resonators with different angular velocities. To pursue this, we has been conducted coupling two rotating resonators with two waveguides to form a four-port device. There are various combinations of angular velocities for the two resonators, each resulting in different outcomes. When the resonators are static or rotate at the same angular velocity, photon transmission is reciprocal. However, with differing angular velocities, it’s been observed that four frequency points of photon circulation can be achieved. Particularly, when the two resonators have equal and opposite angular velocities, two frequency points of photon circulation are attainable. Additionally, there exists a frequency point where photons input from any waveguide can be completely routed to another. We also found that, compared with other nonreciprocal device circulators, single-photon circulators formed by rotating resonators exhibits robustness against the backscattering. Therefore, the routing direction of the photon circulator is dependent on the frequency of incoming photons and the rotational angular velocities of the two resonators. Compared to nonreciprocal devices with two ports, the four-port quantum optical circulator with multi-frequency points enables us to establish two-dimensional and three-dimensional networks to achieve photon quantum simulations[88]. Our results may provide inspiration for multi-frequency points circulator in quantum information.

The paper is organized as follows: In Sec. 2, we outline the theoretical model of the system by presenting Hamiltonian. We give the calculation method and solution to the model. In Sec. 3, we study the single-photon transport properties when two resonators rotate or static. In Sec. 4, we study the effect of adding backscattering in resonators on photon transmission. Finally, we summarize the single-photon transport and give the conclusions in Sec. 5.

Recent experiments have demonstrated the utilization of spinning devices for achieving optical isolators[62], one-way heat flow [63, 89], gyroscopes[64, 65], acoustic amplifiers[90], and rotational doppler effect[91]. Among these, utilizing a spinning resonator can achieve nonreciprocal transmission with an isolation degree of up to 99.6$\%$[62]. In this experiment, a spherical resonator was successfully created by flame polishing the end of a molten silicon glass cylinder and mounting the resonator on a turbine. By properly placing a fiber near the spinning resonator, a stable fiber-resonator coupling was established through a "self-adjusting" aerodynamic process.

In this paper, we propose how to realize a single-photon circulator with multiple frequency points in a system composed of two spinning whispering-gallery-mode (WGM) resonators and two waveguides. As shown in Fig. 1(a), we consider two spinning WGM microresonators $f$ and $d$, coupled to two waveguides a and b, with four input/output ports, respectively. The WGM holds two cavity modes corresponding to clockwise (CW) and counterclockwise (CCW) modes with frequencies $\omega_{cw}=\omega_{c}-\Delta_{F}$ and $\omega_{ccw}=\omega_{c}+\Delta_{F}$, respectively. When the resonator spins at an angular velocity $\Omega$, the rotation-induced Sagnac-Fizeau shift $\Delta_{F}$ is given by [62, 92]

$\displaystyle\Delta_{F}=\frac{nR\Omega\omega_{c}}{c}\left(1-\frac{1}{n^{2}}-\frac{\lambda}{n}\frac{dn}{d\lambda}\right)=\Omega G,$

(1)

where $\omega_{c}$ is the intrinsic frequency of the nonspinning resonator, $c$ and $\lambda$ are the propagation speed and wavelength of light, $R$ and $n$ are the radius and reflectivity of the resonator, respectively. The dispersion term $dn/{d\lambda}$, characterizing the relativistic origin of the Sagnac shift, is relatively small in typical materials ($\sim 1\%$) [92]. $\Omega>0$ ($\Omega<0$) indicates CW (CCW) rotation of the resonator.

$\Omega_{1}$ ($\Omega_{2}$) is the rotational angular velocity of the $f$ ($d$) resonator, and $\Delta_{F1}$ ($\Delta_{F2}$) is the Sagnac shift due to the rotation of the $f$ ($d$) resonator. Under the rotating wave approximation, the total Hamiltonian can be written as ($\hbar=1$)

$\displaystyle\hat{H}=\hat{H}_{0}+\hat{H}_{\mathrm{int}}.$

(2)

Here, the first term $\hat{H}_{0}$ describes the free part,

	$\displaystyle\hat{H}_{0}$	$\displaystyle=$	$\displaystyle\sum_{\alpha=cw,ccw}\left(\omega_{\alpha}\hat{f}_{\alpha}^{\dagger}\hat{f}_{\alpha}+\omega_{d,\alpha}\hat{d}_{\alpha}^{\dagger}\hat{d}_{\alpha}\right)-iv_{g}\int dx\hat{a}_{R_{x}}^{\dagger}\frac{\partial}{\partial x}\hat{a}_{R_{x}}+iv_{g}\int dx\hat{a}_{L_{x}}^{\dagger}\frac{\partial}{\partial x}\hat{a}_{L_{x}}$		(3)
			$\displaystyle-iv_{g}\int dx\hat{b}_{R_{x}}^{\dagger}\frac{\partial}{\partial x}\hat{b}_{R_{x}}+iv_{g}\int dx\hat{b}_{L_{x}}^{\dagger}\frac{\partial}{\partial x}\hat{b}_{L_{x}},$

where $\omega_{\alpha}=\omega_{c}\pm\Delta_{F1}$ ($\omega_{d,\alpha}=\omega_{c}\pm\Delta_{F2}$) is the effective frequency for $\alpha$ $(\alpha=cw,ccw)$ travelling modes in the $f$ ($d$) resonator. $\hat{f}_{\alpha}^{\dagger}$ ($\hat{d}_{\alpha}^{\dagger}$) is the creation operators in the $f$ ($d$)resonator. $\hat{a}^{\dagger}_{R_{x}}$ ($\hat{a}^{\dagger}_{L_{x}}$) is the creation operators for the right-moving (left-moving) photon along the waveguide $a$ at position $x$. $\hat{b}^{\dagger}_{R_{x}}$ ($\hat{b}^{\dagger}_{L_{x}}$) is the creation operators for the right-moving (left-moving) photon along the waveguide $(b)$ at position $x$. The group velocities have been assumed to be $v_{g}$. The second terms $\hat{H}_{int}$ in Eq. (1) describes the interacting part.

	$\displaystyle\hat{H}_{\mathrm{int}}$	$\displaystyle=$	$\displaystyle g_{a}(\hat{a}_{R_{0}}^{\dagger}\hat{f}_{cw}+\hat{a}_{L_{0}}^{\dagger}\hat{f}_{ccw})+g_{b}(\hat{b}_{L_{0}}^{\dagger}\hat{d}_{cw}+\hat{b}_{R_{0}}^{\dagger}\hat{d}_{ccw})$		(4)
			$\displaystyle+J(\hat{f}_{cw}^{\dagger}\hat{d}_{ccw}+\hat{f}_{ccw}^{\dagger}\hat{d}_{cw})+\mathrm{H.c.}$

where $g_{a}$ ($g_{b}$) is the $f$ ($d$) resonator and $a$ ($b$) waveguide coupling strength. $J$ is the coupling strength of resonator $f$ and $d$.

In the case of a single excitation, the state vector of the system can be written as

	$\displaystyle\left|\psi\right\rangle$	$\displaystyle=$	$\displaystyle\sum_{\alpha=cw,ccw}\left(C_{\alpha}\hat{f}_{\alpha}^{\dagger}\left|\varnothing\right\rangle+D_{\alpha}\hat{d}_{\alpha}^{\dagger}\left|\varnothing\right\rangle\right)$		(5)
			$\displaystyle+\sum_{\beta=L,R}\left(\int dxA_{\beta}\left(x\right)\hat{a}_{\beta_{x}}^{\dagger}+\int dxB_{\beta}\left(x\right)\hat{b}_{\beta_{x}}^{\dagger}\right)\left|\varnothing\right\rangle,$

where $\left|\varnothing\right\rangle$ is the vacuum state which indicates that there is zero photon in both the waveguide and the resonator. $C_{\alpha}$ ($D_{\alpha}$) is the probability amplitude of a photon appearing in $f$ ($d$) resonator. $A_{\beta}(x)$ ($B_{\beta}(x)$, $\beta=L,R$) is the probability amplitude of the right- or left-moving photon in the waveguide a (b). According to the Schr$\ddot{o}$dinger equation $\hat{H}\left|\psi\right\rangle=E\left|\psi\right\rangle$, and removing $C_{\alpha}$ and $D_{\alpha}$, the coupled equations can be written

$\displaystyle\begin{aligned} EA_{L}\left(x\right)-iv_{g}\frac{\partial A_{L}\left(x\right)}{\partial x}&=\delta\left(x\right)\frac{g_{a}^{2}\left(E-\omega_{d,cw}\right)A_{L}\left(0\right)+Jg_{a}g_{b}B_{L}\left(0\right)}{\left(E-\omega_{ccw}\right)\left(E-\omega_{d,cw}\right)-J^{2}},\\ EB_{L}\left(x\right)-iv_{g}\frac{\partial B_{L}\left(x\right)}{\partial x}&=\delta\left(x\right)\frac{g_{b}^{2}\left(E-\omega_{ccw}\right)B_{L}\left(0\right)+Jg_{a}g_{b}A_{L}\left(0\right)}{\left(E-\omega_{ccw}\right)\left(E-\omega_{d,cw}\right)-J^{2}},\\ EA_{R}\left(x\right)+iv_{g}\frac{\partial A_{R}\left(x\right)}{\partial x}&=\delta\left(x\right)\frac{g_{a}^{2}\left(E-\omega_{d,cw}\right)A_{R}\left(0\right)+Jg_{a}g_{b}B_{R}\left(0\right)}{\left(E-\omega_{cw}\right)\left(E-\omega_{d,ccw}\right)-J^{2}},\\ EB_{R}\left(x\right)+iv_{g}\frac{\partial B_{R}\left(x\right)}{\partial x}&=\delta\left(x\right)\frac{g_{b}^{2}\left(E-\omega_{cw}\right)B_{R}\left(0\right)+Jg_{a}g_{b}A_{R}\left(0\right)}{\left(E-\omega_{cw}\right)\left(E-\omega_{d,ccw}\right)-J^{2}}.\end{aligned}$

(6)

The photon enters through port 1 of the $a$ waveguide, and the wave function is

$\displaystyle\begin{aligned} A_{R}\left(x\right)&=e^{i\frac{E}{v_{g}}x}\left(\theta\left(-x\right)+t_{1\rightarrow 2}\theta\left(x\right)\right),\\ A_{L}\left(x\right)&=e^{-i\frac{E}{v_{g}}x}t_{1\rightarrow 1}\theta\left(-x\right),\\ B_{R}\left(x\right)&=e^{i\frac{E}{v_{g}}x}t_{1\rightarrow 3}\theta\left(x\right),\\ B_{L}\left(x\right)&=e^{-i\frac{E}{v_{g}}x}t_{1\rightarrow 4}\theta\left(-x\right),\end{aligned}$

(7)

where $t_{i\rightarrow j}$ $(i,j={1,2,3,4})$ represents the probability amplitude of photon transmission from port $i$ to port $j$. $\theta\left(\pm x\right)$ is a step function. The transmission probability is defined by

$\displaystyle T_{i\rightarrow j}=|t_{i\rightarrow j}|^{2}.$

(8)

Combine Eq. (6) and Eq. (7), we obtain the transmission probability amplitude

	$\displaystyle t_{1\rightarrow 1}$	$\displaystyle=$	$\displaystyle 0,\qquad t_{1\rightarrow 4}=0,$		(9)
	$\displaystyle t_{1\rightarrow 2}$	$\displaystyle=$	$\displaystyle\frac{\left(\delta+\Delta_{F1}-i\frac{g_{a}^{2}}{2v_{g}}\right)\left(\delta-\Delta_{F2}+i\frac{g_{b}^{2}}{2v_{g}}\right)-J^{2}}{\left(\delta+\Delta_{F1}+i\frac{g_{a}^{2}}{2v_{g}}\right)\left(\delta-\Delta_{F2}+i\frac{g_{b}^{2}}{2v_{g}}\right)-J^{2}},$		(10)
	$\displaystyle t_{1\rightarrow 3}$	$\displaystyle=$	$\displaystyle\frac{-i\frac{1}{v_{g}}Jg_{a}g_{b}}{\left(\delta+\Delta_{F1}+i\frac{g_{a}^{2}}{2v_{g}}\right)\left(\delta-\Delta_{F2}+i\frac{g_{b}^{2}}{2v_{g}}\right)-J^{2}},$		(11)

where $\delta=E-\omega_{c}$ is detuning. Since the direction of photon transmission is opposite to the direction of the CCW mode in $f$ resonator, $T_{1\rightarrow 1}=0$. Similarly, since the CW mode of the $f$ resonator is only coupled to the CCW mode of the $d$ resonator, $T_{1\rightarrow 4}=0$. So, it is easily to find that $T_{1\rightarrow 2}+T_{1\rightarrow 3}=1$ which guarantees the probability conservation for the incident photon.

If the photon enters through port 2 of the $a$ waveguide, and the wave function is

$\displaystyle\begin{aligned} A_{L}\left(x\right)&=e^{-i\frac{E}{v_{g}}x}\left(\theta\left(x\right)+t_{2\rightarrow 1}\theta\left(-x\right)\right),\\ A_{R}\left(x\right)&=e^{i\frac{E}{v_{g}}x}t_{2\rightarrow 2}\theta\left(x\right),\\ B_{R}\left(x\right)&=e^{i\frac{E}{v_{g}}x}t_{2\rightarrow 3}\theta\left(x\right),\\ B_{L}\left(x\right)&=e^{-i\frac{E}{v_{g}}x}t_{2\rightarrow 4}\theta\left(-x\right).\end{aligned}$

(12)

The probability amplitude can be obtained by combining Eqs. (6) and (12)

	$\displaystyle t_{2\rightarrow 2}$	$\displaystyle=$	$\displaystyle 0,\qquad t_{2\rightarrow 3}=0,$		(13)
	$\displaystyle t_{2\rightarrow 1}$	$\displaystyle=$	$\displaystyle\frac{\left(\delta-\Delta_{F1}-i\frac{g_{a}^{2}}{2v_{g}}\right)\left(\delta+\Delta_{F2}+i\frac{g_{b}^{2}}{2v_{g}}\right)-J^{2}}{\left(\delta-\Delta_{F1}+i\frac{g_{a}^{2}}{2v_{g}}\right)\left(\delta+\Delta_{F2}+i\frac{g_{b}^{2}}{2v_{g}}\right)-J^{2}},$		(14)
	$\displaystyle t_{2\rightarrow 4}$	$\displaystyle=$	$\displaystyle\frac{-i\frac{1}{v_{g}}\lambda g_{a}g_{b}}{\left(\delta-\Delta_{F1}+i\frac{g_{a}^{2}}{2v_{g}}\right)\left(\delta+\Delta_{F2}+i\frac{g_{b}^{2}}{2v_{g}}\right)-J^{2}}.$		(15)

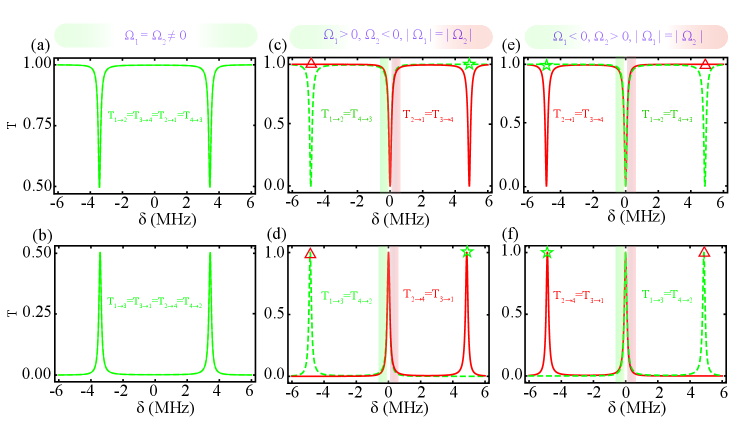
Using the same method, we can also obtain transmission probabilities $T_{3\rightarrow 4}$, $T_{3\rightarrow 1}$, $T_{4\rightarrow 3}$ and $T_{4\rightarrow 2}$. They satisfy the relationships $T_{1\rightarrow 2}=T_{4\rightarrow 3}$, $T_{1\rightarrow 3}=T_{4\rightarrow 2}$, $T_{2\rightarrow 1}=T_{3\rightarrow 4}$ and $T_{2\rightarrow 4}=T_{3\rightarrow 1}$. From Eqs. (10-11) and (14-15), it can be observed that if $\Delta_{F1}=\Delta_{F2}$ and $g_{a}=g_{b}$, we can observe that $T_{1\rightarrow 2}=T_{2\rightarrow 1}$, $T_{1\rightarrow 3}=T_{2\rightarrow 4}$. That is to say, when two resonators are static ($\Omega_{1}=\Omega_{2}=0$) or rotate with the same angular velocity ($\Omega_{1}=\Omega_{2}\neq 0$), the photon transmission in the same waveguide is reciprocal.

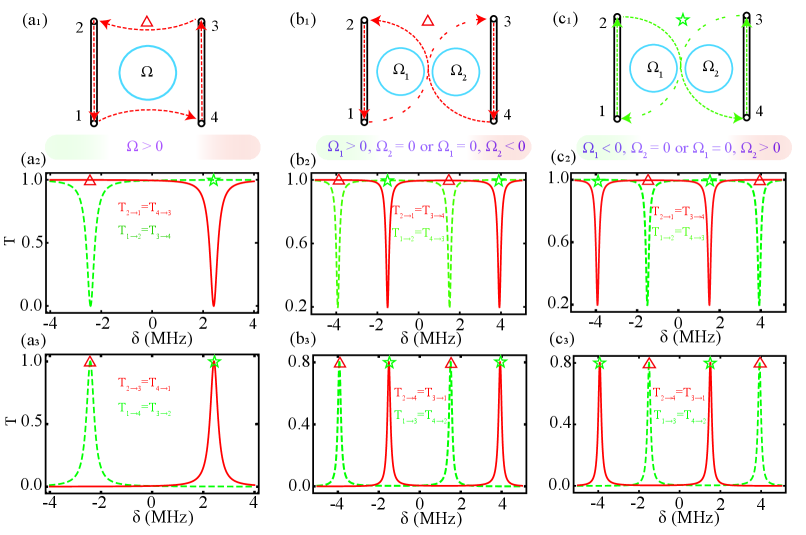
In this section, the main focus of these results is to analyze how different spinning direction in the resonator can impact the frequency of the realized photon circulator. For this purpose, we will focus on the following cases: 1) One resonator spins while the other remains static. 2) Both resonators spin in the same direction. 3) Both resonators spin in opposite directions. In our calculations, we have selected the experimentally feasible parameters [93, 94, 95]: $R=30$ $\mu$m, $n=1.4$, $Q=10^{9}$, $\lambda=1.55\times 10^{-6}$ m, $\omega_{c}=2\pi c/\lambda$, $g_{a}=g_{b}=6\omega_{c}/Q$, $c=v_{g}=3\times 10^{8}$ m/s, and $J=2.4$ MHz.

For comparisons, we first consider the single resonator case illustrated in Fig. 2($\mathrm{a_{1}}$). In Figs. 2($\mathrm{a_{2}}$) and 2($\mathrm{a_{3}}$), transmission probability distribution as a function of detuning $\delta$ for single resonator. The photon transmitted with circulation in the counterclockwise direction $1\rightarrow 4\rightarrow 3\rightarrow 2\rightarrow 1$, at $\delta=\Delta_{F1}$ [see Fig. 2($\mathrm{a_{1}}$)]. In addition, the photon also can transmit with circulation in the clockwise direction $1\rightarrow 2\rightarrow 3\rightarrow 4\rightarrow 1$, at $\delta=-\Delta_{F1}$. The above circulation can be seen from the transmission spectra as shown in Fig. 2($\mathrm{a_{2}}$-$\mathrm{a_{3}}$). The results are consistent with those in Ref. [78].

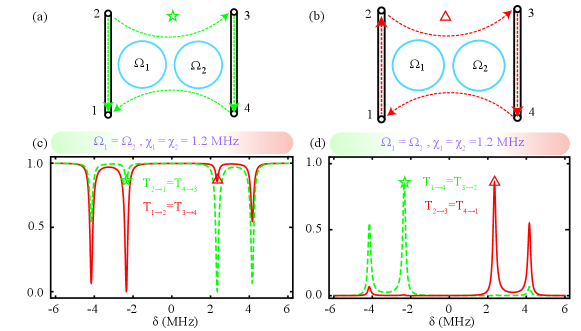
For two resonators case with $\Omega_{1}>0$ and $\Omega_{2}=0$ (or $\Omega_{1}=0$ and $\Omega_{2}<0$), when $\delta=\pm\sqrt{g_{a}^{2}g_{b}^{2}+4v_{g}^{2}J^{2}+v_{g}^{2}\Delta_{F1}^{2}}/(2v_{g})-\Delta_{F1}/2$, the photon transmitted with circulation in the reverse $8$-word direction $2\rightarrow 1\rightarrow 3\rightarrow 4\rightarrow 2$, see Fig. 2($\mathrm{b_{1}}$) (The position marked by a red triangle). The circulation can be seen from the transmission spectra as shown in Figs. 2($\mathrm{b_{2}}$-$\mathrm{b_{3}}$). In this case, the photon can not be transmitted from ports 2 and 3 to ports 4 and 1 , respectively. Due to the large frequency detuning, the photon entering from port 2 can not be transmitted to the CCW mode of the $f$ resonator. It also cannot couple with the CW mode of the $f$ resonator, as the direction of photon transmission is opposite to it. So that the photon from port 2 transmits through the $a$ waveguide directly to port 1. Also, because of the large frequency detuning, the photon entering from port 3 can not be transmitted to the CW mode of the $d$ resonator. It also cannot couple with the CCW mode of the $d$ resonator, as the direction of photon transmission is opposite to it. So that the photon from port 3 transmits through the $b$ waveguide directly to port 4. In contrast, the photon entering from port 1 (4) couples to the CW (CCW) travelling mode with the couping $g_{a}(g_{b})$, so that the photon can be transferred to port 3 (2). Therefore, four frequency point photon circulators can be achieved in this system.

The circulator can also be in the direction of a positive $8$ character, i.e. $1\rightarrow 2\rightarrow 4\rightarrow 3\rightarrow 1$, at $\delta=\pm\sqrt{g_{a}^{2}g_{b}^{2}+4v_{g}^{2}J^{2}+v_{g}^{2}\Delta_{F1}^{2}}/(2v_{g})+\Delta_{F1}/2$, see Fig. 2($\mathrm{c_{1}}$) (The position marked by a green star). The routing behavior can be understood in a similar way as given above. The photon can not be transmitted from ports 1 and 4 to ports 4 and 2 , respectively. Due to the large frequency detuning, the photon entering from port 1 can not be transmitted to the CW mode of the $f$ resonator. It also cannot couple with the CCW mode of the $f$ resonator, as the direction of photon transmission is opposite to it. So that the photon from port 1 transmits through the $a$ waveguide directly to port 2. The photon entering from port 4 can not be transmitted to the CCW mode of the $d$ resonator. It also cannot couple with the CW mode of the $d$ resonator, as the direction of photon transmission is opposite to it. So that the photon from port 4 transmits through the $b$ waveguide directly to port 3. In contrast, the photon entering from port 2 (3) couples to the CCW (CW) travelling mode with the couping $g_{a}$ $(g_{b})$, so that the photon can be transferred to port 4 (1). In addition, when $\Omega_{1}<0$ and $\Omega_{2}=0$ (or $\Omega_{1}=0$ and $\Omega_{2}>0$), we have plotted the transmission probability distribution as a function of detuning $\delta$, as shown in Fig. 2($\mathrm{c_{1}}$-$\mathrm{c_{3}}$). We found that Fig. 2($\mathrm{c_{2}}$-$\mathrm{c_{3}}$) is mirror symmetric in Fig. 2($\mathrm{b_{2}}$-$\mathrm{b_{3}}$) with $\delta=0$ as the mirror surface.

Then, we consider the photon transmission spectra of two resonators rotating in the same directions (e.g., $\Omega_{1}=\Omega_{2}>0$), as shown in the Figs. 3(a-b). Consistent with our previous calculation results, the probability of phohton transmission from any port is $1/2$, and the photon transmission is reciprocal in the same waveguide. In Figs. 3(c-f), we have plotted the photon transmission spectra of two resonator rotating in opposite directions, e.g., $\Omega_{1}>0$, $\Omega_{2}<0$, and $|\Omega_{1}|=|\Omega_{2}|$ or $\Omega_{1}<0$, $\Omega_{2}>0$, and $|\Omega_{1}|=|\Omega_{2}|$. Here, we found that a frequency point $\delta=\pm\sqrt{g_{a}^{2}g_{b}^{2}+4v_{g}^{2}J^{2}+v_{g}^{2}\left(\Delta_{F1}+\Delta_{F2}\right)^{2}}/(2v_{g})+(\Delta_{F2}-\Delta_{F1})/2$ ($\delta=\pm\sqrt{g_{a}^{2}g_{b}^{2}+4v_{g}^{2}J^{2}+v_{g}^{2}\left(\Delta_{F1}+\Delta_{F2}\right)^{2}}/(2v_{g})+(\Delta_{F2}+\Delta_{F1})/2$) can achieve an reverse or positive $8$ circulator, which means to realize the two photon circulator frequency point. Besides, we also found that at a specific angular velocity $|\Omega_{1}|=|\Omega_{2}|=M/G$ ($M=\sqrt{g_{a}^{2}g_{b}^{2}+4v_{g}^{2}J^{2}}/(2v_{g})$, $G=R\omega_{c}\left(n^{2}-1\right)/(cn)$), there was one frequency point that the photon entering from any waveguide can be completely routed to the other waveguide. We also found that Figs. 3(c-d) is mirror symmetric in Figs. 3(e-f) with $\delta=0$ as the mirror surface.

Comparad to a single resonator case, two resonators can have four frequency points for photon circulators, due to the coupling between resonators caused energy level splitting and the Fizeau drag induced splitting of the resonance frequencies of the two counter-travelling optical modes. In addition, we also found that there was one frequency point that the photon entering from any waveguide can be completely routed to the other waveguide. The direction of the photon circulator has also changed, form clockwise (counterclockwise) to reverse (positive) 8-word. The different directions of the photon circulator are due to the coupling between the CW (CCW) mode of the $f$ resonator and the CCW (CW) mode of the $d$ resonator.

The WGM resonators has two degenerate modes corresponding to CW and CCW modes. In practical devices, backscattering is unavoidable. They may be coupled together if the surface of the resonator is rough or the material is uneven[96, 97, 98]. So the Hamiltonian of the system is added with a term

$\displaystyle\hat{H}_{bs}=\chi_{1}\hat{f}_{cw}^{\dagger}\hat{f}_{ccw}+\chi_{2}\hat{d}_{ccw}^{\dagger}\hat{d}_{cw}+\mathrm{H.c.}$

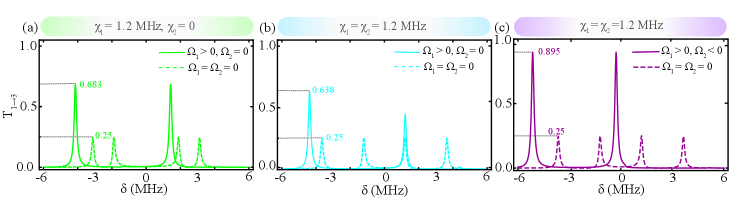
where $\chi_{1}$ ($\chi_{2}$) is the coupling strength of CW and CCW modes inside the $f$ $(d)$ resonator due to backscatter. Using the same method as in the previous section, we can calculate the probability $T_{i\rightarrow j}$ for each port. Figure 4 shows the probability of the photon transitioning from port 1 to port 3 under different conditions.

In Fig. 4(a), the dashed line indicates no rotation, but the $f$ resonator has backscattering, e.g. $\Omega_{1}=\Omega_{2}=0,\chi_{1}=1.2$ MHz, $\chi_{2}=0$. The solid line indicates rotation of the $f$ resonator under the condition of the dashes line, e.g. $\Omega_{1}>0,\Omega_{2}=0,\chi_{1}=1.2$ MHz, $\chi_{2}=0$. We found that the maximum value of $T_{1\rightarrow 3}$ increased from 0.25 to 0.683. So the results indicate that rotation is robust against backscattering. We also found that the frequency points that can be transmitted have shifted to the left, which is caused by the clockwise rotation of the resonator. On the contrary, when the resonator rotates counterclockwise, the transmission frequency point shift to the right. In Fig. 4(b), the dashed line indicates that both resonators are static but have backscattering, e.g. $\Omega_{1}=\Omega_{2}=0$, $\chi_{1}=\chi_{2}=1.2$ MHz. In contrast to Figure 4(a) a resonator has backscatter, we found that adding backscattering in another resonator does not change the value of $T_{1\rightarrow 3}=0.25$, bacause the four ports are transmitted with equal paobability. In the case of backscatter in both resonators, the soild line indicates tthe $f$ resonator rotates clockwise and the $d$ resonator static, e.g. $\Omega_{1}>0$, $\Omega_{2}=0$, $\chi_{1}=\chi_{2}=1.2$ MHz. The maximum value of $T_{1\rightarrow 3}$ has decreased from 0.683 to 0.638. This is cauesd by the backscatter of the $d$ resonator. When the $f$ resonator rotates clockwise and the $d$ resonator rotates counterclockwise ($\Omega_{1}>0$, $\Omega_{2}<0$, $|\Omega_{1}|=|\Omega_{2}|$), the transmission probability $T_{1\rightarrow 3}$ can reach 0.895, as shown in Fig. 4(c). In addition, if $\Omega_{1}<0$, $\Omega_{2}>0$, $|\Omega_{1}|=|\Omega_{2}|$, its transmission spectrum can be obtained in Fig. 4(b) though mirror reflection symmetry with $\delta=0$ as the mirror surface.

In the previous section, when the rotational angular velocities of the two resonators are equal and the direction is the same, the photon transmission is reciprocal in the same waveguide. Here, due to the addition of backscattering, we have broken this reciprocity. In Fig. 5, the transmission spectra of photons are plotted by adding backscattering to the resonators when the rotational angular velocities of the two resonators are equal and the direction is the same. We found two frequency points that can implement a single photon circulator, and the routing behavior is shown in Figs. 5(a-b). The circulator can be seen from the transmission spectra as shown in Figs. 5(c-d). Unlike the 8-word circulator, the direction of the circulator is clockwise or counterclockwise circulator.

We studied the coherent transmission of a single photon in a coupled system of two rotating WGM resonators and two waveguides. This system could form a four-port circulator, whose routing direction depended on the frequency of the incident photon, and the direction of rotation of the two resonators. We found that when both resonators rotated at identical angular velocities, single-photon transmission exhibited reciprocity within the same waveguide. When the angular velocities differed, usually there were four frequency points capable of facilitating single-photon circulation. However, when two resonators rotated in opposite directions with equal angular velocities, besides photon circulates at two frequency points, there is one frequency point at which a single photon input from any waveguide is completely routed to another. When the backscattering of a resonator is present, the single-photon circulation suppressed by the internal defect-induced backscattering can be restored by rotating the resonator, which is witnessed by enhancement of the probability of a single photon transfer.

We note that the presence of the reciprocity shut down the circulator for photons with arbitrary frequency. To turn on the circulator, the resonator must rotate at different angular velocities, so that the reciprocity of photon transmission is broken. Furthermore, one can tune the angular velocity to turn on or off circulating photons with a given frequency. The nonreciprocity of quantum circulators can be used to design novel quantum photonic device, which may have extensive applications in future quantum technologies.

\bmsection

Funding This work was supported by NSFC Grants No.11935006, No. 12075082, No. 12247105, No. 12205054, the science and technology innovation Program of Hunan Province (Grant No. 2020RC4047), National Key R $\&$ D Program of China (No. 2024YFE0102400), the Hunan Provincial major Sci-Tech Program (2023ZJ1010) and PH. D. Research Foundation (BSJJ202122). \bmsectionDisclosures The authors declare no conflicts of interest.