Open quantum dynamics of strongly coupled oscillators with multi-configuration time-dependent Hartree propagation and Markovian quantum jumps

For Markovian open quantum systems Breuer et al. (2002); Carmichael (1999); *Carmichael-book2, the evolution for system density matrix $\hat{\rho}_{S}$ in Liouville space is determined by a quantum master equation, which in Lindblad form reads ($\hbar\equiv 1$ is used throughout) Manzano (2020)

where $\hat{H}_{\mathrm{S}}$ is the system Hamiltonian and $\hat{L}_{j}$ are Lindblad jump operators that describe the interaction between the system and the $j$-th reservoir channel. The square brackets denote the commutator and curly brackets the anticommutator. The Lindblad form of the master equation is a dynamical semi-group that ensures the positivity of the density matrix Manzano (2020).The Monte Carlo wavefunction technique avoids the direct integration of the quantum master equation by propagating an initial wavefunction $\Psi(0)$ over a sequence of non-Hermitian evolution intervals that are interrupted at random times by quantum jumps that encode the physics of the Lindblad operators $\hat{L}_{j}$ *Molmer93.

Figure 1 summarizes the proposed Monte Carlo MCTDH (MC-MCTDH) algorithm. Starting from a reference time $t$, the wavefunction $|\Psi(t)\rangle$ is propagated with the MCTDH method up to $t+\Delta t$ with the effective non-Hermitian Hamiltonian

For small $\Delta t$, the wavefunction norm is reduced as

where $\delta p=\sum_{j}\delta p_{j}$ is determined by the instantaneous jump probabilities $\delta p_{j}=\Delta t\left\langle\Psi(t)\right|\hat{L}_{j}^{\dagger}\hat{L}_{j}\left|\Psi(t)\right\rangle$. At the end of the interval, a pseudo-random number $0<\epsilon<1$ is generated from a uniform distribution, and compared with $\delta p$. If $\delta p\leq\epsilon$, no quantum jump occurs and the wavefunction is renormalized as

before another interval begins. If $\delta p>\epsilon$ a quantum jump occurs and a Lindblad jump operator is chosen to act on the wavefunction. The $j$-th reservoir channel is chosen such that the operator $\hat{L}_{j}$ gives the smallest jump probability $\delta_{j}$ that is greater than $\epsilon$. The new wavefunction after the jump becomes

and a new interval begins. This algorithm (see Fig. 1) is sequentially repeated until the propagation ends, resulting in a piecewise quantum trajectory for the system wavefunction.

Observables are computed by averaging instantaneous expectation values over multiple trajectories *Molmer93. For the $k$-th quantum trajectory, expectation values $\langle\Psi^{(k)}(t)|\hat{O}|\Psi^{(k)}(t)\rangle$ are computed at the end of each interval, after normalizing the wavefunction. The procedure is straightforward to extend for computing two-time correlation functions Breuer et al. (2002). By construction, any trajectory-averaged observable

asymptotically converges to the density matrix solution $\langle\hat{O}\rangle\equiv\mathrm{Tr}[\hat{\rho}_{\mathrm{S}}(t)\hat{O}]$ with increasing number of trajectories $n_{\rm T}$. The convergence proof can be found in Ref. *Molmer93 and is reproduced in Appendix A. In practice, quantum optics problems allow for $n_{\rm T}\sim 10^{2}$. Mean-square errors (MSE) of the average observables can be defined by comparing with the exact density matrix solutions (see Appendix A). The independence of each trajectory facilitates computational parallelization strategies.

We use the MCTDH method for the deterministic propagation step in Fig. 1. The method was developed by Meyer, Manthe and Cederbaum in 1990 Meyer et al. (1990) as a generalization of the time-dependent Hartree ansatz McLachlan (1964) for solving the time-dependent Schrödinger equation. MCTDH is widely used in chemical physics due to its ability for obtaining essentially exact fully-quantum results for complex molecular systems with a large number of vibrational modes and strong non-adiabatic interactions Raab et al. (1999); Meyer et al. (2009).

The standard ansatz for solving the time-dependent Schrödinger equation is an expansion in a time-independent basis with time-dependent coefficients of the form

where $q_{k}$ are system coordinates, $C_{j_{1}...j_{f}}(t)$ are dynamical expansion coefficients and $\chi^{(k)}_{j_{k}}$ are the time-independent basis functions that describe the $k$-th degree of freedom. For example, in molecular vibration problems there would be $f$ degrees of freedom (e.g., vibrational modes) in this expansion, each described by complete basis of $N_{j_{k}}$ basis functions (e.g., vibrational eigenfunctions) represented on a one-dimensional coordinate grid using discrete variable representation (DVR) techniques Light and Carrington (2000).

MCTDH generalizes the static product basis in Eq. (7) with a linear combination of time-dependent Hartree products of the form

where the collective index $J$ labels the set of basis functions $\phi_{j_{k}}$ in a given tensor product configuration that contributes to the wavefunction, the tensor $\bm{A}_{J}(t)\equiv A_{j_{1}...j_{f}}(t)$ contains the time-dependent amplitudes of each product configuration, and $\bm{\Phi}_{J}(t)\equiv\prod_{k=1}^{f}\phi_{j_{k}}^{(k)}(q_{k},t)$ denotes the instantaneous product basis configurations. The number of relevant basis states per configuration and degree of freedom $n_{k}$ in Eq. (8) is typically smaller than the number of DVR basis functions $N_{k}$ needed for convergence the static ansatz in Eq. (7). As a result of this dynamical Hilbert space contraction, the number of product configurations $n_{1}\times n_{2}\times\dots\times n_{f}$ needed for convergence is usually smaller than the number of static configurations in the standard method because $n_{k}<N_{k}$ for each of the $k$-th degrees of freedom, which becomes important when solving high-dimensional quantum dynamics problems.

The time-dependent Schrödinger equation is solved with the MCTDH ansatz [Eq. (8)] and the Dirac-Frenkel variational principle Meyer et al. (2009). Coupled non-linear equations for the $\mathbf{A}_{J}$ and $\mathbf{\Phi}_{J}$ tensors are usually derived by introducing projectors over individual degrees of freedom $\hat{P}^{(k)}\equiv\sum_{j=1}^{n_{k}}|\phi_{j}^{(k)}\rangle\langle\phi_{j}^{(k)}|$, are complete in the limit $n_{k}\rightarrow\infty$. Projecting Eq. (8) over the $k$-th degree of freedom gives

which for the $k=1$ degree-of-freedom, for example, would give an expansion in the complementary space of the form $\bm{\Psi}_{l}^{(1)}=\sum_{j_{2}}^{n_{2}}\cdots\sum_{j_{f}}^{n_{f}}A_{lj_{2}\cdots j_{f}}(t)\phi_{j_{2}}^{(2)}\cdots\phi_{j_{f}}^{(f)}$. Variations of the time-dependent coefficients $\mathbf{A}_{J}$ and one-dimensional time-dependent functions $\bm{\Phi}_{J}$ are given by

Equations of motion for tensor coefficients $\mathbf{A}(t)$ are derived using Eqs. (8), (10) and (12) in the Dirac-Frenkel variational principle $\langle\delta\bm{\Psi}|\hat{H}|\bm{\Psi}\rangle=\dot{\imath}\left\langle\delta\bm{\Psi}\left|\frac{\partial}{\partial t}\right|\bm{\Psi}\right\rangle$ to get the set of coupled nonlinear equations

and

with the constraint $g^{(k)}_{jl}=\dot{\imath}\langle\phi_{j}^{(k)}|\dot{\phi}_{l}^{(k)}\rangle=\dot{\imath}\langle\phi_{j}^{(k)}|\hat{g}^{(k)}|\phi_{l}^{(k)}\rangle$. In Eq. (14), the tensor elements per degree of freedom are denoted as $\bm{A}_{J^{k}_{l}}\equiv A_{j_{1}\cdots l\cdots j_{f}}$.

The equations of motion for the functions $\phi_{j_{k}}^{(k)}$ are also found variationally from the time-dependent Schrödinger equation. In terms of the projection operators $\hat{P}^{(k)}$ they read

where $\rho^{(k)}_{j_{k}l_{k}}\equiv\langle\bm{\Psi}^{(k)}_{j_{k}}|\bm{\Psi}^{(k)}_{l_{k}}\rangle$ is a reduced density matrix, and $\langle\hat{H}\rangle_{jl}^{(k)}=\langle\bm{\Psi}_{j}^{(k)}|\hat{H}|\bm{\Psi}_{l}^{(k)}\rangle$ the mean-field Hamiltonian of the $k$-th degree of freedom. The solution of the MCTDH equations of motion preserve the norm and total energy for time-independent Hermitian Hamiltonians. In this work we use an extension of the method that includes non-Hermitian (complex) potentials. Additional details about MCTDH can be found in Refs. Meyer et al. (2009); Beck et al. (2000); Meyer (2011).

Consider a cavity mode with resonance frequency $\omega_{\rm c}$ in a structure with imperfect mirror reflectivity. The mode is modeled as a quantum harmonic oscillator with annihilation operator $\hat{a}$. Cavity photons leak out to the far field at rate $\kappa$. A minimal decoherence model for radiative decay can be constructed with the Lindblad operator $\hat{L}_{\kappa}=\sqrt{\kappa}\,\hat{a}$. The effective Hamiltonian for the deterministic steps of the Monte Carlo propagation method is thus given by

The Heisenberg equation of motion for the number operator $\hat{n}=\hat{a}^{\dagger}\hat{a}$ has the simple solution $\langle\hat{n}(t)\rangle=\langle\hat{n}(0)\rangle\,{\rm exp}[-\kappa t]$, i.e., exponential decay of initial occupation number $\left\langle\hat{n}(0)\right\rangle$ with population decay time $T_{1}=1/\kappa$. In Fig. 2 we show the MC-MCTDH evolution of an initial Fock state with $\left\langle\hat{n}(0)\right\rangle=8$ photons, together with the analytical solution. The inset shows that ${\rm MSE}\approx 1\%$ can be achieved with about $n_{\rm T}=400$ quantum trajectories.

This one-dimensional example is not exploiting the MCTDH tensor ansatz, but demonstrates the stochastic quantum jumps on a DVR grid for an excited Fock state. In general, most photonic states of interest in quantum optics (Fock state, coherent states, squeezed light) can be accurately represented with DVR grids Triana et al. (2018), which could be advantageous in comparison with more elaborate phase-space representations Zhu et al. (2019); Koessler et al. (2022).

Our next case study is two bilinearly coupled quantum harmonic oscillators in the rotating wave approximation. For an initial state with a single excitation in one of the oscillators, i.e., $\left|\Psi(0)\right\rangle=\left|1\right\rangle\left|0\right\rangle$, we expect the MC-MCTDH algorithm to describe damped Rabi oscillations of the subsystem variables. For a harmonic oscillator with annihilation operator $\hat{b}$ and resonance frequency $\omega_{0}$ (e.g., molecular vibration) interacting with the a cavity field $\hat{a}$ of frequency $\omega_{c}$, the effective Hamiltonian is given by

where $g$ is the coupling strength (Rabi frequency). Dissipation of the $b$-oscillator at rate $\gamma$ is modeled with the Lindblad operator $\hat{L}_{\gamma}=\sqrt{\gamma}\,\hat{b}$, and cavity dissipation is described as before.

Figure 3 shows the evolution of the occupation number $\langle\hat{b}^{\dagger}\hat{b}\rangle$ obtained with MC-MCTDH for strong resonant coupling ($\omega_{\rm c}=\omega_{0}$ and $g/\omega_{\rm c}>0.1$). The exact density matrix solution is also shown for comparison. For the chosen system parameters, averaging over $n_{\mathrm{T}}=50$ quantum trajectories gives good short-time accuracy, although errors tend to accumulate at longer times ($t>20\times 2\pi/\omega_{\rm c}$). Increasing the number of trajectories ($n_{\mathrm{T}}\sim 200$) gives results that match better the exact Liouville-space solution.

We now study the coupling of a two-level atom (qubit) with a cavity field $\hat{a}$ prepared in a coherent state $\left|\alpha\right\rangle$ with (real) amplitude $\alpha$. In the number (Fock) basis, the coherent state gives a Poissonian distribution with $\langle\hat{a}^{\dagger}\hat{a}\rangle=|\alpha|^{2}$ Carmichael (1999). Unitary dynamics is governed by the Jaynes-Cummings Hamiltonian Jaynes and Cummings (1963); Gerry and Knight (2005)

$\hat{\sigma}_{z}$ and $\hat{\sigma}_{\pm}$ are the Pauli spin-$1/2$ operators, $\omega_{0}$ is the qubit frequency, and $g$ the Rabi frequency. Since spins do not have a coordinate dependence, we represent the two spin projections $m_{z}=\pm 1/2$ in a DVR grid using two flat potentials separated in energy by $\omega_{0}$, i.e., $V_{\pm}(q)=\pm\,\omega_{0}/2$. This is equivalent to having two electronic states in the MCTDH package Worth et al. (2007). Pauli operators can be constructed accordingly. Atomic relaxation at the rate $\gamma$ is given by the Lindblad operator $\hat{L}_{\gamma}=\sqrt{\gamma}\,\hat{\sigma}_{-}$, and cavity decay is described before. The effective Hamiltonian for deterministic propagation is given by $\hat{H}=\hat{H}_{0}-i(\kappa/2)\,\hat{a}^{\dagger}\hat{a}-i(\gamma/2)\,\hat{\sigma}_{+}\hat{\sigma}_{-}$, with $\hat{H}_{0}$ in Eq. (19).

Figure 4 shows the evolution of the inversion $W(t)=\rho_{ee}(t)-\rho_{gg}(t)$, where $\rho_{ii}$ denotes level population. The qubit is initialized in the excited level ($W(0)=1$) and strongly couples to a cavity that has initially $|\alpha|^{2}=5$ photons on average. The Rabi frequency is $g=0.13\,/\omega_{0}$. For the small damping rates used ($\kappa=\gamma\sim 10^{-3}\omega_{0}$), the MC-MCTDH reproduces the long-time revivals of the population inversion expected due to the exchange of coherence between qubit and Fock sub-levels that compose the coherent state Gerry and Knight (2005), using only $n_{\rm T}=400$ quantum trajectories. Deviations from the exact Liouville-space solution are negligible at short times, but grow over longer timescales. The inset in Fig. 4 shows the drop of the MSE with increasing number of trajectories.

In this example, we consider a set of $N$ independent oscillators $\hat{b}_{i}$ that couple with a common quantized cavity field $\hat{a}$. The non-Hermitian effective Hamiltonian of the system is given by

with jump operators for the $b$-oscillators $\hat{L}_{i\gamma}=\sqrt{\gamma}\hat{b}_{i}$, and cavity dissipation described as before. We focus on the coherent population transfer between oscillators beyond the single-excitation manifold.

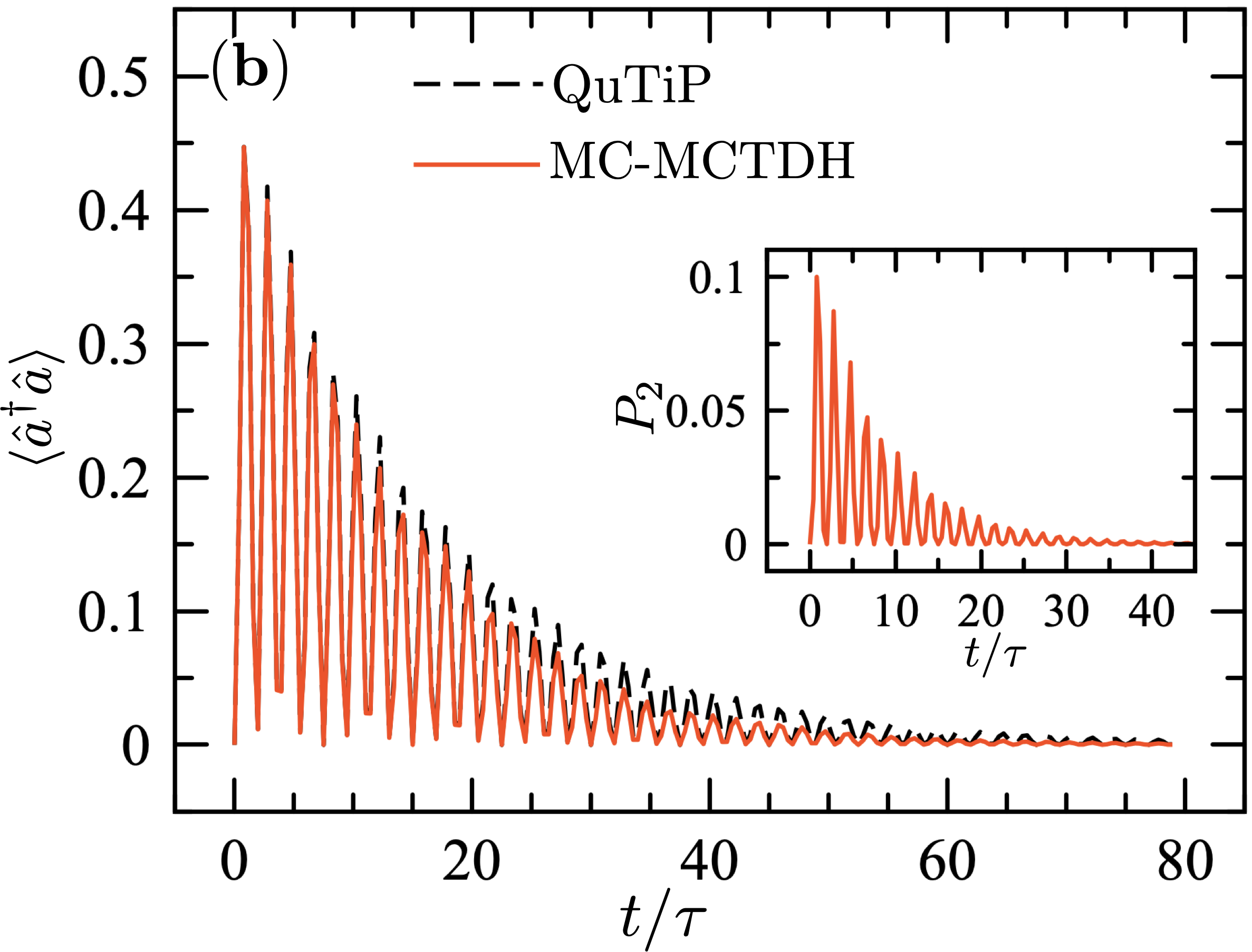
Figure 5a shows the MC-MCTDH evolution of the occupation numbers $\langle\hat{b}_{1}^{\dagger}\hat{b}_{1}\rangle$ and $\langle\hat{b}_{3}^{\dagger}\hat{b}_{3}\rangle$ for a set of $N=4$ oscillators in a cavity that initially has one excitation in $b_{1}$ and another excitation in $b_{2}$, with the cavity field in the vacuum, i.e., $|\Psi(0)\rangle=|1,1,0,0,n=0\rangle$. The results converge to the exact Liouville-space solution for the $b$-variables for $n_{T}=200$ quantum trajectories. However, Fig. 5b shows that long-time errors of about $4\%$ tend to accumulate for the photon number $\langle\hat{a}^{\dagger}\hat{a}\rangle$ after several population transfer cycles, which could be reduced by increasing $n_{T}$. The inset of 5b shows that the method captures the short-time rise and long-time decay of the $n=2$ Fock state population $P_{2}$. Since the amount of ground state bleaching is significant ($>10\%$), the Hilbert space dimension needed to converge the Liouville-space solution is higher than the previous examples. For the parameters in Fig. 5, QuTiP solutions converge with a minimum Hilbert space dimension of $d\equiv(\nu_{\rm max}+1)^{N}\times(n_{\rm max}+1)=324$, where $\nu_{\rm max}=2$ is the maximum quantum number used for each of the $b$-oscillators and $n_{\rm max}=3$ is the highest Fock state included.

As a final example, we compute the dynamics of a circular array of quantum harmonic oscillators of size $N$ with periodic boundary conditions. The array oscillator couple strongly to a common cavity field. We monitor the population transfer dynamics between oscillators in the array with the MC-MCTDH method assuming strong bilinear coupling between sites. The effective Hamiltonian is given by

where $\lambda$ is the nearest-neighbor coupling and the other variables are defined as before.

In Fig. 6 we show the occupation numbers of the cavity field and the oscillator $\hat{b}_{1}$, for an array of size $N=4$ and an initially excited cavity with $n=2$ photons. Two array excitation levels are studied. In Fig. 6a the oscillator array is set to the ground state ($\nu_{\rm max}=0$). In this case, the initial cavity excitations are transferred rapidly to the oscillator array creating a many-particle wavepacket that eventually decays within a few vibrational lifetimes. The evolution can be converged in Liouville space with a truncated Hilbert space that includes up to $\nu_{\mathrm{max}}=3$ excitations per site and $n_{\mathrm{max}}=5$ photons, giving the Hilbert space dimension $d=1536$. Converged MC-MCTDH calculations involved $N_{k}=41$ grid points for each degree of freedom in a harmonic oscillator-DVR primitive basis, with $n_{k}=4$ time-dependent functions, giving 1844 equations of motion to solve. Fig. 6a shows that the MC-MCTDH expectation values agree with the converged Liouville-space results within $\sim 1$% with only $n_{T}=300$ quantum trajectories.

In Fig. 6b, we informally probe the efficiency of the MC-MCTDH method by increasing the initial excitation density of the array to two excitations: one excitation in oscillator $b_{1}$ and another excitation in oscillator $b_{2}$, again with two initial cavity photons, i.e., $|\Psi(0)\rangle=|1,1,0,0,n=2\rangle$. For the same Hamiltonian and dissipative parameters in Fig. 6a, convergence of the Liouville space solution was not possible on the same machine where MC-MCTDH was implemented, due to RAM constraints. We obtained converged density matrix solutions with QuTiP implemented in a high-perfomance computing (HCP) workstation. The minimum Hilbert space dimension needed for $1\%$ convergence was found to be $d=10368$, which included $\nu_{\rm max}=5$ excitations per site and $n_{\rm max}=7$ cavity Fock states. Fig. 6b shows that the MC-MCTDH solution obtained in the low-RAM machine agrees well with the numerically-exact Liouville space solutions for $\hat{a}$ and $\hat{b}$ oscillators in the HCP workstation, using only 300 quantum trajectories.