Open Cluster Dynamics under the Influence of Outflow-Ambient Interactions
Abstract
Stars with outflows impinging on ambient gas experience accelerations due to the gravitational feedback from the interaction morphology between the outflow and the ambient gas. Such “negative dynamical friction” (NDF), in contrast to the conventional “dynamical friction” (DF), is studied for its impact on the dynamics of open clusters (OCs) immersed in a uniform ambient gas. We modify the -body integration code REBOUND with both NDF and DF implemented according to the outflow conditions of each star in a consistently constructed OC. The evolution of stars is also involved in determining the gas-star interactions throughout their stellar lives. Compared to DF-only and gas-free models with identical initial conditions, the NDF-affected cluster is puffier and evaporates faster, as indicated by various diagnostics, including lower velocity dispersions and larger half-mass and half-light radii. Neutron stars with fast winds are expelled from the cluster due to their intensive NDF effect, even without the “kicks” by asymmetric supernovae. Exploration of parameter space confirms that the NDF effect is generally enhanced with higher ambient gas densities, in qualitative agreement with the expression of acceleration. Outflow-ambient interactions should be considered for the proper interpretation of the stellar dynamics evolution in clusters.
1 Introduction
OC offer valuable insights into the formation and evolution of stars. Comprised of approximately to stars that are gravitationally bound to each other (Binney & Tremaine, 2008), OCs represent well-defined single stellar populations. They form from a common molecular cloud collapse (Krumholz et al., 2019), with the same metallicity and age. As a result, open clusters serve as valuable tracers of star formation, chemical evolution, kinematics, and gravitational dynamics (see, e.g., Friel, 1995; Maschberger & Kroupa, 2007, 2011; Krumholz et al., 2019; Cantat-Gaudin, 2022; Fu et al., 2022; Magrini et al., 2023). For instance, they can be utilized to determine the metallicity of stellar populations in different regions of the Milky Way, as their distances can be constrained by their color-magnitude diagrams (see, e.g., Sandage, 1953). Moreover, the kinematic properties of OCs can be used to trace the rotation curve of the Milky Way (see, e.g., Tarricq et al., 2021). Thanks to the contributions of missions like Gaia (Gaia Collaboration et al., 2016) in providing stellar astrometry information, including precise position, parallax, and proper motion, significant advancements have been made (e.g., Gaia Collaboration et al., 2018, 2021, 2023). The member stars of OCs and the properties of several thousand clusters have been determined based on Gaia data (see, e.g., Cantat-Gaudin, 2022; Hunt & Reffert, 2023). Some OCs show tidal structures and indicate interactions with their environments (see, e.g., Pang et al., 2022; Tarricq et al., 2022). These advancements enable the dynamical characteristics study of OCs through observations and facilitate comparison with theoretical models.
Most Galactic OCs travel in the Milky Way thin disk on near-circular orbits that pass through the Galactic mid-plane several times in one orbital revolution (see, e.g., Fu et al., 2022). The impact of the detailed interactions between the cluster member stars and the gas clouds in the Galactic plane remains unclear. Do the interactions change the morphology of the star clusters (Jerabkova et al., 2021; Pang et al., 2021) and lead to the loss of member stars? Do the interactions differ among different kinds of stars? These are still open questions.
The ambient gas density likely will affect the dynamical characteristics of an OC as it travels through a gas cloud. A massive object moving through a giant gas cloud experiences dynamic friction (DF) (Chandrasekhar, 1943; Ostriker, 1999; Edgar, 2004). According to the standard Bondi-Hoyle-Lyttleton accretion model (Hoyle & Lyttleton, 1939; Bondi & Hoyle, 1944; Edgar, 2004), it is understood that due to the long-range nature of gravity, the gas outside the Bondi radius is also influenced by gravity, resulting in the formation of an overdense tail downstream of the massive object. This overdense region exerts a pulling force on the object in the opposite direction of its motion, causing it to decelerate. This force is known as DF force. Works such as Kim & Kim (2007) and Baruteau et al. (2011) have shown that gas DF can lead to the hardening of binaries, and Tagawa et al. (2020) have pointed out that binaries can form through single-single interactions by dissipating kinetic energy in a gaseous medium. Other works, such as Tanaka et al. (2002), have shown that DF force can dampen the velocity dispersion of black holes and stars, and Just et al. (2012) have demonstrated that this dissipative force acting on stars in the disk can result in an increased mass flow toward the supermassive BH and an asymmetry in the phase space distribution due to a rotating accretion disk.
However, the situation changes if stellar objects launch powerful winds. Gruzinov et al. (2020) demonstrated that when the wind speed is sufficiently high, the extent of the underdense region becomes substantial, resulting in an overall gravitational force from the gas that aligns with the object’s motion. Consequently, the DF becomes negative in this scenario, causing the object to accelerate. This phenomenon is known as negative dynamic friction (NDF). In other related works, Li et al. (2020) employed hydrodynamic simulations to explore the changes in accretion rate and the strength of NDF in the presence of outflows from compact objects. Additionally, Wang & Li (2022) conducted a study on NDF in the context of a binary system using global 3D hydrodynamic simulations. This work uses the -body integrator REBOUND (Rein & Liu, 2012) to study the NDF impact on the dynamics of OCs immersed in a uniform ambient gas. Thanks to the support of REBOUND in allowing the incorporation of additional physics, both NDF and DF are implemented according to the outflow conditions of each star in a consistently constructed OC.
This paper is structured as follows. §2 provides comprehensive descriptions of the gas-star interactions incorporated, the stellar evolution model, and the setup of the fiducial model. §3 analyzes and compares the impacts of different types of gas-star interactions—namely, “DF”, “NDF”, and “None”—on the dynamics and stellar evolution of the fiducial model OC, both with and without bulk motion. §4 explores scenarios with various ambient gas densities. Discussion and a summary are given in §5.
2 Methods
This work simulates the dynamics of gas-coupled OCs using -body simulations by adding modules to REBOUND. For accuracy, we adopt the IAS15 integrator (Rein & Spiegel, 2015), which is a 15th order scheme with adaptive step size control. In order to model the clusters properly, stellar particles are created with proper mass distributions and evolved with stellar evolution models that include compact objects epochs along with the dynamics.
2.1 Gas-star Interactions
The interaction between gas and stars can generate either friction or anti-friction, depending on the strength of the stellar outflows. For stars that have no outflows, the analytic approximations for DF are adopted from Ostriker (1999):
| (1) |
where is the stellar velocity, is the ambient gas density, is the Mach number in the gas, and is the Coulomb factor. In this work, we assume that the direction is always aligned with the relative motion direction, because the timescales of hydrodynamic phenomena are typically much shorter than the stellar orbital dynamic timescales ,
| (2) |
in which and are the typical spatial scale of the hydrodynamic process and the stellar dynamics, respectively. The overdense structures causing DF is typically a few times the stellar size in absence of outflows (see e.g., Ostriker 1999), and the typical orbital scales of stars in OCs are no less than about (see e.g., Nilakshi et al. 2002) (unless in close encounter events, which are typically rapid and dwarf DF effects by the ambient gas). Therefore, it is almost always eligible to assume that the star-gas interaction structures settle at the steady or quasi-steady states, and the direction of DF stays along the stellar motion relative to the gas. We use the Bondi radius of each star, , for the minimum impact parameter, and we approximate with the size upper limit of a giant molecular cloud ( in this work; e.g., Solomon et al. 1987; Miville-Deschênes et al. 2017; Sun et al. 2018).
Whenever a star has outflows, the gravitational feedback coming from the interactions between such outflows and the ambient gas will likely accelerate the star. We adopt the analytic approximation described in Gruzinov et al. (2020) and Li et al. (2020),
| (3) |
where is the standoff distance (where the total pressure of the incoming medium equals that of the outflow), is the outflow wind mass-loss rate, is the wind radial velocity and . is the contact discontinuity location at the polar angle (where the gas over-densities are located) in spherical coordinates for which the star is at the origin, and the axis is in the opposite direction of . In general, for typical OCs, spans (e.g., Tarricq et al., 2021; Soubiran et al., 2018; Mathieu, 1984), which is significantly lower than the of almost all stellar outflows. Even asymptotic giant branch (AGB) stars, which are known for their slow outflows, still have (Habing & Olofsson, 2004; Ramstedt et al., 2008). Therefore, one can take the limit of eq. (3) and adopt a simple analytic approximation, (see also Li et al., 2020).
Similar to the DF case, the NDF direction stays along the direction of star to gas relative motion. While the stellar dynamic timescales are estimated similar to eq. (2), the estimation of hydrodynamic timescales approximately reads,
| (4) |
where the spatial scale should stand for the distance from the star to the bow shock, and is the stellar wind velocity. As one can easily observe, the inequality still holds in the NDF cases.
There are multiple types of stars in an OC, and their interactions with the ambient gas are different. Unless otherwise noted, we use the anti-friction recipes for main sequence stars, red giant branch (RGB) stars, and neutron stars (NSs), while we assume that white dwarfs (WDs) and BHs have no outflows and thus obey in eq. (1). Admittedly, WDs and BHs in binaries can accrete and have consequent activities (e.g., disk winds, decretions, and jets), yet detailed discussions on those phenomena only add to the complications and obscure the effects concerned, and are beyond the scope of the current paper. For main sequence stars and giants, the wind properties are calibrated for stars with solar metallicity. The mass-loss rates are approximated by Reimers formula (e.g., Kudritzki & Reimers 1978; see also Choi et al. 2016),
| (5) |
where we use the approximate scaling laws (Kuiper, 1938) and (Demircan & Kahraman, 1991), with as the stellar luminosity, as the stellar radius, and as the stellar mass. Such mass-loss rates are on the high end of typical values, yet stars in an OC are generally young and tend to have stronger stellar winds. The stellar wind velocity has significant variations and uncertainties from star to star. We adopt a simplified power-law fitting for main sequence stars,
| (6) |
which yields observed values of for solar-mass stars (e.g., Brooks et al., 2015), and for type O8 stars (e.g., Bernabeu et al., 1989). The uncertainties of wind properties are even greater for RGB stars; for simplicity, we assume all of them have and (Habing & Olofsson, 2004; Ramstedt et al., 2008). NSs can have significant outflows due to complex acceleration mechanisms, such as winds originating from young and intensely hot neutron stars are propelled by photons and neutrons near the stellar surface (Salpeter & Shapiro, 1981; Duncan et al., 1986). We assume ( for the speed of light), and (e.g., Kato, 1983; Paczynski, 1990; Mor et al., 2023).
2.2 Stellar Evolution Properties
Stars in an OC evolve for hundreds of millions of years before the cluster evaporates (Portegies Zwart et al., 2010; Krumholz et al., 2019; Krause et al., 2020). Given that the main sequence lifetime of an 8 star with solar metallicity is about 35 Myr (see stellar model PARSEC v1.2s 111https://people.sissa.it/sbressan/parsec.html; Bressan et al., 2012; Tang et al., 2014; Chen et al., 2015), before the cluster evaporates all massive stars will have evolved off the main sequence. Very massive stars () are not considered in this work. We assume that each star has finished its main sequence phase and entered its RGB stage at the time we consider significant gas-star interactions to occur. The evolution time of the RGB phase is approximated by a piecewise function in line with the solar metallicity and solar composition stellar models (Z=0.017, Y=0.279) of PARSEC v1.2s:
| (7) |
After the RGB stage, we assume that stars of will undergo their AGB phase and end up as WDs. Because the AGB stage experiences massive outflows that lose about of the stellar mass within a relatively short period (), the impact of AGB outflows due to anti-friction can be accounted as a pulse momentum injection, by integrating assuming and . The increments regarding the velocity is then better estimated by the change in ,
| (8) |
where is the proton mass. and are the total mass-loss and the increment of during the period , respectively. We assume that the consequent WD has (here is for the progenitor RGB star mass), and is given by the decrease of mass before becoming a WD. For stars with , we estimate their similarly, assuming that the expansion period of the supernova ejecta is , , and is also deduced from and the progenitor mass . Note that we consider this pulse momentum injection by AGB outflow in all types of gas-star interactions and intentionally ignore the “kicks” in NS (WD) momenta induced by the asymmetries of supernovae (mass-loss in WD progenitor), so as not to obscure the NDF by such kicks (while NDF only adds to the effects of the kicks). Other epochs of stellar evolution are ignored as they have negligible impact on the stellar cluster dynamics.
| Name | Description | ||||||
|---|---|---|---|---|---|---|---|
| (1) | (2) | (3) | (4) | (5) | (6) | ||
| S1500 | 1500 | 1193 | 2.0 | 5.0 | 0.40 | 0 | Fiducial sample (§3; §4) |
| S500 | 500 | 401 | 2.0 | 5.0 | 0.22 | 0 | Reduced star number (§3.1) |
| S3000 | 3000 | 2302 | 2.0 | 5.0 | 0.56 | 0 | Increased star number (§3.1) |
| S1500b | 1500 | 1198 | 2.0 | 5.0 | 28.82 | 100 | All stars in binary systems (§3.1) |
| S1500-seg | 1500 | 1121 | 2.0 | 5.0 | 0.33 | 0 | Completely segregated sample (§3.2) |
Note. — All samples are in virial equilibrium without the influence of a Galactic tidal field. Except for S1500-seg, all samples are unsegregated.
(1) Number of stars; (2) Total mass; (3) Half-mass radius; (4) Concentration parameter, (5) Velocity dispersion; (6) Fraction of binaries.
| Series | Name | Description† |
|---|---|---|
| CNMF† | Fiducial model (Cold Neutral Media; §3.1 - 3.4) | |
| Fiducial | CNM3† | (§3.3) |
| studies | CNM5† | (§3.3) |
| CNMF-tidal† | Incorporating the Galactic potential (§3.5) | |
| WNM0† | , (Warm Neutral Media) | |
| WNM1† | , (Warm Neutral Media) | |
| Various ambient | MD∗ | , (Diffuse Molecular Regions) |
| gas models | M4∗ | , (Molecular Clouds) |
| (§4) | M5∗ | , (Molecular Clouds) |
| M7∗ | , (Molecular Clouds) | |
| AGND∗ | , (AGN Disk Gases) |
Note. — All models presented here use the S1500 initial sample (see Table 1). Except for CNMF-tidal, the external Galaxy’s potential is exclude. Only the properties different from the fiducial model are described; .
: . : .
2.3 Setup of Fiducial and Other Models
The cluster samples used in the studies on open clusters are usually generated in initial virial equilibrium that can be achieved through various numerical methods (Aarseth et al., 1974), such as N-body integration, the Monte Carlo method, and the fluid dynamical approach (e.g., Aarseth, 1973; Spitzer & Hart, 1971a, b; Larson, 1970a, b). In this work, the initial sample is generated by McLuster, which is an open-source tool that can set initial conditions for N-body simulations or generate artificial star clusters for direct study (Küpper et al., 2011). The virial equilibrium cluster samples generated using McLuster are detailed in Table 1. All generated samples use the broken power-law initial mass function over the stellar mass range (Kroupa et al., 1993; Kroupa, 2002; Reid et al., 2002).
| (9) |
with the parameter in the King (1966) model, specifying model concentration, set to 5.0, and the half-mass radius along the line of sight set to .
With the help of McLuster, different initial conditions can be set when generating cluster samples by modifying the default parameter values. For example, “-Q” sets the virial ratio to ensure the cluster is in virial equilibrium, “-S” adjusts the degree of mass segregation, and “-b” sets the binary fraction. The method used for generating samples with specified degrees of mass segregation and binary fraction is based on the approaches of Baumgardt et al. (2008); Kroupa (1995a, 2008). The fiducial sample is a 1500-star ensemble S1500 without segregation and binaries (see Figures 1–2), which will be used for studying different physical scenarios (§3 and 4). S500 and S3000 are two samples with different numbers of stars, used for comparison with S1500 in the fiducial model study. With the same stellar number as S1500, S1500-seg is a fully mass-segregated cluster, where the most massive star occupies the lowest energy orbit, and the least massive star occupies the highest energy orbit. Note that the previously mentioned samples do not include initial binaries, as introducing binaries would complicate internal interactions within the cluster. For example, collisions could occur between the outflows of stars in binary systems (e.g., Wang & Li, 2022). Such complicated interactions would require further study using hydrodynamic simulations, which is beyond the scope of this current paper and reserved for future works.
Following Kroupa et al. (2001), this work generates a sample with a binary fraction through random pairing (S1500b) to study simplified physical scenarios (considering only gas-star interactions). The binary fraction is defined as
| (10) |
where is the number of binary and is the number of single stars. The method of identifying binaries follows Parker et al. (2009), which is calculating pairs with negative relative energy.


The fiducial model studies an OC immersed in the cold neutral medium (CNM), one of the phases of the interstellar medium (ISM) in the Galaxy, which has and (Draine, 2011). The OC then evolved for within the bounding box. An important assumption is that star formation in the cluster is a single-age event, and once the cluster is formed, all the gas is expelled. Different models exploring physical parameters (especially those about the ambient gas properties) use the same initial fiducial sample S1500 (see Table 1-2). Simulations for each model, including the fiducial model specific to the CNM, are conducted with three types of gas-star interactions, indicated as “NDF”, “DF” and “None” as the suffixes of the models, to emphasize the modes of the gas-star interactions. Note that the stars that do not launch winds (e.g., WDs) always experience the DF effect even in the model marked as “NDF”.
2.4 Basic Characterizations
Statistics about cluster sizes require a clear definition of the cluster center. This work uses the center of mass of the bounded stars, calculated through these two steps:
-
1.
Select all stars within the simulation bounding box and calculate their total energy (the summation of kinetic and gravitational energy) with respect to the center of mass. Stars with negative total energy are considered bounded.
-
2.
Calculate the location and velocity of the center of mass for the bounded stars, which are used as the origin points in the configuration and momentum spaces in subsequent analyses.
Similar to the center of mass, the “center of light” is also desired for the analyses of stellar luminosity distribution, which is defined as the luminosity-weighted average coordinates for the bounded stars identified in the Step 1. Considering the observational conditions, unless specifically emphasized, all half-mass and half-light radii in this paper represent 2D values projected along the line of sight, calculated by averaging over three lines of sight as samples,
| (11) |
where are the projected half-mass or half-light radii calculated on the planes, respectively.
For better presentations of fluctuations in the cluster characterizations, the uncertainties about statistical results in this work are estimated by the non-parametric bootstrap resampling method, which is a widely accepted and commonly used statistical method in astrophysics (see also Efron, 1979; Feigelson & Babu, 2012; Malofeeva et al., 2023). In detail, the bootstrap method generates datasets of the same length as the original data through resampling with replacement, repeated 1000 times. The standard deviations in each bin were then computed based on the results from these 1000 bootstrapped datasets.
3 Fiducial Model Results
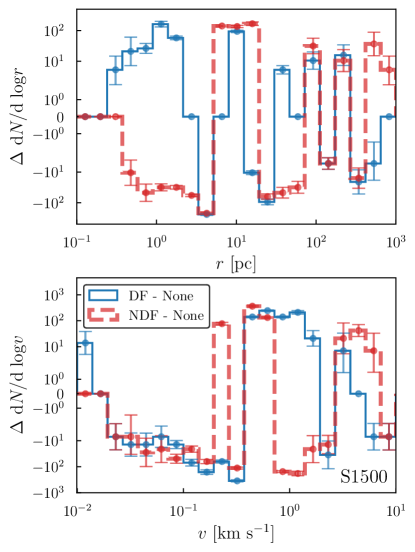

The impacts of the gas-star interactions on the model OC immersed in the fiducial uniform CNM gas (CNMF hereafter for this case) are illustrated by the histograms in Figures 3. Thanks to the NDF acceleration, the stars generally reside on the side with higher total energy in the CNMF-NDF run, compared to its CNMF-DF and CNMF-None counterparts. The distribution of distances to the cluster center (“distances” hereafter) tilts to the more distant side, while the velocity tends to be smaller as the stars are statistically farther from the global gravitational potential minimum.
For a sun-like star orbiting the Galaxy embedded in the CNM gas, the velocity changes caused by NDF are as,
| (12) |
where is the stellar velocity variation caused by NDF. Based on the conservation of angular momentum and assuming the star moves along a circular orbit, the orbital radius of the solar-like star will decrease by
| (13) |
where is the orbital radius and is the orbital variation caused by NDF. The above calculations show that after of evolution, the orbit and velocity change by only , which is insignificant. Additionally, the gas component that occupies the largest volume in the galaxy’s ISM is the warm neutral medium (WNM), which has a lower density than the CNM (see §4 for different gas density cases). This implies that the influence of NDF will be even smaller. Hence, for a solar-like star embedded in the ISM orbiting the galaxy, NDF will not significantly affect its orbital motion unless it interacts with higher density gas.
3.1 Cluster Sizes and Velocity Dispersions
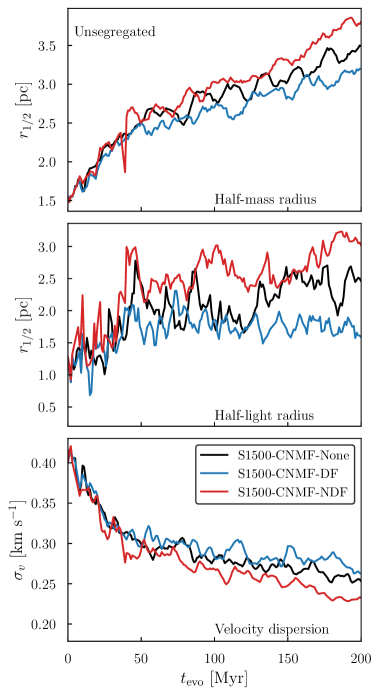
Statistics directly related to observables are presented in the left column of Figure 4. All three models exhibit the same trend of dynamical evaporation, indicated by their increasing half-mass and half-light radii (in each time interval without star deaths), and decreasing velocity dispersions. The half-mass radii for the CNMF-NDF model are larger than the gas-free CNMF-None model by about , while those for the CNMF-DF model are smaller by approximately the same percentage. Acceleration forces (NDF) tend to increase the total energy of stars, relocating them to shallower regions in the potential well and reducing the magnitude of the velocity dispersion. The deceleration forces (DF), in contrast, tend to result in larger velocity dispersions and smaller cluster sizes.
One can observe “cliffs” at in both the half-mass and half-light radii for the unsegregated NDF model in Figure 4. These cliffs are the consequences of both the expulsion of massive stars () due to NDF acceleration , and the termination of massive stars on the main sequence as well. They are more pronounced in the half-light radius, as the luminosity is more sensitive to stellar mass (). In contrast, the DF models slow down the massive stars more efficiently, delaying their evaporation and resulting in a slower increase in cluster size compared to the case without gas-star interaction.
To illustrate the influence of the star numbers, the results for samples S500 and S3000 with different numbers of stars are presented in the right column of Figure 4. The increasing cluster size and decreasing velocity dispersion over time are qualitatively similar to S1500, while the cluster size grows much faster with NDF in S500 and slower in S3000. With decreasing star numbers, the evaporation timescale comes closer to the crossing timescale (; see also Binney & Tremaine 2008), making the cluster more susceptible to the acceleration caused by NDF, and vice versa.

The formation and evolution of binaries within OCs has long been a topic of concern (e.g., Kroupa, 1995b, a, c; Li & Mao, 2018). Figure 5 illustrates the evolution of the binary fraction. For both S1500 and S1500b, the three runs for the CNMF model do not exhibit significant differences in . For S1500b, binary systems are rapidly disrupted in the first 1 Myr, during which the soft binaries are destroyed. Subsequently, the clusters reach an equilibrium where the binary fraction becomes roughly stable. This behavior is consistent with Kroupa (1995b, a); Kroupa et al. (1999); Parker et al. (2009).
3.2 Mass-segregated Clusters


Actual stellar clusters may have different extents of mass segregation during their formation and early evolution, that more massive stars tend to be distributed closer to the cluster center (e.g. Chandrasekhar, 1943; Chandrasekhar & von Neumann, 1942). We study a completely segregated cluster sample S1500-seg generated by McLuster (see also Table 1 and Figure 6), and present the evolution of properties in Figure 7.
The differences in the half-light radii and half-mass radii between NDF and the other two models are more significant than for the fiducial model S1500. After evolution, the half-light radii for the NDF model are about twice as large as in the DF and gas-free models. The NDF model “overturns” the segregation by raising more massive stars to larger distances due to stronger acceleration, while the DF and gas-free models only add to the segregation during the evolution. With more numerical experiments not presented here, we confirm the general trend that the more mass-segregated the clusters are initially, the more important the NDF becomes along the dynamical evolution of OCs.
3.3 Bulk Motion of Clusters

The gas-star interactions–both NDF and DF–are the results of stellar outflows and motion. Although the CNMF model runs assume no bulk motion of the whole cluster, the real situation is usually more complicated. The centers of mass of an OC and a gas cloud can move on their own tracks when evolving in galaxies, and the relative bulk motion between the two objects should be expected. We hence introduce models CNM3 and CNM5 to study such bulk motions at center of mass speeds and , respectively (see also Table 2).

Due to the morphologies of the stellar wind-ambient interaction regions, the magnitudes of NDF acceleration decreases with faster stellar velocities (eq. 3). This relation qualitatively yields the phenomena in Figure 8, where the increase in total energy caused by NDF is slightly suppressed with higher . Regarding the increase in half-mass and half-light radii, a similar suppression is observed in Figure 9. Concerning velocity dispersion, the NDF suppression results in stars settling in deeper regions of the potential well, leading to larger velocity dispersion than in the CNMF model. While these patterns can be qualitatively anticipated for higher velocities, detailed analyses should be based on cluster-specific calculations rather than extrapolations.
3.4 Stellar Evolution and Compact Objects


Outflowing stars are expected to be pushed further away from the cluster center once NDF is in action. For typical main sequence stars immersed in the CNM, however, such effects are generally obscured by the overall trend of OC dynamical evaporation. When an outflowing star travels at a low initial speed in a uniform medium, the asymptotic relation near between the travel distance and the time roughly reads, using the approximate expression for eq. (3) and integrating ,
| (14) |
In the meantime, the velocity scales as asymptotically. These estimations also give the lower limit of time required to drive a star out of the cluster even without the gravitational potential well. When the potential well is present, direct exclusion of a solar-mass main sequence star only via NDF is not possible.
For objects with intensive outflows, however, the accelerations are much more significant dynamically. Although increases sub-linearly with , the NS with can still escape from the stellar ensemble well before the evaporation of OCs. Figure 10 illustrates the efficient expulsion of NS (upper panel) by NDF (solid lines), compared to the DF (dotted lines) and gas-free (dashed lines) cases where the ordinary “evaporation” process of an OC and the increment of a star’s velocity by AGB-outflow-induced pulse are present. NS are driven out to from the center of the cluster within only about , shorter than the lifetime of a typical OC. After escaping from the OC potential, the scaling and eq. (14) holds semi-quantitatively for each of the NS at large distances (). Assuming that the gaseous disk half-thickness is about in the Galaxy, such expulsion process will eventually take about to remove an NS from the disk. Such quick expulsions will likely lead to the scarcity of NS in OCs, and probably in the whole gaseous galactic disk. Figure 11 illustrates a reduced expulsion of NSs attributed to the attenuation of the NDF effect by the bulk motion. The NS expulsion is ubiquitous for gas-immersed OCs unless the cluster bulk motion is too fast relative to the gas. Previous works often attribute the NS exclusion from clusters to the “kicks” during asymmetric supernovae explosions (e.g., Fragione & Banerjee, 2020). With the NDF effects, however, NS exclusion can still take place without these “kicks”. Note that even in the case of intensive outflows from stars, the winds of the stars cannot combine to drive a wind from the OC. This is because the standoff distance of the contact discontinuity,
| (15) |
is much smaller than the distance between member stars (e.g., the minimum distance in the initial OC of the fiducial case is about ).
In contrast to NS, WDs do not launch outflows in our models. This causes the absence of NDF during their WD epochs, and the pulsive acceleration in their AGB stages is clearly insufficient to exclude them from the OCs. However, the deficiency of WDs in young OCs has been proved by observations (e.g. Kalirai et al., 2001). Once the WD outflows due to binary accretion processes are included (which requires detailed modeling in feedback and the non-isotropic outflow patterns, e.g. Li et al. 2020, and is also postponed to future works), WDs are also expected to experience expulsion in their dynamical evolution. To illustrate another possible exclusion mechanism of WDs, we set up a model that enables pulses in velocity for newly formed WDs with a magnitude of and random directions, following Fellhauer et al. (2003). As one can see from Figure 12, such pulses can indeed cause the exclusion of WDs regardless to the condition of gas-star interactions.

3.5 Cluster in Galactic Potential
As a star departs from its cluster, its path is computed considering the Galaxy’s external potential. Incorporating the Galactic potential in models of OC offers a more realistic scenario. Following Allen & Santillan (1991), the Galactic potential is composed of three parts: the central part , the disc , and the halo , i.e., . These three parts of the potential can be expressed in cylindrical coordinates () as follows:
| (16) |
where
| (17) |
The parameters for the above equations are , , , , , , and . The OC is positioned on a circular orbits at a speed of , specifically , at a distance of from the Galactic center.

The impacts of the gas-star interactions in this galactic scenario are illustrated by Figure 13. While the overall trend is consistent with Figure 4 that both the half-mass and half-light radii increase over time, the tidal fields dominate the dynamical evolution and generally dwarf the differences in the half-mass radii and velocity dispersions for the three gas-star interaction models. The half-light radii, which are more sensitive to massive stars, are greater for NDF and DF models compared to the gas-free case. Dinnbier & Kroupa (2020) studied the dynamical evolution of the tidal tails of OCs in detail and provided a semi-analytical model, concluding that such oscillations in the velocity dispersions solely depend on the local galactic dynamical properties, especially the orbital frequency and the epicycle frequency, rather than any cluster properties (e.g., the initial velocity dispersion or mass).
It is expected that the tidal field could be one of the significant effects of the evolution of internal dynamical features within OC. However, this work focuses on the effect of gas-star interactions. While incorporating the tidal field would render the scenario more realistic, it also complicates the physical mechanisms, making it challenging to analyze the effects of different mechanisms clearly. Therefore, the tidal field will not be considered in subsequent scenarios, meaning the external Galaxy’s potential will be excluded. In future work, the influence of both tidal fields and gas interactions on the dynamical characteristics of stars or clusters should be included.
4 Models Exploring Ambient Gas Properties
The Galaxy contains multiple phases of the ISM in its disk, whereas the CNM phase that we have explored in §3 only occupies a relatively small volume fraction (typically a few percent, see e.g., Ferrière 2001; Draine 2011). We therefore conduct various simulations to study the interactions between OCs and other types of gases, including the WNM, diffuse molecular regions (MD), dense and intermediate molecular clouds, and even the mid-plane of active galactic nucleus (AGN) disks (Draine, 2011; Cantiello et al., 2021). Properties of these gases are summarized in Table 2. Note that all simulations in this section use the fiducial sample S1500.



4.1 Distributions in the Configuration and
Velocity Spaces
In a virialized self-gravitating system, stars staying at larger distances from the cluster center generally move at slower velocities. When the NDF and DF accelerations are sufficiently low and gradual, their impact on the cluster configurations is mostly adiabatic, and the system remains virialized during the evolution. When the ambient gas density is raised to in the model AGND, however, the NDF acceleration for a solar-mass star moving at becomes , which is about the gravitational acceleration by a cluster at . A cluster evolving under such strong NDF or DF accelerations no longer remains adiabatic; the dispersal takes place directly within the first resulting in a quickly expanding spatial size and higher velocity dispersions (Figure 14). This phenomenon also appears in the models M7 and M5 that stand for typical molecular clouds, while the models for more diffuse gas (WNM0, WNM1) are qualitatively similar to the CNMF case.
Another effect that emerges in various ambient models is the stratification of stars. The acceleration by NDF on stars tend to increase their energy, which is similar to some “buoyancy” in self-gravitating OCs. As more massive stars launch more powerful stellar winds (§2.2), they tend to move quicker to the “surfaces” of OCs under NDF, and vice versa. We notice that such “buoyancy” will not make the young OCs “inversely segregated” initially, as the timescales required to fully “inversely segregate” the cluster (about ) (see e.g. Figure 15) is longer than the time period of star formation () (Palla & Stahler, 1999; Palla et al., 2005).
Since the stellar luminosity scales as , the half-light radii are considerably greater than half-mass radii in NDF-affected clusters. For those models that have dense ambients (e.g. M4, M5), the half-light radii are greater than the half-mass radii after only about , indicating an obvious radial stratification in terms of stellar types. When attempting to infer the age of an observed OC by the observations in astrometry and dynamics, one should take care of the possible encounters with dense clouds, whose effect in puffing up the OCs is similar to the intrinsic evaporation of clusters. Statistics on the radial distributions of mass and light in such clusters, therefore, may be helpful in reducing this type of parameter degeneracies.
4.2 Puff-up and Dispersal of Open Clusters in Gases
According to eq. (3), the magnitude of NDF acceleration depends much more sensitively on than on . Figure 16 illustrates the general trend that the NDF effects increase with denser ambient gas, raising the total energy and easing the evaporation of cluster stars. The scaling relation in eq. (3) is sub-linear with respect to (). Assuming a relatively invariant velocity distribution over the same period of time, one can infer the scaling relation , and subsequently . This pattern is qualitatively seen in Figure 14, yet we note that such simple scaling no longer applies quantitatively when there are significant increases in velocity dispersions.
Models M5 and M7 show that OCs in relatively dense ambients will quickly puff up or even disperse within , a timescale that is comparable or shorter than the crossing time of an OC over a dense molecular cloud. If one adopts the typical sizes (about ) of dense molecular clouds () (Cernicharo, 1991; Bergin & Tafalla, 2007) with an OC crossing time (assuming bulk velocity ), Model M5 indicates that a cluster should puff up to after this crossing. Similar results also occur in Model M7, even if one limits the interaction time to the typical lifetime of dense molecular clouds (about a few Myr). The encounter with molecular clouds can lead to significant changes in its speed due to NDF or DF, scaled with respect to the data of solar-like stars,
| (18) |
For AGB stars with massive outflows (see also eq.(8) in §2.1), the increment in stellar velocity caused by NDF could raise further to after .
AGN disks are also considered as places where stars can form, whose lifetimes are at the order of (Marconi et al., 2004; Martini & Weinberg, 2001). If a OC forms and stays inside the AGN disk for , it could evaporate almost completely before it is no longer considered as a cluster anymore, even if the destruction processes by orbital motion shears and tidal forces are taken into account. In other words, the likelihood that one can find OCs formed in AGN disks should not be significant.
4.3 Compact Objects and Binaries


As elaborated in §3.3 and 4.1, higher stellar velocities and lower ambient gas densities suppress the NDF acceleration. In various models, the expulsion of NS via NDF behaves accordingly. Figure 17 illustrates that, even for Model WNM1 whose ambient density is merely , such expulsion mechanism is still working, although the time required is considerably longer. This effect is, nevertheless, still more perceptible than the CNM5 case (see Figure 11). For Model WNM0, the expulsion mechanism weakened compared to WNM1, but all NSs still tend to move away from the OC.
The binary fraction corresponding to various models does not show any considerable changes compared to the fiducial CNMF model, except for the AGND model with DF only (Figure 18). The binary fraction increased drastically in the first of evolution. Strong deceleration caused by DF shrinks the separations between stars and reduces stellar velocities, facilitating the formation of binaries. Several studies have explored this phenomenon. Rafikov (2013, 2016) proposed that gas-assisted inspirals efficiently merge supermassive BH binaries within a Hubble time. The NDF would nonetheless overturn this scenario, widening the binary separations. Wang & Li (2022) demonstrated in simulations of AGB star-outflowing pulsars that a dense and slow outflow exerts a positive torque on the binary, causing orbit expansion. Extrapolating these mechanisms to the OCs immersed in dense gas can cause a severe inhibition of binary occurrence rates.
5 Discussion and Summary
In this paper, we study the evolution of OCs immersed in the ISM. Overall, the introduction of NDF makes the OC puffier and eases the evaporation of cluster stars, resulting in reduced velocity dispersions and increased half-mass and half-light radii. This effect scales sub-linearly with the ambient density and is mostly irrelevant to the ambient temperature as the ram pressures on both sides of the contact discontinuity dominate the gas-star interactions. NS with powerful winds are expelled from the cluster due to the intense NDF effect, while WD stars undergo conventional evaporation due to the absence of a WD-driven wind.
5.1 Impacts of the NDF Effects on Cluster Evolution
While gas DF has garnered most of the attention, NDF has been relatively overlooked. Opposite to DF, NDF accelerates stars along their motion direction. Such difference in the effects between NDF versus DF can “flip” the signs of multiple physical mechanisms. For instance, one may expect that the OC evaporation is suppressed or even inhibited by DF when encountered with gas, while the actual scenario could be right the opposite due to NDF. In the densest gases including dark molecular clouds, AGN disks, and AGN tori (whose average column density is as high as about ; see, e.g., Zhao et al. 2021), dispersal of OCs can be almost instant compared to their dynamical lifetimes as clusters. Interpretations about observations on cluster kinetics should take the possibility of NDF into account. Pflamm-Altenburg & Kroupa (2009) argued that massive stellar clusters over a certain critical mass can act as cloud condensation nuclei and accrete gas from the ambient medium. Such critical mass is required for the cluster to accrete gas and induce density instability in the ISM roughly satisfies (where is the cluster mass, is the gas temperature, and is the Plummer parameter; see also Plummer 1911). Admittedly, massive clusters can suppress the NDF effect by accreting from the ambient gas, which is also beyond the scope of the current study and will be addressed in future works. In the scenarios considered in this work, nevertheless, the cluster mass is insufficient to initiate this type of accretion.
Observation missions like Gaia (Gaia Collaboration et al., 2016) provide abundant astrometric data for stars in our galaxy, facilitating the study of OCs’ dynamical evolution (e.g., Maurya et al., 2023). Because of the radial stratification in stellar masses (§4.1), one can prospectively tell the effects of gas-star interactions by measuring the half-mass and half-light radii, as well as the velocity dispersions. The combination of high precision photometry with astrometry can further help the researchers to find out the radial distribution functions of different stellar types. These measurements can be a direct characterization of gas-star interaction history that are potentially important for identifying an OC’s “invasion” into dense gases during its evolution history.
5.2 Neutron Star Depletion
Due to substantial outflows, NSs gradually drift away from their associated OC under the influence of NDF in all simulations. Conversely, WD stars influenced by NDF experience a pulse momentum injection from the main sequence to the AGB stage and subsequently to the WD stage. However, upon transitioning into the WD phase, WDs decelerate due to DF as they lack outflows. This mechanism ensures that part of WDs remain confined within the OC and experience conventional evaporation. If the kick received by a WD is strong enough, such as through an asymmetric mass loss process (Fragione & Banerjee, 2020), it is more likely to be expelled from the OC (see in Figure 12).
It is commonly assumed that kicks by asymmetric supernovae drive NS to high velocities relative to the cluster centers, and eventually expel them from OCs. Lai (2004) reviewed various physical mechanisms leading to kicks, and Bortolas et al. (2017) suggested that NSs are generally scattered away from SgrA* due to such kicks. Contenta et al. (2015) indicated that the natal kick of NSs can alter the cluster’s lifetime by almost a factor of 4. Admittedly, the kicks serve as an effective expulsion mechanism of NS. However, kicks only entail a one-time momentum injection, whose intensity and direction of momentum injection is stochastic and can well result in the NS’s deceleration. The NDF effects are, in contrast, a much more steady and robust mechanism that almost ensures the expulsion without gravitational scatterings. Such effects can further lead to the reduction of NS binaries and mergers within OCs, which is potentially relevant to the spatial distribution of NS-related mergers and gravitational wave events.
5.3 Future Works
Due to the limitations in physical modeling and computation, this work does have some caveats and issues that should be addressed in future works. For example, simplistic isotropic stellar wind models are adopted for each type of star, which is suitable only for a fraction of NS. Many NS–especially those with accretion disks–may launch directed or bipolar outflows, which could affect the intensity and direction of the NDF forces (Li et al., 2020). The WD model in this study lacks wind and is susceptible to DF only. While stand-alone WD stars may not have outflows, accretion from their companions may cause disk winds and jets. This study ignores the time lag in forming stars within the OC and does not consider the interaction between star and star-forming gas. However, the expulsion of residual star-forming gas does not occur instantaneously after the completion of the star formation process in realistic scenario. Observations reveal that star formation efficiencies within OCs vary widely, ranging from several percent to 30 percent for dense clumps within molecular clouds (Lada & Lada, 2003; Higuchi et al., 2009; Megeath et al., 2016), and from 0.1 percent to a few percent for their associated giant molecular clouds (Evans et al., 2009; Murray, 2011). This implies that newly formed or forming stars (such as protostars and pre-MS stars, which have outflows) would interact with star-forming gas, resulting in the influence of NDF on the initial phase space distribution of stars within young OC. Moreover, the stellar winds from these stars may blow unprocessed gas out of the cluster, inhibiting the ongoing star formation process. Refined models in the future should take the complexities of stellar outflows and the star formation process into account. Besides, this work neglects the interactions between the outflows of stars in binary systems and between binary systems and the outflows of single stars. These effects will be investigated in future work using more refined hydrodynamic simulations.
Although our study considers the highly dense scenario of an AGN disk (AGND scenario), we have omitted multiple physical conditions relevant to AGN in order to isolate and emphasize the impact by NDF. Incorporating the shear effect is crucial for understanding stellar formation and evolution within AGN disks. However, this topic is specific to disks and beyond the scope of this paper, which should be addressed in a separate study. Future studies on AGN disks will require additional considerations, such as orbital motion and vertical stratification of gas. The limited thickness of AGN disks differs substantially from the assumed uniform gas ambient in this paper, especially considering the vertical density gradients. Furthermore, isolated stars would experience the DF effects in the highly dense environment of a galaxy’s circumnuclear regions. Future works shall also explore these possibilities of NDF-affected stars.
In addition, this work focuses on relatively small and sparse OCs with about stars. In high-density environments, particularly in AGN disks, super star clusters are often present instead of OCs, whose star formation efficiencies may be typically high. Investigating larger ensembles of stars such as globular clusters can impose additional challenges. Globular clusters contain about or even more stars, while each of the stars might still be dynamically important. Accurate treatments of frequent close encounters are beyond the capacity of ordinary orbital integrators with tree-based or particle-mesh-based gravity solvers, and special algorithms are required for sufficient accuracy. During close encounters, shock structures caused by gas-star interactions may collide, resulting in highly complex gas morphologies and interaction patterns. Understanding how such complex physical scenarios affect the dynamical evolution of stars within globular clusters could be explored once proper algorithms are prepared for complicated computations. Even without proper treatments of frequent close encounters in more massive clusters, the dynamical evolution of compact objects (NS, WD, and BH) are still qualitatively feasible within the current framework for globular clusters and super star clusters. Detailed discussions are nontheless beyond the scope of the current paper focusing on OCs, and a subsequent paper is being composed specifically addressing this issue.
References
- Aarseth (1973) Aarseth, S. J. 1973, Vistas in Astronomy, 15, 13, doi: 10.1016/0083-6656(73)90003-2
- Aarseth et al. (1974) Aarseth, S. J., Henon, M., & Wielen, R. 1974, A&A, 37, 183
- Allen & Santillan (1991) Allen, C., & Santillan, A. 1991, Rev. Mexicana Astron. Astrofis., 22, 255
- Baruteau et al. (2011) Baruteau, C., Cuadra, J., & Lin, D. N. C. 2011, ApJ, 726, 28, doi: 10.1088/0004-637X/726/1/28
- Baumgardt et al. (2008) Baumgardt, H., De Marchi, G., & Kroupa, P. 2008, ApJ, 685, 247, doi: 10.1086/590488
- Bergin & Tafalla (2007) Bergin, E. A., & Tafalla, M. 2007, ARA&A, 45, 339, doi: 10.1146/annurev.astro.45.071206.100404
- Bernabeu et al. (1989) Bernabeu, G., Magazzu, A., & Stalio, R. 1989, A&A, 226, 215
- Binney & Tremaine (2008) Binney, J., & Tremaine, S. 2008, Galactic Dynamics: Second Edition (Princeton University Press)
- Bondi & Hoyle (1944) Bondi, H., & Hoyle, F. 1944, MNRAS, 104, 273, doi: 10.1093/mnras/104.5.273
- Bortolas et al. (2017) Bortolas, E., Mapelli, M., & Spera, M. 2017, MNRAS, 469, 1510, doi: 10.1093/mnras/stx930
- Bressan et al. (2012) Bressan, A., Marigo, P., Girardi, L., et al. 2012, MNRAS, 427, 127, doi: 10.1111/j.1365-2966.2012.21948.x
- Brooks et al. (2015) Brooks, D. H., Ugarte-Urra, I., & Warren, H. P. 2015, Nature Communications, 6, 5947, doi: 10.1038/ncomms6947
- Cantat-Gaudin (2022) Cantat-Gaudin, T. 2022, Universe, 8, 111, doi: 10.3390/universe8020111
- Cantiello et al. (2021) Cantiello, M., Jermyn, A. S., & Lin, D. N. C. 2021, ApJ, 910, 94, doi: 10.3847/1538-4357/abdf4f
- Cernicharo (1991) Cernicharo, J. 1991, in NATO Advanced Study Institute (ASI) Series C, Vol. 342, The Physics of Star Formation and Early Stellar Evolution, ed. C. J. Lada & N. D. Kylafis, 287, doi: 10.1007/978-94-011-3642-6_8
- Chandrasekhar (1943) Chandrasekhar, S. 1943, ApJ, 97, 255, doi: 10.1086/144517
- Chandrasekhar & von Neumann (1942) Chandrasekhar, S., & von Neumann, J. 1942, ApJ, 95, 489, doi: 10.1086/144420
- Chen et al. (2015) Chen, Y., Bressan, A., Girardi, L., et al. 2015, MNRAS, 452, 1068, doi: 10.1093/mnras/stv1281
- Choi et al. (2016) Choi, J., Dotter, A., Conroy, C., et al. 2016, ApJ, 823, 102, doi: 10.3847/0004-637X/823/2/102
- Contenta et al. (2015) Contenta, F., Varri, A. L., & Heggie, D. C. 2015, MNRAS, 449, L100, doi: 10.1093/mnrasl/slv026
- Demircan & Kahraman (1991) Demircan, O., & Kahraman, G. 1991, Ap&SS, 181, 313, doi: 10.1007/BF00639097
- Dinnbier & Kroupa (2020) Dinnbier, F., & Kroupa, P. 2020, A&A, 640, A84, doi: 10.1051/0004-6361/201936570
- Draine (2011) Draine, B. T. 2011, Physics of the Interstellar and Intergalactic Medium (Princeton University Press)
- Duncan et al. (1986) Duncan, R. C., Shapiro, S. L., & Wasserman, I. 1986, ApJ, 309, 141, doi: 10.1086/164587
- Edgar (2004) Edgar, R. 2004, New A Rev., 48, 843, doi: 10.1016/j.newar.2004.06.001
- Efron (1979) Efron, B. 1979, The Annals of Statistics, 7, 1 , doi: 10.1214/aos/1176344552
- Evans et al. (2009) Evans, Neal J., I., Dunham, M. M., Jørgensen, J. K., et al. 2009, ApJS, 181, 321, doi: 10.1088/0067-0049/181/2/321
- Feigelson & Babu (2012) Feigelson, E. D., & Babu, G. J. 2012, Modern Statistical Methods for Astronomy (Cambridge University Press), doi: 10.48550/arXiv.1205.2064
- Fellhauer et al. (2003) Fellhauer, M., Lin, D. N. C., Bolte, M., Aarseth, S. J., & Williams, K. A. 2003, ApJ, 595, L53, doi: 10.1086/379005
- Ferrière (2001) Ferrière, K. M. 2001, Reviews of Modern Physics, 73, 1031, doi: 10.1103/RevModPhys.73.1031
- Fragione & Banerjee (2020) Fragione, G., & Banerjee, S. 2020, ApJ, 901, L16, doi: 10.3847/2041-8213/abb671
- Friel (1995) Friel, E. D. 1995, ARA&A, 33, 381, doi: 10.1146/annurev.aa.33.090195.002121
- Fu et al. (2022) Fu, X., Bragaglia, A., Liu, C., et al. 2022, A&A, 668, A4, doi: 10.1051/0004-6361/202243590
- Gaia Collaboration et al. (2016) Gaia Collaboration, Prusti, T., de Bruijne, J. H. J., et al. 2016, A&A, 595, A1, doi: 10.1051/0004-6361/201629272
- Gaia Collaboration et al. (2018) Gaia Collaboration, Brown, A. G. A., Vallenari, A., et al. 2018, A&A, 616, A1, doi: 10.1051/0004-6361/201833051
- Gaia Collaboration et al. (2021) —. 2021, A&A, 649, A1, doi: 10.1051/0004-6361/202039657
- Gaia Collaboration et al. (2023) Gaia Collaboration, Vallenari, A., Brown, A. G. A., et al. 2023, A&A, 674, A1, doi: 10.1051/0004-6361/202243940
- Gruzinov et al. (2020) Gruzinov, A., Levin, Y., & Matzner, C. D. 2020, MNRAS, 492, 2755, doi: 10.1093/mnras/staa013
- Habing & Olofsson (2004) Habing, H. J., & Olofsson, H. 2004, Asymptotic Giant Branch Stars (Springer-Verlag New York), doi: 10.1007/978-1-4757-3876-6
- Higuchi et al. (2009) Higuchi, A. E., Kurono, Y., Saito, M., & Kawabe, R. 2009, ApJ, 705, 468, doi: 10.1088/0004-637X/705/1/468
- Hoyle & Lyttleton (1939) Hoyle, F., & Lyttleton, R. A. 1939, Proceedings of the Cambridge Philosophical Society, 35, 405, doi: 10.1017/S0305004100021150
- Hunt & Reffert (2023) Hunt, E. L., & Reffert, S. 2023, A&A, 673, A114, doi: 10.1051/0004-6361/202346285
- Jerabkova et al. (2021) Jerabkova, T., Boffin, H. M. J., Beccari, G., et al. 2021, A&A, 647, A137, doi: 10.1051/0004-6361/202039949
- Just et al. (2012) Just, A., Yurin, D., Makukov, M., et al. 2012, ApJ, 758, 51, doi: 10.1088/0004-637X/758/1/51
- Kalirai et al. (2001) Kalirai, J. S., Ventura, P., Richer, H. B., et al. 2001, AJ, 122, 3239, doi: 10.1086/324463
- Kato (1983) Kato, M. 1983, PASJ, 35, 33
- Kim & Kim (2007) Kim, H., & Kim, W.-T. 2007, ApJ, 665, 432, doi: 10.1086/519302
- King (1966) King, I. R. 1966, AJ, 71, 64, doi: 10.1086/109857
- Krause et al. (2020) Krause, M. G. H., Offner, S. S. R., Charbonnel, C., et al. 2020, Space Sci. Rev., 216, 64, doi: 10.1007/s11214-020-00689-4
- Kroupa (1995a) Kroupa, P. 1995a, MNRAS, 277, 1507, doi: 10.1093/mnras/277.4.1507
- Kroupa (1995b) —. 1995b, MNRAS, 277, 1491, doi: 10.1093/mnras/277.4.1491
- Kroupa (1995c) —. 1995c, MNRAS, 277, 1522, doi: 10.1093/mnras/277.4.1522
- Kroupa (2002) —. 2002, Science, 295, 82, doi: 10.1126/science.1067524
- Kroupa (2008) —. 2008, in The Cambridge N-Body Lectures, ed. S. J. Aarseth, C. A. Tout, & R. A. Mardling, Vol. 760 (Springer-Verlag Berlin Heidelberg), 181, doi: 10.1007/978-1-4020-8431-7_8
- Kroupa et al. (2001) Kroupa, P., Aarseth, S., & Hurley, J. 2001, MNRAS, 321, 699, doi: 10.1046/j.1365-8711.2001.04050.x
- Kroupa et al. (1999) Kroupa, P., Petr, M. G., & McCaughrean, M. J. 1999, New A, 4, 495, doi: 10.1016/S1384-1076(99)00038-X
- Kroupa et al. (1993) Kroupa, P., Tout, C. A., & Gilmore, G. 1993, MNRAS, 262, 545, doi: 10.1093/mnras/262.3.545
- Krumholz et al. (2019) Krumholz, M. R., McKee, C. F., & Bland-Hawthorn, J. 2019, ARA&A, 57, 227, doi: 10.1146/annurev-astro-091918-104430
- Kudritzki & Reimers (1978) Kudritzki, R. P., & Reimers, D. 1978, A&A, 70, 227
- Kuiper (1938) Kuiper, G. P. 1938, ApJ, 88, 472, doi: 10.1086/143999
- Küpper et al. (2011) Küpper, A. H. W., Maschberger, T., Kroupa, P., & Baumgardt, H. 2011, MNRAS, 417, 2300, doi: 10.1111/j.1365-2966.2011.19412.x
- Lada & Lada (2003) Lada, C. J., & Lada, E. A. 2003, ARA&A, 41, 57, doi: 10.1146/annurev.astro.41.011802.094844
- Lai (2004) Lai, D. 2004, in Cosmic explosions in three dimensions, ed. P. Höflich, P. Kumar, & J. C. Wheeler, 276, doi: 10.48550/arXiv.astro-ph/0312542
- Larson (1970a) Larson, R. B. 1970a, MNRAS, 150, 93, doi: 10.1093/mnras/150.1.93
- Larson (1970b) —. 1970b, MNRAS, 147, 323, doi: 10.1093/mnras/147.4.323
- Li et al. (2020) Li, X., Chang, P., Levin, Y., Matzner, C. D., & Armitage, P. J. 2020, MNRAS, 494, 2327, doi: 10.1093/mnras/staa900
- Li & Mao (2018) Li, Z., & Mao, C. 2018, ApJ, 859, 36, doi: 10.3847/1538-4357/aabc09
- Magrini et al. (2023) Magrini, L., Viscasillas Vázquez, C., Spina, L., et al. 2023, A&A, 669, A119, doi: 10.1051/0004-6361/202244957
- Malofeeva et al. (2023) Malofeeva, A. A., Mikhnevich, V. O., Carraro, G., & Seleznev, A. F. 2023, AJ, 165, 45, doi: 10.3847/1538-3881/aca666
- Marconi et al. (2004) Marconi, A., Risaliti, G., Gilli, R., et al. 2004, MNRAS, 351, 169, doi: 10.1111/j.1365-2966.2004.07765.x
- Martini & Weinberg (2001) Martini, P., & Weinberg, D. H. 2001, ApJ, 547, 12, doi: 10.1086/318331
- Maschberger & Kroupa (2007) Maschberger, T., & Kroupa, P. 2007, MNRAS, 379, 34, doi: 10.1111/j.1365-2966.2007.11891.x
- Maschberger & Kroupa (2011) —. 2011, MNRAS, 411, 1495, doi: 10.1111/j.1365-2966.2010.17783.x
- Mathieu (1984) Mathieu, R. D. 1984, ApJ, 284, 643, doi: 10.1086/162447
- Maurya et al. (2023) Maurya, J., Joshi, Y. C., Samal, M. R., Rawat, V., & Gour, A. S. 2023, Journal of Astrophysics and Astronomy, 44, 71, doi: 10.1007/s12036-023-09959-3
- Megeath et al. (2016) Megeath, S. T., Gutermuth, R., Muzerolle, J., et al. 2016, AJ, 151, 5, doi: 10.3847/0004-6256/151/1/5
- Miville-Deschênes et al. (2017) Miville-Deschênes, M.-A., Murray, N., & Lee, E. J. 2017, ApJ, 834, 57, doi: 10.3847/1538-4357/834/1/57
- Mor et al. (2023) Mor, R., Livne, E., & Piran, T. 2023, MNRAS, 518, 623, doi: 10.1093/mnras/stac2775
- Murray (2011) Murray, N. 2011, ApJ, 729, 133, doi: 10.1088/0004-637X/729/2/133
- Nilakshi et al. (2002) Nilakshi, Sagar, R., Pandey, A. K., & Mohan, V. 2002, A&A, 383, 153, doi: 10.1051/0004-6361:20011719
- Ostriker (1999) Ostriker, E. C. 1999, ApJ, 513, 252, doi: 10.1086/306858
- Paczynski (1990) Paczynski, B. 1990, ApJ, 363, 218, doi: 10.1086/169332
- Palla et al. (2005) Palla, F., Randich, S., Flaccomio, E., & Pallavicini, R. 2005, ApJ, 626, L49, doi: 10.1086/431668
- Palla & Stahler (1999) Palla, F., & Stahler, S. W. 1999, ApJ, 525, 772, doi: 10.1086/307928
- Pang et al. (2021) Pang, X., Li, Y., Yu, Z., et al. 2021, ApJ, 912, 162, doi: 10.3847/1538-4357/abeaac
- Pang et al. (2022) Pang, X., Tang, S.-Y., Li, Y., et al. 2022, ApJ, 931, 156, doi: 10.3847/1538-4357/ac674e
- Parker et al. (2009) Parker, R. J., Goodwin, S. P., Kroupa, P., & Kouwenhoven, M. B. N. 2009, MNRAS, 397, 1577, doi: 10.1111/j.1365-2966.2009.15032.x
- Pflamm-Altenburg & Kroupa (2009) Pflamm-Altenburg, J., & Kroupa, P. 2009, MNRAS, 397, 488, doi: 10.1111/j.1365-2966.2009.14954.x
- Plummer (1911) Plummer, H. C. 1911, MNRAS, 71, 460, doi: 10.1093/mnras/71.5.460
- Portegies Zwart et al. (2010) Portegies Zwart, S. F., McMillan, S. L. W., & Gieles, M. 2010, ARA&A, 48, 431, doi: 10.1146/annurev-astro-081309-130834
- Rafikov (2013) Rafikov, R. R. 2013, ApJ, 774, 144, doi: 10.1088/0004-637X/774/2/144
- Rafikov (2016) —. 2016, ApJ, 827, 111, doi: 10.3847/0004-637X/827/2/111
- Ramstedt et al. (2008) Ramstedt, S., Schöier, F. L., Olofsson, H., & Lundgren, A. A. 2008, A&A, 487, 645, doi: 10.1051/0004-6361:20078876
- Reid et al. (2002) Reid, I. N., Gizis, J. E., & Hawley, S. L. 2002, AJ, 124, 2721, doi: 10.1086/343777
- Rein & Liu (2012) Rein, H., & Liu, S. F. 2012, A&A, 537, A128, doi: 10.1051/0004-6361/201118085
- Rein & Spiegel (2015) Rein, H., & Spiegel, D. S. 2015, MNRAS, 446, 1424, doi: 10.1093/mnras/stu2164
- Salpeter & Shapiro (1981) Salpeter, E. E., & Shapiro, S. L. 1981, ApJ, 251, 311, doi: 10.1086/159466
- Sandage (1953) Sandage, A. R. 1953, AJ, 58, 61, doi: 10.1086/106822
- Solomon et al. (1987) Solomon, P. M., Rivolo, A. R., Barrett, J., & Yahil, A. 1987, ApJ, 319, 730, doi: 10.1086/165493
- Soubiran et al. (2018) Soubiran, C., Cantat-Gaudin, T., Romero-Gómez, M., et al. 2018, A&A, 619, A155, doi: 10.1051/0004-6361/201834020
- Spitzer & Hart (1971a) Spitzer, Lyman, J., & Hart, M. H. 1971a, ApJ, 164, 399, doi: 10.1086/150855
- Spitzer & Hart (1971b) —. 1971b, ApJ, 166, 483, doi: 10.1086/150977
- Sun et al. (2018) Sun, J., Leroy, A. K., Schruba, A., et al. 2018, ApJ, 860, 172, doi: 10.3847/1538-4357/aac326
- Tagawa et al. (2020) Tagawa, H., Haiman, Z., & Kocsis, B. 2020, ApJ, 898, 25, doi: 10.3847/1538-4357/ab9b8c
- Tanaka et al. (2002) Tanaka, H., Takeuchi, T., & Ward, W. R. 2002, ApJ, 565, 1257, doi: 10.1086/324713
- Tang et al. (2014) Tang, J., Bressan, A., Rosenfield, P., et al. 2014, MNRAS, 445, 4287, doi: 10.1093/mnras/stu2029
- Tarricq et al. (2022) Tarricq, Y., Soubiran, C., Casamiquela, L., et al. 2022, A&A, 659, A59, doi: 10.1051/0004-6361/202142186
- Tarricq et al. (2021) —. 2021, A&A, 647, A19, doi: 10.1051/0004-6361/202039388
- Wang & Li (2022) Wang, L., & Li, X. 2022, ApJ, 932, 108, doi: 10.3847/1538-4357/ac6ce6
- Zhao et al. (2021) Zhao, X., Marchesi, S., Ajello, M., et al. 2021, A&A, 650, A57, doi: 10.1051/0004-6361/202140297