Online conformal prediction with decaying step sizes

We now describe our prediction set construction. Borrowing from conformal prediction, consider a bounded conformal score function $s_{t}:\mathcal{X}\times\mathcal{Y}\to[0,B]$, at each time $t$. This score $s_{t}=s_{t}(X_{t},Y_{t})$ is large when the predictions of the base model disagree greatly with the observed label; an example would be the residual score, $s_{t}(x,y)=|y-\hat{f}_{t}(x)|$, for a model $\hat{f}_{t}:\mathcal{X}\to\mathbb{R}$ trained online. This concept is standard in conformal prediction (Vovk et al., 2005), and we refer the reader to Angelopoulos and Bates (2023) for a recent overview. Given this score function, define

where the threshold $q_{t}$ is updated with the rule

In particular, if we fail to cover $Y_{t}$ at time $t$, then the threshold increases to make the procedure slightly more conservative at the next time step (and vice versa).

Familiar readers will notice the similarity of the update step (4) to that of Gibbs and Candes (2021); Bhatnagar et al. (2023); Feldman et al. (2023); Angelopoulos et al. (2023), the main difference being that here, $\eta_{t}$ can change over time—later on we will see that $\eta_{t}\propto t^{-1/2-\epsilon}$, for some small $\epsilon\in(0,1/2)$, leads to guarantees (1) and (2) as described above. We remark also that the update step for $q_{t}$ can be interpreted as an online (sub)gradient descent algorithm on the quantile loss $\rho_{1-\alpha}(t)=(1-\alpha)\max\{t,0\}+\alpha\max\{-t,0\}$  (Koenker and Bassett Jr, 1978), i.e., we can equivalently write the update step (4) as

In this work, we will consider two different settings:

Our method, like all conformal methods, has coverage guarantees that hold for any underlying model and data stream. Still, the quality of the output (e.g., the size of the prediction sets) does critically depend on the quality of the underlying model. This general interplay between conformal methods and models is discussed throughout the conformal literature (e.g., Vovk et al., 2005; Angelopoulos and Bates, 2023).

We begin by reviewing the most closely related literature. Set constructions of the form in (3), which “invert” the score function, are commonplace in conformal prediction (Vovk et al., 2005), with $q_{t}$ chosen as a sample quantile of the previous conformal scores. However, the exchangeability-based arguments of the standard conformal framework cannot give any guarantees in Setting 1. The idea to set $q_{t}$ via online gradient descent with a fixed step size appears first in Gibbs and Candes (2021), which introduced online conformal prediction in the adversarial setting. The version we present here builds also on the work of Bhatnagar et al. (2023), Feldman et al. (2023), and  Angelopoulos et al. (2023); in particular, Angelopoulos et al. (2023) call the update in (4) the “quantile tracker”. These papers all have long-run coverage guarantees in Setting 1, but do not have convergence guarantees in Setting 2.

Subsequent work to these has explored time-varying step sizes that respond to distribution shifts, primarily for the purpose of giving other notions of validity, such as regret analyses (Gibbs and Candès, 2022; Zaffran et al., 2022; Bastani et al., 2022; Noarov et al., 2023; Bhatnagar et al., 2023). From an algorithmic perspective, these methods depart significantly from the update in (4), generally by incorporating techniques from online learning—such as strongly adaptive online learning (Daniely et al., 2015), adaptive regret (Gradu et al., 2023), and adaptive aggregation of experts (Cesa-Bianchi and Lugosi, 2006). To summarize, the long-run coverage and regret bounds in these papers apply to substantially different, usually more complicated algorithms than the simple expression we have in (4). We remark that “best of both worlds” guarantees appear in the online learning literature (e.g., Bubeck and Slivkins, 2012; Koolen et al., 2016; Zimmert and Seldin, 2021; Jin et al., 2021; Chen et al., 2023; Dann et al., 2023), where the aim is to find a single algorithm whose regret is optimal both in a stochastic setting (i.e., data sampled from a distribution) and in an adversarial setting. A crucial difference, however, is that our paper’s guarantees are concerned with inference and predictive coverage, rather than with estimation or regret.

Farther afield from our work, there have been several other explorations of conformal prediction in time-series, but these are quite different. For example, the works of Barber et al. (2022) and Chernozhukov et al. (2018) provide conformal-type procedures with coverage guarantees under certain relaxations of exchangeability; both can provide marginal coverage in Setting 2, but cannot give any guarantees in Setting 1. Xu and Xie (2021, 2023) study the behavior of conformal methods under classical nonparametric assumptions such as model consistency and distributional smoothness for its validity, and thus cannot give distribution-free guarantees in Settings 1 or 2. Lin et al. (2022) studies the problem of cross-sectional coverage for multiple exchangeable time-series. The online conformal prediction setup was also considered early on by Vovk (2002) for exchangeable sequences. These works are not directly comparable to ours, the primary point of difference being the adversarial guarantee we can provide in Setting 1.

Finally, traditional solutions to the prediction set problem have historically relied on Bayesian modeling (e.g., Foreman-Mackey et al., 2017) or distributional assumptions such as autoregression, smoothness, or ergodicity (e.g., Biau and Patra, 2011). A parallel literature on calibration exists in the adversarial sequence model (e.g., Foster and Vohra, 1998). Our work, like that of Gibbs and Candes (2021), is clearly related to the literatures on both calibration and online convex optimization (Zinkevich, 2003), and we hope these connections will continue to reveal themselves; our work takes online conformal prediction one step closer to online learning by allowing the use of decaying step sizes, which is typical for online gradient descent.

We provide the first analysis of the online conformal prediction update in (4) with an arbitrary step size. Our analysis gives strong long-run coverage bounds for appropriately decaying step sizes, even in the adversarial setting (Setting 1). We also give a simultaneous convergence guarantee in the I.I.D. setting (Setting 2), showing that the parameter $q_{t}$ converges to the optimal value $q^{*}$. Importantly, this type of convergence does not hold with a fixed step size (the case previously analyzed in the online conformal prediction literature). In fact, we show that with a fixed step size, online conformal prediction returns meaningless prediction sets (i.e., either $\emptyset$ or $\mathcal{Y}$) infinitely often. From the theoretical point of view, therefore, our method is the first to provide this type of “best-of-both-worlds” guarantee.

While these theoretical results show an improvement (relative to the fixed-step-size method) in an I.I.D. setting, from the practical perspective we will see that a decaying step size also enables substantially better results and more stable behavior on real time series data, which lies somewhere between the I.I.D. and the adversarial regime.

Our first main result shows that, for a nonincreasing step size sequence, the long-run coverage rate

will converge to the nominal level $1-\alpha$.

As a special case, if we choose a constant step size $\eta_{t}\equiv\eta$ then this result is analogous to Gibbs and Candes (2021, Proposition 4.1). On the other hand, if we choose $\eta_{t}\propto t^{-a}$ for some $a\in(0,1)$, then the long-run coverage at time $T$ has error bounded as $\mathcal{O}(\frac{1}{T^{1-a}})$.

As discussed above, if the data appears to be coming from the same distribution then a decaying step size can be advantageous, to stabilize the behavior of the prediction sets over time. However, if we detect a sudden distribution shift and start to lose coverage, we might want to increase the step size $\eta_{t}$ to recover coverage more quickly. To accommodate this, the above theorem can be generalized to an arbitrary step size sequence, as follows.

We can see that Theorem 1 is indeed a special case of this more general result, because in the case of a nonincreasing sequence $\eta_{t}$, we have $\max_{1\leq t\leq T}\eta_{t}=\eta_{1}$, and

But Theorem 2 can be applied much more broadly. For example, we might allow the step size to decay during long stretches of time when the distribution seems stationary, but then reset to a larger step size whenever we believe the distribution may have shifted. In this case, we can obtain an interpretable error bound from the result of Theorem 2 by observing that $\|\Delta_{1:T}\|_{1}\leq\frac{2N_{T}}{\min_{1\leq t\leq T}\eta_{t}}$, where $N_{T}=\sum_{t=2}^{T}{\mathbbm{1}}_{{\eta_{t}>\eta_{t-1}}}$ is the number of times we increase the step size. Thus, as long as the step size does not decay too quickly, and the number of “resets” $N_{T}$ is $\mathrm{o}(T)$, the upper bound of Theorem 2 will still be vanishing.

To begin, we assume that the score function is pretrained, i.e., that $s_{1}=s_{2}=\dots$ are all equal to some fixed function $s:\mathcal{X}\times\mathcal{Y}\rightarrow[0,B]$. The reader should interpret this as the case where the underlying model is not updated online (e.g., $s(x,y)=|y-\hat{f}(x)|$ for a pretrained model $\hat{f}$ that is no longer being updated). This simple case is intended only as an illustration of the trends we might see more generally; in Section 3.2 below we will study a more realistic setting, where model training is carried out online as the data is collected.

In this setting, since the score function does not vary with $t$, we have $\mathsf{Coverage}_{t}(\cdot)\equiv\mathsf{Coverage}(\cdot)$ where

i.e., instantaneous coverage at time $t$ is $\mathsf{Coverage}(q_{t})$.

First, we will see that choosing a constant step size leads to undesirable behavior: while coverage will hold on average over time (as recorded in Theorem 1 and in the earlier work of Gibbs and Candes (2021)), there will be high variability in $\mathsf{Coverage}(q_{t})$ over time—for instance, we may have $\mathcal{C}_{t}(X_{t})=\emptyset$ infinitely often.

On the other hand, if we choose a sequence of step sizes $\eta_{t}$ that decays at an appropriate rate (such as $\eta_{t}\propto t^{-1/2-\epsilon}$, for some $\epsilon\in(0,1/2)$, as mentioned earlier) then over time, this highly variable behavior can be avoided. Instead, we will typically see coverage converging to $1-\alpha$ for each constructed prediction set $\mathcal{C}_{t}(X_{t})$, i.e., $\mathsf{Coverage}(q_{t})\rightarrow 1-\alpha$. We will need one more assumption: defining $q^{*}$ as the $(1-\alpha)$-quantile of $s(X,Y)$, we assume that $q^{*}$ is unique:

With an additional assumption, this immediately implies convergence of the coverage, $\mathsf{Coverage}(q_{t})$:

That is, instead of the high variance in coverage incurred by a constant step size (as in Proposition 1), here the coverage converges to the nominal level $1-\alpha$. Finally, with additional assumptions, we can also characterize the rate at which the threshold $q_{t}$ converges to $q^{*}$:

The result of Theorem 3 above is restricted to a very simple setting, where the score functions are given by $s_{t}\equiv s$ for some fixed $s$, i.e., we are using a pretrained model. We now consider the more interesting setting where the model is trained online. Formally, we consider Setting 2 where we allow the score function $s_{t}$ to depend arbitrarily on the data observed before time $t$, i.e., on $\{(X_{r},Y_{r})\}_{r<t}$.

First, we will consider a constant step size $\eta_{t}\equiv\eta$.

This result is analogous to Proposition 1 for the case of a pretrained score function (but with a slightly weaker conclusion due to the more general setting). As before, the conclusion we draw is that a constant step size inevitably leads to high variability in $\mathsf{Coverage}_{t}(q_{t})$.

On the other hand, if we take a decaying step size, Theorem 3 established a convergence result given a pretrained score function. We will now see that similar results hold in for the online setting as long as the model converges in some sense. In many settings, we might expect $s_{t}$ to converge to some score function $s$—for example, if our fitted regression functions, $\hat{f}_{t}$, converge to some “true” model $f^{*}$, then $s_{t}(x,y)=|y-\hat{f}_{t}(x)|$ converges to $s(x,y)=|y-f^{*}(x)|$. As before, we let $\mathsf{Coverage}(q)=\mathbb{P}_{{P}}\left({s(X,Y)\leq q}\right)$, and write $q^{*}$ to denote the $(1-\alpha)$-quantile of this distribution. We now extend the convergence results of Theorem 3 to this setting.

As in the previous section, an additional assumption implies convergence of the coverage, $\mathsf{Coverage}_{t}(q_{t})$:

To summarize, the results of this section show that the coverage of each prediction set $\mathcal{C}_{t}(X_{t})$, given by $\mathsf{Coverage}_{t}(q_{t})$, will converge even in a setting where the model is being updated in a streaming fashion, as long as the fitted model itself converges over time.

In particular, if we choose $\eta_{t}\propto t^{-1/2-\epsilon}$ for some $\epsilon\in(0,1/2)$, then in the adversarial setting the long-run coverage error is bounded as $\mathcal{O}(\frac{1}{T^{1/2-\epsilon}})$ by Theorem 1, while in the I.I.D. setting, Theorem 4 guarantees convergence. In other words, this choice of $\eta_{t}$ simultaneusly achieves both types of guarantees.

While the results of this section have assumed I.I.D. data, the proof techniques used here can be extended to handle broader settings—for example, a stationary time series, where despite dependence we may still expect to see convergence over time. We leave these extensions to future work.

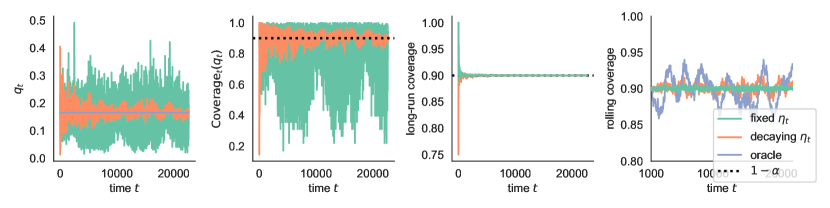
Figures 2 and 2 display the results of the experiment for the Elec2 data and the Imagenet data, respectively. We now discuss our findings.

The Elec2 (Harries et al., 1999) dataset is a time-series of 45312 hourly measurements of electricity demand in New South Wales, Australia. We use even-numbered time points as the time series, and odd-numbered time points as a holdout set for estimating $\mathsf{Coverage}_{t}(q_{t})$. The demand measurements are normalized to lie in the interval $Y_{t}\in[0,1]$. The covariate vector $X_{t}=(Y_{1},\ldots,Y_{t-1})$ is the sequence of all previous demand values. The forecast $\hat{Y}_{t}$ is one-day-delayed moving average of $Y_{t}$ (i.e., at time $t$, our predicted value $\hat{Y}_{t}$ is given by the average of observations taken between 24 and 48 hours earlier), and the score is $s_{t}(X_{t},Y_{t})=|Y_{t}-\hat{Y}_{t}|$.

The Imagenet (Deng et al., 2009) is a standard computer vision dataset of natural images. We take the 50000 validation images of Imagenet 2012 and treat them as a time series for the purpose of evaluating our methods. Because the validation split of Imagenet is shuffled, this comprises an exchangeable time series. We use 45000 points for the time series, and the remaining 5000 points as a holdout set for estimating $\mathsf{Coverage}_{t}(q_{t})$. As the score function, we use $s_{t}(X_{t},Y_{t})=1-\max_{y\in\mathcal{Y}}\hat{f}(X_{t})_{y}$ (here $\max_{y\in\mathcal{Y}}\hat{f}(X_{t})_{y}$ is the softmax score of the pretrained ResNet-152 model).

As discussed in Section 2.2, in applications where the distribution of the data may drift or may have changepoints, it might be beneficial to allow $\eta_{t}$ to increase at times to allow for updates in the learning process. To study this empirically, in the Appendix, we include additional experiments in a broader range of settings—we test over 3000 real datasets, and compare the fixed step size method, the decaying step size method, and a “decay+adapt” version of our method where the sequence $\eta_{t}$ adapts to trends in the data (decaying if the distribution of the data appears stationary, but increasing if distribution shift is detected).

First, we need a lemma to verify that the values $q_{t}$ are uniformly bounded over all $t$. This result is essentially the same as that in Lemma 4.1 of Gibbs and Candes (2021), except extended to the setting of decaying, rather than constant, step size. The proof is given in the Appendix.

We are now ready to prove the theorems. As discussed earlier, Theorem 1 is simply a special case, so we only prove the more general result Theorem 2.

By definition of $\Delta$, we have $\eta_{t}^{-1}=\sum_{r=1}^{t}\Delta_{r}$ for all $t\geq 1$. We then calculate

where the last step holds since $q_{r},q_{T+1}$ are bounded by Lemma 1.

First we prove that $\lim\sup_{t\rightarrow\infty}\mathsf{Coverage}_{t}(q_{t})=1$ almost surely. Equivalently, for any fixed $\epsilon>0$, we need to prove that $\mathbb{P}\left({\lim\sup_{t\rightarrow\infty}\mathsf{Coverage}_{t}(q_{t})<1-\epsilon}\right)=0$.

We begin by constructing a useful coupling between the online conformal process, and a sequence of I.I.D. uniform random variables. For each $t\geq 1$, define

drawn independently for each $t$ after conditioning on all the data, $\{(X_{t},Y_{t})\}_{t\geq 1}$. Since $\mathbb{P}\left({Y_{t}\in\mathcal{C}_{t}(X_{t})}\ \middle|\ {\{(X_{r},Y_{r})\}_{r<t}}\right)=\mathsf{Coverage}_{t}(q_{t})$ by construction, we can verify that $U_{t}\stackrel{{\scriptstyle\textnormal{iid}}}{{\sim}}\mathsf{Uniform}[0,1]$.

Next fix any integer $N\geq\frac{B+\eta\alpha}{\eta(1-\alpha)}$. Let $A_{i}$ be the event that

Since the $U_{t}$’s are I.I.D. uniform random variables, we have $\mathbb{P}\left({A_{i}}\right)=\epsilon^{N}$ for each $i$, and the events $A_{i}$ are mutually independent. Therefore, by the second Borel–Cantelli lemma, $\mathbb{P}\left({\sum_{i\geq 1}{\mathbbm{1}}_{{A_{i}}}=\infty}\right)=1$. Now we claim that

Suppose that $A_{i}$ holds and that $\mathsf{Coverage}_{t}(q_{t})\leq 1-\epsilon$ for all $t$ in the range $(i-1)N<t\leq iN$. Then by construction of the $U_{t}$’s, we have $Y_{t}\not\in\mathcal{C}_{t}(X_{t})$ for all $(i-1)N<t\leq iN$. Therefore by (4),

where the last step holds by our choice of $N$, together with the fact that $q_{(i-1)N+1}\geq-\alpha\eta$ by Lemma 1. But since the score function $s_{iN+1}$ takes values in $[0,B]$ by assumption, we therefore have $\mathsf{Coverage}_{iN+1}(q_{iN+1})\geq\mathsf{Coverage}_{iN+1}(B)=1$. Therefore, we have verified the claim (9).

Since $A_{i}$ occurs for infinitely many $i$, almost surely, by (9) we therefore have $\lim\sup_{t\rightarrow\infty}\mathsf{Coverage}_{t}(q_{t})\geq 1-\epsilon$, almost surely, as desired. Since $\epsilon>0$ is arbitrary, this completes the proof that $\lim\sup_{t\rightarrow\infty}\mathsf{Coverage}_{t}(q_{t})=1$ almost surely.

Finally, a similar argument verifies $\lim\inf_{t\rightarrow\infty}\mathsf{Coverage}(q_{t})=0$ almost surely.

Since $s_{t}\equiv s$, we have $\mathsf{Coverage}_{t}(q_{t})=\mathsf{Coverage}(q_{t})$, for each $t$. By Proposition 3, $\lim\inf_{t\rightarrow\infty}\mathsf{Coverage}(q_{t})=0$ and $\lim\sup_{t\rightarrow\infty}\mathsf{Coverage}(q_{t})=1$, almost surely. Since we have assumed that $\alpha$ is a rational number, by the definition of the procedure (4), all values $q_{t}$ must lie on a discrete grid (i.e., if $\alpha=k/K$ for some integers $k,K$ then, for all $t$, $q_{t}-q_{1}$ must be an integer multiple of $\eta/K$). Moreover, by Lemma 1, $q_{t}$ is uniformly bounded above and below for all $t$, so $q_{t}$ can only take finitely many values. This implies $\mathsf{Coverage}(q_{t})$ also can take only finitely many values, and in particular, this means that if $\lim\inf_{t\rightarrow\infty}\mathsf{Coverage}(q_{t})=0$ (respectively, if $\lim\sup_{t\rightarrow\infty}\mathsf{Coverage}(q_{t})=1$) then $\mathsf{Coverage}(q_{t})=0$ (respectively, $\mathsf{Coverage}(q_{t})=1$) for infinitely many $t$.

We observe that Theorem 3 is simply a special case of Theorem 4 (obtained by taking $s_{t}\equiv s$ for all $t$), so we only need to prove Theorem 4.

First, consider the sequence

Define events $\mathcal{E}_{Z}$, the event that $\lim_{t\rightarrow\infty}Z_{t}$ exists, and $\mathcal{E}_{s}$, the event that $s_{t}\stackrel{{\scriptstyle\textnormal{d}}}{{\rightarrow}}s$. In the Appendix, we will verify that

i.e., $\mathbb{P}\left({\mathcal{E}_{Z}}\right)=1$, using martingale theory.

To establish the theorem, then, it suffices for us to verify that on the event $\mathcal{E}_{Z}\cap\mathcal{E}_{s}$, it holds that $q_{t}\rightarrow q^{*}$. From this point on, we assume that $\mathcal{E}_{Z}$ and $\mathcal{E}_{s}$ both hold.

Fix any $\epsilon>0$. Since $q\mapsto\mathsf{Coverage}(q)$ is monotone, it can have at most countably infinitely many discontinuities. Without loss of generality, then, we can assume that this map is continuous at $q=q^{*}-\epsilon/3$ and at $q=q^{*}+\epsilon/3$ (by taking a smaller value of $\epsilon$ if needed).

First, since $Z_{t}$ converges, we can find some finite time $T_{1}$ such that

Moreover, since $\sum_{t}\eta_{t}^{2}<\infty$, we have $\eta_{t}\rightarrow 0$ and so we can find some finite time $T_{2}$ such that $\eta_{t}\leq\frac{\epsilon}{3}$ for all $t\geq T_{2}$. Furthermore, on $\mathcal{E}_{s}$, we have $\mathsf{Coverage}_{t}(q)\rightarrow\mathsf{Coverage}(q)$, at each $q=q^{*}\pm\epsilon/3$. Thus we can find some finite time $T_{3}$ and some $\delta>0$ such that

for all $t\geq T_{3}$ (we are using the fact that $\mathsf{Coverage}(q^{*}-\epsilon/3)<1-\alpha$ by (6)). Similarly we can find a finite $T_{4}$ and some $\delta^{\prime}>0$ such that $\mathsf{Coverage}_{t}(q^{*}+\epsilon/3)\geq 1-\alpha+\delta^{\prime}$ for all $t\geq T_{4}$. Let $T=\max\{T_{1},T_{2},T_{3},T_{4}\}$.

We will now split into cases. If it does not hold that $q_{t}\in q^{*}\pm\epsilon$ for all sufficiently large $t$, then one of the following cases must hold:

• •

  Case 1a: $q_{t}<q^{*}-\epsilon/3$ for all $t\geq T$.

• •

  Case 1b: $q_{t}>q^{*}+\epsilon/3$ for all $t\geq T$.

• •

  Case 2a: for some $t^{\prime}\geq t\geq T$, it holds that $q_{t}\geq q^{*}-\epsilon/3$ and $q_{t^{\prime}}<q^{*}-\epsilon$.

• •

  Case 2b: for some $t^{\prime}\geq t\geq T$, it holds that $q_{t}\leq q^{*}+\epsilon/3$ and $q_{t^{\prime}}>q^{*}+\epsilon$.

The authors thank Isaac Gibbs, Ryan Tibshirani, and Margaux Zaffran for helpful feedback on this work. R.F.B. was partially supported by the National Science Foundation via grant DMS-2023109, and by the Office of Naval Research via grant N00014-20-1-2337.