One-dimensional $\mathbb{Z}$-classified topological crystalline insulator under space-time inversion symmetry

Introduction. Crystalline symmetry plays an important role in classifying topological insulators [1, 2, 3, 4, 5, 6], complementary to the three intrinsic symmetries (i.e. chiral, time-reversal, and particle-hole symmetries). Tremendous topological states protected by crystalline symmetries, known as topological crystalline insulators (TCIs), have been explored [1, 2, 3, 4, 5, 6, 7]. In recent years, systematic search for TCIs has been achieved by analyzing high-symmetry points in momentum space and chemical orbitals in real space [2, 3]. TCIs exhibit nontrivial topological properties such as corner states [8, 9], quantized multipole moments [9, 10], non-Abelian topological charges [6, 11, 12, 13], and period-multiplied Bloch oscillations [14, 15]. These properties show that crystalline symmetries introduce richer topological structures, and may have promising applications in spintronics, quantum computing, and novel electronic devices.

In one dimension (1D), the inversion symmetry is essential for realizing TCI [16, 16, 17, 18, 19, 20, 21]. Given a gapped band, the polarization $p$ related to the Berry-Zak phase is widely used as a $\mathbb{Z}_{2}$-quantized invariant to characterize different 1D TCIs [22, 23, 24, 25, 20, 26], though it may fail to predict the bulk-edge correspondence [27]. For composite multiple bands, one can utilize the inversion eigenvalues at high-symmetry points or the Wilson loop to identify a non-negative integer invariant $\mathbb{Z}^{\geq}$ [16, 17, 10, 28]. In the presence of chiral symmetry, it is well known that the band topology in 1D transcends $\mathbb{Z}_{2}$ classification and falls into the $\mathbb{Z}$ classification, which can be characterized by the chiral winding number [29, 30]. Notably, it has been discovered that the chiral winding number can be equivalently expressed as the polarization difference between the two sublattices (or orbitals) [31, 32, 33], offering a more fundamentally physical perspective on comprehending 1D chiral-symmetric topological insulators. The number of in-gap zero modes is proportional to the chiral winding number, meaning that nontrivial relative polarization between sublattices can give rise to nontrivial boundary states. Therefore, in the absence of chiral symmetry, a natural question arises: Can nontrivial relative inter-sublattice polarization exist as a result of crystalline symmetry and further categorize the band topology in 1D?

In this Letter, we present a theory demonstrating that, under space-time inversion symmetry, exotic topological structures can exist in a large family of 1D TCIs. Space-time inversion symmetry, referring to the combination of inversion symmetry and time-reversal symmetry, is expressed by

$\displaystyle{\cal I\cal T}H\left(k\right){\left({{\cal I\cal T}}\right)^{-1}}=H\left(k\right),$

(1)

where $k$ is the quasi momentum, $\mathcal{I}$ denotes the space-inversion operator and ${\cal T}$ represents the time-reversal operator. The space-time inversion symmetry imposes constraints on the Bloch Hamiltonian and its eigenvectors locally within the momentum space. This phenomenon brings internal topological structures to the Bloch states, enabling a substantial classification of band topology within 1D TCIs. Our work gives insights into systematic exploration of TCIs with hidden topological structures in higher dimensions.

Three-band model and inversion winding number. We consider a simple but general three-band model with space-time inversion symmetry (1). Its Hamiltonian matrix and inversion operator are given by

$$H\left(k\right)=\left({\begin{array}[]{*{20}{c}}{{\Delta_{k}}}&{{g_{k}}}&{{h_{k}}}\\ {{g_{k}}^{*}}&{-{\Delta_{k}}}&{{g_{k}}}\\ {{h_{k}}^{*}}&{{g_{k}}^{*}}&{{\Delta_{k}}}\end{array}}\right),\;\;{\cal I}=\left({\begin{array}[]{*{20}{c}}{0}&{0}&1\\ {0}&1&{0}\\ 1&{0}&{0}\end{array}}\right),$$

(2)

with $g_{k},h_{k}\in\mathbb{C}$ being complex parameters and $\Delta_{k}\in\mathbb{R}$ being real parameter. The time-reversal operation on the Bloch Hamiltonian here is the complex conjugation operation: ${\cal T}H(k){\cal T}^{-1}={H(k)}^{*}$. Clearly, this model has no chiral symmetry. Due to the space-time inversion symmetry, the eigenvector of $H(k)$ can be written as a general form

$${\bm{u}_{k}}={\left({\begin{array}[]{*{20}{c}}{{\alpha_{k}}{e^{-i{\xi_{k}}}}}&{{\beta_{k}}{e^{-i\frac{{{\xi_{k}}}}{2}}}}&{{\alpha_{k}}^{*}}\end{array}}\right)^{\rm{T}}}$$

(3)

with $\xi_{k}\in[0,2\pi)$, $\alpha_{k}\in\mathbb{C}$ and $\beta_{k}\in\mathbb{R}$. For simplicity, we have omitted the band index and assumed that all bands are gapped. Under the inversion transformation, we have ${\left({{\cal I}{\bm{u}_{k}}}\right)^{*}}={e^{i{\xi_{k}}}}{\bm{u}_{k}}$. In particular, the first and third sublattices are related by a space-time inversion operation, and the phase factor associated with $\xi_{k}$ cannot be gauged out. This leads to the possible presence of nontrivial topological structures among the sublattices.

It is important to note that, in 1D chiral-symmetric topological insulators, the polarization difference between two sublattices can lead to nontrivial polarizations and charge accumulations at the edge [31, 33, 34]. This phenomenon is associated with the chiral winding number belonging to the $\mathbb{Z}$ class. Thus, in the 1D TCIs with space-time inversion symmetry, we define a gauge-invariant winding number via the sublattice polarization difference between the first and the third sublattice,

$\displaystyle\nu=\frac{1}{{\pi i}}\int_{0}^{2\pi}{dk\;\left[{\frac{{\langle{u_{k}}|\frac{\partial}{{\partial k}}\left({{{\hat{P}}_{3}}-{{\hat{P}}_{1}}}\right){u_{k}}\rangle}}{{\langle{u_{k}}|{{\hat{P}}_{1}}+{{\hat{P}}_{3}}|{u_{k}}\rangle}}}\right]},$

(4)

where ${{\hat{P}}_{\sigma}}=\sum\nolimits_{k}{|k,\sigma\rangle\langle k,\sigma|}$ is the projector onto the $\sigma=1,2,3$ sublattice with $|k,\sigma\rangle$ being the basis of the momentum space, and ${\langle{u_{k}}|{{\hat{P}}_{1}}+{{\hat{P}}_{3}}|{u_{k}}\rangle}$ denotes the normalization factor. Due to the inversion symmetry, one can find ${\langle{u_{k}}|{{\hat{P}}_{1}}|{u_{k}}\rangle}={\langle{u_{k}}|{{\hat{P}}_{3}}|{u_{k}}\rangle}$. This gauge-invariant quantity is quantized to integers $\nu\in\mathbb{Z}$ and it is directly related to the quantized polarization such that $p=\nu/2\mod 1$ [35]. It is worth noting that the inversion winding number shares some similarities with the mirror Chern number, where the difference of the Chern number between the two sectors having different mirror eigenvalues constitutes the mirror Chern number [36, 37]. In our study, the inversion winding number is obtained via projection onto the two inversion-symmetric sublattices.

Below we discuss the topological stability of the defined inversion winding number (4). It can be found that the inversion winding number becomes ill-defined when $\alpha_{k}=0$ in Eq. (3). To change the value of the inversion winding number, the system must pass this singular point. To find in what condition that $\alpha_{k}=0$, we solve the eigenvalue equation $H(k)u_{k}=E_{k}u_{k}$ by assuming $\alpha_{k}=0$. We find that $g_{k}=0$ is necessary for $\alpha_{k}=0$. It can be concluded that, to change the inversion winding number, one must either break the space-time inversion symmetry, close the spectral gap, or introduce certain terms to ensure that $g_{k}=0$. Generally speaking, the topological protection in TCIs manifests that the target system cannot be adiabatically connected to other distinct TCI phases without closing the spectral gap and breaking the underlying symmetry. In this sense, the inversion winding number here seems unstable, as it may possibly change through tuning $g_{k}=0$. Nevertheless, the inversion winding number is related to the polarization via $p=\nu/2\mod 1$. Strictly speaking, the parity of the inversion winding number is a $\mathbb{Z}_{2}$ topological invariant. Although the inversion winding number becomes ill-defined when $\alpha_{k}=0$, it is still possible to introduce perturbations to ensure that $g_{k}\neq 0$, thereby avoiding this singular point.

Fortunately, the condition $g_{k}\neq 0$ for avoiding the singular point naturally arises in most realistic systems. As the parameter ${g_{k}}\propto\sum\nolimits_{j\leq j^{\prime}}{t_{j,j^{\prime}}^{\sigma,\sigma^{\prime}}{e^{ik\left({j-j^{\prime}}\right)}}}$ describes the coupling strength between $\sigma=\{1,3\}$ and $\sigma^{\prime}=2$ sublattices in momentum space, one can find that $g_{k}=0$ physically requires some very special tunneling terms in real space. Here, $t_{j,j^{\prime}}^{\sigma,\sigma^{\prime}}$ represents the tunneling strength from the $\sigma$ sublattice in the $j$th cell to the $\sigma^{\prime}$ sublattice in the $j^{\prime}$th cell in real space. For example, if we set $g_{k}=0$ for all $k\in\rm{B.Z.}$, some certain lattices become completely isolated, resulting in the system being in the atomic limit. Therefore, we can assert that by excluding those specific conditions to ensure that $g_{k}\neq 0$, the inversion winding number remains topologically stable. This argument remains valid for a large family of systems, offering a more comprehensive classification for space-time inversion-invariant systems. Later, we will provide some evidence to support this point.

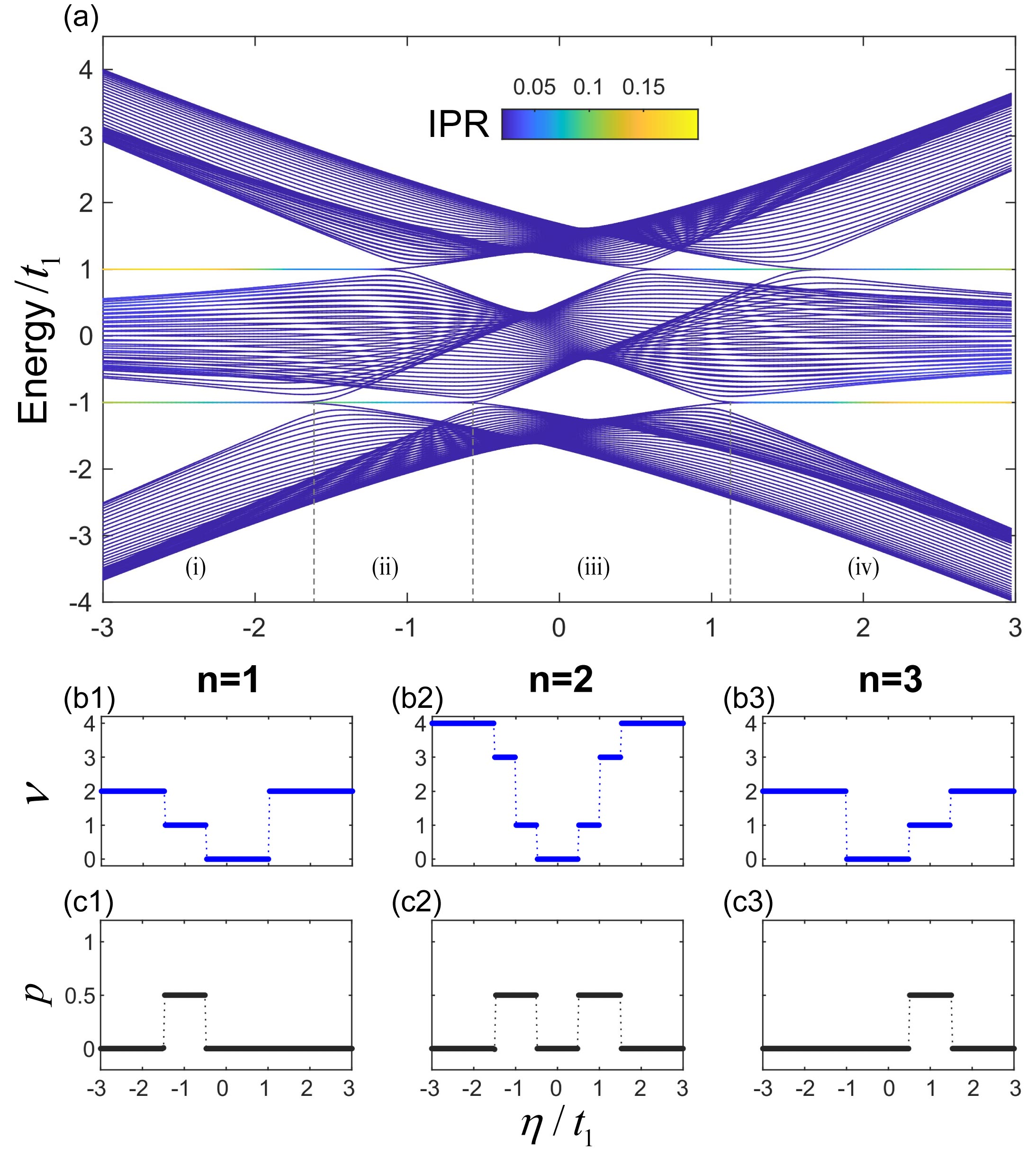
Prototypical model and bulk-edge correspondence. To show the validity of the defined inversion winding number and demonstrate its $\mathbb{Z}$ classification, we choose $g_{k}=-t_{1}$, $h_{k}=-t_{2}e^{-ik}-\eta e^{-2ik}$ and $\Delta_{k}=0$, which corresponds to a system with long-range tunneling in real space. The real-space formulation of this model can be found in Supllementary Material. By varying $\eta/t_{1}$, the spectrum under open boundary condition (OBC) is shown in Fig. 1 (a), comprising three bands labeled as $n=1,2,3$ from the bottom to the top. In both the first and second band gaps, several in-gap states appear. These in-gap states correspond to edge states that are exponentially localized near the two boundaries. To better elucidate the results, we concentrate on the lowest gap and designate four regions (i-iv) separated by gap-closing points and delve into its topological properties. Intriguingly, there are three different phases. We find that the in-gap edge states exhibit a four-fold degeneracy in regions (i) and (iv), and a two-fold degeneracy in region (ii). In region (iii), there is no in-gap edge state. This suggests that these three regions are three distinct phases.

Subsequently, we calculate the inversion winding number (4) under the periodic boundary condition (PBC), see Figs. 1 (b1-b3). Remarkably, the inversion winding number identifies more distinct phases and its variation coincides with the locations of gap-closing points. Under the OBC, the number of edge states closely relates to the inversion winding number of the adjacent bands. For instance, the numbers of in-gap edge states in the first and second gaps are respectively proportional to the inversion winding numbers of the first ($n=1$) and third ($n=3$) bands: $N_{{\rm{edge}}}^{\#1}=2|{\nu_{1}}|$ and $N_{{\rm{edge}}}^{\#2}=2|{\nu_{3}}|$, where $N_{{\rm{edge}}}^{\#m}$ and $\nu_{n}$ respectively denote the number of edge states in the $m$th gap and the inversion winding number of the $n$th band. Regarding the second band ($n=2$), its inversion winding number is the sum of the first and third bands: $\nu_{2}=\nu_{1}+\nu_{3}$, and the change of this inversion winding number requires the closing of either the first or the second band gap. It can be further deduced that the nontrivial topology of the second band contributes to the emergence of in-gap edge states in both band gaps.

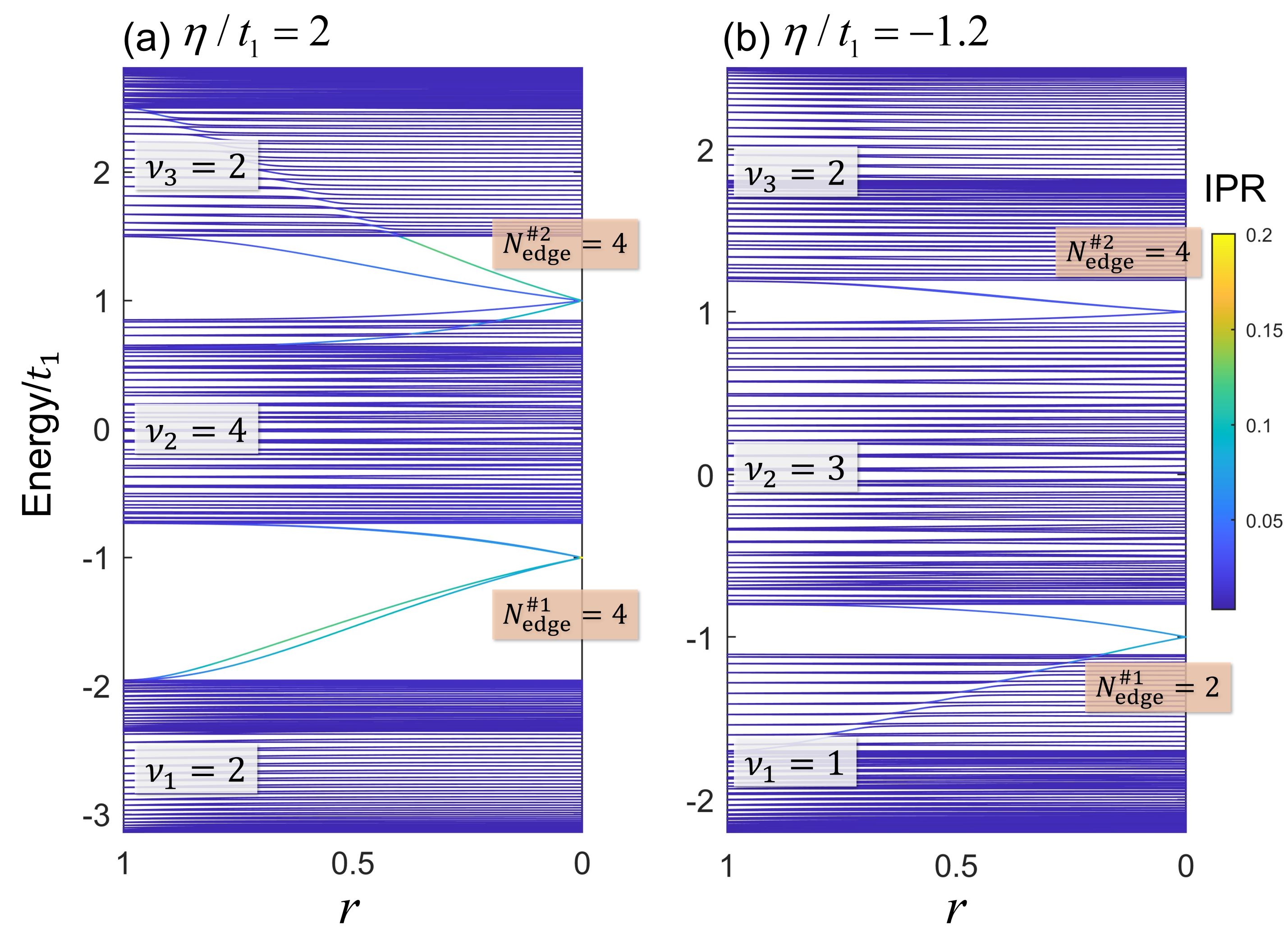
To elucidate the bulk-edge correspondence more profoundly, we consider a continuous connection between the PBC and the OBC. This transition can be effectively modeled by introducing a real-valued parameter $r\in[0,1]$ to the tunneling: $t_{j,j^{\prime}}^{\sigma,\sigma^{\prime}}\to rt_{j,j^{\prime}}^{\sigma,\sigma^{\prime}}$ when $j,j^{\prime}$ crosses the boundary under PBC. Thereby, $r=1$ corresponds to the PBC, while $r=0$ corresponds to the OBC, which allows the emergency of edge states. As depicted in Fig. 2 (a-b), edge states arise from the two adjacent bands, with their number related to the inversion winding number. The number of edge states arising from the second band is equal to the number of edge states arising from the other two bands. These findings not only reveal a more extensive classification of the band topology protected by the space-time inversion symmetry, but also well demonstrate the nature of bulk-edge correspondence for the inversion winding number. More discussions about the bulk-edge correspondence can be found in the Supplementary Material [35].

For comparison, we calculate the polarization for each band, as shown in Figs. 1 (c1-c3). Generally, the emergence of in-gap edge states is expected as a result of non-zero band polarization, which can be calculated using the Berry-phase formalism under PBC [38, 39]: $p_{n}=1/2\pi\int_{{\rm{B}}.{\rm{Z}}.}{dk\;\langle{u^{n}_{k}}|i\partial{u^{n}_{k}}\rangle}\mod 1$, with $n$ being the band index. The polarization provides insights into the center of Wannier function within a unit cell [40]. Owing to the space-time inversion symmetry, the polarization for each gapped band is quantized to either $p_{n}=0$ or $p_{n}=1/2$ [41], which has been widely employed to distinguish the band topology. However, as shown by the numerical results, the polarization is unable to explain the presence of the four-fold degenerate edge states observed above. Therefore, unlike the defined inversion winding number, the polarization fails to identify the rich band topology.

Robustness of inversion winding number. Having established the momentum-space formula of inversion winding number, we then delve into exploring its real-space counterpart to assess the robustness of band topology against disorder that preserves the space-time inversion symmetry. In analogy to the chiral-symmetric system [33, 42], the real-space formula of the inversion winding number can be expressed as a Bott index form,

$$\nu=-\frac{1}{{2\pi}}{\mathop{\rm Im}\nolimits}\left\{{{\rm{Tr}}\left[{{\rm{log}}\left({{{\cal X}_{1}}^{\dagger}{{\cal X}_{3}}}\right)}\right]}\right\},$$

(5)

in which ${{\cal X}_{\sigma}}={{\bf{\Psi}}^{\dagger}}\exp\left({i\frac{{2\pi}}{L}\hat{x}}\right){{\hat{P}}_{\sigma}}{\bf{\Psi}}$ is the projected-position matrix of the $\sigma=1,3$ sublattices and ${\bf{\Psi}}=\left({\cdots,|{\psi_{j}}\rangle,\cdots}\right)$ denotes a set of eigenstates on the target band. Eq. (5) is equivalent to the momentum-space formula in the presence of translation symmetry [35].

The real-space formula enables us to efficiently calculate the inversion winding number in the presence of inversion-invariant disorder. Here, we introduce disorders to the nearest-neighbor tunneling between the first and third sublattice: ${{\hat{H}}_{dis}}=-W\sum\nolimits_{j}{{\delta_{x}}|x,1\rangle\langle x,3|}+{\rm{H.c.}}$, wherein $\delta_{x}\in[-1/2,1/2]$ represents a uniformly distributed random variable and $W$ is the strength of disorder. Here, $|x,\sigma\rangle,x=1,2,\cdots,L$ denotes the position basis. To preserve the space-time inversion symmetry, we enforce $\hat{\mathcal{I}}{{\hat{H}}_{dis}}\hat{\mathcal{I}}^{-1}={\left({{{\hat{H}}_{dis}}}\right)^{*}}$. Meanwhile, this term only entails the coupling between the sublattices $\sigma=1$ and $\sigma=3$. As mentioned earlier, the inversion winding number retains its well-defined nature as long as $t_{1}\neq 0$ in this system.

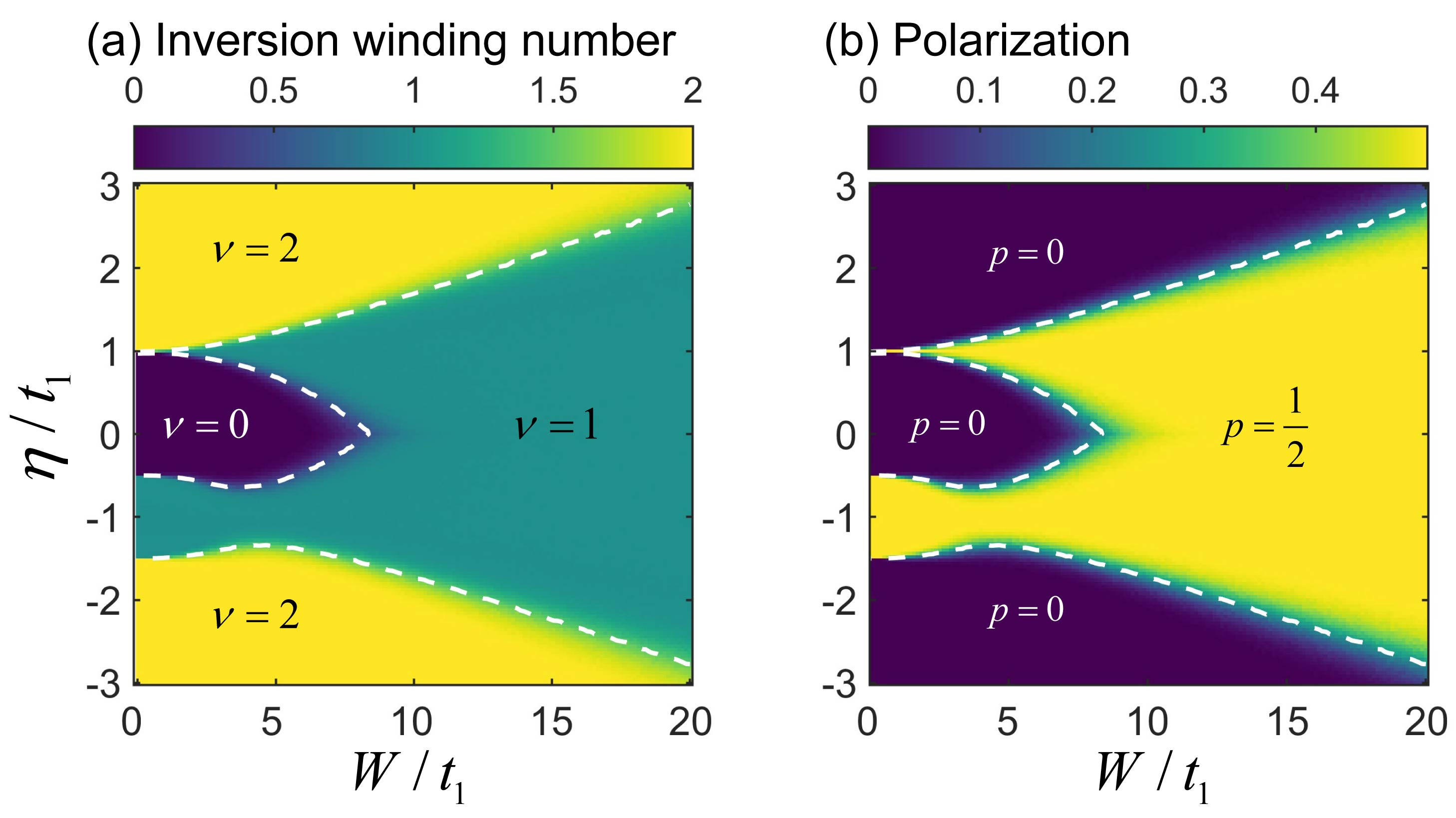
Subsequently, by utilizing Eq. (5), we calculate the $\eta$-$W$ phase diagram of inversion winding number for the lowest band under PBC, see Fig. 3 (a). Remarkably, the real-space formula yields a quantized value in every random realization. For weak disorder strength ($W/t_{1}\ll 1$), the first band gap remains finite and the fluctuations of the inversion winding number are nearly zero, as shown in Figs. 3 (c) and (d). As the disorder strength intensifies, we observe the emergence of a disorder-induced topological transition. Particularly, there is the disorder-induced topological phase ($\nu=0\to\nu=1$), which is identified as the topological Anderson insulating phase [43, 44, 45, 32, 46, 47, 48]. Significant statistical fluctuations in the inversion winding number are observed around all phase transitions. Away from the phase transition points, the inversion winding number remains remarkably stable in broad areas for different random realizations. More detailed discussions, including the evidence for bulk-edge correspondence, can be found in the Supplementary Material [35].

For comparison, we calculate the polarization through the projected position operator methods [49, 10, 50], as shown in Fig. 3 (b). Due to the inversion symmetry, the polarization is also quantized. The polarization $p$ is connected to the inversion winding number $\nu$ through the relation $p=\nu/2\mod 1$. As expected, the polarization fails to distinguish the phase of $\nu=0$ and 2.

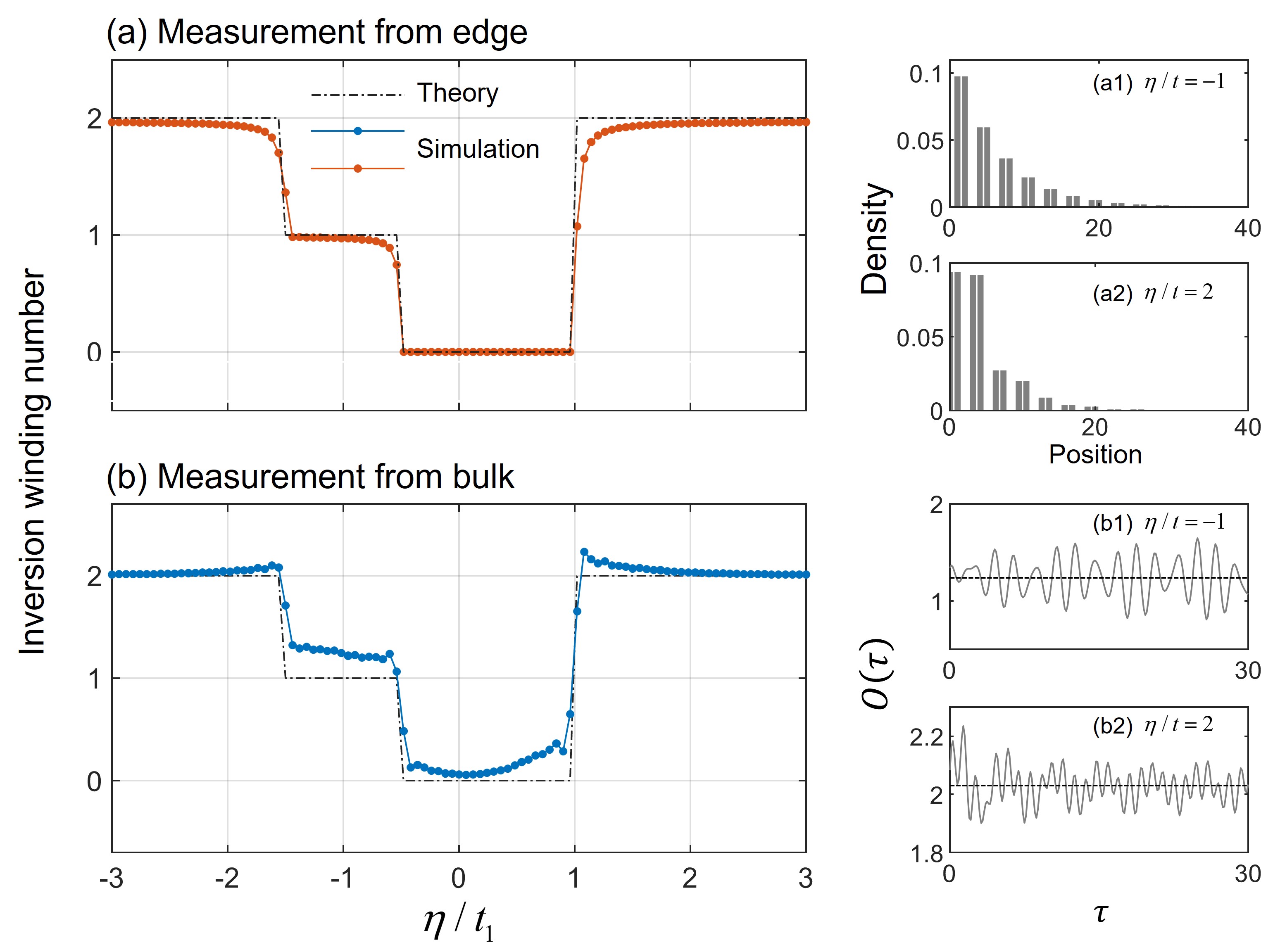
Real-space characterization of band topology. In above, we have found that the inversion winding number is associated with the polarization difference between two sublattices. This offers the feasibility for experimentally characterizing different topological phases. Under the OBC, the inversion winding number can be approximately extracted from bulk states or edge states via

$$\nu=(-1)^{\chi}\frac{2}{L}\sum\limits_{n\in{\rm{target}}}{\frac{{\langle{\psi_{n}}|{{\hat{X}}_{3}}-{{\hat{X}}_{1}}|{\psi_{n}}\rangle}}{{\langle{\psi_{n}}|{{\hat{P}}_{3}}+{{\hat{P}}_{1}}|{\psi_{n}}\rangle}}}$$

(6)

in which $\hat{X}_{\sigma}=\hat{x}\hat{P}_{\sigma}$ is the position operator projected to the $\sigma=\{1,2,3\}$ sublattice. Eq. (6) is a summation over bulk states in a certain band ($\chi=1$) or edge states in a certain gap ($\chi=0$). It implies that one can measure the inversion winding number through the bulk or the edge states. In experiments, the edge states can be probed via versatile approaches and then the information of inversion winding number can be directly extracted. As for the bulk state, it is also feasible to measure the winding number through time-evolution [51, 32, 52, 53, 54, 55, 56]: $\nu\approx\mathrm{lim}_{T\to\infty}\frac{1}{T}\int_{0}^{T}{d\tau\;O\left(\tau\right)}$ with $O\left(\tau\right)=\frac{{\langle\Psi\left(\tau\right)|{{\hat{X}}_{3}}-{{\hat{X}}_{1}}|\Psi\left(\tau\right)\rangle}}{{\langle\Psi\left(\tau\right)|{{\hat{P}}_{3}}+{{\hat{P}}_{1}}|\Psi\left(\tau\right)\rangle}}$ and $|\Psi\left(\tau\right)\rangle$ being a superposition of bulk states in a certain band. In Fig. 4, we present our numerical simulation for the experimental measurement through edge states or bulk states [35]. Remarkably, both methods produces a very prominent results compared with the theoretical prediction. The tiny difference between them can be attributed to the finite-size effect and the relatively small spectral gap, especially for bulk measurement. This again highlights the bulk-edge correspondence principle in this system: the appearance of in-gap edge state is a result of the nontrivial sublattice polarization of a band. The nontrivial inversion winding number has prominent physical consequences. The above results can be verified in various systems, such as, electrical circuits [57, 58], acoustic systems [59, 60] and other photonic or atomic systems [61, 26, 62, 63, 64, 64, 65, 21, 55, 11, 66].

Summary and discussion. We uncover that, under the space-time inversion symmetry, the band topology can be further classified beyond the conventional $\mathbb{Z}_{2}$ classification in a large family of 1D three-band models. Based upon the sublattice polarization difference from the space-time inversion symmetry, we introduce a gauge-invariant winding number: the inversion winding number. The bulk topology and the bulk-edge correspondence can be well characterized by the inversion winding number $\nu\in\mathbb{Z}$. In addition, we give a real-space formula for the inversion winding number. We also find that the inversion winding number remains effective even in the presence of strong symmetry-invariant disorders. With the real-space formula for the inversion winding number, one can experimentally identify distinct topological phases in TCIs.

This work is supported by the National Key Research and Development Program of China (Grant No. 2022YFA1404104), the National Natural Science Foundation of China (Grant No. 12025509, Grant No. 12247134 and Grant No. 12275365), and the Natural Science Foundation of Guangdong Province (Grant No.2023A1515012099).