On uniqueness of elastic scattering from a cavity
Abstract
The paper considers direct and inverse elastic scattering from a cavity in homogeneous medium with Dirichlet and Neumann boundary conditions. For direct scattering, existence and uniqueness are derived by variation approach. For inverse scattering, Frchet derivatives of the solution operators are investigated, which give local stability for Dirichlet case.
keywords:
elastic cavity , variation formulation , Navier equations , existence , uniquenessMSC:
35P25 , 35A15 , 35R30[inst1]organization=School of Mathematical Sciences,addressline=Zhejiang University, city=Hangzhou, postcode=310058, country=P. R. China
[inst2]organization=School of Mathematical Sciences and Institute of Natural Sciences,addressline=Shanghai Jiao Tong University, city=Shanghai, postcode=200240, country=P. R. China
1 Introduction
In this paper, we consider a time-harmonic plane elastic wave incident on a cavity which can be regarded as a local perturbation below the plane with wide-ranging applications as engine inlet ducts, cracks, gaps and so on.
For electromagnetic incident waves, there are considerable research results in literature. For instance, Ammari, Bao and Wood proved uniqueness and existence of electromagnetic cavity problems respectively to TE and TM polarization by variational approaches in [1], and by integral equation methods in [2]. They also extend similar results for Maxwell’s equations in [3] by variational approaches. Recently, Bao et al established a stability result explicitly dependent on wave number for TE polarization based on Fourier analysis in energy space in [4] and TM polarization in [5]. Numerical methods for large cavities can be seen in [6, 7, 8].
Compared to electromagnetic scattering, elastic scattering also has wide applications in seismology and geophysics such as [9, 10, 11] and attracts more attention recently. However, elastic scattering problems have not been studied intensively due to their inherent difficulties arising from the governing equations and boundary conditions. For periodic surface, Arens studied quasi-periodic Green tensor and elastic potentials in [12] and used Rayleigh expansions and Rellich identities to prove uniqueness and integral equation methods to prove existence in [13]. Elschner and Hu applied variational approaches to get similar results in [14]. For general unbounded rough surfaces, Arens studied Green tensor, elastic potentials and upward radiation condition (UPRC), and proved uniqueness by integral equation methods and existence by integral equation methods, see [15, 16, 17]. Elschner and Hu [18] gave an equivalent form of UPRC and proved uniqueness and existence by variational approaches. They [19] also considered solvability in weighted Sobolev spaces and proved existence and uniqueness of elastic scattering from unbounded rough surface with an incident wave. Moreover, Hu, Yuan and Zhao [20] combined variation formula and integral equation to prove uniqueness and existence of two-dimensions local perturbed surface scattering problem with Lipschitz graph. For cavities, Hu, Li and Zhao considered elastic scattering in three-dimensions and proved the uniqueness in [21] for Dirichlet boundary conditions.
Inverse cavity problem is to reconstruct the shape of a cavity by measured far-field data on the artificial boundary. In general, to reconstruct a shape, Frchet derivative is commonly used. For instance, Bao, Gao and Li considered TE and TM polarization in [22] and proved uniqueness for lossy medium and studied the domain derivative and local stability for inverse electromagnetic cavity. A similar results for Maxwell’s equations was extended in [23]. Bao and Lai [24] proposed an optimization scheme to design a cavity for radar cross section reduction. Recently, Hu, Yuan, Zhao considered domain derivative for the inverse elastic scattering by a locally perturbed rough surface in [20]. To the authors’ best knowledge, research on inverse elastic scattering from cavities is still at its infant stage.
This paper intends to extend electromagnetic scattering from a cavity to elastic scattering. By employing transparent boundary conditions given by Dirichlet to Neumann (DtN) and Neumann to Dirichlet (NtD) operators, the boundary value problems can be reduced into a bounded domain so that the Fredholm alternative can be applied. Then, the variational approach is used to prove existence and uniqueness of the elastic scattering problem in two-dimensions with Dirichlet condition or Neumann condition. For Dirichlet problem, the existence in two-dimensions is actually trivial compared to three dimensions in [21]. However, we can obtain the uniqueness for two-dimensions while it is still open for three dimensions. Neumann problem is similar to Dirichlet problem with additional difficulties for the NtD operator. On inverse elastic cavity problem, this paper applies the method of changing variable to give the Frchet derivative for Dirichlet problem and Neumann problem, respectively. The difficulty for inverse Neumann problem lies in the boundary value problem reduced by it in Section 2 has inhomogeneous Neumann boundary condition by directly applying NtD operator. Hence, in order to obtain the TBC deduced by the DtN operator, we use an artificial boundary to rewrite the boundary value problem for Neumann case.
The paper is outlined as follows. In Section 2, the direct problems are reduced into variation problems in a bounded domain by DtN operator and NtD operator. In Section 3 and Section 4, existence and uniqueness for Dirichlet problem and Neumann problem are examined respectively. Moreover, the solutions to variation problems can be extended to satisfy Kurpradze-Sommerfeld radiation condition and Navier equations in upper half-space. In section 5, the Frchet derivatives for Dirichlet problem and Neumann problem are given respectively and a local stability result is given for Dirichlet problem. Conclusion is given in Section 6.
2 Problem formulation
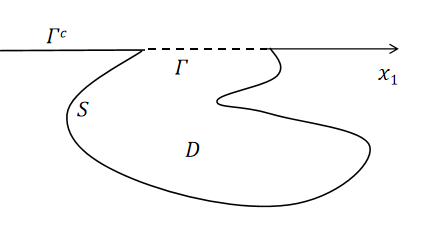
Consider a time-harmonic plane wave incident on a cavity, which is shown in Figure 1, denoted by with boundary , where is bounded and is assumed Lipschitz continuous. It is noted that is not necessary a graph of some function. In addition, denote . The medium is assumed to be homogeneous.
Suppose the incident time-harmonic plane wave takes the form
where
Define the compressional and shear wave numbers by
For simplicity, throughout this paper, it assumes , . Consider total wave field which satisfies the following Navier equations with Lam constants , and frequency
| (2.1) |
For convenience, denote by . This paper considers two kinds of boundary conditions, i.e., Dirichlet condition
| (2.2) |
and Neumann condition
| (2.3) |
where the differential operator is defined . Consider the Helmholtz decomposition for , i.e.,
| (2.4) |
with
| (2.5) |
where and . Then, and satisfy the homogeneous Helmholtz equations
| (2.6) |
The total wave field consists of incident wave , reflected wave and scattering wave , i.e., . Here, the reflected wave satisfies
| (2.7) | |||
| (2.8) |
It is easy to know that the reflected wave exists and can be expressed by the following functions
with and which are linearly independent solutions to Navier equations. Combing the Dirichlet boundary condition gives
And the Neumann boundary condition (2.8) yields
For the scattering wave , it is required to satisfy the following half-plane Kupradze-Sommerfeld radiation condition,
| (2.9) |
and
| (2.10) |
with for , .
Now we can state the following two problems respectively.
Dirichlet problem: Find which satisfies (2.1)-(2.2), where satisfies Kupradze-Sommerfeld radiation condition (2.9)-(2.10).
Neumann problem: Find which satisfies (2.1) and (2.3), where satisfies Kupradze-Sommerfeld radiation condition (2.9)-(2.10).
To investigate the above two problems in an unbounded domain, it is necessary to introduce transparent boundary conditions (TBC) to reduce the model problems into a bounded domain.
By Helmholtz decomposition, we have satisfying (2.4) with corresponding , satisfying (2.5)-(2.6). Applying the Fourier transform to (2.6) with respect to and using radiation condition gives
with
Denote by the Fourier transformation of with respect to . Then the Fourier transformation of is given by
| (2.11) |
Let ,
| (2.12) |
which implies
| (2.13) |
Inserting (2.13) into (2.11) arrives at the following representation for :
| (2.14) |
in with
Recalling the definition of differential operator , we have
| (2.15) |
Combing (2.14)-(2.15) and direct calculation implies that
| (2.16) |
where
| (2.17) |
Then the Dirichlet to Neumann operator can be defined by
So on . Noting that on and on , then TBC for Dirichlet problem can be given by
By TBC, Dirichlet problem can be reformulated as
Denote . Then for , the Betti formula gives
where
| (2.18) |
Define a sesquilinear form as
Now we obtain variation formula of Dirichlet boundary value problem.
Variation problem 1: find such that .
It is similar to give TBC and variation formula corresponding to Neumann problem. Note that in this case, it is not but , which has compact support on . So may not be integrable on . Thus, (2.13) and (2.16) may not hold in this case. However, can be represented by similarly. According to (2.14), we obtain
| (2.19) |
Combing (2.11) and (2.19) yields
Take , then can be represented by . Insert the representation in (2.11), we have
Taking inverse Fourier transformation and gives
Hence NtD operator can be defined by
which implies
Denote and . Then the Neumann problem can be reformulated as
| (2.20) | |||
Define the function space
where
and is zero extension of . In fact, it is clear that is the dual space of in [17]. The sesquilinear form : is defined by
Now we can give the following variation formula by the Betti formula.
Variation problem 2: find such that
Next two sections consider existence and uniqueness of solutions to the above two variation problems. Moreover, they can be extended to satisfying Kurpradze-Sommerfeld radiation condition.
3 Existence and uniqueness for Dirichlet problem
Since this problem is in a bounded domain with Lipschitz continuous boundary, we have the well-known compact embedding result that is a compact subset of . Hence uniqueness of variation problem and Fredholm alternative yield existence directly. To this end, we show that the continuity of DtN operator results in the continuity of the sesquilinear form , which is stated in the following lemma with the proof omitted.
Lemma 3.1.
The DtN operator is a continuous linear operator from to .
In order to use Fredholm alternative, it needs to show the sesquilinear form satisfies the Grding inequality. Take real part of ,
Considering (2.18) gives
It turns out that
| (3.1) |
By Plancherel identity,
where . However, the sign of is undeterminied because it lacks the result that is positive definite or negative definite. Fortunately, for sufficiently large , we know is positive definite, given in Lemma 3.2.
Lemma 3.2.
for .
The proof is also omitted here as it is trivial compared as the results in [18]. Noting that
and using Lemma 3.2, we have
Therefore, it suffices to estimate the intergal in . The following inequality is similar as the three-dimensions case in [20].
Lemma 3.3.
For any , we have , where are positive constants which depend on .
Next the uniqueness and existence of the variation problem can be derived by Lemma 3.3 and the Fredholm alternative.
Theorem 3.1.
Variation problem 1 admits a unique solution .
Proof.
Assume . We have
Combing (2.12) and (2.17) gives
Denote the matrix by
Taking the real part implies
So we have
| (3.2) |
Hence
which implies
Since has compact support on , is analytic with respect to . By unique continuation, for . So and on . By Holmgren’s uniqueness theorem, in which implies uniqueness. Finally, combing Lemma 3.3 and Fredholm alternative yields existence. ∎
Remark. Theorem 3.1 shows that there admits a unique solution to Variation problem 1 in bounded domain . We can extend to by (2.14), though it may not satisfy Kupradze-Sommerfeld radiation condition. In fact, the condition that satisfies (2.14) is weaker than Kupradze-Sommerfeld radiation condition of half-plane (2.9)-(2.10) (see [15]). But we can extend by
| (3.3) |
where is the half-space Green tensor for Dirichlet problem. According to the property of Green tensor we can verify that the corresponding is the solution to Drichlet problem in (see [15]). Then by representation theorem we know that any solution to Dirichlet problem in satisfies (3.3), which means the extension is unique.
4 Existence and uniqueness for Neumann problem
Recalling the two variation problems in Section 2, we can find that the main difference between Dirichlet problem and Neumann one is that in (2.17) is replaced by , i.e.,
| (4.1) |
where
This section shows that has similar properties to though it is more complicated. Before proceed to the uniqueness, we give the following lemma to show that is continuous, which implies the sesquilinear form is also continuous.
Lemma 4.1.
The NtD operator is a bounded linear operator from to .
Proof.
Then we consider similarly as Section 2.
Lemma 4.2.
for sufficiently large .
Proof.
Taking real part of for , we have
with
and
In order to prove , it suffices to verify and . Recall when , and . It turns out that
which means for sufficiently large . Direct calculation gives
for sufficiently large . So is positive definite for sufficiently large . ∎
Using the above lemma, we can estimate and then get the following inequality.
Lemma 4.3.
For any , we have , where are positive constant and they both depend on and .
Proof.
Similar to Section 3, for , we have
| (4.5) |
By Lemma 4.2, there exists such that for . So it can be deduced that
| (4.6) |
Noting for ,
So we have
| (4.7) |
By the trace theorem and the interpolation inequality, we obtain
| (4.8) |
Here are different constants depending on and , is sufficiently small and is dependent on and . By combining (4.5)-(4.8), we obtain the inequality
As is sufficiently small, it turns out that
∎
Next, we can proceed to the uniqueness for the Neumann problem. Though is more complicated than , it is difficult to directly give the representation of the imaginary part of the sesquilinear form like (3.2). But the following proof shows that it is not necessary to get exact representation of the imaginary part of the sesquilinear form.
Theorem 4.1.
Variation problem 2 admits a unique solution .
Proof.
Similar to Section 3, we will prove the uniqueness, which yields existence. Assume (i.e., ) which implies . Taking imaginary part of variation formula gives
For , we have
Then take imaginary part of (4.1) to get . For , we have
Simple calculation gives
It turns out that . For , we have
Direct calculation gives
where
with
In order to prove , it suffices to verify and . By direct calculation,
and
where
Therefore it turns out that , and thus .
In summary,
Hence for . Similarly to Section 3, by unique continuation and Holmgren’s uniqueness theorem, in which implies uniqueness. Combing Lemma 4.3 and Fredholm alternative yields existence.
∎
Remark. Similarly to Section 2, we can extend to by
| (4.9) |
where is the half-space Green tensor for Neumann problem. Obviously by representation theorem, this extension is unqiue. Hence we get the unique solution to Neumann problem in .
5 Inverse cavity problem
In this section, an inverse cavity problem, i.e., to reconstruct the unknown cavity from , is considered by investigating the Frchet derivative of the solution operator. For Dirichlet problem, the Frecht derivative implies a local stability result of inverse cavity problem directly. This can be deduced by the fact that when the Dirichlet data of Frecht derivative on the boundary of the cavity vanishes, the solution to original problem is zero. However, for Neumann case, the Frecht derivative satisfies different boundary value condition, which results in major difference from the Dirichlet case.
5.1 Dirichlet case
Let be and satisfying . Denote by and the domain with boundary . Similarly denote . Define the solution operator : by
where is the solution to variation problem for Dirichlet boundary condition, i.e.,
| (5.1) |
with
| (5.2) |
Extend to and still denote it by such that , which gives
| (5.3) |
Denote by . Obviously, it is invertible for sufficiently small . Then taking the variable transform implies
where , . Hence is a sesquilinear form on . Thus the variation formula (5.1) becomes
| (5.4) |
Next we proceed to derive the Frchet derivative of the solution operator . Let : is the Frchet derivative of at . Notice that is equipped with norm . The following theorem shows for , satisfies the homogeneous Navier equation in , the homogeneous TBC on and an inhomogeneous Dirichlet condition (5.7) on .
Theorem 5.1.
Suppose satisfying on . Let is the solution to the problem
| (5.5) | ||||
| (5.6) | ||||
| (5.7) |
Then .
Proof.
Let . Then implies . So and . By trace theorem,
| (5.8) |
with the constant . For convenience, we denote . Then combining (5.3) and (5.8) yields we only need to prove
For any ,
Firstly consider
where
| (5.9) | ||||
| (5.10) | ||||
| (5.11) |
Consider the Jacobi matrix
Direct calculation implies
| (5.12) |
and
| (5.13) |
Combining (5.12) and (5.13) gives
| (5.14) |
Insert (5.12)-(5.14) into (5.9)-(5.11),
| (5.15) |
where
| (5.16) | ||||
| (5.17) | ||||
| (5.18) |
It is easy to verify
| (5.19) |
Insert (5.19) into (5.15)-(5.18),
| (5.20) |
For , applying the identity
and divergence theorem gives
| (5.21) |
Considering , integration by parts gives
| (5.22) |
Integration by parts again gives
| (5.23) |
Denote and . Notice implies . This turns out that
| (5.24) |
Applying the divergence theorem again and noticing , , we obtain
| (5.25) |
Inserting (5.1)-(5.1) into (5.16) and (5.18) yields
| (5.26) |
For , direct calculation gives
| (5.27) |
and similarly
| (5.28) |
Then applying divergence theorem yields
| (5.29) |
Recalling , we have
| (5.30) |
Together with (5.27)-(5.30) implies
| (5.31) |
Now recalling , and combining the representations of in (5.1) and (5.1) implies
| (5.32) |
Notice satisfies (5.5)-(5.6), so it satisfies the variation formula for any . Hence by (5.1) and (5.1) we can obtain
| (5.33) |
The Dirichlet boundary condition (5.7) and deduces so that . The using Theorem 3.1 we know the sesquilinear form generates an invertible bounded linear operator which is still denoted by . By Banach open map theorem, : is also a bounded linear operator which implies
| (5.34) |
Then combining (5.33)-(5.34) gives
Hence we only need to prove when , . Since . Inserting (5.12)-(5.14) gives
Since
we obtain
Hence
which completes the proof. ∎
Next we consider a local stability result for inverse cavity problem. For two domains in , define the Hausdorff distance between and by
where
Take , where and . It is easy to verify . Our goal is to give the following local stability result.
Theorem 5.2.
Given and is sufficiently small, then
where , and is a constant independent with .
Proof.
For , it is obvious this conclusion is true. So we can assume .
Assume this conclusion is not true. There exists a such that
| (5.35) |
where is some subsequence of . Applying Theorem 5.1 to gives
| (5.36) |
where satisfies
Let , then satisfies
Then by (5.36) we obtain
| (5.37) |
Combining (5.35) and (5.37) yields . Hence
By unique continuation,
Recall
and , there must exist a continuous part such that
which implies
Then by unique continuation in which is a contradiction to on . ∎
5.2 Neumann case
Next consider the Neumann problem. Notice that the boundary value problem deduced by the NtD operator has the inhomogeneous boundary condition (2.20), so it is difficult to directly calculate the Frchet derivative like Dirichlet problem. Here, we still take the advantage of the TBC given by a DtN operator, though its definition on is difficult. Instead, a upper half-circle artificial boundary is taken, see in Figure 2.

Take such that in Figure 2. Denote , and . Let .
Recalling the scattering wave of Neumann problem satisfies and the Green’s representation theorem yields
where is the differential operator with respect to . Taking gives
Define the single-layer operator by
and double-layer operator by
We can choose such that is not the interior Dirichlet eigenvalue of so that is invertible. Then define the DtN operator
where is the identity operator. It is easy to verify this DtN operator implies the TBC
with .
Then rewrite the boundary value problem as
The variation formula is given by
| (5.38) |
where : is defined by
The Dirichlet data on is directly given from the Neumann data on by (4.9). Hence it is enough to consider the reconstruction from the Dirichlet data on .
Let . Define the solution operator : by
where is solution to
| (5.39) |
with
| (5.40) |
Extend to and still denote it by such that
and
with constant . Define by
It is invertible for sufficiently small .
Then taking the variable transform in (5.40) implies
Here is the similarly defined as in Section 5.1 except that , and are replaced by , and respectively. Since , , is a sesquilinear form on . So the variation formula (5.39) becomes
Let : is the Frchet derivative of at . Then result similar as Theorem 5.1 holds for Neumann case.
Theorem 5.3.
Suppose satisfying on . Let is solution to the problem
| (5.41) | ||||
| (5.42) | ||||
| (5.43) |
where is a distribution defined on by
Then .
Proof.
Let . Then implies . So and . Similarly as Theorem 5.1, we only need to prove
where . For any ,
Like Section 5.1, we have
| (5.44) |
where is defined the same as (5.16)-(5.18) except that is replaced by .
For , similarly as (5.1), we obtain
| (5.45) |
By and integration by parts, we have
| (5.46) |
Integration by parts again gives
| (5.47) |
Combining (5.2)-(5.2) and on gives
| (5.48) |
Apply the divergence theorem again, we obtain
| (5.49) |
| (5.50) |
For , similar discussion as (5.27)-(5.1) shows
| (5.51) |
Notice satisfies (5.41)-(5.43), then
| (5.52) |
Combining and (5.2)-(5.2) gives
Then we arrive at
to completes the proof. ∎
Remark. We can not get local stability from the Frchet derivative like the Dirichlet problem. Let with and . Assume . For any , the equality
does not imply . In fact, we can see in [22] for electromagnetic scattering, the local stability holds only for lossy medium, i.e, non-real wave number.
6 Conclusion
In this paper, elastic cavity problem with Dirichlet or Neumann condition is reduced into a bounded domain by the DtN or NtD operator. Variational approaches is utilized to prove the uniqueness and existence of boundary value problem in a bounded domain. For inverse cavity problem, the Frchet derivative is given for shape reconstruction and a local stability result is given for the Dirichlet problem. The stability results explicit with frequency for large elastic cavities like [4, 5] remains unsolved, which will be discussed in a forthcoming paper.
References
- [1] H. Ammari, G. Bao, A. W. Wood, Analysis of the electromagnetic scattering from a cavity, Japan Journal of Industrial and Applied Mathematics 19 (2) (2002) 301–310.
- [2] H. Ammari, G. Bao, A. W. Wood, An integral equation method for the electromagnetic scattering from cavities, Mathematical Methods in the Applied Sciences 23 (12) (2000) 1057–1072.
- [3] H. Ammari, G. Bao, A. W. Wood, A cavity problem for Maxwell’s equations, Methods and Applications of Analysis 9 (2) (2002) 249–260.
- [4] G. Bao, K. Yun, Z. Zhou, Stability of the scattering from a large electromagnetic cavity in two dimensions, SIAM Journal on Mathematical Analysis 44 (1) (2012) 383–404.
- [5] G. Bao, K. Yun, Stability for the electromagnetic scattering from large cavities, Archive for Rational Mechanics and Analysis 220 (3) (2016) 1003–1044.
- [6] G. Bao, W. Sun, A fast algorithm for the electromagnetic scattering from a large cavity, SIAM Journal on Scientific Computing 27 (2) (2005) 553–574.
- [7] Z. Xiang, T.-T. Chia, A hybrid BEM/WTM approach for analysis of the em scattering from large open-ended cavities, IEEE Transactions on Antennas and Propagation 49 (2) (2001) 165–173.
- [8] J.-M. Jin, S. S. Ni, S.-W. Lee, Hybridization of SBR and FEM for scattering by large bodies with cracks and cavities, IEEE Transactions on Antennas and Propagation 43 (10) (1995) 1130–1139.
- [9] I. Abubakar, Scattering of plane elastic waves at rough surfaces. i, in: Mathematical Proceedings of the Cambridge Philosophical Society, Vol. 58, Cambridge University Press, 1962, pp. 136–157.
- [10] J. Fokkema, Reflection and transmission of elastic waves by the spatially periodic interface between two solids (theory of the integral-equation method), Wave Motion 2 (4) (1980) 375–393.
- [11] J. Sherwood, Elastic wave propagation in a semi-infinite solid medium, Proceedings of the Physical Society (1958-1967) 71 (2) (1958) 207.
- [12] T. Arens, A new integral equation formulation for the scattering of plane elastic waves by diffraction gratings, The Journal of Integral Equations and Applications (1999) 275–297.
- [13] T. Arens, The scattering of plane elastic waves by a one-dimensional periodic surface, Mathematical Methods in the Applied Sciences 22 (1) (1999) 55–72.
- [14] J. Elschner, G. Hu, Variational approach to scattering of plane elastic waves by diffraction gratings, Mathematical Methods in the Applied Sciences 33 (16) (2010) 1924–1941.
- [15] T. Arens, Uniqueness for elastic wave scattering by rough surfaces, SIAM Journal on Mathematical Analysis 33 (2) (2001) 461–476.
- [16] T. Arens, Existence of solution in elastic wave scattering by unbounded rough surfaces, Mathematical Methods in the Applied Sciences 25 (6) (2002) 507–528.
- [17] T. Arens, The scattering of elastic waves by rough surfaces, Ph.D. thesis, Brunel University (2000).
- [18] J. Elschner, G. Hu, Elastic scattering by unbounded rough surfaces, SIAM Journal on Mathematical Analysis 44 (6) (2012) 4101–4127.
- [19] J. Elschner, G. Hu, Elastic scattering by unbounded rough surfaces: solvability in weighted Sobolev spaces, Applicable Analysis 94 (2) (2015) 251–278.
- [20] G. Hu, X. Yuan, Y. Zhao, Direct and inverse elastic scattering from a locally perturbed rough surface, Communications in Mathematical Sciences 16 (6) (2018) 1635–1658.
- [21] G. Hu, P. Li, Y. Zhao, Elastic scattering from rough surfaces in three dimensions, Journal of Differential Equations 269 (5) (2020) 4045–4078.
- [22] G. Bao, J. Gao, P. Li, Analysis of direct and inverse cavity scattering problems, Numerical Mathematics: Theory, Methods and Applications 4 (3) (2011) 335–358.
- [23] P. Li, An inverse cavity problem for Maxwell’s equations, Journal of Differential Equations 252 (4) (2012) 3209–3225.
- [24] G. Bao, J. Lai, Radar cross section reduction of a cavity in the ground plane, Communications in Computational Physics 15 (4) (2014) 895–910.