On tunnel numbers of a cable knot and its companion
Abstract.
Let be a nontrivial knot in and its tunnel number. For any -slope in the torus boundary of a closed regular neighborhood of in , denoted by , it is a nontrivial cable knot in . Though , Example 1.1 in Section 1 shows that in some case, . So it is interesting to know when .
After using some combinatorial techniques, we prove that (1) for any nontrivial cable knot and its companion , ; (2) if either admits a high distance Heegaard splitting or is far away from a fixed subset in the Farey graph, then . Using the second conclusion, we construct a satellite knot and its companion so that the difference between their tunnel numbers is arbitrary large.
Key words and phrases:
cable knot, tunnel number, Heegaard distance2010 Mathematics Subject Classification:
57M271. Introduction
Let be a nontrivial knot in and its closed complement in . Then admits a Heegaard splitting with . Let be the minimal Heegaard genus of and the tunnel number . For any pair of pairwise coprime numbers and , there is a slope crossing the meridian times and the longitude times, denoted by , in . Then it is a -cable knot over , denoted by , and is a companion of . Though is also a cable knot of itself, we only consider the nontrivial case and require . Since is contained in the closed neighborhood of , it is interesting to know the difference between and .
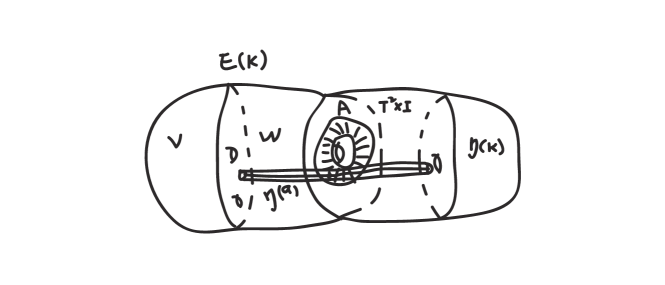
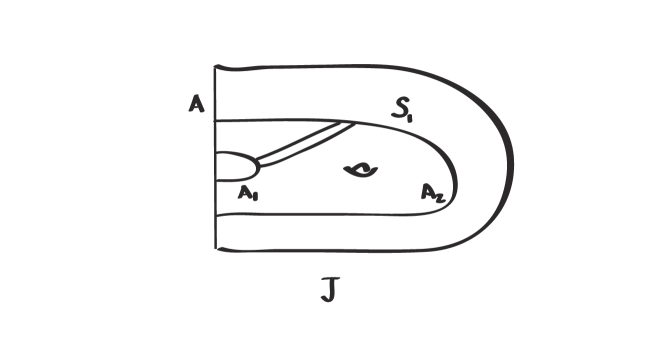
There is a combinatorial description of through , in which way it gives an inequality between and . Let be the closed regular neighborhood of in . Since is a slope in , we can slightly push into the interior of . It is not hard to see that is homeomorphic to the amalgamation of and along an annulus in their common torus boundary, where the core curve of is isotopic to the slope. Then admits a Heegaard splitting as follows: Let be a fiber arc in from to and the closed regular neighborhood in . Then we define and . Since is homeomorphic to the amalgamation of a handlebody and along an once punctured annulus, it is a compression body, see Figure 1. Moreover, . So is a Heegaard splitting of and . Therefore . Hence , see also in [16]. However, is not always the best upper bound of , see Example 1.1 as follows.
Before stating Example 1.1, we introduce the definition of a -primitive knot in . We assume that the torus boundary . Let be a slope in . If there is a spanning annulus with and an essential disk such that is a single point, then is called -primitive. Moreover, if admits a -primitive minimal Heegaard splitting, is called -primitive.
Example 1.1.
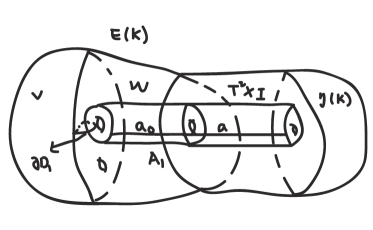
Let be a -primitive knot in . Suppose is a -primitive mininal Heegaard splitting of with . Then there is a spanning annulus and an essential disk so that (1) ; (2) is a slope on . In the above construction of the Heegaard splitting of , let be the spanning arc of which is disjoint from the point . Since , is an essential disk of , denoted by . Note that is an essential disk in and . Then is stabilized, see Figure 2. Hence , see [12].
Then there is a natural question: Can be arbitrarily large? Unfortunately, the answer is negative. More precisely, we have the following theorem.
Theorem 1.1.
For any nontrivial cable knot and its companion , .
Remark 1.1.
In a conference held in Xi’an Jiaotong University 2015, Tao Li announced that for any nontrivial satellite knot and its companion , . But until now, we have found no preprint or publication containing this result.
By Example 1.1, if is a (p,q)-cable knot while is -primitive, then . Hence in this case, . So there is a problem as follows.
Problem 1.1.
For any nontrivial cable knot and its companion , if and only if is a (p,q)-cable knot and is -primitive.
There are some results related to this problem. For example, Moriah [16] proved that if is tunnel number one but no torus knot, then . If we consider as the amalgamation of and along an annulus, it is more or less similar to the complement of the connected sum of two knots in . For any two high distance knots, Gao, Guo and Qiu [3] proved that . Since a -primitive Heegaard splitting has distance at most 2, Example 1.1 doesn’t hold on a high distance knot. Thus we guess that if is a high distance knot, .
Although there are many well properties of a high distance knot, given a knot in , it is a little bit hard to determine whether admits a high distance Heegaard splitting or not. So for an arbitrary nontrivial knot , we consider the problem that how to properly choose so that . In [11], Li introduced an idea to consider a sufficiently complicated gluing map in the calculation of minimal Heegaard genus of an amalgamated 3-manifold. As pointed earlier, is also an amalgamation of two 3-manifolds along an annulus. Then we guess that there should be a similar result on tunnel numbers between and . We present these two ideas in the following theorem.
Theorem 1.2.
Suppose is a -cable knot over a nontrivial knot in .
-
(1)
If admits a distance at least Heegaard splitting, then .
-
(2)
Let be the collection of boundary slopes of essential surfaces properly embedded in . Then there is a constant number depending on so that if
then .
Remark 1.2.
-
•
In fact, there are infinitely many high distance knots in , see [15];
-
•
By the second conclusion in Theorem 1.2, for any given number , we can construct a satellite knot and its companion so that as follows. For any , let be the cable knot so that . And then let be the cable knot of so that . It is not hard to see that lies in the solid torus neighborhood of . By the same argument again and again, we have a knot contained in the solid torus neighborhood of and .
A Heegaard splitting is a Dehn surgery of if there is an embedded simple closed curve in or so that or is a Dehn surgery of or along . Under the second condition in Theorem 1.2, there is no essential surface in with slopes as its boundary slopes. So this phenomenon derives out the following corollary.
Corollary 1.1.
The conclusion of Corollary 1.1 implies that each unstabilized Heegaard splitting of is a Dehn surgery of one of ’s. In reverse, doing a Dehn surgery on each unstabilized Heegaard splitting of also produces a Heegaard splitting of . Then there is a natural question:
Question 1.1.
For any two non isotopic but same genus Heegaard splittings of , is it possible that doing two Dehn surgeries on them simultaneously produce two isotopic Heegaard splittings of ?
Remark 1.3.
To our best knowledge, there is no evidence showing that whether it is true or false.
2. Preliminaries
Let be a Heegaard splitting. It is stabilized if there is a pair of essential disks in and individually so that their boundary curves intersect in one point. Otherwise, it is unstabilized. A Heegaard splitting is reducible if there is an essential simple closed curve in bounding a disk in and also a disk in . Otherwise, it is irreducible. For any irreducible Heegaard splitting, Casson and Gordon [2] introduced a weakly reducible and irreducible Heegaard splitting as follows: is weakly reducible and irreducible if it is irreducible and there are a pair of disjoint essential disks in and individually. Otherwise, it is strongly irreducible. So if is unstabilized, it is either strongly irreducible or weakly reducible and irreducible.
If is a closed orientable and genus at least two surface, then there is a curve complex defined on it as follows, see also in [5]. The vertices are the isotopic classes of essential simple closed curves in . A -simplex is a set of isotopic classes of nonisotopic and pairwise disjoint essential simple closed curves in . Without further notation, we abuse a curve and its isotopic class. Then there is a distance defined on the one-skeleton . Let and be arbitrary two essential simple closed curves on . The distance of and , denoted by , is the minimal number of edges connecting and in , i.e., the minimal integer satisfying is an edge path in where and and is an edge (i.e., is distinct and disjoint from ) . It is not hard to see that linearly extending to the whole is a metric of it. It is well known that is gromov hyperbolic, see [14]. If is a torus, there is also a curve complex defined on it, which is the Farey graph . Similarly, the vertices are the isotopic classes of essential simple closed curves in . We put an edge between two isotopic classes of essential, non isotopic, intersecting one point simple closed curves in . Then for any two vertices and in , the distance is defined to be the minimal number of edges from to in . It is well known that the diameter of is infinite, i.e., .
There is a disk complex defined on either of and as follows. The vertices are the isotopic classes of essential simple closed curves in which bound essential disks in (resp. ). A -simplex is a set of isotopic classes of nonisotopic and pairwise disjoint essential simple closed curves in which bound essential disks in (resp. ). Denote the disk complex of (resp. ) by (resp. ). It is not hard to see that and . Hempel [9] defined the Heegaard distance to be the distance between and in and proved that is weakly reducible and irreducible if and only if ; is strongly irreducible if and only if .
Let be a properly embedded essential surface, i.e., incompressible and -incompressible, in a compact orientable 3-manifold . Hartshorn [4] and Schalemann [19] proved that . Later, Scharlemann and Tomova [21], Li [10] extended this result into a general case.
Definition 2.1.
Let be a separating surface properly embedded in and . Suppose has compressing disks on both sides. We say is strongly irreducible if each compressing disk in meets each compressing disk in . Otherwise, is called weakly reducible.
Definition 2.2.
Let be a strongly irreducible surface. Then is called -strongly irreducible if
-
(1)
every compressing and -compressing disk in meets every compressing and -compressing disk in , and
-
(2)
there is at least one compressing or -compressing disk on each side of .
In Li’s proof of Theorem 1.1 in [10], it contains the following lemma:
Lemma 2.1.
Suppose is a compact orientable irreducible 3-manifold and is a separating strongly irreducible surface in . Let be a properly embedded compact orientable surface in and suppose is either essential or separating strongly irreducible. Then either
-
(1)
, or
-
(2)
after isotopy, for all , where is a level surface in a sweep-out for , or
-
(3)
and are isotopic.
If , there is at least one essential surface with boundary curves. When are some tori, Hatcher [8] studied all boundary curves of essential surface in . In particular, if is a torus, there is a finiteness result about boundary slopes of essential surfaces in as follows. For a general case, there are some results on it, see [6, 7, 13].
Lemma 2.2 (Corollary [8]).
Let be a compact, orientable, irreducible 3-manifold. If , there are finitely many slopes realized by boundary curves of essential surfaces in .
In particular, Bachman, Schleimer and Sedgewick [1] proved the following lemma:
Lemma 2.3 (Lemma 4.8[1]).
Suppose is compact orientable irreducible 3-manifold with a torus boundary. Let be a separating, properly embedded, connected surface in which is strongly irreducible, has non-empty boundary, and is not peripheral. Then either is -strongly irreducible or is at most distance one from the boundary of some properly embedded surface which is both incompressible and boundary-incompressible.
In general, for any essential surface and any strongly irreducible and -strongly irreducible surface in , Li proved that there is an upper bound of distances between any two of their boundary curves in .
Lemma 2.4 (Lemma 3.7 [11]).
Suppose is not an -bundle and has a connected boundary. Let be the collection of orientable surfaces properly embedded in with genus no more than and boundary is essential in . Let and be surfaces in . Suppose is essential and suppose is either essential or strongly irreducible and -strongly irreducible. Then there exists a number that depends only on , such that the distance in .
At the end of this section, we introduce a lemma about essential annuli and disks in a compression body.
Lemma 2.5 (Lemma 3.1 [17]).
Let be a nontrivial compression body, and let be a collection of pairwise disjoint essential annuli properly embedded in . Then there is an essential disk properly embedded in disjoint from .
3.
Let be a minimal genus Heegaard splitting of . Since is irreducible, is either strongly irreducible or weakly reducible and irreducible.
3.1. is strongly irreducible.
Since is an essential annulus in , by Schultens lemma [22], consists of nonzero and finitely many essential simple closed curves in both of them. Under this condition, we assume that is minimal.
Claim 3.1.
One component of is strongly irreducible while the others are incompressible in .
Proof.
Not only but also consist of finitely many essential annuli. For if not, one of them contains at least one boundary parallel annulus. Then we do an isotopy on to reduce , which is against the minimal assumption of . By Lemma 2.5, there is an essential disk (resp. ). Then is contained in one subsurface of , says . Since is strongly irreducible, . Then any essential disk of disjoint from has its boundary curve in . So any essential disk of disjoint from has its boundary curve in . Hence is the only compressible subsurface in . Since is essential, i.e., the inclusion map on its fundamental group is injective, is strongly irreducible.
∎
Let be the strongly irreducible surface of . Recall that . Since its interior is disjoint from , lies in either or the solid torus , abbreviated by . If , then consists of finitely many nested annuli, denoted by , for some .
For each , is a pair of essential curves. Then there is a so that is the innermost in which bounds an annulus . So is an essential annulus in one compression body, says in for example. For if not, we do an isotopy on to reduce . On one side, since , bounds an annulus in . It means that there is a pair of two isotopic essential simple closed curves in bounding an essential annulus in . By the standard outermost disk argument, there is a boundary compression in producing an essential disk . It is not hard to see that is separating and cuts out a solid torus in . On the other side, also bounds a solid torus in , denoted by . Moreover, .
Let be the longitude of . Then we push it a little into the interior of . For simplicity, it is still denoted by . Removing a regular neighbor of , denoted by , in and makes into a torus I-bundle, where the disk is in one of its boundary surface. Since is cutten into the solid torus and a genus less one compression body or handlebody, is still a compression body but with one more negative boundary surface. In , we attach a 2-handle along an essential simple closed curve in and a 3-ball to cancel the resulted 2-sphere so that the resulted solid torus is actually the and also . Similarly we attach a 2-handle addition along the same essential simple closed curve on . So it produces a new compression body , where . Then is still a Heegaard splitting. For simplicity, we replace by , by . Then is a Heegaard splitting. As we do the Dehn surgery in , the 3-manifold is an amalgamation of and a solid torus along . Moreover,
Claim 3.2.
is a Heegaard splitting of .
Proof.
Since consists of finitely many nested annuli in which are not parallel to , by doing the Dehn surgery in , the solid torus bounded by is changed into a new solid torus so that is parallel to . It means that among of all these annuli , each one is parallel to . So we do an isotopy on so that it is disjoint from . Therefore, is in either or . Since has the same core curve with , is incompressible. Therefore, is boundary parallel in or . So cuts out the I-bundle in . It means that is homeomorphic to . ∎
By Claim 3.2, . Since is a minimal Heegaard genus of , . So .
Otherwise, lies in the solid torus . Recall that a strongly irreducible surface is bicompressible, i.e., being compressed in its two sides, and weakly incompressible, i.e., no disjoint compression disks from its two sides. Scharlemann[18] studied the bicompressible but weakly incompressible surfaces in a solid torus, proved the following lemma.
Lemma 3.1 (Proposition 3.2[18]).
Let be essential simple closed curve in so that it neither bounds a disk in nor intersects the essential disk in in one point. Then for any bicompressible, weakly incompressible surface with as its boundary curve, it is either a boundary parallel incompressible annulus with a tube parallel to an arc in attached or the tube sum of two boundary parallel incompressible annuli and the tube is parallel to an arc in .
So is either a boundary parallel annulus with a tube attached or the tube sum of two boundary parallel annuli in . In case of a long argument, we divide its proof into these two lemmas 3.2 and 3.3.
Lemma 3.2.
If is a boundary parallel annulus with a tube attached in , then .
Proof.
Since bounds a subannulus , is parallel to either or its complement annulus in .
(1) If is parallel to a subannulus , then up to isotopy, see Figure 3. For if not, then there is an annulus in parallel to . So we do an isotopy along this annulus to reduce . Then is an essential annulus in one of and . Without loss of generality, we assume that . The other case is similar. So we omit it. Then cutting along produces two handlebodies or one handlebody and a compression body. Let be the compression body or the handlebody containing no .

By Claim 3.1, except , all other components of are nested annuli in . If there is no annulus in , there are a pair of two spanning annuli, says and so that one component of , says , lies in . It is not hard to see that is a handlebody and . Let be I-bundle in . Then we remove this I-bundle from and attach it to along these two annuli . So is changed into a new 3-manifold, says . In this case, contains . Let be a vertical arc connecting in . So is a fiber arc in connecting and the other boundary surface of . We remove the union of a regular neighborhood of and a regular neighborhood of in from . Then is changed into a 3-manifold , which is also the amalgamation of and a tubed annulus I-bundle along two essential annuli. It is not hard to see that is also a handlebody and furthermore is the disk sum of and , denoted by . So is a compression body and is a Heegaard splitting of . During the process of this surgery, . It means that and .
So we assume that there is at least one annulus in . Let be the innermost annulus in , i.e., no other component of lies between it and . Then is not boundary parallel into . For if not, then we can do an isotopy on to reduce . Let be the handlebody or compression body as above. Then contains a smaller copy of . Then we do a Dehn surgery on this smaller copy of along its longitude so that is parallel to . Then is changed into a new 3-manifold, denoted by again. By the same argument of the case that is incompressible, is homeomorphic to . Since bounds an annulus I-bundle, let be a fiber arc connecting and in this I-bundle. Then we remove a regular neighborhood of and then is changed into a 3-manifold . By the same argument as above, is a compression body or handlebody. Without loss of generality, we assume that is a handlebody. Meanwhile, the union of and the closed regular neighborhood of is a compression body. So is a Heegaard splitting of . By the same argument, .
(2) If is parallel to the complement annulus of in , then . For if not, by Claim 3.1, then there is an innermost annulus of so that its boundary curves lie in the interior of . By minimality of , is not boundary parallel to . Then bounds a smaller copy of . By the similar argument as above, we do a Dehn surgery on this smaller copy of and get a Heegaard splitting of . Moreover, .
It is not hard to see that the dual core curve of the tube in bounds an essential disk , says in . Then we do a compression on along the disk and get a new 3-manifold . Moreover, is changed into an annulus in . Then bounds a smaller copy of in . Denote . If is an essential annulus in , then is an amalgamation of a handlebody or a compression body and a smaller copy of along . So we do a Dehn surgery as above so that the smaller copy of is changed into the I-bundle and is changed into a 3-manifold , where is the union of and . Then is homeomorphic to . By the same argument as above, is a Heegaard splitting of and .
Otherwise, is an essential annulus in . Then both of and are in , where they bound a smaller copy of . Then we do a Dehn surgery on this smaller copy of so that they are parallel. Hence is changed into a compression body or handlebody . Replace by . So is a Heegaard splitting of and . ∎
Lemma 3.3.
If is the tube sum of two annuli in , then .
Proof.
Let be the tube sum of two annuli and in . We say there is no other component of in the region between and in . For if not, then the tube would not connect them. It is not hard to see that (resp. ) bounds an annulus in . Without loss of generality, we assume that the annulus bounded by in doesn’t contain . Then we say that there is no other component of , of which boundary curves lies in the annulus bounded by in . Otherwise, we either do an isotopy on to reduce or do a Dehn surgery as above and get .
There are three types of and as follows:
-
•
(1) one of them is parallel to , says while not;
-
•
(2) both of them are parallel to ;
-
•
(3) neither of them is parallel to .
For the first case, either separate in or not. If separate , then bounds a smaller copy of . Then we do a compression on this tube along the disk bounded by the core curve. Without loss of generality, we assume that . So is changed into a new 3-manifold, denoted by , which is also a compression body or handlebody. Denoted by . Again we do a Dehn surgery on as in the proof of Lemma 3.2 and so the smaller copy of is changed into the annulus I-bundle . So is changed into and . Let be the vertical arc of , which connects . Then is a compression body or handlebody. Meanwhile, the union of and the closed regular neighborhood of is a handlebody or compression body, denoted by . Moreover, . So . If doesn’t separate , then there is a smaller copy of bounded by . So we do a dehn surgery as above. Then .
For the second case, and are not nested. Without loss of generality, we assume that the disk bounded by core curve of this tube lies in . Then we do a compression on along an essential disk in . So is changed into a new compression body or handlebody, says . Since and bound two essential annuli in , cutting along them produce a handlebody or compression body, says . Then is the amalgamation of and an annulus I-bundle or a smaller copy of . For the first case, removing a closed neighborhood of a fiber arc in this I-bundle changes into a handlebody or compression body . For the later case, we do a dehn surgery on this smaller copy of so that it is changed into an annulus I-bundle. In both of these two cases, .
For the third case, and are parallel in and there is a smaller copy of bounded by a subannulus in and . For if not, then both of and lie in an I-bundle of . Then we do an isotopy to reduce . We do a compression on this tube along the disk bounded by the core curve. Without loss of generality, we assume that . So is changed into a new 3-manifold, denoted by , which is also a compression body or handlebody. Denoted by . Since there is no other component of lie between and , this smaller copy of lies in . By the same argument in the proof of Lemma 3.2, we do a Dehn surgery on this smaller copy of so that it is changed into . So is changed into a new compression body or handlebody . Moreover, . On one side, we attach a closed regular neighborhood of a vertical fiber arc in the I-bundle bounded by and to so that is changed into a compression body or handlebody, says . On the other side, is still a handlebody or compression body and . During this process, and . ∎
3.2. is weakly reducible and irreducible.
By the main result in [20], has an untelescoping, says . We assume that each component of is essential in both of them up to isotopy. Under this condition, we assume that is minimal. Then each component of is an incompressible annulus in , which is not boundary parallel to in . So are nested annuli in . Let be the innermost one among . Since bounds an annulus , bounds a smaller copy of , denoted by . Then lies in some , for some .
By Claim 3.1, contains at most one strongly irreducible surface, denoted by . If there is no strongly irreducible surface in , by the similar argument as above, we do a Dehn surgery on so that is changed into the annulus I-bundle . Then the Heegaard splitting is changed into . So the amalgamation is a Heegaard splitting of . Hence and hence .
So we assume that is strongly irreducible in . By Lemma 3.1, is either a boundary parallel annulus with a tube attached or the tube sum of two boundary parallel annuli in . Though the argument is almost same to the proofs in Lemma 3.2 and 3.3, it is slightly different. Without loss of generality, we assume that the dual disk to the tube lies in . For the first case, we do a compression on along a non-separating essential disk in . On one hand, is changed into a genus less one compression body or handlebody . On the other hand, bounds an incompressible annulus . So is an essential annulus in . Then one component of contains no , denoted by . It is not hard to see that is a handlebody or compression body. Since is a genus one, two boundary curves compact surface, is changed into an annulus and . It means that the complement of in , denoted by , is the amalgamation of and the solid torus bounded by along .
It is known that is incompressible in . Then either is parallel to or there is a smaller copy of bounded by . If is parallel to , then is homeomorphic to . So it is a handlebody or compression body, denoted by . It means that is a genus Heegaard splitting of , which is impossible. So bounds a smaller copy of . Then by the same argument in Lemma 3.3, we do a Dehn surgery on in so that is changed into a compression body or handlebody . And is a genus Heegaard splitting. By the similar argument, is a Heegaard splitting of . So .
The left case is that is the tube sum of two boundary parallel annuli in . By the same argument in Lemma 3.3, is changed into , where . Moreover, is a Heegaard splitting of . So .
4. The proof of Theorem 1.2
Let , , , , and be the same as in Section 1. We rewrite Theorem 1.2 as the following proposition:
Proposition 4.1.
Suppose is a -cable knot over a nontrivial knot in .
-
(1)
If admits a distance at least Heegaard splitting, then .
-
(2)
Let be the collection of boundary slopes of essential surfaces properly embedded in . Then there is a constant depending on so that if
then .
Proof.
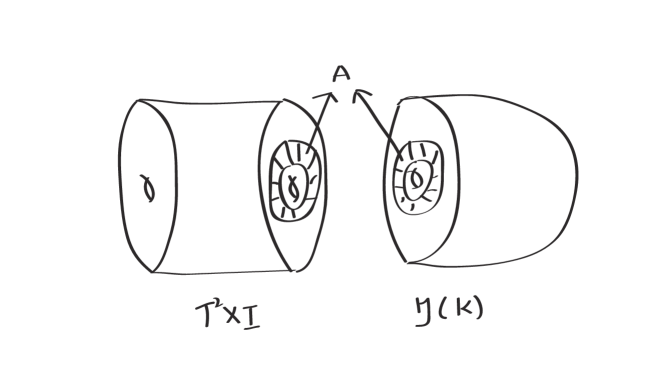
Since is in , we can slightly push into the interior of . Then where , see Figure 5.
4.1. Proof of Proposition 4.1 (1)
Let be a minimal genus Heegaard splitting of with . Then it is either strongly irreducible or weakly reducible and irreducible.
Lemma 4.1.
is weakly reducible and irreducible.
Proof.
Suppose the conclusion is false. Then is strongly irreducible. Since is essential, then intersects nontrivially up to isotopy. By Schultens’ lemma [22], we assume that (1) is minimal; (2) each simple closed curve of is essential in both and .
Claim 4.1.
There is at most one strongly irreducible component in while others are essential in .
Proof.
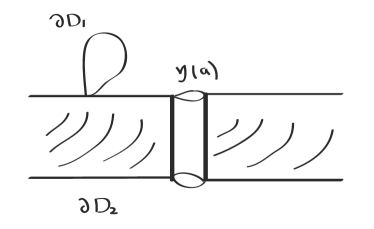
Since (resp. ) is a collection of disjoint essential annuli in (resp. ), by Lemma 2.5, there is a compressible disk (resp. ) in (resp. ) so that (resp. ) disjoint from (resp. ). Since is strongly irreducible, both and lie in or . Furthermore, and lie in a same component of . Moreover, is strongly irreducible while other components of are essential. For if not, then there is another compressible component of . It means that is weakly reducible, see Figure 6. ∎
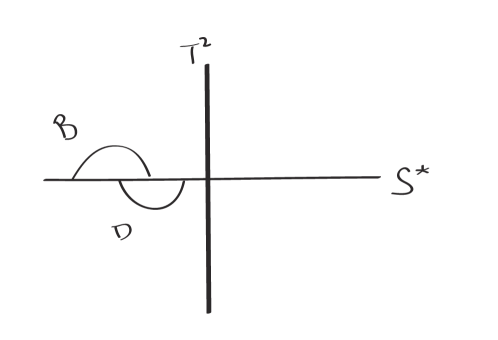
Let be a distance at least Heegaard splitting of . Then is strongly irreducible in both and . By Claim 4.1, there is at most one strongly irreducible component in while others are essential in . If contains only one strongly irreducible component , then is separating. Since intersects nontrivially up to isotopy, and are not well-separated. Moreover, is not isotopic to . Then by Lemma 2.1, . Since is essential in , . Then . A contradiction. Otherwise, contains an essential subsurface in . Then by the same argument, . A contradicition.
∎
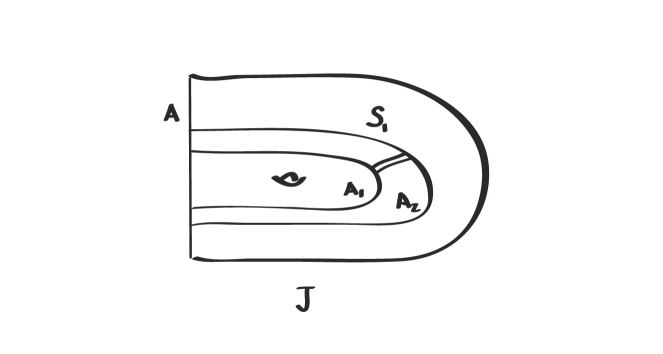
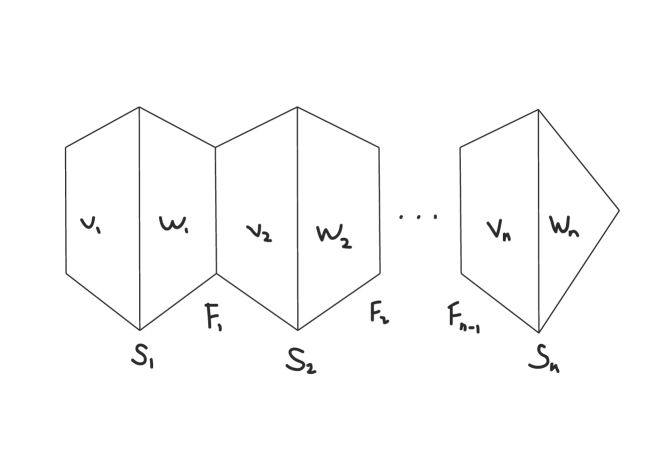
So is weakly reducible and irreducible. By [20], has an untelescoping , for , so that (1) is essential in , for any ; (2) is a strongly irreducible Heegaard splitting, for any , see Figure 7.
Since
and
we have
If for some , intersects nontrivially up to isotopy, then each component of is essential in . Let be an essential surface in . Then by Lemma 2.1, . It contradicts the assumption that . So for any , is disjoint from . By the similar argument in the proof of Lemma 4.1, for any , is disjoint from . Hence is disjoint from .
Then lies in some or , for some . Without loss of generality, we assume that lies in . Since is essential in , . It is known that there is no essential closed surface in a compression body or handlebody. So is isotopic to . Therefore is an amalgamation of a Heegaard splitting of and a Heegaard splitting of along .
Fact 4.1.
.
Proof.
Since , runs around the longitude of at least twice. So is not a torus -bundle. On one hand, consists of two tori. Then . On the other hand, there is a genus two Heegaard splitting of . Let and be a fiber arc in with one endpoint in and the other in and . Then both and are genus two compression bodies with , see Figure 8. So is a genus two Heegaard splitting of and . Hence . ∎
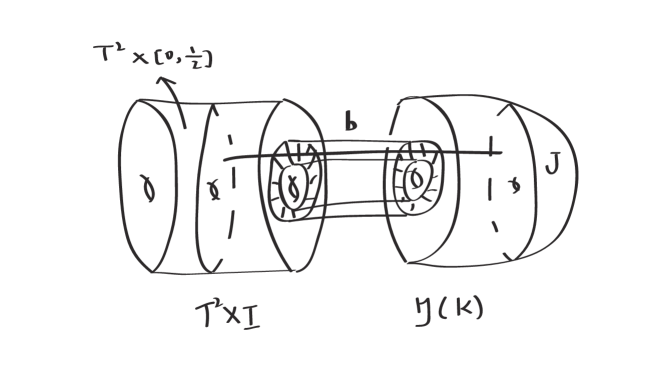
Therefore, . And . However, . Hence .
4.2. Proof of Proposition 4.1 (2)
Recall that is the collection of isotopy classes of boundary slopes of properly embedded essential surfaces in . Then by Lemma 2.2, contains finitely many vertices in depending on . So there is a constant depending on so that .
Claim 4.2.
is not a twisted -bundle over a compact non-orientable surface.
Proof.
Suppose the conclusion is false. Then is a twisted -bundle over a compact non-orientable surface . Then . Since is a torus, . So is either a Mobius band or Klein bottle. We say that is not a Mobius band. For if not, then is the twisted I-bundle of a Mobius band, i.e., a solid torus. So is a trivial knot in . A contradiction. So is a Klein bottle. Let be a double cover of . Then is a torus and , i.e., a torus I-bundle, is a double covering of . For any slope , is a double covering of . However, when is the meridian of , is a Lens space or while is . It means that is not simple connected. A contradiction. ∎
Let be a boundary slope of an essential surface properly embedded in such that the genus of is minimal. Let . By Claim 4.2, is not a twisted -bundle over a non-orientable surface. Since is nontrivial, is incompressible. So is not a product -bundle over an orientable compact surface. By Lemma 2.4, for any properly embedded, strongly irreducible and -strongly irreducible, genus at most surface in , there is a number depending only on so that . Let .
Let be a minimal genus Heegaard splitting of with . Since is irreducible, is either strongly irreducible or weakly reducible and irreducible.
Lemma 4.2.
is weakly reducible and irreducible.
Proof.
Suppose that the conclusion is false. Then is strongly irreducible. Since is essential in , intersects nontrivially up to isotopy. By Claim 4.1, there is at most one strongly irreducible component in while others are essential in . Moreover, are isotopic to the slope in .
If contains an essential surface in , then and . A contradiction. Otherwise, contains only one strongly irreducible component . By Lemma 2.3, either is strongly irreducible, -irreducible or there is an incompressible and boundary incompressible surface so that For the first case, . Then , i.e., . Hence . A contradiction. For the second case, . A contradiction. ∎
So is weakly reducible and irreducible. By the main result in [20], has an untelescoping , so that (1) for any , is incompressible in and not parallel to ; (2) for any , is a strongly irreducible Heegaard splitting. We say that is disjoint from . For if not, (1) either up to isotopy for some . Then each component of is essential in . Note that are isotopic to in . Then . A contradiction. Or, (2) . By the similar argument in the proof of Lemma 4.2, . A contradiction.
Therefore is an amalgamation of a Heegaard splitting of and a Heegaard splitting of along . So and . However, it is known that . So .
∎
5. The proof of Corollary 1.1
Let and be the same as in Theorem 1.2 (2). For any unstabilized Heegaard splitting of , since is irreducible, it is either strongly irreducible or weakly reducible and irreducible. So we divide it into two cases: (1) is strongly irreducible; (2) is weakly reducible and irreducible. We firstly prove Corollary 1.1 for the strongly irreducible case.
Since is an essential annulus in , by Schultens lemma [22], each curve of is essential in both and . Then by the same argument in the proof of Claim 3.1, one subsurface of is strongly irreducible while the others are incompressible in their corresponding components of . Moreover, each subsurface of has slopes as its boundary curves. By the condition that
is connected and strongly irreducible while each component of is essential and an annulus. So is a collection of nested annuli in . By the similar argument of Case 1 of Theorem 1.1 in Section 3, we do a Dehn surgery on and obtain a Heegaard splitting of . In reverse, is also a Dehn surgery of .
Otherwise, is weakly reducible and irreducible. Then it has an untelescoping, says , for , where is incompressible in . By the same argument as above, is disjoint from . So is contained in , for some . Then by the same argument as the strongly irreducible case, we do a Dehn surgery on so that it is changed into . Moreover, is a Heegaard splitting of . In reverse, is also a Dehn surgery of .
References
- [1] Bachman, D., Schleimer, S. and Sedgwick, E., Sweepouts of amalgamated 3-manifolds, Algebr. Geom. Topol., 6, 2006, 171-194.
- [2] Casson, A. J. and Gordon C. McA., Reducing Heegaard splittings, Topology Appl. 27 (1987), no. 3, 275-283.
- [3] Gao X. T., Guo Q. L. and Qiu R. F., A note on tunnel number of composite knots, Topology Appl. 158 (2011), no. 16, 2240-2243.
- [4] Hartshorn K., Heegaard splittings of Haken manifolds have bounded distance, Pacific J. Math. 204 (2002), no. 1, 61-75.
- [5] Harvey W. J., Boundary structure of the modular group. Riemann surfaces and related topics: Proceedings of the 1978 Stony Brook Conference (State Univ. New York, Stony Brook, N.Y., 1978), pp. 245-251, Ann. of Math. Stud., 97, Princeton Univ. Press, Princeton, N.J., 1981.
- [6] Hass J., Rubinstein J. H. and Wang S. C., Boundary slopes of immersed surfaces in 3-manifolds, J. Differential Geom. 52 (1999), no. 2, 303-325.
- [7] Hass J., Wang S. C. and Zhou Q., On finiteness of the number of boundary slopes of immersed surfaces in 3-manifolds, Proc. Amer. Math. Soc. 130 (2002), no. 6, 1851-1857.
- [8] Hatcher A. E., On the boundary curves of incompressible surfaces, Pacific J. Math. 99 (1982), no. 2, 373-377.
- [9] Hempel J., 3-manifolds as viewed from the curve complex, Topology 40 (2001), no. 3, 631-657.
- [10] Li T., Saddle tangencies and the distance of Heegaard splittings, Algebr. Geom. Topol. 7 (2007), 1119-1134.
- [11] ——, Heegaard surfaces and the distance of amalgamation, Geom. Topol. 14 (2010), no. 4, 1871-1919.
- [12] Li T., Qiu R. F., On the degeneration of tunnel numbers under a connected sum, Trans. Amer. Math. Soc. 368 (2016), no. 4, 2793-2807.
- [13] Li T., Qiu R. F. and Wang S. C., A quadratic bound on the number of boundary slopes of essential surfaces with bounded genus, Geom. Dedicata 147 (2010), 131-138.
- [14] Masur H. and Minsky Y.N., Geometry of the complex of curves. I. Hyperbolicity, Invent. Math. 138 (1999), no. 1, 103-149.
- [15] Minsky Y. N., Moriah Y., Schleimer S., High distance knots, Algebr. Geom. Topol. 7 (2007), 1471-1483.
- [16] Moriah Y., A note on satellites and tunnel number, Kobe J. Math. 8 (1991), no. 1, 73-79.
- [17] Morimoto K., On the super additivity of tunnel number of knots, Math. Ann. 317 (2000), no. 3, 489-508.
- [18] Scharlemann M., Local detection of strongly irreducible Heegaard splittings, Topology Appl. 90 (1998), 135-147.
- [19] ——, Proximity in the curve complex: boundary reduction and bicompressible surfaces, Pacific J. Math. 228 (2006), no. 2, 325-348.
- [20] Scharlemann M. and Thompson A., Thin position for 3-manifolds, Geometric topology (Haifa, 1992), 231-238, Contemp. Math., 164, Amer. Math. Soc., Providence, RI, 1994.
- [21] Scharlemann M. and Tomova M., Alternate Heegaard genus bounds distance, Geom. Topol. 10 (2006), 593-617.
- [22] Schultens J., Additivity of tunnel number for small knots, Comment. Math. Helv. 75 (2000), no. 3, 353-367.