On the special role of class-selective neurons in early training

Omkar Ranadive [email protected]
Alchera X
Northwestern University Nikhil Thakurdesai [email protected]
Independent Researcher Ari S Morcos [email protected]
Meta AI (FAIR) Matthew Leavitt²²footnotemark: 2 [email protected]
MosaicML Stéphane Deny²²footnotemark: 2 [email protected]
Aalto University Corresponding authorCo-last authors

Abstract

It is commonly observed that deep networks trained for classification exhibit class-selective neurons in their early and intermediate layers. Intriguingly, recent studies have shown that these class-selective neurons can be ablated without deteriorating network function. But if class-selective neurons are not necessary, why do they exist? We attempt to answer this question in a series of experiments on ResNet-50s trained on ImageNet. We first show that class-selective neurons emerge during the first few epochs of training, before receding rapidly but not completely; this suggests that class-selective neurons found in trained networks are in fact vestigial remains of early training. With single-neuron ablation experiments, we then show that class-selective neurons are important for network function in this early phase of training. We also observe that the network is close to a linear regime in this early phase; we thus speculate that class-selective neurons appear early in training as quasi-linear shortcut solutions to the classification task. Finally, in causal experiments where we regularize against class selectivity at different points in training, we show that the presence of class-selective neurons early in training is critical to the successful training of the network; in contrast, class-selective neurons can be suppressed later in training with little effect on final accuracy. It remains to be understood by which mechanism the presence of class-selective neurons in the early phase of training contributes to the successful training of networks.

1 Introduction

A significant body of research has attempted to understand the role of single neuron class-selectivity in the function of artificial (Zhou et al., 2015; Radford et al., 2017; Bau et al., 2017; Morcos et al., 2018; Olah et al., 2018; Rafegas et al., 2019; Dalvi et al., 2019; Meyes et al., 2019; Dhamdhere et al., 2019; Leavitt & Morcos, 2020a; Kanda et al., 2020; Leavitt & Morcos, 2020b), and biological (Sherrington, 1906; Adrian, 1926; Granit, 1955; Hubel & Wiesel, 1959; Barlow, 1972) neural networks. Neurons responding selectively to specific classes are typically found throughout networks trained for image classification, even in early and intermediate layers. Interestingly, these class-selective neurons can be ablated (i.e. their activation set to 0; Morcos et al. 2018) or class selectivity substantially reduced via regularization Leavitt & Morcos (2020a) with little consequence to overall network accuracy—sometimes even improving it. These findings demonstrate that class selectivity is not necessary for network function, but it remains unknown why class selectivity is learned if it is largely not necessary for network function.

One notable limitation of many previous studies examining selectivity is that they have largely overlooked the temporal dimension of neural network training; single unit ablations are performed only at the end of training (Morcos et al., 2018; Amjad et al., 2018; Zhou et al., 2018; Meyes et al., 2019; Kanda et al., 2020), and selectivity regularization is mostly constant throughout training (Leavitt & Morcos, 2020a; b). However, there are numerous studies demonstrating substantial differences in training dynamics during the early vs. later phases of neural network training (Sagun et al., 2018; Gur-Ari et al., 2018; Golatkar et al., 2019; Frankle et al., 2020b; Jastrzebski et al., 2020). Motivated by these studies, we asked a series of questions about the dynamics of class selectivity during training in an attempt to elucidate why neural networks learn class selectivity: When in training do class-selective neurons emerge? Where in networks do class-selective neurons first emerge? Is class selectivity uniformly (ir)relevant for the entirety of training, or are there critical periods during which class selectivity impacts later network function? We addressed these questions in experiments conducted in ResNet-50 trained on ImageNet, which led to the following results (Fig 1):

•

The emergence of class-selective neurons in early and intermediate layers follow a non-trivial and surprising path: after a prominent rise during the first few epochs of training, class selectivity subsides quickly during the next few epochs, before returning to a baseline level specific to each layer.
•

During this early training phase where average class selectivity is high in early and intermediate layers, class-selective neurons in these layers are much more important for network function compared to later in training, as assessed with single-unit ablation.
•

During this early, high-selectivity phase of training, the representations of early and latter layers are much more similar than during later in training, implying that selectivity in early layers could be leveraged to solve the classification problem by transmission to the latter layers via skip connections.
•

In a causal experiment where we prevent class selectivity from rising sharply in early and intermediate layers during the first epochs of training, we show the network training accuracy suffers from the suppression of this phenomenon. This indicates that the rapid emergence of class-selective neurons in early and intermediate layers during the first phase of training plays a useful role in the successful training of the network.

Together, our results demonstrate that class-selective neurons in early and intermediate layers of deep networks are a vestige of their emergence during the first few epochs of training, during which they play a useful role to the successful training of the network.

Refer to caption — (a) Dynamics of class selectivity throughout training

2 Related Work

2.1 The Role of Selectivity in Deep Networks

Numerous studies have examined the causal role of class selectivity for network performance, nearly all of which have relied on single unit ablation as their method of choice. Morcos et al. 2018 examined a number of different CNN architectures trained to perform image classification and found that class selectivity for individual units was uncorrelated (or negatively correlated) with test-set generalization. This finding was replicated by Kanda et al. 2020 and Amjad et al. 2018, though the latter study also observed that the effects can vary when ablating groups of neurons, in which case, selectivity can be beneficial. Furthermore, Zhou et al. 2018 found that ablating class-selective units can impair accuracy for specific classes, but a corresponding increase in accuracy for other classes can leave overall accuracy unaffected.

Studies using NLP models have also shown varied results. Donnelly & Roegiest 2019 ablated the "sentiment neuron" reported by Radford et al. 2017 and found mixed effects on performance, while Dalvi et al. 2019 found networks were more negatively impacted when class-selective units were ablated.

Of particular importance is the work of Leavitt & Morcos 2020a, which introduced a regularizer for fine-grained control over the amount of selectivity learned by a network. This regularizer makes it possible to test whether the presence of selectivity is beneficial, and whether networks need to learn selectivity, two questions that ablation methods cannot test. By regularizing to discourage or promote the learning of selectivity, they found that selectivity is neither strictly necessary nor sufficient for network performance. In follow-up work they also showed that promoting class selectivity with their regularizer confers robustness to adversarial attacks, while reducing selectivity confers robustness to naturalistic perturbations (Leavitt & Morcos, 2020b). However, they did not scale their experiments beyond ResNet18 (He et al., 2016) and Tiny-ImageNet (Fei-Fei et al., 2015). Additionally, with the exception of one set of controls in which the regularizer was linearly warmed up during the first five epochs of training (Leavitt & Morcos, 2020a), they did not examine the dynamics of class selectivity’s importance over the training process. Most importantly, they did not attempt to address why selectivity is learned.

2.2 The Early Phase of Neural Network Training

A breadth of approaches have been used to characterize the differences between the early and later phases of neural network training and highlight the impact of early-phase interventions on late-phase behavior. The application of iterative magnitude pruning in the Lottery Ticket approach (Frankle & Carbin, 2018) requires rewinding to a sufficiently early point in training—within the first few thousand iterations—to prune without negatively impacting model quality (Frankle et al., 2020a; b). The local loss landscape also changes rapidly early in training (Sagun et al., 2018); the subspace in which gradient descent occurs quickly shrinks into a very restricted subspace (Gur-Ari et al., 2018). Achille et al. 2018 characterized a critical period of training by perturbing the training process with corrupted data labels early in training and found that the network’s final performance was irreparably impaired. Similarly, Golatkar et al. 2019 found that removing some forms of regularization after the early phase of training, or imposing them after the early phase, had little effect on network performance. These results emphasize the outsize importance of interventions applied during the early phase of neural network training, and the relevance of the early phase of training for understanding why networks learn class selectivity.

3 Approach

3.1 Model Architecture

We use ResNet-50s (He et al., 2016) trained on ImageNet for all our experiments. ResNet-50s are formed of a convolutional stem followed by four successive modules. We define the early and intermediate layers as the layers present inside the early and intermediate modules shown in Fig 2(a). Each module is composed of multiple bottleneck layers. Each bottleneck layer contains one residual (or "skip") connection to the next bottleneck layer. Further details on the structure of the model can be found in Appendix A.1. Details on model training can be found in Appendix A.2.

3.2 Class Selectivity Index

We refer to the individual channels of the bottleneck layers as "units" or "neurons" for the purpose of our experiments (Fig 2(b)). We compute a class selectivity index for each unit of each bottleneck layer of every module. This index is a measure of how much the unit favors a specific ImageNet class. It is defined as (Leavitt & Morcos, 2020a):

SI=\frac{\mu_{max}-\mu_{-max}}{\mu_{max}+\mu_{-max}+\epsilon}

(1)

where $\mu_{max}$ is the largest class-conditional mean activation over all possible classes, averaged within samples of a class, and averaged over spatial locations for that channel, $\mu_{-max}$ is the mean response to the remaining (i.e. non- $\mu_{max}$ ) classes, and $\epsilon$ is a small value to prevent division by zero (here $10^{-6}$ ) in the case of a dead unit. All activations are assumed to be positive because they are extracted after a ReLU layer. The selectivity index can range from 0 to 1. A unit with identical average activity for all classes would have a selectivity of 0, and a unit that only responds to a single class would have a selectivity of 1. We compute such class selectivity indices across all epochs of training and then we perform various experiments to see how class selectivity affects learning at different stages of training.

3.3 Quantifying the Relevance of Class-Selective Neurons

We used the following methods to determine whether class-selective neurons are relevant to network function.

Single neuron ablation:

This method consists in setting the channel outputs of the bottleneck layers to 0. In our experiments, we perform progressive ablation of the channels in all bottleneck layer of a given module, ordered by class selectivity index and starting with the most class-selective channels, or by random ordering of channels (random control condition). On a fully-trained ResNet-50, we found that ablation of class-selective neurons is less damaging to network accuracy than ablation of random neurons (Appendix A.3), consistent with previous reports.

Class-selectivity regularizer:

We used Leavitt & Morcos (2020a)’s selectivity regularizer to either promote or suppress the emergence of class-selective neurons in different modules and at different epochs of training. The regularization term is as follows:

\mu_{SI}=\frac{1}{M}\sum_{m}^{M}\frac{1}{B}\sum_{b}^{B}SI_{b}

(2)

where M is the total number of modules, m is the current module, B is the total number of bottleneck layer in current module M and b is the current bottleneck layer. $SI_{b}$ represents the selectivity indices of the channels in the current bottleneck layer b.

This term can be added to the loss function as follows:

loss=-\sum_{c}^{C}y_{c}\log(\hat{y_{c}})-\alpha\mu_{SI}

(3)

The left hand term of the loss function is the cross-entropy loss where C is the total number of classes, c is class index, $y_{c}$ is true class label and $\hat{y_{c}}$ is the predicted class probability. The right hand side of the loss function is the regularization term ( $-\alpha\mu_{SI}$ ). The $\alpha$ parameter controls the strength of the regularizer. A negative value of $\alpha$ will regularize against selectivity and a positive value of $\alpha$ will regularize in favor of selectivity.

4 Results

4.1 Class-selective neurons emerge during early epochs of training

We began by examining the dynamics of class selectivity in each module over the course of training. It is possible that selectivity follows a similar pattern as accuracy: increasing quickly over the first few epochs, then gradually saturating over the remainder of training. We consider this to be the most likely scenario, as it is follows the dynamics of early and rapid change followed by stabilization observed in many other quantities during training. Indeed, class selectivity sharply rises during the first epoch of training (Fig 3; analysis of evolution of selectivity throughout training for individual bottleneck layers can be found in Appendix A.4), but after that, the effect varies depending on layer depth: earlier layers (Modules 4-6) show rapid decreases in selectivity over 3-5 epochs, followed by slow approach to an asymptote over the remainder of training. In contrast, latter layers (Module 7) do not exhibit any substantial decrease in selectivity after the initial jump, and selectivity remains high in latter layers throughout training. These dynamic, depth-dependent changes in selectivity during the first few epochs of training indicate that the role of selectivity could also vary during training, and in a layer-dependent manner.

4.2 Class-selective neurons support the decision of the network more during early epochs of training than latter epochs

In order to determine whether the role of class selectivity in network behavior varies over the course of training, we performed class-selective and random ablations (Section 3.3) at different points during training and measured the effect on accuracy. We normalize accuracy between 0 and 100 so that the curves for each epoch can be plotted together and compared. The right-hand side of Fig 5 shows that the effect on accuracy is more prominent in the earlier epochs of class-selective ablations. Compared to this, random ablation curves do not show any significant difference across epochs.

To quantify this phenomenon further, we calculated the area under the ablation curves for each epoch, obtaining one value per epoch summarizing the sensitivity of the network to ablation, and plotted these values across epochs. If class-selective ablations were more damaging in the earlier epochs, then this would correspond to less area under the curve (AUC) in the earlier epochs compared to the latter epochs i.e., the curve should show a positive slope across epochs. As illustrated in Fig 5, the class-selective curves for module 4 and module 6 indeed show a positive slope which is steeper especially at early epochs compared to the random ablation curve which is relatively flat. These results indicate that class-selective neurons are more important in the earlier epochs of training compared to the latter epochs as they are more damaging to the normalized accuracy in the earlier epochs compared to latter epochs. Interestingly, module 5 doesn’t exhibit this trend as clearly and the effect is much stronger in module 6.

However, the AUC curves in Fig 5 also show that random ablations remain more damaging than class-selective ablations at all epochs, as they exhibit overall less area under the curve. The important distinction is that class-selective ablations are more damaging in the earlier epochs relative to the class-selective ablations in latter epochs while random ablations are roughly equally damaging throughout training. This phenomenon reverses in module 7 (Fig 5), where class-selective ablations are more damaging throughout training, which is expected from the role of these layers to provide class-selective information for the network decision.

4.3 The network is linear at initialization and in early epochs of training, which might explain the emergence of shortcut decision strategies

Why are neurons learning class-selective features in early and intermediate modules during the early epochs of training? Here, we postulated that the network is close to being linear at random weight initialization, such that the neurons of all layers jointly learn to be class-selective, with neurons from latter layers relying on class-selective features emerging in early and intermediate layers, effectively producing crude shortcut decision strategies at these early epochs of training.

To test out this hypothesis, we calculated the Centered Kernel Alignment (CKA) (Kornblith et al., 2019; Nguyen et al., 2020) similarity between all modules. CKA can be used to find representational similarity between different components of a network. The CKA similarity between early module and latter module and between early module and the fully connected layer (FC) is indeed high during the first few epochs, and then recedes to a low level for the rest of the training (Fig 6). The CKA similarity across all other pairs of modules shows a similar trend (Appendix A.5).

From these results, the following picture emerges: at the early stages of training where the network is close to being linear, all layers jointly learn class-selective features, with latter layers piggy-backing on class-selective features learned by early layers.

4.4 The emergence of class-selective neurons early in training is essential to successful training: suppressing it impairs learning

Is the emergence of class-selective neurons early in training crucial to learning? To test whether the spike observed in selectivity during the early epochs (Fig 3) is important to learning, we conducted a series of regularization experiments. The question which we want to answer is - Will the model be able to learn if we regularize against selectivity and suppress that spike in selectivity in the early epochs?

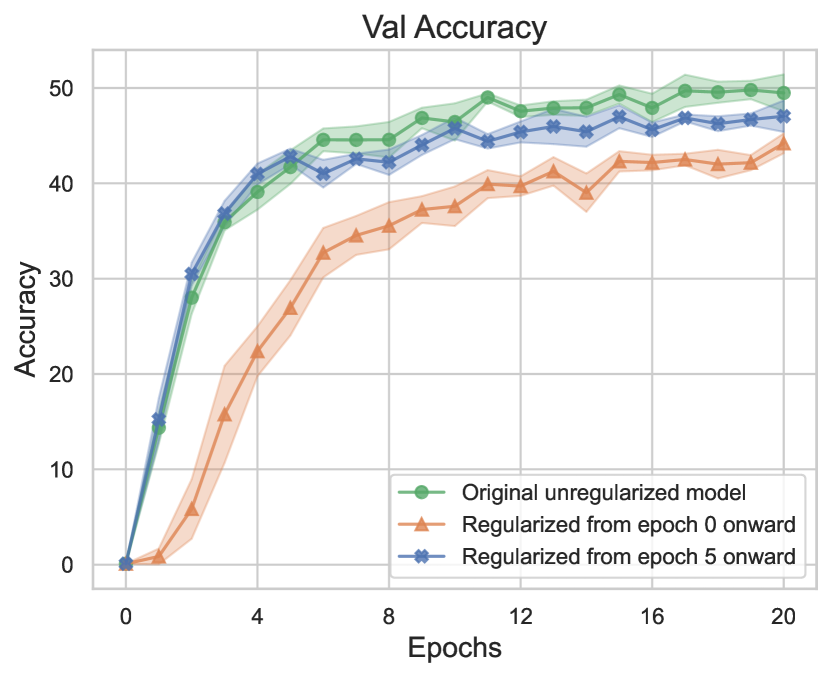
We performed experiments to test two scenarios: regularizing against class-selectivity from epoch 0 onward VS regularizing from epoch 5 onward. Epoch 0 is the randomly initialized model and epoch 5 is approximately after the spike in selectivity (Fig 3). We hypothesized that if selectivity is important to learning in those early epochs, then regularizing from epoch 0 onward should lead to a greater decrease in the model accuracy later on in training as compared to regularizing from epoch 5 onward. As we already know that selectivity is important to learning in the latter module and as we are interested in understanding the emergence of class-selective neurons in early and intermediate modules, we only regularized the early and intermediate modules against selectivity.

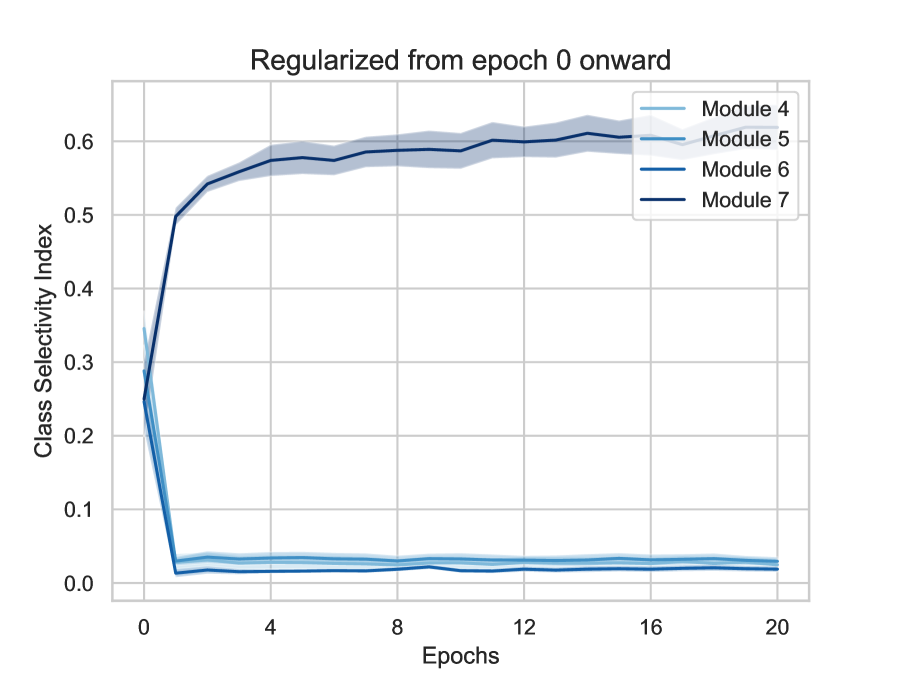
We used a regularizing strength of $\alpha=-20$ and found that the regularizer prevents the peak of emergence of class-selective neurons in early epochs of training and that it impairs training and validation accuracy throughout training if regularized from epoch 0 (Fig 7). However, in the second scenario where the regularizer was turned on from epoch 5 onward, the model performed almost as well as the original unregularized model. These results indicate that the emergence of class-selective neurons in intermediate modules in early epochs of training is a phenomenon that plays a crucial role in the correct training of the network. Other sets of experiments with different values of $\alpha$ can be found in Appendix A.6.1. It is worth noting that Leavitt & Morcos (2020a) found that regularizing beyond the range of $\alpha=[-1,-5]$ —depending on the model and dataset—had significant negative effects on network performance, while we were able to increase the magnitude of $\alpha$ all the way to $-20$ with minimal effect on network performance, so long as we did not regularize until epoch 5. Regularizing against class selectivity in early epochs also degrades performance of smaller versions of ResNets i.e., ResNet18 and ResNet34 (Appendix A.8.3).

The model never fully recovers the performance if the regularization is kept on, but if the regularization is turned off after the first few epochs of training then the network is slowly able to recover from the perturbation after 20+ epochs of training (Appendix A.6.3).

4.5 Class Selectivity is most important during the first epoch of training

In the previous set of experiments, we regularized against class-selectivity from epoch 5 onward, which starts after the spike in selectivity. But the next question which arises is what happens if we regularize in-between epochs 0 and 5? Fig 8 shows that learning is only impaired if the model is regularized from epoch 0 onward. Models regularized from epoch 1-5 onward performed similarly to the unregularized model, suggesting that the most critical phase for class selectivity happens during the very first epoch of training.

4.6 Regularizing in favor of class selectivity does not improve learning

As class-selective neurons are crucial to learning in the early epochs, could increasing the selectivity in those early epochs further improve learning? To answer this question, we regularized in favor of class-selectivity (i.e. with positive values of $\alpha$ ) during those early epochs. We found that increasing the selectivity in those early epochs did not improve performance further (Fig 15, Fig 16). Therefore, both an increase and a decrease in selectivity is harmful to learning, suggesting that the network roughly learns the "right" amount of selectivity for optimal learning. More details on the regularization for selectivity experiments can be found in Appendix A.6.2.

4.7 Effect of class selectivity regularization on the balance of class representation

We next explored how the regularization in favor and against class selectivity affects the balance of class representation in the predictions of the network. We found that, both increasing and decreasing class selectivity in early and intermediate modules resulted in a poorer diversity of class representation in the predictions of the network (Appendix A.6.4). This effect lasted for the few first epochs of training, after which it was no longer visible. We conclude that tampering with class selectivity in early and intermediate layers perturbs the correct learning of the network by over-representing certain classes at the prediction stage during a period which is apparently critical for the correct training of the network.

5 Discussion

Previous experiments have shown that class selectivity in individual units may not be necessary for high accuracy converged solutions (Morcos et al., 2018; Amjad et al., 2018; Donnelly & Roegiest, 2019; Leavitt & Morcos, 2020a; Kanda et al., 2020; Leavitt & Morcos, 2020b). We sought to determine why class selectivity is learned if it is not necessary. In a series of experiments examining the training dynamics of ResNet50 trained on ImageNet, we found that class selectivity in early and intermediate layers is actually necessary during a critical period early in training in order for the network to learn high accuracy converged solutions. Specifically, we observed that class selectivity rapidly emerges within the first epoch of training, before receding over the next 2-3 epochs in early and intermediate layers. Ablating class-selective neurons during this critical period has a much greater impact on accuracy than ablating class-selective neurons at the end of training. Furthermore, we used Leavitt & Morcos (2020a)’s selectivity regularizer and found that strongly regularizing against class selectivity—to a degree that Leavitt & Morcos (2020a) found had catastrophic effects on network performance—had a negligible effect on network performance if regularization doesn’t occur in the initial epochs. We also found that the representations of early and latter layers are much more similar during the early critical period of training compared to later in training, indicating that selectivity in early layers may be leveraged by latter layers in order to solve the classification problem early in training. Taken together, our results show that class-selective neurons in early and intermediate layers of deep networks are a vestige of their emergence during a critical period early in training, during which they are necessary for successful training of the network.

One limitation of the present work is that it is limited to ResNet-50 trained on ImageNet. While Leavitt & Morcos (2020a) found that their results were consistent across a breadth of CNN architectures and image classification datasets, it is possible that our findings may not generalize to networks trained on NLP tasks, in which single neuron selectivity is also a topic of interest.

Our observations add to the list of phenomena occurring during the critical phase early in training (see related work section 2), and prompts more investigations regarding this phase. In particular, it would be interesting to understand why the emergence of class-selectivity is necessary in this early phase of training, and whether this phenomenon connects to other critical-period phenomena, such as the emergence of lottery ticket subnetworks (Frankle & Carbin, 2018; Paul et al., 2022), and critical learning flexibility (Achille et al., 2018).

References

Achille et al. (2018) Alessandro Achille, Matteo Rovere, and Stefano Soatto. Critical Learning Periods in Deep Networks. September 2018. URL https://openreview.net/forum?id=BkeStsCcKQ.
Adrian (1926) E. D. Adrian. The impulses produced by sensory nerve endings. The Journal of Physiology, 61(1):49–72, March 1926. ISSN 0022-3751. URL https://www.ncbi.nlm.nih.gov/pmc/articles/PMC1514809/.
Amjad et al. (2018) Rana Ali Amjad, Kairen Liu, and Bernhard C. Geiger. Understanding Individual Neuron Importance Using Information Theory. April 2018. URL https://arxiv.org/abs/1804.06679v3.
Barlow (1972) H B Barlow. Single Units and Sensation: A Neuron Doctrine for Perceptual Psychology? Perception, 1(4):371–394, December 1972. ISSN 0301-0066. doi: 10.1068/p010371. URL https://doi.org/10.1068/p010371.
Bau et al. (2017) David Bau, Bolei Zhou, Aditya Khosla, Aude Oliva, and Antonio Torralba. Network Dissection: Quantifying Interpretability of Deep Visual Representations. In 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pp. 3319–3327, Honolulu, HI, July 2017. IEEE. ISBN 978-1-5386-0457-1. doi: 10.1109/CVPR.2017.354. URL http://ieeexplore.ieee.org/document/8099837/.
Dalvi et al. (2019) Fahim Dalvi, Nadir Durrani, Hassan Sajjad, Yonatan Belinkov, Anthony Bau, and James Glass. What Is One Grain of Sand in the Desert? Analyzing Individual Neurons in Deep NLP Models. Proceedings of the AAAI Conference on Artificial Intelligence, 33(01):6309–6317, July 2019. ISSN 2374-3468. doi: 10.1609/aaai.v33i01.33016309. URL https://aaai.org/ojs/index.php/AAAI/article/view/4592.
Dhamdhere et al. (2019) Kedar Dhamdhere, Mukund Sundararajan, and Qiqi Yan. How Important is a Neuron. In International Conference on Learning Representations, 2019. URL https://openreview.net/forum?id=SylKoo0cKm.
Donnelly & Roegiest (2019) Jonathan Donnelly and Adam Roegiest. On Interpretability and Feature Representations: An Analysis of the Sentiment Neuron. In Leif Azzopardi, Benno Stein, Norbert Fuhr, Philipp Mayr, Claudia Hauff, and Djoerd Hiemstra (eds.), Advances in Information Retrieval, Lecture Notes in Computer Science, pp. 795–802, Cham, 2019. Springer International Publishing. ISBN 978-3-030-15712-8. doi: 10.1007/978-3-030-15712-8_55.
Fei-Fei et al. (2015) Li Fei-Fei, Andrej Karpathy, and Justin Johnson. Tiny imagenet visual recognition challenge, 2015. URL https://tiny-imagenet.herokuapp.com/.
Frankle & Carbin (2018) Jonathan Frankle and Michael Carbin. The Lottery Ticket Hypothesis: Finding Sparse, Trainable Neural Networks. arXiv:1803.03635 [cs], March 2018. URL http://arxiv.org/abs/1803.03635. arXiv: 1803.03635.
Frankle et al. (2020a) Jonathan Frankle, Gintare Karolina Dziugaite, Daniel Roy, and Michael Carbin. Linear mode connectivity and the lottery ticket hypothesis. In International Conference on Machine Learning, pp. 3259–3269. PMLR, 2020a.
Frankle et al. (2020b) Jonathan Frankle, David J. Schwab, and Ari S. Morcos. The Early Phase of Neural Network Training. arXiv:2002.10365 [cs, stat], February 2020b. URL http://arxiv.org/abs/2002.10365. arXiv: 2002.10365.
Golatkar et al. (2019) Aditya Sharad Golatkar, Alessandro Achille, and Stefano Soatto. Time Matters in Regularizing Deep Networks: Weight Decay and Data Augmentation Affect Early Learning Dynamics, Matter Little Near Convergence. In Advances in Neural Information Processing Systems, volume 32. Curran Associates, Inc., 2019. URL https://proceedings.neurips.cc/paper/2019/hash/87784eca6b0dea1dff92478fb786b401-Abstract.html.
Granit (1955) Ragnar Granit. Receptors and sensory perception. Receptors and sensory perception. Yale University Press, New Haven, CT, US, 1955.
Gur-Ari et al. (2018) Guy Gur-Ari, Daniel A. Roberts, and Ethan Dyer. Gradient Descent Happens in a Tiny Subspace, December 2018. URL http://arxiv.org/abs/1812.04754. arXiv:1812.04754 [cs, stat].
He et al. (2016) Kaiming He, Xiangyu Zhang, Shaoqing Ren, and Jian Sun. Deep residual learning for image recognition. In Proceedings of the IEEE conference on computer vision and pattern recognition, pp. 770–778, 2016.
Hubel & Wiesel (1959) D. H. Hubel and T. N. Wiesel. Receptive fields of single neurones in the cat’s striate cortex. The Journal of Physiology, 148(3):574–591, 1959. ISSN 1469-7793. doi: 10.1113/jphysiol.1959.sp006308. URL https://physoc.onlinelibrary.wiley.com/doi/abs/10.1113/jphysiol.1959.sp006308.
Jastrzebski et al. (2020) Stanislaw Jastrzebski, Maciej Szymczak, Stanislav Fort, Devansh Arpit, Jacek Tabor, Kyunghyun Cho, and Krzysztof Geras. The Break-Even Point on Optimization Trajectories of Deep Neural Networks, February 2020. URL http://arxiv.org/abs/2002.09572. arXiv:2002.09572 [cs, stat].
Kanda et al. (2020) Yuta Kanda, Kota S. Sasaki, Izumi Ohzawa, and Hiroshi Tamura. Deleting object selective units in a fully-connected layer of deep convolutional networks improves classification performance. arXiv:2001.07811 [q-bio], January 2020. URL http://arxiv.org/abs/2001.07811. arXiv: 2001.07811.
Kornblith et al. (2019) Simon Kornblith, Mohammad Norouzi, Honglak Lee, and Geoffrey Hinton. Similarity of neural network representations revisited. In International Conference on Machine Learning, pp. 3519–3529. PMLR, 2019.
Leavitt & Morcos (2020a) Matthew L Leavitt and Ari Morcos. Selectivity considered harmful: evaluating the causal impact of class selectivity in dnns. arXiv preprint arXiv:2003.01262, 2020a.
Leavitt & Morcos (2020b) Matthew L. Leavitt and Ari Morcos. Linking average- and worst-case perturbation robustness via class selectivity and dimensionality, 2020b. URL http://arxiv.org/abs/2010.07693. arXiv:2010.07693 [cs, stat].
Meyes et al. (2019) Richard Meyes, Melanie Lu, Constantin Waubert de Puiseau, and Tobias Meisen. Ablation Studies in Artificial Neural Networks. arXiv:1901.08644 [cs, q-bio], February 2019. URL http://arxiv.org/abs/1901.08644. arXiv: 1901.08644.
Morcos et al. (2018) Ari S. Morcos, David G.T. Barrett, Neil C. Rabinowitz, and Matthew Botvinick. On the importance of single directions for generalization. In International Conference on Learning Representations, 2018. URL https://openreview.net/forum?id=r1iuQjxCZ.
Nguyen et al. (2020) Thao Nguyen, Maithra Raghu, and Simon Kornblith. Do wide and deep networks learn the same things? uncovering how neural network representations vary with width and depth. arXiv preprint arXiv:2010.15327, 2020.
Olah et al. (2018) Chris Olah, Arvind Satyanarayan, Ian Johnson, Shan Carter, Ludwig Schubert, Katherine Ye, and Alexander Mordvintsev. The Building Blocks of Interpretability. Distill, 3(3):e10, March 2018. ISSN 2476-0757. doi: 10.23915/distill.00010. URL https://distill.pub/2018/building-blocks.
Paszke et al. (2019) Adam Paszke, Sam Gross, Francisco Massa, Adam Lerer, James Bradbury, Gregory Chanan, Trevor Killeen, Zeming Lin, Natalia Gimelshein, Luca Antiga, et al. Pytorch: An imperative style, high-performance deep learning library. Advances in neural information processing systems, 32, 2019.
Paul et al. (2022) Mansheej Paul, Brett W Larsen, Surya Ganguli, Jonathan Frankle, and Gintare Karolina Dziugaite. Lottery tickets on a data diet: Finding initializations with sparse trainable networks. arXiv preprint arXiv:2206.01278, 2022.
Radford et al. (2017) Alec Radford, Rafal Jozefowicz, and Ilya Sutskever. Learning to Generate Reviews and Discovering Sentiment. arXiv:1704.01444 [cs], April 2017. URL http://arxiv.org/abs/1704.01444. arXiv: 1704.01444.
Rafegas et al. (2019) Ivet Rafegas, Maria Vanrell, Luis A. Alexandre, and Guillem Arias. Understanding trained CNNs by indexing neuron selectivity. Pattern Recognition Letters, pp. S0167865519302909, October 2019. ISSN 01678655. doi: 10.1016/j.patrec.2019.10.013. URL http://arxiv.org/abs/1702.00382. arXiv: 1702.00382.
Sagun et al. (2018) Levent Sagun, Utku Evci, V. Ugur Guney, Yann Dauphin, and Leon Bottou. Empirical Analysis of the Hessian of Over-Parametrized Neural Networks, May 2018. URL http://arxiv.org/abs/1706.04454. arXiv:1706.04454 [cs].
Sherrington (1906) Charles S. Sherrington. The integrative action of the nervous system. The integrative action of the nervous system. Yale University Press, New Haven, CT, US, 1906. doi: 10.1037/13798-000.
Subramanian (2021) Anand Subramanian. torch_cka, 2021. URL https://github.com/AntixK/PyTorch-Model-Compare.
Waskom (2021) Michael L Waskom. Seaborn: statistical data visualization. Journal of Open Source Software, 6(60):3021, 2021.
Zhou et al. (2015) Bolei Zhou, Aditya Khosla, Agata Lapedriza, Aude Oliva, and Antonio Torralba. Object Detectors Emerge in Deep Scene CNNs. In International Conference on Learning Representations, April 2015. URL http://arxiv.org/abs/1412.6856. arXiv: 1412.6856.
Zhou et al. (2018) Bolei Zhou, Yiyou Sun, David Bau, and Antonio Torralba. Revisiting the Importance of Individual Units in CNNs via Ablation. arXiv:1806.02891 [cs], June 2018. URL http://arxiv.org/abs/1806.02891. arXiv: 1806.02891.

Appendix A Appendix

A.1 Structure of ResNet-50

We define early, intermediate, and latter layers as the layers present in the early, intermediate, and latter modules respectively. (Fig 9(a)). These modules are made up of bottleneck layers (Fig 9(b), 9(c)). We calculate class selectivity index on individual channels extracted after the ReLU layer of each bottleneck layer.

A.2 Model Training

We trained 10 instances of ResNet-50 on ImageNet using standard training procedure using PyTorch (Paszke et al., 2019). All instances were trained for 90 epochs with a batch size of 256, learning rate of 0.1, weight decay of 1e-4, and momentum of 0.9.

The class selectivity indices were calculated over the validation set of 50k images for every epoch from epoch 0 to epoch 90. All plots were generated using Seaborn Library (Waskom, 2021). Accuracies shown in all plots are top-1 ImageNet training/validation accuracy. Error shades in all plots represent the 95% confidence interval (CI) of the mean.

A.3 Class-Selective Ablations on a fully-trained network are less damaging than Random Ablations

We find that in the early and intermediate modules (modules 4, 5, 6), an ablation of units ordered by their class-selectivity rank (i.e. most class-selective units ablated first) affects the network accuracy less than a control experiment where we ablate channels in a random order (Fig 10), consistent with the findings of Morcos et al. (2018). This result is paradoxical, as it seems to indicate that although class-selective channels emerge during training in early modules, these channels do not support the decision of the fully-trained network. In the latter module (module 7), we find that class-selective channels do support the decision of the network more than random channels (Fig 10), consistent with our intuition (i.e. the layers near the end of the network do need to be class-selective for good performance) and previous findings by Morcos et al. (2018).

A.4 Class Selectivity Index Across Bottleneck Layers

Fig 11 shows the evolution of class selectivity throughout training for every bottleneck layer inside each module. An interesting observation here is that for module 6 and 7, the bottleneck layers are increasingly class-selective with network depth i.e, the latter bottleneck layers are more selective than the earlier ones inside those modules. For module 5, they exhibit roughly the same amount of selectivity later in training. However, for module 4, this trend is reversed and the bottleneck layers are decreasingly class-selective with network depth.

A.5 Centered Kernel Alignment (CKA) Analysis

To check the representational similarity between the modules at different stages of learning we used the Centered Kernel Alignment (CKA) (Kornblith et al., 2019; Nguyen et al., 2020) metric. To perform the CKA analysis we used the torch_cka library (Subramanian, 2021). The CKA similarity across all cases is high during the early epochs of training (Fig 12) which suggests that the network is jointly learning to be class-selective, with neurons from latter layers relying on the class-selective features from early and intermediate layers to produce crude shortcut strategies.

Fig 12(a) shows that module 4 has a high representation similarity with module 5, 6, 7 in the first few epochs which then recedes to a low level for the rest of the training period. After the similarity level recedes, consistent with our intuition, the similarity decreases with increasing network depth i.e., after the first few epochs, module 4 is most similar to module 5, then to module 6, and then module 7. The remaining cases show a similar trend (Fig 12(b), Fig 12(c)).

A.6 Regularization Experiments

A.6.1 Regularizing against selectivity

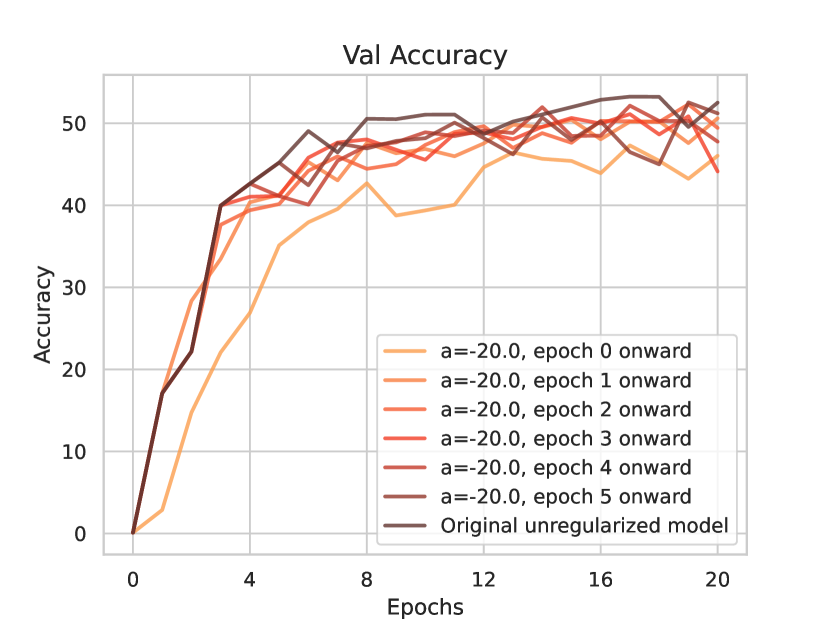
We conduct a set of regularization experiments where we regularize against selectivity for different values of $\alpha$ . We want to test two scenarios: Regularizing from epoch 0 onward VS regularizing from epoch 5 onward (epoch 5 is approximately after the spike in selectivity). We only regularize the early and intermediate modules (i.e. module 4, 5, 6) as we are interested in understanding the emergence of class selectivity in those modules. Also, regularizing only the early and intermediate modules allows us to use a higher values of $\alpha$ without squashing the network accuracy completely. The results for different values of $\alpha$ are shown in Fig 13. The following main observations can be made:

•

For $\alpha$ = -1.0, there isn’t much difference between the unregularized model and the models regularized from epoch 0 and epoch 5 onward.
•

For $\alpha$ = -5.0, the model regularized from epoch 0 onward performed worse than the one regularized from epoch 5 onward.
•

For $\alpha$ = -10.0, -20.0, the models regularized from epoch 0 onward performed significantly worse than the ones regularized from epoch 5 onward.

These results indicate that selectivity is important for learning in those early epochs and suppressing it by a significant amount impairs learning.

A.6.2 Regularizing for selectivity

If selectivity is important for learning in the early epochs, then does increasing selectivity further in early epochs improve learning? To test this, we conducted experiments in which we regularized for selectivity with different values of $\alpha$ . First, we tried regularizing the early and intermediate modules with large values of $\alpha$ (+10, +20) for the first four epochs, after which the regularizer was turned off. The latter module (module 7) was not regularized for selectivity. We found that in both cases, the model performed much worse as compared to the original unregularized model (Fig 15). The large $\alpha$ causes the selectivity index to go close to 1.0. Also, as module 7 was not regularized, its selectivity index ends up being lower than the other modules (Fig 15).

Next, we re-did the experiment with smaller values of $\alpha$ (+1, +5) and we also decided to regularize module 7 for selectivity along with the early and intermediate modules. This time, we tried the experiment on two scenarios:

•

Turning the regularizer on for first four epochs for all modules with $\alpha$ = +1, +5.
•

Turning the regularizer on only for epoch 1 (as it is the most important (Section 4.5)) for all modules with $\alpha$ = +1, +5.

In all cases, the increase in selectivity was harmful to performance (Fig 16). So overall, the results show that increasing selectivity does not improve performance. Therefore, both an increase and a decrease in selectivity is harmful to learning.

A.6.3 Can the model eventually recover its performance from the effects of regularization?

The regularization experiments conducted in Section 4.4 and Appendix A.6.1 are done till epoch 20. So, this naturally leads to the following questions:

Does the model eventually recover from the effects of regularization if it is trained for more epochs?

We trained the models regularized from epoch 0 onward and the one regularized from epoch 5 onward for 60 epochs while keeping the regularizer on with $\alpha$ = -20. The model regularized from epoch 0 onward is never able to recover the lost performance (Fig 17(a)).

Does the model eventually recover from the effects of regularization if the regularization is turned off after the early epochs?

Next, we regularized a third model for only the first four epochs with $\alpha$ = -20 after which the regularizer was turned off. This model was able to eventually recover the lost performance by epoch 20 (Fig 17(b)).

These two experiments confirm that class selectivity plays an important role towards model’s performance.

A.6.4 Effect of regularization on balance of class representation

What happens to the class representation when we regularize against selectivity? To test this, we kept a count of each class predicted by the model on the validation set for each epoch, and then took the mean of top-5 class counts for each epoch. One would expect that if the model is regularized against selectivity then classes won’t be over-represented i.e., the mean of top-5 class counts should be low for each epoch. However, surprisingly, the mean of top-5 class counts is actually higher in case of the model regularized from epoch 0 when compared to the unregularized model (Fig 18). So even if the individual neurons aren’t class-selective, the model ends up over-representing certain classes in the early epochs. We think this might be because if neurons are not class-selective at all, then the model might have difficulty learning in the early epochs and so the model as a whole ends up overfitting to a few classes.

Similarly, when the model is regularized in favor of selectivity, the classes again end up being over-represented. This suggests that tampering with the selectivity in either direction perturbs the correct learning by over-representing classes.

A.7 Analyzing class selectivity at a sub-epoch resolution

To understand how soon class selectivity rises during the first epoch of training, we analyzed selectivity at a sub-epoch resolution (Fig 19). The model was saved 10 times within each epoch, i.e, the model was saved after every 1000 batches of training with a batch size of 128, for the first few epochs. Fig 19(a) shows the evolution of selectivity during the first epoch of training. We can see that the selectivity rises after training the model on the first 2000 batches (Point 0b2 in Fig 19(a)). Fig 19(b) shows the evolution of selectivity at a sub-epoch resolution from epoch 0 to epoch 4. We can observe that the selectivity is most prominent during the first few thousand batches of training after which it starts to settle down.

A.8 Class Selectivity in smaller variants of ResNets

In this section, we investigate whether smaller variants of ResNet (i.e. ResNet18/34) also exhibit similar class selectivity characteristics as a ResNet50. The ResNet18 and ResNet34 variants can also be divided into four modules like the ResNet50 (Fig 9). Both ResNet18 and ResNet34 have fewer layers and also fewer channels in each layer compared to a ResNet50.

A.8.1 Evolution of Class Selectivity in all modules

In both ResNet18 and ResNet34, the rise in selectivity in early epochs can only be observed for module 6 and 7 (Fig 20). The selectivity values then stabilize across all modules just like what was observed in the case of ResNet50. Another interesting observation is that the stabilized class selectivity values for each module are approximately the same across all three ResNet architectures, i.e, for module 7 it is $\approx$ 0.7, for module 6 it is $\approx$ 0.4, for module 5 and 4 it is $\approx$ between 0.2-0.3.

The lower rise in selectivity could possibly be due to smaller depth (fewer layers) and also significantly fewer channels in each layer. For comparison, in a ResNet50 there are 256, 512, 1024, 2048 channels in each layer of module 4, 5, 6 and 7 respectively while in ResNet18/34 there are only 64, 128, 256, 512 channels in each layer of module 4, 5, 6 and 7 respectively.

A.8.2 Evolution of class selectivity in bottleneck layers

The evolution of selectivity in bottleneck layers of ResNet18 and ResNet34 (Fig 21, Fig 22) show a similar trend to that of ResNet50 bottleneck layers (Fig 11). For ResNet34, modules 6 and 7 are increasingly class-selective with network depth and modules 4 and 5 are decreasingly class-selective with network depth (Fig 22). The same effect can be observed for ResNet18 except for module 6 which is decreasingly class-selective with network depth (Fig 21).

A.8.3 Regularizing against selectivity

Both ResNet18 and ResNet34 were regularized against selectivity with $\alpha=-20$ . Interestingly, both the models show a similar regularization result to that of ResNet50. For both ResNet18 and ResNet34, the models regularized from epoch 0 onward performed worse than the models regularized from epoch 5 onward (Fig 23, 24). This indicates that class selectivity is important during the early epochs of training even in the case of smaller variants of ResNet.