On the solution of the coupled steady-state dual-porosity-Navier-Stokes fluid flow model with the Beavers-Joseph-Saffman interface condition¹¹footnotemark: 1

In this section, we consider the steady-state dual-porosity-Navier-Stokes fluid flow model in a bounded open polygonal domain $\Omega\subset\mathbb{R}^{N}(N=2,3)$ with four physically valid interface conditions.

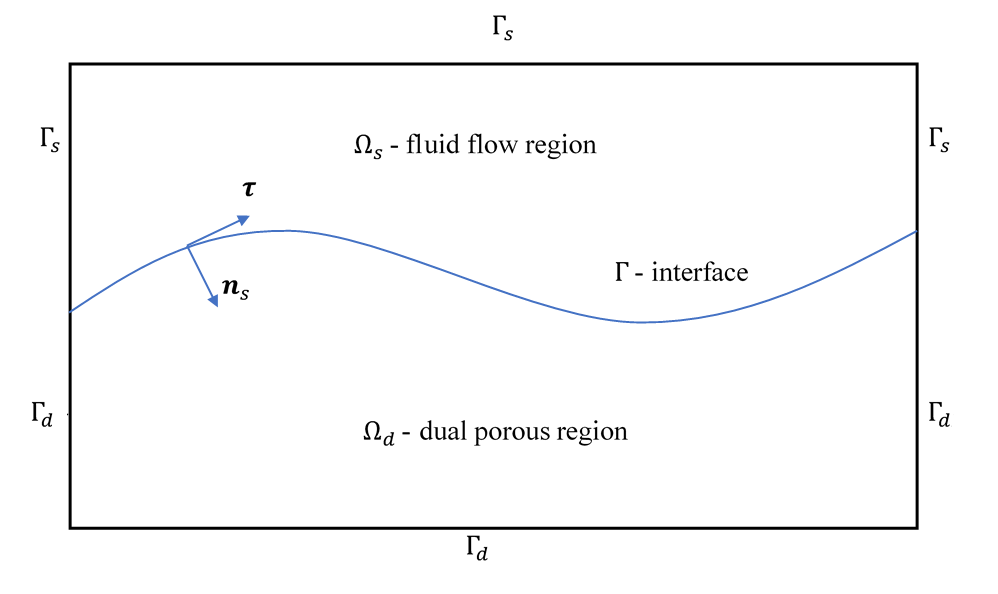
The domain $\Omega$ consists of a fluid flow region $\Omega_{s}$ and a dual-porous medium region $\Omega_{d}$, with interface $\Gamma=\overline{\Omega}_{s}\cap\overline{\Omega}_{d}$ (see Figure 1). Both $\Omega_{s}$ and $\Omega_{d}$ are open, regular, simply connected, and bounded with Lipschitz continuous boundaries $\Gamma_{i}=\partial\Omega_{i}\setminus\Gamma~{}(i=s,d)$, respectively. Here, $\Omega_{s}\cap\Omega_{d}=\emptyset$, $\overline{\Omega}_{s}\cup\overline{\Omega}_{d}=\Omega$. The unit normal vector of the interface $\Gamma$ pointing from $\Omega_{s}$ to $\Omega_{d}$ (from $\Omega_{d}$ to $\Omega_{s}$) is denoted by $\bm{n}_{s}$ (resp. $\bm{n}_{d}$), and the corresponding unit tangential vectors are denoted by $\bm{\tau}_{i}$, $i=1,\cdots,N-1$. In two-dimensional case, if we write $\bm{n}_{s}=(n_{1},n_{2})\in\mathbb{R}^{2}$, then $\bm{\tau}=\bm{n}_{s}^{\top}=(-n_{2},n_{1})$.

In $\Omega_{s}$, the fluid flow is governed by the Navier-Stokes equation [11, 12, 17, 20, 21, 26, 27]:

where $\mathbb{T}(\bm{u}_{s},p_{s})=-p_{s}\mathbb{I}+2\nu\mathbb{D}(\bm{u}_{s})$ is the stress tensor, $\nu$ is the kinetic viscosity, $\mathbb{D}(\bm{u}_{s})=\frac{1}{2}\left[\nabla\bm{u}_{s}+(\nabla\bm{u}_{s})^{\top}\right]$ is the velocity deformation tensor, $\bm{u}_{s}(\bm{x})$ denotes the fluid velocity in $\Omega_{s}$, $p_{s}(\bm{x})$ denotes the kinematic pressure in $\Omega_{s}$, and $\bm{f}_{s}(\bm{x})$ denotes a general body force term that includes gravitational acceleration. As usual, we write formally:

The filtration of an incompressible fluid through porous media is often described using Darcy’s law. So in dual-porous medium domain $\Omega_{d}$, the flow is governed by a traditional dual-porosity model, which is composed of matrix and microfracture equations as follows:

where $\phi_{m}(\bm{x})$, $\phi_{f}(\bm{x})$ denote the matrix and microfracture flow pressure, $\mu$ is the dynamic viscosity, $k_{m}$, $k_{f}$ are the intrinsic permeability of the matrix and microfracture regions, $\sigma$ is the shape factor characterizing the morphology and dimension of the microfractures, $f_{d}$ is the sink/source term for the microfractures, and the term $\frac{\sigma k_{m}}{\mu}(\phi_{m}-\phi_{f})$ describes the mass exchange between matrix and microfractures.

Based on the fundamental properties of the dual-porosity fluid flow model and traditional Stokes–Darcy flow model, Hou et al. [31] introduced four physically valid interface conditions as follows to couple appropriately the dual-porosity-Stokes model, which are also adapted to our problem.

• 1.

  No-exchange condition between the matrix and the conduits/macrofractures:

  $$-\frac{k_{m}}{\mu}\nabla\phi_{m}\cdot\bm{n}_{d}=0\quad\text{on}~{}\Gamma.$$

  (2.3)

• 2.

  Mass conservation:

  $$\bm{u}_{s}\cdot\bm{n}_{s}=\frac{k_{f}}{\mu}\nabla\phi_{f}\cdot\bm{n}_{d}\quad\text{on}~{}\Gamma.$$

  (2.4)

• 3.

  Balance of normal forces:

  $$-\bm{n}_{s}\cdot(\mathbb{T}(\bm{u}_{s},p_{s})\bm{n}_{s})=\frac{\phi_{f}}{\rho}\quad\text{on}~{}\Gamma.$$

  (2.5)

• 4.

  The Beavers-Joseph-Saffman interface condition [7, 33, 35, 41]: for $i=1,\cdots,N-1$,

  $$-\bm{\tau}_{i}\cdot\left(\mathbb{T}(\bm{u}_{s},p_{s})\bm{n}_{s}\right)=\frac{\alpha\nu\sqrt{N}}{\sqrt{\text{trace}(\bm{\Pi})}}\bm{u}_{s}\cdot\bm{\tau}_{i}\quad\text{on}~{}\Gamma.$$

  (2.6)

In (2.3)–(2.6), $\alpha$ is the Beavers-Joseph constant depending on the properties of the dual-porous medium, $\bm{\Pi}$ represents the intrinsic permeability that satisfies the relation $\bm{\Pi}=k_{f}\mathbb{I}$, $\mathbb{I}$ is the $N\times N$ identity matrix, and $\rho$ is the fluid density.

Throughout this paper we use the following standard function spaces. For a Lipschitz domain $\mathcal{D}\subset\mathbb{R}^{N}$, $N\geqslant 1$, we denote by $W^{k,p}(\mathcal{D})$ the Sobolev space with indexes $k\geqslant 0$, $1\leqslant p\leqslant\infty$ of real-valued functions defined on $\mathcal{D}$, endowed with the seminorm $|\cdot|_{W^{k,p}(\mathcal{D})}$ denoted by $|\cdot|_{k,p,\mathcal{D}}$ and norm $\|\cdot\|_{W^{k,p}(\mathcal{D})}$ denoted by $\|\cdot\|_{k,p,\mathcal{D}}$ [1]. When $p=2$, $W^{s,2}(\mathcal{D})$ is denoted as $H^{k}(\mathcal{D})$ and the corresponding seminorm and norm are written as $|\cdot|_{k,\mathcal{D}}$ and $\|\cdot\|_{k,\mathcal{D}}$, respectively. In addition, with $|\mathcal{D}|$ we denote the $N$-dimensional Hausdorff measure of $\mathcal{D}$.

To perform the variational formulation, we define some necessary Hilbert spaces given by

We also need the trace space $\bm{H}_{00}^{1/2}(\Gamma):=\bm{X}_{s}|_{\Gamma}$ (resp. $H_{00}^{1/2}(\Gamma):=X_{d}|_{\Gamma}$), which is a nonclosed subspace of $\bm{H}^{1/2}(\Gamma)$ (resp. $H^{1/2}(\Gamma)$) and has a continuous zero extension to $\bm{H}^{1/2}(\partial\Omega_{s})$ (resp. $H^{1/2}(\partial\Omega_{d})$) [14, 15, 20]. For the trace space $\bm{H}_{00}^{1/2}(\Gamma)$ and its dual space $(\bm{H}_{00}^{1/2}(\Gamma))^{\prime}$, we have the following continuous imbedding result [15]:

One can see more details in [15, 34, 45] and the references therein. For any bounded domain $\mathcal{D}\subset\mathbb{R}^{N}$, $(\cdot,\cdot)_{\mathcal{D}}$ denotes the $L^{2}$ inner product on $\mathcal{D}$, and $\langle\cdot,\cdot\rangle_{\partial\mathcal{D}}$ denotes the $L^{2}$ inner product (or duality pairing) on the boundary $\partial\mathcal{D}$. We also consider the following product Hilbert space $\underline{\bm{Y}}:=\bm{X}_{s}\times X_{d}\times X_{d}$ with norm

In addition, based on the following formula:

we introduce the trilinear form $b(\cdot;\cdot,\cdot)$ given by $\forall\,\bm{u}_{s},\bm{v}_{s},\bm{w}_{s}\in\bm{X}_{s}$,

Hence, the Galerkin variational formulation of the coupled problem (2.1)–(2.6) is proposed that: to find $(\underline{\bm{u}},p_{s})\in\underline{\bm{Y}}\times Q_{s}$ such that

where $\underline{\bm{u}}=(\bm{u}_{s},\phi_{m},\phi_{f})$, $\underline{\bm{v}}=(\bm{v}_{s},\psi_{m},\psi_{f})$, the bilinear forms $a(\cdot,\cdot)$ and $d(\cdot,\cdot)$ are defined as

Thanks to [17, 26], we have the following important result:

Firstly, throughout this paper we use $C$ to denote a generic positive constant independent of discretization parameters, which may take different values in different occasions. Then, based on general Sobolev inequalities, the trace theorem and the Sobolev embedding theorem [1], we have that for any bounded open set $\mathcal{D}\subset\mathbb{R}^{N}$ with Lipschitz continuous boundary $\partial\mathcal{D}$ and for all $v\in H^{1}(\mathcal{D})$,

which can be also found in [17, 26]. We also need Poincaré inequality and Korn’s inequality [15] that for all $\bm{v}_{s}\in\bm{X}_{s}$ and for all $\psi\in X_{d}$,

Moreover, for the trilinear form $b(\cdot;\cdot,\cdot)$, the following lemma holds with the help of [4, 8], (3.1), (3.4) and (3.6).

Let us introduce the following divergence-free space:

and we consider the new product Hilbert space:

which equipped with the same norm as $\underline{\bm{Y}}$.

Thanks to [26], it provides a lower constant bound $\beta_{0}>0$ depending only on $\Omega$ to guarantee the following inf-sup condition:

Hence, by (3.12) and the same argument in [25], the Galerkin variational formulation (2.9) is equivalent to the following problem: to find $\underline{\bm{u}}\in\underline{\bm{W}}$ such that

Let $\mathcal{R}_{i,h}$ be a quasi-uniform regular triangulation of the domain $\Omega_{i}$, $i=s,d$, respectively. If assuming that the two meshes $\mathcal{R}_{s,h}$ and $\mathcal{R}_{d,h}$ coincide along the interface $\Gamma$, then we can define $\mathcal{R}_{h}:=\mathcal{R}_{s,h}\cup\Gamma\cup\mathcal{R}_{d,h}$, which is also a quasi-uniform regular triangulation of $\Omega$. The diameter of element $K\in\mathcal{R}_{h}$ is denoted as $h_{K}$, and we set the mesh parameter $h=\max_{K\in\mathcal{R}_{h}}h_{K}$.

Then we denote by $\bm{X}_{h}\subset\bm{H}_{0}^{1}(\Omega)$ a finite element space defined on $\Omega$. The discrete space $\bm{X}_{h}$ can be naturally restricted to $\Omega_{s}$, so we set $\bm{X}_{s,h}=\bm{X}_{h}|_{\Omega_{s}}\subset\bm{X}_{s}$. Following the same technique, we establish other finite element spaces $Q_{s,h}\subset Q_{s}$ and $X_{d,h}\subset X_{d}$. We assume that $(\bm{X}_{s,h},Q_{s,h})$ is a stable finite element space pair. Further we define the following vector-valued Hilbert space on $\Omega_{d}$:

In addition, we need a finite element subspace $\bm{V}_{h}\subset\bm{X}_{h}$ defined on $\Omega$ given by

Similarly, we have

where $\bm{V}_{s,h}$ is a weakly divergence-free finite element space on $\Omega_{s}$, and any function $\bm{v}_{d,h}\in\bm{X}_{d,h}$ has an implicit restriction that $\int_{\Gamma}\bm{v}_{d,h}\cdot\bm{n}_{d}\mathrm{d}s=0$ because of the continuity of $\bm{V}_{h}$ across the interface $\Gamma$.

According to [26], the difficulty of obtaining an a priori estimate of the Navier-Stokes/Darcy fluid flow model comes from the energy unbalance due to the nonlinear convection term $(\bm{u}_{s}\cdot\nabla)\bm{u}_{s}$ in (2.1). It motivates us to construct an auxiliary discrete Galerkin variational problem defined on $\Omega_{d}$ with compatible boundary conditions, so that the auxiliary problem can compensate the nonlinear convection term in the energy balance of the Navier-Stokes equations.

To fix ideas, we first define a lifting operator $\mathcal{L}:\,\bm{H}_{00}^{1/2}(\Gamma)\rightarrow\bm{X}_{d}$ as follows: for any $\bm{\eta}\in\bm{H}_{00}^{1/2}(\Gamma)$ with $\int_{\Gamma}\bm{\eta}\mathrm{d}s=0$ such that

Then, we introduce the Scott-Zhang interpolator $\Pi_{s,h}:\,\bm{X}_{s}\rightarrow\bm{X}_{s,h}$ satisfying the following properties [42]:

Now, with the mesh parameter $h$, the interpolator $\Pi_{s,h}$ and any given $\bm{u}_{s}\in\bm{V}_{s}$, we consider the following auxiliary discrete Galerkin variational problem: to find $\bm{u}_{d,h}\in\bm{X}_{d,h}$ with $\bm{u}_{d,h}|_{\Gamma}=(\Pi_{s,h}\bm{u}_{s})|_{\Gamma}$ such that for all $\bm{v}_{d,h}\in\bm{X}_{d,h}$,

where $\bm{u}_{d}^{0}=\mathcal{L}(\bm{u}_{s}|_{\Gamma})\in\bm{X}_{d}$, and $\kappa>0$ is a certain positive constant specified later. Furthermore, the discrete problem (3.16) is uniquely solvable in $\bm{X}_{d,h}$ from Lemma 3.1 in [32].

We realize that (3.13) and (3.16) can form a larger coupled system because of the convection term $\bm{u}_{d}^{0}$ and the constraint $\bm{u}_{d,h}|_{\Gamma}=(\Pi_{s,h}\bm{u}_{s})|_{\Gamma}$ for the unknown variable $\bm{u}_{d,h}$ over the interface $\Gamma$, and we also stress that the new coupled system has no energy exchange via the interface $\Gamma$. It implies that (3.16) is subjected to (3.13) but any possible solution of (3.13) has nothing to do with the auxiliary problem (3.16).