On the size and complexity of scrambles

Throughout this paper, a graph $G=(V,E)$ is a finite, connected, loopless multigraph with vertex set $V=V(G)$ and undirected edge multiset $E=E(G)$. This means that in edge multiset $E$, we allow multiple edges between any two distinct vertices of $V$ but disallow edges from a vertex to itself. If there is at most one edge between any two vertices, graph $G$ is known to be simple. The girth of a graph is the length of its smallest cycle.

The degree of a vertex $v$, denoted $d(v)$, counts the number of edges incident to $v$. For a subset $V^{\prime}\subseteq V$, subgraph $G[V^{\prime}]$ induced by $V^{\prime}$ has vertex set $V^{\prime}$ and edge set $E^{\prime}=\{(u,v)\in E|u,v\in V^{\prime}\}\subseteq E$. The vertex connectivity of a graph $G$, denoted $\kappa(G)$, is the minimum cardinality of a set $T\subseteq V$ for which $G[V\backslash T]$ is disconnected. Similarly, the edge connectivity of a graph $G$, denoted, $\lambda(G)$, is the minimum cardinality of a set $W\subseteq E$ for which the graph $G^{\prime}=(V,E\backslash W)$ is disconnected. In general, the k-restricted edge connectivity of a graph $G$, denoted $\lambda_{k}(G)$, is the minimum cardinality of a set $W\subseteq E$ for which the graph $G^{\prime}=(V,E\backslash W)$ is disconnected and every component of $G^{\prime}$ has size $\geq k$ (if such a set $W$ exists; otherwise $\lambda_{k}(G)$ is undefined). We let $\xi_{k}(G)$ denote the minimum outdegree of any $k$-vertex connected subgraph of $G$. If $\lambda_{k}=\xi_{k}(G)$, we say that $G$ is $\lambda_{k}$-optimal.

The independence number of a graph $G$, denoted $\alpha(G)$, is the maximum cardinality subset $S\subseteq V$ for which no two vertices in $S$ share an edge. In general, the k-component independence number of a graph $G$, denoted $\alpha_{k}(G)$, is the maximum cardinality of subset $S\subseteq V$ for which every component of $G[S]$ has size $\leq k$.

We now recall several operations and transformations on graphs. The Cartesian product of graphs $G=(V_{G},E_{G})$ and $H=(V_{H},E_{H})$, denoted by $G\square H$, has vertex set $V_{G}\times V_{H}$ with edges between vertices $(u,u^{\prime})$ and $(v,v^{\prime})$ if and only if $u=v$ and $(u^{\prime},v^{\prime})\in E_{H}$ or $u^{\prime}=v^{\prime}$ and $(u,v)\in E_{G}$; if $G$ and $H$ are not both simple, edges in the multiset $E_{G\square H}$ appear as many times as the corresponding edge in $E_{G}$ or $E_{H}$.

A degree 2 vertex $v$ with distinct neighbors $s$ and $w$ in $G$ can be smoothed by deleting $v$, deleting the edges $(u,v)$ and $(v,w)$, and adding edge $(u,w)$. A graph $H$ obtained via a series of smoothings of $G$ is known as a refinement of $G$. An edge subdivision is the opposite of smoothing: given vertices $u,w$ and the edge $(u,w)$, this operation deletes $(u,w)$, creates a new vertex $v$, and creates the edges $(u,v)$ and $(v,w)$. A graph $H$ obtained from a series of edge subdivisions of $G$ is a subdivision of $G$.

Distinct vertices $u,v,w$ with edges $(u,v)$ and $(v,w)$ can be lifted by deleting edges $(u,v)$ and $(v,w)$ while creating edge $(u,w)$. A graph $H$ obtained via a series of lifts of $G$ is known as an immersion minor of $G$. A function $f$ is immersion minor monotone if for every $H$ that is an immersion minor of $G$, we have $f(H)\leq f(G)$.

An edge contraction is an operation in which two vertices connected by an edge are merged into one vertex; formally,given a graph $G$ with $u,v\in V$ and $(u,v)\in E$, an edge contraction is a map that is the identity on $V\setminus\{u,v\}$ and maps $u$ and $v$ to a new vertex $w$; for all $(x,z)\in E$ with $x,z\notin\{u,v\}$, it is again the identity, while the edges $(x,u)$ or $(x,v)$ are mapped to $(x,w)$. A graph $H$ obtained via a series of edge deletions, vertex deletions, and edge contractions of $G$ is known as a minor of $G$. A function $f$ is said to be minor monotone if $f(H)\leq f(G)$ when $H$ is a minor of $G$. A graph family $\mathcal{G}$ is said to be minor closed if for every $G\in\mathcal{G}$, every minor of $G$ is also in $\mathcal{G}$.

The treewidth of a graph $G$, denoted $\operatorname{tw}(G)$, is a well-studied invariant that serves as a lower bound on gonality [26]. We omit the usual definition of treewidth in terms of tree-decompositions, and instead present an equivalent characterization with an invariant known as bramble number.

A bramble $\mathcal{B}$ on a graph $G$ is a collection of nonempty connected subgraphs of $G$ for which any two have non-empty intersection or are joined by an edge. The order of bramble $\mathcal{B}$ is its hitting number $h(\mathcal{B})$, the smallest cardinality of a vertex subset $H\subset V(G)$ such that $V(B)\cap H\neq\emptyset$ for all $B\in\mathcal{B}$. The bramble number of a graph $G$, denoted $\operatorname{bn}(G)$ is then the maximum order of a bramble on $G$. In [24], Seymour and Thomas proved that $\operatorname{tw}(G)=\operatorname{bn}(G)-1$.

To find a more powerful bound on graph gonality, [18] generalized brambles to scrambles. A scramble $\mathcal{S}$ on a graph $G$ is a nonempty collection of nonempty connected subgraphs of $G$, which we call the eggs of the scramble.

The order of a scramble is defined in terms of its hitting number $h(\mathcal{S})$ and another quantity known as its egg-cut number. An egg-cut of $\mathcal{S}$ is collection of edges in $E(G)$ that, when deleted, disconnect $G$ into two components, each containing an egg from $\mathcal{S}$. The egg-cut number of $\mathcal{S}$, denoted $e(\mathcal{S})$, is the minimum size of an egg-cut of $\mathcal{S}$; if no egg-cut exists (that is, if all pairs of eggs of $\mathcal{S}$ overlap in at least one vertex), we set $e(\mathcal{S})=\infty$. The order of a scramble $\mathcal{S}$, denoted $||\mathcal{S}||$ is then defined as the minimum of $h(\mathcal{S})$ and $e(\mathcal{S})$. The size of a scramble, denoted $|\mathcal{S}|$, is the number of eggs in scramble $\mathcal{S}$.

Finally, the scramble number of a graph $G$, written $\operatorname{sn}(G)$, is the largest possible order of a scramble on $G$:

The following result shows that scramble number forms a strictly better lower bound on gonality than treewidth.

A disjoint scramble $\mathcal{S}$ on some graph $G$ is a scramble on $G$ such that the eggs of $\mathcal{S}$ are pairwise disjoint, i.e. for any eggs $e_{1},e_{2}\in\mathcal{S}$ necessarily $e_{1}\cap e_{2}=\emptyset$. Note that the hitting number of a disjoint scramble is simply its size. The disjoint scramble number of a graph $G$, written $\operatorname{dsn}(G)$, is the largest order of a disjoint scramble on $G$. Note that $\operatorname{dsn}(G)\leq\operatorname{sn}(G)$; sometimes this inequality is strict [13, Proposition 5.2].

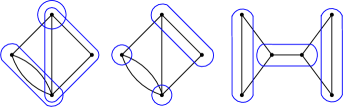
Figure 1 illustrates several scrambles, the first two on the same graph $G_{1}$. The first scramble $\mathcal{S}_{1}$ on $G_{1}$ has $h(\mathcal{S}_{1})=2$ and $e(\mathcal{S}_{1})=3$, so that $||\mathcal{S}_{1}||=2$. The second scramble $\mathcal{S}_{2}$ on $G_{1}$ has $h(\mathcal{S}_{2})=3$ and $e(\mathcal{S}_{2})=3$, so that $||\mathcal{S}_{2}||=3$. This turns out to be the maximum order of a scramble on $G$: to have a larger hitting number, each vertex must be its own egg, but then there would exist an egg-cut of size $2$. Thus we have $\operatorname{sn}(G_{1})=3$, and since this can be achieved by the disjoint scramble $\mathcal{S_{2}}$ we have $\operatorname{dsn}(G_{1})=3$. The third scramble $\mathcal{S}_{3}$ on the final graph $G_{2}$ has order $1$, since the middle edge forms an egg-cut; this illustrates that there may be smaller egg-cuts than the minimum number of edges leaving any egg.

Given a scramble $\mathcal{S}$ on some graph $G$, a subset scramble of $\mathcal{S}$ is simply another scramble $\mathcal{S}^{\prime}$ on $G$ such that $\mathcal{S}^{\prime}\subseteq\mathcal{S}$, i.e. each egg in $\mathcal{S}^{\prime}$ is also an egg in $\mathcal{S}$. Given a graph $G$ and a positive integer $k$, the $k$-uniform scramble, denoted $\varepsilon_{k}$, on $G$ is the scramble whose eggs are all the connected subgraphs of $G$ on $k$ vertices [6]. In particular, the $1$-uniform scramble is the scramble where the eggs are precisely the vertices of $G$; these are sometimes called verteggs. The 2-uniform scramble is the scramble where the eggs are all pairs of vertices that are connected by an edge; it is sometimes known as the edge scramble.

The scramble number of many families of graphs has been studied before [6, 14, 25]. While scramble number is NP-Hard to compute [14, Theorem 1.1], its inclusion in NP is unknown. Scrambles seem to be a natural NP-certificate candidate for lower-bounding scramble number, but the size of maximal order scrambles may be exponentially large in the size of the graph. Bounding the size of maximal order scrambles makes brute force computation of scramble number, where every possible combination of scrambles is considered, more efficient. In particular, a polynomial upper bound on the size of maximum order scrambles implies that scramble number is in NP. With this in mind, we define the carton number of a graph $G$, denoted $\operatorname{cart}(G)$, as the smallest number of eggs with which a scramble $\mathcal{S}$ with order $\operatorname{sn}(G)$ can be constructed. In other words, it is the minimal size of a maximal order scramble; or formulaically,

A carton scramble on a graph $G$ is a scramble with order $\operatorname{sn}(G)$ and $\operatorname{cart}(G)$ many eggs.

For instance, Figure 2 presents two scrambles, both of order $3$, on a graph $G$ of scramble number $3$. The first scramble has size $5$, while the second has size $3$. No scramble of maximal order on the graph has size smaller than $3$, since $h(\mathcal{S})\leq|\mathcal{S}|$. Thus $\textrm{cart}(G)=3$, and the second scramble is a carton scramble while the first is not.

While lower-bounding scramble number is possible with a specific scramble, upper-bounding is more subtle, especially if there is a gap between scramble number and gonality. One useful invariant for providing upper bounds is screewidth, recently developed in [7]. There are no known cases where screewidth is larger than gonality, meaning it is in practice a more useful lower bound.

For a graph $G$, a tree-cut decomposition of $G$ is a pair $\mathcal{T}=(T,\mathcal{X})$ of a tree¹¹1A tree is a connected acyclic graph. $T$ a set $\mathcal{X}$ of subsets $X_{b}$ of $V(G)$, one for each vertex $b\in V(T)$, such that

• •

  $\bigcup_{b\in V(T)}=V(G)$, and

• •

  $X_{a}\cap X_{b}=\emptyset$ for $a\neq b$.

Thus $\mathcal{X}$ forms a near-partition of $V(G)$, which is the same as a partition with empty sets allowed. For clarity, we refer to the vertices and edges of $T$ as nodes and links, respectively, reserving ther terms vertices and edges for $G$. We refer to the set $X_{b}$ as the bag associated to the node $b\in V(T)$.

The adhesion of a link $l\in E(T)$, denoted as $\operatorname{adh}(l)$, is the set of edges $(v_{a},v_{b})\in E(G)$ where $v_{a}$ and $v_{b}$ are in different components of $T-l$. Similarly, the adhesion of a non-leaf²²2The adhesion of a leaf node, with degree equal to $1$, is taken to be the empty set. node $b\in V(T)$ is the set of edges $(v_{a},v_{b})\in E(G)$ where $v_{a}$ and $v_{b}$ are in different components of $T-b$. The width of tree-cut decomposition $\mathcal{T}$ is then defined to be $w(\mathcal{T})=\max(\operatorname{lw}(\mathcal{T}),\operatorname{bw}(\mathcal{T}))$ where

Finally, the screewidth of $G$ is $\operatorname{scw}(G)=\min_{\mathcal{T}}w(\mathcal{T})$. By [7], we have $\operatorname{sn}(G)\leq\operatorname{scw}(G)$ for any graph $G$.

Geometrically, we illustrate a tree-cut decomposition by drawing a thickened copy of $T$, drawing the vertices of $G$ inside of their corresponding nodes, and drawing the edges $(u,v)\in E(G)$ passing through the unique path in $T$ connecting the vertices $u$ and $v$ in their respective bags. The adhesion of a link is then the set of edges passing through it; and the adhesion of a non-leaf node is the set of edges “tunneling” through the node, without either endpoint in that node. Thus $\operatorname{lw}(\mathcal{T})$ is the maximum number of edges passing through a link; and $\operatorname{bw}(\mathcal{T})$ is the maximum over all nodes of the number of vertices plus the number of tunneling edges.

Two examples of tree-cut decompositions $\mathcal{T}_{1}$ and $\mathcal{T}_{2}$ of the same graph $G$ are illustrated in Figure 3. The first has $\operatorname{lw}(\mathcal{T}_{1})=5$ and $\operatorname{bw}(\mathcal{T}_{1})=6$, so $w(\mathcal{T}_{1})=6$. The second has $\operatorname{lw}(\mathcal{T}_{2})=3$ and $\operatorname{bw}(\mathcal{T}_{2})=2$, so $w(\mathcal{T}_{2})=3$. It follows that $\operatorname{scw}(\mathcal{T})\leq 3$. As previously established, this graph has scramble number $3$, implying that $\operatorname{scw}(G)=3$ since $\operatorname{sn}(G)\leq\operatorname{scw}(G)$.

Below, we show or recall results that will be useful throughout the paper. Some follow quickly from definitions and others come from related work.

Since $\operatorname{dsn}(G)\leq\operatorname{sn}(G)$, we have that disjoint scramble number also serves as a lower bound on graph gonality, although it will never perform better than scramble number. We will see in Section 5 that disjoint scramble number may be larger than, smaller than, or equal to treewidth, meaning it also does not consistently perform better than treewidth as a lower bound on gonality. However, disjoint scramble number has the advantage that the problem of deciding whether $\operatorname{dsn}(G)\geq k$ is in NP, with a disjoint scramble of order $k$ serving as a polynomial size certificate verifiable in polynomial time (for a disjoint scramble $\mathcal{S}$ we have $h(\mathcal{S})=|\mathcal{S}|$, and $e(\mathcal{S})$ can be computed in polynomial time as there are polynomially many eggs [6]). Lower bounding treewidth or scramble number is not known to be in NP; indeed, since upper bounding treewidth is NP-complete, lower bounding could only be in NP if NP$=$co-NP, which is generally expected not to be the case.

This inequality can be strict in some cases, as $\mathcal{S}$ might contain pairs of eggs that $\mathcal{S}^{\prime}$ does not contain which can be separated by removing fewer than $e(\mathcal{S}^{\prime})$ edges. An extreme example is where $\mathcal{S}^{\prime}$ contains only one egg, so $e(\mathcal{S}^{\prime})=\infty$, even for $\mathcal{S}$ with $e(\mathcal{S})$ finite.