On the series expansion of a square-free zeta series

In the recent work of Wolf [7] who investigated the divergence of a certain zeta series involving the Möbius function $\mu(n)$ [3, p. 304], (thus essentially running over square-free integers) as such

$$\sum_{n=1}^{x}\frac{|\mu(n)|}{n}=O(\log x)$$

(1)

(as $x\to\infty$) and determined a more refined estimate

$$\sum_{n=1}^{x}\frac{|\mu(n)|}{n}=\gamma^{M}+\frac{6}{\pi^{2}}\log x+O(\frac{1}{x}),$$

(2)

where a new constant

	$\displaystyle\gamma^{M}$	$\displaystyle=\lim_{x\to\infty}\left(\sum_{n=1}^{x}\frac{|\mu(n)|}{n}-\frac{6}{\pi^{2}}\log x\right)$		(3)
		$\displaystyle=1.04389451571193829740\ldots,$

can be extracted in the limit in a much the same way as the classical Euler-Mascheroni constant

	$\displaystyle\gamma$	$\displaystyle=\lim_{x\to\infty}\left(\sum_{n=1}^{x}\frac{1}{n}-\log x\right)$		(4)
		$\displaystyle=0.57721566490153286060\ldots$

Recalling that the Riemann zeta function is defined by the simplest Dirichlet series

$$\zeta(s)=\sum_{n=1}^{\infty}\frac{1}{n^{s}}$$

(5)

is absolutely convergent for $\Re(s)>1$, and admits the Laurent series expansion about $s=1$ is given by

$$\zeta(s)=\frac{1}{s-1}+\sum_{n=0}^{\infty}\gamma_{n}\frac{(-1)^{n}(s-1)^{n}}{n!},$$

(6)

which analytically extends $\zeta$ to $\mathbb{C}\backslash 1$ with residue $1$ and an only pole at $s=1$. With the Euler’s constant ($\gamma_{0}=\gamma$) appearing as the $0^{th}$ order coefficient in the series, and consequently, the next higher order Stieltjes constants $\gamma_{n}$ [4, p. 561] can be similarly generated by the well-known formula

$$\gamma_{n}=\lim_{x\to\infty}\Bigg{\{}\sum_{k=1}^{x}\frac{\log^{n}(k)}{k}-\frac{\log^{n+1}(x)}{n+1}\Bigg{\}}.$$

(7)

And in a similar fashion, a certain fraction of the zetas

$$\frac{\zeta(s)}{\zeta(2s)}=\sum_{n=1}^{\infty}\frac{|\mu(n)|}{n^{s}}$$

(8)

involves the Möbius function as in (1) [6, p.5], and based on some previous analysis its Laurent series expansion is given by

$$\frac{\zeta(s)}{\zeta(2s)}=\frac{6}{\pi^{2}(s-1)}+\sum_{n=0}^{\infty}\gamma_{n}^{M}\frac{(-1)^{n}(s-1)^{n}}{n!},$$

(9)

also with a pole at $s=1$ and residue $\frac{6}{\pi^{2}}$, and the proposed formula by Wolf for these expansion coefficients

$$\gamma^{M}_{n}=\lim_{x\to\infty}\Bigg{\{}\sum_{k=1}^{x}\frac{|\mu(k)|\log^{n}(k)}{k}-\frac{6}{\pi^{2}}\frac{\log^{n+1}(x)}{n+1}\Bigg{\}}$$

(10)

is an analogue of the Stieltjes formula (7) [7]. We also note that the radius of convergence of (9) is only limited to $R=2$ due to the pole at the first trivial zero when $2s=-2$ for $s=-1$ from the center at $s=1$.

We now prove (10) by following exactly the proof in Bohman-Fröberg [2][4, p. 561-562], but additionally inserting the Möbius function. We begin the proof by introducing a self-canceling telescoping series

$$\sum_{k=1}^{\infty}(|\mu(k)|k^{1-s}-|\mu(k+1)|(k+1)^{1-s})=1$$

(11)

then one has

$$(s-1)\frac{\zeta(s)}{\zeta(2s)}=1+\sum_{k=1}^{\infty}\left(|\mu(k+1)|(k+1)^{1-s}-|\mu(k)|k^{1-s}+(s-1)|\mu(k)|k^{-s}\right)$$

(12)

which is still valid for $\Re(s)>1$, but since for $s=1$ the (lhs) limit is

$$\lim_{s\to 1}(s-1)\frac{\zeta(s)}{\zeta(2s)}=\frac{6}{\pi^{2}}$$

(13)

is inconsistent with (rhs) of (12). So if we consider another re-scaled sequence instead

$$(s-1)\frac{\zeta(s)}{\zeta(2s)}=\frac{6}{\pi^{2}}+\sum_{k=1}^{\infty}\left(\frac{6}{\pi^{2}}|\mu(k+1)|(k+1)^{1-s}-\frac{6}{\pi^{2}}|\mu(k)|k^{1-s}+(s-1)|\mu(k)|k^{-s}\right)$$

(14)

such that the (lhs) equals (rhs) at $s=1$, and then proceeding with the exp-log expansion exactly about $s=1$, then one obtains

	$\displaystyle(s-1)\frac{\zeta(s)}{\zeta(2s)}=$	$\displaystyle\frac{6}{\pi^{2}}+\sum_{k=1}^{\infty}\Big{[}\frac{6}{\pi^{2}}\exp(-|\mu(k+1)|(1-s)\log(k+1))+$		(15)
		$\displaystyle-\frac{6}{\pi^{2}}\exp(|\mu(k)|(1-s)\log(k))+(s-1)\frac{1}{k}\exp(-(s-1)|\mu(k)|\log(k))\Big{]}$
	$\displaystyle=$	$\displaystyle\frac{6}{\pi^{2}}+\sum_{k=1}^{\infty}\Bigg{[}\frac{6}{\pi^{2}}\sum_{n=0}^{\infty}\frac{(-1)^{n}(s-1)^{n}}{n!}\Big{[}|\mu(k+1)|^{n}\log^{n}(k+1)-|\mu(k)|^{n}\log^{n}(k)\Big{]}+$
		$\displaystyle+(s-1)\frac{1}{k}\sum_{n=0}^{\infty}\frac{(-1)^{n}(s-1)^{n}|\mu(k)|^{n}\log^{n}(k)}{n!}\Bigg{]}$

and by collecting the $(s-1)$ terms (with $(s-1)^{0}=1$) and since $|\mu(k)|^{n}=|\mu(k)|$, we obtain

$$\frac{\zeta(s)}{\zeta(2s)}=\frac{6}{\pi^{2}(s-1)}+\sum_{n=0}^{\infty}\gamma^{M}_{n}\frac{(-1)^{n}(s-1)^{n}}{n!}$$

(16)

where

$$\gamma^{M}_{n}=\sum_{k=1}^{\infty}\left[\frac{|\mu(k)|\log^{n}(k)}{k}-\frac{6}{\pi^{2}}\frac{\log^{n+1}(k+1)-\log^{n+1}(k)}{k}\right]$$

(17)

and last term as self-cancels again leaving only the $n+1$ term leading to the final limit formula

$$\gamma^{M}_{n}=\lim_{x\to\infty}\Bigg{\{}\sum_{k=1}^{x}\frac{|\mu(k)|\log^{n}(k)}{k}-\frac{6}{\pi^{2}}\frac{\log^{n+1}(x)}{n+1}\Bigg{\}}.$$

(18)

We next consider an alternative representation for these coefficients. If we take the Laurent series expansion about $s=1$ of

$$\zeta(s)=\frac{1}{s-1}+\gamma+O(|s-1|)$$

(19)

to the $0^{th}$ order, and another expansion of

$$\frac{1}{\zeta(2s)}=\frac{1}{\zeta(2)}-2\frac{\zeta^{\prime}(2)}{\zeta(2)^{2}}(s-1)+O(|s-1|^{2})$$

(20)

to the $1^{st}$ order, then by multiplying them together yields

$$\frac{\zeta(s)}{\zeta(2s)}=\frac{6}{\pi^{2}(s-1)}+\frac{\gamma}{\zeta(2)}-2\frac{\zeta^{\prime}(2)}{\zeta(2)^{2}}+O(|s-1|).$$

(21)

As a result, the $0^{th}$ order coefficient in (21) is collected in the limit $s\to 1$ as

$$\gamma^{M}=\frac{6\gamma}{\pi^{2}}-\frac{72\zeta^{\prime}(2)}{\pi^{4}}$$

(22)

gives a better closed-form formula in terms of other known constants. And the value for the zeta derivative $\zeta^{\prime}(2)$ can be computed directly from (5) as

$$\zeta^{\prime}(2)=\sum_{k=1}^{\infty}\frac{\log(k)}{k^{2}}.$$

(23)

In Table 1, we compute the first $10$ higher order $\gamma^{M}_{n}$ coefficients to high-precision ($30$ decimal places) by the $n^{th}$ differentiation of the (lhs) of (16) in the limit as

$$\gamma^{M}_{n}=(-1)^{n}\frac{d^{n}}{ds^{n}}\Bigg{[}\frac{\zeta(s)}{\zeta(2s)}-\frac{6}{\pi^{2}(s-1)}\Bigg{]}\Bigr{\rvert}_{s\to 1}$$

(24)

which is easily possible to do in software packages such as Mathematica or Pari/GP [5][8]. The error term for $\gamma^{M}$ in (1) is $O(\frac{1}{x})$, and this would roughly imply that in order to get $30$ decimal places using (3), one needs to compute the limit with $x$ on the order of $\sim 10^{30}$, which is so large that even on modern computer workstations is still completely unfeasible to do in reasonable time (but perhaps on a supercomputer it could run faster), but one can still easily compute these constants to thousands of digits by differentiation in (24).

We saw earlier that the square-free Dirichlet series

$$\frac{\zeta(s)}{\zeta(2s)}=\sum_{n=1}^{\infty}\frac{|\mu(n)|}{n^{s}}$$

(25)

is convergent for $\Re(s)>1$. In the previous Section, the telescoping series (12) is also convergent for $\Re(s)>1$, but with the introduction of a scaling constant we propose that (14) is actually valid for $\Re(s)>\frac{1}{4}$ (except at $s=1$) and assuming (RH). We reformulate the expression and bring over $(s-1)$ to the (rhs) we have

$$\frac{\zeta(s)}{\zeta(2s)}=\frac{6}{\pi^{2}(s-1)}+\frac{1}{s-1}\sum_{k=1}^{\infty}\left[\frac{6}{\pi^{2}}\left(|\mu(k+1)|(k+1)^{1-s}-|\mu(k)|k^{1-s}\right)+(s-1)|\mu(k)|k^{-s}\right]$$

(26)

and in another form

$$\frac{\zeta(s)}{\zeta(2s)}=\lim_{x\to\infty}\Bigg{\{}\sum_{k=1}^{x}\frac{|\mu(k)|}{k^{s}}+\frac{6}{\pi^{2}(s-1)}\left[1+\sum_{k=1}^{x}\left(|\mu(k+1)|(k+1)^{1-s}-|\mu(k)|k^{1-s}\right)\right]\Bigg{\}}$$

(27)

and then self-canceling the telescoping series to last term we get

$$\frac{\zeta(s)}{\zeta(2s)}=\lim_{x\to\infty}\Bigg{\{}\sum_{n=1}^{x}\frac{|\mu(n)|}{n^{s}}-\frac{6}{\pi^{2}(1-s)}x^{1-s}\Bigg{\}}$$

(28)

which we numerically find is valid $\Re(s)>\frac{1}{4}$ as stated. This limitation is due to the poles that arise at $\frac{1}{2}\rho$, where $\rho$ is the non-trivial root of $\zeta$. As evidenced by numerical computations, for example, for $s=0.8$ we compute the (lhs) of (28) to $-1.9413794172\ldots$, while the (rhs) with $x=10^{8}$ is $-1.941\underline{3}8634\ldots$, an agreement to $4$ digits. And if $s=0.5$ then the (lhs) of (28) is $0$, while the (rhs) with $x=10^{8}$ is computed as $-0.00173997\ldots$, where we see it is going to zero. And we checked many more random points and see that this formula is clearly converging to right values in the new domain $\Re(s)>\frac{1}{4}$, and as shown by the plot in Fig. 1, where we compare the (lhs) and (rhs) of equation (28) for $x=10^{8}$, and observe a deviation starts to happen near $\frac{1}{4}$. This means that all non-trivial roots are also roots of the (rhs) of (28).

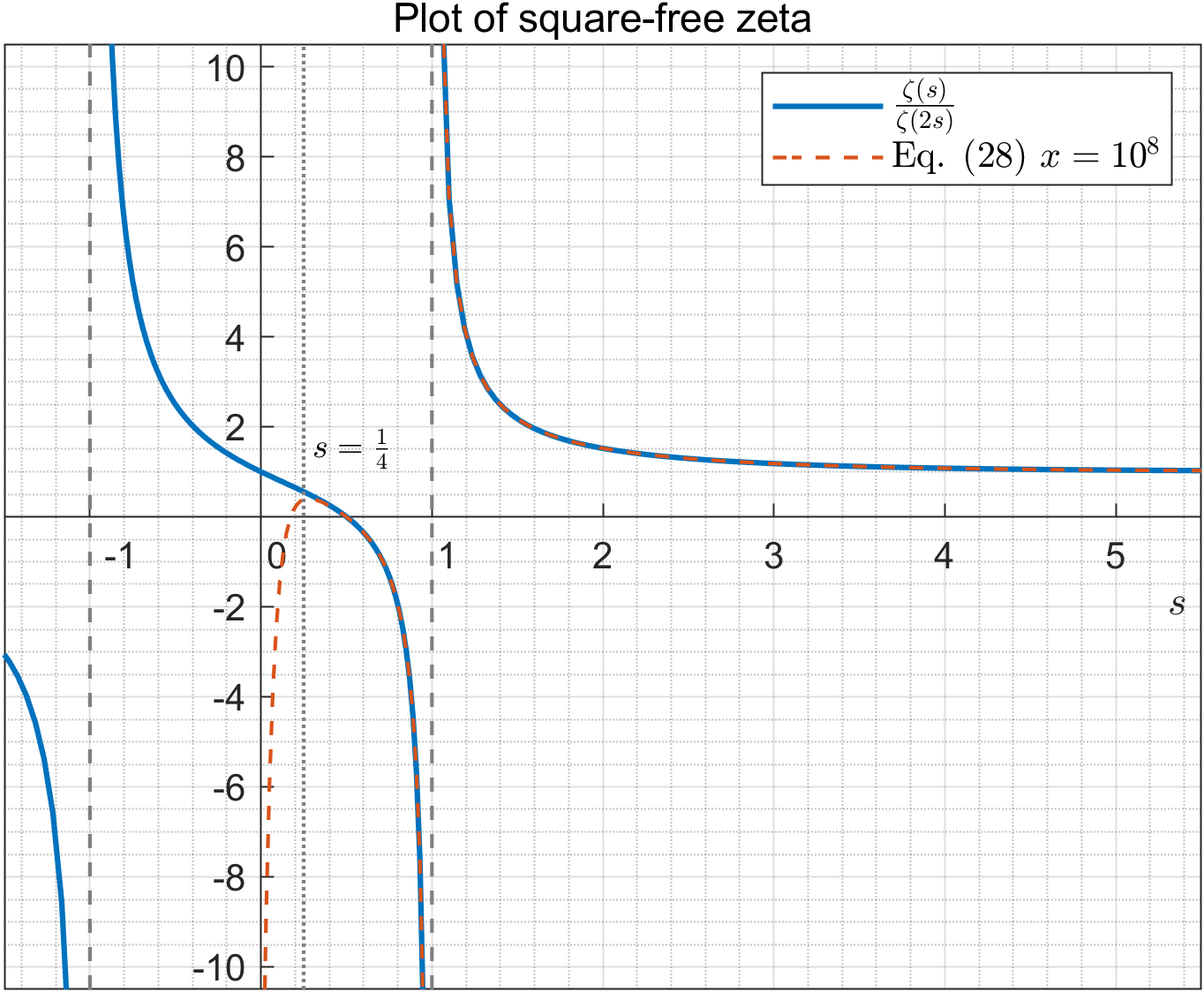
Equation (28) can give many more interesting results. As previously seen, $s=\frac{1}{2}$ is a zero of (28), and so we obtain a special case

$$\sum_{n=1}^{x}\frac{|\mu(n)|}{\sqrt{n}}\sim\frac{12}{\pi^{2}}\sqrt{x}$$

(29)

as $x\to\infty$, or expressing in another way

$$\lim_{x\to\infty}\frac{1}{\sqrt{x}}\sum_{n=1}^{x}\frac{|\mu(n)|}{\sqrt{n}}=\frac{12}{\pi^{2}}.$$

(30)

We also consider another expansion about $s=\frac{1}{2}$ of

$$\frac{\zeta(s)}{\zeta(2s)}=2\zeta(\frac{1}{2})(s-\frac{1}{2})+O(|s-\frac{1}{2}|^{2})$$

(31)

and seek to extract the first order zeta value by differentiation of the (rhs) of (28). We obtain the formula

$$\zeta(\frac{1}{2})=\lim_{x\to\infty}\Bigg{\{}-\frac{1}{2}\sum_{n=1}^{x}\frac{|\mu(n)|\log(n)}{\sqrt{n}}+\frac{6}{\pi^{2}}\sqrt{x}\left(-2+\log(x)\right)\Bigg{\}}$$

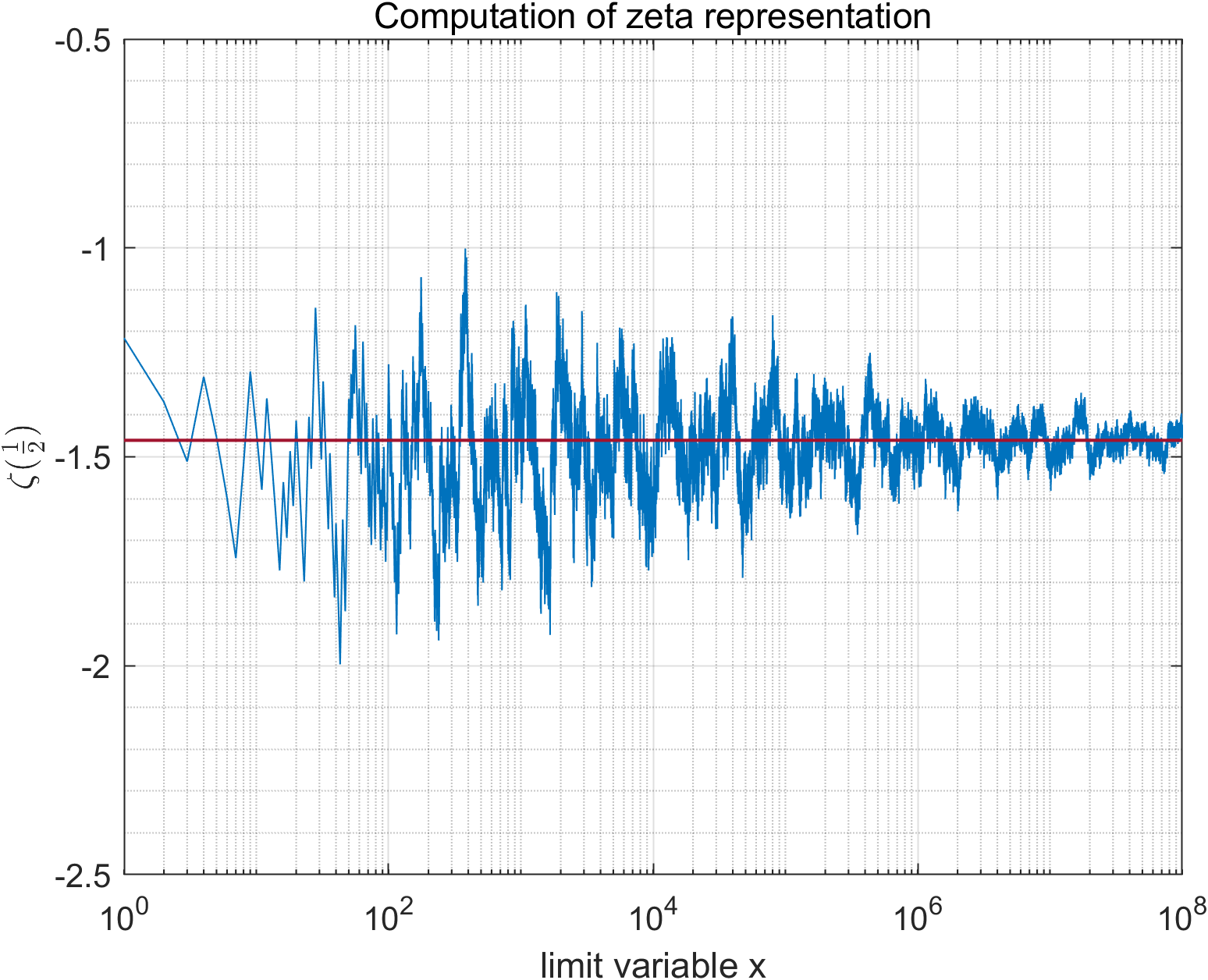
(32)

which is converging to this zeta value. We next verify this formula numerically and find that it is a rather noisy and fluctuating series. In Fig. 2, we plot (32) as a function of $x$ from $x=10^{0}$ to $10^{8}$ in increments of $1$, on a logarithmic scale on the x-axis to capture all points. We note how it is fluctuating about the value $\zeta(\frac{1}{2})=-1.4603545088\ldots$, with a gradual decrease in amplitude as $x$ increases. Another form can be simplified by plugging in (30) into (32) to have

$$\zeta(\frac{1}{2})=\lim_{x\to\infty}\Bigg{\{}-\frac{1}{2}\sum_{n=1}^{x}\frac{|\mu(n)|(\log(n)+2)}{\sqrt{n}}+\frac{6}{\pi^{2}}\sqrt{x}\log(x)\Bigg{\}}$$

(33)

and when we test this formula we reproduce an almost the same plot as in Fig. 2.

There is a common alternating series representation for the zeta function

$$\zeta(s)=\frac{1}{1-2^{1-s}}\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n^{s}}$$

(34)

which is valid for $\Re(s)>0$ (but except at those points $t$ on the line $1+it$ where the leading factor becomes singular). A similar relation can be obtained for the square-free zeta series inspired by the MathOverflow post [9] by taking advantage of a certain connection to the Euler product

$$\frac{\zeta(s)}{\zeta(2s)}=\sum_{n=1}^{\infty}\frac{|\mu(n)|}{n^{s}}=\prod_{p}\left(1+\frac{1}{p^{s}}\right)$$

(35)

valid for $\Re(s)>1$, where $p$ runs over all primes $p=\{2,3,5,7,\ldots\}$. Then, the application of the general Dirichlet series [3, p. 326] reads

$$\sum_{n=1}^{\infty}\frac{f(n)}{n^{s}}=\prod_{p}\sum_{k=0}^{\infty}\frac{f(p^{k})}{p^{ks}},$$

(36)

where $f(n)$ is a multiplicative function, meaning that for any positive integers $a$ and $b$ must satisfy the relation $f(1)=1$ and $f(a)f(b)=f(ab)$ whenever $a$ and $b$ are co-prime holds. It turns out that an alternating sign function $f(n)=(-1)^{n+1}$ is multiplicative, and hence $f(n)=(-1)^{n+1}|\mu(n)|$ is multiplicative, then we get the following transformation

	$\displaystyle\sum_{n=1}^{\infty}(-1)^{n+1}\frac{|\mu(n)|}{n^{s}}$	$\displaystyle=\prod_{p}\sum_{k=0}^{\infty}\frac{(-1)^{p^{k}+1}|\mu(p^{k})|}{p^{ks}}$		(37)
		$\displaystyle=\left(1-\frac{1}{2^{s}}\right)\prod_{p\geq 3}\left(1+\frac{1}{p^{s}}\right)$
		$\displaystyle=\left(1-\frac{1}{2^{s}}\right)\left(1+\frac{1}{2^{s}}\right)^{-1}\prod_{p\geq 2}\left(1+\frac{1}{p^{s}}\right)$
		$\displaystyle=\left(\frac{2^{s}-1}{2^{s}+1}\right)\frac{\zeta(s)}{\zeta(2s)}$

since $\mu(0)=1$, and $\mu(p)=-1$ and $\mu(p^{k})=0$ for $k>1$. And this leads to the form analogue to the alternating zeta series (34) as

$$\frac{\zeta(s)}{\zeta(2s)}=\left(\frac{2^{s}+1}{2^{s}-1}\right)\sum_{n=1}^{\infty}(-1)^{n+1}\frac{|\mu(n)|}{n^{s}}.$$

(38)

It is rare get such a coincidence, since this transformation depends on the existence of such a Euler product form. But unfortunately, the domain of convergence of (37) is only valid for $\Re(s)>1$ instead of $\Re(s)>0$ as in the alternating zeta (34). One reason is that at $s=1$ the summation in (34) is conditionally convergent as

$$\sum_{n=1}^{\infty}\frac{(-1)^{n+1}}{n}=\log(2)$$

(39)

while the for square-free alternating zeta at $s=1$ diverges for the reason being by equating (8) with (34), where they only differ by a factor of $\frac{1}{3}$. And this leads to consider an estimate

$$\sum_{n=1}^{x}(-1)^{n+1}\frac{|\mu(n)|}{n}=\bar{\gamma}^{M}+\frac{2}{\pi^{2}}\log x+O(\frac{1}{x}),$$

(40)

as $x\to\infty$, and an analogue constant for the alternating series

	$\displaystyle\bar{\gamma}^{M}$	$\displaystyle=\lim_{x\to\infty}\left(\sum_{n=1}^{x}\frac{(-1)^{n+1}|\mu(n)|}{n}-\frac{2}{\pi^{2}}\log x\right)$		(41)
		$\displaystyle=0.53524615263113376955\ldots,$

where the closed-form formula can be computed by

$$\bar{\gamma}^{M}=\frac{1}{3}\gamma^{M}+\frac{8}{3\pi^{2}}\log(2)$$

(42)

by the virtue of expansion of the factor

$$\frac{2^{s}-1}{2^{s}+1}=\frac{1}{3}+\frac{4}{9}\log(2)(s-1)+O(|s-1|^{2})$$

(43)

in conjunction with (19) to (22).

I would like to thank Professor Wolf for comments and suggestions for improving the paper.