commentComment
On The Scale Dependence and Spacetime Dimension of the Internet with Causal Sets
Abstract
A statistical measure of dimension is used to compute the effective average space dimension for the Internet and other graphs, based on typed edges (links) from an ensemble of starting points. The method is applied to CAIDA’s ITDK data for the Internet. The effective dimension at different scales is calibrated to the conventional Euclidean dimension using low dimensional hypercubes. Internet spacetime has a ‘foamy’ multiscale containment hierarchy, with interleaving semantic types. There is an emergent scale for approximate long range order in the device node spectrum, but this is not evident at the AS level, where there is finite distance containment. Statistical dimension is thus a locally varying measure, which is scale-dependent, giving an visual analogy for the hidden scale-dependent dimensions of Kaluza-Klein theories. The characteristic exterior dimensions of the Internet lie between and , and maximal interior dimensions rise to .
I Introduction
The Internet is large graph for which we can explicitly and empirically measure the average statistical space(time) dimension. The concept of a statistical dimension was introduced in [1], and has since attracted interest in causal set theory and discrete approaches to quantum gravity [1, 2, 3, 4]. There is dual scientific interest in determining the dimension of an actual phenomenological network: it helps to set aside any prejudices about what dimension we might expect from a virtually interacting processes by straightforward measurement, and it allows us to calibrate the technique for a more intuitive assessment using graph theoretic methods. With the introduction of modern graph databases, this task becomes quite easy. On a technological level, the average dimension of the Internet indicates the availability of redundant paths through the mesh and is thus a measure of the robustness of the Internet to failure.
Conventionally, the idea of space(time) dimension is rooted in long standing traditions of Euclidean geometry and Cartesian vector spaces. This is a geometric idealization, inferred more by the convenience of symmetry than observed directly. In physics, the underlying structure of spacetime is reasoned to be discrete on some scale (the Planck scale is typically assumed), but the dimension of a discrete spacetime is not as simple to define as in a continuous Euclidean space. We also have to deal with different ‘semantics’, or the roles for which we count dimensions. For example, the ‘kinetic dimension’ of a space is conventionally equal to half the number of independent spatial degrees of freedom (or forward directions) available to a process (see figure 1). Here, there is an implicit notion of continuity of momentum in selecting forward directions only. In solid state and lattice field theories of physics, a finite spacing is maintained between points in the parameter space to avoid infinities associated with the differential coincidence limit, and to separate the effects of bound states. This makes a direct connection between classically Newtonian causality and computational processes over multiple timescales.
Definitions of dimension vary, but most stay close to a tradition in philosophy of studying trajectories of rigid bodies within an idealized ambient ‘theatre’. The parameters characterizing such paths are continuous real-valued coordinates. The success of this approach was affirmed by Newton’s treatise on mechanics and many later theories, which have etched the truth of this model into the collective consciousness. However, the attractively simple idea of a Euclidean vector space is insufficient to characterize the effective degrees of freedom of more general processes, including those found in biology and computer science, where the parameters form discrete graphs, so its a happy occasion to find phenomenological data to study. In graph theory, the dimension of a graph may be defined in several ways: both in terms of the same dynamical counting of degrees of freedom above, and even by the embedding of the graph into a Euclidean space as a last resort. The latter is popular in developing approximations in network Machine Learning for instance, because it keeps reasoning within a familiar Pythagorean regime.


II Measuring graph space
In a directed graph, locations are nodes (vertices), and the forward or outgoing degree , or number of links (edges) are the dimension at that point. This idea is scale dependent (figure 1 again), which may feel unfamiliar–though a similar idea is invoked in modern Kaluza-Klein theories, where hidden degrees of freedom are considered to be short range or ‘rolled up’ on a small scale.
Most lay-persons probably think of the Internet as a network of cables stretched around the globe, but this is not a representation of its dynamics. The functional behaviour of the Internet is built on the outcomes of interfering virtual phenomena, just as the behaviour of a quantum multi-slit experiment is based on the behaviour of waves not the slits by themselves. Empirically, we probe the Internet as a graph, from within the graph itself, by sampling data about neighbouring nodes from within a ‘radius’ defined as a certain number of hops along graph edges from a given random origin. The collection of the data is non-trivial, and involves assimilating data from multiple patches into a covering; but, luckily the data exist at the Center for Applied Internet Data Analysis (CAIDA)[5]. By letting a known process run over all possible acyclic trajectories from the origin, and looking at reflections—a bit like a sonar map. In the case of the Internet, one uses the ECHO protocol, or the well-known traceroute program. These reflections are then collated and averaged to create a map, which is held in a graph database (ArangoDB). The resulting map is somewhat fictitious, being a representation of a sum over multiple ephemeral dynamical processes–in much the way that a television cathode ray image is a convenient illusion, or a quantum wavefunction is a representation of possible energy channels, because its points are never observed simultaneously–we rely on a persistence timescale to collate and define effective simultaneity.
To probe the dimension of the map, we can now repeat the same process on the aggregate map, using the database to search for all nodes reachable by acyclic paths within a certain number of hops. These data samples are deterministic, and thus without uncertainty, but they are not local and representative of the whole graph. They can be collected into ensembles by randomizing the origin—choosing sample sets which have either closely separated origins or widely separated origins to study the locality of characters. In each case, we can easily retrieve the number of reachable points as a function of integer number of hops with a single database query. This can now be reported on average, with associated error bars. The effect is to probe spacetime from the perspective of ‘open balls’, mimicking the basic topological construction of a manifold, albeit with discrete integral adjacent jumps. In essence, we deal only with time-average point correlations, and the directionality of the original probes is averaged away by the methodology. This may be presumptuous, if we’re interested in behaviour on a detailed level, especially when inhomogeneous characteristics of processes are taken into account, but it fits most people’s intuitions of what a space should be[6].

This process assumes that all reachable nodes are of homogeneous type, and that all links are traversable in both directions. Both these assumptions are presumptuous in the case of the a general network. In collating the data, we have applied a semantic spacetime model to separate out independent semantic degrees of freedom which allows us to probe the graph through different virtual process channels (see figure 3). These channels can be associated with different protocols (which are the computer science equivalent of force carriers in physics). Different types of connection and different kinds of node have different semantics, and we can (indeed should) separate them. However, there is also an effective picture of what it means for nodes to be adjacent.
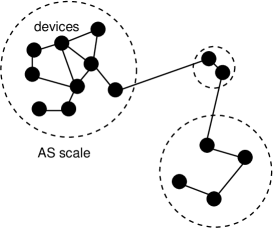
In what follows, we look at two channels: one that correspond approximately to network ‘devices’ (what CAIDA call Nodes, or entities that appear to share IP interfaces) and so-called Autonomous Systems (AS) which represent large organizations hosting the devices. Owing to the unobservability of certain regions, there are also ‘wormholes’ or ‘hyperlinks’ where traces may appear to tunnel through several regions without being observable. We take those into account, but they distort the underlying picture with an additional virtual phenomenon. The channels communicate by the IP protocol and the BGP protocols respectively. BGP travels virtually on top of IP, but is still semantically independent of it. We can perform the same measurement process on each independent graph to measure a result.


For calibration of a statistical method, we remark here that regular (crystalline) lattices (figure 8), exhibiting long range order, have a special significance for our intuition about spacetime dimension, since these are ubiquitous and for the basis for Cartesian coordinates, thus we use these for calibrating our measure. However, the likeness of a graph to a lattice or other continuum manifold is of mainly heuristic interest in the case of more complex multiscale systems, like the Internet, since the concept of dimensionality is mainly associated with predicting degrees of available states and dynamical freedoms locally. Nevertheless, it is of interest to test the method and the intuitiveness of its results. The study closest to our, in spirit, is perhaps the use of causal sets to explore the science citation process [7].
III Related physics
A brief contextual placement for measuring dimension by this method is in order. Studies of graph-like spacetimes in physics nearly always look for the emergence of manifold (quasi-Euclidean) behaviour from random probabilistic process distributions, since their purpose is to imagine the emergence of our quasi-Euclidean large scale experience in some limit. This is not our purpose here. Directed graphs are more like causal (kinetic) processes of Feynman diagrams or other process diagrams. These are of direct interest to Internet design, as well being suitable for comparison with other dynamical systems.
Continuum space is a precise abstraction, but discrete spacetime is less constrained by requirements of symmetry, so we are cautious in making assumptions. Myrheim [1] was characteristically early in pointing out that for discrete spacetime we can only define dimension statistically. Detailed mathematical work by Meyer [2] developed a language for so-called Causal Sets as an abstraction based on a theoretical model for node adjacency; this used Poisson distributed sprinklings of nodes to form directed graphs. Although arbitrary, this allows results to be calculated analytically. A more recent mathematical formulation in [8] exploring the probabilistic aspect of point filling and its relationship to manifold structures. In these modern renditions, one refers to Alexandrov sets over the limits of a causal interval . This is defined over an interval of values : , for finite cardinality.
In our case, the data form a cumulative map of such channels, which is a summary of many overlapping probes, in which the boundary conditions may be both quickly or slowly varying. For this to make sense, we infer the notion of persistent channels of communication (edges) between the quasi-pointlike vertices of the graph. We wish to preserve these explicit communications channels in the model, with an effective connectivity given by the overlap of their promised open sets: , which is equivalent to the Alexandrov set in the continuum[9, 8]. This leads to rather different topologies than the scale-free Poisson processes, and requires some modification of the approach to estimating bulk space-filling.
In nearly all studies of statistical dimension, the points, which are effectively nodes or vertices of a graph, are all of a single featureless kind—formally ‘typeless’ in a computer science sense and are generated probabilistically. However, this is not the case in technology, nor in chemistry and biology, etc, where the concept of a variegated semantic space becomes useful[6]. Spatiotemporal homogeneity is convenient for invoking an implicit ensemble, i.e. an accumulation of processes into a distribution that leads to continuous fractional scaling. These more complex systems are of interest both on a practical and theoretical level, since they are much more accessible and can be observed directly, and have very predictable functional characteristics. Semantic spacetime is a (promise) graph theoretical model of discrete processes, with arbitrary set-valued overlap criteria that may have any number of types, equivalences, and orderings. Spacelike features are introduced through the semantics of spatial relationships (adjacency, containment, interior properties, etc) rather than by quantitative measure arguments. The relationship between Semantic Spacetime and Causal Sets has been discussed in [10].
Our ability to detect dimension depends on the ‘channel depth’ in the process hierarchy to which we can probe. Pathways through space may be resolved from ‘routes’ between locations, captured and accumulated from virtual and ephemeral transits with long-term invariant characteristics. The relationship between routes and cables is not necessarily single valued nor deterministic, just as the relationship between quantum measurements and spatiotemporal boundary conditions is not deterministic and may not plumb the true depth of a process hierarchy. In this sense, an Internet packet route is quite like a quantum multi-slit experiment, with several parallel processes interfering over sampling subtimes. Invariant links are discerned by the observation of these interior sampling process channels over the elapsed (exterior) time of the experiment. This sampling takes many days. The resulting interference paths may be sewn together into a persistent hypersurface.
IV The degree distribution
The first characterization for any graph is its description in terms of nodes (also called vertices) and links (also called edges). Since every graph maps to a process and vice versa, this is also an initial indication of the dimensionality of kinetic behaviour.

In a continuum vector space, the number of independent local basis vectors yields the usual dimension of space. In a continuum, these basis vectors are only completely independent when they are orthogonal to one another. The continuity (or relative absence of holes) allows us to make sense of dimension at a single point, as a limit. The homogeneity of the continuum allows us to characterize the dimension for the whole space, as the same everywhere. Graphs, however, are different at every point. The closest corresponding idea in a graph is the node degree at a point. The independence of neighbouring nodes is obvious at one hop, but their independence over many hops remains to bee seen. How do we know that two directions are not mainly parallel over long distances and arrive at the same final destination? We can’t know this except statistically; counting exact trajectories and looking at their interference patterns is possible in principle, but impractical in practice for a discrete spacetime.
For a directed process, the outgoing node degree is the number of edges leaving the node, following the implicit ordering of the directed edges. This is usually what we want to use for trajectories. Any class of edges constitutes a partial ordering of the nodes they connect, and the sum of outgoing possibility leads to a ‘future cone’ of reachable points. However, in a graph (at each point) different outgoing paths are always initially independent, as long as they lead to different neighbouring nodes, because there is no way to deform one edge into a sum of others without passing through some kind of speculative, i.e. non-existent, embedding space in which we visualize it. The ability to do so may depend on the number of links over which we try (see figure 1). The number of incoming and outgoing edges that connect a node (vertex) to its neighbours can be different at every single node. Thus, the effective local dimension at a point can be different at every location too.
Counting the half average total node degree distribution for the Devices channel and computing the dimension at one hop.
| (1) |
where . For mutual information channels, we can simply take half This gives an average local point dimension of for the device channel. This definition of dimension is the relevant microscopic dimension for instantaneous stepwise dynamics, but it isn’t representative of large scale phenomena. On a larger scale, path degrees of freedom that appear independent over shorter path segments might not be independent over longer segments (figure 1). Consider a path that forks into two but then reconverges into a single path after some distance. In this case, the dimension at point is two, but the dimension on a larger scale is only 1, since all paths lead to a single direction. We can measure the characteristics of the graph on different semantic as well as dynamical scales (see figure 7), from its hierarchical composition.


The degree distribution for AS supernodes (containing each many device nodes) is given in figure 9. For the AS (BGP) supernodes, the effective dimension as average . This is significantly higher, since there are many more outgoing paths between AS providers.
V Statistical geometry
To overcome the scale dependence of node degree, we can look for a method that can be adapted to any scale with a suitable renormalization. A statistical approach was proposed by Myrheim[1] and by Meyer[2], based on the assumption of a probabilistic Poisson scattering process. The advantage of empirical data is that we don’t have to postulate the existence of a prior probability concept to explore the dynamics of the Internet’s process evolution; however, this means we need a somewhat different formula for dimension–one that has the semantics appropriate to small number processes, but which matches our intuitions about dimension from Euclidean schooling. A simple form of this can be understood by imagining space to be an virtual representation of degrees of freedom, as in kinetic processes.
The effective volume of an -cube of side length is just , and the volume of a ball of radius in dimensions is:
| (2) |
If we imagine trying to fill a volume of space with unit cubes or balls, then the number is determined by the dimension of the space (or vice versa) and some assumptions about the symmetry of volumes. We can estimate the effective dimension of a process by thinking of the vertices of a graph as -balls that touch when linked by edges. In order for a space to accommodate such linkage, it requires a minimum number of dimensions, given roughly by the ratio of volumes. After a certain number of such edges (hops or links), we can think of the process as a radius from the origin. The number of nodes after a certain radius us thus:
| (3) |
or
| (4) |
This ratio of logs means that we can only usefully measure the dimension for hop lengths of greater than two, so there’s no contradiction with a result for node degree. There is clearly freedom in defining the details too. The formula is based on a spherical geometry from the origin, with radius equal to the graph hop count. In particular, when using the number of hops from a starting point as the only measurable form of distance, there is some freedom in imagining the filling geometry (see figure 8), because the result is effectively an open ball without a boundary of corners or faces, so there’s a discrepancy in calculating volume from nodes or links. For a Cartesian ‘orthogonal’ geometry, we would tend to count volumes in terms of a cube of side-length ; now, the paths of length may undergo right angle turns—they can’t be assumed purely radial, which complicates the notion of distance by hop alone (this is one reason why many researchers immediately look to embed graphs in a Euclidean container). To complete what we think of as a cubic volume, we may have to go through additional hops to include corners, so a simple radial path length will progressively underestimate dimension in a geometry that undergoes right angle turns at the end, as a function of the distance. A counting estimate actually lies closer to a count from one hop length greater (at least for small hop counts and dimensions), so
There are two possible methods for using (4).
-
1.
We can measure the dimension as a function of distance (number of hops traversed along all paths of fixed length from the source) and sum the nodes enclosed by this region. This gives a deterministic answer for the dimension as a function of scale at that point, due to the Long Range Order of the lattice.
-
2.
We can select a random sample of points and perform the same method, but now average over the results to give a statistical estimate of a wider area.
VI Scale dependence of statistical measures
The scale dependence of the results is of interest here. In the middle of an -cube, far away from edge effects, we would expect the dimension to be quite stable. If we think of the volume of an -cube as and , then the dimension would be , which makes sense. But this is not how we measure volume from a graph (see figure 8). The corner nodes are not part of the volume found at one hop in all directions (giving a side length of 2). Only the open core is counted. There is no way to speculate about completing some kind of idealized geometry to get this nice simple number. Instead, we have to live with empirical and fractional approximations from inside the graph.
Closer to an edge we might expect the dimensionality of a volume to be reduced by the effect of edges. This is the case, but it never reaches the dimension of the face (). More interesting, we find that the dimension reaches a maximum value, due to the efficiency of dividing a virtual volume into balls, which we may then fall off again with distance (see figures 4 and 5) to reach a stable value as long as we don’t get close to edges.
A Euclidean spatial lattice has a singular degree distribution (a delta function at some fixed number of nearest neighbours). However, such networks are special cases, typically due to some Long Range Order; few networks that represent processes have such uniform crystalline bindings. Internet is known to have a power law distribution of node degrees, which means that error bars are only convenient scale markers, not Gaussian measures, and they will be large.
In inhomogeneous graphs, the non-simply connected topologies may lead to dimension being different on short and long scales, due to the inherent scale of Long Range Order (molecules or cells are not uniform on a short scale, but may form materials that are uniform on a large scale). This presents a dilemma: we restrict the size of measurement to capture local variations, while trying to avoid data that are merely incomplete. The only solution is to probe as a function of length and use any emergent scales to identify a natural granularity in space. Within grains of a certain size, there can be “hidden extra dimensions” or the opposite “holes through the dimensionality” that affect the result on a smaller scale. This is it the graphical analogue of “hidden dimensions” known from speculative physics models, e.g. Kaluza-Klein theory.
For anyone who believes the true nature of spacetime to be some kind of metric space, this inconsistency of dimensionality might feel weird, but this is what one has to expect of any discrete process structure. The infinitesimal limit (to which we’ve become unquestioningly accustomed) is the only case in which dimensionality can be abstracted to a constant. As we move towards theories in which the primacy of processes over things and spaces begins to dominate, this strangeness will become simply natural.
We can calibrate the expression defining scale-dependent graph dimension using -dimensional hypercubes, which are easy to generate as lattice graphs . For a cube of discrete side length (i.e. links joining nodes along an edge), we can calculate the numbers of links and nodes :
| (5) | |||||
| (6) |
Using these measures, we can check the correctness of the graph and the links in data, as well as perform Taylor expansions to estimate the discrepancy between an idealized cube and an effective spanning tree volume. A graph database (here we used ArangoDB) makes this task quite easy, with machine validation for large graphs.
| 2 | 2.3 | |
| 3 | 3.1 | |
| 4 | 4.3 | |
| 5 | 5.2 | |
| ITDK-dev | 8.7 | |
| ITDK AS | 7.70 |
When dealing with expressions involving powers, it’s hard to find an expression that doesn’t require one to know the power in order to find the power, so we resort to linearizing the expressions with logs and expansions. Ultimately, we can choose simply to define a heuristic statistical dimension , based on hop lengths from an origin, by:
| (7) |
where the additional corrective terms in the denominator are the first terms in a Taylor expansion for large , and offer an approximate calibration to cubic lattices up to dimension 5. Since our intuition about dimension is limited to these low numbers, this seems like a fair compromise.
VII Semantic channels
Figure 3 shows the different channels for which data were collected in the ITDK probes. Device nodes are the basic meeting point for information channels. They form the interior structure of AS nodes, for example, so they form an entirely different metric and semantic scale of the functional behaviour. There is an independent set of IPv4 and IPv6 addresses (the latter currently empty in the data). Finally, we have Autonomous System Numbers (ASN) and partial information about geo-spatial coordinates for the city a node is close to—a very coarse location on the Earth’s surface. We examine only Devices and ASes here. The dimensionality of these different channels need not be the same.
Although the probe process trajectories are directed (directional) in nature, the ITDK data treat connections as symmetric or undirected, in keeping with the usual interpretation of a background space. This is a weakness in the method for the ITDK, which assumes that reflection paths are the same as outgoing paths. This is not true in general, but there is currently no way to determine this using available technology. Locations are the average remnants of processes that could move in any direction (the process memory, in a computational sense). Formally, we use NEAR type links of the Semantic Spacetime model as correlations with respect to ensembles of probe trajectories.
In the case of the AS channel, connections are much more sparse and we need to collect an order of magnitude more samples in order to get an estimation of the error. This is intuitively in keeping with the fact that, if we call Device nodes semantic scale then AS has logarithmic scale . More interesting, perhaps, the AS graph seems to exhibit confinement, i.e. there is a maximum path length: paths don’t propagate beyond 7 or 8 hops. The reason for this is unclear, and we can’t rule out the idea that it is an artifact of the data collection limitations. The Autonomous Systems (AS) are private organizations, and may not allow probing of their interior structures. The interiors may also be connected through ‘Unknown’ nodes, which are tunnels or wormholes through the Internet, unobservable jumps of often indeterminate length. On the other hand, one would expect the maximum number of hops between all reachable locations to be finite and the range is shorter on the scale of ASes than for Devices. Evidence of maximum ranges above 20 hops were also seen in the Devices channel, but the computational expense or going beyond this prohibited further study. It’s at least suggestive that the finite horizon is a real effect rather than an artifact of the data.


The AS supernode graph has a fundamentally different character to the device graph. Cluster radii of less than 8 hops characterize the observable data. At 8 hops, the effective dimension appear to be about 5. This continues to fall with hop length, because no new points are expressed into the expanding volume of the search, thus it falls off exponentially without a clear limit. That is not the say that there are no new AS bubbles beyond this distance, only that they are disconnected by paths that are not out of scope. Some of these could be connected by anonymous tunnels (wormholes or hyperlinks) which have not been considered here because their passage through ASes can’t be established.
VIII Summary
In a dynamical system, we have to be clear about the distinction between infrastucture carriers and the virtual processes that multiply on top of it, over different semantic channels. We can only ever characterize processes using other processes, so at one level everything is virtual. This relativity trap may require us to modify certain prejudices about the nature of reality from observation alone.
It’s possible to calibrate and measure the dimension of the Internet across two of its process channels: device nodes and ASes. The spacelike hypersections of the Internet’s routing device channel have a short range dimension rising from 1.65 to an intermediate cell size of 8.7. Over distances at around 20 hops, the effective average dimension settles to . The scale dependence is evidence of the ‘foamy’ honeycomb structure of the graph. For the AS channel, there is a similar pattern and evidence of containment at a maximum length of paths is no more than 7 or 8 hops.
Last mile ‘edge’ connections of devices are conspicuously absent from the data in the map. This includes subnets where broadcast domains effectively group endpoints into coarse grains of order devices. This number of direct edge to edge tunnelling is growing all the time, and will likely be impacted in reality by telecommunication 5G services and beyond.
We can thus compute the dimension of the Internet as an abstract spacetime. The discreteness of the Internet scale favour a higher number of dimensions than a continuum embedding space would, since it is unconstrained by continuity or analyticity. At around six dimensions per slice, and higher dimensionality on a small scale, we see that it is quite ‘foamy’ more like a honeycomb than a uniform Euclidean space. On a practical level, this means that for every possible route between two points, there is an average redundancy of about 6 alternatives. On a policy level, this indicates a measure of the robustness and even resilience of the Internet to outages.
Due to the absence of timelike process information in the ITDK sets, we can’t comment on the long timescale dimension for slow changes. It’s not clear how to measure this timelike evolution of the Internet as a whole, in either a Newtonian or Minkowskian sense. The proper time of a process is intrinsically local and short range. The global time assumption is a convenient mathematical approximation for an embedding space, but it isn’t really physical within the interior of a system. Locally, individual observations express time inseparably from space, and may have any dimensionality (in principle) between 1 and some natural number. The default traceroute probe is to send three probes in parallel to initiate three parallel paths, subject to underlying routing behaviour; but over long distances observations those probe paths grow only with a lower number of dimensions over the expanding cone of reachable states. The computational expense of exploring path lengths of longer than 20 nodes is very high, even with a sparse graph, since path number grows exponentially with length.
The study here is limited by the maps we can construct of Internet processes. This, in turn, is limited by politics and security policy, as well as by technology. The Internet wasn’t explicitly designed to be observed (much like the universe as a whole) so we have to make do with what we have. Recognizing certain dynamical similarities between virtual network processes and quantum systems, we could imagine a future methodology based on interferometry for revealing more of the dynamical effects; however, this remains in the realm of speculation for now.
I’m grateful to kc claffy and Bradley Huffaker of CAIDA for helpful discussions and for the use of their resources.
References
- [1] J. Myrheim. Statistical geometry. CERN preprint TH.2538, August 1978.
- [2] D.A. Meyer. The Dimension of Causal Sets. PhD thesis, MIT, 1988.
- [3] L. Bombelli, D. Meyer, and R.D. Sorkin. Spacetime as a causal set. Phys. Rev. Lett., 59:521–524, 1988.
- [4] C. Moore. Comment on: Spacetime as a causal set. Phys. Rev. Lett., 60:655, 1988.
- [5] Young Hyun K. Keys, M. Luckie, and K. Claffy. Internet-scale ipv4 alias resolution with midar. Technical report, CAIDA, 2013. DOI:10.1109/TNET.2012.2198887.
- [6] M. Burgess. Spacetimes with semantics (i). arXiv:1411.5563, 2014.
- [7] James R. Clough and Tim S. Evans. What is the dimension of citation space? Physica A: Statistical Mechanics and its Applications, 448:235–247, Apr 2016.
- [8] M Aghili, L Bombelli, and B B Pilgrim. Discrete spacetime: a web of chains. Classical and Quantum Gravity, 36(18):185015, Aug 2019.
- [9] J.A. Bergstra and M. Burgess. Promise Theory: Principles and Applications (second edition). Press, 2014,2019.
- [10] M. Burgess. Notes on causal sets and semantic spacetime. available on Researchgate, June 2019.
- [11] M. Burgess. Semantic spacetime and data analytics appendix 1: Exploring the digital barrier reef with caida and arangodb. Medium article, December 2021.