On the pitchfork bifurcation of the folded node and other unbounded time-reversible connection problems in $\mathbb{R}^{3}$

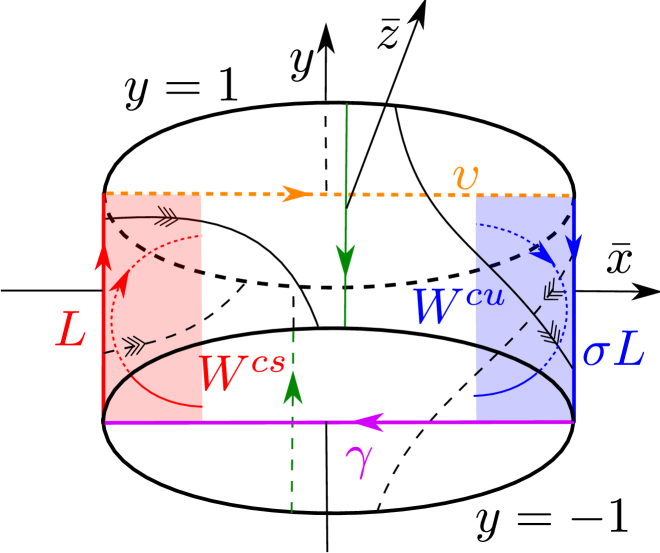
In slow-fast systems with one fast variable and two slow ones, the folded node $p$ is a singularity of the slow flow on the fold line of a critical manifold $C$. See an illustration in Fig. 1. Upon desingularization $p$ corresponds to a stable node with eigenvalues $\lambda_{s}<\lambda_{w}<0$, and its strong stable manifold $\upsilon$, tangent to the eigenvector associated with $\lambda_{s}$, produces a funnel region on the critical manifold, where orbits approach the singularity tangent to the weak eigendirection (associated with the eigenvalue $\lambda_{w}$). Due to the contraction within the funnel region, the folded node – upon composition with a global return mapping – provides a mechanism for producing attracting limit cycles $\Gamma_{\epsilon}$, see [2]. In fact, a blowup of the folded node reveals one orbit $\gamma$, along which extended versions $W^{cu}$ and $W^{cs}$ of the attracting and repelling critical manifolds, respectively, twist or rotate; the number of rotations being described by $\mu:=\lambda_{s}/\lambda_{w}>1$. The twisting is such that these manifolds intersect transversally whenever $\mu\notin\mathbb{N}$. As a consequence, for these values of $\mu$, there exists a ‘weak canard’ connecting extended versions of the Fenichel slow manifolds. This orbit acts, due to the twisting of $W^{cu}$ along $\gamma$, as a ‘center of rotation’ and trajectories on either side will therefore experience small oscillations before they leave a neighborhood of $p$ by following its unstable set; in Fig. 1 this unstable set coincides with the positive $z$-axis. Consequently, the limit cycles $\Gamma_{\epsilon}$ will be of mixed-mode type where small oscillations are followed by larger ones. Such oscillations appear in many applications, perhaps most notably in chemical reaction dynamics, and the folded node has therefore gained glory as a (relatively) simple mathematical model of this phenomenon, see e.g. the review article [4].

Bifurcations of the weak canard occurs whenever $\mu\in\mathbb{N}$; in this case, for $\epsilon=0$, the twisting of $W^{cu}$ and $W^{cu}$ is such that these manifolds intersect tangentially along $\gamma$. These bifurcations were described for $\epsilon=0$ by the reference [28], working on the ‘normal form’

and using the Melnikov approach developed in [27], following [26]. The system (1.1) is related to the blowup of the folded node $p$ for $\epsilon=0$. In particular for (1.1), $\gamma$ takes the following form

For each odd $n$, it was shown that there is a transcritical bifurcation of ‘canards’ connecting $W^{cu}(\mu)$ and $W^{cs}(\mu)$. For all $0<\epsilon\ll 1$, this bifurcation produces additional transversal intersections of the slow manifold. The resulting new canards – the ‘secondary canards’ – produce bands on the attracting slow manifold where different number of small oscillations occur, see [2, 4, 28]. For any even $n$, it was conjectured that a pitchfork bifurcation occurs. This was supported by numerical computations. Furthermore, in [18, App. A] a way was found to compute a ‘third order’ Melnikov integral using Mathematica for all even $n$ and explicit computations demonstrated that the integral was nonzero for even values of $n$ up to $20$. Following the work of [28] this also shows that a pitchfork bifurcation occurs, at least for these values.

In this paper, we prove the pitchfork bifurcation for every even $n$ by evaluating the third order Melnikov integral analytically. Our approach is based upon a time-reversible version of the Melnikov theory of [27]. However, the most important insight of this paper is to characterize the manifolds $W^{cs}(\mu)$ and $W^{cu}(\mu)$ locally by solutions to higher order variational equations; this is in contrast to [28] which uses an integral representation of these manifolds. We show that this approach, relying on reducing these variational equations to an inhomogeneous Weber equation, extends to a very general class of time-reversible, quadratic, unbounded connection problems in $\mathbb{R}^{3}$. Regardless, for the folded node the ‘time-reversible approach’ also allows us to provide a more detailed blowup picture of the folded node, including a rigorous description of the additional transverse intersections of $W^{cs}$ and $W^{cu}$ that arise due to the pitchfork bifurcation.

The bifurcations of canards for (1.1), is closely related to bifurcations of periodic orbits from heteroclinic cycles at infinity. The Falkner-Skan equation

and the Nosé equation:

are well-known examples of systems (without equilibria) possessing such bifurcations, see e.g. [23], and [17] for other examples. The Falkner-Skan equation (1.3) initially appeared in the study of boundary layers in fluid dynamics, see [6]. In this context, the physical relevant parameter regime is $\mu\in(0,2)$. However, the equation has subsequently been studied by other authors [22, 21, 23] for all $\mu>0$ on the basis of the rich dynamics it possesses (including chaotic dynamics and a novel bifurcation of periodic orbits from infinity). On the other hand, the Nosé equations (1.4) model the interaction of a particle with a heat bath [19]. The system also has interesting dynamics without any equilibrium and possesses many similar properties to (1.1) and (1.3). Nevertheless, the description of the bifurcating periodic orbits in both of these systems, is – as noted by [23] – long and cumbersome, and to a large extend, independent of standard methods of dynamical systems theory. Therefore, although the folded node will be our primary focus, a subsequent aim of the paper, is to apply the Melnikov theory, and our classification of $W^{cs}$ and $W^{cu}$ through solutions of an inhomogeneous Weber equation, to these bifurcations and present a simpler description of the emergence of periodic orbits, based on normal form theory and invariant manifolds and therefore more in tune with dynamical systems theory.

The reference [27] describes a Melnikov theory for connection problems of nonhyperbolic points at infinity. In this section, we will review this approach in the context of time-reversible systems. For simplicity, we restrict to $\mathbb{R}^{3}$ and consider a general smooth ODE

for $x=x(t)\in\mathbb{R}^{3}$, depending on a parameter $\alpha\in\mathbb{R}$, and assume the following:

• (H1)

  There exists a time-reversible symmetry

  $\displaystyle(x,t)\mapsto(\sigma x,-t),$

  (2.2)

  with $\sigma\in\mathbb{R}^{3\times 3}$ being an involution: $\sigma^{2}=\textnormal{id}$, $\textnormal{id}=\text{diag}(1,1,1)$ being the identity matrix in $\mathbb{R}^{3\times 3}$, such that

  $$f(\sigma x,\alpha)=-\sigma f(x,\alpha),$$

  for all $x$ and all $\alpha$.

Therefore:

As is standard, we say that an orbit $x$ with parametrization $x(t)$, which is a fix-point of the symmetry: $x(t)=\sigma x(-t)$ for all $t$, is ‘symmetric’. On the other hand, in general two orbits $x_{1}\neq x_{2}$, for which $x_{2}(t)=\sigma x_{1}(-t)$, is said to be ‘symmetrically related’.

Furthermore, we say that a solution $x(t)$ of (2.1) has algebraic growth for $t\rightarrow\infty$ if there exists a $\nu>0$ such that $\sup_{t\geq 0}|x(t)|(|t|+1)^{-\nu}<\infty$ for $\nu>0$ large enough. Specifically, we define the Banach space

for $\nu>0$ fixed, see [27]. Similarly, a solution $x(t)$ of (2.1) has algebraic growth for $t\rightarrow-\infty$ if $\sup_{t\leq 0}|x(t)|(|t|+1)^{-\nu}<\infty$ for $\nu>0$ large enough. Accordingly, we define

We will suppress $\nu$ in $C_{b,+}(\nu)$ and $C_{b,-}(\nu)$ whenever it is convenient to do so.

Next, we assume

• (H2)

  For $\alpha=0$ there exists a symmetric solution $\gamma$ with parametrization $\gamma(t)$, $t\in\mathbb{R}$, of at most algebraic growth for $t\rightarrow\pm\infty$, i.e. $\gamma(t)\in C_{b,+}(\nu)$ with $\nu>0$ large enough. Without loss of generality we suppose that

  $\displaystyle\gamma(0)=0.$

• (H3)

  There exists a three-dimensional smooth invariant manifold $W^{cs}$ in the extended system

  $\displaystyle\begin{split}\dot{x}&=f(x,\alpha),\\ \dot{\alpha}&=0.\end{split}$

  (2.3)

  Here $W^{cs}$ denotes the center-stable manifold consisting of all solution curves $(x(t),\alpha)$ of (2.1) near (and including) $(x,\alpha)=(\gamma(t),0)$ (in a sense specified below) for which $x(t)\in C_{b,+}(\nu)$, for $\nu>0$ large enough.

$W^{cs}$ is foliated by two-dimensional invariant manifolds $W^{cs}(\alpha)$ of (2.1) for fixed values of $\alpha$, sufficiently small.

By (H1) and (H3), there exists a center-unstable manifold

consisting of all solution curves $(z(t),\alpha)$ of (2.1) near (and including) $(x,\alpha)=(\gamma(t),0)$ for which $x(t)\in C_{b,-}(\nu)$.

• (H4)

  Let $U:=\textnormal{span}(\dot{\gamma}(0))$. Then for $\alpha=0$ there exists a one-dimensional linear space $V$ such that

  $$T_{\gamma(0)}W^{cs}(0)\cap T_{\gamma(0)}W^{cu}(0)=U\oplus V,$$

  is a two-dimensional subspace.

(H4) implies that the manifolds $W^{cs}(0)$ and $W^{cu}(0)$ intersect tangentially along $\gamma$ for $\alpha=0$. In fact, seeing that $W^{cu}=\sigma W^{cs}$ we have

Next, following [28] let

Then $\mathbb{R}^{3}=U\oplus V\oplus W$. Let $e_{u}$, $e_{v}$ and $e_{w}$ be unit vectors spanning $U$, $V$ and $W$, respectively, and denote the coordinates of any $x\in\mathbb{R}^{3}$ with respect to this basis $\{e_{u},e_{v},e_{w}\}$ by $(u,v,w)$. Fix $r>0$ small and let $B_{r}$ be the ball of radius $r$ centered at $\gamma(0)$. We then define a local section $\Sigma$ transverse to $\gamma$ at $\gamma(0)=0$ by

Notice that $\Sigma$ – in the $(u,v,w)$-coordinates – is contained within the $(v,w)$-plane. Next, we write $x=z+\gamma(t)$ following [27] such that

where $g(t,z,\alpha)=f(\gamma(t)+z,\alpha)-f(\gamma(t),0)-A(t)z$. Also $g(t,0,0)=0,D_{z}g(t,0,0)=0$ and notice that (2.5) is the variational equation along $\gamma(t)$. Furthermore:

Let $\Phi(t,s)$ be the state-transition matrix of (2.5). Then by (H3) and (H4) there exists a continuous projection $P:[0,\infty)\rightarrow\mathbb{R}^{3}$ such that

and

for all $t,s\geq 0$. Furthermore, if $Q(s)=I-P(s)$ then

and it follows that

for some $K\geq 1$, $\theta,\eta\geq 0$ and all $0\leq s\leq t$, see e.g. [27, 26]. By assumption (H1), Lemma 2.2 and (2.9) we also have:

Consider the adjoint equation of (2.5):

and notice that

is a time-reversible symmetry for (2.10) by (H1). Then

In the following, we fix a specific $\psi_{*}(t)$ by setting $\psi_{*}(0)=e_{w}$. Since $\Phi^{T}(s,t)=\Phi^{-T}(t,s)$ is a state-transition matrix of (2.10), we can then write $\psi_{*}(t)$ as

We now have the following important result.

In fact, in the $(u,v,w)$-coordinates

Next, for (2.7), it can by variation of constants – following [27] – be shown that $z(t)\in C_{b,+}$, with $z(0)\in\Sigma$, if and only if there exists a $v\in V$ such that

This enables an analytic characterization of the (nonunique) invariant manifold $W^{cs}(\mu)$, which is essential for the Melnikov approach, as follows. Let the mapping $z\mapsto T(z)$ be defined on $C_{b,+}$ so that $T(z)(t)$ is the right hand side of (2.14) and consider a sufficiently small neighborhood $N$ of $(v,\alpha)=(0,0)$. Then, upon possible modification (or cut-off) of $f$ (and therefore of $g$ in (2.7)), as in center manifold theory [3], we obtain for each $(v,\alpha)\in N$, a unique fix-point $z_{*}(v,\alpha)$ of $T$: $T(z_{*})=z_{*}$, see [27]. Henceforth we will assume that such a modification of $f$ (and therefore of $g$) has been made. It is also standard, see also [27], to show that $z_{*}$ is smooth, with each partial derivative belonging to $C_{b,+}(\nu)$ for $\nu$ large enough. In this way,