This paper was converted on www.awesomepapers.org from LaTeX by an anonymous user.
Want to know more? Visit the Converter page.

[1]\fnmZachary \surFrangella \equalcontThese authors contributed equally to this work.

\equalcont

These authors contributed equally to this work.

1]\orgdivManagement Science and Engineering, \orgnameStanford University, \orgaddress\street475 Via Ortega, \cityStanford, \postcode94305, \stateCA

2]\orgdivSystems Engineering, \orgnameCornell University, \orgaddress\street136 Hoy Rd, \cityIthaca, \postcode14850, \stateNY

3]\orgdivElectrical Engineering and Computer Science, \orgnameMassachusetts Institute of Technology, \orgaddress\street50 Vassar St, Cambridge, \cityCambridge, \postcode02139, \stateMA

4]\orgdivOperations Research and Financial Engineering, \orgnamePrinceton University, \orgaddress\street98 Charlton St, \cityPrinceton, \postcode08540, \stateNJ

On the (linear) convergence of Generalized Newton Inexact ADMM

[email protected]    \fnmShipu \surZhao [email protected]    \fnmTheo \surDiamandis [email protected]    \fnmBartolomeo \surStellato [email protected]    \fnmMadeleine \surUdell [email protected] [ [ [ [
Abstract

This paper presents GeNI-ADMM, a framework for large-scale composite convex optimization that facilitates theoretical analysis of both existing and new approximate ADMM schemes. GeNI-ADMM encompasses any ADMM algorithm that solves a first- or second-order approximation to the ADMM subproblem inexactly. GeNI-ADMM exhibits the usual 𝒪​(1/t)\mathcal{O}(1/t)-convergence rate under standard hypotheses and converges linearly under additional hypotheses such as strong convexity. Further, the GeNI-ADMM framework provides explicit convergence rates for ADMM variants accelerated with randomized linear algebra, such as NysADMM and sketch-and-solve ADMM, resolving an important open question on the convergence of these methods. This analysis quantifies the benefit of improved approximations and can inspire the design of new ADMM variants with faster convergence.

keywords:
ADMM, Inexactness, Linearization, Randomized Numerical Linear Algebra

1 Introduction

The Alternating Direction Method of Multipliers (ADMM) is one of the most popular methods for solving composite optimization problems, as it provides a general template for a wide swath of problems and converges to an acceptable solution within a moderate number of iterations [1]. Indeed, [1] implicitly promulgates the vision that ADMM provides a unified solver for various convex machine learning problems. Unfortunately, for the large-scale problem instances routinely encountered in the era of Big Data, ADMM scales poorly and cannot provide a unified machine learning solver for problems of all scales. The scaling issue arises as ADMM requires solving two subproblems at each iteration, whose cost can increase superlinearly with the problem size. As a concrete example, in the case of ℓ1\ell_{1}-logistic regression with an n×dn\times d data matrix, ADMM requires solving an ℓ2\ell_{2}-regularized logistic regression problem at each iteration [1]. With a fast-gradient method, the total complexity of solving the subproblem is 𝒪~​(n​d​κ)\tilde{\mathcal{O}}(nd\sqrt{\kappa}) [2], where κ\kappa is the condition number of the problem. When nn and dd are in the tens of thousands or larger—a moderate problem size by contemporary machine learning standards—and κ\kappa is large, such a high per-iteration cost becomes unacceptable. Worse, ill-conditioning is ubiquitous in machine learning problems; often κ=Ω​(n)\kappa=\Omega(n), in which case the cost of the subproblem solve becomes superlinear in the problem size.

Randomized numerical linear algebra (RandNLA) offers promising tools to scale ADMM to larger problem sizes. Recently [3] proposed the algorithm NysADMM, which uses a randomized fast linear system solver to scale ADMM up to problems with tens of thousands of samples and hundreds of thousands of features. The results in [3] show that ADMM combined with the RandNLA primitive runs 3 to 15 times faster than state-of-the-art solvers on machine learning problems from LASSO to SVM to logistic regression. Unfortunately, the convergence of randomized or approximate ADMM solvers like NysADMM is not well understood. NysADMM approximates the xx-subproblem using a linearization based on a second-order Taylor expansion, which transforms the xx-subproblem into a Newton-step, i.e., a linear system solve. It then solves this system approximately (and quickly) using a randomized linear system solver. The convergence of this scheme, which combines linearization and inexactness, is not covered by prior theory for approximate ADMM; prior theory covers either linearization [4] or inexact solves [5] but not both.

In this work, we bridge the gap between theory and practice to explain the excellent performance of a large class of approximate linearized ADMM schemes, including NysADMM [3] and many methods not previously proposed. We introduce a framework called Generalized Newton Inexact ADMM, which we refer to as GeNI-ADMM (pronounced genie-ADMM). GeNI-ADMM includes NysADMM and many other approximate ADMM schemes as special cases. The name is inspired by viewing the linearized xx-subproblem in GeNI-ADMM as a generalized Newton-step. GeNI-ADMM allows for inexactness in both the xx-subproblem and the zz-subproblem. We show GeNI-ADMM exhibits the usual 𝒪​(1/t)\mathcal{O}(1/t)-convergence rate under standard assumptions, with linear convergence under additional assumptions. Our analysis also clarifies the value of using curvature in the generalized Newton step: approximate ADMM schemes that take advantage of curvature converge faster than those that do not at a rate that depends on the conditioning of the subproblems. As the GeNI-ADMM framework covers any approximate ADMM scheme that replaces the xx-subproblem by a linear system solve, our convergence theory covers any ADMM scheme that uses fast linear system solvers. Given the recent flurry of activity on fast linear system solvers within the (randomized) numerical linear algebra community [6, 7, 8], our results will help realize these benefits for optimization problems as well. To demonstrate the power of the GeNI-ADMM framework, we establish convergence of NysADMM and another RandNLA-inspired scheme, sketch-and-solve ADMM, whose convergence was left as an open problem in [9].

1.1 Contributions

Our contributions may be summarized concisely as follows:

  1. 1.

    We provide a general ADMM framework GeNI-ADMM, that encompasses prior approximate ADMM schemes as well as new ones. It can take advantage of second-order information and allows for inexact subproblem solves.

  2. 2.

    We show that GeNI-ADMM converges ergodically with the usual ergodic 𝒪​(1/t)\mathcal{O}(1/t) rate, despite all the approximations it makes. Further, it converges at a linear rate under strong convexity.

  3. 3.

    We apply our framework to show some RandNLA-based approximate ADMM schemes converge at the same rate as vanilla ADMM, answering some open questions regarding their convergence [9, 3]. In the case of sketch-and-solve ADMM, we show modifications to the naive scheme are required to ensure convergence.

1.2 Roadmap

In Section 2, we formally state the optimization problem that we focus on in this paper and briefly introduce ADMM. In Section 3 we introduce the Generalized Newton Inexact ADMM framework and review ADMM and its variants. Section 4 gives various technical backgrounds and assumptions needed for our analysis. Section 5 establishes that GeNI-ADMM converges at an 𝒪​(1/t)\mathcal{O}(1/t)-rate in the convex setting. Section 6 then shows that, when the objective is strongly convex, GeNI-ADMM converges linearly. In Section 7, we apply our theory to establish convergence rates for two methods that naturally fit into our framework, and we illustrate these results numerically in Section 8.

1.3 Notation and preliminaries

We call a matrix psd if it is positive semidefinite. We denote the convex cone of n×nn\times n real symmetric psd matrices by 𝕊n+\mathbb{S}^{+}_{n}. We denote the Loewner ordering on 𝕊n+\mathbb{S}^{+}_{n} by ⪯\preceq, that is A⪯BA\preceq B if and only if B−AB-A is psd. Given a matrix HH, we denote its spectral norm by ‖H‖\|H\|. If ff is a smooth function we denote its smoothness constant by LfL_{f}. We say a positive sequence {εk}k≥1\{\varepsilon^{k}\}_{k\geq 1} is summable if ∑k=1∞εk<∞\sum_{k=1}^{\infty}\varepsilon^{k}<\infty.

2 Problem statement and ADMM

Let 𝒳,𝒵,ℋ\mathcal{X},\mathcal{Z},\mathcal{H} be finite-dimensional inner-product spaces with inner-product ⟨⋅,⋅⟩\langle\cdot,\cdot\rangle and norm ∥⋅∥\|\cdot\|. We wish to solve the convex constrained optimization problem

minimizef​(x)+g​(z)subject toM​x+N​z=0x∈X,z∈Z,\begin{array}[]{ll}\mbox{minimize}&f(x)+g(z)\\ \mbox{subject to}&Mx+Nz=0\\ &x\in X,~{}z\in Z,\end{array} (1)

with variables xx and zz, where X⊂𝒳X\subset\mathcal{X} and Z⊂𝒵Z\subset\mathcal{Z} are closed convex sets, ff is a smooth convex function, gg is a convex proper lower-semicontinuous (lsc) function, and M:𝒳↦ℋM:\mathcal{X}\mapsto\mathcal{H} and N:𝒵↦ℋN:\mathcal{Z}\mapsto\mathcal{H} are bounded linear operators.

Remark 1.

Often, the constraint is presented as M​x+N​z=cMx+Nz=c for some non-zero vector cc however, by increasing the dimension of 𝒵\mathcal{Z} by 11 and replacing NN by [N​c][N~{}c], we can make c=0c=0. Thus, our setting of c=0c=0 is without loss of generality.

We can write problem (1) as the saddle point problem

minimizex∈X,z∈Z​maximizey∈Y​f​(x)+g​(z)+⟨y,M​x+N​z⟩,\underset{{x\in X,z\in Z}}{\mbox{minimize}}\;\underset{y\in Y}{\mbox{maximize}}\;f(x)+g(z)+\langle y,Mx+Nz\rangle, (2)

where Y⊂𝒵Y\subset\mathcal{Z} is a closed convex set. The saddle-point formulation will play an important role in our analysis. Perform the change of variables u=y/ρu=y/\rho and define the Lagrangian

Lρ​(x,z,u)≔f​(x)+g​(z)+⟨ρ​u,M​x+N​z⟩.L_{\rho}(x,z,u)\coloneqq f(x)+g(z)+\langle\rho u,Mx+Nz\rangle.

Then (2) may be written concisely as

minimizex∈X,z∈Z​maximizeu∈U​Lρ​(x,z,u).\underset{x\in X,z\in Z}{\mbox{minimize}}\;\underset{{u\in U}}{\mbox{maximize}}\;L_{\rho}(x,z,u). (3)

The ADMM algorithm (Algorithm 1) is a popular method for solving (1). Our presentation uses the scaled form of ADMM [1, 10], which uses the change of variables u=y/ρu=y/\rho, this simplifies the algorithms and analysis, so we maintain this convention throughout the paper.

Algorithm 1 ADMM
convex proper lsc functions ff and gg, constraint matrix MM, stepsize ρ\rho
repeat
     xk+1=argminx∈X​{f​(x)+ρ2​‖M​x+N​zk+uk‖2}x^{k+1}=\underset{x\in X}{\mathop{\rm argmin}}\{f(x)+\frac{\rho}{2}\|Mx+Nz^{k}+u^{k}\|^{2}\}
     zk+1=argminz∈Z​{g​(z)+ρ2​‖M​xk+1+N​z+uk‖2}z^{k+1}=\underset{z\in Z}{\mathop{\rm argmin}}\{g(z)+\frac{\rho}{2}\|Mx^{k+1}+Nz+u^{k}\|^{2}\}
     uk+1=uk+M​xk+1+N​zk+1u^{k+1}=u^{k}+Mx^{k+1}+Nz^{k+1}
until convergence
solution (x⋆,z⋆)(x^{\star},z^{\star}) of problem (1)

3 Generalized Newton Inexact ADMM

As shown in Algorithm 1, at each iteration of ADMM, two subproblems are solved sequentially to update variables xx and zz. ADMM is often the method of choice when the zz-subproblem has a closed-form solution. For example, if g​(x)=‖x‖1g(x)=\|x\|_{1}, the zz-subproblem is soft thresholding, and if g​(x)=1𝒮​(x)g(x)=1_{\mathcal{S}}(x) is the indicator function of a convex set 𝒮\mathcal{S}, the zz-subproblem is projection onto 𝒮\mathcal{S} [11, §6]. However, it may be expensive to compute even with a closed-form solution. For example, when g​(x)=1𝒮​(x)g(x)=1_{\mathcal{S}}(x) and 𝒮\mathcal{S} is the psd cone, the zz-subproblem requires an eigendecomposition to compute the projection, which is prohibitively expensive for large problems [12].

Let us consider the xx-subproblem

xk+1=argminx∈X​{f​(x)+ρ2​‖M​x+N​zk+uk‖2}.x^{k+1}=\underset{x\in X}{\mathop{\rm argmin}}\left\{f(x)+\frac{\rho}{2}\|Mx+Nz^{k}+u^{k}\|^{2}\right\}. (4)

In contrast to the zz-subproblem, there is usually no closed-form solution for the xx-subproblem. Instead, an iterative scheme is often used to solve it inaccurately, especially for large-scale applications. This solve can be very expensive when the problem is large. To reduce computational effort, many authors have suggested replacing this problem with a simplified subproblem that is easier to solve. We highlight several strategies to do so below.

Augmented Lagrangian linearization.

One strategy is to linearize the augmented Lagrangian term ρ2​‖M​x+N​zk+uk‖2\frac{\rho}{2}\|Mx+Nz^{k}+u^{k}\|^{2} in the ADMM subproblem and replace it by the quadratic penalty 12​‖x−xk‖P2\frac{1}{2}\|x-x^{k}\|^{2}_{P} for some (carefully chosen) positive definite matrix PP. More formally, the strategy adds a quadratic term to form a new subproblem

xk+1=argminx∈X​{f​(x)+ρ2​‖M​x+N​zk+uk‖2+12​‖x−xk‖P2},x^{k+1}=\underset{x\in X}{\mathop{\rm argmin}}\left\{f(x)+\frac{\rho}{2}\|Mx+Nz^{k}+u^{k}\|^{2}+\frac{1}{2}\|x-x^{k}\|^{2}_{P}\right\},

which is substantially easier to solve for an appropriate choice of PP. One canonical choice is P=η​I−ρ​MT​MP=\eta I-\rho M^{T}M, where η>0\eta>0 is a constant. For this choice, the quadratic terms involving MM cancel, and we may omit constants with respect to xx, resulting in the subproblem

xk+1=argminx∈X​{f​(x)+ρ​⟨M​x,M​xk−zk+uk⟩+η2​‖x−xk‖2}.x^{k+1}=\underset{x\in X}{\mathop{\rm argmin}}\left\{f(x)+\rho\langle Mx,Mx^{k}-z^{k}+u^{k}\rangle+\frac{\eta}{2}\|x-x^{k}\|^{2}\right\}.

Here, an isotropic quadratic penalty replaces the augmented Lagrangian term in (4). This strategy allows the subproblem solve to be replaced by a proximal operator with a (possibly) closed-form solution. This strategy has been variously called preconditioned ADMM, proximal ADMM, and (confusingly) linearized ADMM [13, 14, 4].

Function approximation.

The second strategy to simplify the xx-subproblem, is to approximate the function ff by a first- or second-order approximation [4, 10, 3], forming the new subproblem

xk+1=argminx∈X​{f​(xk)+⟨∇f​(xk),x−xk⟩+12‖x−xk∥H2+ρ2​‖M​x+N​zk+uk‖2}x^{k+1}=\underset{x\in X}{\mathop{\rm argmin}}\left\{f(x^{k})+\langle\nabla f(x^{k}),x-x^{k}\rangle+\frac{1}{2}\|x-x^{k}\|_{H}^{2}+\frac{\rho}{2}\|Mx+Nz^{k}+u^{k}\|^{2}\right\} (5)

where HH is the Hessian of ff at xkx^{k}. The resulting subproblem is quadratic and may be solved by solving a linear system or (for M=IM=I) performing a linear update, as detailed below in Section 3.1.1.

Inexact subproblem solve.

The third strategy is to solve the ADMM subproblems inexactly to achieve some target accuracy, either in absolute error or relative error. An absolute-error criterion chooses the subproblem error a priori [5], while a relative error criterion requires the subproblem error to decrease as the algorithm nears convergence, for example, by setting the error target at each iteration proportional to ‖uk+1−uk−ρ​(zk+1−zk)‖\|u^{k+1}-u^{k}-\rho(z^{k+1}-z^{k})\| [15].

Approximations used by GeNI-ADMM.

The GeNI-ADMM framework allows for any combination of the three strategies: augmented Lagrangian linearization, function approximation, and inexact subproblem solve. Consider the generalized second-order approximation to ff

f​(x)≈f1​(x)+f2​(x~k)+⟨∇f2​(x~k),x−x~k⟩+12​‖x−x~k‖Θk2,\displaystyle f(x)\approx f_{1}(x)+f_{2}(\tilde{x}^{k})+\langle\nabla f_{2}(\tilde{x}^{k}),x-\tilde{x}^{k}\rangle+\frac{1}{2}\|x-\tilde{x}^{k}\|^{2}_{\Theta^{k}}, (6)

where f1+f2=ff_{1}+f_{2}=f and {Θk}k≥1\{\Theta^{k}\}_{k\geq 1} is a sequence of psd matrices that approximate the Hessian of ff. GeNI-ADMM uses this approximation in the xx-subproblem, resulting in the new subproblem

x~k+1=argminx∈X\displaystyle\tilde{x}^{k+1}=\underset{x\in X}{\textrm{argmin}} {f1(x)+⟨∇f2(x~k),x−x~k⟩+12∥x−x~k∥Θk2\displaystyle\{f_{1}(x)+\langle\nabla f_{2}(\tilde{x}^{k}),x-\tilde{x}^{k}\rangle+\frac{1}{2}\|x-\tilde{x}^{k}\|^{2}_{\Theta^{k}} (7)
+ρ2∥Mx+Nz~k+u~k∥2}.\displaystyle+\frac{\rho}{2}\|Mx+N\tilde{z}^{k}+\tilde{u}^{k}\|^{2}\}.

We refer to (7) as a generalized Newton step. The intuition for the name is made plain when X=ℝdX=\mathbb{R}^{d}, f1=0,f2=ff_{1}=0,f_{2}=f in which case the update becomes

(Θk+ρ​MT​M)​x~k+1=Θk​x~k−∇f​(x~k)−ρ​MT​(u~k−z~k).\displaystyle\left(\Theta^{k}+\rho M^{T}M\right)\tilde{x}^{k+1}=\Theta^{k}\tilde{x}^{k}-\nabla f(\tilde{x}^{k})-\rho M^{T}(\tilde{u}^{k}-\tilde{z}^{k}). (8)

Equation (8) shows that the xx-subproblem reduces to a linear system solve, just like the Newton update. We can also interpret GeNI-ADMM as a linearized proximal augmented Lagrangian (P-ALM) method [16, 17]. From this point of view, GeNI-ADMM replaces ff in the P-ALM step by its linearization and adds a specialized penalty defined by the Θk\Theta^{k}-norm.

GeNI-ADMM also replaces the zz-subproblem of ADMM with the following problem

z~k+1=argminz∈Z​{g​(z)+ρ2​‖M​x~k+1+N​z+u~k‖2+12​‖z−z~k‖Ψk2}.\tilde{z}^{k+1}=\underset{z\in Z}{\mathop{\rm argmin}}\{g(z)+\frac{\rho}{2}\|M\tilde{x}^{k+1}+Nz+\tilde{u}^{k}\|^{2}+\frac{1}{2}\|z-\tilde{z}^{k}\|^{2}_{\Psi^{k}}\}. (9)

Incorporating the quadratic Ψk\Psi^{k} term allows us to linearize the augmented Lagrangian term, which is useful when NN is very complicated.

However, even with the allowed approximations, it is unreasonable to assume that (7), (9) are solved exactly at each iteration. Indeed, the hallmark of the NysADMM scheme from [3] is that it solves (7) inexactly (but efficiently) using a randomized linear system solver. Thus, the GeNI-ADMM framework allows for inexactness in the xx and zz-subproblems, as seen in Algorithm 2.

Algorithm 2 Generalized Newton Inexact ADMM (GeNI-ADMM)
penalty parameter ρ\rho, sequence of psd matrices {Θk}k≥1,{Ψk}k≥1\{\Theta^{k}\}_{k\geq 1},\{\Psi^{k}\}_{k\geq 1}, forcing sequences {εxk}k≥1,{εzk}k≥1,\{\varepsilon_{x}^{k}\}_{k\geq 1},\{\varepsilon_{z}^{k}\}_{k\geq 1},
repeat
     x~k+1​≈εxk​argminx∈X​{f1​(x)+⟨∇f2​(x~k),x−x~k⟩+12‖x−x~k∥Θk2+ρ2​‖M​x+N​z~k+u~k‖2}\tilde{x}^{k+1}\overset{\varepsilon_{x}^{k}}{\approx}\underset{x\in X}{\mathop{\rm argmin}}\{f_{1}(x)+\langle\nabla f_{2}(\tilde{x}^{k}),x-\tilde{x}^{k}\rangle+\frac{1}{2}\|x-\tilde{x}^{k}\|^{2}_{\Theta^{k}}+\frac{\rho}{2}\|Mx+N\tilde{z}^{k}+\tilde{u}^{k}\|^{2}\}
     z~k+1​≊εzk​argminz∈Z​{g​(z)+ρ2​‖M​x~k+1+N​z+u~k‖2+12​‖z−z~k‖Ψk2}\tilde{z}^{k+1}\overset{\varepsilon_{z}^{k}}{\approxeq}\underset{z\in Z}{\mathop{\rm argmin}}\{g(z)+\frac{\rho}{2}\|M\tilde{x}^{k+1}+Nz+\tilde{u}^{k}\|^{2}+\frac{1}{2}\|z-\tilde{z}^{k}\|^{2}_{\Psi^{k}}\}
     u~k+1=u~k+M​x~k+1+N​z~k+1\tilde{u}^{k+1}=\tilde{u}^{k}+M\tilde{x}^{k+1}+N\tilde{z}^{k+1}
until convergence
solution (x⋆,z⋆)(x^{\star},z^{\star}) of problem (1)

Algorithm 2 differs from ADMM (Algorithm 1) in that a) the xx and zz-subproblems are now given by (7) and (9) and b) both subproblems may be solved inexactly. Given the inexactness and the use of the generalized Newton step in place of the original xx-subproblem, we refer to Algorithm 2 as Generalized Newton Inexact ADMM (GeNI-ADMM). The inexactness schedule is controlled by the forcing sequences {εxk}k≥1,{εzk}k≥1\{\varepsilon_{x}^{k}\}_{k\geq 1},\{\varepsilon_{z}^{k}\}_{k\geq 1} that specify how accurately the xx and zz-subproblems are solved at each iteration. These subproblems have different structures that require different notions of accuracy. To distinguish between them, we make the following definition.

Definition 1 (ε\varepsilon-minimizer and ε\varepsilon-minimum).

Let h:𝒯↦ℝh:\mathcal{T}\mapsto\mathbb{R} be strongly-convex and let t⋆=argmint′∈𝒯h​(t′)t^{\star}=\mathop{\rm argmin}_{t^{\prime}\in\mathcal{T}}h(t^{\prime}).

  • •

    (ε\varepsilon-minimizer) Given t∈𝒯t\in\mathcal{T}, we say tt is an ε\varepsilon-minimizer of minimizet∈𝒯​h​(t)\textrm{minimize}_{t\in\mathcal{T}}h(t) and write

    t​≈𝜀​argmint′∈𝒯h​(t′)if and only if‖t−t⋆‖≤ε.t\overset{\varepsilon}{\approx}\mathop{\rm argmin}_{t^{\prime}\in\mathcal{T}}h(t^{\prime})\quad\textrm{if and only if}\quad\|t-t^{\star}\|\leq\varepsilon.

    In words, tt is nearly equal to the argmin of h​(t)h(t) in set 𝒯\mathcal{T}.

  • •

    (ε\varepsilon-minimum) Given t∈𝒯t\in\mathcal{T}, we say tt gives an ε\varepsilon-minimum of minimizet∈𝒯​h​(t)\textrm{minimize}_{t\in\mathcal{T}}h(t) and write

    t​≊𝜀​argmint′∈𝒯h​(t′)if and only ifh​(t)−h​(t⋆)≤ε.t\overset{\varepsilon}{\approxeq}\mathop{\rm argmin}_{t^{\prime}\in\mathcal{T}}h(t^{\prime})\quad\textrm{if and only if}\quad h(t)-h(t^{\star})\leq\varepsilon.

    In words, tt produces nearly the same objective value as the argmin of h​(t)h(t) in set 𝒯\mathcal{T}.

Thus, from Definition 1 and Algorithm 2, we see for each iteration kk that x~k+1\tilde{x}^{k+1} is an εxk\varepsilon_{x}^{k}-minimizer of the xx-subproblem, while z~k+1\tilde{z}^{k+1} gives an εzk\varepsilon_{z}^{k}-minimum of the zz-subproblem.

3.1 Related work

The literature on the convergence of ADMM and its variants is vast, so we focus on prior work most relevant to our setting. Section 3.1 lists some of the prior work that developed and analyzed the approximation strategies described in Section 3. GeNI-ADMM differs from all prior work in Section 3.1 by allowing (almost) all these approximations and more. It also provides explicit rates of convergence to support choices between algorithms. Moreover, many of these algorithms can be recovered from GeNI-ADMM.

Reference Convergence
rate Problem
class Augmented Lagrangian Linearization Function
approximation Subproblem
inexactness
Eckstein and Bertsekas [5] ✗ Convex ✗ ✗ x,zx,z
absolute error
He and Yuan [14] Ergodic 𝒪​(1/t)\mathcal{O}(1/t) Convex xx ✗ ✗
Monteiro and Svaiter [18] Ergodic 𝒪​(1/t)\mathcal{O}(1/t) Convex ✗ ✗ ✗
Ouyang et al. [19] 𝒪​(1/t)\mathcal{O}(1/\sqrt{t}) Stochastic
convex ✗ ff
stochastic first-order ✗
Ouyang et al. [4] Ergodic 𝒪​(1/t)\mathcal{O}(1/t) Convex xx ff
first-order ✗
Deng and Yin [13] Linear Strongly convex x,zx,z ✗ ✗
Eckstein and Yao [15] ✗ Convex ✗ ✗ xx
relative error
Hager and Zhang [20] Ergodic 𝒪​(1/t),\mathcal{O}(1/t),
𝒪​(1/t2)\mathcal{O}(1/t^{2}) Convex,
Strongly convex xx ✗ xx
relative error
Yuan et al. [21] Locally
linear Convex x,zx,z ✗ ✗
Ryu and Yin [10] ✗ Convex x,zx,z f,gf,g
partial first-order ✗
This work Ergodic 𝒪​(1/t),\mathcal{O}(1/t),
Linear Convex,
Strongly convex x,zx,z ff
partial generalized second-order x,zx,z
absolute error
Table 1: A structured comparison of related work on the convergence of ADMM and its variants. The “xx” (“zz”) in the table denotes that a paper uses the corresponding strategy of the column to simplify the xx-subproblem (zz-subproblem). In the “Function approximation” column, the “ff” (“gg”) indicates that a paper approximates function “ff” (“gg”) in the xx-subproblem (zz-subproblem). “stochastic first-order” means a paper uses first-order function approximation but replace the gradient term with a stochastic gradient. “partial generalized second-order” means a paper uses second-order function approximation as (7), but HH is not necessarily the Hessian.

3.1.1 Algorithms recovered from GeNI-ADMM

Various ADMM schemes in the literature can be recovered by appropriately selecting the parameters in Algorithm 2. Let us consider a few special cases to highlight important prior work on approximate ADMM, and provide concrete intuition for the general framework provided by Algorithm 2.

NysADMM

The NysADMM scheme [3] assumes the problem is unconstrained M=I,N=−IM=I,N=-I. We maintain this assumption for simplicity of exposition, although it is unnecessary. GeNI-ADMM specializes to NysADMM taking Θk=η​(Hfk+σ​I)\Theta^{k}=\eta(H_{f}^{k}+\sigma I), and Ψk=0\Psi^{k}=0, where HfkH_{f}^{k} denotes the Hessian of ff at the kkth iteration. Unlike the original NysADMM scheme of [3], we include the regularization term σ​I\sigma I, where σ>0\sigma>0. This inclusion is required for theoretical analysis but seems unnecessary in practice (see Section 7.1 for a detailed discussion). Substituting this information into (8) leads to the following update for the xx-subproblem.

x~k+1=x~k−(η​Hfk+(ρ+η​σ)​I)−1​(∇f​(x~k)+ρ​(x~k−z~k+u~k)).\tilde{x}^{k+1}=\tilde{x}^{k}-\left(\eta H_{f}^{k}+(\rho+\eta\sigma)I\right)^{-1}\left(\nabla f(\tilde{x}^{k})+\rho(\tilde{x}^{k}-\tilde{z}^{k}+\tilde{u}^{k})\right). (10)
Sketch-and-solve ADMM

If M=I,N=−IM=I,N=-I, Ψk=0\Psi^{k}=0, and Θk\Theta^{k} is chosen to be a matrix such that Θk+ρ​I\Theta^{k}+\rho I is easy to factor, we call the resulting scheme sketch-and-solve ADMM. The name sketch-and-solve ADMM is motivated by the fact that such a Θk\Theta^{k} can often be obtained via sketching techniques. However, the method works for any Θk\Theta^{k}, not only ones constructed by sketching methods. The update is given by

x~k+1=x~k−(Θk+ρ​I)−1​(∇f​(x~k)+ρ​(x~k−z~k+u~k)).\tilde{x}^{k+1}=\tilde{x}^{k}-\left(\Theta^{k}+\rho I\right)^{-1}\left(\nabla f(\tilde{x}^{k})+\rho(\tilde{x}^{k}-\tilde{z}^{k}+\tilde{u}^{k})\right).

We provide the full details of sketch-and-solve ADMM in Section 7.2. To our knowledge, sketch-and-solve ADMM has not been previously proposed or analyzed.

Proximal/Generalized ADMM

Set f1=f,f2=0f_{1}=f,f_{2}=0, and fix Θk=Θ\Theta^{k}=\Theta and Ψk=Ψ\Psi^{k}=\Psi, where Θ\Theta and Ψ\Psi are symmetric positive definite matrices. Then GeNI-ADMM simplifies to

x~k+1=argminx∈X{f​(x)+ρ2​‖M​x+N​z~k+u~k‖2+12​‖x−x~k‖Θ2},\displaystyle\tilde{x}^{k+1}=\mathop{\rm argmin}_{x\in X}\left\{f(x)+\frac{\rho}{2}\|Mx+N\tilde{z}^{k}+\tilde{u}^{k}\|^{2}+\frac{1}{2}\|x-\tilde{x}^{k}\|_{\Theta}^{2}\right\},
z~k+1=argminz∈Z{g​(z)+ρ2​‖M​x~k+1+N​z+u~k‖2+12​‖z−z~k‖Ψ2},\displaystyle\tilde{z}^{k+1}=\mathop{\rm argmin}_{z\in Z}\left\{g(z)+\frac{\rho}{2}\|M\tilde{x}^{k+1}+Nz+\tilde{u}^{k}\|^{2}+\frac{1}{2}\|z-\tilde{z}^{k}\|_{\Psi}^{2}\right\},

which is the Proximal/Generalized ADMM of Deng and Yin [13].

Linearized ADMM

Set Θk=α−1​I−ρ​MT​M\Theta^{k}=\alpha^{-1}I-\rho M^{T}M and Ψ=β−1​I−ρ​NT​N\Psi=\beta^{-1}I-\rho N^{T}N, for all k≥1k\geq 1. Then GeNI-ADMM simplifies to

x~k+1=proxα​f​(x~k−α​ρ​MT​(M​x~k+N​z~k+u~k)),\displaystyle\tilde{x}^{k+1}=\textup{prox}_{\alpha f}\left(\tilde{x}^{k}-\alpha\rho M^{T}(M\tilde{x}^{k}+N\tilde{z}^{k}+\tilde{u}^{k})\right),
z~k+1=proxβ​g​(z~k−β​ρ​NT​(M​x~k+1+N​z~k+u~k)),\displaystyle\tilde{z}^{k+1}=\textup{prox}_{\beta g}\left(\tilde{z}^{k}-\beta\rho N^{T}(M\tilde{x}^{k+1}+N\tilde{z}^{k}+\tilde{u}^{k})\right),

which is exactly Linearized ADMM [11, §4.4.2].

Primal Dual Hybrid Gradient

The Primal Dual Hybrid Gradient (PDHG) or Chambolle-Pock algorithm of Chambolle and Pock [22] is a special case of GeNI-ADMM since PDHG is a special case of Linearized ADMM (see section 3.5 of [10]).

Gradient descent ADMM

Consider two linearization schemes from Ouyang et al. [4]. The first scheme we call gradient descent ADMM (GD-ADMM) is useful when it is cheap to solve a least-squares problem with MM. GD-ADMM is obtained from GeNI-ADMM by setting f1=0,f2=ff_{1}=0,f_{2}=f, and Θk=η​I\Theta^{k}=\eta I for all kk. The x~k+1\tilde{x}^{k+1} update (8) for GD-ADMM simplifies to

x~k+1=x~k−(ρ​MT​M+η​I)−1​(∇f​(x~k)+ρ​MT​(M​x~k+N​z~k+u~k)).\tilde{x}^{k+1}=\tilde{x}^{k}-(\rho M^{T}M+\eta I)^{-1}\left(\nabla f(\tilde{x}^{k})+\rho M^{T}(M\tilde{x}^{k}+N\tilde{z}^{k}+\tilde{u}^{k})\right). (11)

The second scheme, linearized-gradient descent ADMM (LGD-ADMM), is useful when MM is not simple, so that the update (11) is no longer cheap. To make the xx-subproblem update cheaper, it linearizes the augmented Lagrangian term by setting Θk=α−1​I−ρ​MT​M\Theta^{k}=\alpha^{-1}I-\rho M^{T}M for all kk in addition to linearizing ff. In this case, (8) yields the x~k+1\tilde{x}^{k+1} update

x~k+1=x~k−α​(∇f​(x~k)+ρ​MT​(M​x~k+N​z~k+u~k)).\tilde{x}^{k+1}=\tilde{x}^{k}-\alpha\left(\nabla f(\tilde{x}^{k})+\rho M^{T}(M\tilde{x}^{k}+N\tilde{z}^{k}+\tilde{u}^{k})\right). (12)

Observe in the unconstrained case, when M=IM=I, the updates (11) and (12) are equivalent and generate the same iterate sequences when initialized at the same point [23]. Indeed, they are both generated by performing a gradient step on the augmented Lagrangian (7), for suitable choices of the parameters. Notably, this terminology differs from [4], who refer to (11) as “linearized ADMM” (L-ADMM) and (12) as “linearized preconditioned ADMM” (LP-ADMM). We choose our terminology to emphasize that GD-ADMM accesses ff via its gradient, as in the literature the term “linearized ADMM” is usually reserved for methods that access ff through its prox operator  [14, 11, 13].

In the remainder of this paper, we will prove convergence of Algorithm 2 under appropriate hypotheses on the sequences {Θk}k≥1,{Ψk}k≥1,{εxk}k≥1,\{\Theta^{k}\}_{k\geq 1},\{\Psi^{k}\}_{k\geq 1},\{\varepsilon_{x}^{k}\}_{k\geq 1}, and {εzk}k≥1\{\varepsilon_{z}^{k}\}_{k\geq 1}.

4 Technical preliminaries and assumptions

We introduce some important concepts that will be central to our analysis. The first is Θ\Theta-relative smoothness, which is crucial to establish that GeNI-ADMM benefits from curvature information provided by the Hessian.

Definition 2 (Θ\Theta-relative smoothness).

We say f:𝒟→ℝf:\mathcal{D}\to\mathbb{R} is Θ\Theta-relatively smooth with respect to the bounded function Θ:𝒟→𝕊+n\Theta:\mathcal{D}\to\mathbb{S}_{+}^{n} if there exists L^Θ>0\hat{L}_{\Theta}>0 such that for all x,y∈𝒟x,y\in\mathcal{D}

f​(x)≤f​(y)+⟨∇f​(y),x−y⟩+L^Θ2​‖x−y‖Θ​(y)2.f(x)\leq f(y)+\langle\nabla f(y),x-y\rangle+\frac{\hat{L}_{\Theta}}{2}\|x-y\|^{2}_{\Theta(y)}. (13)

That is, the function ff is smooth with respect to the Θ\Theta-norm. Definition 2 generalizes relative smoothness, introduced in [24] to analyze Newton’s method. The definition in [24] takes Θ\Theta to be the Hessian of ff, HfH_{f}. When ff belongs to the popular family of generalized linear models, then (13) holds with a value of L^Hf\hat{L}_{H_{f}} that is independent of the conditioning of the problem [24]. For instance, if ff is quadratic and Θ​(y)=Hf\Theta(y)=H_{f}, then (13) holds with equality for L^Hf=1\hat{L}_{H_{f}}=1. Conversely, if we take Θ=I\Theta=I, which corresponds to GD-ADMM, then L^Θ=Lf\hat{L}_{\Theta}=L_{f}, the smoothness constant of ff. Our theory uses the fact that L^Θ\hat{L}_{\Theta} is much smaller than the smoothness constant LfL_{f} for methods that take advantage of curvature, and relies on L^Θ\hat{L}_{\Theta} to characterize the faster convergence speed of these methods.

The other important idea we need is the notion of an ε\varepsilon-subgradient [25, 26].

Definition 3 (ε\varepsilon-subgradient).

Let r:𝒟→ℝr:\mathcal{D}\to\mathbb{R} be a convex function and ε>0\varepsilon>0. We say that s∈𝒟∗s\in\mathcal{D}^{*} is an ε\varepsilon-subgradient for rr at z∈𝒟z\in\mathcal{D} if, for every z′∈𝒟z^{\prime}\in\mathcal{D}, we have

r​(z′)−r​(z)≥⟨s,z′−z⟩−ε.r(z^{\prime})-r(z)\geq\langle s,z^{\prime}-z\rangle-\varepsilon.

We denote the set of ε\varepsilon-subgradients for rr at zz by ∂εr​(z)\partial_{\varepsilon}r(z).

Clearly, any subgradient is an ε\varepsilon-subgradient, so Definition 3 provides a natural weakening of a subgradient. The ε\varepsilon-subgradient is critical for analyzing zz-subproblem inexactness, and our usage in this context is inspired by the convergence analysis of inexact proximal gradient methods [27]. We shall need the following proposition whose proof may be found in [25, Proposition 4.3.1].

Proposition 1.

Let rr, r1r_{1}, and r2r_{2} be convex functions. Then for any zz, the following holds:

  1. 1.

    0∈∂εr​(z)0\in\partial_{\varepsilon}r(z) if and only if r​(z)​≊𝜀​argminz′r​(z′)r(z)\overset{\varepsilon}{\approxeq}\mathop{\rm argmin}_{z^{\prime}}r(z^{\prime}), that is zz gives an ε\varepsilon-minimum of minimizez′​r​(z′)\textup{minimize}_{z^{\prime}}r(z^{\prime}).

  2. 2.

    ∂ε(r1+r2)​(z)⊂∂εr1​(z)+∂εr2​(z).\partial_{\varepsilon}(r_{1}+r_{2})(z)\subset\partial_{\varepsilon}r_{1}(z)+\partial_{\varepsilon}r_{2}(z).

With Proposition 1 recorded, we prove the following lemma in Section A.2 of the appendix, which will play a critical role in establishing the convergence of GeNI-ADMM.

Lemma 1.

Let z~k+1\tilde{z}^{k+1} give an εzk\varepsilon^{k}_{z}-minimum of the zz-subproblem. Then there exists an s~\tilde{s} with ‖s~‖≤C​εzk\|\tilde{s}\|\leq C\sqrt{\varepsilon_{z}^{k}} such that

−ρ​NT​u~k+1+Ψk​(z~k−z~k+1)+s~∈∂εzkg​(z~k+1).-\rho N^{T}\tilde{u}^{k+1}+\Psi_{k}(\tilde{z}^{k}-\tilde{z}^{k+1})+\tilde{s}\in\partial_{\varepsilon_{z}^{k}}g(\tilde{z}^{k+1}).

4.1 Assumptions

In this section, we present the main assumptions required by our analysis.

Assumption 1 (Existence of saddle point).

There exists an optimal primal solution (x⋆,z⋆)∈X×Z(x^{\star},z^{\star})\in X\times Z for (1) and an optimal dual solution u⋆∈Uu^{\star}\in U such that (x⋆,z⋆,u⋆)(x^{\star},z^{\star},u^{\star}) is a saddle point of (2). Here, U⊂𝒵U\subset\mathcal{Z} is a closed convex set and ρ​U=Y\rho U=Y. We denote the optimal objective value of (1) as p⋆p^{\star}.

Assumption 1 is standard and merely assumes that (1) has a solution.

Assumption 2 (Regularity of ff and gg).

The function ff is twice-continuously differentiable and is 11-relatively smooth with respect to Θ\Theta. The function gg is finite-valued, convex, and lower semi-continuous.

Assumption 2 is also standard. It ensures that it makes sense to talk about the Hessian of ff and that ff is relatively smooth. Note assuming L^Θ=1\hat{L}_{\Theta}=1 is without loss of generality, for we can always redefine Θ′=L^Θ​Θ\Theta^{\prime}=\hat{L}_{\Theta}\Theta, and ff will be 11-relatively smooth with respect to Θ′\Theta^{\prime}.

Assumption 3 (Forcing sequence summability and approximate subproblem oracles).

Let {εxk}k≥1\{\varepsilon^{k}_{x}\}_{k\geq 1} and {εzk}k≥1\{\varepsilon^{k}_{z}\}_{k\geq 1} be given forcing sequences, we assume they satisfy

ℰx=∑k=1∞εxk<∞,ℰz=∑k=1∞εzk<∞.\mathcal{E}_{x}=\sum_{k=1}^{\infty}\varepsilon_{x}^{k}<\infty,\quad\mathcal{E}_{z}=\sum^{\infty}_{k=1}\sqrt{\varepsilon_{z}^{k}}<\infty.

Further we define the constants Kεx≔supk≥1εxkK_{\varepsilon_{x}}\coloneqq\sup_{k\geq 1}\varepsilon_{x}^{k}, Kεz≔supk≥1εzkK_{\varepsilon_{z}}\coloneqq\sup_{k\geq 1}\sqrt{\varepsilon_{z}^{k}}. Observe KεxK_{\varepsilon_{x}} and KεzK_{\varepsilon_{z}} are finite owing to the summability hypotheses. Moreover, we assume Algorithm 2 is equipped with oracles for solving the xx and zz-subproblems, which at each iteration produce approximate solutions x~k+1\tilde{x}^{k+1}, z~k+1\tilde{z}^{k+1} satisfying:

x~k+1​≈εxk​argminx∈X​{f1​(x)+⟨∇f2​(x~k),x−x~k⟩+12‖x−x~k∥Θk2+ρ2​‖M​x+N​z~k+u~k‖2},\displaystyle\tilde{x}^{k+1}\overset{\varepsilon_{x}^{k}}{\approx}\underset{x\in X}{\mathop{\rm argmin}}\{f_{1}(x)+\langle\nabla f_{2}(\tilde{x}^{k}),x-\tilde{x}^{k}\rangle+\frac{1}{2}\|x-\tilde{x}^{k}\|^{2}_{\Theta^{k}}+\frac{\rho}{2}\|Mx+N\tilde{z}^{k}+\tilde{u}^{k}\|^{2}\},
z~k+1​≊εzk​argminz∈Z​{g​(z)+ρ2​‖M​x~k+1+N​z+u~k‖2+12​‖z−z~k‖Ψk2}.\displaystyle\tilde{z}^{k+1}\overset{\varepsilon_{z}^{k}}{\approxeq}\underset{z\in Z}{\mathop{\rm argmin}}\{g(z)+\frac{\rho}{2}\|M\tilde{x}^{k+1}+Nz+\tilde{u}^{k}\|^{2}+\frac{1}{2}\|z-\tilde{z}^{k}\|^{2}_{\Psi^{k}}\}.

The conditions on the xx and zz subproblem oracles are consistent with those of [5], which requires the sum of the errors in the subproblems to be summable. The approximate solution criteria of Assumption 3 are also easily met in practical applications, as the subproblems are either simple enough to solve exactly, or can be efficiently solved approximately via iterative algorithms. For instance, with LGD-ADMM the xx-subproblem is simple to solve enough exactly, while for NysADMM the xx-subproblem is efficiently solved via conjugate gradient with a randomized preconditioner.

Assumption 4 (Regularity of {Θk}k≥1\{\Theta^{k}\}_{k\geq 1} and {Ψk}k≥1\{\Psi^{k}\}_{k\geq 1}).

We assume there exists constants θmax,θmin,ψmax,\theta_{\textup{max}},~{}\theta_{\textup{min}},~{}\psi_{\textup{max}}, and ν>0\nu>0, such that

θmax​I⪰Θk⪰θmin​I,ψmax​I⪰Ψk,Ψk+ρ​NT​N⪰ν​I,for all​k≥1.\theta_{\textup{max}}I\succeq\Theta^{k}\succeq\theta_{\textup{min}}I,~{}\psi_{\textup{max}}I\succeq\Psi^{k},~{}\Psi^{k}+\rho N^{T}N\succeq\nu I,\quad\text{for all}~{}k\geq 1. (14)

Moreover, we also assume that The sequences {Θk}k≥1,{Ψk}k≥1\{\Theta^{k}\}_{k\geq 1},\{\Psi^{k}\}_{k\geq 1} satisfy

‖x~k−x⋆‖Θk2≤(1+ζk−1)​‖x~k−x⋆‖Θk−12,\displaystyle\|\tilde{x}^{k}-x^{\star}\|^{2}_{\Theta^{k}}\leq(1+\zeta^{k-1})\|\tilde{x}^{k}-x^{\star}\|^{2}_{\Theta^{k-1}}, (15)
‖z~k−z⋆‖Ψk2≤(1+ζk−1)​‖z~k−z⋆‖Ψk−12,\displaystyle\|\tilde{z}^{k}-z^{\star}\|^{2}_{\Psi^{k}}\leq(1+\zeta^{k-1})\|\tilde{z}^{k}-z^{\star}\|^{2}_{\Psi^{k-1}},

where {ζk}k≥1\{\zeta^{k}\}_{k\geq 1} is a non-negative summable sequence, that is, ∑k=1∞ζk<∞\sum^{\infty}_{k=1}\zeta^{k}<\infty.

The first half of Assumption 4 is standard, and essentially requires that Θk\Theta^{k} and Ψk+ν​NT​N\Psi^{k}+\nu N^{T}N define norms. For most common choices of Θk\Theta^{k} and Ψk\Psi^{k} these assumptions are satisfied, they are also readily enforced by adding on a small multiple of the identity. The addition of a small regularization term is common practice in popular ADMM solvers, such as OSQP [28], as it avoids issues with degeneracy and increases numerical stability.

The second part of the assumption requires that Θk\Theta^{k} (Ψk)\Psi^{k}) and Θk−1\Theta^{k-1} (Ψk−1\Psi^{k-1}) eventually not differ much on the distance of x~k\tilde{x}^{k} (z~k\tilde{z}^{k}) to x⋆x^{\star} (z⋆z^{\star}). Assumptions of this form are common in analyses of optimization algorithms that use variable metrics. For instance, He et al. [29] which develops an alternating directions method for monotone variational inequalities, assumes their equivalents of the sequences {Θk}\{\Theta^{k}\} and {Ψk}\{\Psi^{k}\} satisfy

(1−ζk−1)​Θk−1⪯Θk⪯(1+ζk−1)​Θk−1,(1−ζk−1)​Ψk−1⪯Ψk⪯(1+ζk−1)​Ψk−1.(1-\zeta^{k-1})\Theta^{k-1}\preceq\Theta^{k}\preceq(1+\zeta^{k-1})\Theta^{k-1},~{}(1-\zeta^{k-1})\Psi^{k-1}\preceq\Psi^{k}\preceq(1+\zeta^{k-1})\Psi^{k-1}. (16)

More recently, Rockafellar [30] analyzed the proximal point method with variable metrics, under the assumption the variable metrics satisfy (16). Thus, Assumption 4 is consistent with the literature and is, in fact, weaker than prior work, as (16) implies (15). Assumption 4 may always be enforced by changing the Θk\Theta^{k}’s and Ψk\Psi^{k}’s only finitely many times.

We also define the following constants which shall be useful in our analysis,

τζ≔∏k≥2(1+ζk),ℰζ=τζ​(∑k=1∞ζk)<∞.\tau_{\zeta}\coloneqq\prod_{k\geq 2}(1+\zeta^{k}),\quad\mathcal{E}_{\zeta}=\tau_{\zeta}\left(\sum^{\infty}_{k=1}\zeta^{k}\right)<\infty.

Note Assumption 4 implies τζ<∞\tau_{\zeta}<\infty. Moreover, for any k≥1k\geq 1 it holds that

‖x~k−x⋆‖Θk2≤τζ​‖x~k−x⋆‖Θ12,‖z~k−z⋆‖Ψk2≤τζ​‖z~k−z⋆‖Ψ12.\|\tilde{x}^{k}-x^{\star}\|^{2}_{\Theta^{k}}\leq\tau_{\zeta}\|\tilde{x}^{k}-x^{\star}\|^{2}_{\Theta^{1}},~{}\|\tilde{z}^{k}-z^{\star}\|^{2}_{\Psi^{k}}\leq\tau_{\zeta}\|\tilde{z}^{k}-z^{\star}\|^{2}_{\Psi^{1}}.

5 Sublinear convergence of GeNI-ADMM

This section establishes our main theorem, Theorem 1, which shows that Algorithm 2 enjoys the same 𝒪​(1/t)\mathcal{O}(1/t)-convergence rate as standard ADMM.

Theorem 1 (Ergodic convergence).

Define constants dx⋆,Θ1=‖x~1−x⋆‖Θ1d_{x^{\star},\Theta^{1}}=\|\tilde{x}^{1}-x^{\star}\|_{\Theta^{1}}, du⋆=‖u~1−u⋆‖d_{u^{\star}}=\|\tilde{u}^{1}-u^{\star}\|, dz⋆,Ψρ,N1=‖z~1−z⋆‖Ψ1+ρ​NT​Nd_{z^{\star},\Psi^{1}_{\rho,N}}=\|\tilde{z}^{1}-z^{\star}\|_{\Psi^{1}+\rho N^{T}N}. Let p⋆p^{\star} denote the optimum of (1). For each t≥1t\geq 1, denote x¯t+1=1t​∑k=2t+1x~k\bar{x}^{t+1}=\frac{1}{t}\sum^{t+1}_{k=2}\tilde{x}^{k}, and z¯t+1=1t​∑k=2t+1z~k\bar{z}^{t+1}=\frac{1}{t}\sum^{t+1}_{k=2}\tilde{z}^{k}, where {x~k}k≥1\{\tilde{x}^{k}\}_{k\geq 1} and {z~k}k≥1\{\tilde{z}^{k}\}_{k\geq 1} are the iterates produced by Algorithm 2 with forcing sequences {εxk}k≥1\{\varepsilon^{k}_{x}\}_{k\geq 1} and {εzk}k≥1\{\varepsilon^{k}_{z}\}_{k\geq 1} with u~1=0\tilde{u}^{1}=0 and M​x~1=−N​z~1M\tilde{x}^{1}=-N\tilde{z}^{1}. Instate Assumptions 1-4. Then, the suboptimality gap satisfies

Furthermore, the feasibility gap satisfies

‖M​x¯t+1+N​z¯t+1‖≤2t​Γρ+du⋆2,\|M\bar{x}^{t+1}+N\bar{z}^{t+1}\|\leq\frac{2}{t}\sqrt{\frac{\Gamma}{\rho}+d^{2}_{u^{\star}}},

Consequently, after 𝒪​(1/ϵ)\mathcal{O}(1/\epsilon) iterations,

f​(x¯t+1)+g​(z¯t+1)−p⋆≤ϵ,and​‖M​x¯t+1+N​z¯t+1‖≤ϵ.f(\bar{x}^{t+1})+g(\bar{z}^{t+1})-p^{\star}\leq\epsilon,\;\text{and}\;\;\;\|M\bar{x}^{t+1}+N\bar{z}^{t+1}\|\leq\epsilon.

Theorem 1 shows that, with a constant value of η\eta and appropriate forcing sequences, the suboptimality gap and the feasibility residuals both go to zero at a rate of 𝒪​(1/t)\mathcal{O}(1/t). Hence, the overall convergence rate of ADMM is preserved despite all the approximations involved in GeNI-ADMM. However, some schemes yield better constants than others.

To see this difference, consider the case when ff is a convex quadratic function and M=IM=I. Let HfH_{f} be the Hessian of ff. Consider (a) NysADMM Θk=Hf\Theta^{k}=H_{f} (10) and (b) GD-ADMM Θk=I\Theta^{k}=I (11). Further, suppose that NysADMM and GD-ADMM are initialized at 0. The rates of convergence guaranteed by Theorem 1 for Algorithm 2 for both methods are outlined in Table 2.

Table 2: Convergence rate comparison of NysADMM and GD-ADMM when initialized at 0 for quadratic ff.

Method NysADMM (Θk=Hf)\left(\Theta^{k}=H_{f}\right) GD-ADMM (Θk=I)\left(\Theta^{k}=I\right)
Feasibility gap 𝒪​(1t​(2ρ​‖x⋆‖Hf+σ​I2))\mathcal{O}\left(\frac{1}{t}\left(\sqrt{\frac{2}{\rho}\|x^{\star}\|^{2}_{H_{f}+\sigma I}}\right)\right) 𝒪​(1t​(2ρ​λ1​(Hf)​‖x⋆‖2))\mathcal{O}\left(\frac{1}{t}\left(\sqrt{\frac{2}{\rho}\lambda_{1}\left(H_{f}\right)\|x^{\star}\|^{2}}\right)\right)
Suboptimality gap 𝒪​(12​t​‖x⋆‖Hf+σ​I2)\mathcal{O}\left(\frac{1}{2t}\|x^{\star}\|^{2}_{H_{f}+\sigma I}\right) 𝒪​(12​t​λ1​(Hf)​‖x⋆‖2)\mathcal{O}\left(\frac{1}{2t}\lambda_{1}\left(H_{f}\right)\|x^{\star}\|^{2}\right)

In the first case, the relative smoothness constant satisfies L^Θ=1\hat{L}_{\Theta}=1, while in the second, L^Θ=λ1​(Hf)\hat{L}_{\Theta}=\lambda_{1}\left(H_{f}\right), which is the largest eigenvalue of HfH_{f}. Comparing the rates in Table 2, we see NysADMM improves over GD-ADMM whenever

(λ1​(Hf)−σ)​‖x⋆‖2≥‖x⋆‖Hf2.\left(\lambda_{1}\left(H_{f}\right)-\sigma\right)\|x^{\star}\|^{2}\geq\|x^{\star}\|^{2}_{H_{f}}.

Hence NysADMM improves significantly over GD-ADMM when HfH_{f} exhibits a decaying spectrum, provided x⋆x^{\star} is not concentrated on the top eigenvector of HfH_{f}. We formalize the latter property in the following definition.

Definition 4 (μ𝐯\mu_{\mathbf{v}}-incoherence).

Let (λ1​(Hf),𝐯)(\lambda_{1}(H_{f}),\mathbf{v}) be the largest eigenpair of HfH_{f}. We say x⋆x^{\star} is μ𝐯\mu_{\mathbf{v}}-incoherent if there exists 0≤μ𝐯<10\leq\mu_{\mathbf{v}}<1 such that:

|⟨𝐯,x⋆⟩|2≤μ𝐯​‖x⋆‖2.|\langle\mathbf{v},x^{\star}\rangle|^{2}\leq\mu_{\mathbf{v}}\|x^{\star}\|^{2}. (17)

Definition 4 is a weak form of the incoherence condition from compressed sensing and matrix completion, which plays a key role in signal and low-rank matrix recovery [31, 32]. In words, x⋆x^{\star} is μ𝐯\mu_{\mathbf{v}}-incoherent if its energy is not solely concentrated on the top eigenvector of HfH_{f} and can be expected to hold generically. The parameter μ𝐯\mu_{\mathbf{v}} controls the allowable concentration. When μ𝐯=0\mu_{\mathbf{v}}=0, x⋆x^{\star} is orthogonal to 𝐯\mathbf{v}, so its energy is distributed amongst the other eigenvectors. Conversely, the closer μ𝐯\mu_{\mathbf{v}} is to 11, the more x⋆x^{\star} is allowed to concentrate on 𝐯\mathbf{v}.

Using μ𝐯\mu_{\mathbf{v}}-incoherence, we can say more about how NysADMM improves on GD-ADMM.

Proposition 2.

Suppose x⋆x^{\star} is μ𝐯\mu_{\mathbf{v}}-incoherent and σ=τ​λ1​(Hf)\sigma=\tau\lambda_{1}(H_{f}) where τ∈(0,1)\tau\in(0,1). Then, the following bound holds

(λ1​(Hf)−σ)​‖x⋆‖2‖x⋆‖Hf2≥(1−τ)​(μ𝐯+λ2​(Hf)λ1​(Hf))−1.\frac{\left(\lambda_{1}(H_{f})-\sigma\right)\|x^{\star}\|^{2}}{\|x^{\star}\|^{2}_{H_{f}}}\geq(1-\tau)\left(\mu_{\mathbf{v}}+\frac{\lambda_{2}(H_{f})}{\lambda_{1}(H_{f})}\right)^{-1}.

Hence if μ𝐯+λ2​(Hf)/λ1​(Hf)≤(1−τ)​α−1\mu_{\mathbf{v}}+\lambda_{2}(H_{f})/\lambda_{1}(H_{f})\leq(1-\tau)\alpha^{-1}, where α≥1\alpha\geq 1, then

λ1​(Hf)​‖x⋆‖2‖x⋆‖Hf2≥α.\frac{\lambda_{1}(H_{f})\|x^{\star}\|^{2}}{\|x^{\star}\|^{2}_{H_{f}}}\geq\alpha.

The proof of Proposition 2 is given in Section A.2. Proposition 2 shows when x⋆x^{\star} is μ𝐯\mu_{\mathbf{v}}-incoherent and HfH_{f} has a decaying spectrum, NysADMM yields a significant improvement over GD-ADMM. As a concrete example, consider when α=2\alpha=2, then Proposition 2 implies the ergodic convergence of NysADMM is twice as fast as GD-ADMM. We observe this performance improvement in practice; see Section 8 for corroborating numerical evidence. Just as Newton’s method improves on gradient descent for ill-conditioned problems, NysADMM is less sensitive to ill-conditioning than GD-ADMM.

We now move to proving Theorem 1.

5.1 Our approach

To prove Theorem 1, we take the approach in Ouyang et al. [4], and analyze GeNI-ADMM by viewing Eq. 1 through its formulation as saddle point problem Eq. 2. Let W=X×Z×UW=X\times Z\times U, w^=(x^,z^,u^)\hat{w}=(\hat{x},\hat{z},\hat{u}), and w=(x,z,u)w=(x,z,u), where w,w^∈Ww,\hat{w}\in W. Define the gap function

Q​(w^,w)≔[f​(x)+g​(z)+⟨ρ​u^,M​x+N​z⟩]−[f​(x^)+g​(z^)+⟨ρ​u,M​x^+N​z^⟩].Q(\hat{w},w)\coloneqq[f(x)+g(z)+\langle\rho\hat{u},Mx+Nz\rangle]-[f(\hat{x})+g(\hat{z})+\langle\rho u,M\hat{x}+N\hat{z}\rangle]. (18)

The gap function naturally arises from the saddle-point formulation Eq. 2. By construction, it is concave in its first argument and convex in the second, and satisfies the important inequality

Q​(w⋆,w)=Lρ​(x,z,u⋆)−Lρ​(x⋆,z⋆,u)≥0,Q(w^{\star},w)=L_{\rho}(x,z,u^{\star})-L_{\rho}(x^{\star},z^{\star},u)\geq 0,

which follows by definition of (x⋆,z⋆,u⋆)(x^{\star},z^{\star},u^{\star}) being a saddle-point. Hence the gap function may be viewed as measuring the distance to the saddle w⋆w^{\star}.

Further, given a closed set U⊂𝒵U\subset\mathcal{Z} and v∈𝒵v\in\mathcal{Z} we define

ℓU​(v,w)\displaystyle\ell_{U}(v,w) ≔supu^∈U{Q​(w^,w)+⟨v,ρ​u^⟩∣w^=(x^,z^,u^),x^=x⋆,z^=z⋆}\displaystyle\coloneqq\sup_{\hat{u}\in U}\{Q(\hat{w},w)+\langle v,\rho\hat{u}\rangle\mid\hat{w}=(\hat{x},\hat{z},\hat{u}),~{}\hat{x}=x^{\star},~{}\hat{z}=z^{\star}\} (19)
=f​(x)+g​(z)−p⋆+supu^∈U⟨ρ​u^,v−(M​x+N​z)⟩.\displaystyle=f(x)+g(z)-p^{\star}+\sup_{\hat{u}\in U}\langle\rho\hat{u},v-(Mx+Nz)\rangle.

The following lemma of Ouyang et al. [4] relates the gap function to the suboptimality and feasibility gaps. As the proof is elementary, we provide it in Section A.2 for completeness.

Lemma 2.

For any U⊆𝒵U\subseteq\mathcal{Z}, suppose ℓU​(M​x+N​z,w)≤ϵ<∞\ell_{U}(Mx+Nz,w)\leq\epsilon<\infty and ‖M​x+N​z‖≤δ\|Mx+Nz\|\leq\delta, where w=(x,z,u)∈Ww=(x,z,u)\in W. Then

f​(x)+g​(z)−p⋆≤ϵ.f(x)+g(z)-p^{\star}\leq\epsilon. (20)

In other words, (x,z)(x,z) is an approximate solution of (1) with suboptimality gap ϵ\epsilon and feasibility gap δ\delta. Further, if U=𝒵U=\mathcal{Z}, for any vv such that ℓU​(v,w)≤ϵ<∞\ell_{U}(v,w)\leq\epsilon<\infty and ‖v‖≤δ\|v\|\leq\delta, we have v=M​x−zv=Mx-z.

Lemma 2 shows that if we can find ww such that ℓU​(M​x+N​z,w)≤ϵ\ell_{U}(Mx+Nz,w)\leq\epsilon and ‖M​x+N​z‖≤δ\|Mx+Nz\|\leq\delta, then we have an approximate optimal solution to (1) with gaps ϵ\epsilon and δ\delta, that is, ℓU​(M​x+N​z,w)\ell_{U}(Mx+Nz,w) controls the suboptimality and feasibility gaps.

5.2 Controlling the gap function

Lemma 2 shows the key to establishing convergence of GeNI-ADMM is to achieve appropriate control over the gap function. To accomplish this, we use the optimality conditions of the xx and zz subproblems. However, as the subproblems are only solved approximately, the inexact solutions satisfy perturbed optimality conditions. To be able to reason about the optimality conditions under inexact solutions, the iterates must remain bounded. Indeed, if the iterates are unbounded, they can fail to satisfy the subproblem optimality conditions arbitrarily badly. Fortunately, the following proposition shows the iterates remain bounded.

Proposition 3 (GeNI-ADMM iterates remain bound).

Let {εxk}k≥1,{εzk}k≥1,{Θk}k≥1,{Ψk}k≥1\{\varepsilon_{x}^{k}\}_{k\geq 1},\{\varepsilon_{z}^{k}\}_{k\geq 1},\{\Theta^{k}\}_{k\geq 1},\{\Psi^{k}\}_{k\geq 1}, and ρ>0\rho>0 be given. Instate Assumptions 1-4. Run Algorithm 2, then the output sequences {x~k}k≥1,{z~k}k≥1,{u~k}k≥1\{\tilde{x}^{k}\}_{k\geq 1},\{\tilde{z}^{k}\}_{k\geq 1},\{\tilde{u}^{k}\}_{k\geq 1} are bounded. That is, there exists R>0R>0, such that

{x~k}k≥1⊂B​(x⋆,R),{z~k}k≥1⊂B​(z⋆,R),{u~k}k≥1⊂B​(u⋆,R).\{\tilde{x}^{k}\}_{k\geq 1}\subset B(x^{\star},R),\quad\{\tilde{z}^{k}\}_{k\geq 1}\subset B(z^{\star},R),\quad\{\tilde{u}^{k}\}_{k\geq 1}\subset B(u^{\star},R).

The proof of Proposition 3 is provided in Section A.2.

As the iterates remain bounded, we can show that the optimality conditions are approximately satisfied at each iteration. The precise form of these perturbed optimality conditions is given in Lemmas 3 and 4. Detailed proofs establishing these lemmas are given in Section A.2.

Lemma 3 (Inexact xx-optimality condition).

Instate Assumptions 1-4. Suppose x~k+1\tilde{x}^{k+1} is an εxk\varepsilon^{k}_{x}-minimizer of the xx-subproblem under Assumption 3. Then for some absolute constant Cx>0C_{x}>0 we have

⟨∇f1​(x~k+1)+∇f2​(x~k),x⋆−x~k+1⟩≤⟨Θk​(x~k+1−x~k),x⋆−x~k+1⟩\displaystyle\langle\nabla f_{1}(\tilde{x}^{k+1})+\nabla f_{2}(\tilde{x}^{k}),x^{\star}-\tilde{x}^{k+1}\rangle\leq\langle\Theta^{k}(\tilde{x}^{k+1}-\tilde{x}^{k}),x^{\star}-\tilde{x}^{k+1}\rangle (21)
+ρ​⟨M​x~k+1+N​z~k+u~k,M​(x⋆−x~k+1)⟩+Cx​εxk.\displaystyle+\rho\langle M\tilde{x}^{k+1}+N\tilde{z}^{k}+\tilde{u}^{k},M(x^{\star}-\tilde{x}^{k+1})\rangle+C_{x}\varepsilon_{x}^{k}.
Lemma 4 (Inexact zz-optimality condition).

Instate Assumptions 1-4. Suppose z~k+1\tilde{z}^{k+1} is an εzk\varepsilon^{k}_{z}-minimum of the zz-subproblem under Definition 1. Then for some absolute constant Cz>0C_{z}>0 we have

g​(z⋆)−g​(z~k+1)≥⟨−ρ​NT​u~k+1+Ψk​(z~k−z~k+1),z⋆−z~k+1⟩−Cz​εzk.g(z^{\star})-g(\tilde{z}^{k+1})\geq\langle-\rho N^{T}\tilde{u}^{k+1}+\Psi^{k}(\tilde{z}^{k}-\tilde{z}^{k+1}),z^{\star}-\tilde{z}^{k+1}\rangle-C_{z}\sqrt{\varepsilon_{z}^{k}}. (22)

When εxk=εzk=0\varepsilon_{x}^{k}=\varepsilon_{z}^{k}=0 the approximate optimality conditions of Lemmas 3 and 4 collapse to the exact optimality conditions. We also note while Lemma 3 (Lemma 4) necessarily holds when x~k+1\tilde{x}^{k+1} (z~k+1)\tilde{z}^{k+1}) is an εxk\varepsilon_{x}^{k}-approximate minimizer (εzk\varepsilon_{z}^{k}-minimum), the converse does not hold. With Lemmas 3 and 4 in hand, we can establish control of the gap function for one iteration.

Lemma 5.

Instate Assumptions 1-4.. Let w~k+1=(x~k+1,z~k+1,u~k+1)\tilde{w}^{k+1}=(\tilde{x}^{k+1},\tilde{z}^{k+1},\tilde{u}^{k+1}) denote the iterates generated by Algorithm 2 at iteration kk. Set w=(x⋆,z⋆,u)w=(x^{\star},z^{\star},u), then the gap function QQ satisfies

Q​(w,w~k+1)\displaystyle Q(w,\tilde{w}^{k+1}) ≤12​(‖x~k−x⋆‖Θk2−‖x~k+1−x⋆‖Θk2)+12​(‖z~k−z⋆‖Ψk+ρ​NT​N2−‖z~k+1−z⋆‖Ψk+ρ​NT​N2)\displaystyle\leq\frac{1}{2}\left(\|\tilde{x}^{k}-x^{\star}\|^{2}_{\Theta^{k}}-\|\tilde{x}^{k+1}-x^{\star}\|^{2}_{\Theta^{k}}\right)+\frac{1}{2}\left(\|\tilde{z}^{k}-z^{\star}\|_{\Psi^{k}+\rho N^{T}N}^{2}-\|\tilde{z}^{k+1}-z^{\star}\|_{\Psi^{k}+\rho N^{T}N}^{2}\right)
+ρ2​(‖u~k−u‖2−‖u~k+1−u‖2)+Cx​εxk+Cz​εzk.\displaystyle+\frac{\rho}{2}\left(\|\tilde{u}^{k}-u\|^{2}-\|\tilde{u}^{k+1}-u\|^{2}\right)+C_{x}\varepsilon_{x}^{k}+C_{z}\sqrt{\varepsilon_{z}^{k}}.
Proof.

From the definition of QQ,

Q​(w,w~k+1)=f​(x~k+1)−f​(x⋆)+g​(z~k+1)−g​(z⋆)+⟨ρ​u,M​x~k+1+N​z~k+1⟩−⟨ρ​u~k+1,M​x⋆+N​z⋆⟩.\displaystyle Q(w,\tilde{w}^{k+1})=f(\tilde{x}^{k+1})-f(x^{\star})+g(\tilde{z}^{k+1})-g(z^{\star})+\langle\rho u,M\tilde{x}^{k+1}+N\tilde{z}^{k+1}\rangle-\langle\rho\tilde{u}^{k+1},Mx^{\star}+Nz^{\star}\rangle.

Our goal is to upper bound Q​(w,w~k+1)Q(w,\tilde{w}^{k+1}). We start by bounding f​(x~k+1)−f​(x⋆)f(\tilde{x}^{k+1})-f(x^{\star}) as follows:

f​(x~k+1)−f​(x⋆)=(f1​(x~k+1)−f1​(x⋆))+(f2​(x~k+1)−f2​(x~k))+(f2​(x~k)−f2​(x⋆))\displaystyle f(\tilde{x}^{k+1})-f(x^{\star})=\left(f_{1}(\tilde{x}^{k+1})-f_{1}(x^{\star})\right)+\left(f_{2}(\tilde{x}^{k+1})-f_{2}(\tilde{x}^{k})\right)+\left(f_{2}(\tilde{x}^{k})-f_{2}(x^{\star})\right)
≤(1)​⟨∇f1​(x~k+1),x~k+1−x~⋆⟩+⟨∇f1​(x~k),x~k+1−x~k⟩+12​‖x~k+1−x~k‖Θk2+f2​(x~k)−f2​(x⋆)\displaystyle\overset{(1)}{\leq}\langle\nabla f_{1}(\tilde{x}^{k+1}),\tilde{x}^{k+1}-\tilde{x}^{\star}\rangle+\langle\nabla f_{1}(\tilde{x}^{k}),\tilde{x}^{k+1}-\tilde{x}^{k}\rangle+\frac{1}{2}\|\tilde{x}^{k+1}-\tilde{x}^{k}\|^{2}_{\Theta_{k}}+f_{2}(\tilde{x}^{k})-f_{2}(x^{\star})
≤(2)​⟨∇f1​(x~k+1),x~k+1−x~⋆⟩+⟨∇f2​(x~k),x~k+1−x~k⟩+12​‖x~k+1−x~k‖Θk2+⟨∇f2​(x~k),x~k−x⋆⟩\displaystyle\overset{(2)}{\leq}\langle\nabla f_{1}(\tilde{x}^{k+1}),\tilde{x}^{k+1}-\tilde{x}^{\star}\rangle+\langle\nabla f_{2}(\tilde{x}^{k}),\tilde{x}^{k+1}-\tilde{x}^{k}\rangle+\frac{1}{2}\|\tilde{x}^{k+1}-\tilde{x}^{k}\|^{2}_{\Theta_{k}}+\langle\nabla f_{2}(\tilde{x}^{k}),\tilde{x}^{k}-x^{\star}\rangle
=⟨∇f1​(x~k+1)+∇f2​(x~k),x~k+1−x⋆⟩+12​‖x~k+1−x~k‖Θk2,\displaystyle=\langle\nabla f_{1}(\tilde{x}^{k+1})+\nabla f_{2}(\tilde{x}^{k}),\tilde{x}^{k+1}-x^{\star}\rangle+\frac{1}{2}\|\tilde{x}^{k+1}-\tilde{x}^{k}\|^{2}_{\Theta^{k}},

where (1)(1) uses convexity of f1f_{1} and 11-relative smoothness of f2f_{2}, and (2)(2) uses convexity of f2f_{2}. Inserting the upper bound on f​(x~k+1)−f​(x)f(\tilde{x}^{k+1})-f(x) into the expression for Q​(w,w~k+1)Q(w,\tilde{w}^{k+1}), we find

Q​(w,w~k+1)≤\displaystyle Q(w,\tilde{w}^{k+1})\leq ⟨∇f1​(x~k+1)+∇f2​(x~k),x~k+1−x⋆⟩+12​‖x~k+1−x~k‖Θk2+g​(z~k+1)−g​(z⋆)\displaystyle\langle\nabla f_{1}(\tilde{x}^{k+1})+\nabla f_{2}(\tilde{x}^{k}),\tilde{x}^{k+1}-x^{\star}\rangle+\frac{1}{2}\|\tilde{x}^{k+1}-\tilde{x}^{k}\|^{2}_{\Theta^{k}}+g(\tilde{z}^{k+1})-g(z^{\star}) (23)
+⟨ρ​u,M​x~k+1−z~k+1⟩−⟨ρ​u~k+1,M​x⋆−z⋆⟩.\displaystyle+\langle\rho u,M\tilde{x}^{k+1}-\tilde{z}^{k+1}\rangle-\langle\rho\tilde{u}^{k+1},Mx^{\star}-z^{\star}\rangle.

Now, using the inexact optimality condition for the xx-subproblem (Lemma 3), the above display becomes

Q​(w,w~k+1)≤⟨Θk​(x~k+1−x~k),x⋆−x~k+1⟩+ρ​⟨M​x~k+1+N​z~k+u~k,M​(x⋆−x~k+1)⟩+Cx​εxk\displaystyle Q(w,\tilde{w}^{k+1})\leq\langle\Theta^{k}(\tilde{x}^{k+1}-\tilde{x}^{k}),x^{\star}-\tilde{x}^{k+1}\rangle+\rho\langle M\tilde{x}^{k+1}+N\tilde{z}^{k}+\tilde{u}^{k},M(x^{\star}-\tilde{x}^{k+1})\rangle+C_{x}\varepsilon_{x}^{k} (24)
+12​‖x~k+1−x~k‖Θk2+g​(z~k+1)−g​(z⋆)+⟨ρ​u,M​x~k+1+N​z~k+1⟩−⟨ρ​u~k+1,M​x⋆+N​z⋆⟩.\displaystyle+\frac{1}{2}\|\tilde{x}^{k+1}-\tilde{x}^{k}\|^{2}_{\Theta^{k}}+g(\tilde{z}^{k+1})-g(z^{\star})+\langle\rho u,M\tilde{x}^{k+1}+N\tilde{z}^{k+1}\rangle-\langle\rho\tilde{u}^{k+1},Mx^{\star}+Nz^{\star}\rangle. (25)

Similarly, applying the inexact optimality for the zz-subproblem (Lemma 4), we further obtain

Q​(w,w~k+1)≤⟨Θk​(x~k+1−x~k),x⋆−x~k+1⟩+ρ​⟨M​x~k+1+N​z~k+u~k,M​(x⋆−x~k+1)⟩+Cx​εxk\displaystyle Q(w,\tilde{w}^{k+1})\leq\langle\Theta^{k}(\tilde{x}^{k+1}-\tilde{x}^{k}),x^{\star}-\tilde{x}^{k+1}\rangle+\rho\langle M\tilde{x}^{k+1}+N\tilde{z}^{k}+\tilde{u}^{k},M(x^{\star}-\tilde{x}^{k+1})\rangle+C_{x}\varepsilon_{x}^{k}
+12​‖x~k+1−x~k‖Θk2−ρ​⟨NT​u~k+1,z~k+1−z⋆⟩+⟨Ψk​(z~k+1−z~k),z⋆−z~k+1⟩+Cz​εzk\displaystyle+\frac{1}{2}\|\tilde{x}^{k+1}-\tilde{x}^{k}\|^{2}_{\Theta^{k}}-\rho\langle N^{T}\tilde{u}^{k+1},\tilde{z}^{k+1}-z^{\star}\rangle+\langle\Psi^{k}(\tilde{z}^{k+1}-\tilde{z}^{k}),z^{\star}-\tilde{z}^{k+1}\rangle+C_{z}\sqrt{\varepsilon_{z}^{k}} (26)
+⟨ρ​u,M​x~k+1+N​z~k+1⟩−⟨ρ​u~k+1,M​x⋆+N​z⋆⟩.\displaystyle+\langle\rho u,M\tilde{x}^{k+1}+N\tilde{z}^{k+1}\rangle-\langle\rho\tilde{u}^{k+1},Mx^{\star}+Nz^{\star}\rangle.

We now simplify (5.2) by combining terms. Some basic manipulations show the terms on line 2 of (5.2) may be rewritten as

−ρ​⟨NT​u~k+1,z~k+1−z⋆⟩+ρ​⟨u,M​x~k+1+N​z~k+1⟩−ρ​⟨u~k+1,M​x⋆+N​z⋆⟩\displaystyle-\rho\langle N^{T}\tilde{u}^{k+1},\tilde{z}^{k+1}-z^{\star}\rangle+\rho\langle u,M\tilde{x}^{k+1}+N\tilde{z}^{k+1}\rangle-\rho\langle\tilde{u}^{k+1},Mx^{\star}+Nz^{\star}\rangle
=ρ​⟨u−u~k+1,M~​x~k+1+N​z~k+1⟩−ρ​⟨u~k+1,M​(x⋆−x~k+1)⟩.\displaystyle=\rho\langle u-\tilde{u}^{k+1},\tilde{M}\tilde{x}^{k+1}+N\tilde{z}^{k+1}\rangle-\rho\langle\tilde{u}^{k+1},M(x^{\star}-\tilde{x}^{k+1})\rangle.

We can combine the preceding display with the second term of line 1 in (5.2) to reach

ρ​⟨M​x~k+1+N​z~k+u~k,M​(x⋆−x~k+1)⟩−ρ​⟨u~k+1,M​(x⋆−x~k+1)⟩+ρ​⟨u−u~k+1,M​x~k+1+N​z~k+1⟩\displaystyle\rho\langle M\tilde{x}^{k+1}+N\tilde{z}^{k}+\tilde{u}^{k},M(x^{\star}-\tilde{x}^{k+1})\rangle-\rho\langle\tilde{u}^{k+1},M(x^{\star}-\tilde{x}^{k+1})\rangle+\rho\langle u-\tilde{u}^{k+1},M\tilde{x}^{k+1}+N\tilde{z}^{k+1}\rangle
=ρ​⟨u~k+1+N​(z~k−z~k+1),M​(x⋆−x~k+1)⟩−ρ​⟨u~k+1,M​(x⋆−x~k+1)⟩+ρ​⟨u−u~k+1,M​x~k+1+N​z~k+1⟩\displaystyle=\rho\langle\tilde{u}^{k+1}+N(\tilde{z}^{k}-\tilde{z}^{k+1}),M(x^{\star}-\tilde{x}^{k+1})\rangle-\rho\langle\tilde{u}^{k+1},M(x^{\star}-\tilde{x}^{k+1})\rangle+\rho\langle u-\tilde{u}^{k+1},M\tilde{x}^{k+1}+N\tilde{z}^{k+1}\rangle
=ρ⟨N(z~k−z~k+1),M(x⋆−x~k+1)+ρ⟨u−u~k+1,Mx~k+1+Nz~k+1⟩\displaystyle=\rho\langle N(\tilde{z}^{k}-\tilde{z}^{k+1}),M(x^{\star}-\tilde{x}^{k+1})+\rho\langle u-\tilde{u}^{k+1},M\tilde{x}^{k+1}+N\tilde{z}^{k+1}\rangle
=ρ​⟨N−​(z~k+1−z~k),M​(x⋆−x~k+1)⟩+ρ​⟨u~k+1−u,u~k−u~k+1⟩,\displaystyle=\rho\langle N^{-}(\tilde{z}^{k+1}-\tilde{z}^{k}),M(x^{\star}-\tilde{x}^{k+1})\rangle+\rho\langle\tilde{u}^{k+1}-u,\tilde{u}^{k}-\tilde{u}^{k+1}\rangle,

where N−=−N.N^{-}=-N. Inserting the preceding simplification into (5.2), we reach

Q​(w,w~k+1)\displaystyle Q(w,\tilde{w}^{k+1}) ≤⟨Θk​(x~k+1−x~k),x⋆−x~k+1⟩+ρ​⟨u~k+1−u,u~k−u~k+1⟩\displaystyle\leq\langle\Theta^{k}(\tilde{x}^{k+1}-\tilde{x}^{k}),x^{\star}-\tilde{x}^{k+1}\rangle+\rho\langle\tilde{u}^{k+1}-u,\tilde{u}^{k}-\tilde{u}^{k+1}\rangle (27)
+⟨Ψk​(z~k+1−z~k),z⋆−z~k+1⟩+ρ​⟨N−​(z~k+1−z~k),M​(x⋆−x~k+1)⟩\displaystyle+\langle\Psi^{k}(\tilde{z}^{k+1}-\tilde{z}^{k}),z^{\star}-\tilde{z}^{k+1}\rangle+\rho\langle N^{-}(\tilde{z}^{k+1}-\tilde{z}^{k}),M(x^{\star}-\tilde{x}^{k+1})\rangle
+12​‖x~k+1−x~k‖Θk2+Cx​εxk+Cz​εzk.\displaystyle+\frac{1}{2}\|\tilde{x}^{k+1}-\tilde{x}^{k}\|_{\Theta^{k}}^{2}+C_{x}\varepsilon_{x}^{k}+C_{z}\sqrt{\varepsilon^{k}_{z}}.

Now, we bound the first two leading terms in line 1 of (27) by invoking the identity ⟨a−b,Υ​(c−d)⟩=1/2​(‖a−d‖Υ2−‖a−c‖Υ2)+1/2​(‖c−b‖Υ2−‖d−b‖Υ2)\langle a-b,\Upsilon(c-d)\rangle=1/2\left(\|a-d\|^{2}_{\Upsilon}-\|a-c\|^{2}_{\Upsilon}\right)+1/2\left(\|c-b\|^{2}_{\Upsilon}-\|d-b\|^{2}_{\Upsilon}\right) to obtain

⟨Θk​(x~k+1−x~k),x⋆−x~k+1⟩+ρ​⟨u~k+1−u,z~k+1−M​x~k+1⟩=\displaystyle\langle\Theta^{k}(\tilde{x}^{k+1}-\tilde{x}^{k}),x^{\star}-\tilde{x}^{k+1}\rangle+\rho\langle\tilde{u}^{k+1}-u,\tilde{z}^{k+1}-M\tilde{x}^{k+1}\rangle=
12​(‖x⋆−x~k‖Θk2−‖x⋆−x~k+1‖Θk2)−12​‖x~k+1−x~k‖Θk2+ρ2​(‖u~k−u‖2−‖u~k+1−u‖2−‖u~k−u~k+1‖2).\displaystyle\frac{1}{2}\left(\|x^{\star}-\tilde{x}^{k}\|^{2}_{\Theta^{k}}-\|x^{\star}-\tilde{x}^{k+1}\|^{2}_{\Theta^{k}}\right)-\frac{1}{2}\|\tilde{x}^{k+1}-\tilde{x}^{k}\|^{2}_{\Theta^{k}}+\frac{\rho}{2}\left(\|\tilde{u}^{k}-u\|^{2}-\|\tilde{u}^{k+1}-u\|^{2}-\|\tilde{u}^{k}-\tilde{u}^{k+1}\|^{2}\right).

Similarly, to bound the third and fourth terms in (27), we again invoke (a−b)T​Υ​(c−d)=1/2​(‖a−d‖Υ2−‖a−c‖Υ2)+1/2​(‖c−b‖Υ2−‖d−b‖Υ2)(a-b)^{T}\Upsilon(c-d)=1/2\left(\|a-d\|^{2}_{\Upsilon}-\|a-c\|^{2}_{\Upsilon}\right)+1/2\left(\|c-b\|^{2}_{\Upsilon}-\|d-b\|^{2}_{\Upsilon}\right) which yields

⟨Ψk​(z~k+1−z~k),z⋆−z~k+1⟩=12​(‖z~k−z⋆‖Ψk2−‖z~k+1−z⋆‖Ψk2)−12​‖z~k+1−z~k‖Ψk2,\displaystyle\langle\Psi^{k}(\tilde{z}^{k+1}-\tilde{z}^{k}),z^{\star}-\tilde{z}^{k+1}\rangle=\frac{1}{2}\left(\|\tilde{z}^{k}-z^{\star}\|^{2}_{\Psi^{k}}-\|\tilde{z}^{k+1}-z^{\star}\|^{2}_{\Psi^{k}}\right)-\frac{1}{2}\|\tilde{z}^{k+1}-\tilde{z}^{k}\|_{\Psi^{k}}^{2},
ρ​⟨N−​(z~k−z~k+1),M​(x~k+1−x⋆)⟩\displaystyle\rho\langle N^{-}(\tilde{z}^{k}-\tilde{z}^{k+1}),M(\tilde{x}^{k+1}-x^{\star})\rangle
=ρ2​(‖N−​z~k−M​x⋆‖2−‖z~k+1−M​x⋆‖2+‖N−​z~k+1−M​x~k+1‖2−‖N−​z~k−M​x~k+1‖2)\displaystyle=\frac{\rho}{2}\left(\|N^{-}\tilde{z}^{k}-Mx^{\star}\|^{2}-\|\tilde{z}^{k+1}-Mx^{\star}\|^{2}+\|N^{-}\tilde{z}^{k+1}-M\tilde{x}^{k+1}\|^{2}-\|N^{-}\tilde{z}^{k}-M\tilde{x}^{k+1}\|^{2}\right)
=ρ2​(‖N​z~k−N​z⋆‖2−‖N​z~k+1−N​z⋆‖2−‖M​x~k+1+N​z~k‖2)+ρ2​‖u~k−u~k+1‖2.\displaystyle=\frac{\rho}{2}\left(\|N\tilde{z}^{k}-Nz^{\star}\|^{2}-\|N\tilde{z}^{k+1}-Nz^{\star}\|^{2}-\|M\tilde{x}^{k+1}+N\tilde{z}^{k}\|^{2}\right)+\frac{\rho}{2}\|\tilde{u}^{k}-\tilde{u}^{k+1}\|^{2}.

Putting everything together, we conclude

Q​(w,w~k+1)\displaystyle Q(w,\tilde{w}^{k+1}) ≤12​(‖x~k−x⋆‖Θk2−‖x~k+1−x⋆‖Θk2)+12​(‖z~k−z⋆‖Ψk+ρ​NT​N2−‖z~k+1−z⋆‖Ψk+ρ​NT​N2)\displaystyle\leq\frac{1}{2}\left(\|\tilde{x}^{k}-x^{\star}\|^{2}_{\Theta^{k}}-\|\tilde{x}^{k+1}-x^{\star}\|^{2}_{\Theta^{k}}\right)+\frac{1}{2}\left(\|\tilde{z}^{k}-z^{\star}\|_{\Psi^{k}+\rho N^{T}N}^{2}-\|\tilde{z}^{k+1}-z^{\star}\|_{\Psi^{k}+\rho N^{T}N}^{2}\right)
+ρ2​(‖u~k−u‖2−‖u~k+1−u‖2)+Cx​εxk+Cz​εzk.\displaystyle+\frac{\rho}{2}\left(\|\tilde{u}^{k}-u\|^{2}-\|\tilde{u}^{k+1}-u\|^{2}\right)+C_{x}\varepsilon_{x}^{k}+C_{z}\sqrt{\varepsilon_{z}^{k}}.

as desired. ∎

5.3 Proof of Theorem 1

With Lemma 5 in hand, we are ready to prove Theorem 1.

Proof.

From Lemma 5, we have for each kk that

Q​(w,w~k+1)\displaystyle Q(w,\tilde{w}^{k+1}) ≤12​(‖x~k−x⋆‖Θk2−‖x~k+1−x⋆‖Θk2)+12​(‖z~k−z⋆‖Ψk+ρ​NT​N2−‖z~k+1−z⋆‖Ψk+ρ​NT​N2)\displaystyle\leq\frac{1}{2}\left(\|\tilde{x}^{k}-x^{\star}\|^{2}_{\Theta^{k}}-\|\tilde{x}^{k+1}-x^{\star}\|^{2}_{\Theta^{k}}\right)+\frac{1}{2}\left(\|\tilde{z}^{k}-z^{\star}\|_{\Psi^{k}+\rho N^{T}N}^{2}-\|\tilde{z}^{k+1}-z^{\star}\|_{\Psi^{k}+\rho N^{T}N}^{2}\right)
+ρ2​(‖u~k−u‖2−‖u~k+1−u‖2)+Cx​εxk+Cz​εzk.\displaystyle+\frac{\rho}{2}\left(\|\tilde{u}^{k}-u\|^{2}-\|\tilde{u}^{k+1}-u\|^{2}\right)+C_{x}\varepsilon_{x}^{k}+C_{z}\sqrt{\varepsilon_{z}^{k}}.

Now, summing up the preceding display from k=1k=1 to tt and using w=(x⋆,z⋆,u)w=(x^{\star},z^{\star},u), we obtain

∑k=2t+1Q​(x⋆,z⋆,u;w~k)\displaystyle\sum^{t+1}_{k=2}Q(x^{\star},z^{\star},u;\tilde{w}^{k}) ≤12​∑k=1t(‖x~k−x⋆‖Θk2−‖x~k+1−x⋆‖Θk2)⏟T1\displaystyle\leq\frac{1}{2}\underbrace{\sum^{t}_{k=1}\left(\|\tilde{x}^{k}-x^{\star}\|^{2}_{\Theta^{k}}-\|\tilde{x}^{k+1}-x^{\star}\|^{2}_{\Theta^{k}}\right)}_{T_{1}}
+ρ2​∑k=1t(‖z~k−z⋆‖Ψk+ρ​NT​N2−‖z~k+1−z⋆‖Ψk+ρ​NT​N2)⏟T2\displaystyle+\underbrace{\frac{\rho}{2}\sum^{t}_{k=1}\left(\|\tilde{z}^{k}-z^{\star}\|_{\Psi^{k}+\rho N^{T}N}^{2}-\|\tilde{z}^{k+1}-z^{\star}\|_{\Psi^{k}+\rho N^{T}N}^{2}\right)}_{T_{2}}
+ρ2​∑k=1t(‖u~k−u‖2−‖u~k+1−u‖2)⏟T3+Cx​ℰx+Cz​ℰz.\displaystyle+\underbrace{\frac{\rho}{2}\sum^{t}_{k=1}\left(\|\tilde{u}^{k}-u\|^{2}-\|\tilde{u}^{k+1}-u\|^{2}\right)}_{T_{3}}+C_{x}\mathcal{E}_{x}+C_{z}\mathcal{E}_{z}.

We now turn to bounding T1T_{1}. Using the definition of T1T_{1}, we find

T1\displaystyle T_{1} =12​∑k=1t(‖x~k−x⋆‖Θk2−‖x~k+1−x⋆‖Θk2)\displaystyle=\frac{1}{2}\sum^{t}_{k=1}\left(\|\tilde{x}^{k}-x^{\star}\|^{2}_{\Theta^{k}}-\|\tilde{x}^{k+1}-x^{\star}\|^{2}_{\Theta^{k}}\right)
=12​(‖x~1−x⋆‖Θ12−‖x~t+1−x⋆‖Θt2)+12​∑k=2t(‖x~k−x⋆‖Θk2−‖x~k−x⋆‖Θk−12).\displaystyle=\frac{1}{2}\left(\|\tilde{x}^{1}-x^{\star}\|^{2}_{\Theta^{1}}-\|\tilde{x}^{t+1}-x^{\star}\|^{2}_{\Theta^{t}}\right)+\frac{1}{2}\sum_{k=2}^{t}\left(\|\tilde{x}^{k}-x^{\star}\|^{2}_{\Theta^{k}}-\|\tilde{x}^{k}-x^{\star}\|^{2}_{\Theta^{k-1}}\right).

Now using our hypotheses on the sequence {Θk}k\{\Theta^{k}\}_{k} in (15), we obtain

‖x~k−x⋆‖Θk2−‖x~k−x⋆‖Θk−12\displaystyle\|\tilde{x}^{k}-x^{\star}\|^{2}_{\Theta^{k}}-\|\tilde{x}^{k}-x^{\star}\|^{2}_{\Theta^{k-1}} =(x~k−x⋆)T​(Θk−Θk−1)​(x~k−x⋆)≤ζk−1​‖x~k−x⋆‖Θk−12\displaystyle=(\tilde{x}^{k}-x^{\star})^{T}(\Theta^{k}-\Theta^{k-1})(\tilde{x}^{k}-x^{\star})\leq\zeta^{k-1}\|\tilde{x}^{k}-x^{\star}\|^{2}_{\Theta^{k-1}}
≤τζ​ζk−1​‖x~k−x⋆‖Θ12.\displaystyle\leq\tau_{\zeta}\zeta^{k-1}\|\tilde{x}^{k}-x^{\star}\|^{2}_{\Theta^{1}}.

Inserting the previous bound into T1T_{1}, we reach

T1\displaystyle T_{1} ≤12​‖x~1−x⋆‖Θ12+12​τζ​∑k=1tζk−1​‖x~k−x⋆‖Θ12−12​‖x~t+1−x⋆‖Θt2\displaystyle\leq\frac{1}{2}\|\tilde{x}^{1}-x^{\star}\|^{2}_{\Theta^{1}}+\frac{1}{2}\tau_{\zeta}\sum_{k=1}^{t}\zeta^{k-1}\|\tilde{x}^{k}-x^{\star}\|^{2}_{\Theta^{1}}-\frac{1}{2}\|\tilde{x}^{t+1}-x^{\star}\|^{2}_{\Theta^{t}}
≤12​(‖x~1−x⋆‖Θ12+Cζ​ℰζ)−12​‖x~t+1−x⋆‖Θt2\displaystyle\leq\frac{1}{2}\left(\|\tilde{x}^{1}-x^{\star}\|^{2}_{\Theta^{1}}+C_{\zeta}\mathcal{E}_{\zeta}\right)-\frac{1}{2}\|\tilde{x}^{t+1}-x^{\star}\|^{2}_{\Theta^{t}}
≤12​(dx⋆,Θ12+Cζ​ℰζ).\displaystyle\leq\frac{1}{2}\left(d^{2}_{x^{\star},\Theta^{1}}+C_{\zeta}\mathcal{E}_{\zeta}\right).

Next, we bound T2T_{2}.

T2\displaystyle T_{2} =12​∑k=1t(‖z~k−z⋆‖2−‖z~k+1−z⋆‖2)+12​∑k=1t(‖z~k−z⋆‖Ψk+ρ​NT​N2−‖z~k+1−z⋆‖Ψk+ρ​NT​N2)\displaystyle=\frac{1}{2}\sum^{t}_{k=1}\left(\|\tilde{z}^{k}-z^{\star}\|^{2}-\|\tilde{z}^{k+1}-z^{\star}\|^{2}\right)+\frac{1}{2}\sum_{k=1}^{t}\left(\|\tilde{z}^{k}-z^{\star}\|_{\Psi^{k}+\rho N^{T}N}^{2}-\|\tilde{z}^{k+1}-z^{\star}\|_{\Psi^{k}+\rho N^{T}N}^{2}\right)
≤ρ2​∑i=1t(‖z~k−z⋆‖2−‖z~k+1−z⋆‖2)+12​(‖z~1−z⋆‖Ψ12+Cζ​ℰζ)\displaystyle\leq\frac{\rho}{2}\sum^{t}_{i=1}\left(\|\tilde{z}^{k}-z^{\star}\|^{2}-\|\tilde{z}^{k+1}-z^{\star}\|^{2}\right)+\frac{1}{2}\left(\|\tilde{z}^{1}-z^{\star}\|^{2}_{\Psi^{1}}+C_{\zeta}\mathcal{E}_{\zeta}\right)
=12​‖z~1−z⋆‖Ψ1+ρ​I2=12​dz⋆,Ψρ,N12+Cζ2​ℰζ.\displaystyle=\frac{1}{2}\|\tilde{z}^{1}-z^{\star}\|_{\Psi^{1}+\rho I}^{2}=\frac{1}{2}d_{z^{\star},\Psi^{1}_{\rho,N}}^{2}+\frac{C_{\zeta}}{2}\mathcal{E}_{\zeta}.

Last, T3T_{3} is a telescoping sum, hence

T2\displaystyle T_{2} =ρ2​∑k=1t(‖u~k−u‖2−‖u~k+1−u‖2)=ρ2​(‖u~1−u‖2−‖u~t+1−u‖2).\displaystyle=\frac{\rho}{2}\sum^{t}_{k=1}\left(\|\tilde{u}^{k}-u\|^{2}-\|\tilde{u}^{k+1}-u\|^{2}\right)=\frac{\rho}{2}\left(\|\tilde{u}^{1}-u\|^{2}-\|\tilde{u}^{t+1}-u\|^{2}\right).

Using our bounds on T1T_{1} through T3T_{3}, we find

∑k=2t+1Q​(x⋆,z⋆,u;w~k)\displaystyle\sum^{t+1}_{k=2}Q(x^{\star},z^{\star},u;\tilde{w}^{k}) ≤12​(dx⋆,Θ12+Cζ​ℰζ)+12​dz⋆,Ψρ,N12+12​Cζ​ℰζ+Cx​ℰx+Cz​ℰz\displaystyle\leq\frac{1}{2}\left(d^{2}_{x^{\star},\Theta^{1}}+C_{\zeta}\mathcal{E}_{\zeta}\right)+\frac{1}{2}d_{z^{\star},\Psi^{1}_{\rho,N}}^{2}+\frac{1}{2}C_{\zeta}\mathcal{E}_{\zeta}+C_{x}\mathcal{E}_{x}+C_{z}\mathcal{E}_{z}
+ρ2​(‖u~1−u‖2−‖u~t+1−u‖2)\displaystyle+\frac{\rho}{2}\left(\|\tilde{u}^{1}-u\|^{2}-\|\tilde{u}^{t+1}-u\|^{2}\right)
=12​dx⋆,Θ12+12​dz⋆,Ψρ,N12+Cx​ℰx+Cz​ℰz+Cζ​ℰζ+ρ2​(‖u~1−u‖2−‖u~t+1−u‖2),\displaystyle=\frac{1}{2}d^{2}_{x^{\star},\Theta^{1}}+\frac{1}{2}d_{z^{\star},\Psi^{1}_{\rho,N}}^{2}+C_{x}\mathcal{E}_{x}+C_{z}\mathcal{E}_{z}+C_{\zeta}\mathcal{E}_{\zeta}+\frac{\rho}{2}\left(\|\tilde{u}^{1}-u\|^{2}-\|\tilde{u}^{t+1}-u\|^{2}\right),

Now, as w¯t+1=1t​∑k=2t+1w~k\bar{w}^{t+1}=\frac{1}{t}\sum^{t+1}_{k=2}\tilde{w}^{k}, the convexity of QQ in its second argument yields

Q​(x⋆,z⋆,u;w¯t+1)\displaystyle Q(x^{\star},z^{\star},u;\bar{w}^{t+1}) ≤1t​∑k=2t+1Q​(x⋆,z⋆,u;w~k)\displaystyle\leq\frac{1}{t}\sum_{k=2}^{t+1}Q(x^{\star},z^{\star},u;\tilde{w}^{k}) (28)
≤1t​(12​dx⋆,Θ12+ρ2​dz⋆,Ψρ,N12+Cx​ℰx+Cz​ℰz+Cζ​ℰζ+ρ2​(‖u~1−u‖2−‖u~t+1−u‖2)).\displaystyle\leq\frac{1}{t}\left(\frac{1}{2}d^{2}_{x^{\star},\Theta^{1}}+\frac{\rho}{2}d_{z^{\star},\Psi_{\rho,N}^{1}}^{2}+C_{x}\mathcal{E}_{x}+C_{z}\mathcal{E}_{z}+C_{\zeta}\mathcal{E}_{\zeta}+\frac{\rho}{2}\left(\|\tilde{u}^{1}-u\|^{2}-\|\tilde{u}^{t+1}-u\|^{2}\right)\right).

Define Γ≔12​dx⋆,Θ12+12​dz⋆,Ψρ,N12+Cx​ℰx+Cz​ℰz+Cζ​ℰζ\Gamma\coloneqq\frac{1}{2}d^{2}_{x^{\star},\Theta^{1}}+\frac{1}{2}d^{2}_{z^{\star},\Psi^{1}_{\rho,N}}+C_{x}\mathcal{E}_{x}+C_{z}\mathcal{E}_{z}+C_{\zeta}\mathcal{E}_{\zeta}. Since Q​(w⋆,w¯t+1)≥0Q(w^{\star},\bar{w}^{t+1})\geq 0, by (28) we reach

‖u~t+1−u⋆‖2≤2ρ​Γ+du⋆2.\|\tilde{u}^{t+1}-u^{\star}\|^{2}\leq\frac{2}{\rho}\Gamma+d^{2}_{u^{\star}}.

Let v~t+1=1t​(u~1−u~t+1)\tilde{v}^{t+1}=\frac{1}{t}\left(\tilde{u}^{1}-\tilde{u}^{t+1}\right). Then we can bound ‖v~t+1‖2\|\tilde{v}_{t+1}\|^{2} as

‖v~t+1‖2≤\displaystyle\|\tilde{v}^{t+1}\|^{2}\leq 2t2​(‖u~1−u⋆‖2+‖u~t+1−u⋆‖2)≤4t2​(Γρ+du⋆2).\displaystyle\frac{2}{t^{2}}\left(\|\tilde{u}^{1}-u^{\star}\|^{2}+\|\tilde{u}^{t+1}-u^{\star}\|^{2}\right)\leq\frac{4}{t^{2}}\left(\frac{\Gamma}{\rho}+d^{2}_{u^{\star}}\right).

By (28), given the fact u~1=0\tilde{u}^{1}=0, we also have

Q​(x⋆,z⋆,u;w¯t+1)\displaystyle Q(x^{\star},z^{\star},u;\bar{w}^{t+1}) ≤Γ−ρ​⟨u~1−u~t+1,u⟩t=Γt−ρ​⟨v~t+1,u⟩,\displaystyle\leq\frac{\Gamma-\rho\langle\tilde{u}^{1}-\tilde{u}^{t+1},u\rangle}{t}=\frac{\Gamma}{t}-\rho\langle\tilde{v}^{t+1},u\rangle,

where the equality follows from the definition of v~t+1\tilde{v}^{t+1}. Hence for any uu

Q​(x⋆,z⋆,u;w¯t+1)+⟨v~t+1,ρ​u⟩\displaystyle Q(x^{\star},z^{\star},u;\bar{w}^{t+1})+\langle\tilde{v}^{t+1},\rho u\rangle ≤Γt,\displaystyle\leq\frac{\Gamma}{t},

and therefore

ℓU​(v~t+1,w¯t+1)≤1t​(12​dx⋆,Θ12+12​dz⋆,Ψρ,N12+Cx​ℰx+Cz​ℰz+Cζ​ℰζ).\ell_{U}(\tilde{v}^{t+1},\bar{w}^{t+1})\leq\frac{1}{t}\left(\frac{1}{2}d^{2}_{x^{\star},\Theta^{1}}+\frac{1}{2}d_{z^{\star},\Psi^{1}_{\rho,N}}^{2}+C_{x}\mathcal{E}_{x}+C_{z}\mathcal{E}_{z}+C_{\zeta}\mathcal{E}_{\zeta}\right).

We finish the proof by invoking Lemma 2. □\Box

6 Linear convergence of GeNI-ADMM

In this section, we seek to establish linear convergence results for Algorithm 2. In general, the linear convergence of ADMM relies on strong convexity of the objective function [1, 33, 11]. Consistently, the linear convergence of GeNI-ADMM also requires strong convexity. Many applications of GeNI-ADMM fit into this setting, such as elastic net [34]. However, linear convergence is not restricted to strongly convex problems. It has been shown that local linear convergence of ADMM can be guaranteed even without strong convexity [21]. Experiments in Section 8 show the same phenomenon for GeNI-ADMM: it converges linearly after a couple of iterations when the iterates reach some manifold containing the solution. The linear convergence theory of GeNI-ADMM provides a way to understand this phenomenon. We first list the additional assumptions required for linear convergence:

Assumption 5 (Optimization is over the whole space).

The sets XX and ZZ in (1) satisfy

X=𝒳,and​Z=𝒵.X=\mathcal{X},~{}\text{and}~{}Z=\mathcal{Z}.

Assumption 5 states that the optimization problem in (1) is over the entire spaces 𝒳\mathcal{X} and 𝒵\mathcal{Z}, not closed subsets. This assumption is met in many practical optimization problems of interest, where 𝒳=𝒵=ℋ=ℝd\mathcal{X}=\mathcal{Z}=\mathcal{H}=\mathbb{R}^{d}. Moreover, it is consistent with prior analyses such as Deng and Yin [13], who specialize their analysis to the setting of the last sentence.

Assumption 6 (Regularity of ff).

The function ff is finite valued, strongly convex with parameter σf\sigma_{f}, and smooth with parameter LfL_{f}.

Assumption 6 imposes standard regularity conditions on ff, in addition to the conditions of Assumption 2.

Assumption 7 (Non-degeneracy of constraint operators).

The linear operators M​MTMM^{T} and NT​NN^{T}N are invertible.

Assumption 7 is consistent with prior analyses of ADMM-type schemes under strong convexity, such as Deng and Yin [13], who make this assumption in their analysis of Generalized ADMM. Moreover, the assumption holds in many important application problems, especially those that arise from machine learning where, typically, M=IM=I and N=−IN=-I.

Assumption 8 (Geometric decay of the forcing sequences).

There exists a constant q>0q>0 such that the forcing sequences {εxk}k≥1\{\varepsilon^{k}_{x}\}_{k\geq 1}, {εzk}k≥1\{\varepsilon^{k}_{z}\}_{k\geq 1} satisfy

εxk+1≤εxk/(1+q),and​εzk+1≤εzk/(1+q)2.\varepsilon^{k+1}_{x}\leq\varepsilon^{k}_{x}/(1+q),\;\text{and}\;\;\varepsilon^{k+1}_{z}\leq\varepsilon^{k}_{z}/(1+q)^{2}. (29)

Moreover, we assume Algorithm 2 is equipped with oracles for solving the xx and zz-subproblems, which at each iteration produce approximate solutions x~k+1\tilde{x}^{k+1}, z~k+1\tilde{z}^{k+1} satisfying:

x~k+1​≈εxk​argminx∈X​{f1​(x)+⟨∇f2​(x~k),x−x~k⟩+12‖x−x~k∥Θk2+ρ2​‖M​x+N​z~k+u~k‖2},\displaystyle\tilde{x}^{k+1}\overset{\varepsilon_{x}^{k}}{\approx}\underset{x\in X}{\mathop{\rm argmin}}\{f_{1}(x)+\langle\nabla f_{2}(\tilde{x}^{k}),x-\tilde{x}^{k}\rangle+\frac{1}{2}\|x-\tilde{x}^{k}\|^{2}_{\Theta^{k}}+\frac{\rho}{2}\|Mx+N\tilde{z}^{k}+\tilde{u}^{k}\|^{2}\},
z~k+1​≊εzk​argminz∈Z​{g​(z)+ρ2​‖M​x~k+1+N​z+u~k‖2+12​‖z−z~k‖Ψk2}.\displaystyle\tilde{z}^{k+1}\overset{\varepsilon_{z}^{k}}{\approxeq}\underset{z\in Z}{\mathop{\rm argmin}}\{g(z)+\frac{\rho}{2}\|M\tilde{x}^{k+1}+Nz+\tilde{u}^{k}\|^{2}+\frac{1}{2}\|z-\tilde{z}^{k}\|^{2}_{\Psi^{k}}\}.

Assumption 8 replaces Assumption 3 and requires the inexactness sequences to decay geometrically. Compared with the sublinear convergence result, linear convergence requires more accurate solutions to the subproblems. Again, since the zz-subproblem inexactness is weaker than the xx-subproblem inexactness, {εzk}k≥1\{\varepsilon^{k}_{z}\}_{k\geq 1} should have a faster decay rate (1+q)2(1+q)^{2} than the decay rate (1+q1+q) of {εxk}k≥1\{\varepsilon^{k}_{x}\}_{k\geq 1}.

The requirement that the forcing sequences decay geometrically is somewhat burdensome, as it leads to the subproblems needing to be solved to higher accuracy sooner than if the forcing sequences were only summable. Fortunately, this condition seems to be an artifact of the analysis; our numerical experiments with strongly convex ff (Section 8.2) only use summable forcing sequences but show linear convergence of GeNI-ADMM.

6.1 Our approach

Inspired by Deng and Yin [13], we take a Lyapunov function approach to proving linear convergence. Let w~=(x~,z~,u~)\tilde{w}=(\tilde{x},\tilde{z},\tilde{u}), and w⋆=(x⋆,z⋆,u⋆)w^{\star}=(x^{\star},z^{\star},u^{\star}). We define the Lyapunov function:

Φk=1ρ​‖x~k−x⋆‖Θk2+1ρ​‖z~k−z~⋆‖Ψk+ρ​NT​N2+‖u~k−u⋆‖2=‖w~k−w⋆‖Gk2,\Phi^{k}=\frac{1}{\rho}\|\tilde{x}^{k}-x^{\star}\|_{\Theta^{k}}^{2}+\frac{1}{\rho}\|\tilde{z}^{k}-\tilde{z}^{\star}\|_{\Psi^{k}+\rho N^{T}N}^{2}+\|\tilde{u}^{k}-u^{\star}\|^{2}=\|\tilde{w}^{k}-w^{\star}\|_{G^{k}}^{2},

where

Gk≔(1ρ​Θk0001ρ​Ψk+NT​N000I).G^{k}\coloneqq\begin{pmatrix}\frac{1}{\rho}\Theta^{k}&0&0\\ 0&\frac{1}{\rho}\Psi^{k}+N^{T}N&0\\ 0&0&I\end{pmatrix}.

Our main result in this section is the following theorem, which shows the Lyapunov function converges linearly to 0.

Theorem 2.

Instate Assumptions 1-2, and Assumptions 4-8. Moreover, suppose that θmin\theta_{\textup{min}} in (14) satisfies θmin>Lf2/σf\theta_{\textup{min}}>L^{2}_{f}/\sigma_{f}. Then there exist constants δ\delta and S>0S>0 such that if q>δq>\delta,

(1+δ)k​Φk≤τζ​Φ1+S.(1+\delta)^{k}\Phi^{k}\leq\tau_{\zeta}\Phi^{1}+S. (30)

Hence after k=𝒪​(1δ​log⁡(τζ​Φ1ϵ))k=\mathcal{O}\left(\frac{1}{\delta}\log\left(\frac{\tau_{\zeta}\Phi^{1}}{\epsilon}\right)\right) iterations,

Φk≤ϵ.\Phi^{k}\leq\epsilon.

The proof of Theorem 2 is deferred to Section 6.3. As Gk≻0G^{k}\succ 0 for all kk, Theorem 2 implies the iterates (x~k,z~k,u~k)(\tilde{x}^{k},\tilde{z}^{k},\tilde{u}^{k}) converge linearly to optimum (x⋆,z⋆,u⋆)(x^{\star},z^{\star},u^{\star}). Thus, despite inexactly solving approximations of the original ADMM subproblems, GeNI-ADMM still enjoys linear convergence when the objective is strongly convex. An unattractive aspect of Theorem 2 is the requirement that θmin\theta_{\textup{min}} satisfy θmin>Lf2/σf\theta_{\textup{min}}>L_{f}^{2}/\sigma_{f}. Although this condition can be enforced by adding a damping term σ​I\sigma I to Θk\Theta^{k}, this is undesirable as a large regularization term can lead GeNI-ADMM to converge slower. We have found that this condition is unnecessary—our numerical experiments do not enforce this condition, yet GeNI-ADMM achieves linear convergence. We believe this condition to be an artifact of the analysis, which stems from lower bounding the term −⟨∇f2​(x~k+1)−∇f2​(x~k),x~k+1−x⋆⟩-\langle\nabla f_{2}(\tilde{x}^{k+1})-\nabla f_{2}(\tilde{x}^{k}),\tilde{x}^{k+1}-x^{\star}\rangle in Lemma 7.

6.2 Sufficient descent

From Theorem 2, to establish linear convergence of GeNI-ADMM, it suffices to show Φk\Phi^{k} decreases geometrically. We take two steps to achieve this. First, we show that ‖w~k−w⋆‖Gk2−‖w~k+1−w⋆‖Gk2\|\tilde{w}^{k}-w^{\star}\|_{G^{k}}^{2}-\|\tilde{w}^{k+1}-w^{\star}\|_{G^{k}}^{2} decreases for every iteration kk (Lemma 7). Second, we show that Φk+1\Phi^{k+1} decreases geometrically by a factor of 1/(1+δ)1/(1+\delta) with respect to Φk\Phi^{k} and some small error terms that stem from inexactness (Lemma 8).

As in the convex case, the optimality conditions of the subproblems play a vital role in the analysis. Since the subproblems are only solved approximately, we must again consider the inexactness of the solutions in these two steps. For the first step, we use strong convexity of ff and convexity of gg with appropriate perturbations to account for the inexactness. We call these conditions perturbed convexity conditions, as outlined in Lemma 6.

Lemma 6 (Perturbed convexity).

Instate the assumptions of Theorem 2. Let x~k+1\tilde{x}^{k+1} and z~k+1\tilde{z}^{k+1} be the inexact solutions of xx and zz-subproblems under Definition 1. Recall (x⋆,z⋆,u⋆)(x^{\star},z^{\star},u^{\star}) is a saddle point of (1). Then for some constant C≥0C\geq 0, the following inequalities are satisfied:

  1. 1.

    (Semi-inexact ff-strong convexity)

    ⟨x~k−x~k+1,x~k+1−x⋆⟩Θk+ρ​⟨N​(z~k+1−z~k)+u⋆−u~k+1,M​(x~k+1−x⋆)⟩+C​εxk\displaystyle\langle\tilde{x}^{k}-\tilde{x}^{k+1},\tilde{x}^{k+1}-x^{\star}\rangle_{\Theta^{k}}+\rho\langle N(\tilde{z}^{k+1}-\tilde{z}^{k})+u^{\star}-\tilde{u}^{k+1},M(\tilde{x}^{k+1}-x^{\star})\rangle+C\varepsilon_{x}^{k} (31)
    ≥σf​‖x~k+1−x⋆‖2−⟨∇f2​(x~k+1)−∇f2​(x~k),x~k+1−x⋆⟩,\displaystyle\geq\sigma_{f}\|\tilde{x}^{k+1}-x^{\star}\|^{2}-\langle\nabla f_{2}(\tilde{x}^{k+1})-\nabla f_{2}(\tilde{x}^{k}),\tilde{x}^{k+1}-x^{\star}\rangle,
  2. 2.

    (Semi-inexact gg-convexity)

    ⟨z~k+1−z⋆,ρ​NT​(u⋆−u~k+1)+Ψk​(z~k−z~k+1)⟩≥−C​εzk.\langle\tilde{z}^{k+1}-z^{\star},\rho N^{T}(u^{\star}-\tilde{u}^{k+1})+\Psi^{k}(\tilde{z}^{k}-\tilde{z}^{k+1})\rangle\geq-C\sqrt{\varepsilon_{z}^{k}}. (32)

A detailed proof of Lemma 6 is presented in Section A.3. In Lemma 6, we call (31) and (32) semi-inexact (strong) convexity because x⋆x^{\star} (z⋆z^{\star}) is part of the exact saddle point but x~k+1\tilde{x}^{k+1} (z~k+1\tilde{z}^{k+1}) is an inexact subproblem solution. With Lemma 6, we establish a descent-type inequality, which takes into inexactness.

Lemma 7 (Inexact sufficient descent).

Define εwk=εxk+εzk\varepsilon_{w}^{k}=\varepsilon_{x}^{k}+\sqrt{\varepsilon_{z}^{k}}, then the following descent condition holds.

‖w~k−w⋆‖Gk2−‖w~k+1−w⋆‖Gk2+C​εwk≥12​‖w~k−w~k+1‖Gk2+2​σfρ​‖x~k+1−x⋆‖2\displaystyle\|\tilde{w}^{k}-w^{\star}\|_{G^{k}}^{2}-\|\tilde{w}^{k+1}-w^{\star}\|^{2}_{G^{k}}+C\varepsilon_{w}^{k}\geq\frac{1}{2}\|\tilde{w}^{k}-\tilde{w}^{k+1}\|_{G^{k}}^{2}+\frac{2\sigma_{f}}{\rho}\|\tilde{x}^{k+1}-x^{\star}\|^{2} (33)
−2ρ​⟨∇f2​(x~k+1)−∇f2​(x~k),x~k+1−x⋆⟩.\displaystyle-\frac{2}{\rho}\langle\nabla f_{2}(\tilde{x}^{k+1})-\nabla f_{2}(\tilde{x}^{k}),\tilde{x}^{k+1}-x^{\star}\rangle.
Proof.

Adding the inequalities (31) and (32) together, and using the relation M​(x~k+1−x⋆)=u~k+1−u~k+N​(z⋆−z~k+1)M(\tilde{x}^{k+1}-x^{\star})=\tilde{u}^{k+1}-\tilde{u}^{k}+N(z^{\star}-\tilde{z}^{k+1}), we reach

⟨x~k−x~k+1,x~k+1−x⋆⟩Θk+⟨z~k−z~k+1,z~k+1−z⋆⟩Ψk+ρ​NT​N+ρ​⟨u~k−u~k+1,u~k+1−u⋆⟩+C​εxk\displaystyle\langle\tilde{x}^{k}-\tilde{x}^{k+1},\tilde{x}^{k+1}-x^{\star}\rangle_{\Theta^{k}}+\langle\tilde{z}^{k}-\tilde{z}^{k+1},\tilde{z}^{k+1}-z^{\star}\rangle_{\Psi^{k}+\rho N^{T}N}+\rho\langle\tilde{u}^{k}-\tilde{u}^{k+1},\tilde{u}^{k+1}-u^{\star}\rangle+C\varepsilon_{x}^{k}
≥σf​‖x~k+1−x⋆‖2−⟨∇f2​(x~k+1)−∇f2​(x~k),x~k+1−x⋆⟩−C​εzk+ρ​⟨u~k−u~k+1,N​(z~k+1−z~k)⟩\displaystyle\geq\sigma_{f}\|\tilde{x}^{k+1}-x^{\star}\|^{2}-\langle\nabla f_{2}(\tilde{x}^{k+1})-\nabla f_{2}(\tilde{x}^{k}),\tilde{x}^{k+1}-x^{\star}\rangle-C\sqrt{\varepsilon_{z}^{k}}+\rho\langle\tilde{u}^{k}-\tilde{u}^{k+1},N(\tilde{z}^{k+1}-\tilde{z}^{k})\rangle

Recalling the definitions of w~\tilde{w}, εwk\varepsilon_{w}^{k}, and GkG^{k}, and using the identity ⟨a−b,Υ​(c−d)⟩=1/2​(‖a−d‖Υ2−‖a−c‖Υ2)+1/2​(‖c−b‖Υ2−‖d−b‖Υ2)\langle a-b,\Upsilon(c-d)\rangle=1/2\left(\|a-d\|^{2}_{\Upsilon}-\|a-c\|^{2}_{\Upsilon}\right)+1/2\left(\|c-b\|^{2}_{\Upsilon}-\|d-b\|^{2}_{\Upsilon}\right), we arrive at

‖w~k−w⋆‖Gk2−‖w~k+1−w⋆‖Gk2+εwk≥2​σfρ​‖x~k+1−x⋆‖2+‖w~k+1−w~k‖Gk2\displaystyle\|\tilde{w}^{k}-w^{\star}\|_{G^{k}}^{2}-\|\tilde{w}^{k+1}-w^{\star}\|_{G^{k}}^{2}+\varepsilon_{w}^{k}\geq\frac{2\sigma_{f}}{\rho}\|\tilde{x}^{k+1}-x^{\star}\|^{2}+\|\tilde{w}^{k+1}-\tilde{w}^{k}\|^{2}_{G^{k}}
+⟨u~k−u~k+1,N​(z~k+1−z~k)⟩−2ρ​⟨∇f2​(x~k+1)−∇f2​(x~k),x~k+1−x⋆⟩.\displaystyle+\langle\tilde{u}^{k}-\tilde{u}^{k+1},N(\tilde{z}^{k+1}-\tilde{z}^{k})\rangle-\frac{2}{\rho}\langle\nabla f_{2}(\tilde{x}^{k+1})-\nabla f_{2}(\tilde{x}^{k}),\tilde{x}^{k+1}-x^{\star}\rangle.

Now, for the term ‖w~k+1−w~k‖Gk2+⟨u~k−u~k+1,N​(z~k+1−z~k)⟩\|\tilde{w}^{k+1}-\tilde{w}^{k}\|^{2}_{G^{k}}+\langle\tilde{u}^{k}-\tilde{u}^{k+1},N(\tilde{z}^{k+1}-\tilde{z}^{k})\rangle, Cauchy-Schwarz implies

‖w~k+1−w~k‖Gk2+⟨u~k−u~k+1,N​(z~k+1−z~k)⟩\displaystyle\|\tilde{w}^{k+1}-\tilde{w}^{k}\|_{G^{k}}^{2}+\langle\tilde{u}^{k}-\tilde{u}^{k+1},N(\tilde{z}^{k+1}-\tilde{z}^{k})\rangle
≥‖w~k+1−w~k‖Gk2−12​‖u~k+1−u~k‖2−12​‖z~k+1−z~k‖NT​N2\displaystyle\geq\|\tilde{w}^{k+1}-\tilde{w}^{k}\|_{G^{k}}^{2}-\frac{1}{2}\|\tilde{u}^{k+1}-\tilde{u}^{k}\|^{2}-\frac{1}{2}\|\tilde{z}^{k+1}-\tilde{z}^{k}\|^{2}_{N^{T}N}
≥‖w~k+1−w~k‖Gk2−12​‖u~k+1−u~k‖2−12​‖z~k+1−z~k‖1/ρ​Ψk+NT​N2\displaystyle\geq\|\tilde{w}^{k+1}-\tilde{w}^{k}\|_{G^{k}}^{2}-\frac{1}{2}\|\tilde{u}^{k+1}-\tilde{u}^{k}\|^{2}-\frac{1}{2}\|\tilde{z}^{k+1}-\tilde{z}^{k}\|^{2}_{1/\rho\Psi^{k}+N^{T}N}
=12​‖w~k+1−w~k‖Gk2.\displaystyle=\frac{1}{2}\|\tilde{w}^{k+1}-\tilde{w}^{k}\|_{G^{k}}^{2}.

Hence we obtain

‖w~k−w⋆‖Gk2−‖w~k+1−w⋆‖Gk2+C​εwk≥2​σfρ​‖x~k+1−x⋆‖2+12​‖w~k+1−w~k‖Gk2\displaystyle\|\tilde{w}^{k}-w^{\star}\|_{G^{k}}^{2}-\|\tilde{w}^{k+1}-w^{\star}\|_{G^{k}}^{2}+C\varepsilon_{w}^{k}\geq\frac{2\sigma_{f}}{\rho}\|\tilde{x}^{k+1}-x^{\star}\|^{2}+\frac{1}{2}\|\tilde{w}^{k+1}-\tilde{w}^{k}\|^{2}_{G^{k}}
−2ρ​⟨∇f2​(x~k+1)−∇f2​(x~k),x~k+1−x⋆⟩,\displaystyle-\frac{2}{\rho}\langle\nabla f_{2}(\tilde{x}^{k+1})-\nabla f_{2}(\tilde{x}^{k}),\tilde{x}^{k+1}-x^{\star}\rangle,

as desired. □\Box ∎

Given the inexact sufficient descent condition (33), the next step in proving linear convergence is to show (33) leads to a contraction relation between Φk+1\Phi^{k+1} and Φk\Phi^{k}.

Lemma 8 (Inexact Contraction Lemma).

Under the assumptions of Theorem 2, there exists constants δ>0\delta>0, and C≥0C\geq 0 such that

(1+δ)​Φk+1≤(1+ζk)​(Φk+C​εwk).(1+\delta)\Phi^{k+1}\leq(1+\zeta^{k})\left(\Phi^{k}+C\varepsilon_{w}^{k}\right). (34)

The proof of Lemma 8, and an explicit expression for δ\delta, appears in Section A.3. As in Theorem 2, the constant δ\delta gives the rate of linear convergence and depends on the conditioning of ff and the constraint matrices MM and NN. The better the conditioning, the faster the convergence, with the opposite holding true as the conditioning worsens. With Lemma 8 in hand, we now prove Theorem 2.

6.3 Proof of Theorem 2

Proof.

By induction on (34), we have

(1+δ)k​Φk\displaystyle(1+\delta)^{k}\Phi^{k} ≤(∏j=1k(1+ζj))​Φ1+C​∑j=1k(∏i=jk(1+ζi))​(1+δ)j−1​εwj\displaystyle\leq\left(\prod^{k}_{j=1}(1+\zeta^{j})\right)\Phi^{1}+C\sum^{k}_{j=1}\left(\prod^{k}_{i=j}(1+\zeta^{i})\right)(1+\delta)^{j-1}\varepsilon^{j}_{w}
≤τζ​Φ1+C​τζ​∑j=1k(1+δ)j−1​εwj≤τζ​Φ1+C​τζ​∑j=1k(1+δ1+q)j−1\displaystyle\leq\tau_{\zeta}\Phi^{1}+C\tau_{\zeta}\sum_{j=1}^{k}(1+\delta)^{j-1}\varepsilon^{j}_{w}\leq\tau_{\zeta}\Phi^{1}+C\tau_{\zeta}\sum_{j=1}^{k}\left(\frac{1+\delta}{1+q}\right)^{j-1}
≤τζ​Φ1+C​τζ1−1+δ1+q=τζ​Φ1+S,\displaystyle\leq\tau_{\zeta}\Phi^{1}+\frac{C\tau_{\zeta}}{1-\frac{1+\delta}{1+q}}=\tau_{\zeta}\Phi^{1}+S,

where the second inequality uses Assumption 8 to reach εwj≤C(1+q)j\varepsilon^{j}_{w}\leq\frac{C}{(1+q)^{j}}, and the third inequality uses q>δq>\delta to bound the sum by the sum of the geometric series. Hence, we have shown the first claim. The second claim follows immediately from the first via a routine calculation. □\Box

7 Applications

This section applies our theory to establish convergence rates for NysADMM and sketch-and-solve ADMM.

7.1 Convergence of NysADMM

Algorithm 3 NysADMM
penalty parameter ρ\rho, step-size η\eta, regularization σ≥0\sigma\geq 0, forcing sequences {εxk}k≥1\{\varepsilon_{x}^{k}\}_{k\geq 1}, {εzk}k≥1\{\varepsilon_{z}^{k}\}_{k\geq 1}
repeat
    Find εxk\varepsilon_{x}^{k}-approximate solution x~k+1\tilde{x}^{k+1} of
(η​Hfk+(ρ+η​σ)​I)​x=η​(Hfk+σ​I)​x~k−∇f​(x~k)+ρ​(z~k−u~k)(\eta H_{f}^{k}+(\rho+\eta\sigma)I)x=\eta(H^{k}_{f}+\sigma I)\tilde{x}^{k}-\nabla f(\tilde{x}^{k})+\rho(\tilde{z}^{k}-\tilde{u}^{k})
    z~k+1​≊εzk​argminz∈Z​{g​(z)+ρ2​‖M​x~k+1−z+u~k‖2}\tilde{z}^{k+1}\overset{\varepsilon_{z}^{k}}{\approxeq}\underset{z\in Z}{\mathop{\rm argmin}}\{g(z)+\frac{\rho}{2}\|M\tilde{x}^{k+1}-z+\tilde{u}^{k}\|^{2}\}
    u~k+1=u~k+M​x~k+1−z~k+1\tilde{u}^{k+1}=\tilde{u}^{k}+M\tilde{x}^{k+1}-\tilde{z}^{k+1}
until convergence
solution (x⋆,z⋆)(x^{\star},z^{\star}) of problem (1)

We begin with the NysADMM scheme from [3]. Recall NysADMM is obtained from Algorithm 2 by setting f1=0,f2=ff_{1}=0,f_{2}=f, using the exact Hessian Θk=Hf​(x~k)=η​(Hfk+σ​I)\Theta^{k}=H_{f}(\tilde{x}^{k})=\eta(H_{f}^{k}+\sigma I), and setting Ψk=0\Psi^{k}=0. Instantiating these selections into Algorithm 2, we obtain NysADMM, presented as Algorithm 3. Compared to the original NysADMM, Algorithm 3 adds a regularization term σ​I\sigma I to the Hessian. In theory, when ff is only convex, this regularization term is required to ensure the condition Θk⪰θmin\Theta^{k}\succeq\theta_{\textup{min}} of Assumption 2, as the Hessian along the optimization path may fail to be uniformly bounded below. The addition of the σ​I\sigma I term removes this issue. However, the need for this term seems to be an artifact of the proof, as Zhao et al. [3] runs Algorithm 3 on non-strongly convex objectives with σ=0\sigma=0, and convergence is still obtained. Similarly, we set σ=0\sigma=0 in all our experiments, and convergence consistent with our theory is obtained. Hence, in practice, we recommend setting σ=0\sigma=0, or some small value, say σ=10−8\sigma=10^{-8}, so that convergence isn’t slowed by unneeded regularization.

The xx-subproblem for NysADMM is a linear system. NysADMM solves this system using the Nyström PCG method from [7]. The general convergence of NysADMM was left open in [3], which established convergence only for quadratic ff. Moreover, the result in [3] does not provide an explicit convergence rate. We shall now rectify this state of affairs using Theorem 1. We obtain the following convergence guarantee by substituting the parameters defining NysADMM (with the added σ​I\sigma I term) into Theorem 1.

Corollary 1 (Convergence of NysADMM).

Instate the assumptions of Theorem 1. Let σ>0\sigma>0. Set f1=0,f2=ff_{1}=0,f_{2}=f, η=L^f\eta=\hat{L}_{f}, Θk=η​(Hfk+σ​I)\Theta^{k}=\eta(H^{k}_{f}+\sigma I), and Ψk=0\Psi^{k}=0 in Algorithm 2. Then

f​(x¯t+1)+g​(z¯t+1)−p⋆≤Γtf(\bar{x}^{t+1})+g(\bar{z}^{t+1})-p^{\star}\leq\frac{\Gamma}{t}

and

‖M​x¯t+1+N​z¯t+1‖≤2t​Γρ+du⋆2.\|M\bar{x}^{t+1}+N\bar{z}^{t+1}\|\leq\frac{2}{t}\sqrt{\frac{\Gamma}{\rho}+d^{2}_{u^{\star}}}.

Here Γ\Gamma and du⋆2d_{u^{\star}}^{2} are the same as in Theorem 1.

NysADMM converges at the same 𝒪​(1/t)\mathcal{O}(1/t)-rate as standard ADMM, despite all the approximations it makes. Thus, NysADMM offers the same level of performance as ADMM, but is much faster due to its use of inexactness. This result is empirically verified in Section 8, where NysADMM converges almost identically to ADMM. Corollary 1 supports the empirical choice of a constant step-size η=1\eta=1, which was shown to have excellent performance uniformly across tasks in [3]: the theorem sets η=L^f\eta=\hat{L}_{f} and L^f=1\hat{L}_{f}=1 for quadratic functions, and satisfies L^f=𝒪​(1)\hat{L}_{f}=\mathcal{O}(1) for loss functions such as the logistic loss. We recommend setting η=1\eta=1 as the default value for GeNI-ADMM. Given NysADMM’s superb empirical performance in [3] and the firm theoretical grounding given by Corollary 1, we conclude that NysADMM provides a reliable framework for solving large-scale machine learning problems.

7.2 Convergence of sketch-and-solve ADMM

Algorithm 4 Sketch-and-solve ADMM
penalty parameter ρ\rho, step-size η\eta, {εzk}k≥1\{\varepsilon_{z}^{k}\}_{k\geq 1}
repeat
    Find solution x~k+1\tilde{x}^{k+1} of
(η​H^k+(ρ+η​γk)​I)​x=η​(H^k+γk​I)​x~k−∇f​(x~k)+ρ​(z~k−u~k)(\eta\hat{H}^{k}+(\rho+\eta\gamma^{k})I)x=\eta\left(\hat{H}^{k}+\gamma^{k}I\right)\tilde{x}^{k}-\nabla f(\tilde{x}^{k})+\rho(\tilde{z}^{k}-\tilde{u}^{k})
    z~k+1​≊εzk​argminz∈Z​{g​(z)+ρ2​‖M​x~k+1−z+u~k‖2}\tilde{z}^{k+1}\overset{\varepsilon_{z}^{k}}{\approxeq}\underset{z\in Z}{\mathop{\rm argmin}}\{g(z)+\frac{\rho}{2}\|M\tilde{x}^{k+1}-z+\tilde{u}^{k}\|^{2}\}
    u~k+1=u~k+M​x~k+1−z~k+1\tilde{u}^{k+1}=\tilde{u}^{k}+M\tilde{x}^{k+1}-\tilde{z}^{k+1}
until convergence
solution (x⋆,z⋆)(x^{\star},z^{\star}) of problem (1)

Sketch-and-solve ADMM is obtained from GeNI-ADMM by setting Θk\Theta^{k} to be an approximate Hessian computed by a sketching procedure. The two most popular sketch-and-solve methods are the Newton sketch [35, 36, 37] and Nyström sketch-and-solve [38, 39, 7]. Both methods use an approximate Hessian that is cheap to compute and yields a linear system that is fast to solve. ADMM together with sketching techniques, provides a compelling means to handle massive problem instances. The recent survey [9] suggests using sketching to solve a quadratic ADMM subproblem for efficiently solving large-scale inverse problems. However, it was previously unknown whether the resulting method would converge. Here, we formally describe the sketch-and-solve ADMM method and prove convergence.

Sketch-and-solve ADMM is obtained from Algorithm 2 by setting

Θk=η​(H^k+γk​I),\Theta^{k}=\eta\left(\hat{H}^{k}+\gamma^{k}I\right), (35)

where H^k\hat{H}^{k} is an approximation to the Hessian Hf​(x~k)H_{f}(\tilde{x}^{k}) at the kkth iteration, and γk≥0\gamma^{k}\geq 0 is a constant chosen to ensure convergence. The term γk​I\gamma^{k}I ensures that the approximate linearization satisfies the Θ\Theta-relative smoothness condition when γk\gamma^{k} is chosen appropriately, as in the following lemma:

Lemma 9.

Suppose ff is L^f\hat{L}_{f}-relatively smooth with respect to its Hessian HfH_{f}. Construct {Θk}k≥1\{\Theta^{k}\}_{k\geq 1} as in (35) and select γk>0\gamma^{k}>0 such that γk≥‖Ek‖=‖Hf​(x~k)−H^k‖\gamma^{k}\geq\|E^{k}\|=\|H_{f}(\tilde{x}^{k})-\hat{H}^{k}\| for every kk. Then

f​(x)≤f​(x~k)+⟨∇f​(x~k),x−x~k⟩+L^f2​‖x−x~k‖Θk2.f(x)\leq f(\tilde{x}^{k})+\langle\nabla f(\tilde{x}^{k}),x-\tilde{x}^{k}\rangle+\frac{\hat{L}_{f}}{2}\|x-\tilde{x}^{k}\|^{2}_{\Theta^{k}}.
Proof.

By L^f\hat{L}_{f} relative smoothness we have,

f​(x)≤f​(x~k)+⟨∇f​(x~k),x−x~k⟩+L^f2​‖x−x~k‖Hf​(x~k)2.f(x)\leq f(\tilde{x}^{k})+\langle\nabla f(\tilde{x}^{k}),x-\tilde{x}^{k}\rangle+\frac{\hat{L}_{f}}{2}\|x-\tilde{x}^{k}\|^{2}_{H_{f}(\tilde{x}^{k})}.

Now,

‖x−x~k‖Hf​(x~k)2\displaystyle\|x-\tilde{x}^{k}\|^{2}_{H_{f}(\tilde{x}^{k})} =‖x−x~k‖H^k2+(x−x~k)T​(Hf​(x~k)−H^k)​(x−x~k)\displaystyle=\|x-\tilde{x}^{k}\|^{2}_{\hat{H}^{k}}+(x-\tilde{x}^{k})^{T}(H_{f}(\tilde{x}^{k})-\hat{H}^{k})(x-\tilde{x}^{k})
≤‖x−x~k‖H^k2+‖Ek‖​‖x−x~k‖2≤‖x−x~k‖H^k2+γk​‖x−x~k‖2\displaystyle\leq\|x-\tilde{x}^{k}\|^{2}_{\hat{H}^{k}}+\|E^{k}\|\|x-\tilde{x}^{k}\|^{2}\leq\|x-\tilde{x}^{k}\|^{2}_{\hat{H}^{k}}+\gamma^{k}\|x-\tilde{x}^{k}\|^{2}
=‖x−x~k‖Θk2.\displaystyle=\|x-\tilde{x}^{k}\|^{2}_{\Theta^{k}}.

The desired claim now immediately follows. □\Box

Lemma 9 shows we can ensure relative smoothness by selecting γk>0\gamma^{k}>0 appropriately. Assuming relative smoothness, we may invoke Theorem 1 to guarantee that sketch-and-solve ADMM converges. Unlike with NysADMM, we find it is necessary to select γk\gamma^{k} carefully (such as in Lemma 9) to ensure the relative smoothness condition holds, otherwise sketch-and-solve ADMM will diverge, see Section 8.3 for numerical demonstration. This condition is somewhat different from those in prior sketching schemes in optimization, such as the Newton Sketch [35, 36], where convergence is guaranteed as long as the Hessian approximation is invertible.

Corollary 2.

Suppose ff is L^f\hat{L}_{f}-relatively smooth with respect to its Hessian HfH_{f} and instate the assumptions of Theorem 1. In Algorithm 2, Set Θk=η​(H^k+γk​I)\Theta^{k}=\eta(\hat{H}^{k}+\gamma^{k}I) with η=L^f\eta=\hat{L}_{f}, γk=‖Ek‖=‖H^k−Hf​(x~k)‖\gamma^{k}=\|E^{k}\|=\|\hat{H}^{k}-H_{f}(\tilde{x}^{k})\|, and Ψk=0\Psi^{k}=0. Then

f(x¯t+1)+g(z¯t+1)−p⋆≤1t(L^f(dx⋆,Hf​(x~1)2+∥E1∥dx⋆2)+ρ2dz⋆2+Cxℰx+Czℰz+Cζℰζ)=:1tΓ^f(\bar{x}^{t+1})+g(\bar{z}^{t+1})-p^{\star}\leq\frac{1}{t}\left(\hat{L}_{f}\left(d^{2}_{x^{\star},H_{f}(\tilde{x}^{1})}+\|E^{1}\|d^{2}_{x^{\star}}\right)+\frac{\rho}{2}d^{2}_{z^{\star}}+C_{x}\mathcal{E}_{x}+C_{z}\mathcal{E}_{z}+C_{\zeta}\mathcal{E}_{\zeta}\right)=:\frac{1}{t}\hat{\Gamma}

and

‖M​x¯t+1−z¯t+1‖≤2t​Γ^ρ+du⋆2.\|M\bar{x}^{t+1}-\bar{z}^{t+1}\|\leq\frac{2}{t}\sqrt{\frac{\hat{\Gamma}}{\rho}+d^{2}_{u^{\star}}}.

Here variables x¯t+1\bar{x}^{t+1} and z¯t+1\bar{z}^{t+1}, diameters dx⋆,Hf​(x~1)2d^{2}_{x^{\star},H_{f}(\tilde{x}^{1})}, dz⋆2d^{2}_{z^{\star}}, and du⋆2d^{2}_{u^{\star}}, and constants CxC_{x}, CzC_{z}, ℰx\mathcal{E}_{x}, ℰz\mathcal{E}_{z}, ℰζ\mathcal{E}_{\zeta}, R⋆R_{\star}, and p⋆p^{\star} are all defined as in Theorem 1.

Remark 2.

It is not hard to see Corollary 2 also holds for any γ>0\gamma>0 if the {Θk}k≥1\{\Theta^{k}\}_{k\geq 1} satisfy

(1−τ)​(Hfk+γ​I)⪯Θk⪯(1+τ)​(Hfk+γ​I),(1-\tau)(H_{f}^{k}+\gamma I)\preceq\Theta^{k}\preceq(1+\tau)(H_{f}^{k}+\gamma I),

for some τ∈(0,1)\tau\in(0,1), and η≥L^f/(1−τ)\eta\geq\hat{L}_{f}/(1-\tau). Many sketching methods can ensure this relative error condition with high probability [40] by choosing the sketch size proportional to the effective dimension of Hf+γ​IH_{f}+\gamma I [7, 36].

Corollary 2 shows sketch-and-solve ADMM obtains an 𝒪​(1/t)\mathcal{O}(1/t)-convergence rate. The main difference between NysADMM and sketch-and-solve is the additional error term due to the use of the approximate Hessian, which results in a slightly slower convergence rate. In this sense, sketch-and-solve ADMM can be regarded as a compromise between NysADMM (Θk=η​(Hf​(x~k)+σ​I)\Theta^{k}=\eta(H_{f}(\tilde{x}^{k})+\sigma I)) and gradient descent ADMM (Θk=η​I\Theta^{k}=\eta I) — with the convergence rate improving as the accuracy of the Hessian approximation increases.

8 Numerical experiments

In this section, we numerically illustrate the convergence results developed in Section 5 and Section 6 for several methods highlighted in Section 3.1.1 that fit into the GeNI-ADMM framework: sketch-and-solve ADMM (Algorithm 4), NysADMM (Algorithm 3), and “gradient descent” ADMM (GD-ADMM) (11). As a baseline, we also compare to exact ADMM (Algorithm 1) to see how various approximations or inexactness impact the convergence rate. We conduct three sets of experiments that verify different aspects of the theory:

  • •

    Section 8.1 verifies that NysADMM, GD-ADMM and sketch-and-solve ADMM converge sublinearly for convex problems. Moreover, we observe a fast transition to linear convergence, after which all methods but GD-ADMM converge quickly to high accuracy.

  • •

    Section 8.2 verifies that NysADMM, GD-ADMM, and sketch-and-solve ADMM converge linearly for strongly convex problems.

  • •

    Section 8.3 verifies that, without the correction term, sketch-and-solve ADMM diverges, showing the necessity of the correction term in Section 7.2.

We consider three common problems in machine learning and statistics in our experiments: lasso [41], elastic net regression [42], and ℓ1\ell_{1}-logistic regression[43]. All experiments use the realsim dataset from LIBSVM [44], accessed through OpenML [45], which has 72,30972,309 samples and 20,95820,958 features. Our experiments use a subsample of realsim, consisting of 10,00010,000 random samples, which ensures the objective is not strongly convex for lasso and ℓ1\ell_{1}-logistic regression.

All methods solve the zz-subproblem exactly, and every method, except NysADMM, solves their xx-subproblem exactly. NysADMM solves the linear system in Algorithm 3 inexactly using Nyström PCG. At each iteration, the following absolute tolerance on the PCG residual is used for determining the termination of Nyström PCG:

εxk=min⁡{rpk−1​rdk−1k1.5,1},\varepsilon^{k}_{x}=\min\left\{\frac{\sqrt{r_{p}^{k-1}r_{d}^{k-1}}}{k^{1.5}},1\right\},

where rpk−1r_{p}^{k-1} and rdk−1r_{d}^{k-1} are the ADMM primal and dual residuals at the previous iteration. We multiply a summable sequence by the geometric mean of the primal and dual residuals at the previous iteration. The geometric mean of the primal and dual residuals is a commonly used tolerance for PCG in practical ADMM implementations such as OSQP [46]—despite this sequence not being apriori summable.

For NysADMM, a sketch size of 5050 is used to construct the Nyström preconditioner, and for sketch-and-solve ADMM, we use a sketch size 500500 to form the Hessian approximation. For sketch-and-solve ADMM, the parameter γk\gamma^{k} in (35) is chosen by estimating the error of the Nyström sketch using power iteration.

We use a bound on the duality gap as the stopping criterion for each algorithm. The details of how the bound on the duality gap bound is computed are presented in Appendix B. All our experiments use a tolerance of ϵ=10−4\epsilon=10^{-4}. An algorithm is terminated when the bound on the duality falls below ϵ\epsilon or has completed 500 iterations.

All experiments are performed in the Julia programming language [47] on a MacBook Pro with a M1 Max processor and 64GB of RAM. To compute the “true” optimal values, we use the commercial solver Mosek [48] (with tolerances set low for high accuracy and presolve turned off to preserve the problem scaling) and the modeling language JuMP [49, 50].

8.1 GeNI-ADMM converges sublinearly and locally linearly on convex problems

To illustrate the global sublinear convergence of GeNI-ADMM methods on convex objectives, we look at the performance of ADMM, NysADMM, GD-ADMM, and sketch-and-solve ADMM on solving a lasso and ℓ1\ell_{1}-logistic regression problem with the realsim dataset. Note, as the number of samples is smaller than the number of features, the corresponding optimization problems are convex but not strongly convex.

Lasso regression
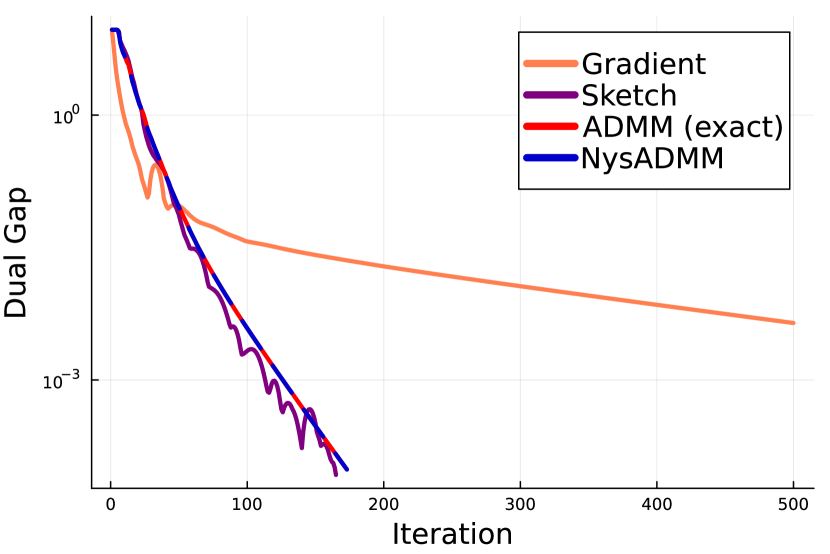
Refer to caption
(a) Primal residual convergence
Refer to caption
(b) Dual residual convergence
Refer to caption
(c) Dual gap convergence
Refer to caption
(d) Objective value convergence
Figure 1: Convergence of lasso regression for NysADMM, sketch-and-solve ADMM, and gradient descent ADMM.

The lasso regression problem is to minimize the ℓ2\ell_{2} error of a linear model with an ℓ1\ell_{1} penalty on the weights:

minimize (1/2)​‖A​x−b‖22+γ​‖x‖1.\displaystyle({1}/{2})\|Ax-b\|_{2}^{2}+\gamma\|x\|_{1}.

This can be easily transformed into the form (1) by taking f​(x)=(1/2)​‖A​x−b‖22f(x)=(1/2)\|Ax-b\|_{2}^{2}, g​(z)=γ​‖z‖1g(z)=\gamma\|z\|_{1}, M=IM=I, N=−IN=-I, and X=Z=ℝnX=Z=\mathbb{R}^{n}. We set γ=0.05⋅γmax\gamma=0.05\cdot\gamma_{\mathrm{max}}, where γmax=‖AT​b‖∞\gamma_{\mathrm{max}}=\|A^{T}b\|_{\infty} is the value above which the all zeros vector is optimal111This can be seen from the optimality conditions, which we state in Appendix B of the appendix.. We stop the algorithm when the gap is less than 10−410^{-4}, or after 500500 iterations.

The results of lasso regression are illustrated in Figure 1. Figure 1 shows all methods initially converge at sublinear rate, but quickly transition to a linear rate of convergence after reaching some manifold containing the solution. ADMM, NysADMM, and sketch-and-solve ADMM (which use curvature information) all converge converge much faster then GD-ADMM, confirming the predictions of Section 5 that methods which use curvature information will converge faster than methods that do not. Moreover, the difference in convergence between NysADMM and ADMM is negligible, despite the former having a much cheaper iteration complexity due to the use of inexact linear system solves.

Logistic Regression
Refer to caption
(a) Primal residual convergence
Refer to caption
(b) Dual residual convergence
Refer to caption
(c) Dual gap convergence
Refer to caption
(d) Objective value convergence
Figure 2: Convergence of logistic regression for NysADMM, sketch-and-solve ADMM, and gradient descent ADMM.

For the logistic regression problem, with data (a~i,b~i)(\tilde{a}_{i},\tilde{b}_{i}), where b~i∈{±1}\tilde{b}_{i}\in\{\pm 1\}. We define

ℙ​(b~i∣a~i)=11+exp⁡(b~i​(a~iT​x))=11+exp⁡(aiT​x),\mathbb{P}\left({\tilde{b}_{i}\mid\tilde{a}_{i}}\right)=\frac{1}{1+\exp\left(\tilde{b}_{i}(\tilde{a}_{i}^{T}x)\right)}=\frac{1}{1+\exp(a_{i}^{T}x)},

where we define ai=b~i​a~ia_{i}=\tilde{b}_{i}\tilde{a}_{i}. The loss is the negative of the log likelihood, −log⁡(∏i=1mℙ​(b~i∣a~i))-\log\left(\prod_{i=1}^{m}\mathbb{P}(\tilde{b}_{i}\mid\tilde{a}_{i})\right). Thus, the optimization problem is

minimize ∑i=1mlog⁡(1+exp⁡(aiT​x))+γ​‖x‖1.\displaystyle\sum_{i=1}^{m}\log\left(1+\exp(a_{i}^{T}x)\right)+\gamma\|x\|_{1}.

We set γ=0.05⋅γmax\gamma=0.05\cdot\gamma_{\mathrm{max}}, where γmax=(1/2)​‖AT​𝟏‖∞\gamma_{\mathrm{max}}=(1/2)\|A^{T}\mathbf{1}\|_{\infty} is the value above which the all zeros vector is optimal. For NysADMM, the preconditioner is re-constructed after every 20 iterations. For sketch-and-solve ADMM, we re-construct the approximate Hessian at every iteration. Since the xx-subproblem is not a quadratic program, we use the L-BFGS [51] implementation from the Optim.jl package [52] to solve the xx-subproblem.

Figure 2 presents the results for logistic regression. The results are consistent with the lasso experiment—all methods initially converge sublinearly before quickly transitioning to linear convergence, and methods using better curvature information, converge faster. In particular, although sketch-and-solve-ADMM converges slightly faster than GD-ADMM, its convergence is much slower than NysADMM, which more accurately captures the curvature due to using the exact Hessian. The convergence of NysADMM and ADMM is essentially identical, despite the former having a much cheaper iteration cost due to approximating the xx-subproblem and using inexact linear system solves.

8.2 GeNI-ADMM converges linearly on strongly convex problems

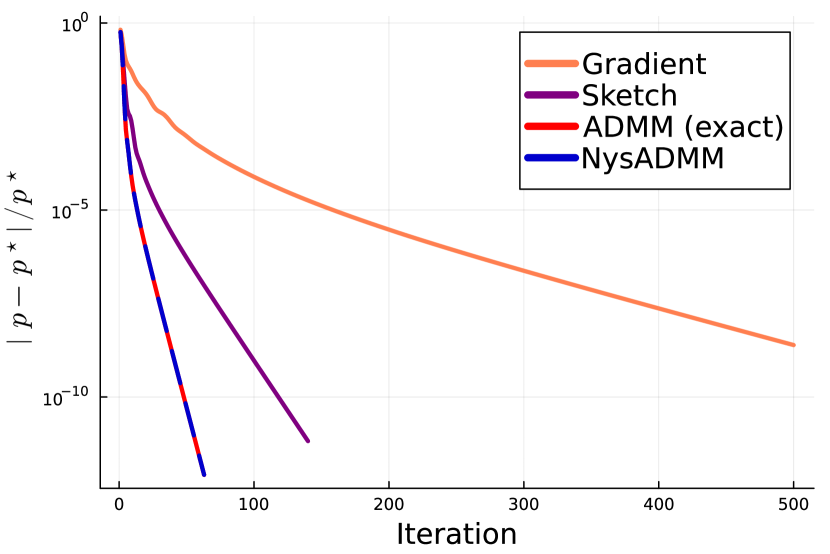
Refer to caption
(a) Primal residual convergence
Refer to caption
(b) Dual residual convergence
Refer to caption
(c) Objective value convergence
Figure 3: Convergence of elastic net regression for NysADMM, sketch-and-solve ADMM, and gradient descent ADMM.

To verify the linear convergence of GeNI-ADMM methods in the presence of strong convexity, we experiment with the elastic net problem:

minimize (1/2)​‖A​x−b‖22+γ​‖x‖1+(μ/2)​‖x‖22.\displaystyle({1}/{2})\|Ax-b\|_{2}^{2}+\gamma\|x\|_{1}+(\mu/2)\|x\|_{2}^{2}.

We set μ=1\mu=1, and use the same problem data and value of γ\gamma as the lasso experiment. The results of the elastic-net experiment are presented in Figure 3. Comparing Figures 1 and 3, we clearly observe the linear convergence guaranteed by the theory in Section 6. Although in Figure 1, ADMM and NysADMM quickly exhibit linear convergence, Figure 3 clearly shows strong convexity leads to an improvement in the number of iterations required to converge. Moreover, we see methods that make better use of curvature information converge faster than methods that do not, consistent with the results of the lasso and logistic regression experiments.

Refer to caption
(a) Lasso regression
Refer to caption
(b) Logistic regression
Figure 4: We show the convergence or lack thereof for sketch-and-solve ADMM with (solid lines) and without (dashed lines) the correction term required by the theoretical results (see section 7.2). When this term is not included, the algorithm does not converge.

8.3 Sketch-and-solve ADMM fails to converge without the correction term

To demonstrate the necessity of the correction term in Section 7.2, we run sketch-and-solve ADMM on lasso and ℓ1\ell_{1}-logistic regression without the correction term. Figure 4 presents the results of these simulations. Without the correction term in (35), sketch-and-solve ADMM quickly diverges on the lasso problem. For the logistic regression problem, it oscillates and fails to converge. These results highlight the importance of selecting this term appropriately as discussed in Section 7.2.

9 Conclusion and future work

In this paper, we have developed a novel framework, GeNI-ADMM, that facilitates efficient theoretical analysis of approximate ADMM schemes and inspires the design of new, practical approximate ADMM methods. GeNI-ADMM generalizes prior approximate ADMM schemes as special cases by allowing various approximations to the xx and zz-subproblems, which can then be solved inexactly. We have established the usual ergodic 𝒪​(1/t)\mathcal{O}(1/t)-convergence rate for GeNI-ADMM under standard hypotheses, and linear convergence under strong convexity. We have shown how to derive explicit rates of convergence for ADMM variants that exploit randomized numerical linear algebra using the GeNI-ADMM framework, We have provided convergence results for NysADMM and sketch-and-solve ADMM as special cases, resolving whether these schemes are globally convergent. Numerical experiments on real-world data generally show an initial sublinear phase followed by linear convergence, validating the theory we developed.

There are several interesting directions for future work. Our analysis shows that in approximate ADMM schemes, a better approximation usually leads to faster convergence. However, a better approximation usually makes {Θk}k≥1\{\Theta^{k}\}_{k\geq 1} more complex and the resulting subproblem harder to solve. A comprehensive study of the trade-off between theoretical convergence speed and subproblem complexity depending on the choice of {Θk}k≥1\{\Theta^{k}\}_{k\geq 1} will be an important future research direction. Our numerical experiments show that GeNI-ADMM can achieve linear convergence locally in the neighborhood of the optimal solution, even for problems that are not strongly convex. Existing studies have proved that exact ADMM exhibits local linear convergence without strong convexity [21]. It would be interesting to establish local linear convergence for GeNI-ADMM schemes without strong convexity, a phenomenon observed in all our experiments (Section 8). Extending GeNI-ADMM to the multiblock setting is another exciting avenue for future work. Such an extension will likely be nuanced, as standard multi-block ADMM can diverge on convex objectives [53]. Our theoretical analysis shows that curvature information provides an advantage in approximate ADMM schemes. This observation can help the design of efficient ADMM-type methods for a broader range of applications, including stochastic and nonconvex optimization.

Appendix A Proofs not appearing in the main paper

A.1 Proofs for Section 4

We begin with the following lemma, which plays a key role in the proof of Lemma 1. For a proof, see Example 1.2.2. in Chapter XI of [26].

Lemma 10 (ε\varepsilon-subdifferential of a quadratic function).

Let h​(z)=⟨b,z⟩+12​‖z‖A2h(z)=\langle b,z\rangle+\frac{1}{2}\|z\|_{A}^{2}, where AA is a symmetric positive definite linear operator. Then

∂εh​(z)\displaystyle\partial_{\varepsilon}h(z) ={b+A​(z+v)|‖v‖A22≤ε}.\displaystyle=\left\{b+A(z+v)\hskip 2.0pt\middle|\hskip 2.0pt\frac{\|v\|_{A}^{2}}{2}\leq\varepsilon\right\}.

With Lemma 10 in hand, we now prove Lemma 1.

Proof of Lemma 1
Proof.

Observe the function defining the zz-subproblem may be decomposed as G​(z)=g​(z)+h​(z)G(z)=g(z)+h(z) with

h​(z)=ρ2​‖M​x~k+1+N​z+u~k‖22+12​‖z−z~k‖Ψk2.h(z)=\frac{\rho}{2}\|M\tilde{x}^{k+1}+Nz+\tilde{u}^{k}\|^{2}_{2}+\frac{1}{2}\|z-\tilde{z}^{k}\|_{\Psi^{k}}^{2}.

Now, by hypothesis z~k+1\tilde{z}^{k+1} gives an εzk\varepsilon_{z}^{k}-minimum of G​(z)G(z). Hence by Proposition 1,

0∈∂εzkG​(z~k+1)​and​∂εzkG​(z~k+1)⊂∂εzkg​(z~k+1)+∂εzkh​(z~k+1).0\in\partial_{\varepsilon_{z}^{k}}G(\tilde{z}^{k+1})~{}\text{and}~{}\partial_{\varepsilon^{k}_{z}}G(\tilde{z}^{k+1})\subset\partial_{\varepsilon^{k}_{z}}g(\tilde{z}^{k+1})+\partial_{\varepsilon^{k}_{z}}h(\tilde{z}^{k+1}).

Thus, we have 0=sg+sh0=s_{g}+s_{h} where s∈∂εzkg​(z~k+1)s\in\partial_{\varepsilon_{z}^{k}}g(\tilde{z}^{k+1}) and sh∈∂εzkh​(z~k+1)s_{h}\in\partial_{\varepsilon_{z}^{k}}h(\tilde{z}^{k+1}). Applying Lemma 10, with A=Ψk+ρ​NT​NA=\Psi^{k}+\rho N^{T}N and b=ρ​NT​(M​x~k+1+u~k)−Ψk​z~kb=\rho N^{T}(M\tilde{x}^{k+1}+\tilde{u}^{k})-\Psi^{k}\tilde{z}^{k}, we reach

sh=ρ​NT​(M​x~k+1+N​z~k+1+u~k)+Ψk​(z~k+1−z~k)+v.s_{h}=\rho N^{T}(M\tilde{x}^{k+1}+N\tilde{z}^{k+1}+\tilde{u}^{k})+\Psi^{k}(\tilde{z}^{k+1}-\tilde{z}^{k})+v.

The desired claim now immediately follows from using s=−shs=-s_{h}. □\Box

A.2 Proofs for Section 5

Proof of Proposition 2
Proof.

Using the eigendecomposition, we may decompose HfH_{f} as

Hf=λ1​(Hf)​𝐯𝐯T+∑i=2dλi​(Hf)​𝐯i​𝐯iT.H_{f}=\lambda_{1}(H_{f})\mathbf{v}\mathbf{v}^{T}+\sum^{d}_{i=2}\lambda_{i}(H_{f})\mathbf{v}_{i}\mathbf{v}^{T}_{i}.

So

‖x⋆‖Hf2\displaystyle\|x^{\star}\|^{2}_{H_{f}} =λ1​(Hf)​⟨𝐯,x⋆⟩2+∑i=2dλi​(Hf)​⟨𝐯i,x⋆⟩2\displaystyle=\lambda_{1}(H_{f})\langle\mathbf{v},x^{\star}\rangle^{2}+\sum^{d}_{i=2}\lambda_{i}(H_{f})\langle\mathbf{v}_{i},x_{\star}\rangle^{2}
≤λ1​(Hf)​μ𝐯​‖x⋆‖2+λ2​(Hf)​∑i=2d⟨𝐯i,x⋆⟩2\displaystyle\leq\lambda_{1}(H_{f})\mu_{\mathbf{v}}\|x^{\star}\|^{2}+\lambda_{2}(H_{f})\sum^{d}_{i=2}\langle\mathbf{v}_{i},x^{\star}\rangle^{2}
≤(μ𝐯+λ2​(Hf)λ1​(Hf))​λ1​(Hf)​‖x⋆‖2.\displaystyle\leq\left(\mu_{\mathbf{v}}+\frac{\lambda_{2}(H_{f})}{\lambda_{1}(H_{f})}\right)\lambda_{1}(H_{f})\|x^{\star}\|^{2}.

Recalling that σ=τ​λ1​(Hf)\sigma=\tau\lambda_{1}(H_{f}) with τ∈(0,1)\tau\in(0,1), we may put everything together to conclude

(λ1​(Hf)−σ)​‖x⋆‖2‖x⋆‖Hf2≥(1−τ)​λ1​(Hf)​‖x⋆‖2‖x⋆‖Hf2≥(1−τ)​(μ𝐯+λ2​(Hf)λ1​(Hf))−1,\displaystyle\frac{(\lambda_{1}(H_{f})-\sigma)\|x^{\star}\|^{2}}{\|x^{\star}\|^{2}_{H_{f}}}\geq(1-\tau)\frac{\lambda_{1}(H_{f})\|x^{\star}\|^{2}}{\|x^{\star}\|^{2}_{H_{f}}}\geq(1-\tau)\left(\mu_{\mathbf{v}}+\frac{\lambda_{2}(H_{f})}{\lambda_{1}(H_{f})}\right)^{-1},

proving the first claim. The second claim follows immediately from the first. □\Box

Proof of Lemma 2
Proof.

By definition of ℓU​(v,w)\ell_{U}(v,w)

ℓU​(v,w)=f​(x)+g​(z)−p⋆+supu^∈U⟨ρ​u^,v−(M​x+N​z)⟩.\ell_{U}(v,w)=f(x)+g(z)-p^{\star}+\sup_{\hat{u}\in U}\langle\rho\hat{u},v-(Mx+Nz)\rangle. (36)

Hence if v=M​x+N​zv=Mx+Nz and ℓU​(v,w)≤ϵ\ell_{U}(v,w)\leq\epsilon, (36) yields

f​(x)+g​(z)−p⋆≤ϵ.f(x)+g(z)-p^{\star}\leq\epsilon.

Thus, we obtain the first statement.

Now, suppose ℓU​(v,w)≤ϵ\ell_{U}(v,w)\leq\epsilon, ‖v‖≤δ\|v\|\leq\delta and U=𝒵U=\mathcal{Z}. Then, combining these hypotheses with (36) and using p⋆p^{\star} that is the optimum, we reach

supu^∈𝒵⟨ρ​u^,v−(M​x+N​z)⟩≤ϵ.\sup_{\hat{u}\in\mathcal{Z}}\langle\rho\hat{u},v-(Mx+Nz)\rangle\leq\epsilon.

Observe if v≠M​x+N​zv\neq Mx+Nz then supu^∈𝒵⟨ρ​u^,v−(M​x+N​z)⟩=∞\sup_{\hat{u}\in\mathcal{Z}}\langle\rho\hat{u},v-(Mx+Nz)\rangle=\infty, contradicting the preceding inequality. Thus v=M​x+N​zv=Mx+Nz, which yields the second statement, and completes the proof. □\Box

Proof of Proposition 3
Lemma 11 (Exact Gap function 1-step bound ).

Let wk+1=(xk+1,zk+1,uk+1)w^{k+1}=(x^{k+1},z^{k+1},u^{k+1}) denote the iterates generated by Algorithm 2 at iteration k+1k+1, when we solve the subproblems exactly. Then, the following inequality holds

Q​(w,wk+1)\displaystyle Q(w,w^{k+1}) ≤12​(‖z−x~k‖Θk2−‖x−xk+1‖Θk2)+12​(‖z−z~k‖Ψk2−‖z−zk+1‖Ψk2)\displaystyle\leq\frac{1}{2}\left(\|z-\tilde{x}^{k}\|^{2}_{\Theta^{k}}-\|x-x^{k+1}\|^{2}_{\Theta^{k}}\right)+\frac{1}{2}\left(\|z-\tilde{z}^{k}\|^{2}_{\Psi^{k}}-\|z-z^{k+1}\|^{2}_{\Psi^{k}}\right)
ρ2​(‖z~k−M​x‖2−‖zk+1−M​x‖2)+ρ2​(‖u~k−u‖2−‖uk+1−u‖2).\displaystyle\frac{\rho}{2}\left(\|\tilde{z}^{k}-Mx\|^{2}-\|z^{k+1}-Mx\|^{2}\right)+\frac{\rho}{2}\left(\|\tilde{u}^{k}-u\|^{2}-\|u^{k+1}-u\|^{2}\right).
Proof.

The argument is identical to the proof of Lemma 5. Indeed, the only difference is εxk=εzk=0\varepsilon_{x}^{k}=\varepsilon_{z}^{k}=0, as the subproblems are solved exactly. So the same line of argumentation may be applied, except the exact subroblem optimality conditions are used. □\Box

We now prove Proposition 3.

Proof.

First, observe that item 2. is an immediate consequence of item 1, so it suffices to show item 1. To this end, plugging in w=w⋆w=w^{\star}, using Q​(w⋆,wk+1)≥0Q(w^{\star},w^{k+1})\geq 0, and rearranging, we reach

‖xk+1−x⋆‖Θk2+‖zk+1−z⋆‖Ψk+ρ​NT​N2+ρ​‖uk+1−u⋆‖2\displaystyle\|x^{k+1}-x^{\star}\|^{2}_{\Theta^{k}}+\|z^{k+1}-z^{\star}\|_{\Psi^{k}+\rho N^{T}N}^{2}+\rho\|u^{k+1}-u^{\star}\|^{2}
≤‖x~k−x⋆‖Θk2+‖z~k−z⋆‖Ψk+ρ​NT​N2+ρ​‖u~k−u⋆‖2.\displaystyle\leq\|\tilde{x}^{k}-x^{\star}\|^{2}_{\Theta^{k}}+\|\tilde{z}^{k}-z^{\star}\|_{\Psi^{k}+\rho N^{T}N}^{2}+\rho\|\tilde{u}^{k}-u^{\star}\|^{2}.

Defining the norm ‖w‖W,k=‖x‖Θk2+‖z‖Ψk+ρ​NT​N2+ρ​‖u‖2\|w\|_{W,k}=\sqrt{\|x\|^{2}_{\Theta^{k}}+\|z\|^{2}_{\Psi^{k}+\rho N^{T}N}+\rho\|u\|^{2}}, the preceding inequality may be rewritten as

‖wk+1−w⋆‖W,k≤‖w~k−w⋆‖W,k.\|w^{k+1}-w^{\star}\|_{W,k}\leq\|\tilde{w}^{k}-w^{\star}\|_{W,k}.

Now, our inexactness hypothesis (Assumption 3) along with ν\nu-strong convexity of the zz-subproblem (which follows by Assumption 2) implies

‖x~k+1−xk+1‖≤εxk,‖z~k+1−zk+1‖≤εzkν.\|\tilde{x}^{k+1}-x^{k+1}\|\leq\varepsilon_{x}^{k},\quad\|\tilde{z}^{k+1}-z^{k+1}\|\leq\sqrt{\frac{\varepsilon_{z}^{k}}{\nu}}.

Using u~k+1=M​x~k+1+N​z~k+1+u~k\tilde{u}^{k+1}=M\tilde{x}^{k+1}+N\tilde{z}^{k+1}+\tilde{u}^{k} and uk+1=M​xk+1+N​zk+1+u~ku^{k+1}=Mx^{k+1}+Nz^{k+1}+\tilde{u}^{k}, we find

ρ​‖u~k+1−uk+1‖≤εxk+C​εzk.\rho\|\tilde{u}^{k+1}-u^{k+1}\|\leq\varepsilon_{x}^{k}+C\sqrt{\varepsilon_{z}^{k}}.

Hence we have,

‖w~k+1−w⋆‖W,k≤‖wk+1−w⋆‖W,k+‖w~k+1−wk+1‖W,k≤‖w~k−w⋆‖W,k+C​(εxk+εzk).\|\tilde{w}^{k+1}-w^{\star}\|_{W,k}\leq\|w^{k+1}-w^{\star}\|_{W,k}+\|\tilde{w}^{k+1}-w^{k+1}\|_{W,k}\leq\|\tilde{w}^{k}-w^{\star}\|_{W,k}+C\left(\varepsilon_{x}^{k}+\sqrt{\varepsilon_{z}^{k}}\right).

Defining the summable sequence εwk=C​(εxk+εzk)\varepsilon_{w}^{k}=C(\varepsilon_{x}^{k}+\sqrt{\varepsilon_{z}^{k}}), the preceding display may be written as

‖w~k+1−w⋆‖W,k≤‖w~k−w⋆‖W,k+εwk​(△),\|\tilde{w}^{k+1}-w^{\star}\|_{W,k}\leq\|\tilde{w}^{k}-w^{\star}\|_{W,k}+\varepsilon_{w}^{k}\quad(\triangle),

Now, Assumption 4 implies that ‖w~k−w⋆‖W,k≤1+ζk​‖w~k−w⋆‖W,k−1\|\tilde{w}^{k}-w^{\star}\|_{W,k}\leq\sqrt{1+\zeta^{k}}\|\tilde{w}^{k}-w^{\star}\|_{W,k-1}. Combining this inequality with induction on (△)(\triangle), we find

‖w~k+1−w⋆‖W,k≤(∏j=2k1+ζj)​‖w~1−w⋆‖W,1+(∏j=2k1+ζj)​∑j=1kεwj.\|\tilde{w}^{k+1}-w^{\star}\|_{W,k}\leq\left(\prod^{k}_{j=2}\sqrt{1+\zeta^{j}}\right)\|\tilde{w}^{1}-w^{\star}\|_{W,1}+\left(\prod^{k}_{j=2}\sqrt{1+\zeta^{j}}\right)\sum_{j=1}^{k}\varepsilon_{w}^{j}.

Hence,

min⁡{θmin,ν}​‖w~k+1−w⋆‖≤‖w~k+1−w⋆‖W,k≤τζ​(‖w~1−w⋆‖W,1+ℰw).\sqrt{\min\{\theta_{\textup{min}},\nu\}}\|\tilde{w}^{k+1}-w^{\star}\|\leq\|\tilde{w}^{k+1}-w^{\star}\|_{W,k}\leq\sqrt{\tau_{\zeta}}\left(\|\tilde{w}^{1}-w^{\star}\|_{W,1}+\mathcal{E}_{w}\right).

It follows immediately that:

supk≥1‖w~k+1−w⋆‖≤max⁡{τζ​(‖w~1−w⋆‖W,1+ℰw)min⁡{θmin,ν},‖w~0−w⋆‖}<∞,\sup_{k\geq 1}\|\tilde{w}^{k+1}-w^{\star}\|\leq\max\left\{\frac{\sqrt{\tau_{\zeta}}\left(\|\tilde{w}^{1}-w^{\star}\|_{W,1}+\mathcal{E}_{w}\right)}{\sqrt{\min\{\theta_{\textup{min}},\nu\}}},\|\tilde{w}^{0}-w^{\star}\|\right\}<\infty,

and so the sequence {w~k}k≥0\{\tilde{w}^{k}\}_{k\geq 0} is bounded, which in turn implies {x~k}k≥0,{z~k}k≥0,\{\tilde{x}^{k}\}_{k\geq 0},\{\tilde{z}^{k}\}_{k\geq 0}, and {u~k}k≥0\{\tilde{u}^{k}\}_{k\geq 0} are bounded. □\Box

Proof of Lemma 3
Proof.

Throughout the proof, we shall denote by Sxk​(x)S_{x}^{k}(x), the function defining the xx-subproblem at iteration kk. The exact solution of the xx-subproblem shall be denoted by xk+1x^{k+1}. To begin, observe that:

∇Sxk​(x)=∇f1​(x)+∇f2​(x~k)+(Θk+ρ​MT​M)​(x−x~k)+ρ​MT​(M​x~k+N​z~k+u~k).\nabla S^{k}_{x}(x)=\nabla f_{1}(x)+\nabla f_{2}(\tilde{x}^{k})+(\Theta^{k}+\rho M^{T}M)(x-\tilde{x}^{k})+\rho M^{T}(M\tilde{x}^{k}+N\tilde{z}^{k}+\tilde{u}^{k}).

Now,

⟨∇Sxk​(x~k+1),x⋆−x~k+1⟩\displaystyle\langle\nabla S^{k}_{x}(\tilde{x}^{k+1}),x^{\star}-\tilde{x}^{k+1}\rangle =⟨∇Sxk​(x~k+1)−∇Sxk​(xk+1)+∇Sxk​(xk+1),x⋆−xk+1+xk+1−x~k+1⟩\displaystyle=\langle\nabla S^{k}_{x}(\tilde{x}^{k+1})-\nabla S^{k}_{x}(x^{k+1})+\nabla S^{k}_{x}(x^{k+1}),x^{\star}-x^{k+1}+x^{k+1}-\tilde{x}^{k+1}\rangle
=⟨∇Sxk​(x~k+1)−∇Sxk​(xk+1),x⋆−xk+1⟩\displaystyle=\langle\nabla S^{k}_{x}(\tilde{x}^{k+1})-\nabla S^{k}_{x}(x^{k+1}),x^{\star}-x^{k+1}\rangle
+⟨∇Sxk​(x~k+1)−∇Sxk​(xk+1),xk+1−x~k+1⟩\displaystyle+\langle\nabla S^{k}_{x}(\tilde{x}^{k+1})-\nabla S^{k}_{x}(x^{k+1}),x^{k+1}-\tilde{x}^{k+1}\rangle
+⟨∇Sxk​(xk+1),x⋆−xk+1⟩+⟨∇Sxk​(xk+1),xk+1−x~k+1⟩\displaystyle+\langle\nabla S^{k}_{x}(x^{k+1}),x^{\star}-x^{k+1}\rangle+\langle\nabla S^{k}_{x}(x^{k+1}),x^{k+1}-\tilde{x}^{k+1}\rangle
≥(1)​⟨∇f1​(x~k+1)−∇f1​(xk+1),x⋆−x~k+1⟩+⟨x~k+1−xk+1,x⋆−xk+1⟩Θk+ρ​MT​M\displaystyle\overset{(1)}{\geq}\langle\nabla f_{1}(\tilde{x}^{k+1})-\nabla f_{1}(x^{k+1}),x^{\star}-\tilde{x}^{k+1}\rangle+\langle\tilde{x}^{k+1}-x^{k+1},x^{\star}-x^{k+1}\rangle_{\Theta^{k}+\rho M^{T}M}
+⟨∇f1​(x~k+1)−∇f1​(xk+1),x~k+1−xk+1⟩+⟨x~k+1−xk+1,x~k+1−xk+1⟩Θk+ρ​MT​M\displaystyle+\langle\nabla f_{1}(\tilde{x}^{k+1})-\nabla f_{1}(x^{k+1}),\tilde{x}^{k+1}-x^{k+1}\rangle+\langle\tilde{x}^{k+1}-x^{k+1},\tilde{x}^{k+1}-x^{k+1}\rangle_{\Theta^{k}+\rho M^{T}M}
+⟨∇Sxk​(xk+1),xk+1−x~k+1⟩\displaystyle+\langle\nabla S^{k}_{x}(x^{k+1}),x^{k+1}-\tilde{x}^{k+1}\rangle
≥(2)−C1​εxk−C2​(εxk)2+⟨∇Sxk​(xk+1),xk+1−x~k+1⟩.\displaystyle\overset{(2)}{\geq}-C_{1}\varepsilon_{x}^{k}-C_{2}(\varepsilon^{k}_{x})^{2}+\langle\nabla S^{k}_{x}(x^{k+1}),x^{k+1}-\tilde{x}^{k+1}\rangle.

Here (1)(1) uses ∇Sxk​(x)−∇Sxk​(y)=∇f1​(x)−∇f1​(y)+(Θk+ρ​MT​M)​(x−y)\nabla S_{x}^{k}(x)-\nabla S_{x}^{k}(y)=\nabla f_{1}(x)-\nabla f_{1}(y)+(\Theta^{k}+\rho M^{T}M)(x-y), and that xk+1x^{k+1} is the exact solution of the xx-subproblem, while (2)(2) uses that x~k+1\tilde{x}^{k+1} is an εxk\varepsilon_{x}^{k} minimizer of the xx-subproblem and that f1f_{1} has a Lipschitz gradient. Now, as the iterates all belong to a compact set, it follows that supk‖∇Sxk​(xk+1)‖≤C3\sup_{k}\|\nabla S^{k}_{x}(x^{k+1})\|\leq C_{3}. So,

⟨∇Sxk​(x~k+1),x⋆−x~k+1⟩≥−C1​εxk−(εxk)2−C3​εxk≥−Cx​εxk.\displaystyle\langle\nabla S^{k}_{x}(\tilde{x}^{k+1}),x^{\star}-\tilde{x}^{k+1}\rangle\geq-C_{1}\varepsilon_{x}^{k}-(\varepsilon^{k}_{x})^{2}-C_{3}\varepsilon_{x}^{k}\geq-C_{x}\varepsilon_{x}^{k}.

This establishes the first inequality, and the second inequality follows from the first by plugging x~k+1\tilde{x}^{k+1} into the expression for ∇Sxk​(x)\nabla S_{x}^{k}(x). □\Box

Proof of Lemma 4
Proof.

Proof. By hypothesis, z~k+1\tilde{z}^{k+1} is an εzk\varepsilon_{z}^{k}-approximate minimizer of the zz-subproblem, so Lemma 1 shows there exists a vector s~\tilde{s} with ‖s~‖≤C​εzk\|\tilde{s}\|\leq C\sqrt{\varepsilon_{z}^{k}}, such that

g​(z⋆)−g​(z~k+1)≥ρ​⟨u~k+1+Ψk​(z~k−z~k+1)+s~,z⋆−z~k+1⟩−εzk.g(z^{\star})-g(\tilde{z}^{k+1})\geq\rho\langle\tilde{u}^{k+1}+\Psi^{k}(\tilde{z}^{k}-\tilde{z}^{k+1})+\tilde{s},z^{\star}-\tilde{z}^{k+1}\rangle-\varepsilon_{z}^{k}.

Rearranging, using Cauchy-Schwarz, along with the boundedness of the iterates, the preceding display becomes

g​(z⋆)−g​(z~k+1)−ρ​⟨u~k+1+Ψk​(z~k−z~k+1),z⋆−z~k+1⟩≥−C​εzk−εzk≥−Cz​εzk,g(z^{\star})-g(\tilde{z}^{k+1})-\rho\langle\tilde{u}^{k+1}+\Psi^{k}(\tilde{z}^{k}-\tilde{z}^{k+1}),z^{\star}-\tilde{z}^{k+1}\rangle\geq-C\sqrt{\varepsilon_{z}^{k}}-\varepsilon_{z}^{k}\geq-C_{z}\sqrt{\varepsilon_{z}^{k}},

where the last display uses εzk≤Kεz\varepsilon_{z}^{k}\leq K_{\varepsilon_{z}}, and absorbs constant terms to get the constant CzC_{z}. □\Box

A.3 Proofs for Section 6

Proof of Lemma 6
Proof.
  1. 1.

    We begin by observing that strong convexity of ff implies

    ⟨∇f​(x~k+1)−∇f​(x⋆),x~k+1−x⋆⟩≥σf​‖x~k+1−x⋆‖2.\displaystyle\langle\nabla f(\tilde{x}^{k+1})-\nabla f(x^{\star}),\tilde{x}^{k+1}-x^{\star}\rangle\geq\sigma_{f}\|\tilde{x}^{k+1}-x^{\star}\|^{2}.

    Decomposing ff as f=f1+f2f=f_{1}+f_{2}, the preceding display may be rewritten as

    ⟨∇f1​(x~k+1)+∇f2​(x~k)−∇f​(x⋆),x~k+1−x⋆⟩+⟨∇f2​(x~k+1)−∇f2​(x~k),x~k+1−x⋆⟩\displaystyle\langle\nabla f_{1}(\tilde{x}^{k+1})+\nabla f_{2}(\tilde{x}^{k})-\nabla f(x^{\star}),\tilde{x}^{k+1}-x^{\star}\rangle+\langle\nabla f_{2}(\tilde{x}^{k+1})-\nabla f_{2}(\tilde{x}^{k}),\tilde{x}^{k+1}-x^{\star}\rangle
    ≥σf​‖x~k+1−x⋆‖2.\displaystyle\geq\sigma_{f}\|\tilde{x}^{k+1}-x^{\star}\|^{2}.

    Now, the exact solution xk+1x^{k+1} of the xx-subproblem at iteration kk satisfies ∇Sxk​(xk+1)=0\nabla S_{x}^{k}(x^{k+1})=0. Moreover, x~k+1\tilde{x}^{k+1} is an εxk\varepsilon_{x}^{k} minimizer of the xx-subproblem, and ∇Sxk​(x)\nabla S_{x}^{k}(x) is Lipschitz continuous. Combining these three properties, it follows there exists a vector Err∇k\textrm{Err}^{k}_{\nabla} satisfying:

    ∇Sxk​(x~k+1)=∇Sxk​(xk+1)+Err∇k=Err∇k,where​‖Err∇k‖≤C​εxk.\nabla S^{k}_{x}(\tilde{x}^{k+1})=\nabla S_{x}^{k}(x^{k+1})+\textrm{Err}^{k}_{\nabla}=\textrm{Err}^{k}_{\nabla},\quad\text{where}~{}\|\textrm{Err}^{k}_{\nabla}\|\leq C\varepsilon_{x}^{k}.

    Consequently, we have

    ∇f1​(x~k+1)+∇f2​(x~k)=Θk​(x~k−x~k+1)+ρ​MT​N​(z~k+1−z~k)−ρ​MT​u~k+1+Err∇k.\nabla f_{1}(\tilde{x}^{k+1})+\nabla f_{2}(\tilde{x}^{k})=\Theta^{k}(\tilde{x}^{k}-\tilde{x}^{k+1})+\rho M^{T}N(\tilde{z}^{k+1}-\tilde{z}^{k})-\rho M^{T}\tilde{u}^{k+1}+\textrm{Err}^{k}_{\nabla}.

    Utilizing the preceding relation, along with the fact that the iterates are bounded, we reach

    ⟨x~k−x~k+1,x~k+1−x⋆⟩Θk+ρ​⟨N​(z~k+1−z~k)+u⋆−u~k+1,M​(x~k+1−x⋆)⟩+C​εxk\displaystyle\langle\tilde{x}^{k}-\tilde{x}^{k+1},\tilde{x}^{k+1}-x^{\star}\rangle_{\Theta^{k}}+\rho\langle N(\tilde{z}^{k+1}-\tilde{z}^{k})+u^{\star}-\tilde{u}^{k+1},M(\tilde{x}^{k+1}-x^{\star})\rangle+C\varepsilon_{x}^{k}
    ≥σf​‖x~k+1−x⋆‖2−⟨∇f2​(x~k+1)−∇f2​(x~k),x~k+1−x⋆⟩.□\displaystyle\geq\sigma_{f}\|\tilde{x}^{k+1}-x^{\star}\|^{2}-\langle\nabla f_{2}(\tilde{x}^{k+1})-\nabla f_{2}(\tilde{x}^{k}),\tilde{x}^{k+1}-x^{\star}\rangle.~{}\Box
  2. 2.

    As −ρ​NT​u⋆∈∂g​(z⋆)-\rho N^{T}u^{\star}\in\partial g(z^{\star}), and −ρ​NT​u~k+1+Ψk​(z~k−z~k+1)+s~∈∂εzkg​(z~k+1)-\rho N^{T}\tilde{u}^{k+1}+\Psi^{k}(\tilde{z}^{k}-\tilde{z}^{k+1})+\tilde{s}\in\partial_{\varepsilon_{z}^{k}}g(\tilde{z}^{k+1}), we have

    g​(z~k+1)−g​(z⋆)≥⟨−ρ​NT​u⋆,z~k+1−z⋆⟩,\displaystyle g(\tilde{z}^{k+1})-g(z^{\star})\geq\langle-\rho N^{T}u^{\star},\tilde{z}^{k+1}-z^{\star}\rangle,
    g​(z⋆)−g​(z~k+1)≥⟨−ρ​NT​u~k+1+Ψk​(z~k−z~k+1),z⋆−z~k+1⟩−εzk.\displaystyle g(z^{\star})-g(\tilde{z}^{k+1})\geq\langle-\rho N^{T}\tilde{u}^{k+1}+\Psi^{k}(\tilde{z}^{k}-\tilde{z}^{k+1}),z^{\star}-\tilde{z}^{k+1}\rangle-\varepsilon_{z}^{k}.

    So, adding together the two inequalities and rearranging, we reach

    ⟨z~k+1−z⋆,ρ​NT​(u⋆−u~k+1)+Ψk​(z~k−z~k+1)+s~⟩≥−εzk.\langle\tilde{z}^{k+1}-z^{\star},\rho N^{T}(u^{\star}-\tilde{u}^{k+1})+\Psi^{k}(\tilde{z}^{k}-\tilde{z}^{k+1})+\tilde{s}\rangle\geq-\varepsilon_{z}^{k}.

    Now using boundedness of the iterates and ‖s~‖≤C​εzk\|\tilde{s}\|\leq C\sqrt{\varepsilon_{z}^{k}}, Cauchy-Schwarz yields

    ⟨z~k+1−z⋆,ρ​NT​(u~k+1−u⋆)+Ψk​(z~k−z~k+1)⟩≥−C​εzk.\langle\tilde{z}^{k+1}-z^{\star},\rho N^{T}(\tilde{u}^{k+1}-u^{\star})+\Psi^{k}(\tilde{z}^{k}-\tilde{z}^{k+1})\rangle\geq-C\sqrt{\varepsilon_{z}^{k}}.

    □\Box

Proof of Lemma 8

We wish to show for some δ>0\delta>0, that the following inequality holds

‖wk−w⋆‖Gk2−‖wk+1−w⋆‖Gk2+εwk≥δ​‖wk+1−w⋆‖Gk2.\|w^{k}-w^{\star}\|_{G^{k}}^{2}-\|w^{k+1}-w^{\star}\|_{G^{k}}^{2}+\varepsilon_{w}^{k}\geq\delta\|w^{k+1}-w^{\star}\|_{G^{k}}^{2}.

To establish this result, it suffices to show the inequality

‖wk+1−wk‖Gk2+2​σfρ​‖xk+1−x⋆‖2−2ρ​⟨∇f2​(xk+1)−∇f2​(xk),xk+1−x⋆⟩≥δ​‖wk+1−w⋆‖Gk2.\|w^{k+1}-w^{k}\|^{2}_{G^{k}}+\frac{2\sigma_{f}}{\rho}\|x^{k+1}-x^{\star}\|^{2}-\frac{2}{\rho}\langle\nabla f_{2}(x^{k+1})-\nabla f_{2}(x^{k}),x^{k+1}-x^{\star}\rangle\geq\delta\|w^{k+1}-w_{\star}\|_{G^{k}}^{2}.

We accomplish this by upper bounding each term that appears in ‖wk+1−w⋆‖Gk2\|w^{k+1}-w_{\star}\|_{G^{k}}^{2}, by terms that appear in the left-hand side of the preceding equality. To that end, we have the following result.

Lemma 12 (Coupling Lemma).

Under the assumptions of Theorem 2, the following statements hold:

  1. 1.

    Let μ1≥2\mu_{1}\geq 2, c1=12​Lf2ρ2​λmin​(M​MT),c2=4​(2​Lf2+θmax2)ρ2​λmin​(M​MT),c3=8​‖M‖2c_{1}=\frac{12L^{2}_{f}}{\rho^{2}\lambda_{\textup{min}}(MM^{T})},c_{2}=\frac{4\left(2L^{2}_{f}+\theta_{\textup{max}}^{2}\right)}{\rho^{2}\lambda_{\textup{min}}(MM^{T})},c_{3}=8\|M\|^{2}. Then for some constant C≥0C\geq 0, we have

    ‖uk+1−u⋆‖2≤c1​‖x~k+1−x⋆‖2+c2​‖x~k−x~k+1‖2+c3​‖z~k−z~k+1‖1/ρ​Ψk+NT​N2+C​εwk.\|u^{k+1}-u^{\star}\|^{2}\leq c_{1}\|\tilde{x}^{k+1}-x^{\star}\|^{2}+c_{2}\|\tilde{x}^{k}-\tilde{x}^{k+1}\|^{2}+c_{3}\|\tilde{z}^{k}-\tilde{z}^{k+1}\|_{1/\rho\Psi^{k}+N^{T}N}^{2}+C\varepsilon_{w}^{k}.
  2. 2.

    There exists constants c4=2​(‖N‖2+ψmax/ρσmin2​(N))​‖M‖2c_{4}=2\left(\frac{\|N\|^{2}+\psi_{\textup{max}}/\rho}{\sigma^{2}_{\textrm{min}}(N)}\right)\|M\|^{2}, c5=c4/‖M‖2c_{5}=c_{4}/\|M\|^{2}, such that

    ‖zk+1−z⋆‖1/ρ​Ψk+NT​N2≤c4​‖xk+1−x⋆‖2+c5​‖uk+1−uk‖2.\|z^{k+1}-z^{\star}\|_{1/\rho\Psi^{k}+N^{T}N}^{2}\leq c_{4}\|x^{k+1}-x^{\star}\|^{2}+c_{5}\|u^{k+1}-u^{k}\|^{2}.
  3. 3.

    For all μ>0\mu>0, we have

    ⟨∇f2​(xk+1)−∇f2​(xk),xk+1−x⋆⟩≤μ/2​‖xk+1−x⋆‖2+Lf22​μ​‖xk+1−xk‖2.\displaystyle\langle\nabla f_{2}(x^{k+1})-\nabla f_{2}(x^{k}),x^{k+1}-x^{\star}\rangle\leq\mu/2\|x^{k+1}-x^{\star}\|^{2}+\frac{L^{2}_{f}}{2\mu}\|x^{k+1}-x^{k}\|^{2}.

Taking Lemma 12 as given, let us prove Lemma 8.

Proof.

Observe Lemma 12 implies

12​‖wk+1−wk‖Gk2+2​σfρ​‖xk+1−x⋆‖2−2ρ​⟨∇f2​(xk+1)−∇f2​(xk),xk+1−x⋆⟩−δ​‖wk+1−w⋆‖Gk2\displaystyle\frac{1}{2}\|w^{k+1}-w^{k}\|^{2}_{G^{k}}+\frac{2\sigma_{f}}{\rho}\|x^{k+1}-x^{\star}\|^{2}-\frac{2}{\rho}\langle\nabla f_{2}(x^{k+1})-\nabla f_{2}(x^{k}),x^{k+1}-x^{\star}\rangle-\delta\|w^{k+1}-w_{\star}\|_{G_{k}}^{2}
≥(2​σf−μ2ρ−δ​(c1+c4))​‖x~k+1−x⋆‖2+(θmin2​ρ−Lf22​ρ​μ2−δ​c2)​‖x~k−x~k+1‖2\displaystyle\geq\left(\frac{2\sigma_{f}-\mu_{2}}{\rho}-\delta(c_{1}+c_{4})\right)\|\tilde{x}^{k+1}-x^{\star}\|^{2}+\left(\frac{\theta_{\textup{min}}}{2\rho}-\frac{L_{f}^{2}}{2\rho\mu_{2}}-\delta c_{2}\right)\|\tilde{x}^{k}-\tilde{x}^{k+1}\|^{2}
+(1/2−δ​c3)​‖z~k−z~k+1‖1/ρ​Ψk+NT​N2+(1/2−δ​c5)​‖u~k−u~k+1‖2−C​εwk.\displaystyle+\left(1/2-\delta c_{3}\right)\|\tilde{z}^{k}-\tilde{z}^{k+1}\|_{1/\rho\Psi^{k}+N^{T}N}^{2}+\left(1/2-\delta c_{5}\right)\|\tilde{u}^{k}-\tilde{u}^{k+1}\|^{2}-C\varepsilon_{w}^{k}.

Setting μ2=σf\mu_{2}=\sigma_{f}, and using θmin>Lf2/σf=κf​Lf\theta_{\textup{min}}>L^{2}_{f}/\sigma_{f}=\kappa_{f}L_{f}, we find by setting

δ=min⁡{σfρ​(c1+c4),θmin−κf​Lf2​ρ​c2,12​c3,12​c5}>0,\delta=\min\left\{\frac{\sigma_{f}}{\rho(c_{1}+c_{4})},\frac{\theta_{\textup{min}}-\kappa_{f}L_{f}}{2\rho c_{2}},\frac{1}{2c_{3}},\frac{1}{2c_{5}}\right\}>0,

that

‖w~k−w⋆‖Gk2−‖w~k+1−w⋆‖Gk2+C​εwk≥δ​‖w~k+1−w⋆‖Gk2,\|\tilde{w}^{k}-w^{\star}\|^{2}_{G^{k}}-\|\tilde{w}^{k+1}-w^{\star}\|^{2}_{G^{k}}+C\varepsilon_{w}^{k}\geq\delta\|\tilde{w}^{k+1}-w^{\star}\|^{2}_{G^{k}},

as desired. □\Box

We now turn to to the proof of Lemma 12.

Proof of Lemma 12
Proof.
  1. 1.

    Observe by LfL_{f}-smoothness of ff, that

    2​Lf2​(‖x~k+1−x⋆‖2+‖x~k−x⋆‖2)\displaystyle 2L^{2}_{f}\left(\|\tilde{x}^{k+1}-x^{\star}\|^{2}+\|\tilde{x}^{k}-x^{\star}\|^{2}\right) ≥‖∇f1​(x~k+1)−∇f1​(x⋆)+∇f2​(x~k)−∇f2​(x⋆)‖2\displaystyle\geq\|\nabla f_{1}(\tilde{x}^{k+1})-\nabla f_{1}(x^{\star})+\nabla f_{2}(\tilde{x}^{k})-\nabla f_{2}(x^{\star})\|^{2}
    =‖Θk​(x~k−x~k+1)+ρ​MT​N​(z~k−z~k+1)+ρ​MT​(u⋆−u~k+1)+Err∇k‖2\displaystyle=\|\Theta^{k}(\tilde{x}^{k}-\tilde{x}^{k+1})+\rho M^{T}N(\tilde{z}^{k}-\tilde{z}^{k+1})+\rho M^{T}(u^{\star}-\tilde{u}^{k+1})+\textrm{Err}^{k}_{\nabla}\|^{2}
    ≥12​ρ2​‖MT​(u~k+1−u⋆)‖2−‖Θk​(x~k−x~k+1)+ρ​MT​N​(z~k−z~k+1)+Err∇k‖2.\displaystyle\geq\frac{1}{2}\rho^{2}\|M^{T}(\tilde{u}^{k+1}-u^{\star})\|^{2}-\|\Theta^{k}(\tilde{x}^{k}-\tilde{x}^{k+1})+\rho M^{T}N(\tilde{z}^{k}-\tilde{z}^{k+1})+\textrm{Err}^{k}_{\nabla}\|^{2}.

    Here the last inequality uses with μ=2\mu=2, the identity (valid for all μ>1\mu>1)

    ‖a+b‖2≥(1−μ−1)​‖a‖2+(1−μ)​‖b‖2.\|a+b\|^{2}\geq(1-\mu^{-1})\|a\|^{2}+(1-\mu)\|b\|^{2}.

    So, rearranging and using ‖a+b‖2≤2​‖a‖2+2​‖b‖2\|a+b\|^{2}\leq 2\|a\|^{2}+2\|b\|^{2}, we reach

    ρ22​‖MT​(u~k+1−u⋆)‖2\displaystyle\frac{\rho^{2}}{2}\|M^{T}(\tilde{u}^{k+1}-u^{\star})\|^{2} ≤6​Lf2​‖x~k+1−x⋆‖2+2​(2​Lf2+‖Θk‖2)​‖x~k−x~k+1‖2\displaystyle\leq 6L^{2}_{f}\|\tilde{x}^{k+1}-x^{\star}\|^{2}+2\left(2L^{2}_{f}+\|\Theta^{k}\|^{2}\right)\|\tilde{x}^{k}-\tilde{x}^{k+1}\|^{2}
    +4​ρ2​‖M‖2​‖N​(z~k−z~k+1)‖2+4​‖Err∇k‖2.\displaystyle+4\rho^{2}\|M\|^{2}\|N(\tilde{z}^{k}-\tilde{z}^{k+1})\|^{2}+4\|\textrm{Err}^{k}_{\nabla}\|^{2}.

    Now, using ‖Err∇k‖2≤C​εxk≤C​εwk\|\textrm{Err}^{k}_{\nabla}\|^{2}\leq C\varepsilon_{x}^{k}\leq C\varepsilon_{w}^{k} and ‖v‖NT​N≤‖v‖1/ρ​Ψk+NT​N\|v\|_{N^{T}N}\leq\|v\|_{1/\rho\Psi^{k}+N^{T}N}, we reach

    ‖u~k+1−u⋆‖2≤12​Lf2ρ2​λmin​(M​MT)​‖x~k+1−x⋆‖2+4​(2​Lf2+θmax2)ρ2​λmin​(M​MT)​‖x~k−x~k+1‖2\displaystyle\|\tilde{u}^{k+1}-u^{\star}\|^{2}\leq\frac{12L^{2}_{f}}{\rho^{2}\lambda_{\textup{min}}(MM^{T})}\|\tilde{x}^{k+1}-x^{\star}\|^{2}+\frac{4\left(2L^{2}_{f}+\theta_{\textup{max}}^{2}\right)}{\rho^{2}\lambda_{\textup{min}}(MM^{T})}\|\tilde{x}^{k}-\tilde{x}^{k+1}\|^{2}
    8​‖M‖2​‖z~k−z~k+1‖1/ρ​Ψk+NT​N2+C​εwk.□\displaystyle 8\|M\|^{2}\|\tilde{z}^{k}-\tilde{z}^{k+1}\|_{1/\rho\Psi^{k}+N^{T}N}^{2}+C\varepsilon_{w}^{k}.~{}\Box
  2. 2.

    This inequality is a straightforward consequence of the relation

    M​(x~k+1−x⋆)=u~k+1−u~k+N​(z⋆−z~k+1).M(\tilde{x}^{k+1}-x^{\star})=\tilde{u}^{k+1}-\tilde{u}^{k}+N(z^{\star}-\tilde{z}^{k+1}).

    Indeed, using the identity ‖a+b‖2≤2​‖a‖2+2​‖b‖2\|a+b\|^{2}\leq 2\|a\|^{2}+2\|b\|^{2}, we reach

    ‖N​(z~k+1−z⋆)‖2≤2​‖M‖2​‖x~k+1−x⋆‖+2​‖u~k−u~k+1‖2.\displaystyle\|N(\tilde{z}^{k+1}-z^{\star})\|^{2}\leq 2\|M\|^{2}\|\tilde{x}^{k+1}-x^{\star}\|+2\|\tilde{u}^{k}-\tilde{u}^{k+1}\|^{2}.

    Consequently

    ‖z~k+1−z⋆‖1/ρ​Ψk+NT​N2\displaystyle\|\tilde{z}^{k+1}-z^{\star}\|_{1/\rho\Psi^{k}+N^{T}N}^{2} ≤2​(‖N‖2+ψmax/ρσmin2​(N))​‖M‖2​‖x~k+1−x⋆‖\displaystyle\leq 2\left(\frac{\|N\|^{2}+\psi_{\textup{max}}/\rho}{\sigma^{2}_{\textrm{min}}(N)}\right)\|M\|^{2}\|\tilde{x}^{k+1}-x^{\star}\|
    +2​(‖N‖2+ψmax/ρσmin2​(N))​‖u~k−u~k+1‖2,\displaystyle+2\left(\frac{\|N\|^{2}+\psi_{\textup{max}}/\rho}{\sigma^{2}_{\textrm{min}}(N)}\right)\|\tilde{u}^{k}-\tilde{u}^{k+1}\|^{2},

    which is precisely the desired claim. □\Box

  3. 3.

    Young’s inequality implies for all μ>0\mu>0, that

    ⟨∇f2​(x~k+1)−∇f2​(x~k),x~k+1−x⋆⟩≤12​μ​‖∇f2​(x~k+1)−∇f2​(x~k)‖2+μ2​‖x~k+1−x⋆‖2.\langle\nabla f_{2}(\tilde{x}^{k+1})-\nabla f_{2}(\tilde{x}^{k}),\tilde{x}^{k+1}-x^{\star}\rangle\leq\frac{1}{2\mu}\|\nabla f_{2}(\tilde{x}^{k+1})-\nabla f_{2}(\tilde{x}^{k})\|^{2}+\frac{\mu}{2}\|\tilde{x}^{k+1}-x^{\star}\|^{2}.

    The desired claim now follows from LfL_{f}-smoothness of f2f_{2}. □\Box

Appendix B Dual gap bounds for ADMM

In this section, we derive bounds for the duality gap for the machine learning examples we consider in Section 8. The derivation is largely inspired by [54, 55]. We consider problems of the form

minimize ℓ​(x)=∑i=1mf​(aiT​x−bi)+γ​‖x‖1,\displaystyle\ell(x)=\sum_{i=1}^{m}f(a_{i}^{T}x-b_{i})+\gamma\|x\|_{1}, (37)

where f​(⋅)f(\cdot) is some loss function, which we assume to be convex and differentiable. (The latter is not necessary but is convenient for our purposes.)

Dual problem.

We introduce new variable yiy_{i} and reformulate the primal problem (37) as

minimize l​(x)=∑i=1mf​(yi)+γ​‖x‖1\displaystyle l(x)=\sum_{i=1}^{m}f(y_{i})+\gamma\|x\|_{1} (38)
subject to y=A​x−b.\displaystyle y=Ax-b.

The Lagrangian is then

L​(x,y,ν)=∑i=1mf​(yi)+γ​‖x‖1+νT​(A​x−b−y).L(x,y,\nu)=\sum_{i=1}^{m}f(y_{i})+\gamma\|x\|_{1}+\nu^{T}(Ax-b-y).

Taking minimization over xx and yy, we get the dual function

g​(ν)={−∑i=1mf∗​(νi)−bT​ν,‖AT​ν‖∞≤γ−∞,otherwise.g(\nu)=\begin{cases}-\sum_{i=1}^{m}f^{*}(\nu_{i})-b^{T}\nu,&\|A^{T}\nu\|_{\infty}\leq\gamma\\ -\infty,&\text{otherwise}.\end{cases}

Thus, the dual problem is

maximize g​(ν)\displaystyle g(\nu) (39)
subject to ‖AT​ν‖∞≤γ.\displaystyle\|A^{T}\nu\|_{\infty}\leq\gamma.

Importantly, for any dual feasible point ν\nu, we have that

ℓ​(x)≥ℓ​(x⋆)=g​(ν⋆)≥g​(ν),\ell(x)\geq\ell(x^{\star})=g(\nu^{\star})\geq g(\nu),

where x⋆x^{\star} and ν⋆\nu^{\star} are optimal solutions to (37) and (39) respectively. It immediately follows that

ℓ​(x)−g​(ν)max⁡(ℓ​(x),|g​(ν)|)≥ℓ​(x)−ℓ​(x⋆)max⁡(ℓ​(x),|g​(ν)|).\frac{\ell(x)-g(\nu)}{\max\left(\ell(x),\lvert{g(\nu)}\rvert\right)}\geq\frac{\ell(x)-\ell(x^{\star})}{\max\left(\ell(x),\lvert{g(\nu)}\rvert\right)}. (40)

We will call this the relative dual gap.

Dual feasible points.

The optimality conditions of (38) are (after eliminating yy)

νi⋆=f′​(aiT​x⋆−bi)\nu_{i}^{\star}=f^{\prime}(a_{i}^{T}x^{\star}-b_{i}) (41)

Inspired by the second condition, we construct a dual feasible point by taking νi=f′​(aiT​x−bi)\nu_{i}=f^{\prime}(a_{i}^{T}x-b_{i}) and then projecting onto the norm ball constraint. Specifically, we take

νi=γ‖∑i=1mf′​(aiT​x−bi)⋅ai‖∞⋅f′​(aiT​x−bi).\nu_{i}=\frac{\gamma}{\left\|\sum_{i=1}^{m}f^{\prime}(a_{i}^{T}x-b_{i})\cdot a_{i}\right\|_{\infty}}\cdot f^{\prime}(a_{i}^{T}x-b_{i}).

When x≠x⋆x\neq x^{\star}, we can verify that ν\nu is dual feasible:

‖AT​ν‖∞=‖γ‖∑i=1mf′​(aiT​x−bi)⋅ai‖∞⋅(∑i=1mf′​(aiT​x−bi)⋅ai)‖∞=γ.\|A^{T}\nu\|_{\infty}=\left\|\frac{\gamma}{\left\|\sum_{i=1}^{m}f^{\prime}(a_{i}^{T}x-b_{i})\cdot a_{i}\right\|_{\infty}}\cdot\left(\sum_{i=1}^{m}f^{\prime}(a_{i}^{T}x-b_{i})\cdot a_{i}\right)\right\|_{\infty}=\gamma.

Assuming not all xi=0x_{i}=0, then this dual variable is optimal when constructed with x=x⋆x=x^{\star}. This fact can be easily seen by using the optimality conditions of (37), that 0 is contained in the subdifferential, i.e.,

0∈∑i=1mf′​(aiT​x−bi)⋅ai+γ​∂‖x‖1.0\in\sum_{i=1}^{m}f^{\prime}(a_{i}^{T}x-b_{i})\cdot a_{i}+\gamma\partial\|x\|_{1}.

By rearranging, we have the conditions

(∑i=1mf′​(aiT​x−bi)⋅ai)i∈{{+γ}xi<0{−γ}xi>0[−γ,γ]xi=0.\left(\sum_{i=1}^{m}f^{\prime}(a_{i}^{T}x-b_{i})\cdot a_{i}\right)_{i}\in\begin{cases}\{+\gamma\}&x_{i}<0\\ \{-\gamma\}&x_{i}>0\\ [-\gamma,\gamma]&x_{i}=0.\end{cases}

Thus, when constructed with x⋆x^{\star}, ν\nu is contained within the norm ball and therefore optimal by (41). Note that these optimality conditions also tell us that x=0x=0 is a solution to (37) if and only if ‖AT​f′​(−b)‖∞≤γ\|A^{T}f^{\prime}(-b)\|_{\infty}\leq\gamma, where the function f′f^{\prime} is applied elementwise.

This construction and the bound (40) suggest a natural stopping criterion. For any primal feasible point, we construct a dual feasible point ν\nu. Using the dual feasible point, we evaluate the duality gap. We then terminate the solver if the relative gap is less than some tolerance ϵ\epsilon as

l​(x)−g​(ν)max⁡(|g​(ν)|,l​(x))≤ϵ.\frac{l(x)-g(\nu)}{\max\left(\lvert{g(\nu)\rvert},l(x)\right)}\leq\epsilon.

If this condition is met, we are guaranteed that the true relative error is also less than ϵ\epsilon from (40).

References

  • \bibcommenthead
  • Boyd et al. [2011] Boyd, S., Parikh, N., Chu, E., Peleato, B., Eckstein, J.: Distributed optimization and statistical learning via the alternating direction method of multipliers. Foundations and Trends in Machine Learning 3, 1–122 (2011)
  • Bubeck [2015] Bubeck, S.: Convex optimization: Algorithms and complexity. Foundations and Trends® in Machine Learning 8(3-4), 231–357 (2015)
  • Zhao et al. [2022] Zhao, S., Frangella, Z., Udell, M.: NysADMM: faster composite convex optimization via low-rank approximation. In: International Conference on Machine Learning, vol. 162, pp. 26824–26840 (2022). PMLR
  • Ouyang et al. [2015] Ouyang, Y., Chen, Y., Lan, G., Pasiliao, E.: An accelerated linearized alternating direction method of multipliers. SIAM Journal on Imaging Sciences 8(1), 644–681 (2015)
  • Eckstein and Bertsekas [1992] Eckstein, J., Bertsekas, D.P.: On the Douglas—Rachford splitting method and the proximal point algorithm for maximal monotone operators. Mathematical Programming 55(1), 293–318 (1992)
  • Lacotte and Pilanci [2020] Lacotte, J., Pilanci, M.: Effective dimension adaptive sketching methods for faster regularized least-squares optimization. In: Advances in Neural Information Processing Systems (2020)
  • Frangella et al. [2021] Frangella, Z., Tropp, J.A., Udell, M.: Randomized Nyström preconditioning. arXiv preprint arXiv:2110.02820 (2021)
  • Meier and Nakatsukasa [2022] Meier, M., Nakatsukasa, Y.: Randomized algorithms for Tikhonov regularization in linear least squares. arXiv preprint arXiv:2203.07329 (2022)
  • Buluc et al. [2021] Buluc, A., Kolda, T.G., Wild, S.M., Anitescu, M., Degennaro, A., Jakeman, J.D., Kamath, C., Kannan, R.-R., Lopes, M.E., Martinsson, P.-G., et al.: Randomized algorithms for scientific computing (RASC). Technical report, Oak Ridge National Lab.(ORNL), Oak Ridge, TN (United States) (2021)
  • Ryu and Yin [2022] Ryu, E.K., Yin, W.: Large-scale Convex Optimization: Algorithms & Analyses Via Monotone Operators, (2022). Cambridge University Press
  • Parikh and Boyd [2014] Parikh, N., Boyd, S.: Proximal algorithms. Foundations and Trends® in Optimization 1(3), 127–239 (2014)
  • Rontsis et al. [2022] Rontsis, N., Goulart, P., Nakatsukasa, Y.: Efficient semidefinite programming with approximate admm. Journal of Optimization Theory and Applications 192(1), 292–320 (2022)
  • Deng and Yin [2016] Deng, W., Yin, W.: On the global and linear convergence of the generalized alternating direction method of multipliers. Journal of Scientific Computing 66(3), 889–916 (2016)
  • He and Yuan [2012] He, B., Yuan, X.: On the o(1/n) convergence rate of the Douglas–Rachford alternating direction method. SIAM Journal on Numerical Analysis 50(2), 700–709 (2012)
  • Eckstein and Yao [2018] Eckstein, J., Yao, W.: Relative-error approximate versions of douglas–rachford splitting and special cases of the admm. Mathematical Programming 170(2), 417–444 (2018)
  • Hermans et al. [2019] Hermans, B., Themelis, A., Patrinos, P.: QPALM: a Newton-type proximal augmented Lagrangian method for quadratic programs. In: 2019 IEEE 58th Conference on Decision and Control (CDC), pp. 4325–4330 (2019). IEEE
  • Hermans et al. [2022] Hermans, B., Themelis, A., Patrinos, P.: QPALM: a proximal augmented Lagrangian method for nonconvex quadratic programs. Mathematical Programming Computation, 1–45 (2022)
  • Monteiro and Svaiter [2013] Monteiro, R.D., Svaiter, B.F.: Iteration-complexity of block-decomposition algorithms and the alternating direction method of multipliers. SIAM Journal on Optimization 23(1), 475–507 (2013)
  • Ouyang et al. [2013] Ouyang, H., He, N., Tran, L., Gray, A.: Stochastic alternating direction method of multipliers. In: International Conference on Machine Learning, pp. 80–88 (2013). PMLR
  • Hager and Zhang [2020] Hager, W.W., Zhang, H.: Convergence rates for an inexact admm applied to separable convex optimization. Computational Optimization and Applications 77(3), 729–754 (2020)
  • Yuan et al. [2020] Yuan, X., Zeng, S., Zhang, J.: Discerning the linear convergence of ADMM for structured convex optimization through the lens of variational analysis. J. Mach. Learn. Res. 21, 83–1 (2020)
  • Chambolle and Pock [2011] Chambolle, A., Pock, T.: A first-order primal-dual algorithm for convex problems with applications to imaging. Journal of Mathematical Imaging and Vision 40, 120–145 (2011)
  • Zhao et al. [2021] Zhao, S., Lessard, L., Udell, M.: An automatic system to detect equivalence between iterative algorithms. arXiv preprint arXiv:2105.04684 (2021)
  • Gower et al. [2019] Gower, R.M., Kovalev, D., Lieder, F., Richtárik, P.: RSN: randomized subspace Newton. In: Advances in Neural Information Processing Systems (2019)
  • Bertsekas et al. [2003] Bertsekas, D., Nedic, A., Ozdaglar, A.: Convex Analysis and Optimization vol. 1, (2003). Athena Scientific
  • Hiriart-Urruty and Lemaréchal [1993] Hiriart-Urruty, J.-B., Lemaréchal, C.: Convex Analysis and Minimization Algorithms II vol. 305, (1993). Springer
  • Schmidt et al. [2011] Schmidt, M., Roux, N., Bach, F.: Convergence rates of inexact proximal-gradient methods for convex optimization. Advances in Neural Information Processing Systems 24 (2011)
  • Stellato et al. [2020] Stellato, B., Banjac, G., Goulart, P., Bemporad, A., Boyd, S.: OSQP: an operator splitting solver for quadratic programs. Mathematical Programming Computation 12(4), 637–672 (2020)
  • He et al. [2002] He, B., Liao, L.-Z., Han, D., Yang, H.: A new inexact alternating directions method for monotone variational inequalities. Mathematical Programming 92, 103–118 (2002)
  • Rockafellar [2023] Rockafellar, R.T.: Generic linear convergence through metric subregularity in a variable-metric extension of the proximal point algorithm. Computational Optimization and Applications, 1–20 (2023)
  • Candes and Romberg [2007] Candes, E., Romberg, J.: Sparsity and incoherence in compressive sampling. Inverse problems 23(3), 969 (2007)
  • Candes and Recht [2012] Candes, E., Recht, B.: Exact matrix completion via convex optimization. Communications of the ACM 55(6), 111–119 (2012)
  • Nishihara et al. [2015] Nishihara, R., Lessard, L., Recht, B., Packard, A., Jordan, M.: A general analysis of the convergence of ADMM. In: International Conference on Machine Learning, pp. 343–352 (2015). PMLR
  • Friedman et al. [2010] Friedman, J., Hastie, T., Tibshirani, R.: Regularization paths for generalized linear models via coordinate descent. Journal of Statistical Software 33(1), 1 (2010)
  • Pilanci and Wainwright [2017] Pilanci, M., Wainwright, M.J.: Newton sketch: A near linear-time optimization algorithm with linear-quadratic convergence. SIAM Journal on Optimization 27(1), 205–245 (2017)
  • Lacotte et al. [2021] Lacotte, J., Wang, Y., Pilanci, M.: Adaptive Newton sketch: Linear-time optimization with quadratic convergence and effective Hessian dimensionality. In: International Conference on Machine Learning, pp. 5926–5936 (2021). PMLR
  • Derezinski et al. [2021] Derezinski, M., Lacotte, J., Pilanci, M., Mahoney, M.W.: Newton-less: Sparsification without trade-offs for the sketched newton update. Advances in Neural Information Processing Systems 34, 2835–2847 (2021)
  • Bach [2013] Bach, F.: Sharp analysis of low-rank kernel matrix approximations. In: Conference on Learning Theory (2013)
  • Alaoui and Mahoney [2015] Alaoui, A., Mahoney, M.W.: Fast randomized kernel ridge regression with statistical guarantees. In: Advances in Neural Information Processing Systems (2015)
  • Karimireddy et al. [2018] Karimireddy, S.P., Stich, S.U., Jaggi, M.: Global linear convergence of Newton’s method without strong-convexity or Lipschitz gradients. arXiv (2018). https://arxiv.org/abs/1806.00413
  • Tibshirani [1996] Tibshirani, R.: Regression selection and shrinkage via the lasso. Journal of the Royal Statistical Society Series B 58(1), 267–288 (1996)
  • Zou and Hastie [2005] Zou, H., Hastie, T.: Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society Series B: Statistical Methodology 67(2), 301–320 (2005)
  • Hastie et al. [2015] Hastie, T., Tibshirani, R., Wainwright, M.: Statistical Learning with Sparsity: the Lasso and Generalizations, (2015). CRC press
  • Chang and Lin [2011] Chang, C.-C., Lin, C.-J.: LIBSVM: a library for support vector machines. ACM Transactions on Intelligent Systems and Technology (TIST) 2(3), 1–27 (2011)
  • Vanschoren et al. [2013] Vanschoren, J., Rijn, J.N., Bischl, B., Torgo, L.: Openml: networked science in machine learning. SIGKDD Explorations 15(2), 49–60 (2013)
  • Schubiger et al. [2020] Schubiger, M., Banjac, G., Lygeros, J.: Gpu acceleration of admm for large-scale quadratic programming. Journal of Parallel and Distributed Computing 144, 55–67 (2020)
  • Bezanson et al. [2017] Bezanson, J., Edelman, A., Karpinski, S., Shah, V.B.: Julia: A fresh approach to numerical computing. SIAM Review 59(1), 65–98 (2017)
  • ApS [2022] ApS, M.: The MOSEK Optimization Toolbox for MATLAB Manual. Version 10.0. (2022). http://docs.mosek.com/9.0/toolbox/index.html
  • Dunning et al. [2017] Dunning, I., Huchette, J., Lubin, M.: Jump: A modeling language for mathematical optimization. SIAM Review 59(2), 295–320 (2017) https://doi.org/10.1137/15M1020575
  • Legat et al. [2021] Legat, B., Dowson, O., Dias Garcia, J., Lubin, M.: MathOptInterface: a data structure for mathematical optimization problems. INFORMS Journal on Computing 34(2), 672–689 (2021) https://doi.org/10.1287/ijoc.2021.1067
  • Liu and Nocedal [1989] Liu, D.C., Nocedal, J.: On the limited memory bfgs method for large scale optimization. Mathematical Programming 45(1), 503–528 (1989)
  • Mogensen and Riseth [2018] Mogensen, P.K., Riseth, A.N.: Optim: A mathematical optimization package for Julia. Journal of Open Source Software 3(24), 615 (2018) https://doi.org/10.21105/joss.00615
  • Chen et al. [2016] Chen, C., He, B., Ye, Y., Yuan, X.: The direct extension of admm for multi-block convex minimization problems is not necessarily convergent. Mathematical Programming 155(1-2), 57–79 (2016)
  • Kim et al. [2007] Kim, S.-J., Koh, K., Lustig, M., Boyd, S., Gorinevsky, D.: An interior-point method for large-scale ℓ​_​1\ell\_1-regularized least squares. IEEE journal of selected topics in signal processing 1(4), 606–617 (2007)
  • Koh et al. [2007] Koh, K., Kim, S.-J., Boyd, S.: An interior-point method for large-scale l1-regularized logistic regression. Journal of Machine Learning Research 8(Jul), 1519–1555 (2007)